Optimal Tests for Combining p-Values

Abstract

Combining information (p-values) obtained from individual studies to test whether there is an overall effect is an important task in statistical data analysis. Many classical statistical tests, such as chi-square tests, can be viewed as being a p-value combination approach. It remains challenging to find powerful methods to combine p-values obtained from various sources. In this paper, we study a class of p-value combination methods based on gamma distribution. We show that this class of tests is optimal under certain conditions and several existing popular methods are equivalent to its special cases. An asymptotically and uniformly most powerful p-value combination test based on constrained likelihood ratio test is then studied. Numeric results from simulation study and real data examples demonstrate that the proposed tests are robust and powerful under many conditions. They have potential broad applications in statistical inference.

1. Introduction

In statistical inference and decision making, it is critical but challenging to appropriately aggregate information from different sources. p-value combination approaches provide possible solutions. A p-value combination method usually combines the transformed statistics via the original individual p-values, and then, an overall p-value is obtained. The development of combining p-value has a long history. Many pioneer statisticians, including R. A. Fisher [1] and K. Pearson [2], had important contributions in this area. Their methods (e.g., Fisher test), along with others, such as the z-test [3] and the minimal p-test [4], are still widely used in today’s statistical practice. Many studies have been conducted to compare the performances among those p-value combination tests [5,6,7]; it turned out that no test is uniformly most powerful although some methods may perform better than others under certain conditions. Combining dependent p-values is another research direction, as many robust and powerful methods have been proposed in the literature, including a recently proposed test based on Cauchy distribution (CCT) [8]. Although the CCT can be applied to both independent and dependent p-values, it has been shown that this test can never obtain a p-value less than the smallest p-value to be combined, and therefore, is not recommended for combining independent p-values [9]. In this paper, we focus on the situation where we have independent p-values to be combined.

It is well known that combining p-value methods have important applications in meta-analysis [10,11]. However, it is less recognized that combining p-value methods are more frequently but implicitly used in statistical testing. For instance, the commonly used chi-square tests, including the likelihood ratio test, the score test, and the Wald test, with degrees of freedom (df) greater than one can be viewed as p-value combination methods, which are special cases of our proposed gamma distribution-based tests (see Section 2). In other words, the popular chi-square tests only provide possible and special ways to combine p-values that are not necessarily optimal; more powerful methods for combining p-value may be found and used instead.

With recent technical developments, larger volume data, such as genome-wide genomic data, are generated more easily and rapidly. Consequently, advanced statistical methods, including p-value combination tests, are highly desirable [12,13,14,15,16,17,18,19,20]. For instance, meta-analyses, which combine information from different genome-wide association studies (GWASs), have identified many associated genetic variants that could not be identified from a single GWAS [21,22]. It is expected that with more powerful p-value combination tests being developed and available, more and more significant associated genetic variants will be discovered in cancer genomics.

Unfortunately, as Birnbaum [23] already noticed, there exists no uniformly most powerful (UMP) p-value combination test for all alternative hypotheses. However, it is possible that a method is UMP under a certain condition. Moreover, if the true condition is unknown, it is desirable to choose a robust p-value combination method in the sense that it has reasonable detection power under many conditions.

In this paper, we first propose a class of p-value combination methods based on gamma distribution. We show that several existing popular methods are equivalent to certain special cases of this class of tests. Then, we show that the proposed tests are UMP when the p-values to be combined are from certain distributions. When the p-values to be combined are from certain type of distributions whose parameters are partially or fully unknown, asymptotically UMP tests based on constrained likelihood ratio test (CLRT) are proposed and studied.

The rest of the manuscript is organized as follows: In Section 2, we first introduce some existing popular p-value combination tests, describe our proposed tests based on gamma distributions, and then study their connections to existing popular methods and their properties as of UMP tests. Finally, some asymptotically UMP tests based on CLRT are proposed and studied. In Section 3, we compare the performances of the proposed tests with some existing popular methods through a simulation study. In Section 4, two examples of real data applications are demonstrated to illustrate the desired performance of the proposed tests. This paper concludes in Section 5 with discussion and conclusions.

2. Methods

Suppose we have $n$ independent p-values, denoted as $P_i\left(i=1,\cdots ,n\right),$ obtained from testing the individual null hypothesis $H_{i0}$ versus the alternative hypothesis $H_{i1}$, respectively. In addition, throughout this paper, we assume $P_i~\mathrm{U}\left(0,1\right)$ under $H_{i0}$, where $\mathrm{U}\left(0,1\right)$ stands for the uniform distribution between 0 and 1. For a combining p-value test, in this paper, we consider testing the global null hypotheses, $H_0$= ${{\displaystyle \cap }}^{}{H}_{i0}$ vs. the global alternative hypothesis, $H_1={{\displaystyle \cup }}^{}{H}_{i1}$. In statistical literature, several p-value combination tests were proposed long time ago but are still widely used today. We introduce some of the most popular ones as follows.

2.1. Some Existing Popular Tests

2.1.1. The Minimal p-Value (Min p) Test

This test is denoted as $T_p$, with the test statistic defined as [4]:

$$\min \left(P_1, P_2, \cdots ,P_n\right)$$

(1)

whose null distribution is the beta distribution $Beta\left(1,n\right)$ and its p-value is defined as $1-{\left(1-P_{\left(1\right)}\right)}^n$, where $P_{\left(1\right)}=\min \left(P_1, P_2, \cdots ,P_n\right)$. The Tippett’s Min p test in (1) is closely related to the Bonferroni method [24]. When the minimal p-value $p_{\left(1\right)}$ is small, the two tests obtain similar results, and both are close to $n{p}_{\left(1\right)}$.

2.1.2. The Chi-Square Test with $n$ Degrees of Freedom

Denoted as ${\chi }_n^2$, it has the test statistic [25,26]:

$${\displaystyle \sum }_{i=1}^n{\left({\mathsf{\Phi }}^{-1}\left(1-P_i\right)\right)}^2$$

(2)

where ${\mathsf{\Phi }}^{-1}(·)$ is the inverse function of the cumulative distribution function (CDF) of the standard normal distribution, $N\left(0,1\right)$. The null distribution of the test ${\chi }_n^2$ in (2) is the chi-square distribution with $n$ df.

2.1.3. The Fisher Test

Denoted as $F_p$, it has the following test statistic [1]:

$$-2{\displaystyle \sum }_{i=1}^n\ln \left(P_i\right)$$

(3)

whose null distribution is ${\chi }_{2n}^2$, the chi-square distribution with $2n$ df.

2.1.4. The z Test

Denoted as $Z_p$, it has the test statistic [3]:

$${\displaystyle \sum }_{i=1}^n{\mathsf{\Phi }}^{-1}\left(1-P_i\right)/\sqrt{n}$$

(4)

whose null distribution is $N\left(0,1\right)$.

Note that for all of the above tests, their overall one-sided p-values are calculated based on the right-tails, i.e., the areas beyond the test statistics from the right sides of their null distributions, to reflect the fact that smaller individual p-values provide stronger evidence to support the global alternative hypothesis.

2.2. New Tests Based on Gamma Distribution

We use $Gamma\left(\alpha ,\beta \right)$ to denote a random variable that has a gamma distribution with shape parameter $\alpha$ and rate parameter $\beta ,$ where both parameters are positive. The probability density function (PDF) of Gamma($\alpha ,\beta$) is:

$$f_{G\left(\alpha ,\beta \right)}\left(x\right)={\beta }^{\alpha }{x}^{\alpha -1}\exp \left(-\beta x\right)/\mathsf{\Gamma }\left(\alpha \right)$$

(5)

for $x>0$, where the gamma function $\mathsf{\Gamma }\left(z\right)={{\displaystyle \int }}_0^{\infty }{x}^{z-1}{e}^{-x}dx$. Denote the corresponding CDF as $F_{G\left(\alpha ,\beta \right)}\left(x\right).$ We can combine $n$ independent p-values using $Gamma\left(\alpha ,\beta \right)$ and obtain an overall p-value accordingly.

2.2.1. Gamma Distribution-Base Test $T_{G\left(\alpha ,\beta \right)}$

Define the following test statistic:

$$T_{G\left(\alpha ,\beta \right)}\left(P_1,P_2,\cdots ,P_n\right)={\displaystyle \sum }_{i=1}^n{F}_{G\left(\alpha ,\beta \right)}^{-1}\left(1-P_i\right),$$

(6)

where $F_{G\left(\alpha ,\beta \right)}^{-1}\left(y\right)$ is the inverse function of the CDF $F_{G\left(\alpha ,\beta \right)}\left(x\right).$

We also define the following right-tailed p-value for $T_{G\left(\alpha ,\beta \right)}$:

$$P=\mathrm{Pr}\left(Gamma\left(n\alpha ,\beta \right)>t\right)=1-F_{G\left(n\alpha ,\beta \right)}\left(t\right)=S_{G\left(n\alpha ,\beta \right)}\left(t\right)$$

(7)

where $t$ is the observed value for the test $T_{G\left(\alpha ,\beta \right)},$ and $F_{G\left(n\alpha ,\beta \right)}(·)$ and $S_{G\left(n\alpha ,\beta \right)}(·)$ are the CDF and the survival function of Gamma($n\alpha ,\beta$), respectively.

The above test determined by the test statistic $T_{G\left(\alpha ,\beta \right)}$ in (6) and the p-value $P$ in (7) is called $T_{G\left(\alpha ,\beta \right)}$. The p-value for a specific test $T$ is also denoted as $P_T$. Therefore, the p-value in (7) can also be written as $P_{T_{G\left(\alpha ,\beta \right)}}$. Based on the properties of gamma distributions, we have the following result for the test $T_{G\left(\alpha ,\beta \right)}$:

Proposition 1.

The test$T_{G\left(\alpha ,\beta \right)}$with statistic defined in (6) and p-value defined in (7) controls type I error rate exactly at given significance level.

To study the properties of the new tests, we use the following definitions:

Definition 1.

Two tests$T_1$and$T_2$are called equivalent and denoted as$T_1\equiv T_2$if$p_{T_1}\left(x\right)=p_{T_2}\left(x\right)$for any observed data$x$, where$p_{T_i}\left(x\right)$is the p-value obtained by test$T_i\left(i=1,2\right)$from given data$x$.

Based on the properties of the gamma distributions, we can easily verify the following result:

Proposition 2.

For any$\alpha >0$and$\beta >0,$ $T_{G\left(\alpha ,\beta \right)}\equiv T_{G\left(\alpha ,1\right)}$.

Therefore, the rate parameter of the gamma distribution has no effect on the test $T_{G\left(\alpha ,\beta \right)}$. For convenience, in this paper, we set $\beta =1$ and use $T_{G\left(\alpha \right)}$ to denote $T_{G\left(\alpha ,1\right)}$ hereafter unless otherwise specified.

Definition 2.

A positively-valued function$c(\theta$) is called the exact slope of the sequence of tests$T_n$if$\underset{n\to \infty }{lim}\left[\left(-2/n\right)ln\left(1-F_n\left(T_n\right)\right)\right]=c(\theta$) with probability 1, where$F_n\left(T_n\right)$is the CDF of$T_n$. A test is called asymptotically Bahadur optimal (ABO) if its exact slope is maximal at every θ$\in \Theta -{\Theta }_0$, where$\Theta$is the parameter space, and${\Theta }_0$is the parameter space under the null hypothesis. The exact slope is a measure of the rate at which the attained p-value of a test statistic tends to 0 and is a measure of asymptotic efficiency.

It has been proven that $T_{G\left(\alpha ,1/2\right)}$ is ABO for any $\alpha \in \left(0,\infty \right)$ [27]. Hence, from proposition 2, we have the following property:

Proposition 3.

The test$T_{G\left(\alpha \right)}$is ABO for any$\alpha \in \left(0,\infty \right).$

Previously, we proposed a different p-value combination test based on gamma distribution with the test statistic $T={\displaystyle \sum }_{i=1}^n{F}_{G\left(1/P_i,1\right)}^{-1}\left(1-P_i\right)$, which uses the random shape parameter $a_i=1/P_i$ for p-value $P_i$, and its null distribution is intractable, and a resampling method is used to estimate the p-value. While in the current proposed tests, the same shape parameter is used for all individual p-values.

2.2.2. Connections between $T_{G\left(\alpha \right)}$ and Existing Popular Tests

Although the existing popular tests described in Section 2.1 were proposed a long time ago, and their theoretical properties and empirical performances have been extensively studied and compared [6,7,25,28,29], surprisingly, their relationships have not been fully investigated, and the theoretical explanation on the differences of their performances is lacking. In this subsection, we show that they are connected to the aforementioned gamma distribution-based tests $T_{G\left(\alpha \right)}$with different $\alpha$ values. In fact, we have the following results:

Theorem 1.

The class of gamma distribution-based tests$T_{G\left(\alpha \right)}$include special cases that are equivalent to the aforementioned existing popular methods. More specifically,

$$\begin{array}{l}{T}_{G\left(0\right)}\triangleq \underset{\alpha \to 0+}{\lim }{T}_{G\left(\alpha \right)}\equiv T_p;\\ T_{G\left(0.5\right)}\equiv {\chi }_n^2;\\ T_{G\left(1\right)}\equiv F_p;\mathit{and}\\ T_{G(\infty )}\triangleq \underset{\alpha \to \infty }{\lim }{T}_{G\left(\alpha \right)}\equiv Z_p.\end{array}$$

The proof of Theorem 1 is given in the Appendix A.

2.2.3. T_(α) as the Uniformly Most Powerful Test

Besides the ABO property, there is another attractive property for the gamma distribution-based test $T_{G\left(\alpha \right)}$: under certain conditions, it is UMP. We thus have the following theorem:

Theorem 2.

Suppose$P_1,P_2,\cdots ,P_n$are$iid$from the following common density function with parameters$\alpha >0$and$0<c<1$

$$f_{\alpha ,c}\left(p\right)={\left(1-c\right)}^{\alpha }exp\left[c{F}_{G\left(\alpha \right)}^{-1}\left(1-p\right)\right]\mathrm{for}p\in \left(0,1\right),$$

(8)

If both $\alpha$ and $c$ are known, then test $T_{G\left(\alpha \right)}$ is UMP.

The proof is given in the Appendix A.

Remark 1.

(i) For$p\in \left(0,1\right)$, when$c=0$, $f_{\alpha ,0}\left(p\right)=1$. Therefore, $f_{\alpha ,0}\left(p\right)$corresponds to the global null hypothesis. (ii) Under the condition$f_{\alpha ,c}\left(p\right)={\left(1-c\right)}^{\alpha }exp\left[c{F}_{G\left(\alpha \right)}^{-1}\left(1-p\right)\right]$with$0<c<1$, from Theorem 1, the existing tests$T_p,$ ${\chi }_n^2$, $F_p$, and $Z_p$defined in (1)–(4) are UMP for given$\alpha =0, 0.5, 1, \mathrm{and} \infty$, respectively. (iii) Along with Theorem 1, Theorem 2 provides insightful explanations on when and why an existing popular test described in Section 2.1 is preferred. For instance, when the p-values are extremely heterogeneous (e.g., a very small$\alpha$in (8)), the Min p test (i.e., $T_{G\left(0\right)}$i) s more powerful than the other gamma distribution-based tests. On the other hand, when the p-values are more homogeneous (e.g., a large$\alpha$in (8)), the z test (i.e., $T_{G(\infty )}$) is preferred. (iv) The function$f_{\alpha ,c}\left(p\right)={\left(1-c\right)}^{\alpha }{e}^{c{F}_{G\left(\alpha \right)}^{-1}\left(1-p\right)}$with two parameters$\alpha (\alpha >0) \mathrm{and}c$ ($0<c<1$) represents a large class of densities and can be used to approximate the true density functions under the alternative hypotheses. Based on simulation study, we found that under many situations, the true density functions under the alternative hypotheses can be closely approximated by $f_{\alpha ,c}\left(p\right)$ with the two parameters being estimated from the data (see Figures S1–S19 in the Supplementary File).

2.3. Constrained Likelihood Ratio Tests

In Section 2.2, we have shown that $T_{G\left(\alpha \right)}$ is UMP if the p-values to be combined are from the common density as described in (8) with known constants $\alpha$ and $c$. When $c$ is unknown, or both $\alpha$ and $c$ are unknown, constrained likelihood ratio tests (CLRTs) can be constructed accordingly. In this subsection, we study those CLRT-based tests when parameter $c$ is unknown with $\alpha$ being known or unknown.

2.3.1. CLRT-Based Tests with Known $\alpha$ Values

Under (8), with known $\alpha ={\alpha }_0$, the CLRT-based tests can be constructed based on the constrained MLE of $c$ obtained through maximizing $l\left({\alpha }_0,c\right)=l\left(c\right)=n{\alpha }_{0}ln\left(1-c\right)+c{\displaystyle \sum }_{i=1}^n{F}_{G\left({\alpha }_0\right)}^{-1}\left(1-P_i\right)$. More specifically, we define the following test statistic:

$$T_{CLRT,{\alpha }_0}\left(P_1,\cdots ,P_n\right)=2{\alpha }_{0}nln\left(1-{\widehat{c}}_{CLRT,{\alpha }_0}\right)+2\left({\widehat{c}}_{CLRT,{\alpha }_0}\right){\displaystyle \sum }_{i=1}^n{F}_{G\left({\alpha }_0\right)}^{-1}\left(1-P_i\right),$$

(9)

where ${\widehat{c}}_{CLRT,{\alpha }_0}$ is the constrained MLE of $c$ through maximizing the log-likelihood $l\left({\alpha }_0,c\right)$ with the constrain $0<c<1$. We will reject the overall null hypothesis if the test statistic is large. In other words, a one-sided p-value will be calculated from the test.

For the above CLRT-based test $T_{CLRT,{\alpha }_0}$ in (9), we have the following result [30]:

Proposition 4.

The asymptotic distribution of the test$T_{CLRT,{\alpha }_0}$is a mixture of chi-square distributions${\displaystyle \sum }_{i=0}^1{w}_i{\chi }_i^2$, where${\chi }_i^2$is the chi-square distribution with$df=i$, ${\chi }_0^2$is the random variable with probability 1 of being 0, and the weights$w_0$, $w_1$are determined by the null and the alternative hypothesis.

In practice, the p-values of the test $T_{CLRT,{\alpha }_0}$ can be estimated through resampling methods (e.g., see Section 2.3.2 for an example). However, the following result shows that this test is tightly connected with the gamma distribution-based test $T_{G\left({\alpha }_0\right)}$, whose p-value can be calculated directly.

Theorem 3.

Let$t_{CLRT,{\alpha }_0}$be the observed statistic of test$T_{CLRT,{\alpha }_0}$; the p-value of$T_{CLRT,{\alpha }_0}$is determined by the gamma distribution-based test$T_{G\left({\alpha }_0\right)}={\displaystyle \sum }_{i=1}^n{F}_{G\left({\alpha }_0\right)}^{-1}\left(1-P_i\right)$as follows:

$$Pr\left[T_{CLRT,{\alpha }_0}>t_{CLRT,{\alpha }_0}\right]=\{\begin{array}{c}{P}_{T_{G\left({\alpha }_0\right)}} \mathit{if} t_{CLRT,{\alpha }_0}>0 \\ Pr\left[T_{G\left({\alpha }_0\right)}<n{\alpha }_0\right] if t_{CLRT,{\alpha }_0}=0\end{array}$$

(10)

The proof is given in the Appendix A.

Proposition 5.

Under the conditions specified in (8), if the parameter$\alpha ={\alpha }_0$is known, then asymptotically$T_{G\left({\alpha }_0\right)}\equiv T_{CLRT,{\alpha }_0}$.

Proof. 

From the proof of Theorem 3, we know that under (8), when $0\le c<1$, $Pr\left[T_{G\left({\alpha }_0\right)}<n{\alpha }_0\right]=Pr\left[{\widehat{c}}_{{\alpha }_0}\le 0\right]\to 0 \left(as n\to \infty \right),$ and hence, the two p-values from tests $T_{G\left({\alpha }_0\right)}$ and $T_{CLRT,{\alpha }_0}$ are asymptotically equal with probability 1. □

Theorem 4.

Under the conditions specified in (8), if the parameter$\alpha ={\alpha }_0$is known, then the gamma distribution-based test$T_{G\left({\alpha }_0\right)}$and the CLRT-based test$T_{CLRT,{\alpha }_0}$are both asymptotically UMP.

Proof. 

When $\alpha ={\alpha }_0$ is known, it can be shown that the constrained MLEs for $c$ is consistent (see, for instance, Theorem 1 of Self and Liang [30]). Hence, from Theorem 2, $T_{G\left({\alpha }_0\right)}$ is asymptotically UMP. From Proposition 5, $T_{CLRT,{\alpha }_0}$ is asymptotically UMP. □

2.3.2. The Optimal CLRT-Based Test When $\alpha$ Is Unknown

When both parameters $\alpha$ and $c$ in (8) are unknown, they need to be estimated via the constrained MLEs, from which the following constrained likelihood ratio test is defined:

$$T_{CLRT}\left(P_1,\cdots ,P_n\right)=2{\widehat{\alpha }}_{CLRT}nln\left(1-{\widehat{c}}_{CLRT}\right)+2\left({\widehat{c}}_{CLRT}\right){\displaystyle \sum }_{i=1}^n{F}_{G\left({\widehat{\alpha }}_{CLRT}\right)}^{-1}\left(1-P_i\right)$$

(11)

where ${\widehat{\alpha }}_{CLRT}$ and ${\widehat{c}}_{CLRT}$ are the constrained MLEs for parameters $\alpha$ and $c$, respectively, through maximizing the log-likelihood function $l\left(\alpha ,c\right)=n\alpha ln\left(1-c\right)+c{\displaystyle \sum }_{i=1}^n{F}_{G\left(\alpha \right)}^{-1}\left(1-P_i\right)$ with the constrains $0<c<1$ and $\alpha >0$. The R function “nlminb” can be applied to find the constrained MLEs and the corresponding test statistic. The proposed test was implemented using R; the R package “opt” (optimal p-value combination test) can be freely download from https://github.com/zchen2020/opt (accessed on 15 November 2021).

For the above CLRT-based test $T_{CLRT}$, similar to Proposition 4, we have the following result [30]:

Proposition 6.

The asymptotic distribution of the test$T_{CLRT}$is a mixture of chi-square distributions${\displaystyle \sum }_{i=0}^2{w}_i{\chi }_i^2$, where${\chi }_i^2$is the chi-square distribution with$df=i$, ${\chi }_0^2$is the random variable with probability 1 of being 0, and the weights$w_0$, $w_1$,$w_2$are determined by the null and the alternative hypothesis.

The above asymptotic result may not be directly applicable to estimate the p-value for this test, as the number of p-values $n$ is usually small, and more seriously, the weights ${w_i}^{\prime }s$ are difficult to obtain. Instead, a simple resampling method can be used to approximate the null distribution and to estimate the p-value of $T_{CLRT}$. More specifically, for given sample size $n$, randomly sample $n$ null p-values evenly distributed between 0 and 1, then calculate the test statistic using (10). Repeat this process many times (e.g., ${10}^5$); then, the empirical distribution of the test statistic can be used to approximate the null distribution and therefore the p-value of $T_{CLRT}$.

Similar to Theorem 4, we have the following result for $T_{CLRT}$:

Theorem 5.

Under the conditions specified in (8), the CLRT-based test$T_{CLRT}$is asymptotically UMP.

Proof. 

Under conditions (8), it can be shown that the constrained MLEs for $\alpha$ and $c$ are consistent (see, for instance, Theorem 1 of Self and Liang [30]). Hence, $T_{CLRT}$ is asymptotically equivalent to $T_{CLRT,{\alpha }_0}$ for known $\alpha ={\alpha }_0$ in (8). Then from Theorem 4, $T_{CLRT}$ is asymptotically UMP. □

Remark 2.

(i) When $\alpha ={\alpha }_0$ is known, compared with test $T_{CLRT,{\alpha }_0}$, the test $T_{G\left({\alpha }_0\right)}$ is preferred because (a) its test statistic and p-value are easier to get and (b) the two tests in general have very similar performances. (ii) When both $\alpha$ and $c$ are unknown, the test $T_{CLRT}$ is asymptotically UMP, while, in general, neither $T_{CLRT,{\alpha }_0}$nor $T_{G\left({\alpha }_0\right)}$ for preset $\alpha ={\alpha }_0$ is UMP or asymptotically UMP. Therefore, it is expected that $T_{CLRT}$ is more robust, and overall, it has better performance than each individual gamma distribution-based test $T_{G\left(\alpha \right)}$, including the existing popular ones described in Section 2.1.1, Section 2.1.2, Section 2.1.3 and Section 2.1.4.

3. Numeric Studies

In this section, we assess the performances of the proposed tests through a simulation study. In the simulation, we compare the optimal CLRT-based test $T_{CLRT}$ with the popular and representative gamma distribution-based tests, $T_{G\left(0\right)}$, $T_{G\left(1\right)}$, and $T_{G(\infty )}$ (i.e., the Min p, Fisher, and z test, respectively).

In the simulation study, fifty ($n=50$) independent p-values are simulated and combined. Among these 50 p-values, $m \left(m=0, 10, 20, 40, 50\right)$ are assumed from the true individual alternative hypotheses, and the rest ($n-m$) are from the true individual null hypotheses. When m = 0, all 50 individual null hypotheses are true, and the empirical power obtained under this condition is the empirical type I error rate. The p-values from the true null hypotheses are randomly sampled between 0 and 1 from the uniform distribution. For a true individual alternative hypothesis $H_{i1} \left(i=1,\cdots ,m\right)$, we assume the p-value $p_i$ is obtained via a random variable $z_i~N\left({\mu }_i,1\right)$. We randomly set $k$ of the $m$ $u_i^{\prime }s$ as positive or negative (those alternative hypotheses with the same direction of the effects are called concordant alternatives) and the rest of $m-k$ having the other direction. A two-sided p-value for each true individual alternative hypothesis are obtained via the standard z test by comparing the test statistic with the standard normal distribution $N\left(0,1\right)$.

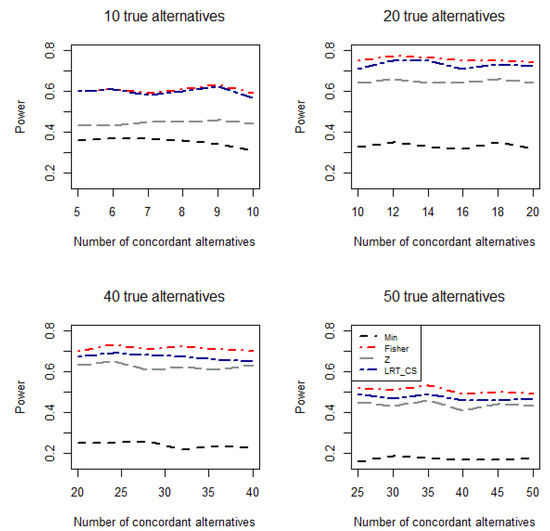
For the true alternative hypotheses, we consider three different scenarios for the effects of ${{\mu }_i}^{\prime }s$. Scenario 1: $\left|{\mu }_i\right|=\mu v_i/{\displaystyle \sum }_{i=1}^m{v}_i$, where $v_i={10}^{r_i}$; $r_i~N\left(0.3,1\right)$; and $\mu =0.8, 0.6, 0.4, 0.3$ when there are 10, 20, 40, and 50 true individual alternatives, respectively. Scenario 2: $\left|{\mu }_i\right|=\mu v_i/{\displaystyle \sum }_{i=1}^m{v}_i$, where $v_i~U\left(1,100\right)$ and $\mu =1.2, 1.0, 0.6, 0.5$ when the number of true individual alternatives is $m=10, 20, 40, \mathrm{and} 50$, respectively. Scenario 3:$\left|{\mu }_i\right|=\mu /m$, and $\mu =1.5, 1.2, 0.8, \mathrm{and} 0.6$ when $m=10, 20, 40, \mathrm{and} 50$, respectively. Note that (i) the constants (e.g., $\mu$, the parameters in the normal distribution for $r_i$ and the uniform distribution for $v_i$) are chosen in the way so that the empirical powers are appreciable for comparison. (ii) For all the three scenarios, the sum of the absolute effect sizes is equal to $\mu$; and (iii) for given $m$, the degree of heterogeneity of the effect sizes among the true individual alternatives decreases from Scenario 1 to Scenario 3. More specifically, in scenario 1, the effect sizes are extremely heterogenous when the number of the true individual alternatives is small. In Scenario 3, the effect sizes are more homogenous. The situations in Scenario 2 are between those in Scenarios 1 and 3. By considering those different conditions, we tried to conduct a reasonable and realistic simulation study to fairly compare our proposed tests with others.

The empirical power values of the tests are estimated using the rejection proportions based on $1000$ replicates at the significance level of 0.05. For the new tests, $T_{CLRT}$ ${10}^5$ replicates are used to estimate their p-values from the resampling method described in Section 2.3.2. Under the overall null hypotheses (i.e., all individual null hypotheses are true), the empirical type I error rates for all methods with different significance levels were obtained. From the simulation study, all methods controlled type I error rate quite well (see Table S4 in the Supplementary File).

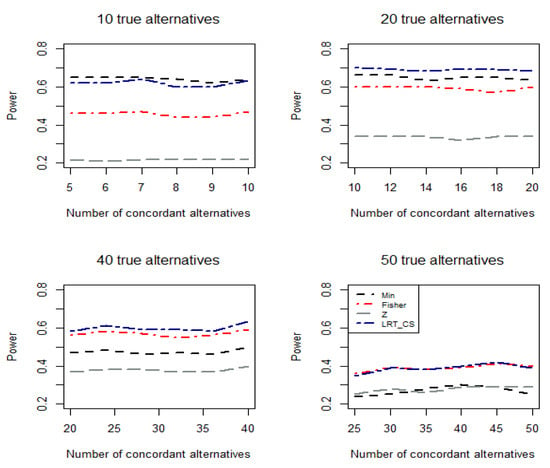
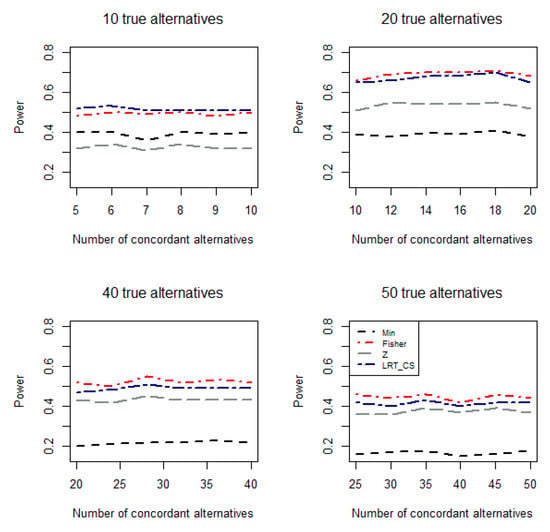
Figure 1, Figure 2 and Figure 3 plot the empirical power values of the Min p (Min), Fisher (Fisher), z test (Z), and the proposed CLRT-based test $T_{CLRT}$ (LRT_CS) when p-values are combined under Scenarios 1 to 3, respectively. We have the following observations: First, for Scenario 1 (Figure 1), where the effect sizes from the true individual alternative hypotheses are extremely heterogeneous, the Min p test (i.e., $T_{G\left(0\right)}$) usually performs better than the Fisher test ($T_{G\left(1\right)}$), which in turn performs better than the z test ($T_{G(\infty )}$). Second, when the degree of heterogeneity of the effect sizes among individual alternative hypotheses are less extreme, as in Scenarios 2 and 3 (Figure 2 and Figure 3), Fisher test and the z test usually perform better or much better than the Min p test. Third, for the Min p, Fisher, and z test, one may perform very well for some conditions but very poorly under others. For instance, under Scenario 1 (extremely heterogeneous effect sizes among the alternatives), the Min p test is more powerful than the other two, while it is much less powerful under scenario 3 (homogeneous effect sizes among the alternatives). The opposite direction was observed for the z test. Fourth, under all conditions considered, the new test $T_{CLRT}$ is either the best or very comparable to the best one. When the number of p-values to be combined is small, we observed similar patterns (see the simulation results in Tables S1–S3 in the Supplementary Materials when n = 10). This demonstrates that, as expected, $T_{CLRT}$ is a robust test in the sense that under many conditions, it has reasonable detection power compared with other tests. We would like to point out that, as expected, the empirical power values from the CLRT-based test $T_{CLRT,{\alpha }_0}$ are very close to those from the corresponding gamma distribution-based tests $T_{G\left(\alpha \right)},$ with $\alpha =0, 1, \infty$ being fixed (data not shown).

4. Real Data Examples

In this section, we apply the proposed tests along with others to two real-world problems to demonstrate the usefulness of the proposed test.

4.1. Example 1: A Meta-Analysis

In a meta-analysis, 12 randomized trials examining the effect of patient rehabilitation designed for geriatric patients versus usual care on improving functional outcome at 3–12 month follow-up were used [31,32]. The estimated odds ratios (ORs) from the 12 trials are listed in

Table 1. Estimated odds ratio and its 95% CI from each study in a meta-analysis with 12 trials. Data were taken from Bachmann et al. and Riley et al.

Study	OR	95% CI	Study	OR	95% CI	Study	OR	95% CI
1	1.11	0.51, 2.39	5	0.88	0.39, 1.95	9	1.06	0.63, 1.79
2	0.97	0.78, 1.21	6	1.28	0.71, 2.30	10	2.95	1.54, 5.63
3	1.13	0.73, 1.72	7	1.19	0.69, 2.08	11	2.36	1.18, 4.72
4	1.08	0.42, 2.75	8	3.82	1.37, 10.60	12	1.68	1.05, 2.70

.

The p-value from the Cochran’s test for homogeneity was 0.021, indicating that the commonly used fixed effect model of meta-analysis was inadequate for this data set. Therefore, the authors ran the meta-analysis with a random effect model and estimated the overall OR as 1.36 with 95% CI (1.08, 1.71) [32]. However, the goodness-of-fit test for the random effect model obtained a p-value of 0.025 [33], indicating the lack of fit of the random effect model for this data set. Therefore, instead of using the problematic fixed or random effect models to combine information from the 12 trials, we use p-value combination methods to test whether there is an overall effect.

In order to use the p-value combination methods, for each trial, we calculate its p-value based on its reported 95% CI. Denote U and L the upper and lower limits of the 95% CI; the test statistic can be approximated as $t=\ln \left(U\times L\right)/\sqrt{4\ln \left(U/L\right)/3.92}$, whose asymptotic null distribution is $N\left(0,1\right)$. The sample sizes of these 12 trials were relatively large, ranging from 108 and 1388; therefore, we can reasonably estimate their p-values using the asymptotic null distribution. We calculate the two-sided p-value for each trial and apply the gamma distribution-based tests. The p-values from the Min p (i.e., $T_{G\left(0\right)}$), Fisher ($T_{G\left(1\right)}$), z test ($T_{G(\infty )}$), and $T_{CLRT}$ for combining those two-sided p-values are 0.013, 0.0068, 0.075, and 0.0047, respectively. Except for the z test, which is known to be less powerful for this heterogeneous situation, all methods obtained p-values less than 0.05, and the proposed test $T_{CLRT}$ had the smallest p-value, indicating that the proposed test is more powerful than the other tests under this specific situation.

4.2. Example 2: A Survival Analysis from a Clinical Trial

The second data set is from the randomized, double-blinded Digoxin Intervention Trial [34]. In this trial, patients with left ventricular ejection fractions of 0.45 or less were randomly assigned to digoxin (3397 patients) or placebo (3403 patients) groups. A primary outcome was the mortality due to worsening heart failure (see Figure S20 in the Supplementary Materials). In the original study, the authors used the log-rank (LR) test and obtained a p-value of 0.061, indicating that the evidence of the effectiveness of digoxin, in terms of reducing the mortality due to worsening heart failure, is at most marginal.

However, it is well known that the LR test may fail to detect the difference between two survival functions if their hazard rate functions are crossing [35,36]. We apply the two-stage approach [35,36] to this data set and obtained two p-values of 0.06 and 0.04 for the two stages. Since, under the null hypothesis, the two p-values from the two stages are asymptotically independent [35,36], we can combine them using the proposed test $T_{CLRT}$ and the gamma distribution-based tests. The p-values are 0.078, 0.017, 0.0099, and 0.011 from the Min p, Fisher, z test, and $T_{CLRT}$, respectively. The proposed test obtained the second smallest p-value, which is slightly larger than the smallest one obtained by the z test.

In addition, the drug effect may differ between males and females. To investigate the possible interaction between sex and treatment, we divide the data into four groups based on the combinations of sex and treatment: Male—Placebo (MP), Male—Drug (MD), Female—Placebo (FP), and Female—Drug (FD). The sample sizes for the four groups are 2639, 2642, 764, and 755, respectively. We then compare the survival functions in the following three pairs of groups: MP vs. MD, (MP + MD) vs. FP, and (MP + MD + FP) vs. FD, where (MP + MD) is a new group with pooled data from groups MP and MD, and (MP + MD + FP) includes all the subjects from groups MP, MD, and FP (see Figure S21 in the Supplementary Materials). For each comparison, the two-stage approach is applied. We obtain the following six p-values: 0.019, 0.026, 0.504, 0.092, 0.975, and 0.050. It has been shown that under the null hypothesis, the six p-values obtained from the above approach are asymptotically independent [36]. Applying the gamma distribution-based tests, along with $T_{CLRT}$, to the six asymptotically independent p-values, we obtain p-values of 0.11, 0.0067, 0.020, and 0.013 from the Min p, Fisher, z test, and $T_{CLRT}$, respectively. It noticeable that the proposed test obtained the second smallest p-value, while Fisher test obtained the smallest one among those methods. These results show that except for the Min p test, all other tests obtain p-values less than 0.05. In addition, the p-values from $T_{CLRT}$ in general are close to the smallest ones, while the popular tests, Fisher and z test, may get quite different p-values under different situations (two groups vs. four groups).

Compared with the original analysis, the results of the proposed optimal test $T_{CLRT}$ using p-values from the two-stage approach applied to either two groups (placebo vs. drug) or four groups (combinations of sex and drug) provide stronger evidence against the null.

5. Discussion and Conclusions

In this paper, we studied a class of gamma distribution-based p-value combination methods, which include special cases that are equivalent to some existing popular methods. This class of tests provide unlimited choices for combining independent p-values. However, under a given situation, some of them may perform very poorly. Therefore, arbitrarily picking one of them may result in failing to detect true alternatives. On the other hand, if we try many different methods and report the smallest p-value, we need to adjust this p-value due to multiple comparison issue; otherwise, we will have more false findings than expected due to inflated type I error rate. Therefore, it is desirable to develop methods that can adaptively find the optimal approach from candidate tests. Our proposed CLRT-based test $T_{CLRT}$ is one of such methods. We have shown that if the p-values to be combined are from a common density function $f_{\alpha ,c}\left(p\right)={\left(1-c\right)}^{\alpha }{e}^{c{F}_{G\left(\alpha \right)}^{-1}\left(1-p\right)}$ for $p\in \left(0,1\right)$, the gamma distribution-based test $T_{G\left(\alpha \right)}$ is UMP when both parameters $\alpha \mathrm{and} c$ are known. When $\alpha ={\alpha }_0$ is known but $c$ unknown, both $T_{G\left(\alpha \right)}$ and the CLRT-based test $T_{CLRT,{\alpha }_0}$ are asymptotically UMP. Furthermore, when both $\alpha \mathrm{and} c$ are unknown, the proposed CLRT-based test $T_{CLRT}$ is asymptotically UMP.

In a meta-analysis, it is natural to assign different weights to individual studies [5,7,37,38]. For instance, a larger weight can be assigned to a study with more subjects; hence, in the z test, a p-value from a larger study may receive a greater weight. Weights can also be assigned based on other quantities, such as the variances of the estimated effect sizes. However, there is no consensus on weight assignment. For our proposed tests, we can easily incorporate weights assigned to each individual p-value. For instance, the weighted gamma distribution-based tests can be constructed using $T_{G\left(\alpha \right)}^w={\displaystyle \sum }_{i=1}^n{F}_{G\left(w_i\alpha \right)}^{-1}\left(1-P_i\right)$, where $w_i$ is the weight assigned to study $i \left(i=1,\cdots ,n\right)$. Based on the properties of gamma distributions, it is not difficult to show that $\underset{\alpha \to \infty }{\lim }{T}_{G\left(\alpha \right)}^w\equiv {\displaystyle \sum }_{i=1}^n{w}_i{\mathsf{\Phi }}^{-1}\left(1-P_i\right)/\sqrt{{\displaystyle \sum }_{i=1}^n{w}_i{}^2}$, the weighted z test. Therefore, the class of weighted gamma distribution-based tests $T_{G\left(\alpha \right)}^w$ are generalizations of the weighted z test. Likewise, the weighted log-likelihood function with given weights becomes $l^w\left(\alpha ,c\right)=\alpha ln\left(1-c\right){\displaystyle \sum }_{i=1}^n{w}_i+c{\displaystyle \sum }_{i=1}^n{F}_{G\left(w_i\alpha \right)}^{-1}\left(1-p_i\right)$, from which the corresponding weighted CLRT-based optimal test $T_{CLRT}^W$ can be constructed accordingly.

Our proposed tests have much broader applications than in meta-analysis. In fact, they can be applied to almost all statistical testing problems when (asymptotically) independent p-values from individual components are available. For instance, in model selection, a typical step is to test whether a set of variables (or a single categorical variable with multiple levels) should be included in the final model. Often the time, the parameters, and the covariances of their estimates are estimated simultaneously through maximum likelihood estimation. Then the LRT via comparing the log-likelihood values from two models with and without the candidate variables, or the Wald chi-square test of the weighted sum of the squared estimated effect sizes, can be applied. For both LRT and the Wald test, a set of asymptotically independent p-values can be obtained through their asymptotically independent components (see, e.g., Chapter 16 of [39]). Hence, our proposed p-value combination methods, such as $T_{CLRT}$, can be applied and may result in a better final model.

Another example is the association test for two categorical variables in a two-way contingency table to which the Pearson chi-square test is usually applied. It is known that the Pearson’s chi-square test statistic with $k$ df can be partitioned into $k$ asymptotically independent components whose null distributions are asymptotically $iid$ chi-square distribution with 1 df [40]. For instance, the partition can be done through the Lancaster approach [41]. Hence, we can calculate a set of asymptotically independent p-values to which our proposed CLRT-based test is applicable.

The performance of the proposed approaches can be improved if the p-values to be combined are obtained from an individual study using more powerful tests. For instance, if we already know the direction of the effect (positive or negative) when we compare two group means, we can use a one-sided rather than a two-sided test to obtain the individual p-value. However, it should be pointed out that sometimes one-sided tests may not be always applicable to individual studies. Nevertheless, our proposed approaches can still be used.

In this paper, we focus on using gamma distribution to combine independent p-values. Our future direction will be developing gamma distribution-based methods to combine dependent p-values. The difficulty in this direction is how to choose the “optimal”-shape parameter so that the resulting test has good detection power and can control type I error rate for arbitrary dependency structure of the p-values to be combined. Our preliminary results indicate that this direction is promising. A follow-up paper will be published.