Transmission Network Expansion Planning Considering Optimal Allocation of Series Capacitive Compensation and Active Power Losses
Abstract
:1. Introduction
2. Mathematical Modeling
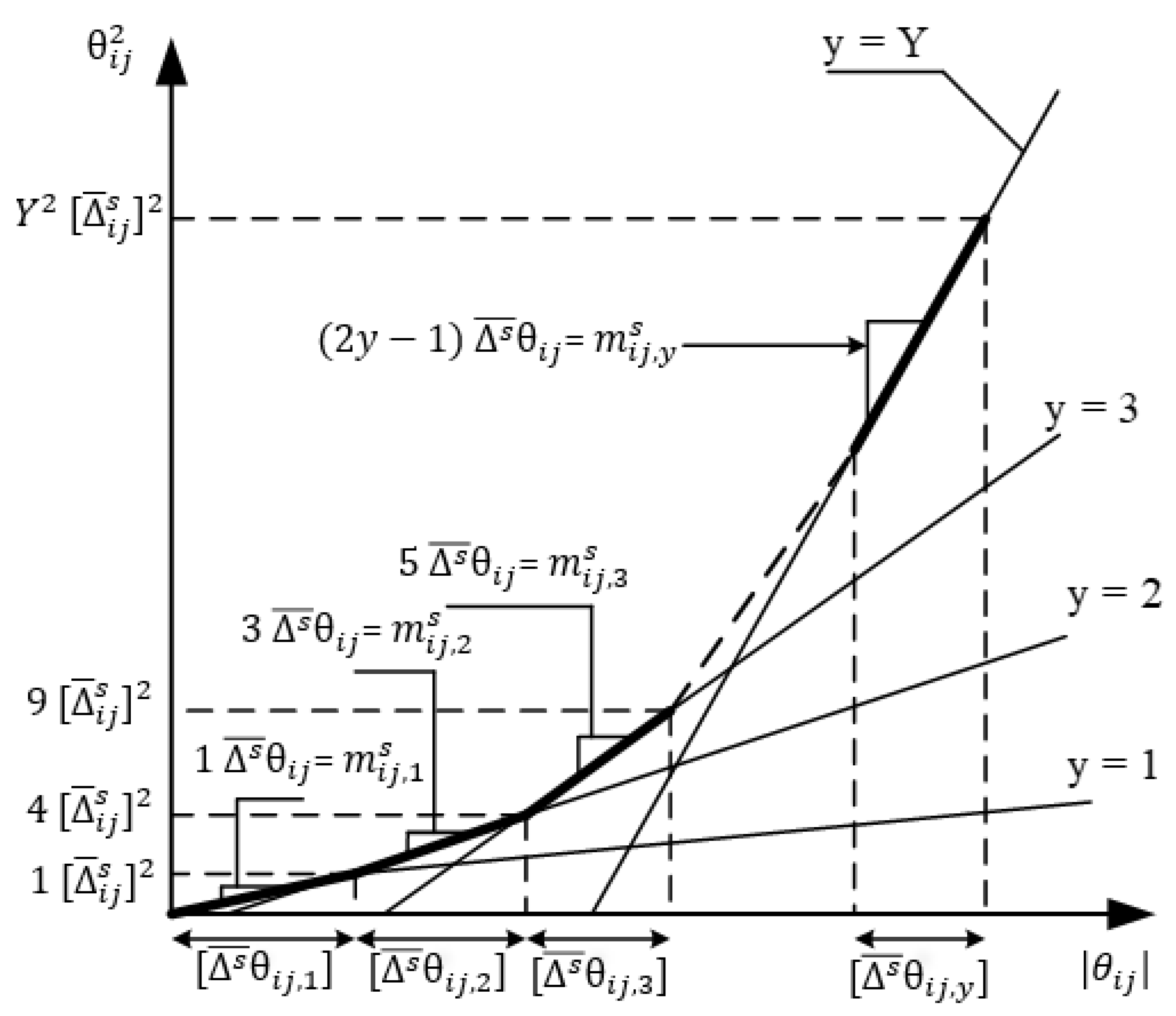
2.1. Linearization of Active Power Losses
2.2. Series Capacitive Compensation
2.3. Modeling of SCC Devices and Active Power Losses in the TNEP Problem
3. Highly Efficient Genetic Algorithm (HEGA)
3.1. Codification
3.2. Initial Population
3.3. Selection
3.4. Recombination
3.5. Mutation
3.6. Local Improvement
3.6.1. Improvement of the Unfitness Function
3.6.2. Improvement of the Fitness Function
3.7. Acceptation Criterion
3.8. Stopping Criterion
4. Test and Results
4.1. Static TNEP
4.1.1. Garver System
4.1.2. IEEE 24-Bus System
4.1.3. South Brazilian 46-Bus System
4.2. Multistage TNEP Problem
4.2.1. Garver System
4.2.2. IEEE 24-Bus System
4.2.3. South Brazilian 46-Bus System
5. Critical Analysis of the Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Escobar, A.H.; Gallego, R.A.; Romero, R. Multistage and coordinated planning of the expansion of transmission systems. IEEE Trans. Power Syst. 2004, 19, 735–744. [Google Scholar] [CrossRef]
- Gallego, L.A.; Garcés, L.P.; Rahmani, M.; Romero, R.A. High-performance hybrid genetic algorithm to solve transmission network expansion planning. IET Gener. Transm. Distrib. 2017, 11, 1111–1118. [Google Scholar] [CrossRef]
- Orfanos, G.A.; Georgilakis, P.S.; Hatziargyriou, N.D. Transmission expansion planning of systems with increasing wind power integration. IEEE Trans. Power Syst. 2013, 28, 1355–1362. [Google Scholar] [CrossRef]
- Dominguez, A.H.; Macedo, L.H.; Escobar, A.H.; Romero, R. Multistage security-constrained HVAC/HVDC transmission expansion planning with a reduced search space. IEEE Trans. Power Syst. 2017, 32, 4805–4817. [Google Scholar] [CrossRef]
- Romero, R.; Rider, M.J.; Silva, I.D.J. A Metaheuristic to Solve the Transmission Expansion Planning. IEEE Trans. Power Syst. 2007, 22, 2289–2291. [Google Scholar] [CrossRef]
- Huang, S.; Dinavahi, V. A Branch-and-Cut Benders Decomposition Algorithm for Transmission Expansion Planning. IEEE Syst. J. 2019, 13, 659–669. [Google Scholar] [CrossRef]
- Choi, J.; El-Keib, A.; Tran, T. A fuzzy branch and bound-based transmission system expansion planning for the highest satisfaction level of the decision maker. IEEE Trans. Power Syst. 2005, 20, 476–484. [Google Scholar] [CrossRef]
- Asada, E.N.; Carreno, E.; Romero, R.; Garcia, A.V. A branch-and-bound algorithm for the multi-stage transmission expansion planning. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; Volume 1, pp. 171–176. [Google Scholar] [CrossRef]
- Garver, L. Transmission Network Estimation Using Linear Programming. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 1688–1697. [Google Scholar] [CrossRef]
- Villasana, R.; Garver, L.L.; Salon, S.J. Transmission Network Planning Using Linear Programming. IEEE Power Eng. Rev. 1985, PER-5, 36–37. [Google Scholar] [CrossRef]
- Gbadamosi, S.L.; Nwulu, N.I.; Damisa, U. Impact of Power Losses on Optimal Expansion Planning using Quadratic Programming. In Proceedings of the 2019 IEEE 6th International Conference on Engineering Technologies and Applied Sciences (ICETAS), Kuala Lumpur, Malaysia, 20–21 December 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Alguacil, N.; Motto, A.L.; Conejo, A.J. Transmission expansion planning: A mixed-integer LP approach. IEEE Trans. Power Syst. 2003, 18, 1070–1077. [Google Scholar] [CrossRef] [Green Version]
- Hamouz, Z.; Al-Faraj, A. Transmission expansion planning using nonlinear programming. Proc. IEEE Power Eng. Soc. Transm. Distrib. Conf. 2002, 1, 50–55. [Google Scholar] [CrossRef]
- Tejada, D.; López-Lezama, J.M.; Rider, M.J.; Vinasco, G. Transmission network expansion planning considering repowering and reconfiguration. Int. J. Electr. Power Energy Syst. 2015, 69, 213–221. [Google Scholar] [CrossRef]
- Romero, R.; Monticelli, A.; Garcia, A.; Haffner, S. Test systems and mathematical models for transmission network expansion planning. Gener. Transm. Distrib. IEE Proc. 2002, 149, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Du, X.; Gu, W.; Zhang, X.; Li, J. Automatic Selection Method for Candidate Lines in Transmission Expansion Planning. IEEE Access 2018, 6, 11605–11613. [Google Scholar] [CrossRef]
- Mendonça, I.; Junior, I.; Dias, B.; Marcato, A. Identification of relevant routes for static expansion planning of electric power transmission systems. Electr. Power Syst. Res. 2016, 140, 769–775. [Google Scholar] [CrossRef]
- Gallego, R.A.; Monticelli, A.; Romero, R. Transmission system expansion planning by extended genetic algorithm. IEE Proc.-Gener. Transm. Distrib. 1998, 145, 329–335. [Google Scholar] [CrossRef]
- Chu, P.C.; Beasley, J.E. A genetic algorithm for the generalised assignment problem. Comput. Oper. Res. 1997, 24, 17–23. [Google Scholar] [CrossRef]
- Da Silva, E.; Ortiz, J.; De Oliveira, G.; Binato, S. Transmission network expansion planning under a Tabu Search approach. IEEE Trans. Power Syst. 2001, 16, 62–68. [Google Scholar] [CrossRef]
- Romero, R.; Gallego, R.A.; Monticelli, A. Transmission system expansion planning by simulated annealing. IEEE Trans. Power Syst. 1996, 11, 364–369. [Google Scholar] [CrossRef]
- Leeprechanon, N.P.; Limsakul, S.P. Optimal Transmission Expansion Planning Using Ant Colony Optimization. J. Sustain. Energy Environ. 2010, 1, 71–76. [Google Scholar]
- Martínez-Álvarez, F.; Cortés, G.; Torres, J.; Gutiérrez-Avilés, D.; Melgar-García, L.; Pérez-Chacón, R.; Rubio-Escudero, C.; Riquelme, J.; Troncoso, A. Coronavirus Optimization Algorithm: A bioinspired metaheuristic based on the COVID-19 propagation model. Big Data 2020, 8, 308–322. [Google Scholar] [CrossRef]
- Rahmani, M.; Romero, R.A.; Rider, M.J.; Paredes, M. Domain reduction using GRASP construction phase for transmission expansion planning problem. In Proceedings of the 12th European Conference on Evolutionary Computation in Combinatorial Optimization, Málaga, Spain, 11–13 April 2012; pp. 87–98. [Google Scholar]
- Mori, H.; Shimomugi, K. Transmission network expansion planning with Scatter Search. In Proceedings of the 2007 IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; pp. 3749–3754. [Google Scholar] [CrossRef]
- Escobar Zuluaga, A.; Gallego, R.; Toro, E. Path-Relinking algorithm applied to transmission system expansion planning problem. Rev. Fac. Ing. Univ. Antioq. 2010, 53, 185–195. [Google Scholar]
- de Sena Taglialenha, S.L.; Lázaro, R.A.R. Electric Transmission Network Expansion Planning with the Metaheuristic Variable Neighbourhood Search; IntechOpen: London, UK, 2019. [Google Scholar]
- Maghouli, P.; Hosseini, S.H.; Buygi, M.O.; Shahidehpour, M. A Multi-Objective Framework for Transmission Expansion Planning in Deregulated Environments. IEEE Trans. Power Syst. 2009, 24, 1051–1061. [Google Scholar] [CrossRef]
- Ugranli, F.; Karatepe, E. Multi-objective transmission expansion planning considering minimization of curtailed wind energy. Int. J. Electr. Power Energy Syst. 2015, 65, 348–356. [Google Scholar] [CrossRef]
- Mori, H.; Iimura, Y. Transmission Network Expansion Planning with a Hybrid Meta-heuristic Method of Parallel Tabu Search and Ordinal Optimization. In Proceedings of the 2007 International Conference on Intelligent Systems Applications to Power Systems, ISAP, Kaohsiung, Taiwan, 5–8 November 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Cortes-Carmona, M.; Palma-Behnke, R.; Moya, O. Transmission Network Expansion Planning by a Hybrid Simulated Annealing Algorithm. In Proceedings of the 2009 15th International Conference on Intelligent System Applications to Power Systems, Curitiba, Brazil, 8–12 November 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Wong, L. A Review of Transmission Losses in Planning Studies; California Energy Commission: Sacramento, CA, USA, 2011.
- Dominguez, A.; Escobar Zuluaga, A.; Gallego, R. An MILP model for the static transmission expansion planning problem including HVAC/HVDC links, security constraints and power losses with a reduced search space. Electr. Power Syst. Res. 2016, 143, 611–623. [Google Scholar] [CrossRef]
- de la Torre, S.; Conejo, A.J.; Contreras, J. Transmission Expansion Planning in Electricity Markets. IEEE Trans. Power Syst. 2008, 23, 238–248. [Google Scholar] [CrossRef]
- Zhang, H.; Heydt, G.T.; Vittal, V.; Quintero, J. An Improved Network Model for Transmission Expansion Planning Considering Reactive Power and Network Losses. IEEE Trans. Power Syst. 2013, 28, 3471–3479. [Google Scholar] [CrossRef]
- de Oliveira, E.J.; da Silva, I.C.; Pereira, J.L.R.; Carneiro, S. Transmission system expansion planning using a sigmoid function to handle integer investment variables. IEEE Trans. Power Syst. 2005, 20, 1616–1621. [Google Scholar] [CrossRef]
- De Oliveira, E.; Moraes, C.; Oliveira, L.; Honório, L.; Poubel, R. Efficient hybrid algorithm for transmission expansion planning. Electr. Eng. 2018, 100, 2765–2777. [Google Scholar] [CrossRef]
- Fitiwi, D.Z.; Olmos, L.; Rivier, M.; Cuadra, F.; Pérez-Arriaga, I.J. Finding a representative network losses model for large-scale transmission expansion planning with renewable energy sources. Energy 2016, 101, 343–358. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, D.; Wang, Z.; Zeng, B.; Wang, X.; Tomsovic, K.; Jin, Y. Optimal Allocation of Series FACTS Devices Under High Penetration of Wind Power Within a Market Environment. IEEE Trans. Power Syst. 2018, 33, 6206–6217. [Google Scholar] [CrossRef] [Green Version]
- Rahmani, M.; Vinasco, G.; Rider, M.J.; Romero, R.; Pardalos, P.M. Multistage Transmission Expansion Planning Considering Fixed Series Compensation Allocation. IEEE Trans. Power Syst. 2013, 28, 3795–3805. [Google Scholar] [CrossRef]
- Zhang, X.; Tomsovic, K.; Dimitrovski, A. Security Constrained Multi-Stage Transmission Expansion Planning Considering a Continuously Variable Series Reactor. IEEE Trans. Power Syst. 2017, 32, 4442–4450. [Google Scholar] [CrossRef] [Green Version]
- Luburić, Z.; Pandžić, H.; Carrión, M. Transmission Expansion Planning Model Considering Battery Energy Storage, TCSC and Lines Using AC OPF. IEEE Access 2020, 8, 203429–203439. [Google Scholar] [CrossRef]
- Gallego, L.; Garcés, L.; Contreras, J. Optimal Placement of Series Capacitive Compensation in Transmission Network Expansion Planning. J. Control. Autom. Electr. Syst. 2019, 31, 165–176. [Google Scholar] [CrossRef]
- Zhang, H.; Vittal, V.; Heydt, G.T.; Quintero, J. A mixed-integer linear programming approach for multi-stage security-constrained transmission expansion planning. IEEE Trans. Power Syst. 2011, 27, 1125–1133. [Google Scholar] [CrossRef]
- Gallego, R. Long Term Transmission Systems Planning Using Combinatorial Optimization. Ph.D. Thesis, State University Campinas, Campinas, Brazil, 1997. (In Portuguese). [Google Scholar]






| Type | Compensation Rate | Compensation Cost |
|---|---|---|
| (% of Circuit Reactance) | (% of Circuit Inves. Cost) | |
| 1 | 30% | 10% |
| 2 | 40% | 15% |
| 3 | 50% | 20% |
| Test | Total Cost (106 US$) | Power Losses (MW) | LPs Executed | Time (min) | Configuration | Compensated Lines |
|---|---|---|---|---|---|---|
| 1 | 110.00 | – | 40 | 0.045 | , | – |
| 2 | 110.00 | – | – | – | , | No compensated lines |
| 3 | 130.00 | 29.51 | 129 | 0.121 | , , | – |
| 4 | 116.00 | 36.62 | 139 | 0.181 | , , | (type 1) |
| Planning Type | Total Cost (106 US$) | Power Losses (MW) | LPs Executed | Time (min) | Configuration | Compensated Lines |
|---|---|---|---|---|---|---|
| 1 | 152.00 | – | 46 | 0.045 | , , , | – |
| 2 | 152.00 | – | 120 | 0.605 | , , , | No compensated lines |
| 3 | 182.00 | 216.19 | 20 | 0.121 | , , , , | – |
| 4 | 154.40 | 225.52 | 8170 | 3.3 | , , , | (type 1) |
| Test | Total Cost (106 US$) | Power Losses (MW) | LPs Executed | Time (min) | Configuration | Compensated Lines |
|---|---|---|---|---|---|---|
| 1 | 72.87 | – | 274 | 0.131 | , , , , , , | – |
| 2 | 63.16 | – | 3154 | 2.28 | , , , , | (type 1), (type 2) |
| 3 | 75.90 | 603.18 | 608 | 0.36 | , , , , , | – |
| 4 | 75.45 | 642.66 | 16,698 | 9.84 | , , , , , | (type 1) |
| Test | Total Cost (106 US$) | LPs | Time (min) | Stage | Stage Cost (P106 US$) | Power Losses (MW) | Configuration | Compensated Lines |
|---|---|---|---|---|---|---|---|---|
| 1 | 80.79 | 924 | 0.277 | 1 | 30.00 | – | – | |
| 2 | 36.45 | – | , | – | ||||
| 3 | 14.34 | – | – | |||||
| 2 | 80.79 | 924 | 0.277 | 1 | 30.00 | – | No compensated lines | |
| 2 | 36.45 | – | , | No compensated lines | ||||
| 3 | 14.34 | – | No compensated lines | |||||
| 3 | 90.35 | 571 | 0.241 | 1 | 30.00 | 19.267 | – | |
| 2 | 36.45 | 27.673 | , | – | ||||
| 3 | 17.21 | 31.643 | , | – | ||||
| 4 | 82.22 | 12,415 | 3.94 | 1 | 30.00 | 19.607 | No compensated lines | |
| 2 | 36.45 | 27.531 | , | No compensated lines | ||||
| 3 | 15.77 | 36.045 | (type 1) |
| Test | Total Cost (106 US$) | LPs | Time (min) | Stage | Stage Cost (106 US$) | Power Losses (MW) | Configuration | Compensated Lines |
|---|---|---|---|---|---|---|---|---|
| 1 | 220.286 | 1685 | 0.481 | 1 | 164.00 | – | , , , , , | – |
| 2 | 21.87 | – | , | – | ||||
| 3 | 14.34 | – | , | – | ||||
| 2 | 209.243 | 190,375 | 44.09 | 1 | 152.00 | – | , , , | No compensated lines |
| 2 | 48,114 | – | No compensated lines | |||||
| 3 | 9.129 | – | No add circuits | (type 3), (type 2) | ||||
| 3 | 238.35 | 15,395 | 5.82 | 1 | 152.00 | 220.47 | , , , | – |
| 2 | 48.114 | 169.40 | – | |||||
| 3 | 38.240 | 115.27 | , | – | ||||
| 4 | 227.264 | 179,863 | 60.48 | 1 | 152.00 | 220.47 | , , , | No compensated lines |
| 2 | 48.114 | 232.373 | No compensated lines | |||||
| 3 | 27.150 | 263.243 | (type 3), (type 1), (type 3) |
| Test | Total Cost (106 US$) | LPs | Time (min) | Stage | Stage Cost (106 US$) | Power Losses (MW) | Configuration | Compensated Lines |
|---|---|---|---|---|---|---|---|---|
| 1 | 183.213 | 8988 | 2.68 | 1 | 116.00 | – | , , , , , , | – |
| 2 | 40.015 | – | , , , , | – | ||||
| 3 | 27.198 | – | , , , , | – | ||||
| 2 | 183.213 | 8988 | 2.68 | 1 | 116.00 | – | , , , , , , | No compensated lines |
| 2 | 40.015 | – | , , , , | No compensated lines | ||||
| 3 | 27.198 | – | , , , , | No compensated lines | ||||
| 3 | 195.08 | 34,326 | 13.74 | 1 | 116.100 | 495.40 | , , , , , , | – |
| 2 | 43.557 | 936.00 | , , , , | – | ||||
| 3 | 35.415 | 488.15 | , , , , | – | ||||
| 4 | 191.68 | 782,938 | 287.88 | 1 | 116.10 | 406.39 | , , , , , , | No compensated lines |
| 2 | 43.558 | 943.51 | , , , , | No compensated lines | ||||
| 3 | 31.433 | 1064.23 | , , , , , | (type 2) |
| Metaheuristic | Garver System | South Brazilian |
|---|---|---|
| Proposed HEGA | 40–50 | 200–300 |
| GA [5] | 50–70 | 100–1500 |
| EGA [45] | 700–1000 | 3500–4500 |
| SA [45] | 1000–1300 | 4000–5000 |
| TS [45] | 600–700 | 4100–6900 |
| TS-SA [45] | 600–700 | 1700–2500 |
| TS-EGA [45] | 500–620 | 1400–1900 |
| TS-SA-EGA [45] | 550–700 | 1450–2000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huanca, D.H.; Gallego, L.A.; López-Lezama, J.M. Transmission Network Expansion Planning Considering Optimal Allocation of Series Capacitive Compensation and Active Power Losses. Appl. Sci. 2022, 12, 388. https://doi.org/10.3390/app12010388
Huanca DH, Gallego LA, López-Lezama JM. Transmission Network Expansion Planning Considering Optimal Allocation of Series Capacitive Compensation and Active Power Losses. Applied Sciences. 2022; 12(1):388. https://doi.org/10.3390/app12010388
Chicago/Turabian StyleHuanca, Dany H., Luis A. Gallego, and Jesús M. López-Lezama. 2022. "Transmission Network Expansion Planning Considering Optimal Allocation of Series Capacitive Compensation and Active Power Losses" Applied Sciences 12, no. 1: 388. https://doi.org/10.3390/app12010388
APA StyleHuanca, D. H., Gallego, L. A., & López-Lezama, J. M. (2022). Transmission Network Expansion Planning Considering Optimal Allocation of Series Capacitive Compensation and Active Power Losses. Applied Sciences, 12(1), 388. https://doi.org/10.3390/app12010388







