Abstract
The purpose of this article was to present an algorithm for creating an ellipse for any data set represented on a two-dimensional reference frame. The study objective was to verify the developed method on real results of experimental tests with different subject matter. This article contains a mathematical algorithm to describe a set of points with elliptical areas. In addition, four results of tests with different subject matter are cited, based on which the developed method was verified. The verification of the method included checking the deviation of the geometric dimensions of the ellipse, the number of points contained within the ellipse, and the area of the ellipse. The implemented research methodology allowed to demonstrate the possibility of using the method of describing a set of points with elliptical areas, in order to determine quantitative parameters evaluating the results of the test. The presented results show the method’s applicability for the results obtained in four different operational tests: measurement of the human body’s gravity center position for a person propelling a wheelchair, measurement of marker position using motion capture methods, measurement of particulate emissions when using equipment powered by an internal combustion engine, and measurement of the muscle activity of the upper limb when propelling a hybrid manual-electric wheelchair. The performed experiments demonstrated that the method allows to describe about 85% of all measurement points with an ellipse.
1. Introduction
Currently developed technical devices are characterized by the complexity of their functional structure. Such a trend can be observed in all types of equipment, ranging from mechanisms [1,2,3], to rehabilitation equipment [4,5,6], machines [7,8], vehicles [9,10], and transport infrastructure [11]. The complex functionality and variety of configurations of operating parameters characterizing the innovative technical solutions result in studies of their effect on the surrounding environment consisting of several experiments measuring the same physical quantity. Tests of exhaust emissions into the atmosphere [12,13] and tests of the effects of technical devices on the biomechanics of anthropotechnical systems [14,15,16] are excellent examples of such tests. In both cases, operating parameters and design features that affect the value of one physical quantity can be controlled during operational tests. This translates into the ability of the device to perform a single function that, depending on the configuration, generates different values of the studied physical quantities.
When analyzing the results of modern tests, one can notice this is caused by different functions describing the same physical value measured for different configurations and parameters of the tested device. Examples of such tests include measurements of emissions of various chemical substances into the atmosphere, depending on the engine design, fuel type, or operating conditions [17,18,19] and tests of human muscular activity during operation of technical equipment with different design features [20,21]. The performance of tests that depend on numerous test parameters and design features is problematic when analyzing the results and when drawing conclusions from the tests performed. Furthermore, in some tests, it is necessary to determine the range of variation of the analyzed physical quantity for different device settings. Examples of such tests include energy consumption tests [22,23] during grinding of different materials with a single device, or tests comparing the effect of different configurations on technical device operation [24]. In the majority of such tests, the experiment result can be presented on two axes: the vertical axis showing the variation of tested physical quantity, and the horizontal axis showing the change of argument of the function. The results placed on such a graph are represented by measurement points defined on the vertical axis by the measured physical value, and on the horizontal axis by the value of the measurement sample variable. Because of the possibility of multiple operational parameters and design features, these points can be grouped by transforming them into a set of linear functions. In the case of such a result presentation, it is difficult to compare two independent experiments measuring the same physical value for two different devices characterized by an individual set of parameters affecting the way the main function of the device is performed. Because of that, there is a noticeable need for a method that allows converting a set of points or a set of functions into a single quantitative parameter or a set of several parameters describing a certain area in which the measured physical value changes.
When having two sets of points relating to the same physical quantities, the simplest way to compare them is to determine the area of presence for the points in the same reference frame. According to this, any issue related to assessing the results of operational tests for technical devices can be reduced to the evaluation of geometric properties of plane figures representing the area of presence for measured points [25]. There are numerous methods known for describing a set of points with an envelope forming a plane figure. One such method is the alpha shape method [26,27], which is characterized by plotting the perimeter of a plane figure based on all extreme points from the analyzed set. This method demonstrates the advantage of possible application in sets of points generating a plane figure with a concave perimeter. The disadvantage of this method is its complex algorithm that can only be implemented in a separate, complex software used for post-processing of the data measured in the study experiment. Another disadvantage of the method is its inability to generate a function defining the perimeter of the determined plane figure. The convex hull method [28,29] and the Delaunay triangulation method [30,31] are similar to the alpha shape method. These methods also have the same disadvantages as the alpha shape method. Moreover, the convex hall method makes it impossible to represent plane figures with a concave perimeter. The main disadvantage of these three methods is defining the delimited region of the plane figure by a set of vertex points. The irregularity of the perimeter plotted on the basis of these points makes it impossible to correctly approximate the perimeter of the figure determined by a mathematical function.
In the case of operational tests aimed at comparing two devices or two configurations of a single device, it is important that the geometric areas replacing the analyzed sets of measurement points are expressed by a mathematical function. Such an assumption results in the possibility of fitting such an area to various sets of points, and mathematical operations performed on it require less complicated mathematical methods. Having considered the foregoing, it is possible to develop an algorithm to describe any two-dimensional data set with a plane figure as an ellipse. The choice of the ellipse as the boundary describing the set of points results from the possibility of its description by means of two parametric equations, and its ease of implementation in the measurement results characterized by a normal distribution. The main objective of this paper was to present an algorithm for creating an ellipse for any data set represented on a two-dimensional reference frame. Verifying the developed method on real results of experimental tests with different subject matter was an additional objective of the study.
2. Materials and Methods
The method of describing a set of n points with elliptical areas allows us to replace any number of points with an ellipse, representing the area of their occurrence in a single plane (Figure 1). The described method should be applied to sets of points in which the number of radius vectors of the points Ri (1) larger than the mean length of the radius vector (2) is close to the number of vectors smaller than the mean length of the radius vector. This dependence can be verified by determining the value of the distribution uniformity ratio ΔP (3) of the analyzed points Pi (xi; yi) with respect to the geometric center of gravity of the analyzed set (; ) (4, 5). For the method described, the value of ΔP should be close to 0.5.
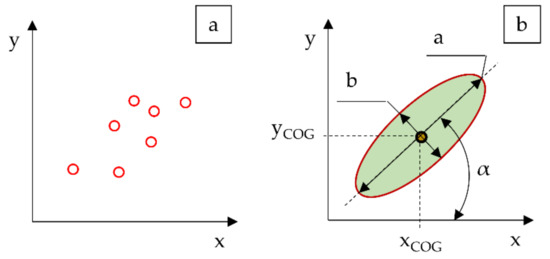
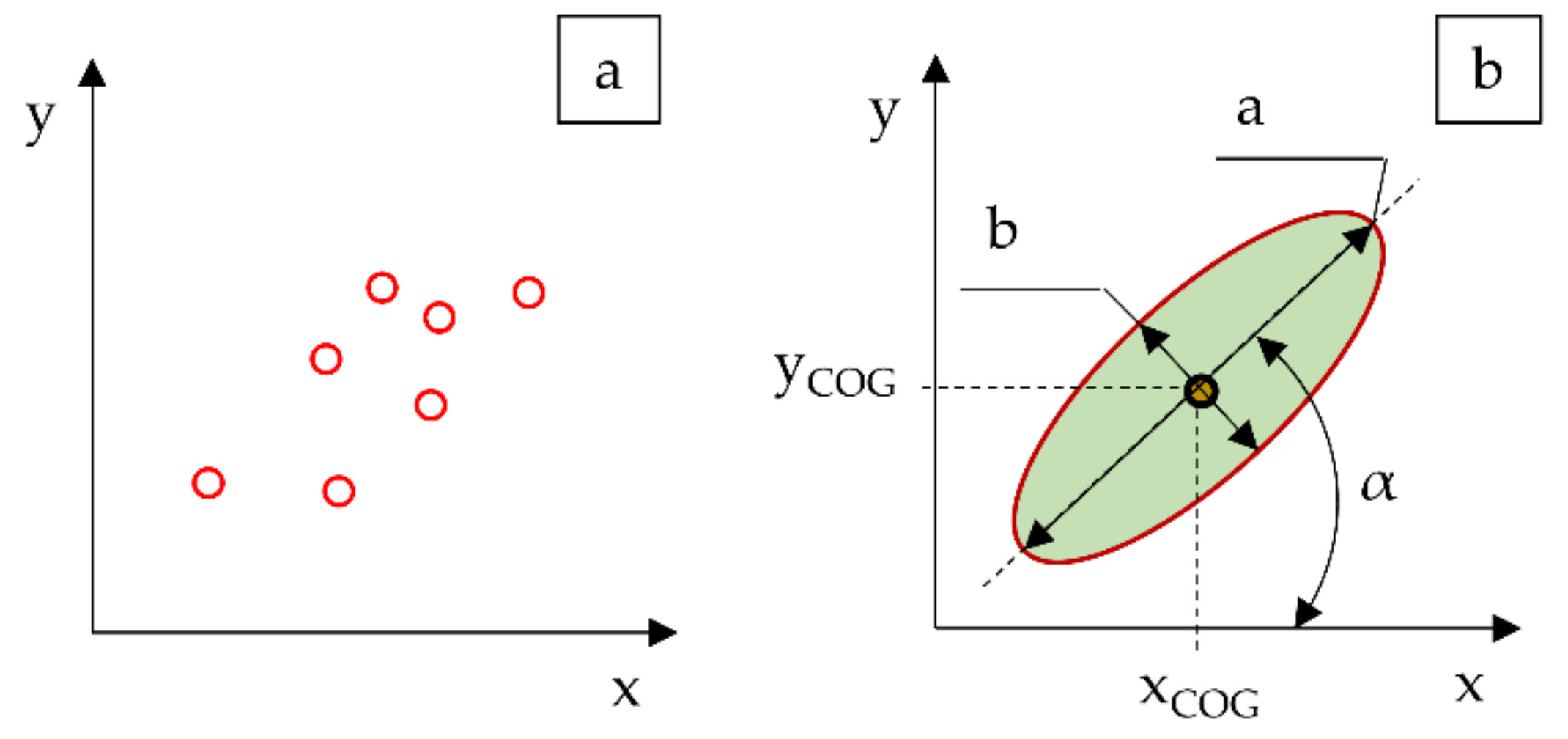
Figure 1.
Schematic illustration of the method replacing an arbitrary set of points (a) with an ellipse defining the area of presence for points on the analyzed plane (b).
Applying the method on a set of points satisfying the properties discussed above results in replacing it with an ellipse defined by five parameters for the position of the center of the ellipse xCOG and yCOG; the angle of inclination of the directional line α; the length of the semiaxis a, parallel to the directional line; and the length of the semiaxis b, perpendicular to the directional line.
2.1. Mathematical Description of the Method
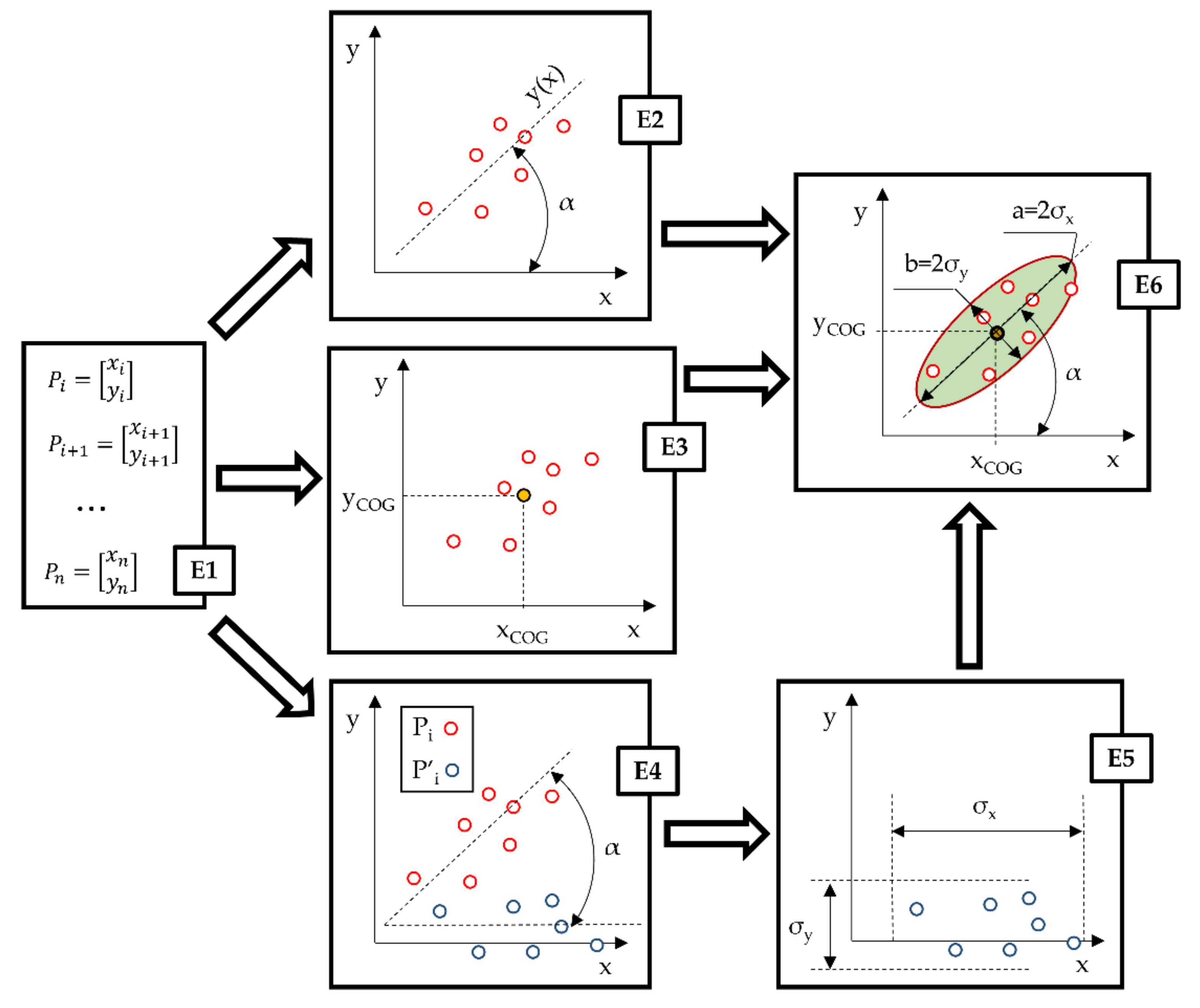
The algorithm of the method (Figure 2) requires providing it with a set of Cartesian coordinates describing the position of the analyzed points Pi (xi; yi) from the analyzed set of points (E1). The provided set is used to determine the linear trend function y(x) (6) first, with the inclination angle of the trendline α (7) (E2) being determined subsequently based on it. The inclination angle of the trendline is the target ellipse inclination angle, which is the angle between the ellipse’s longer semiaxis and the horizontal axis of the reference frame.
where y(x)—the value of the linear function of the trend, n—the number of points in the analyzed set, xi—the coordinate of the position on the horizontal axis of any point from the set, —the mean coordinate of the position on the horizontal axis from the coordinates of the analyzed set of points, yi—the coordinate of the position on the vertical axis of any point from the set, —the mean coordinate of the position on the vertical axis for the coordinates of the analyzed set of points, x—any coordinate on the horizontal axis, and α—the angle of inclination of the trendline with respect to the horizontal axis.
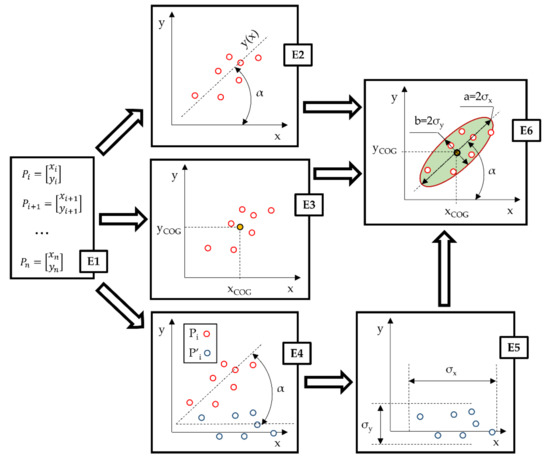
Figure 2.
Schematic of the algorithm allowing to describe a set of points with an ellipse.
In the next step (E3), the position of the ellipse center on the horizontal xCOG (8) and vertical yCOG (9) axes is calculated. These coordinates correspond to the position of the center of the plotted COG ellipse.
where xCOG—mean position on the horizontal axis of the analyzed set of points, yCOG—mean position on the vertical axis of the analyzed set of points, xi—position coordinate on the horizontal axis of any point from the set, yi—position coordinate on the vertical axis of any point from the set, and n—the number of points in the analyzed set.
The next step of the algorithm (E4) requires rotating the analyzed points by the negative value of the angle of inclination of the ellipse. This step is only a mathematical transformation necessary to calculate the dimensions of the ellipse and it does not affect the shape or position of the area approximating the set of points in the next steps. The rotation should result in a set of points with their trendline parallel to the horizontal axis. The rotation of the analyzed points is performed using the rotation matrix R(−α) (10), which is multiplied by all the analyzed points Pi, resulting in points (11) with coordinates rotated by angle α.
where R (α)—rotation matrix, α—the angle of inclination of the ellipse, xi—position coordinate on the horizontal axis of any point from the set, yi—position coordinate on the vertical axis of any point from the set, and —points after rotation by negative value by the angle of inclination of the ellipse α.
Knowing the horizontal and vertical coordinates for the rotated points is necessary to determine the dimensions of the semiaxis a and the semiaxis b of the ellipse (E5). In order to determine the dimensions of the semiaxis of the ellipse, the method uses the standard deviation of the horizontal and vertical coordinates of the analyzed set of points Pi. Depending on the type of distribution, this approach allows to control the percentage of points inside the ellipse by controlling a multiple of the standard deviation. For a set of points with a normal distribution, the dimension of the semiaxis a (12) corresponds to twice the standard deviation of the horizontal coordinate 2σx and the dimension of the semiaxis b (13) corresponds to twice the standard deviation of the vertical coordinate 2σy. Assuming a double standard deviation for normal distributions results in 95.4% of all analyzed Pi points being inside the plotted ellipse. In order to implement the method for non-normal point distributions, it is advisable to express the lengths of the semiaxes a and b as the product of the conformity coefficient ρ of the semiaxis dimensions to the point distribution and the standard deviation (14, 15). In this case, changes in the coefficient ρ translate into the percentage of measurement points that will be included in the plotted ellipse, and thus into the degree of similarity in the representation of the space of presence for the analyzed points Pi.
where a—the longer semiaxis of the ellipse parallel to the trendline of the analyzed set of points Pi, b—the shorter semiaxis of the ellipse perpendicular to the trendline of the analyzed set of points Pi, σx—standard deviation of horizontal coordinates of the set of inverted points , σy—standard deviation of vertical coordinates of inverted set of points , —horizontal coordinate of any point from set of inverted points , —vertical coordinate of any point from the set of inverted points , —mean of horizontal coordinates of the inverted set of points , —mean of vertical coordinates of the inverted set of points , and ρ—conformity coefficient for fitting the semiaxis dimensions to the analyzed distribution.
The last step of the presented algorithm is to plot the ellipse (E6). In order to do this, it is necessary to follow the previous steps, which will provide information about the parameters describing the ellipse. These parameters include the angle of inclination of the directional line of the ellipse α (E2), the coordinates of the position of the center of the ellipse xCOG and yCOG (E3), the dimension of the semiaxis a (E5), and the dimension of the semiaxis b (E5). In the adopted method, the parametric Equation (16) with parameter t∈ ⟨0; 2π⟩ was used to determine the coordinates of the points Ei located on the perimeter of the ellipse.
where Ei—point located on the perimeter of the ellipse, xiE—horizontal position of the ellipse’s envelope point, yiE—horizontal position of the ellipse’s envelope point, a—length of the ellipse’s long axis, b—length of the ellipse’s short axis, and t—parameter of the parametric equation of the ellipse.
Based on the known values of horizontal coordinates xEi and vertical coordinates yEi of the ellipse, taking into account the dimensions of the semiaxes a and b, one should then rotate the ellipse by the angle of inclination of the directional line α and its shift by the coordinates of the position of the center of the ellipse xCOG and yCOG (17). These mathematical operations result in the calculation of coordinates for the perimeter of the ellipse rotated in accordance with the angle of inclination of the trendline of analyzed points, and shifted relative to the beginning of the coordinate system, so that it covers 95.4% of all measured points.
where —point located on the perimeter of the ellipse by the angle α, Ei—point located on the perimeter of the ellipse, R(α)—rotation matrix, α—the angle of inclination of the ellipse, COG—midpoint of the ellipse and the set of analyzed points Pi, a—length of the longer semiaxis of the ellipse, b—length of the shorter semiaxis of the ellipse, t—parameter of the parametric equation of the ellipse, xCOG—mean position on the horizontal axis of the analyzed set of points, and yCOG—mean position on the vertical axis of the analyzed set of points.
2.2. Procedures for the Verification of the Method
The developed method of describing sets of points with elliptical areas was verified using real measurement results from four different tests. Using these data, the effect of the number of measured points for the same measurement sample on the dimensions of the ellipse was checked, as well as the effect of the value of the conformity coefficient ρ for the distribution of points on the percentage of points contained in the plotted ellipse. In addition, the practical application of the method in operational testing of mechanical equipment was evaluated based on two independent tests with different subject matter. Data from a measurement of the gravity center position for the human body while propelling a wheelchair (SAMPE 1), a motion capture measurement of a point moving on a circle of constant radius (SAMPLE 2), a ground-based measurement of PM 2.5 emissions from an internal combustion engine designed for low-power wood chipping machines (SAMPLE 3), and a measurement of muscle activity resulting from propelling a hybrid wheelchair (SAMPLE 4) were used for verification.
The methodology for verifying the algorithm provided that, for each data set analyzed, the dimensions of the semiaxes of the ellipse a and b, the angle of inclination of the ellipse α, the horizontal coordinate xCOG and vertical coordinate yCOG of the location of the center of the ellipse, and the distribution uniformity ratio ΔP were determined. Additionally, in order to assess the correctness of mapping a set of points with an ellipse, a set of criteria individually selected to the type of test providing the measurement points was checked. The classification of the determined parameters and evaluated criteria assigned to each dataset is provided in Table 1.

Table 1.
Summary of measured parameters and evaluated criteria for analyzed data sets, where a—length of the longer semiaxis of the ellipse, b—length of the shorter semiaxis of the ellipse, α—angle of inclination of the directional line of the ellipse, xCOG—mean position on the horizontal axis of the analyzed set of points, yCOG—mean position on the vertical axis of the analyzed set of points, ΔP—distribution uniformity ratio, k—percentage of analyzed points inside the area plotted by the ellipse ΔR—difference between the standard radius of curvature and the mean radius of curvature of the ellipse, A—area of the plotted ellipse σa—standard deviation of the semiaxis a, and σb—standard deviation of the semiaxis b.
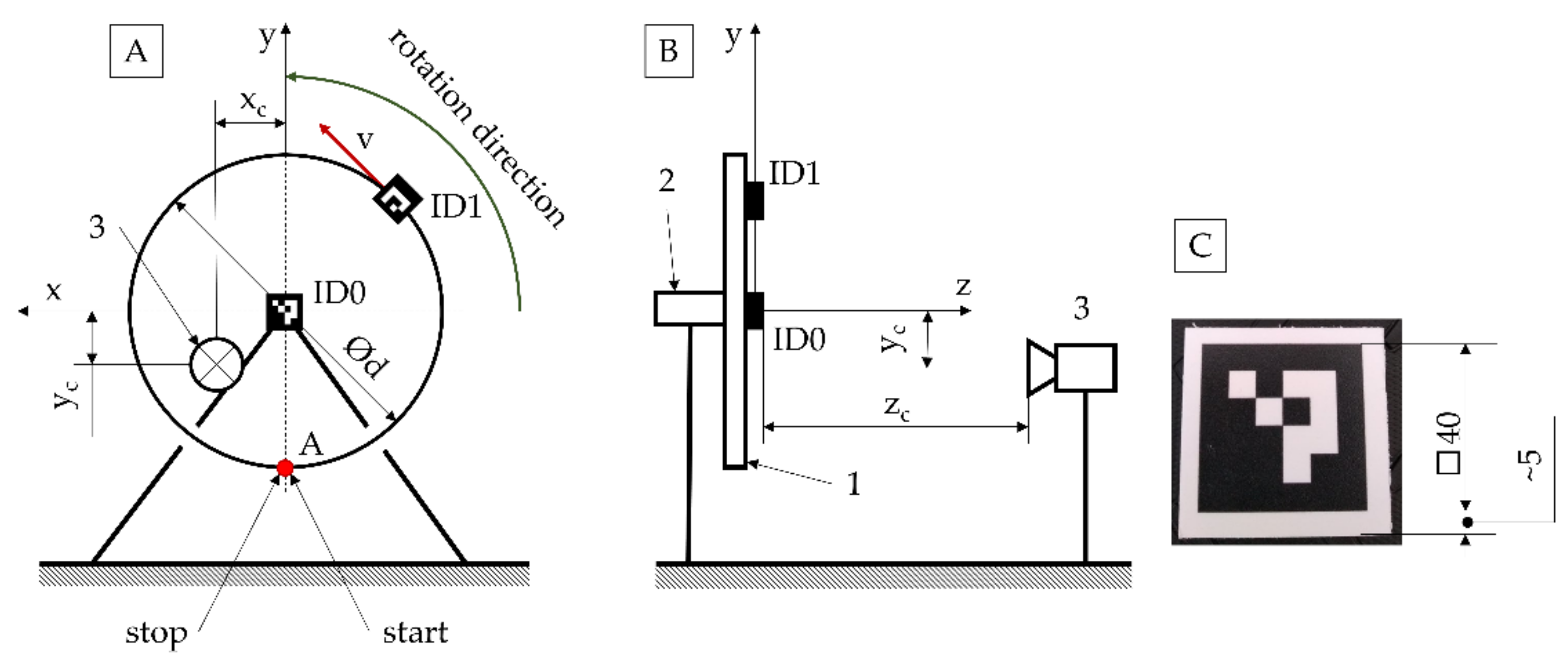
The evaluation of the effect of different sampling frequencies for a single measurement sample on the geometric dimensions of the determined ellipse was carried out on the example of the variation measurement for the position of the human body’s center of gravity when propelling a wheelchair [32,33,34,35] (SAMPLE 1). The data were obtained from the measuring stand (Figure 3), which consisted of weighing scales enabling the determination of coordinates for the center of gravity on a plane parallel to the surface on which the stand was located. The weighing scales were equipped with traction rollers, allowing measurement of the human body’s center of gravity in dynamic conditions corresponding to the propulsion of a wheelchair [36].

Figure 3.
Test stand for the implementation of biomechanical tests with the specified elements for measuring the position of the center of gravity (A) and the test stand during the test (B), where 1—weighing pan, 2—strain gauges supporting the test stand, 3—linear guides stabilizing the weighing pan, and 4—rollers that connect the wheel of the wheelchair with the weighing scales.
The set of analyzed points contained coordinates for the position of the human body’s center of gravity measured in the Cartesian system located in the horizontal plane. The analyzed points were the result of the wheelchair user performing five full propulsion cycles. However, because of the type of evaluation performed, this measurement sample was recorded with eight different frequencies f, taking the following values: 25 Hz, 29 Hz, 33 Hz, 40 Hz, 50 Hz, 67 Hz, 100 Hz, and 200 Hz. The variation in sampling frequency during the test translated into the number of points provided to the algorithm of the verified method.
The effect of the conformity coefficient value of the semiaxis dimensions for the distribution of points ρ on the percentage of points contained inside the plotted ellipse was evaluated with the example of data obtained from the motion capture measurement of the point ID1 position in space (SAMPLE 2), moving with constant speed v on a circle of constant radius d [37].
The test station (Figure 4) used to generate the data consisting of a measuring wheel with a fixed reference diameter d of 520 mm. The ID1 marker was placed on this wheel moving with a constant velocity v of 0.2 m/s2. The position data collected were the coordinates of the ID1 marker’s position relative to the ID0 marker. These data were obtained after processing the image recorded by a camera capturing video at 240 fps, with original software.
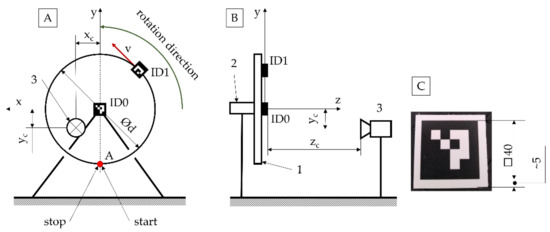
Figure 4.
Schematic of the test station (A,B) for ArUco markers (C) used for motion capture tests, where 1—reference wheel; 2—motor setting the reference wheel in rotation; 3—camera recording the image; xc, yc, zc—coordinates of the camera position relative to the stationary marker ID0; and v—rotational speed of the movable marker ID1.
An application example of the method for describing a set of points with elliptical areas for real operational tests of technical devices is presented using the example of measuring PM 2.5 particulate matter concentration (SAMPLE 3) and measuring the muscular activity of upper limb muscles (SAMPLE 4). The concentration of PM 2.5 particulate matter was measured in a city park, simulating the performance of greenery maintenance using equipment driven by an internal combustion engine (Figure 5). The test was performed in a circular working area (WA) with a 17 m diameter. In the center of this area, there was a Lifan internal combustion engine, with a power of 10 KW, 390 cm3 capacity, powered by gasoline, which was a particulate matter emitter [38]. Measurement of PM 2.5 concentration was performed in different points of WA area using an ATMON FL sensor.

Figure 5.
Photograph of the used engine and PM 2.5 sensor (A) and a view of the test area (B), where 1—engine, 2—particle sensor, and WA—area of the analysis.
Muscle activity (SAMPLE 4) was measured on a wheelchair dynamometer (Figure 3), where a manual-hybrid wheelchair [39] was tested (Figure 6). In these tests, a wheelchair user propelled the wheelchair on a dynamometer that generated three different moments of resistance to motion: 8.14 Nm, 9.67 Nm, and 11.19 Nm. The procedure for propelling the wheelchair was to push off the push rings using the upper limb. During this propulsive movement, an electric motor built into the hub of the drive wheel additionally supported the propulsive force generated by the upper limb. During the performed measurement tests, the electric motor assist gain factor was 0%, 25%, 30%, 40%, 50%, 60%, 70%, and 75%. The value of maximal muscular activity MVCmax expressed in percentage was determined for the parameters changed as such. Muscle activity was determined by surface electromyography using a Noraxon Mini DTS device.

Figure 6.
A hybrid cart used in muscle activity tests, where 1—drive wheel, 2—push rings, and 3—electric motor built into the hub of the drive wheel.
3. Results
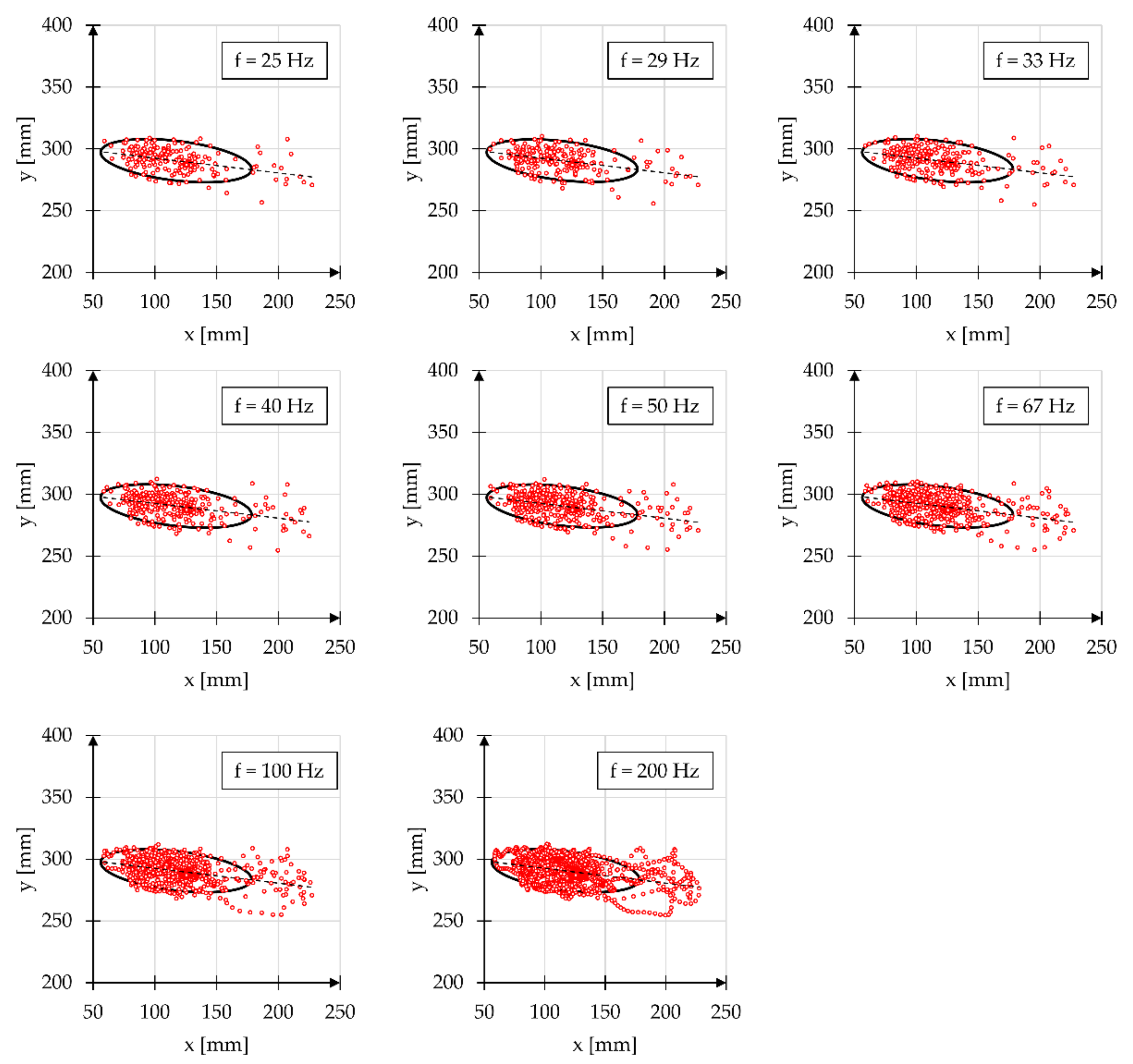
One of the most important factors affecting the quality of the presented tests is the sampling frequency. This is particularly noticeable when measuring physical quantities characterized by large changes in a short time. The tests in which the sampling frequency affects the final result of the analysis include the measurement of speed [40,41], measurement of force in dynamic conditions [42,43], and measurement of the change in position [44,45]. The results of the experiment checking the effect of sampling frequency on changes in dimensions of the ellipses are presented using the example of a set of points illustrating the variability of the human body’s gravity center position after performing five complete propelling cycles [46] (Figure 7) on a manual wheelchair. It should be noted that the presented results refer to the same measurement sample recorded simultaneously with eight different sampling frequencies.
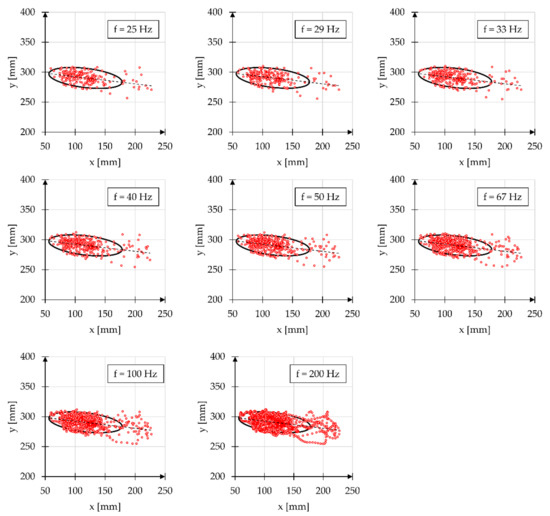
Figure 7.
Plots showing variation in the human body’s gravity center during manual wheelchair propulsion measured with different sampling frequencies f, with marked ellipses approximating the area of presence for the set of the analyzed points.
Changes in parameters describing the shape of the ellipse, the percentage of points described by the ellipse, the area and standard deviations in the dimensions of the semiaxes a and b were checked by evaluating the effect of sampling frequency (Table 2).

Table 2.
List of ellipse parameters and assessed criteria for one measurement test of the gravity center position made with different frequencies, where f—sampling frequency, n—number of points in the set of analyzed points, a—semiaxis of the ellipse parallel to the direction line, b—semiaxis of the ellipse perpendicular to direction line, α—angle of inclination of the direction line, xCOG—position of the center of the ellipse on the horizontal axis, yCOG—position of the center of the ellipse on the vertical axis, ΔP—uniformity ratio of points distribution in relation to the mean value of the radius vector for the points of the analyzed set, k—percentage of points located inside the area defined by the ellipse, A—ellipse area, μ—mean, and σ—standard deviation.
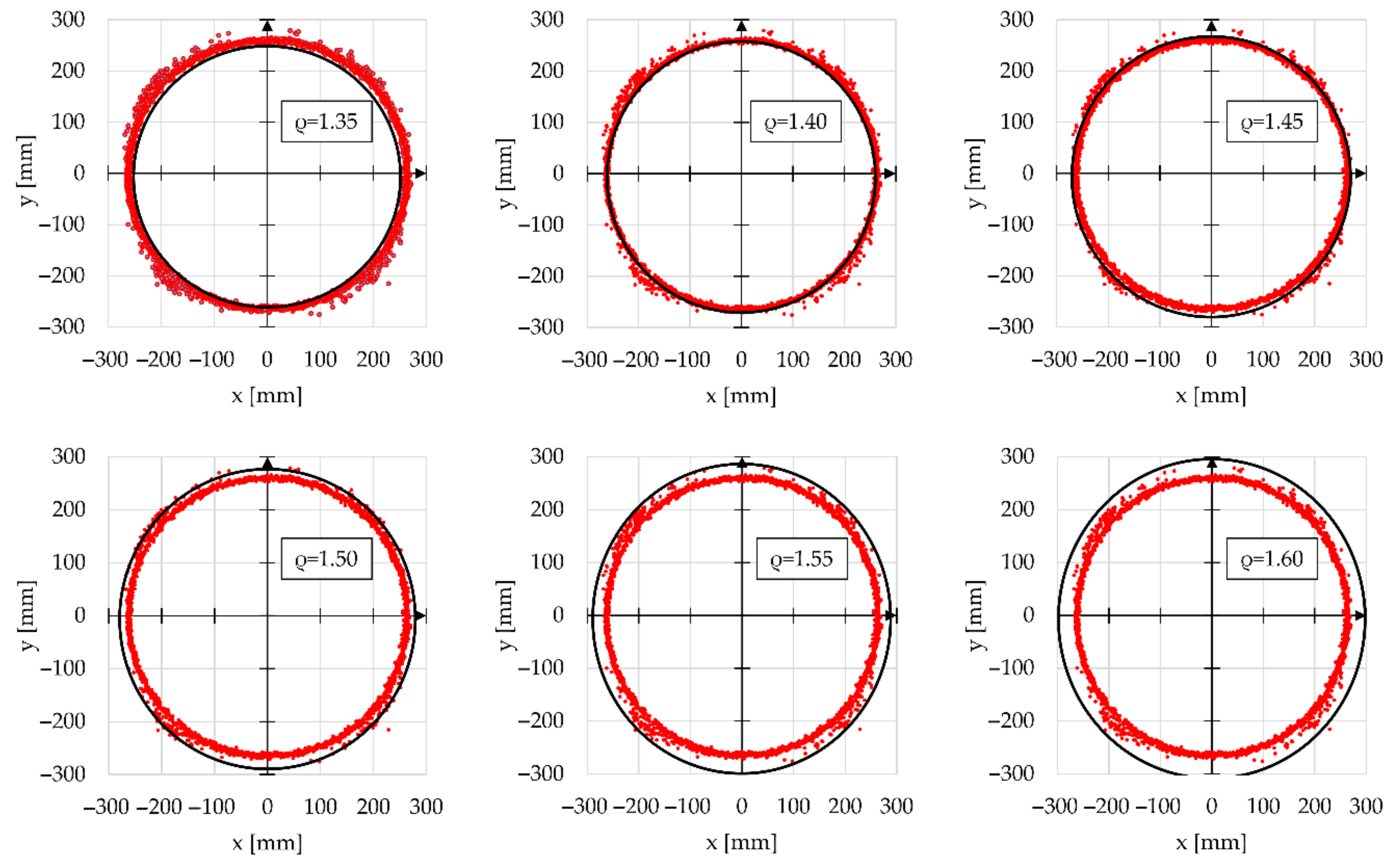
The performed operational tests do not always end with measuring a set of measurement points characterized by normal distribution. Motion capture tests are such a test type, in which the analyzed markers and their spatial position depend on the testing scenario, and in their case, the distribution of measured points is random. Measurement of human body segment kinematics can be taken as an example of such tests [47,48]. The effect of the conformity coefficient ρ value of the ellipse semiaxis dimensions for the set of points with distribution other than normal was performed with the example of data obtained during the motion capture measurement of a marker moving with a constant speed v = 0.2 m/s2 on a circle with a constant radius of curvature d = 520 mm. The data provided to the algorithm of the evaluated method were horizontal and vertical coordinates of the marker measured relative to a single stationary point (Figure 8). The performed evaluation included criteria to check the difference between the radius of the reference circle and the radius determined by the plotted ellipse ΔR (18), as well as the percentage of points included inside the area plotted by the ellipse k (Table 3).
where ΔR—difference between the reference radius of curvature and the mean radius of curvature of the ellipse, a—semiaxis of the target ellipse parallel to the trendline of the analyzed set of points, b—semiaxis of the target ellipse perpendicular to the trendline of the analyzed set of points, and d—diameter of the reference circle on which the ArUco marker was placed.
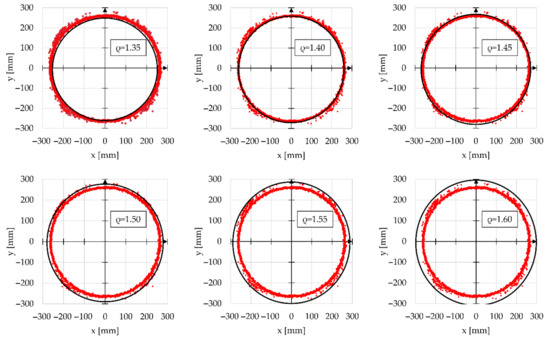
Figure 8.
Graphs of the motion capture measurement of a point moving on a constant-radius circle with ellipses plotted taking into account different values of the conformity coefficient ρ for the dimensions of the ellipse semiaxes.

Table 3.
Summary of the parameters of ellipses plotted with different values of the ellipse semiaxis dimension conformity coefficient ρ and the evaluated criteria for a single motion capture measurement sample, where ρ—the conformity coefficient of the ellipse’s semiaxis dimensions, a—semiaxis of the ellipse parallel to the directional line, b—semiaxis of the ellipse perpendicular to the directional line, α—angle of inclination of the directional line, xCOG—location of the ellipse’s center on the horizontal axis, yCOG—location of the ellipse’s center on the vertical axis, ΔP—uniformity ratio of the distribution of points with respect to the mean value of the radius vector, k—percentage of points inside the area plotted by the ellipse, and ΔR—difference between the reference radius of curvature and the mean radius of curvature of the ellipse.
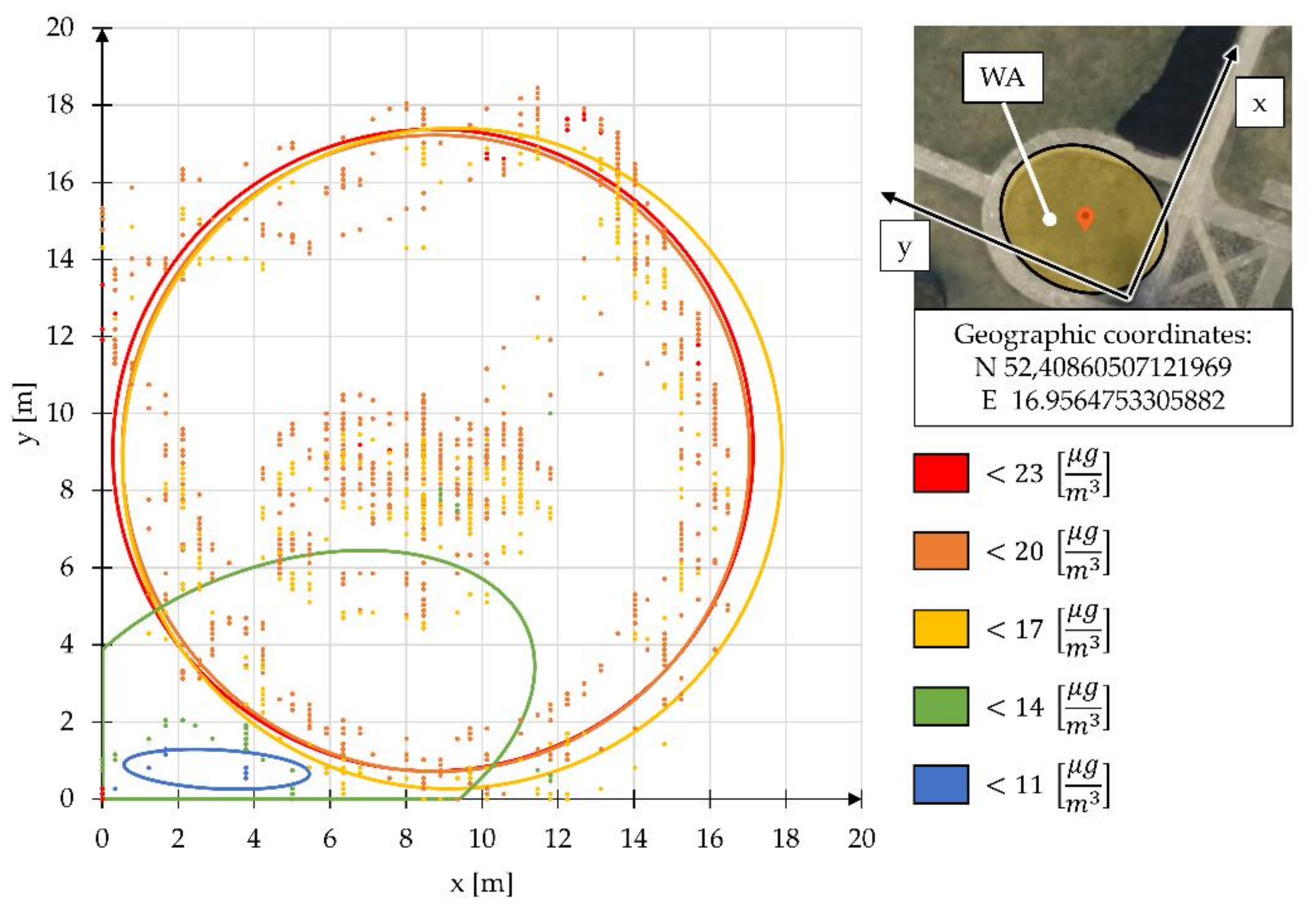
An example of an application of the method in real operational tests is presented using the example of PM 2.5 particulate matter emission measurement. The data used to present the method consisted of a set of coordinates for the sensor’s position in the horizontal plane, with assigned particulate matter concentration values. The applied test verified how performing maintenance work using tools with an internal combustion engine affects the value of air pollutant emissions. Based on such a data set, elliptical areas were plotted, with one of the five adopted ranges of PM 2.5 concentration measured in them (Figure 9).
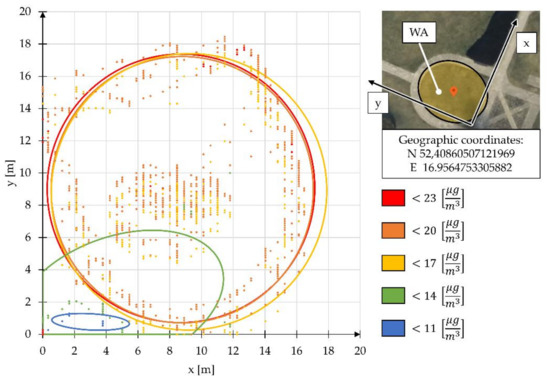
Figure 9.
Graph of areas of different concentrations of PM 2.5 solid particles during maintenance work in the green area with the use of tools powered by an internal combustion engine.
Using the method of describing a set of points with elliptical areas, it was possible to replace the points with areas of known centers xCOG and yCOG, semiaxis dimensions a and b of the ellipse, angle of inclination α of the directional line of the ellipse, and total area. The fact that sorting of points taken into account when plotting the ellipse was used is important in the implementation of the method. The criterion according to which sorting was performed was the concentration of PM 2.5 particulate matter (Table 4).

Table 4.
List of parameters describing dimensions of areas with different values of PM 2.5 particulate matter concentration, where a—semiaxis of the ellipse parallel to the direction line, b—semiaxis of the ellipse perpendicular to direction line, α—angle of inclination of the direction line, xCOG—position of the center of the ellipse on the horizontal axis, yCOG—position of the center of the ellipse on the vertical axis, ΔP—uniformity ratio of points’ distribution in relation to the mean value of the radius vector for the points of the analyzed set, k—percentage of points located inside the area defined by the ellipse, and A—area of the plotted ellipse.
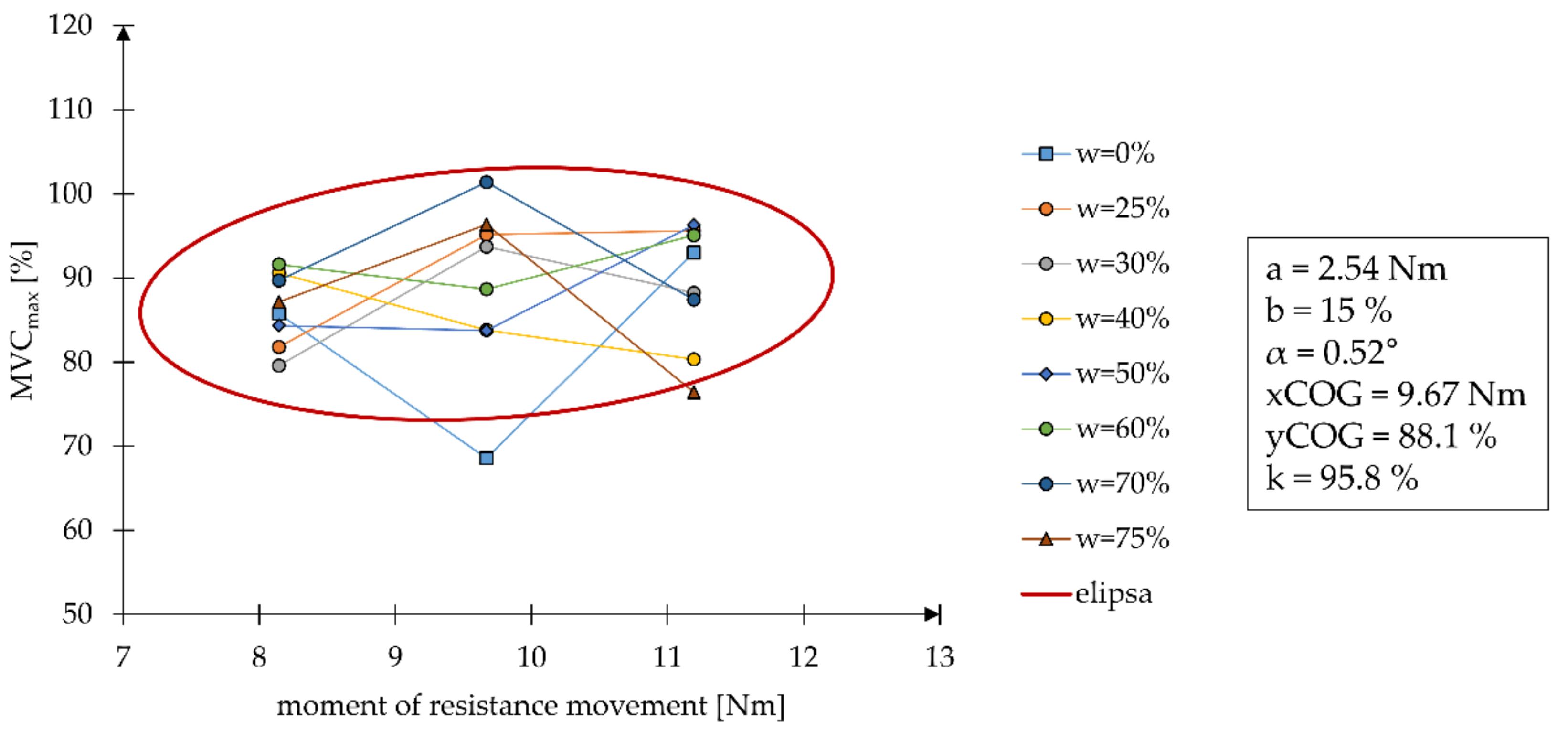
Biochemical tests are another example for the applicability of the method of describing a set of points with elliptical areas. The adopted tests measured the effect of wheelchair resistance moment values on the muscle activity resulting from propelling the wheelchair. The tests involved a hybrid wheelchair that could assist the user with electric motors. These motors could have different settings for the assistance gain factor w. This complexity of variables meant that there were several curves on a single graph representing changes in muscle activity values for different gain factor settings. Using the described method, all these curves were included in a single area, which defines the possible physical activity for a given range of resistance moment values and any values of the assistance gain factor w (Figure 10).
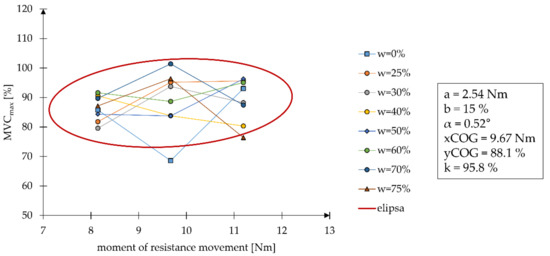
Figure 10.
Graph showing muscle activity values during propulsion of a manual wheelchair dependent on the value of the moment of resistance to motion for different assistance gain factor values w from the electric motor assistance system.
4. Discussion
The presented description of the method of describing a set of points with elliptical areas can be implemented to describe the results of operational tests in which the test results can be presented on two-dimensional graphs. The axes of these graphs may present any units, which is confirmed by the provided examples of method applicability. The application of the method is shown on data obtained during tests measuring the emissions of the internal combustion engine and the muscular activity of the human–wheelchair anthropotechnical system during the propulsion of the push drive. When implementing the method for individual measurement results, one should note that the values presented on the horizontal and vertical axes are of the same order of magnitude because, otherwise, inaccuracies may arise in mapping the set of points with an ellipse. This was noted in the applied example of the muscle activity tests. In this case, the original muscle activity values were expressed as a percentage; therefore, the measured effort ranged from 0 to 1. However, assuming such a size interval on the vertical axis resulted in excessive elongation of the semiaxis a. Because of that, the muscle activity value MVCmax was converted into a percentage value ranging from 0 to 100%. A better ellipse-shaped representation of the area of the measured points was obtained by doing so, and the location of points was determined by the values of the resistance moment on the horizontal axis and by the muscle activity MVCmax on the vertical axis. The results of muscle activity of disabled wheelchair users implemented in the verification are characterized by a similar range of findings as in articles analyzing these results in terms of other aspects [49,50].
When applying the method, the uniformity of distribution for the set of analyzed points with respect to the mean value is important. This uniformity is defined using the uniformity ratio ΔP of the distribution of points with respect to the mean value of the radius vector of the points in the analyzed set. The effect of the ΔP coefficient was particularly noticeable when analyzing the PM 2.5 particulate matter emission areas. In this test, the best elliptical representation of a set of points was obtained for sets in which ΔP was close to 0.5; areas with PM 2.5 concentrations <20 μg/m3 and <17 μg/m3 demonstrate this. In their case, the value of ratio ΔP was 0.58 and 0.59. The least accurate mapping of the set of points with ellipse was obtained for a PM 2.5 concentration of <14 μg/m3. For this set of points, the value of the ratio ΔP was 0.79. The presented example of applying the method on data describing PM 2.5 particulate matter emission has demonstrated the advantage of the described method consisting of simplicity to determine the area occupied by the analyzed set of points. Using this method, determining the area of presence of the analyzed points requires only calculating the area of an ellipse with two known parameters defining the lengths of the semiaxes a and b. The results obtained during the verification of the method confirm that the highest emission of air pollutants is closest to the emission source, i.e., the internal combustion engine [51,52].
The experiments carried out to verify the operation of the method checked how the distribution type and the number of measurement samples affect its applicability. The experiment testing the effect of the number of points on the dimensions of the ellipse showed that, when analyzing a set characterized by a normal distribution, the number of points has little effect on changes in the dimensions of the ellipse. When measuring the variation of gravity center position for the human body propelling the wheelchair, using the set consisting of 230 points, the dimension of semiaxis a was 61.46 mm, while it was 16.00 mm for semiaxis b. However, for the same measurement test measured with the frequency enabling to measure 1835 points, the dimension was 61.37 mm for semiaxis a and 15.83 mm for semiaxis b. Having included these results, it is noticeable that the mapping accuracy of the point presence area increases with the increase in the number of points. Despite that, the obtained small difference in the dimensions of the semiaxes confirms the thesis saying that the increase in the number of points of the analyzed set has little effect on the final dimensions of the ellipse. Based on that, it was found that the method is characterized by high flexibility when the analyzed set of points demonstrates variable size. Additionally, using the example of data from the measurement of the human body’s gravity center position, it was found that, for the distribution of points characterized by the uniformity ratio ΔP at the level of 0.57–0.61, there is an average of 84.08% of all points delivered to the algorithm of the method included in the ellipse. The data on the center of gravity position used for verification during wheelchair propulsion were consistent with the results of other tests measuring and analyzing this parameter in a different aspect [53,54].
An experiment conducted on motion capture data was supposed to demonstrate the effect of the distribution type on the representation of a set of points by an ellipse. Points characterized by a uniform distribution were used in this data set. In the case of such distributions, determining the length of the ellipse semiaxis as a value of double standard deviation is not very precise. It ensures covering over 95.4% of the points with the area plotted by the ellipse, but the plotted area is noticeably larger than the area of presence for the set of analyzed points. In order to also fit this method to uniform distributions, the method of calculating the semiaxis ellipse dimensions was modified. In this case, they are the quotient of the conformity coefficient ρ value of ellipse semiaxis dimensions and the standard deviation value. In one variant of the performed verification, the optimum value of ρ was chosen by searching for the smallest difference between the radius of the reference circle and the mean radius of curvature of the ellipse ΔR. The performed experiment showed that, for the coefficient ρ = 1.4, the smallest difference between the standard radius and the mean radius of ellipse curvature was ΔR equal to 2.50 mm. For such a value of the coefficient ρ, a dimension close to the dimension of the reference wheel diameter d was determined analytically; however, only 33.5% of all measured points were included in the plotted ellipse. This small percentage of points included in the ellipse area is due to the characteristics of the performed test. The use of motion capture testing was characterized by a proportional scatter of the measured marker position relative to a circle defined by a reference diameter d to which the marker was attached. In the case of the second verification variant, the number of points contained within the plotted ellipse was adopted as the criterion of optimality. In this case, the best results were obtained for a coefficient ρ of 1.60, for which the percentage of points inside the ellipse k was 100%. Nevertheless, the difference between the reference radius and the mean radius of curvature of the ellipse ΔR was 40.01 mm in this verification variant. The performed experiment demonstrated that, by controlling the value of the coefficient ρ, the method can be adjusted to different types of distribution, and it is possible to extract various parameters—important for the performed description of the experimental test—from the analyzed set of points. Studies have confirmed the feasibility of analyzing motion capture data over a specific range of speeds [55,56]. As part of the work, the method was verified for four different experimental studies. On this basis, it was found that the method is the most accurate for the results with a normal distribution. In the case of other distributions, the coefficient ρ should be selected independently, which may introduce an additional error.
5. Conclusions
The presented algorithm of the method provides a complete description, enabling its application to the presentation of the experimental results of various physical phenomena. The advantage of the method is describing a set of analyzed points by means of an ellipse, with the possibility to perform various mathematical operations on it. One such operation is calculating the area that, when appropriate units are juxtaposed on the horizontal and vertical axes, can result in the determination of a quantitative coefficient. For example, when measuring the operation of a mechanical system (expressed inwatts) as a function of time (expressed in seconds), the calculated area of the ellipse will represent the energy requirement of the device (expressed in joules). The verification tests performed showed that the method can be successfully applied to sets with any distribution. However, full automation of the described algorithm is achieved for normal distributions characterized by the uniformity ratio of distribution ΔP close to 0.5. In the case of other point distributions, it is necessary to introduce the method of conformity coefficient ρ of the ellipse semiaxis dimensions into the algorithm. This coefficient is chosen with individual optimization criteria for each test. The criteria adopted should result from the research objective adopted, and the target parameters for the analyzed set of points. There are plans to modify the parametric equations of the ellipse used in the further work on developing this method. Successful realization of such an assumption will allow to increase the accuracy of the mapping with the plotted area of the set of analyzed points.
Author Contributions
Conceptualization, B.W.; methodology, B.W.; software, B.W.; validation, B.W., M.K., and Ł.W.; formal analysis, B.W.; investigation, B.W.; resources, B.W.; data curation, B.W., M.K., and Ł.W.; writing—original draft preparation, B.W.; writing—review and editing, B.W.; visualization, B.W.; supervision, B.W.; project administration, B.W.; funding acquisition, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
The test was performed as part of the project LIDER VII “Testing the manual wheelchair propulsion biomechanics for innovative manual and hybrid propulsions” (LIDER/7/0025/L-7/15/2016) financed by the Polish National Centre for Research and Development.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krawiec, P.; Warguła, Ł.; Małozięć, D.; Kaczmarzyk, P.; Dziechciarz, A.; Czarnecka-Komorowska, D. The Toxicological Testing and Thermal Decomposition of Drive and Transport Belts Made of Thermoplastic Multilayer Polymer Materials. Polymers 2020, 12, 2232. [Google Scholar] [CrossRef] [PubMed]
- Krawiec, P.; Różański, L.; Czarnecka-Komorowska, D.; Warguła, Ł. Evaluation of the thermal stability and surface characteristics of thermoplastic polyurethane V-belt. Materials 2020, 13, 1502. [Google Scholar] [CrossRef]
- Sydor, M. Geometry of wood screws: A patent review. Eur. J. Wood Wood Prod. 2019, 77, 93–103. [Google Scholar] [CrossRef]
- Rui, J.; Gao, Q. Design and Analysis of A Multifunctional Wheelchair. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 538, p. 12045. [Google Scholar]
- Rebsamen, B.; Guan, C.; Zhang, H.; Wang, C.; Teo, C.; Ang, M.H.; Burdet, E. A brain controlled wheelchair to navigate in familiar environments. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 590–598. [Google Scholar] [CrossRef]
- Tanaka, K.; Matsunaga, K.; Wang, H.O. Electroencephalogram-based control of an electric wheelchair. IEEE Trans. Robot. 2005, 21, 762–766. [Google Scholar] [CrossRef]
- Minav, T.A.; Heikkinen, J.E.; Pietola, M. Direct driven hydraulic drive for new powertrain topologies for non-road mobile machinery. Electr. Power Syst. Res. 2017, 152, 390–400. [Google Scholar] [CrossRef]
- Lajunen, A.; Sainio, P.; Laurila, L.; Pippuri-Mäkeläinen, J.; Tammi, K. Overview of powertrain electrification and future scenarios for non-road mobile machinery. Energies 2018, 11, 1184. [Google Scholar] [CrossRef]
- Čižiūnienė, K.; Matijošius, J.; Čereška, A.; Petraška, A. Algorithm for Reducing Truck Noise on Via Baltica Transport Corridors in Lithuania. Energies 2020, 13, 6475. [Google Scholar] [CrossRef]
- Szpica, D.; Kusznier, M. Model Evaluation of the Influence of the Plunger Stroke on Functional Parameters of the Low-Pressure Pulse Gas Solenoid Injector. Sensors 2021, 21, 234. [Google Scholar] [CrossRef]
- Kilikevičius, A.; Bačinskas, D.; Selech, J.; Matijošius, J.; Kilikevičienė, K.; Vainorius, D.; Ulbrich, D.; Romek, D. The Influence of Different Loads on the Footbridge Dynamic Parameters. Symmetry 2020, 12, 657. [Google Scholar] [CrossRef]
- Wang, F.; Li, Z.; Zhang, K.; Di, B.; Hu, B. An overview of non-road equipment emissions in China. Atmos. Environ. 2016, 132, 283–289. [Google Scholar] [CrossRef]
- Pirjola, L.; Rönkkö, T.; Saukko, E.; Parviainen, H.; Malinen, A.; Alanen, J.; Saveljeff, H. Exhaust emissions of non-road mobile machine: Real-world and laboratory studies with diesel and HVO fuels. Fuel 2017, 202, 154–164. [Google Scholar] [CrossRef]
- Minetti, A.E. Bioenergetics and biomechanics of cycling: The role of ‘internal work’. Eur. J. Appl. Physiol. 2011, 111, 323–329. [Google Scholar] [CrossRef] [PubMed]
- Vanlandewijck, Y.; Theisen, D.; Daly, D. Wheelchair propulsion biomechanics. Sports Med. 2001, 31, 339–367. [Google Scholar] [CrossRef] [PubMed]
- Kotajarvi, B.R.; Sahick, M.B.; An, K.N.; Zhao, K.D.; Kaufman, K.R.; Basford, J.R. The effect of seat position on wheelchair propulsion biomechanics. J. Rehabil. Res. Dev. 2004, 41, 403–414. [Google Scholar] [CrossRef]
- Van Mierlo, J.; Maggetto, G.; Van de Burgwal, E.; Gense, R. Driving style and traffic measures-influence on vehicle emissions and fuel consumption. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2004, 218, 43–50. [Google Scholar] [CrossRef]
- Brouwer, R.; Falcão, M.P. Wood fuel consumption in Maputo, Mozambique. Biomass Bioenergy 2004, 27, 233–245. [Google Scholar] [CrossRef]
- Lijewski, P.; Merkisz, J.; Fuć, P.; Ziółkowski, A.; Rymaniak, Ł.; Kusiak, W. Fuel consumption and exhaust emissions in the process of mechanized timber extraction and transport. Eur. J. For. Res. 2017, 136, 153–160. [Google Scholar] [CrossRef]
- Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Five basic muscle activation patterns account for muscle activity during human locomotion. J. Physiol. 2004, 556, 267–282. [Google Scholar] [CrossRef]
- Mulroy, S.J.; Gronley, J.K.; Newsam, C.J.; Perry, J. Electromyographic activity of shoulder muscles during wheelchair propulsion by paraplegic persons. Arch. Phys. Med. Rehabil. 1996, 77, 187–193. [Google Scholar] [CrossRef]
- Howey, D.A.; Martinez-Botas, R.F.; Cussons, B.; Lytton, L. Comparative measurements of the energy consumption of 51 electric, hybrid and internal combustion engine vehicles. Transp. Res. Part D Transp. Environ. 2011, 16, 459–464. [Google Scholar] [CrossRef]
- Warguła, Ł.; Kukla, M. Determination of maximum torque during carpentry waste comminution. Wood Res. 2020, 65, 771–784. [Google Scholar] [CrossRef]
- Shrivastava, P.; Verma, T.N.; Pugazhendhi, A. An experimental evaluation of engine performance and emisssion characteristics of CI engine operated with Roselle and Karanja biodiesel. Fuel 2019, 254, 115652. [Google Scholar] [CrossRef]
- Pędzik, M.; Stuper-Szablewska, K.; Sydor, M.; Rogoziński, T. Influence of Grit Size and Wood Species on the Granularity of Dust Particles during Sanding. Appl. Sci. 2020, 10, 8165. [Google Scholar] [CrossRef]
- Liang, J.; Edelsbrunner, H.; Fu, P.; Sudhakar, P.V.; Subramaniam, S. Analytical shape computation of macromolecule. In PROTEINS: Structure, Function, and Genetics; Wiley Periodicals LLC: The Hoboken, NJ, USA, 1998; Volume 33, pp. 1–17. [Google Scholar]
- Giesen, J.; Cazals, F.; Pauly, M.; Zomorodian, A. The conformal alpha shape filtration. Vis. Comput. 2006, 22, 531–540. [Google Scholar] [CrossRef]
- Avis, D.; Bremner, D.; Seidel, R. How good are convex hull algorithms? Comput. Geom. 1997, 7, 265–301. [Google Scholar] [CrossRef]
- Eddy, W.F. A new convex hull algorithm for planar sets. ACM Trans. Math. Softw. (TOMS) 1977, 3, 398–403. [Google Scholar] [CrossRef]
- Lee, D.T.; Schachter, B.J. Two algorithms for constructing a Delaunay triangulation. Int. J. Comput. Inf. Sci. 1980, 9, 219–242. [Google Scholar] [CrossRef]
- Chen, L.; Xu, J.C. Optimal delaunay triangulations. J. Comput. Math. 2004, 22, 299–308. [Google Scholar]
- Wieczorek, B.; Górecki, J.; Kukla, M.; Wojtokowiak, D. The analytical method of determining the center of gravity of a person propelling a manual wheelchair. Procedia Eng. 2017, 177, 405–410. [Google Scholar] [CrossRef]
- Wieczorek, B.; Kukla, M. Methods for measuring the position of the centre of gravity of an anthropotechnic human-wheelchair system in dynamic conditions. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 776, p. 12062. [Google Scholar]
- Wieczorek, B.; Kukla, M.; Warguła, Ł. The Symmetric Nature of the Position Distribution of the Human Body Center of Gravity during Propelling Manual Wheelchairs with Innovative Propulsion Systems. Symmetry 2021, 13, 154. [Google Scholar] [CrossRef]
- Wieczorek, B.; Kukla, M. Biomechanical Relationships between Manual Wheelchair Steering and the Position of the Human Body’s Center of Gravity. J. Biomech. Eng. 2020, 142, 81006. [Google Scholar] [CrossRef]
- Wieczorek, B.; Warguła, Ł. Problems of dynamometer construction for wheelchairs and simulation of push motion. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2019; Volume 254, p. 1006. [Google Scholar]
- Wieczorek, B.; Warguła, Ł.; Kukla, M.; Kubacki, A.; Górecki, J. The effects of ArUco marker velocity and size on motion capture detection and accuracy in the context of human body kinematics analysis. Tech. Trans. 2020, 117, 1–10. [Google Scholar] [CrossRef]
- Warguła, Ł.; Kukla, M.; Lijewski, P.; Dobrzyński, M.; Markiewicz, F. Influence of Innovative Woodchipper Speed Control Systems on Exhaust Gas Emissions and Fuel Consumption in Urban Areas. Energies 2020, 13, 3330. [Google Scholar] [CrossRef]
- Wieczorek, B.; Warguła, Ł.; Rybarczyk, D. Impact of a hybrid assisted wheelchair propulsion system on motion kinematics during climbing up a slope. Appl. Sci. 2020, 10, 1025. [Google Scholar] [CrossRef]
- Veeger, H.E.; Van Der Woude, L.H.; Rozendal, R.H. Effect of handrim velocity on mechanical efficiency in wheelchair propulsion. Med. Sci. Sports Exerc. 1992, 24, 100–107. [Google Scholar] [CrossRef]
- Jiang, R.; Wu, Q.; Zhu, Z. Full velocity difference model for a car-following theory. Phys. Rev. E 2001, 64, 17101. [Google Scholar] [CrossRef]
- Bregman DJ, J.; Van Drongelen, S.; Veeger, H.E.J. Is effective force application in handrim wheelchair propulsion also efficient? Clin. Biomech. 2009, 24, 13–19. [Google Scholar] [CrossRef]
- Robertson, R.N.; Boninger, M.L.; Cooper, R.A.; Shimada, S.D. Pushrim forces and joint kinetics during wheelchair propulsion. Arch. Phys. Med. Rehabil. 1996, 77, 856–864. [Google Scholar] [CrossRef]
- O’Brien, J.F.; Bodenheimer, R.E., Jr.; Brostow, G.J.; Hodgins, J.K. Automatic Joint Parameter Estimation from Magnetic Motion Capture Data; Georgia Institute of Technology: Atlanta, GA, USA, 1999. [Google Scholar]
- Horprasert, T.; Haritaoglu, I.; Wren, C.; Harwood, D.; Davis, L.; Pentland, A. Real-time 3d motion capture. In Second Workshop on Perceptual Interfaces; 1998; Volume 2, Available online: https://xs2.dailyheadlines.cc/scholar?q=Real-time+3d+motion+capture.+In+Second+Workshop+on+Perceptual+Interfaces (accessed on 28 June 2021).
- Van der Woude, L.H.V.; Veeger, H.E.J.; Rozendal, R.H.; Sargeant, A.J. Optimum cycle frequencies in hand-rim wheelchair propulsion. Eur. J. Appl. Physiol. Occup. Physiol. 1989, 58, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Richter, W.M.; Rodriguez, R.; Woods, K.R.; Axelson, P.W. Stroke pattern and handrim biomechanics for level and uphill wheelchair propulsion at self-selected speeds. Arch. Phys. Med. Rehabil. 2007, 88, 81–87. [Google Scholar] [CrossRef]
- Collinger, J.L.; Boninger, M.L.; Koontz, A.M.; Price, R.; Sisto, S.A.; Tolerico, M.L.; Cooper, R.A. Shoulder biomechanics during the push phase of wheelchair propulsion: A multisite study of persons with paraplegia. Arch. Phys. Med. Rehabil. 2008, 89, 667–676. [Google Scholar] [CrossRef] [PubMed]
- Dubowsky, S.R.; Rasmussen, J.; Sisto, S.A.; Langrana, N.A. Validation of a musculoskeletal model of wheelchair propulsion and its application to minimizing shoulder joint forces. J. Biomech. 2008, 41, 2981–2988. [Google Scholar] [CrossRef]
- Van Drongelen, S.; Van der Woude, L.H.; Janssen, T.W.; Angenot, E.L.; Chadwick, E.K.; Veeger, D.H. Mechanical load on the upper extremity during wheelchair activities. Arch. Phys. Med. Rehabil. 2005, 86, 1214–1220. [Google Scholar] [CrossRef] [PubMed]
- Magagnotti, N.; Picchi, G.; Sciarra, G.; Spinelli, R. Exposure of mobile chipper operators to diesel exhaust. Ann. Occup. Hyg. 2014, 58, 217–226. [Google Scholar]
- Neri, F.; Foderi, C.; Laschi, A.; Fabiano, F.; Cambi, M.; Sciarra, G.; Aprea, M.C.; Cenni, A.; Marchi, E. Determining exhaust fumes exposure in chainsaw operations. Environ. Pollut. 2016, 218, 1162–1169. [Google Scholar] [CrossRef]
- Lemaire, E.D.; Lamontagne, M.; Barclay, H.W.; John, T.; Martel, G. A technique for the determination of center of gravity and rolling resistance for tilt-seat wheelchairs. J. Rehabil. Res. Dev. 1991, 28, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Asahara, S.; Yamamoto, S. A method for the determination of center of gravity during manual wheelchair propulsion in different axle positions. J. Phys. Ther. Sci. 2007, 19, 57–63. [Google Scholar] [CrossRef]
- Ukida, H.; Kaji, S.; Tanimoto, Y.; Yamamoto, H. Human motion capture system using color markers and silhouette. In Proceedings of the 2006 IEEE Instrumentation and Measurement Technology Conference Proceedings, Sorrento, Italy, 24–27 April 2006; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar]
- Kok, M.; Hol, J.D.; Schön, T.B. An optimization-based approach to human body motion capture using inertial sensors. IFAC Proc. Vol. 2014, 47, 79–85. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).