Data Augmentation for Audio-Visual Emotion Recognition with an Efficient Multimodal Conditional GAN

Abstract

Audio-visual emotion recognition is the research of identifying human emotional states by combining the audio modality and the visual modality simultaneously, which plays an important role in intelligent human-machine interactions. With the help of deep learning, previous works have made great progress for audio-visual emotion recognition. However, these deep learning methods often require a large amount of data for training. In reality, data acquisition is difficult and expensive, especially for the multimodal data with different modalities. As a result, the training data may be in the low-data regime, which cannot be effectively used for deep learning. In addition, class imbalance may occur in the emotional data, which can further degrade the performance of audio-visual emotion recognition. To address these problems, we propose an efficient data augmentation framework by designing a multimodal conditional generative adversarial network (GAN) for audio-visual emotion recognition. Specifically, we design generators and discriminators for audio and visual modalities. The category information is used as their shared input to make sure our GAN can generate fake data of different categories. In addition, the high dependence between the audio modality and the visual modality in the generated multimodal data is modeled based on Hirschfeld-Gebelein-Rényi (HGR) maximal correlation. In this way, we relate different modalities in the generated data to approximate the real data. Then, the generated data are used to augment our data manifold. We further apply our approach to deal with the problem of class imbalance. To the best of our knowledge, this is the first work to propose a data augmentation strategy with a multimodal conditional GAN for audio-visual emotion recognition. We conduct a series of experiments on three public multimodal datasets, including eNTERFACE’05, RAVDESS, and CMEW. The results indicate that our multimodal conditional GAN has high effectiveness for data augmentation of audio-visual emotion recognition.

1. Introduction

The task of emotion recognition is to detect human affective states. It is crucial for affect-related human-machine interactions, which has attracted a lot of attention from researchers [1,2,3,4,5,6,7,8]. audio-visual emotion recognition is a common type of emotion recognition, which combines the information of audio and visual modalities with multimodal learning [9,10]. Applications can be found in many domains, such as education [11], marketing [12], and gaming [13,14]. In recent years, we have witnessed tremendous progress in audio-visual emotion recognition by using deep neural networks (DNNs) [10,15,16,17,18]. However, these deep learning approaches may suffer from the following two challenges.

Firstly, data acquisition has become a major bottleneck for deep learning [19,20,21]. This is mainly due to two reasons: (i) Differently to traditional machine learning methods, deep learning requires larger amounts of the training data for learning tasks. (ii) The data collection process is often time-consuming and labor-intensive, especially for the multimodal data with different modalities. In consequence, the training data used for deep learning may not be sufficient, which leads to overfitting of deep learning models. Secondly, the emotional data may be class-imbalanced, which means that the minority class contains significantly fewer samples than the majority class. The problem of class imbalance may result in deep learning models showing bias towards the majority class and completely ignoring the minority class in extreme cases [22,23], which can further deteriorate the effectiveness of deep learning for audio-visual emotion recognition.

To address the aforementioned issues, we propose an efficient data augmentation approach with a multimodal conditional generative adversarial network (GAN) for audio-visual emotion recognition. Data augmentation is shown to be an effective way to tackle problems of data insufficiency and class imbalance in many fields, such as speech [24,25,26,27,28], vision [29,30,31,32,33,34], and time series [35,36,37,38]. Different data augmentation techniques are proposed to increase the size of the training data, such as geometric transformations, random occlusion, and photometric transformations [35,39]. GAN was first proposed in [40] to generate new data and is used for data augmentation in many applications [28,30,31,41,42,43,44]. Compared to other data augmentation techniques, GAN has received increasing attention by bringing more variations to the training data through deep learning [45,46]. Our proposed multimodal conditional GAN is a generalization of existing GANs for data augmentation to improve the performance of audio-visual emotion recognition. Figure 1 shows the architecture of our data augmentation approach. We first use our multimodal conditional GAN to generate new data, then augment the training set with the generated data, and finally train a DNN classifier with the augmented training set for the emotion classification task.

To be specific, our multimodal conditional GAN builds generators and discriminators for audio and visual modalities. Additional category information is used as their shared input to generate fake data of different categories. It is shown in [17,47,48,49] that in the real multimodal data, the audio modality and the visual modality are highly dependent, which is beneficial to emotion recognition. Inspired by this, we measure the correlation between the audio modality and the visual modality in the generated multimodal data based on Hirschfeld-Gebelein-Rényi (HGR) maximal correlation [50,51,52], which makes the generated multimodal data close enough to the real multimodal data to help improve the performance of audio-visual emotion recognition. In such a way, our multimodal conditional GAN can (1) effectively generate the multimodal data with audio and visual modalities, and (2) fully consider the correlation between the audio modality and the visual modality in the generated multimodal data. Then, the generated multimodal data are used to augment our training set. Finally, a DNN model is used as the classifier to perform the emotion classification task with the augmented training set. Three public multimodal datasets, including eNTERFACE’05 [53], RAVDESS [54], and CMEW [55,56,57], are used to conduct a series of experiments. The experiment results show that our multimodal conditional GAN can significantly enhance the performance of audio-visual emotion recognition.

To summarize, the main contributions of this paper lie in the following aspects:

• We design an efficient multimodal conditional GAN to augment the multimodal data with audio and visual modalities for emotion recognition.
• We model the correlation between the audio modality and the visual modality in the generated multimodal data to approximate the real multimodal data.
• We conduct experiments on three public multimodal datasets to show that our multimodal conditional GAN can be effectively used for data augmentation of audio-visual emotion recognition.

To the best of our knowledge, this is the first work to propose an efficient data augmentation approach with a multimodal conditional GAN for audio-visual emotion recognition. The rest of this paper is organized as follows. In Section 2, we show related works, including multimodal learning, and GAN and its application for data augmentation. In Section 3, we present our methodology in detail. In Section 4, a series of experiments are conducted to show the effectiveness of our multimodal conditional GAN. Finally, in Section 5, we draw conclusions and point out some future works.

2. Related Works

Our approach is closely related to multimodal learning, and GAN and its application for data augmentation. In this section, we review them in detail.

2.1. Multimodal Learning

Multimodal learning is a hot research topic in the academic community. It processes and relates the information from multiple modalities, and achieves success in many domains [58,59,60,61,62]. Representation and fusion are two key challenges of multimodal learning. The challenge of representation is to study how to learn good feature representations from the multimodal data [63,64,65,66]. It has two common types: joint and coordinated. Joint representations project different modalities into the same representation space. Coordinate representations learn projection functions from each modality and make them have similarity constraints. The challenge of fusion focuses on combining information from different modalities for prediction [67,68], which has three forms: early fusion, late fusion, and hybrid fusion. Early fusion combines the information of different modalities at the feature level, and late fusion works at the decision level. Hybrid fusion is between early fusion and late fusion.

Audio-visual emotion recognition is a specific scenario of multimodal learning by combining audio and visual modalities for emotion recognition. A number of previous works [10,15,16,17,18] has been proposed for audio-visual emotion recognition. For example, in [10], Zhang et al. use convolutional neural networks (CNNs) to extract audio and visual features, and fuse them in a deep belief network. In [15], Kim et al. design deep belief networks for unsupervised feature learning in audio-visual emotion recognition. In [16], multidirectional regression audio features and ridgelet transform-based face image features are captured, and a Bayesian sum rule is used as the fusion strategy. In [17], Ma et al. propose a deep learning approach in order to efficiently utilize common information between the audio modality and the visual modality for emotion recognition by correlation analysis. In [18], Peri et al. explore the disentanglement of multimodal signal representations for the primary task of emotion recognition and a secondary person identification task.

2.2. GAN

The concept of GAN was first proposed in [40] to generate new visual data via adversarial learning. It represents a two-player zero-sum game by adversarially training a generator and a discriminator. The compelling generation capability of GANs has attracted widespread attention from the research community [69,70,71]. Different variants of GANs are proposed. For example, in [72], CycleGAN is proposed for unpaired image-to-image translation by introducing a cycle consistency loss function. In [73], Ledig et al. propose SRGAN for image super-resolution by designing a perceptual loss function. In [74], Karras et al. propose StyleGAN for style transfer by introducing the separation of high-level attributes from stochastic variation in the generated data.

By supplementing the given dataset with the generated data, different forms of GANs are designed for data augmentation in many domains, such as medical image analysis [29,41,75,76], brain-computer interface [42,77], agriculture [43,78,79], and civil engineering [30,80]. In particular, researchers increasingly utilize GANs for data augmentation in the field of emotion recognition, including speech emotion recognition [27,28,81], facial expression recognition [31,82,83], EEG emotion recognition [44,84], and so on. These works have significantly improved the performance of unimodal emotion recognition. However, as far as we know, there are few works using GANs for data augmentation to improve the performance of multimodal emotion recognition, especially audio-visual emotion recognition. This may be due to two facts: (1) Both audio modality and visual modality in multimodal data are high-dimensional. It is difficult to design GANs to effectively extract information from them and generate them simultaneously; (2) In addition, these two modalities are highly correlated in terms of their emotional information [17,85]. Elucidating how to measure their relationship in GANs is also not easy. In our framework, the proposed multimodal condition GAN can effectively tackle the above two issues.

In addition, GANs can be used to deal with class imbalance [86,87,88,89]. For example, in [86], Douzas et al. use a conditional GAN as an oversampling approach to generate synthetic data for the minority class. In [87], Ali-Gombe et al. use multiple fake classes to ensure a fine-grained generation and classification of the minority class instances. In [88], multiple generation modules are adopted for data augmentation of minority classes. In [89], a balanced semisupervised GAN and a balanced batch-sampling strategy are introduced to resolve class imbalance.

3. Methodology

3.1. Overview

In this paper, we design a multimodal GAN for data augmentation in the problem of audio-visual emotion recognition. the pipeline is shown in Figure 1. We first apply our proposed GAN to generate fake multimodal data that is as realistic as possible, then use the generated data to supplement the original training set. Finally, we train a DNN classifier to perform the classification task with the augmented training set. The architecture of our multimodal GAN is shown in Figure 2. It builds generators and discriminators for audio and visual modalities. Generators generate fake data to confuse discriminators, while discriminators are used to distinguish whether the input data is real or fake. They are implemented by parameterized neural networks, which are trained together.

Suppose in the training process, we are given the training set $D=\left\{({\mathbf{x}}_A^{\left(i\right)},{\mathbf{x}}_V^{\left(i\right)},y^{\left(i\right)})\mid y^{\left(i\right)}\in \mathcal{Y}=\{1,2,\cdots ,|\mathcal{Y}\left|\right\},i=1,\cdots ,n\right\}$, where ${\mathbf{x}}_A^{\left(i\right)}$ and ${\mathbf{x}}_V^{\left(i\right)}$ represent the audio modality and the visual modality of the i-th sample, respectively. $y^{\left(i\right)}$ is their corresponding category label. For simplicity, the superscript will be omitted in the following. We denote the generator and discriminator of the visual modality as $G_V$ and $D_V$, respectively. $G_A$ and $D_A$ are expressed in the same way. ${\mathbf{z}}_V$ and ${\mathbf{z}}_A$ are two independent Gaussian noise vectors that are used to generate the visual modality and audio modality, respectively.

3.2. Proposed Multimodal Conditional GAN

To train our multimodal condition GAN, we design loss functions from the following two aspects: (1) The high-dimensional multimodal data with audio and visual modalities should be generated appropriately; (2) The relationship between the audio modality and the visual modality in the generated multimodal data should be fully considered. In order to achieve these goals, we generate the audio modality and the visual modality simultaneously, and model their correlation in our framework. Specifically, to generate the visual modality in the multimodal data, the following loss function $L_V(D_V,G_V)$ is considered:

$$L_V(D_V,G_V)=\mathbb{E}[log{D}_V\left({\mathbf{x}}_V\right|y)]+\mathbb{E}[log(1-D_V\left(G_V\left({\mathbf{z}}_V\right|y)\right))]$$

(1)

where $\mathbb{E}$ represents the expectation. The generator $G_V$ takes the noise vector ${\mathbf{z}}_V$ and the category label y as input, and outputs the fake visual modality. The discriminator $D_V$ can be regarded as a binary classifier. It takes the real or fake visual modality as the input together with the corresponding category label, and outputs a single scalar to distinguish whether the input visual modality is real or fake. $G_V$ and $D_V$ are optimized adversarially. Similarly, to generate the audio modality, we consider the following loss function $L_A(D_A,G_A)$:

$$L_A(D_A,G_A)=\mathbb{E}[log{D}_A\left({\mathbf{x}}_A\right|y)]+\mathbb{E}[log(1-D_A\left(G_A\left({\mathbf{z}}_A\right|y)\right))]$$

(2)

It is worth pointing out that the category label is sent to $G_V$ and $G_A$ as the shared input. In this way, audio and visual modalities in the multimodal data are generated simultaneously, where they share the same emotional information.

In addition, it is shown in [17,47] that the audio modality and the visual modality in the real multimodal data are correlated, which contributes to emotional recognition. This factor inspires us to consider the relationship between different modalities in the generated multimodal data. Here, we adopt a novel correlation loss function based on the Hirschfeld-Gebelein-Rényi (HGR) maximal correlation [50,51,52] to capture the correlation between the audio modality and the visual modality:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill L_{corr}(G_A,G_V)& =-\mathbb{E}[G_A{\left({\mathbf{z}}_A\right|y)}^T\left(G_V\left({\mathbf{z}}_V\right|y)\right]\hfill \\ & +\frac{1}{2}\mathrm{tr}\left(\mathrm{cov}\left(G_A\left({\mathbf{z}}_A\right|y)\right)\mathrm{cov}\left(G_V\left({\mathbf{z}}_V\right|y)\right)\right)\hfill \end{array}\end{array}$$

(3)

where the covariance matrix $\mathrm{cov}\left(G_A\left({\mathbf{z}}_A\right|y)\right)=\mathbb{E}\left[G_A\left({\mathbf{z}}_A\right|y)G_A{\left({\mathbf{z}}_A\right|y)}^T\right]-\mathbb{E}\left[G_A\left({\mathbf{z}}_A\right|y)\right]·\mathbb{E}{\left[G_A\left({\mathbf{z}}_A\right|y)\right]}^T$, $\mathrm{cov}\left(G_V\left({\mathbf{z}}_V\right|y)\right)$ is formulated in the same way, and $\mathrm{tr}(·)$ represents the trace operator. By optimizing the correlation function $L_{corr}$ in our framework, we relate the audio modality and the visual modality in the generated multimodal data with high dependence, which makes the generated multimodal data as realistic as possible to help improve the performance of emotion recognition.

Finally, we use the following loss function to train our multimodal conditional GAN:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill G_A^{*},G_V^{*}=arg\underset{G_A,G_V}{min}\underset{D_A,D_V}{max}{L}_A+L_V+\lambda ·L_{corr}\end{array}\end{array}$$

(4)

where $\lambda$ is a coefficient to measure the importance of the correlation loss in our framework. Different modules are trained simultaneously. After training, optimized generators $G_A^{*}$ and $G_V^{*}$ are used to generate new multimodal data with audio and visual modalities for data augmentation. The procedure to update the parameters of our multimodal conditional GAN is summarized in Algorithm 1.

3.3. DNN Classifier

In fact, we can use the trained generators $G_A^{*}$ and $G_V^{*}$ to generate any number of new multimodal data. However, not all generated data can benefit audio-visual emotion recognition. This may be because some of the generated data does not have sufficient emotional information, thus failing to perform data augmentation. Therefore, inspired by [44,90], we design a strategy to evaluate the generated multimodal data. We first learn a DNN classifier with the original training set D, which is trained with the cross-entropy loss function. Then, we use the trained classifier to predict the emotion labels of the multimodal data generated by our multimodal conditional GAN. If the predicted probability exceeds a certain threshold, we select this data as the final generated data.

After evaluating the generated data, we use the final generated data to supplement the original training set D as the augmented training set. On this set, we train a DNN classifier with the same architecture as the above DNN classifier. Then, we evaluate its classification performance on the test set.

Algorithm 1 Update the parameters of our multimodal conditional GAN.

Input: Coefficient $\lambda$, number of training iterations T, number of steps for discriminators $K_d$, number of steps for generators $K_g$.

for $t=1,\cdots ,T$do

for $k=1,\cdots ,K_d$ do

• Sample m noise samples $\{{\mathbf{z}}_A^{\left(1\right)},\cdots ,{\mathbf{z}}_A^{\left(m\right)}\}$ and m noise samples $\{{\mathbf{z}}_V^{\left(1\right)},\cdots ,{\mathbf{z}}_V^{\left(m\right)}\}$ from two independent prior distributions.

• Sample m real examples $\{({\mathbf{x}}_A^{\left(1\right)},{\mathbf{x}}_V^{\left(1\right)},y^{\left(1\right)}),\cdots ,({\mathbf{x}}_A^{\left(m\right)},{\mathbf{x}}_V^{\left(m\right)},y^{\left(m\right)})\}$ from the training set D.

• Update the discriminators $D_A$ and $D_V$ in Equations (1) and (2).

end for

for $k=1,\cdots ,K_g$ do

• Sample m noise samples $\{{\mathbf{z}}_A^{\left(1\right)},\cdots ,{\mathbf{z}}_A^{\left(m\right)}\}$ and m noise samples $\{{\mathbf{z}}_V^{\left(1\right)},\cdots ,{\mathbf{z}}_V^{\left(m\right)}\}$ from two independent prior distributions.

• Update the generators $G_A$ and $G_V$ in Equations (1)–(3).

end for

end for

4. Experiments

4.1. Datasets

We conduct experiments on three public multimodal datasets: eNTERFACE’05, RAVDESS, and CMEW. eNTERFACE’05 [53] is an audio-visual emotion database that contains 42 subjects, coming from 14 different nationalities. Six basic emotions are considered in this dataset, including anger, disgust, fear, happiness, sadness, and surprise. The data of this dataset are all in video format. Following [17,91], we extract 30 segments from each video. Then, for each segment, we use 94 mel filter banks with a 40 ms Hanning window and a 10 ms overlapping to extract the log mel spectrogram with the size of $94\times 94\times 3$ as the audio modality. In addition, the human face with the size of $160\times 160\times 3$ is detected by the multitask cascaded convolutional neural network (MTCNN) [92] as the visual modality. In this way, segment samples are extracted from the original videos. Then, all samples are divided into three parts: training set, validation set, and test set. To verify that our model can cope with data insufficiency, we conduct experiments by empirically setting up training sets of three sizes: Setting1, where each emotion has 300 segment samples; Setting2, where each emotion has 1200 segment samples; Setting3, where each emotion has 2400 segment samples. It can be seen that Setting1 has the fewest samples, Setting2 has fewer, and Setting3 has the most. In each of the above three cases, our multimodal conditional GAN is trained for data augmentation. The number of segment samples per class in both the validation set and the test set is 990 to evaluate the classification performance of emotion recognition. Under Setting1, the ratio of training set, validation set, and test set is 10:33:33. The ratios of Setting2 and Setting3 are 40:33:33 and 80:33:33, respectively.

RAVDESS [54] is a validated multimodal emotional database. It consists of 24 professional actors, vocalizing lexically-matched statements in a neutral North American accent. The data of this dataset are also in the form of video. The same six basic emotions as the eNTERFACE’05 dataset are studied here. Similar to the eNTERFACE’05 dataset, we also extract segment samples from original videos on the RAVDESS dataset and divide the samples into three parts: training set, validation set, and test set. On this dataset, we conduct experiments on training sets with three different settings: Setting1, where each emotion has 150 segment samples; Setting2, where each emotion has 300 segment samples; Setting3, where each emotion has 1200 segment samples. For the validation and test sets, each class has 870 segment samples. The ratios of training set, validation set, and test set under Setting1, Setting2, and Setting3 are 5:29:29, 10:29:29, and 40:29:29, respectively.

CMEW [55,56,57] is an audio-visual emotion database collected from Chinese TV series and movies. It contains four emotional states, including neutral, sadness, happiness, and anger. Data preprocessing is similar to the eNTERFACE’05 dataset and the RAVDESS dataset. Training sets with three sizes are used to conduct experiments separately: Setting1, where each emotion has 300 segment samples; Setting2, where each emotion has 1200 segment samples; Setting3, where each emotion has 6000 segment samples. There are 3150 segment samples for each class of the validation set and the test set. The ratios of training set, validation set, and test set under Setting1, Setting2, and Setting3 are 2:21:21, 8:21:21, and 40:21:21, respectively.

4.2. Networks

In Section 4.1, we show that the audio modality with the size of $94\times 94\times 3$ and the visual modality with the size of $160\times 160\times 3$ are extracted from original videos. If we directly feed them into our multimodal condition GAN, it will be difficult for our model to learn useful information from audio and visual modalities due to the high dimensionality of the multimodal data. Inspired by [17,44], we utilize the fully connected layer before the softmax layer of ResNet-34 [93] to extract 512-dimensional features from the raw audio and visual modalities as the input of our framework. In other words, the dimensionality of both ${\mathbf{x}}_A$ and ${\mathbf{x}}_V$ is 512. In this way, audio and visual modalities are appropriately represented in our system. The dimensions of Gaussian noise vectors ${\mathbf{z}}_A$ and ${\mathbf{z}}_V$ are set to 50. In addition, the label y corresponding to ${\mathbf{x}}_A$ and ${\mathbf{x}}_V$ are converted into the label embedding, and then sent to the generators of our multimodal conditional GAN along with ${\mathbf{z}}_A$ and ${\mathbf{z}}_V$.

Generators $G_A$ and $G_V$ have the same architecture with four fully connected layers. The first layer is the input layer with the noise vector and the label embedding, the second layer has 128 nodes, the third layer has 256 nodes, and the last layer is the output layer with 512 nodes to generate fake audio modality or fake visual modality. The second and third layers are followed by the LeakyReLU function. Similarly, discriminators $D_A$ and $D_V$ have the same architecture. We first concatenate the label embedding with the input modality, which can be either a real modality or a fake one generated by generators. Then, we send them to the discriminator with four fully connected layers. The first layer is the input layer. Each of the following two layers has 256 LeakyReLU nodes, and the last layer has only one node to determine whether the input data is real or fake.

After generating data with our multimodal conditional GAN, we use classifiers to evaluate the generated data and perform the final emotion classification task. In [94,95,96], DNN is shown to be effective in learning feature representations from audio and visual modalities. Inspired by this, we adopt DNN to design our emotion classifier. To be specific, we first concatenate the audio modality and the visual modality into a feature vector, and then send it into the DNN classifier with four fully connected layers. The first layer is the input layer with 1024 nodes. Each of the following two layers has 128 LeakyReLU nodes. The number of nodes in the last layer is the number of emotion categories (six for eNTERFACE’05 and RAVDESS, and four for CMEW).

4.3. Implementation Details

As far as we know, we are the first to design a multimodal GAN for data augmentation in the problem of audio-visual emotion recognition. Under different experimental settings, we compare our approach (Ours) with the following methods to show the superiority of our framework: (1) Baseline (A), which only uses the audio modality of the original training set for emotion classification. (2) Baseline (V), which only uses the visual modality of the original training set for emotion classification. (3) Baseline (A+V), which only uses the multimodal data of the original training set for emotion classification without data augmentation. In addition, some representative previous works of audio-visual emotion recognition are also compared, including (4) Attention Mechanism [97], (5) Canonical Correlation Analysis (CCA) [98], and (6) Tensor Fusion [99]. Moreover, we report the performance of (7) Ours (wo corr), which first uses our multimodal conditional GAN without the correlation loss to generate data, and then augment the original dataset with the generated data, finally performing emotion classification with the augmented training set. By comparing the performance of Ours and Ours (wo corr), we can show the importance of the proposed correlation loss in our framework.

In the training stage, we use the segment-level samples to perform classification. After obtaining the segment-level classification results, we use the majority rule to predict the video-level emotion labels. To ensure the reliability of the experimental result, we repeat each experiment five times and use the average classification accuracy (%) as the final result. For eNTERFACE’05, RAVDESS, and CMEW, we set $\lambda$ to 0.001, 0.01, and 0.1, respectively. In addition, Adam optimizer [100] with the learning rate of 0.0002 is adopted, and the batch size is set to 100. It is worth noting that our architecture is a GAN conditional on the class label. It can generate samples of different categories, which can internally prevent mode collapse [40,101]. In addition, inspired by [102,103], the above hyperparameters and network weights are carefully set to deal with other training problems of our multimodal conditional GAN. Pytorch [104] is used to implement our architecture on an NVIDIA TITAN V GPU card.

4.4. Experiment Results

To show the effectiveness of our approach, we first compare the classification performance of our method with other methods on different datasets, including eNTERFACE’05, RAVDESS, and CMEW. On each dataset, three settings are used for experiments. Note that to take full advantage of the methods of Ours (wo corr) and Ours, false multimodal data with appropriate sizes should be generated for data augmentation. The classification accuracies of different methods on the test set are reported, as shown in

Table 1. Classification accuracy (%) of different methods on the eNTERFACE’05 dataset. Best results are shown in bold.

Method	Sample Size
	Setting1	Setting2	Setting3
Baseline (A)	25.26	31.95	39.18
Baseline (V)	25.77	44.85	61.34
Baseline (A+V)	26.29	45.88	65.46
Attention Mechanism [97]	26.29	46.39	65.98
CCA [98]	26.80	45.88	66.49
Tensor Fusion [99]	27.32	46.91	67.53
Ours (wo corr)	29.38	48.97	69.07
Ours	31.95	50.52	71.13

,

Table 2. Classification accuracy (%) of different methods on the RAVDESS dataset. Best results are shown in bold.

Method	Sample Size
	Setting1	Setting2	Setting3
Baseline (A)	24.86	34.10	39.88
Baseline (V)	28.90	37.57	54.34
Baseline (A+V)	34.10	45.09	59.53
Attention Mechanism [97]	32.37	45.66	61.27
CCA [98]	33.06	44.51	60.69
Tensor Fusion [99]	33.53	43.35	60.12
Ours (wo corr)	39.88	50.28	64.16
Ours	42.20	52.02	65.90

and

Table 3. Classification accuracy (%) of different methods on the CMEW dataset. Best results are shown in bold.

Method	Sample Size
	Setting1	Setting2	Setting3
Baseline (A)	30.71	36.19	40.24
Baseline (V)	31.43	38.10	41.67
Baseline (A+V)	33.10	40.71	47.38
Attention Mechanism [97]	33.57	41.19	47.86
CCA [98]	34.05	41.43	48.10
Tensor Fusion [99]	32.14	40.00	47.14
Ours (wo corr)	36.90	44.76	50.47
Ours	39.29	46.43	52.14

.

We find the following summarizations: (1) Our approach achieves the highest performance compared to other methods, which shows that the data generated using our multimodal conditional GAN can significantly benefit audio-visual emotion recognition. (2) Although the classification performance of Ours (wo corr) is significantly higher than that of baseline methods, it is still lower than that of Ours, which shows that the correlation between the audio modality and the visual modality is helpful for data augmentation to improve the performance of emotion recognition. (3) In most cases, the classification accuracies of Attention Mechanism, CCA, and Tensor Fusion are higher than those of Baseline (A), Baseline (V), and Baseline (A+V), but still obviously lower than those of Ours (wo corr) and Ours. In addition, when the scale of training data is relatively small, especially in the case of Setting1, the performance of Attention Mechanism, CCA, and Tensor Fusion may be lower than that of Baseline (A+V). These findings show that the above previous works are not as effective as our method to utilize the information from the size-limited training set for classification. (4) We can further find that as the size of the original training set becomes smaller, the classification performance gap between Ours and Baseline (A+V) becomes larger. For example, on the RAVDESS dataset, the accuracy gap between Ours and Baseline (A+V) is 8.10% and 6.37% in the case of Setting1 and Setting3, respectively. This indicates that the fewer the real data, the more obvious the advantages of our approach. (5) In most cases, classification accuracies on the eNTERFACE’05 dataset and the RAVDESS dataset are higher than those on the CMEW dataset, which is consistent with the experimental results of previous works [10,17].

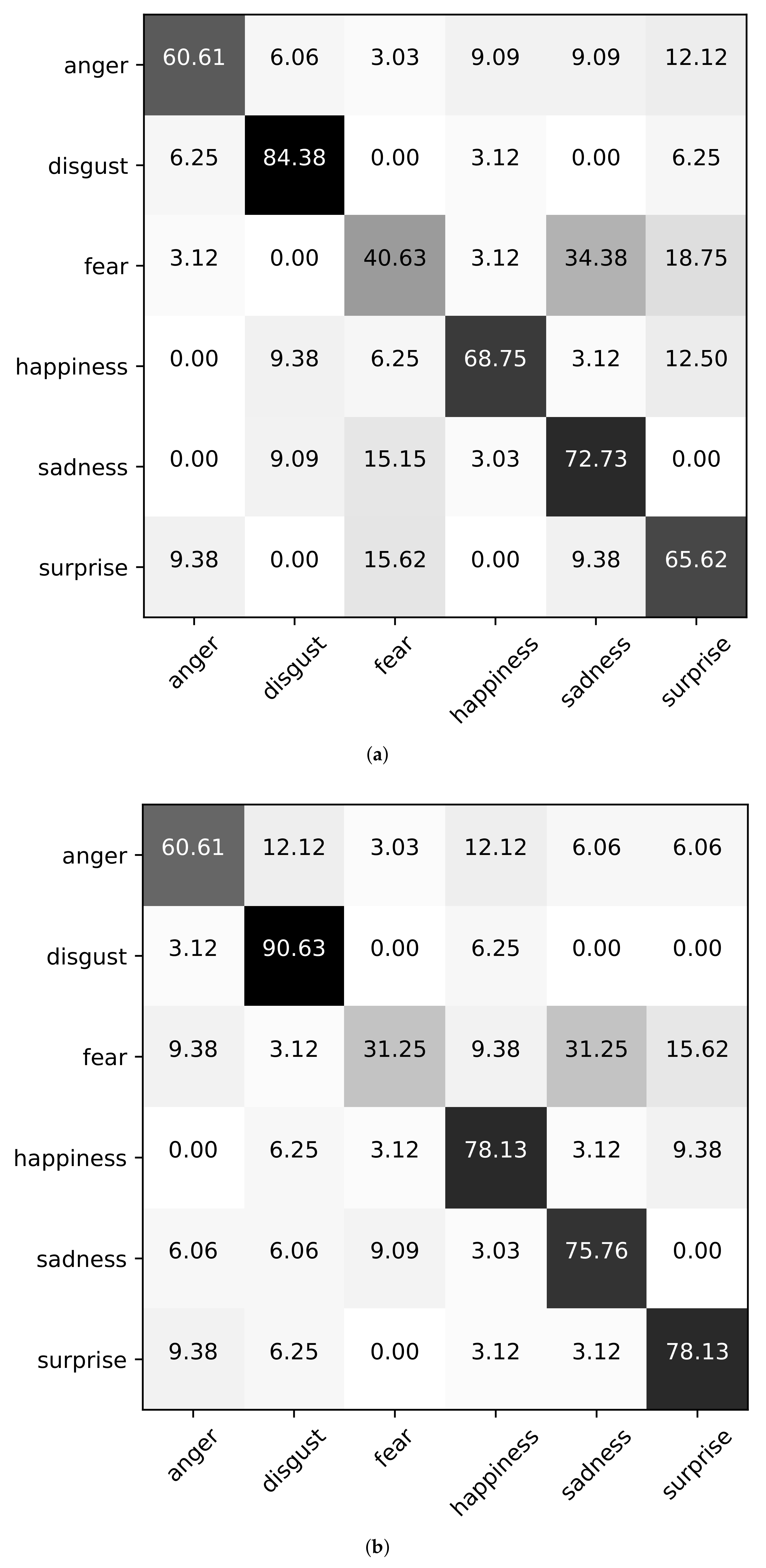
Next, we show the confusion matrices using Baseline (A+V), Ours (wo corr), and Ours in the case of Setting3 on the datasets of eNTERFACE’05, RAVDESS, and CMEW, as shown in Figure 3, Figure 4 and Figure 5. It can be found that on the eNTERFACE’05 dataset, “disgust’’ is the easiest to be recognized. On the RAVDESS dataset, “happiness” is the easiest to be recognized. On the CMEW dataset, “anger” is the easiest to be recognized. This shows that different datasets have different emotional cues. In addition, we can further find that for a few emotions, the classification accuracy using Baseline (A+V) may be higher than that using Ours (wo corr) or Ours, such as “disgust” on the RAVDESS dataset and “anger” on the CMEW dataset. However, for most emotions, the classification accuracy using Ours (wo corr) or Ours is higher. This shows that Ours (wo corr) or Ours can more effectively use the information of most emotions for the classification task.

In the above discussion, we show that our approach can efficiently help improve the classification accuracy on the test set. Inspired by [105], we next study the impact of the data generated by our multimodal conditional GAN on the training speed. On the datasets of eNTERFACE’05, RAVDESS, and CMEW, we plot the training loss with epochs of the DNN classifier in different methods, as shown in Figure 6. It is worth pointing out that the DNN classifier in Baseline (A+V) only uses the original training set for training, while the DNN classifier in the method of Ours (wo corr) or Ours uses the real data and generated data together for training. It can be found that the training loss of our approach decreases the fastest with epochs, which means that its convergence is the fastest, the convergence of Ours (wo corr) is the second fastest, and the convergence of Baseline (A+V) is the slowest. This shows that in addition to helping improve the accuracy of emotion classification, our framework can effectively speed up the training of the emotion classifier.

When analyzing the experimental results in Table 1, Table 2 and Table 3, we mention that when using Ours or Ours (wo corr), it is necessary to generate new data of appropriate size. Here, we discuss what scale of generated data is appropriate under different settings. We name the ratio of the size of the generated data to the size of the original training set as the augmentation ratio. It is used to measure the scale of the generated data compared to the original training set. Then, we analyze the classification performance of the methods of Ours and Ours (wo corr) with six augmentation ratios, including 0.5, 1, 2, 3, 4, and 5. The augmentation ratio of 2 means that the size of the generated data is twice the size of the original training set. Other ratios are represented in the same way. The experimental results on the datasets of eNTERFACE’05, RAVDESS, and CMEW are shown in

Table 4. Classification accuracy (%) with different augmentation ratios on the eNTERFACE’05 dataset. Best results are shown in bold.

Sample Size	Method	Augmentation Ratio
		0.5	1	2	3	4	5
Setting1	Ours (wo corr)	27.32	28.35	27.84	29.38	28.87	27.84
	Ours	28.35	29.38	31.96	31.44	30.93	29.38
Setting2	Ours (wo corr)	46.39	48.45	48.45	48.97	47.94	46.91
	Ours	48.45	49.48	50.00	50.52	50.00	48.97
Setting3	Ours (wo corr)	67.53	69.07	68.56	68.04	68.56	67.01
	Ours	70.10	71.13	70.62	69.59	70.10	69.07

,

Table 5. Classification accuracy (%) with different augmentation ratios on the RAVDESS dataset. Best results are shown in bold.

Sample Size	Method	Augmentation Ratio
		0.5	1	2	3	4	5
Setting1	Ours (wo corr)	37.57	38.73	39.88	39.31	39.31	38.15
	Ours	39.88	40.46	42.20	41.62	41.04	41.04
Setting2	Ours (wo corr)	47.40	49.71	50.29	49.13	47.98	48.55
	Ours	49.71	52.02	52.02	51.45	50.87	50.29
Setting3	Ours (wo corr)	62.43	64.16	63.58	63.01	63.01	62.43
	Ours	63.58	65.90	65.32	64.74	64.16	64.16

and

Table 6. Classification accuracy (%) with different augmentation ratios on the CMEW dataset. Best results are shown in bold.

Sample Size	Method	Augmentation Ratio
		0.5	1	2	3	4	5
Setting1	Ours (wo corr)	35.00	36.43	36.90	36.67	35.95	35.71
	Ours	37.14	38.81	39.29	38.57	38.33	38.33
Setting2	Ours (wo corr)	44.76	44.05	43.57	42.86	42.62	42.62
	Ours	46.43	46.19	45.95	45.24	44.52	44.05
Setting3	Ours (wo corr)	50.48	50.24	50.24	49.76	49.29	48.81
	Ours	51.90	52.14	51.67	51.19	50.24	50.00

, respectively.

We can find that on each setting, there is an augmentation ratio with the highest classification accuracy for Ours or Ours (wo corr). We can call this augmentation ratio the most appropriate augmentation ratio. In most cases, when the augmentation ratio is lower than the most appropriate augmentation ratio and increases, the corresponding classification accuracy also increases, while when the augmentation ratio is higher than the most appropriate augmentation ratio and increases, the corresponding classification accuracy decreases. For example, on Setting2 of the eNTERFACE’05 dataset, the most appropriate augmentation ratio is 3 for Ours. When the augmentation ratio increases from 0.5 to 1, 2, and then to 3, the corresponding classification accuracy also increases. However, when the augmentation ratio increases from 3 to 4 and then to 5, the corresponding classification accuracy becomes smaller. The reason behind this phenomenon may be that when the augmentation ratio is relatively small, the generated data is not enough for data augmentation effectively. Therefore, with the increase of augmentation ratio, the corresponding classification performance is improved. However, when the augmentation ratio is too large, the generated data may obscure the information of the original training set, which weakens the effect of data augmentation. Driven by these factors, we emphasize that the augmentation ratio should be selected appropriately for data augmentation.

From Table 4, Table 5 and Table 6, it can be further found that when the scale of the original training set is relatively small, the augmentation ratio should be set larger, i.e., more generated data can be used for data augmentation, while when the scale of the original data is relatively large, the augmentation ratio should be set smaller. For example, on the eNTERFACE’05 dataset, the sizes of Setting1 and Setting2 are relatively small, and it is more appropriate to set the augmentation ratio to 2 or 3, while Setting3 has more samples, and it is better to set the augmentation ratio to 1. The RAVDESS dataset and the CMEW dataset are similar to the eNTERFACE’05 dataset. In addition, we can see that the classification performances of Ours and Ours (wo corr) have a similar trend with the augmentation ratio, but the classification performance of Ours is higher than that of Ours (wo corr) under each setting. For example, on the eNTERFACE’05 dataset, the most appropriate augmentation ratios of Ours or Ours (wo corr) are 3 and 2, respectively, for Setting2 and Setting3. However, under these two settings, the classification accuracy of Ours is 1.55% and 2.06% higher than that of Ours (wo corr), respectively, which again shows the importance of capturing the correlation between the audio modality and the visual modality in our framework.

Furthermore, we show that our multimodal conditional GAN can deal with the problem of class imbalance of the training data. We conduct experiments on the datasets of eNTERFACE’05, RAVDESS, and CMEW. As shown in previous works [88,106], the majority-to-minority class ratio is high in real-world class imbalance problems. Inspired by this, we consider two different training sets: Case1 and Case2. For the training set of Case1, there are 300 samples for a class, and 1200 samples for each of other classes. For the training set of Case2, there are 150 samples for a class, and 1200 samples for each of other classes. It can be seen that the majority-to-minority class ratio of Case 2 is higher than that of Case 1. We use our multimodal conditional GAN or the multimodal GAN without the correlation loss to augment the unbalanced training set to make an augmented training set containing 2400 samples for each class, which is class-balanced. Then, the augmented training set is further used to train a DNN classifier. In both Case1 and Case2, we also perform experiments with other methods. Additionally, to compare with the class-balanced case, we report the classification performance of different methods on the training set with 1200 samples per class (for Ours (wo corr) or Ours, each class is augmented to 2400 samples). It is worth pointing out that on each dataset, the validation and test sets are still set as in Section 4.1, which means that they are still class-balanced. Under this setting, we report the classification accuracy of the test set on each dataset to evaluate the performance of our framework to cope with the class imbalance of the training data, as shown in

Table 7. Classification accuracy (%) of different methods when the training set is class-imbalanced on the eNTERFACE’05 dataset. Best results are shown in bold.

Method	Class Balance	Class Imbalance
		Case1	Case2
Baseline (A)	31.95	31.44	30.41
Baseline (V)	44.85	38.14	34.54
Baseline (A+V)	45.88	39.69	36.60
Attention Mechanism [97]	46.39	41.24	35.57
CCA [98]	45.88	39.18	36.08
Tensor Fusion [99]	46.91	40.72	37.11
Ours (wo corr)	48.45	43.30	41.75
Ours	$\mathbf{49}.\mathbf{48}$	$\mathbf{44}.\mathbf{33}$	$\mathbf{42}.\mathbf{78}$

,

Table 8. Classification accuracy (%) of different methods when the training set is class-imbalanced on the RAVDESS dataset. Best results are shown in bold.

Method	Class Balance	Class Imbalance
		Case1	Case2
Baseline (A)	39.88	37.57	36.99
Baseline (V)	54.35	51.45	50.29
Baseline (A+V)	59.53	54.34	53.75
Attention Mechanism [97]	61.27	55.49	52.60
CCA [98]	60.69	56.07	53.18
Tensor Fusion [99]	60.12	52.60	51.45
Ours (wo corr)	64.16	59.54	58.95
Ours	$\mathbf{65}.\mathbf{90}$	$\mathbf{61}.\mathbf{85}$	$\mathbf{60}.\mathbf{11}$

and

Table 9. Classification accuracy (%) of different methods when the training set is class-imbalanced on the CMEW dataset. Best results are shown in bold.

Method	Class Balance	Class Imbalance
		Case1	Case2
Baseline (A)	36.19	33.57	29.76
Baseline (V)	38.10	34.76	31.42
Baseline (A+V)	40.71	35.48	34.76
Attention Mechanism [97]	41.19	36.19	33.81
CCA [98]	41.43	36.10	33.10
Tensor Fusion [99]	40.00	35.24	32.86
Ours (wo corr)	44.05	39.05	37.62
Ours	$\mathbf{46}.\mathbf{19}$	$\mathbf{40}.\mathbf{95}$	$\mathbf{39}.\mathbf{04}$

.

We can observe that with the increase of the majority-to-minority class ratio, the classification accuracy of different methods decreases. However, compared with other methods, our approach achieves the highest classification performance in various settings of class imbalance, indicating that our framework can effectively deal with the problem of class imbalance. In addition, it can be found that compared with different baselines, the method of Ours (wo corr) can also improve the performance of emotion classification, but it is weaker than Ours, which indicates that our proposed correlation loss is useful in the scenario of class imbalance.

5. Conclusions

In this paper, we propose an efficient data augmentation framework with a multimodal conditional GAN for audio-visual emotion recognition. To be specific, our framework builds generators and discriminators for audio and visual modalities. Then, we use the category information as their shared input to make our multimodal conditional GAN generate new multimodal data of different categories. In addition, the correlation between the audio modality and the visual modality in the generated multimodal data is fully considered in our framework. Finally, we use the generated data to supplement the original training set for the emotion classification task. To the best of our knowledge, we are the first to propose an efficient multimodal condition GAN to augment the multimodal data for audio-visual emotion recognition.

A series of experiments on the datasets of eNTERFACE’05, RAVDESS, and CMEW show that compared with different baselines, our framework achieves the highest classification accuracy for audio-visual emotion recognition, even when the training data is scarce. In addition, experiments show that the data generated by our multimodal conditional GAN can improve the training speed of DNN-based emotion classifiers. Moreover, the results further point out that the size of the data generated using our multimodal conditional GAN should be set appropriately for data augmentation. Finally, we exploit our approach to cope with the problem of class imbalance. Experiments show that in this scenario, the classification performance of our approach is still significantly higher than that of different baselines.

Despite the progress of our framework, it may have the following limitations: (1) Our approach is used for audio-visual emotion recognition. It does not consider combining information from other modalities, such as text [107] and physiological signals [108,109], which also contribute to emotion recognition. (2) Our architecture focuses on designing a multimodal condition GAN for data augmentation. Previous works such as Attention Mechanism, CCA, and Tensor Fusion are not considered to be integrated in our framework. As shown in Section 4.4, these previous works can also perform emotion recognition to a certain extent. (3) The labels of all samples are assumed to be correctly annotated to train our multimodal architecture. However, in reality, the data collection may suffer from label noise [110,111,112]. To further validate the effectiveness of our approach, we will tackle the above limitations in the future. Firstly, we will generalize our architecture to utilize more modalities. Secondly, we will combine our approach with the above previous works to further improve the performance of our framework. Finally, we will consider coping with label noise in our architecture.