Effect of Impact and Bearing Parameters on Bird Strike with Aero-Engine Fan Blades

Abstract

Bird strikes are one of the most dangerous incidents occurring to aircraft engines and can inflict heavy casualties and economic losses. In this study, a smoothed particle hydrodynamics (SPH) mallard bird model has been used to simulate bird impact to rotary aero-engine fan blades. The simulations were performed using the finite element method (FEM) by means of LS-DYNA. The reliability of the material model and numerical method was verified by comparing the numerical results with Wilbeck’s experimental results. The effects of impact and bearing parameters, including bird impact location, bird impact orientation, initial bird velocity, fan rotational speed, stiffness of the bearing, and the damping of the bearing on the bird impact to aero-engine fan blade are studied and discussed. The results show that both the impact location and bird orientation have significant effects on the bird strike results. Bird impact to blade roots is the most dangerous scenario causing the impact force to reach 390 kN. The most dangerous orientation is the case where the bird’s head is tilted 45° horizontally, which leads to huge fan kinetic energy loss as high as 64.73 kJ. The bird’s initial velocity affects blade deformations. The von Mises stress during the bird strike process can reach 1238 MPa for an initial bird velocity of 225 m/s. The fan’s rotational speed and the bearing stiffness affect the rotor stability significantly. The value of bearing damping has little effect on the bird strike process. This paper presents a procedure for evaluating the strength of fan blades against bird strike in the design stage.

1. Introduction

With increasing developments in commercial aviation, the number of bird strikes is also increasing, and the hazards they pose are becoming more severe. According to the report of the Federal Aviation Administration (FAA), bird strikes have resulted in 363 human injuries and fatalities between the years 1990 and 2020. The economic loss due to bird strikes is also drastic. During the year 2020 alone, a USD (United States dollar) 124 million loss was caused by bird strikes directly or indirectly. The aero-space engine is the most frequently damaged component by bird strikes, accounting for 26% of all damaged components [1,2].

The earliest method of studying bird strikes was the experimental tests, which provided a direct method to assess the bird strike severity [3]. However, it is time-consuming and costly to design and carry-out bird strike experiments [4]. The development of computer technology and improvement of numerical simulation methods after the 2000s have provided a new approach for bird strike studies. Combined experimental and numerical approaches can provide feasible and cost-effective outcomes for bird strike studies [5,6].

Simple geometries such as straight-ended cylinders, spheres, ellipsoids, and hemispherical-ended cylinders are commonly used as bird models in simulations. The noted substitute bird models have been implemented in many studies for many years and have yielded a lot of valuable results [7,8,9,10]. However, as compared to traditional bird models, a realistic bird model provides results that are more consistent with experiments [11,12,13,14]. The Lagrangian, Eulerian, arbitrary Lagrangian–Eulerian (ALE), and smoothed particles hydrodynamics (SPH) methods are the most frequently used techniques to simulate bird strike phenomenon [15,16,17]. Due to the large deformation of the bird during a bird strike event and the complexity of the calculations, the SPH method is widely employed in bird strike simulations [18].

Recently, the parametric study of bird strikes has been increasing. Bird impact to rigid plate scenarios are usually implemented to evaluate the efficiency of different bird model geometries [11,19]. To further understand the influence of the fan structure, the impact target model needs to be changed from a flat plate to a real engine. The impact characteristics of the traditional model on the fan have been obtained [20,21]. In actual bird strike accidents, the orientation of the bird concerning the engine is random. The same holds for impact location. As a result, the effect of the impact location and bird orientation has been studied numerically [22,23,24]. However, due to the limitations of traditional models, such as the sphere model being identical in all orientations, the use of realistic bird models has been increasing recently [19]. The effect of bearing components is also often neglected in fan models impacted by birds. Bird strike impacts can cause transient shocks, and the resulting unbalanced forces can have an impact on the fan [25]. The introduction of bearings into the model is very necessary for accurate bird strike simulation. Furthermore, the mass and flight velocity of the bird also affect the bird strike results [26]. Although many bird strike scenarios have been studied previously, the parametric study of a real bird model striking a rotating fan with bearings has not been investigated before.

In this study, numerical simulations are carried out to study the effect of different impact and bearing parameters on the bird striking aero-engine fan blade process. A realistic bird model based on the SPH method as well as a rotary fan with the bearing is constructed through the finite element (FE) method. The influence of six parameters, including bird impact location, bird impact orientation, bird impact velocity, fan rotational speed, damping and stiffness of the bearing on the bird impact process, is investigated. The contact force, bearing force, kinetic energy change of the bird, von Mises stresses of the blade roots and leading edges are compared and discussed to understand the specific effects of each parameter.

2. Bird and Fan Modeling

2.1. Bird Geometry and Material Modeling

To better simulate the real situation of bird strikes, a real bird was scanned using computed tomography (CT) to obtain the body geometry. In a recent report from FAA [1], during 1990–2020, 1191 mallard strikes were reported in total, accounting for 20% of waterfowl strikes. Huge economic losses have been caused by mallards, so the mallard bird model was chosen for this research. An anesthetized mallard was passed through a CT scanning device to obtain the mallard three-dimensional (3D) geometry. The mallard was 40 cm in length and 45 cm in wingspan weighing 820 g. The SPH method was adopted for bird body modeling based on the mallard 3D model. The model used in the numerical simulation consisted of 41,685 SPH elements each having a mass of 0.0191 g. The SPH bird model is shown in Figure 1.

According to previous studies [27], birds behave similarly to fluids during high-speed impacts where the inhomogeneity and nonuniformity due to other components such as feathers and bones can be neglected. Based on this assumption that all parts of the bird body exhibit the same mechanical behavior, a single material model can effectively predict the impact behavior of the bird body under different conditions [18]. To simulate this material behavior of the bird body, a material model accompanied with an equation of states (EOS) is usually used. The null material model is often used to simulate fluids in high-velocity conditions. The strain of the fluid could be related to its stress by:

$${\sigma }_{ij}=-P{\delta }_{ij}+2\rho \gamma {\dot{e}}_{ij}$$

(1)

where ${\sigma }_{ij}$ is the viscous stress, $P$ is the pressure on the fluid, ${\delta }_{ij}$ is the identity tensor, $\rho$ is the fluid density, $\gamma$ is the dynamic viscosity coefficient, and ${\dot{e}}_{ij}$ is the rate-of-deformation tensor. The material properties of the mallard bird model are listed in

Table 1. Null material parameters for the bird [18].

Parameter	Value
Density	$938 \mathrm{kg}/{\mathrm{m}}^3$
Relative volumetric strain for erosion in tension	1
Relative volumetric strain for erosion in compression	0.8

.

The null material model must be used with an EOS. The EOS is linked to the material’s physical state variables and is often applied in interpreting the properties of fluids and solids. According to Reference [28], the Gruneisen EOS and the Tillosten EOS are mainly used in numerical simulation studies of high-speed collision problems. The Gruneisen EOS was implemented in this study. There are two forms of the Gruneisen equation, corresponding to two different states of compression and expansion. Pressure for materials in compression is expressed as:

$$p=\frac{{\rho }_0{C}^2\mu \left[1+(1-\frac{{\gamma }_0}{2})\mu -\frac{a}{2}{\mu }^2\right]}{{\left[1-(S_1-1)\mu -S_2\frac{{\mu }^2}{\mu +1}-S_3\frac{{\mu }^3}{{(\mu +1)}^2}\right]}^2}+({\gamma }_0+a\mu )E$$

(2)

and in tension is given by:

$$p={\rho }_0{C}^2\mu +({\gamma }_0+a\mu )E$$

(3)

where C is the intercept of the v_s − v_p curve; S₁, S₂, and S₃ are the unitless slope coefficients; ${\gamma }_0$ is the Gruneisen constant; a is the unitless first-order correction of ${\gamma }_0$. The parameter $\mu$ is expressed by:

$$\mu =\frac{\rho }{{\rho }_0}-1$$

(4)

where $\rho$ and ${\rho }_0$ are density of the material and the reference density, respectively. The parameters used in this study are listed in

Table 2. Parameters used in Gruneisen EOS for the mallard bird model [11].

Parameter	Value
C	1480 m/s
S1	1.92
S2	0
S3	0
${\gamma }_0$	0.1
a	0

.

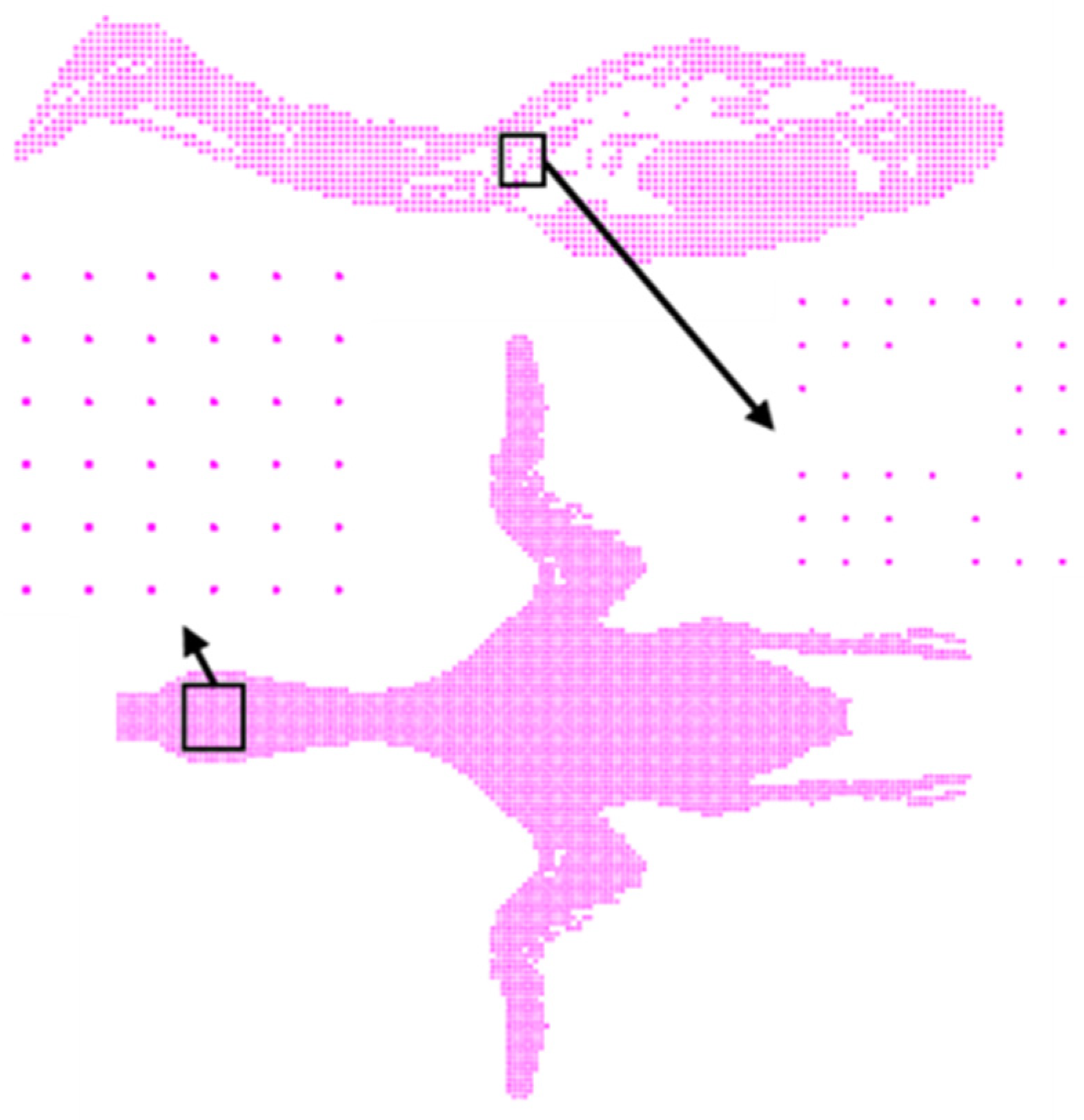
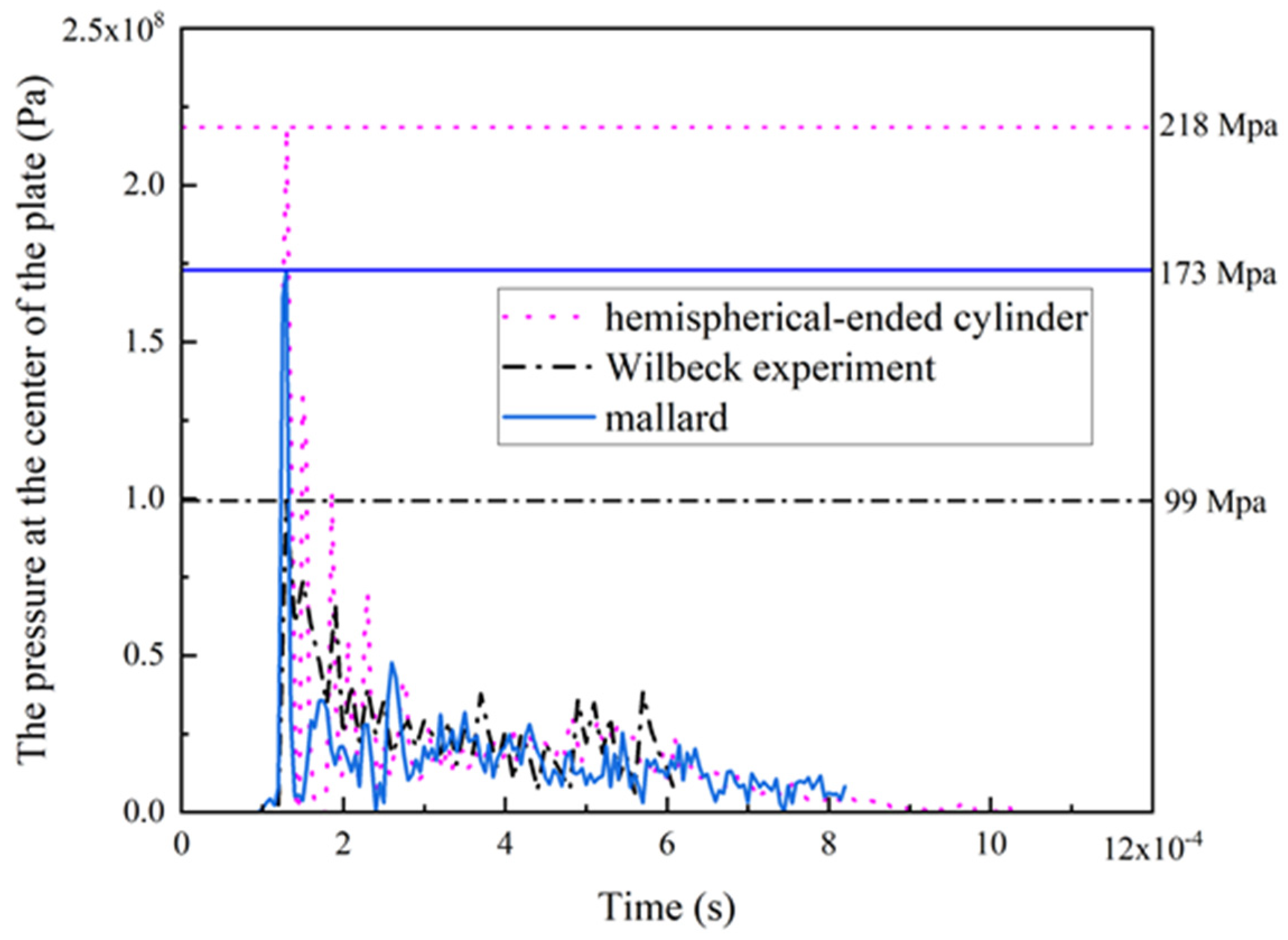
2.2. Model Validation

The model was verified by comparing the numerical results with Wilbeck’s experimental data [29], which used a compressed air cannon device to shoot a bird body with a mass of 1 kg to a rigid target plate with a speed of 253 m/s. In the LS-DYNA, a mallard and a hemispherical-ended cylinder bird model were impacted onto a rigid target with an initial velocity of 253 m/s. A shell unit was positioned at the center of impact, representing a sensor to monitor the pressure variations, as shown in Figure 2.

It can be seen that the pressure variations of the mallard model are closer to that of Wilbeck’s experiment as compared to the bird model with traditional geometry. The peak pressure recorded from the mallard model was 172 MPa, while it was 218 MPa for the hemispherical-ended cylinder model. The initial peak pressure of the experiment was 99 MPa, and it was used as a reference to calculate the error for the two other models. It was found out that the discrepancy between the peak pressure of experimental test and the hemispherical-ended model was 120%, while the error for the mallard model was 73%, which showed a great improvement. Comparing the noted values with the pressure measured by the experiment, the mallard model has improved the accuracy of the impact pressure acquisition. Therefore, the mallard model can better reflect the real bird body impact process.

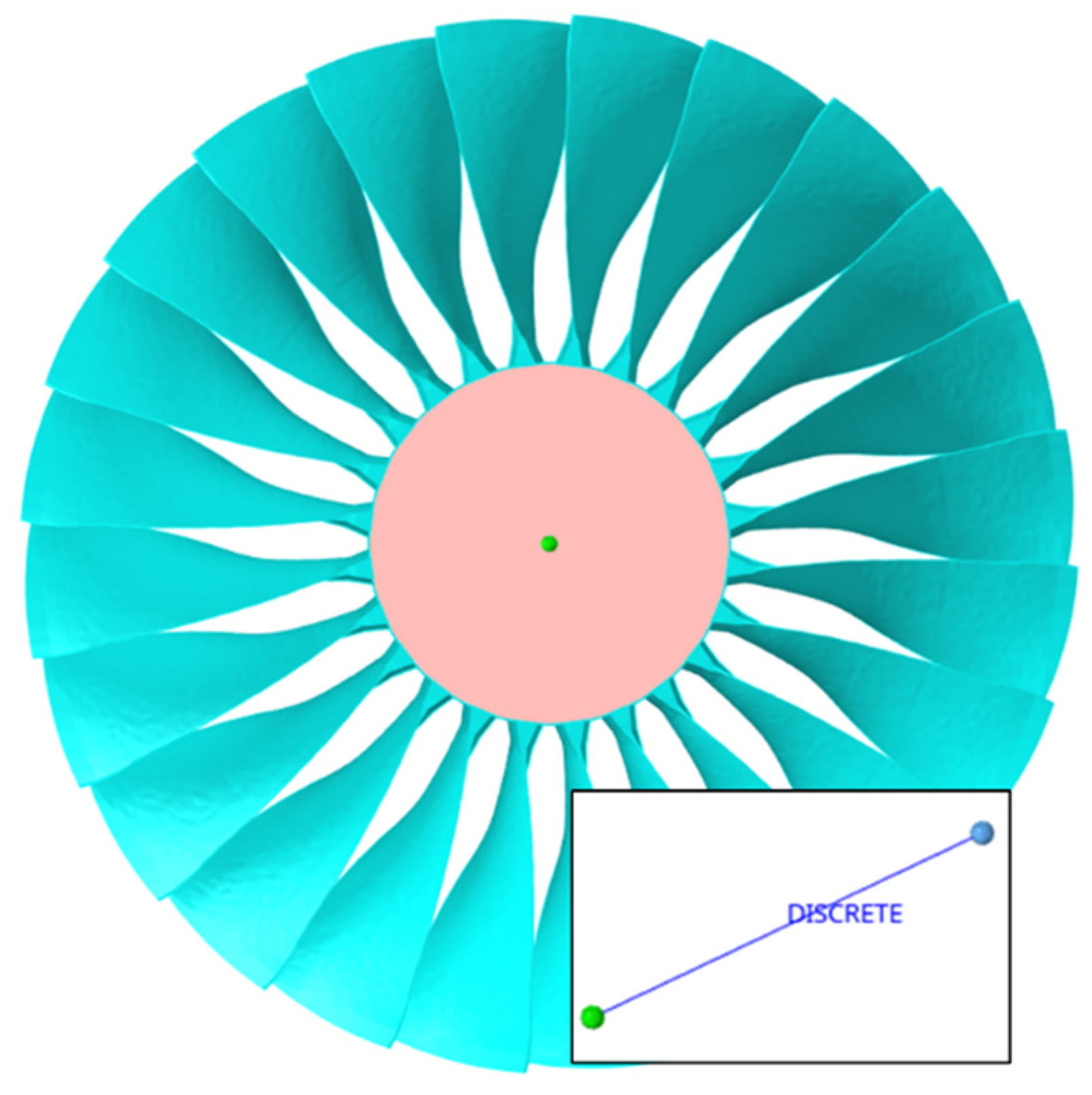
2.3. Geometric Model and Meshing

The bird strike often occurs at the fan of a turbofan engine [1]. To simulate this situation, a real aero-engine fan was used as the impact target in this paper. The geometry of all parts of the fan was extracted from real aircraft engines, and they were discretized, as can be seen in Figure 3. The fan was composed of 24 equally spaced (15°) narrow chord blades connected to the hub. The form of connection between the blades and the disk was ignored, and they were considered as a single body. The initial twist angle of the blades was 61.3° with a measuring height of 603.2 mm. In some studies [9,30], only a few blades were considered for numerical simulation to increase the computational speed. However, because the rotation of the fan and the debris generated by the impact can affect most of the blades, this paper has considered the whole fan for the numerical simulation. Due to the focus of this study on the impact of the blades, the structure of the wheel was simplified. The fan was discretized using the Lagrangian method. Although the shell element helps to improve the computational speed, as the blades did not have uniform thicknesses and they had obvious vibrational characteristics in the thickness direction, this research used solid elements to discretize the blades. The fan was composed of 1,520,213 elements, each blade containing 54,086 elements: 4 elements in thickness, 194 elements in length, and 104 elements in the width directions. The type of finite element is a hexahedral solid element.

When a bird strike occurs, the aero-engine fan blades deform under the high-velocity impact. The blades may even fail if the situation is detrimental. To simulate and reproduce the impact phenomenon and truly reflect the relationship between impact loads and structural response, the Johnson–Cook material model was chosen to simulate the material behavior of the fan. In the Johnson–Cook material model, the flow stress is expressed by [31]:

$${\sigma }_y=(A+B{\overline{\epsilon }}^{p^n})(1+c\ln {\dot{\epsilon }}^{*})(1-T^{*m})$$

(5)

where $A$, $B$, $n$, $c$ and $m$ are the constants of the material; ${\overline{\epsilon }}^p$ is the effective plastic strain; ${\dot{\epsilon }}^{*}$ is a unitless rate which can be obtained by dividing the quasi-static threshold rate by effective plastic strain rate; $T^{*}=\frac{T-T_r}{T_m-T_r}$ is the homologous temperature, $T$ is the current temperature, $T_m$ is the melt temperature of the material, and $T_r$ is the room temperature.

Since the Johnson–Cook model simulates the fracture process by calculating the failure of elements, it is necessary to obtain its strain at failure, which is defined as follows [31]:

$${\epsilon }^f=[D_1+D_2\exp D_3{\sigma }^{*}][1+D_4\ln {\dot{\epsilon }}^{*}][1+D_5{T}^{*}]$$

(6)

where ${\epsilon }^f$ is the strain at fracture; $D_1, D_2, D_3, D_4,D_5$ are the failure parameters depending on the material; and ${\sigma }^{*}$ is the stress triaxiality.

Since the stress state, strain rate, and temperature are changing during the failure process, the failure of the material is determined by the following equation:

$$D=\sum \frac{\Delta {\overline{\epsilon }}^p}{{\epsilon }^f}$$

(7)

where D is the damage parameter and $\Delta {\overline{\epsilon }}^p$ is incremental changes in the effective plastic strain. The $\sum$ is a summation notation. When the value of D reaches 1, the material can be considered as failed. Titanium alloy Ti-6Al-4V material properties were assigned to aero-engine fan blades (

Table 3. Johnson–Cook material parameters for Ti-6Al-4V used in the simulation [32].

Parameter	Symbol	Value
Density	$\rho$	$4420 \mathrm{kg}/{\mathrm{m}}^3$
Shear modulus	$G$	41.9 GPa
Yield stress	$A$	1098 MPa
Strain hardening modulus	$B$	1092 MPa
Strain hardening exponent	$n$	0.93
Strain rate dependence coefficient	$c$	0.014
Softening exponent	$m$	1.1
Melting temperature	$T_M$	1878 K
Room temperature	$T_R$	293 K
Specific heat	$C_P$	612 J/kg·K
Failure parameters	$D_1$	0.112
	$D_2$	0.123
	$D_3$	0.48
	$D_4$	0.014
	$D_5$	3.87

).

In this paper, solid elements are used in the simulation, so the Johnson–Cook material model should be accompanied by an EOS [19]. The Gruneisen EOS, which was introduced above, also works for this model. The parameters are given in

Table 4. Parameters used in Gruneisen EOS for Ti-6Al-4V [9].

Parameter	Value
$C$	5130 m/s
$S_1$	1.028
$S_2$	0
$S_3$	0
${\gamma }_0$	1.23
$a$	0.17

.

2.4. The Elastic Support

In previous studies [19,33], bearings were often ignored in the modeling of the fan, and fixed constraints were set at the center of the hub. This resulted in the fan not moving as a whole upon impact, and only the deformation of the blades was simulated. However, in a real-life scenario, after the fan is hit by a bird, there will be radial movement in the hub, after which the vibration is suppressed due to the presence of bearings. In extreme cases, the bearing might be destroyed if the vibration is very severe. As a result, it is beneficial to add bearings to the fan model and study the effect of bearings on the bird strike damage. The bearings of the aero-engine are of rolling type, which can be considered as a stiffness-damping system. In this paper, two nodes are set at the center of the hub, one is fixed at the center, and the other is connected to all the nodes on the hub to simulate the motion of the fan. Two discrete elements (SECTION_DISCRETE) are used to connect the two noted nodes, and then stiffness and damping are assigned to these two discrete elements. The keywords MAT_SPRING and MAT_DAMPER determine whether the elements are of spring or damping type, see Figure 4.

3. Simulation of Bird Striking on a Rotating Fan

3.1. Pre-Stress of Fan Blades

To analyze the results of bird strike engines, it is necessary to perform a pre-stress analysis of the fan prior to the impact analysis [22]. The pre-stress analysis of the fan can determine the stress distribution and deformation of the blade due to centrifugal force, which helps to obtain more accurate results from bird strike simulation.

The analysis of pre-stress is performed using the method of dynamic relaxation, and the explicit–implicit analysis is carried out in LS-DYNA for the fan speed of 600 rad/s (direction: counterclockwise). The pre-stress of the blade can be calculated after adding the speed condition, see Figure 5. The maximum stress of the blades was about 1000 MPa, lower than the set yield strength. Therefore, the operation of the engine was normal before the bird strike occurred. After the pre-stress analysis of the fan, the bird impact onto the rotating fan can be simulated.

3.2. Contact and Boundary Conditions

The good handling of friction and impact problems at the interacting surfaces is one of the important advantages of LS-DYNA, and the accuracy of the simulation is determined by the definition of a contact interface. As a result, the selection of a suitable contact algorithm is crucial in modeling the interaction of the SPH particles and the FE elements accurately. The commonly used method for contact and sliding interface processing is the penalty method. To improve the accuracy of simulating the phenomenon of the blade being damaged during the impact, the contact type CONTACT_ERODING_NODES_TO_SURFACE was used in this research.

The key bird ingestion parameters, including bird strike location, bird strike orientation, the rotational speed of the fan, and initial bird velocity, need to be based on realistic aero-engine operating conditions. The termination time was set to 6 ms, as at this time, the impact process is completed, and the obtained data can reflect the influence of bird impact. The time interval for outputs was set to 0.06 ms. The initial impact location of the bird was 1/2 of the blade height, the initial impact orientation of the bird was the head striking the fan, the rotational speed of the fan was set to 600 rad/s, the bird’s initial velocity was set to 253 m/s. The bird’s initial velocity was the initial relative speed of the bird and the engine, i.e., the ingestion speed. The elastic support parameters: the stiffness and the damping values were set to ${10}^8$ N/m and 500 Ns/m, respectively.

To study the effect of different impact parameters on the bird strike, different case scenarios of the above-mentioned parameters were chosen for simulation using the control variable method. The effect of bearings in bird strikes was also studied by giving different values of stiffness and damping to the elastic bearing.

Three impact locations on the blade were chosen. Since the height of the bird is about 1/6 of the blade height, impact points were chosen to be at 1/6, 3/6 and 5/6 of the blade height, representing the root, the middle, and the tip locations of the blade, respectively (Figure 6).

Figure 7 shows the bird striking on the rotating fan from seven different impact orientations. Figure 7a shows the initial rotation of the bird model for 90°, 180°, and 270° around the Y axis. Figure 7b demonstrates the initial rotation of the bird model for 45°, 90°, and 135° around the Z axis. The seven considered impact orientations represent the head-, abdomen-, tail-, back-, and wing-first impacts.

Referring to other examples [9,19,22], the rotational speed of the fan was set to three typical stage speeds of 600, 395, and 88 rad/s, corresponding to different operating phases. The ingestion speed of the bird corresponds to the experimental settings of Wilbeck [29], which was chosen to be 253, 225 and 118 m/s. According to the actual aero-engine rolling bearing stiffness and damping value ranges, the stiffness was set to ${10}^8$, $5\times {10}^7$ and ${10}^7$ N/m values, and the damping was set to 500, 5000, and 10,000 Ns/m values. Different case studies are listed in

Table 5. Different case studies considered for studying different parameters in the bird strike simulations.

Case	Impact Location	Impact Orientation	Bird Initial Velocity (m/s)	Rotational Speed of the Engine (rad/s)	Support Stiffness (N/m)	Support Damping (Ns/m)
G	Middle	0°	253	600	${10}^8$	500
L1	Root	0°	253	600	${10}^8$	500
L2	Tip	0°	253	600	${10}^8$	500
O1	Middle	Y-90°	253	600	${10}^8$	500
O2	Middle	Y-180°	253	600	${10}^8$	500
O3	Middle	Y-270°	253	600	${10}^8$	500
O4	Middle	Z-45°	253	600	${10}^8$	500
O5	Middle	Z-90°	253	600	${10}^8$	500
O6	Middle	Z-135°	253	600	${10}^8$	500
V1	Middle	0°	225	600	${10}^8$	500
V2	Middle	0°	116	600	${10}^8$	500
R1	Middle	0°	253	88	${10}^8$	500
R2	Middle	0°	253	395	${10}^8$	500
S1	Middle	0°	253	600	$5\times {10}^7$	500
S2	Middle	0°	253	600	${10}^7$	500
D1	Middle	0°	253	600	${10}^8$	5000
D2	Middle	0°	253	600	${10}^8$	10,000

. The letter G stands for the control group, and letters L, O, V, R, S and D stand for impact location, impact orientation, initial bird velocity, rotational speed, support stiffness and support damping, respectively. The simulations for different bird collision parameter settings were performed using LS-DYNA.

4. Results and Discussion

The effect of the bird strike fan was analyzed according to the key impact parameters proposed in Federal Aviation Regulation Section 33 (FAR–33) [34]. The selected parameters are used to reflect the blade damage during the engine airworthiness verification test and can be used to determine the severity of the bird strike.

The stress at the blade root is a common parameter to study. According to the maximum distortion energy theory [35], excessive von Mises stress in the blades leads to torsional deformation and even fracture of the blade. At the beginning of bird collision, the deformation of the contact point is the largest, changing the aerodynamic shape of the blade and making the rotor motion unstable. The relative displacement of the blade tip can be sufficiently large to cause blade-casing rubbing, triggering secondary failure. The rotating blade has kinetic energy. In the bird strike process, the bird body obtains kinetic energy from the blade, which can explain the loss of blade kinetic energy. The more kinetic energy the blade loses, the more serious the damage of the blade is [36]. The contact force between the bird and the blade should not be neglected, as this force can reflect the force on the fan in the entire impact process [19].

In summary, this paper investigates the parameters of stress on the blade root, the contact force, the bearing force, and the kinetic energy of the bird body as the main indicators of bird strike transient response.

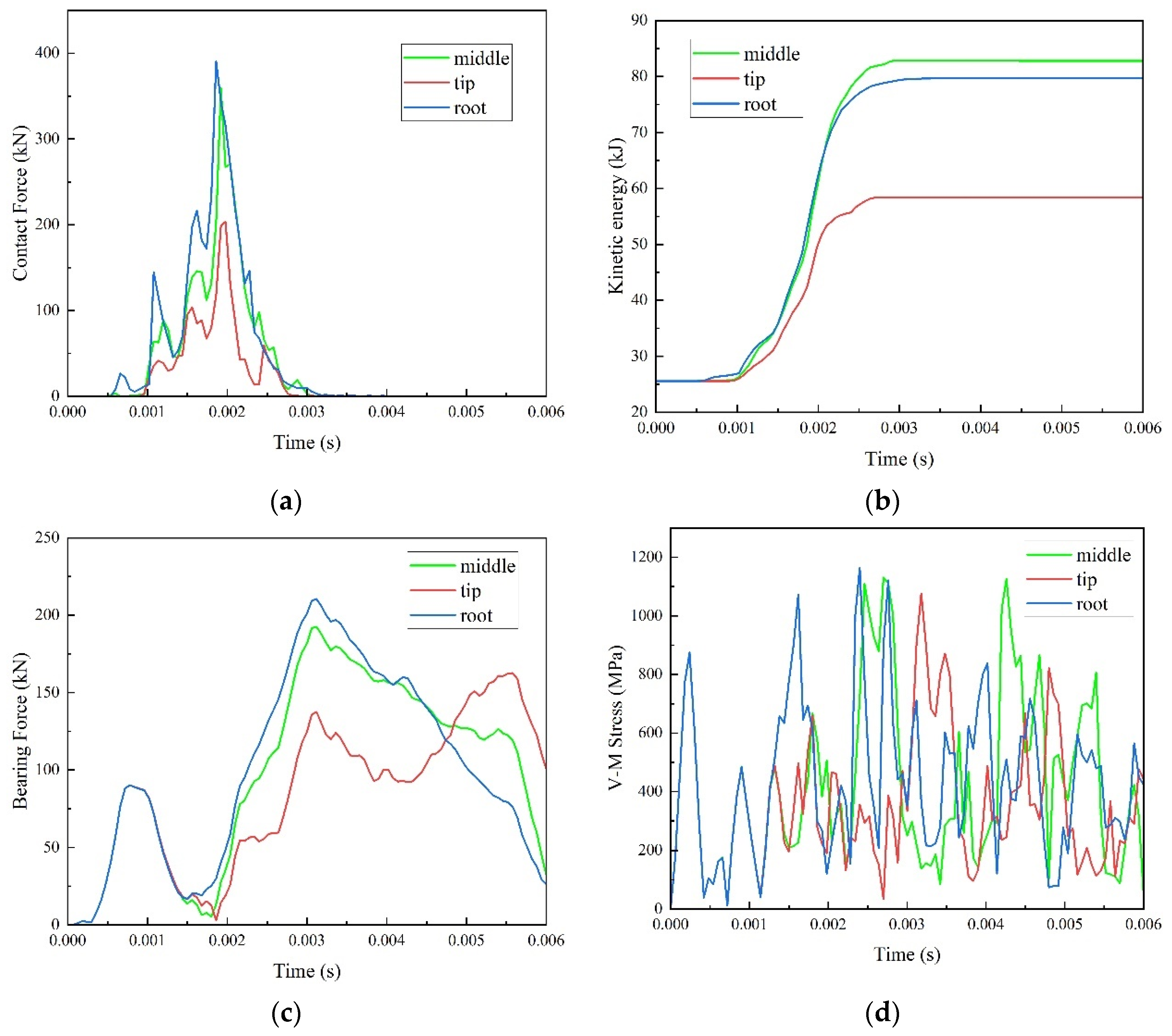
4.1. The Influence of Bird Impact Location

The impact-location analysis comprised three locations (Cases G, L1, L2) along the fan length to study the relationship between the damage of blades and bird impact location. From Figure 8a, with the change of impact location, the maximum value of the bird’s impact force also changes. The maximum bird impact force is recorded for the case of the bird impacting the blade root (390 kN), followed by the case of the bird impacting the middle of the blade. The maximum impact force recorded for the case of the bird impacting the blade tip is much lower being about half of the two other cases. This is due to the twist angle of the blade and increases in its width as the height increases, thus causing the reduction in the bird’s impact force.

It can also be observed from Figure 8b that the kinetic energy obtained by the bird impacting the root and the middle of the blade is almost twice that obtained when the bird hits the blade tip. The maximum kinetic energy of the bird was 83 kJ when the fan lost the maximum energy. It can be seen in Figure 8c that before the bird comes into contact with the blade, the bearing force is the same for all three cases. After the bird strike, the change in the bearing forces has a lag compared to the instances the bird-blade contact start. This is due to fact that it takes some time for the force to be transferred from the blade to the bearing unit, after which it quickly rises to its maximum value. When striking the blade root, the bearing force reaches a peak value of 211 kN. Due to the different twist angles along the blade height direction, there is a large bird block impacting the blade tip at 0.0055 s in the case L2, thus generating a peak impact force.

The comparison of blade-root von Mises stress is shown in Figure 8d. Bird impact does not create a big difference in the value of von Mises stress at different impact locations. The maximum stress recorded was 1164 MPa and it was for the case of a bird impacting the blade root. When the stress exceeds the yield stress, the blade deforms and fails, which makes the whole system prone to danger. The response of the fan heavily depends on the impact location, and the closer to the root, the greater damage the blade undergoes.

Vignjevic et al. studied the effect of impact location along the length of the blade and found out that the bird strike location has a considerable effect on the blade response [9] due to the change in the blade pitch along the height. This was similar to our conclusion, and based on this, we proposed that the most dangerous impact location was the blade root.

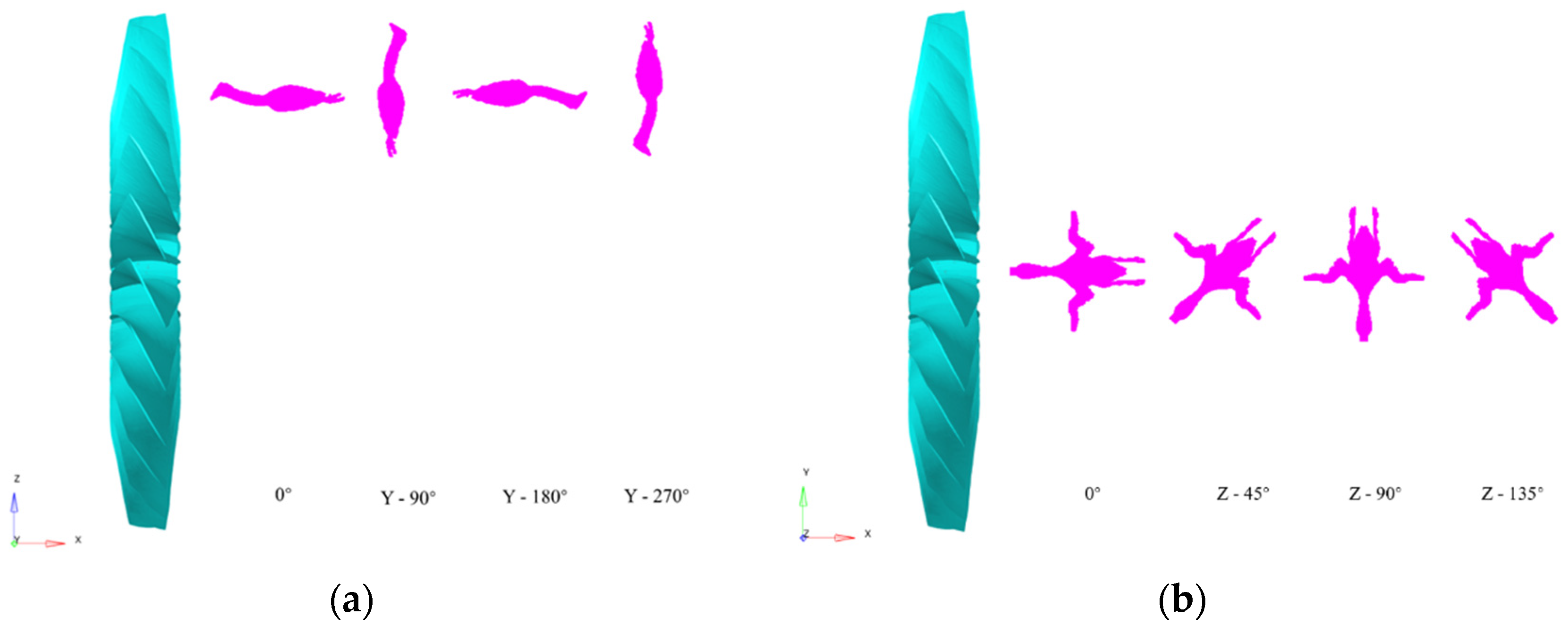
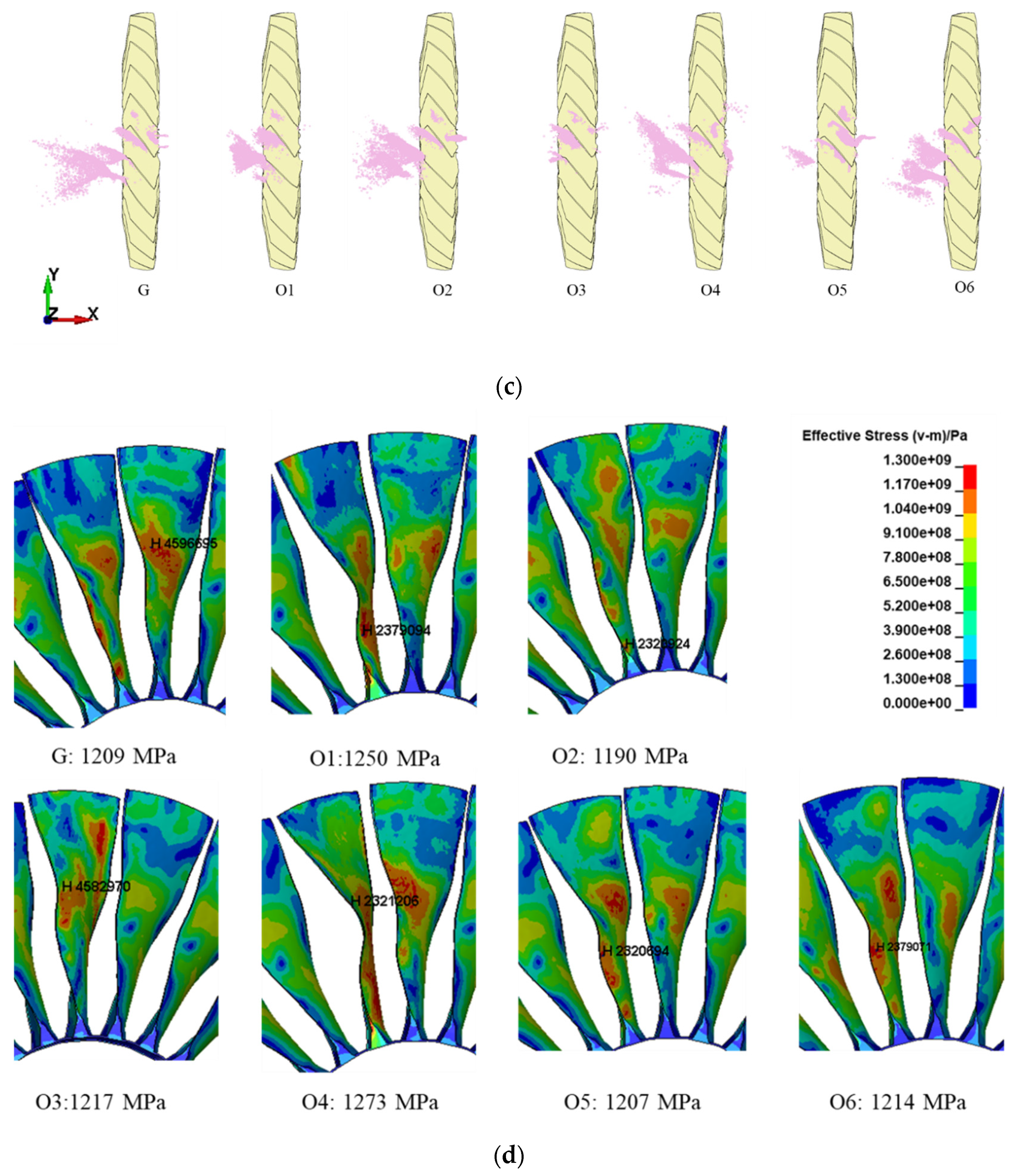
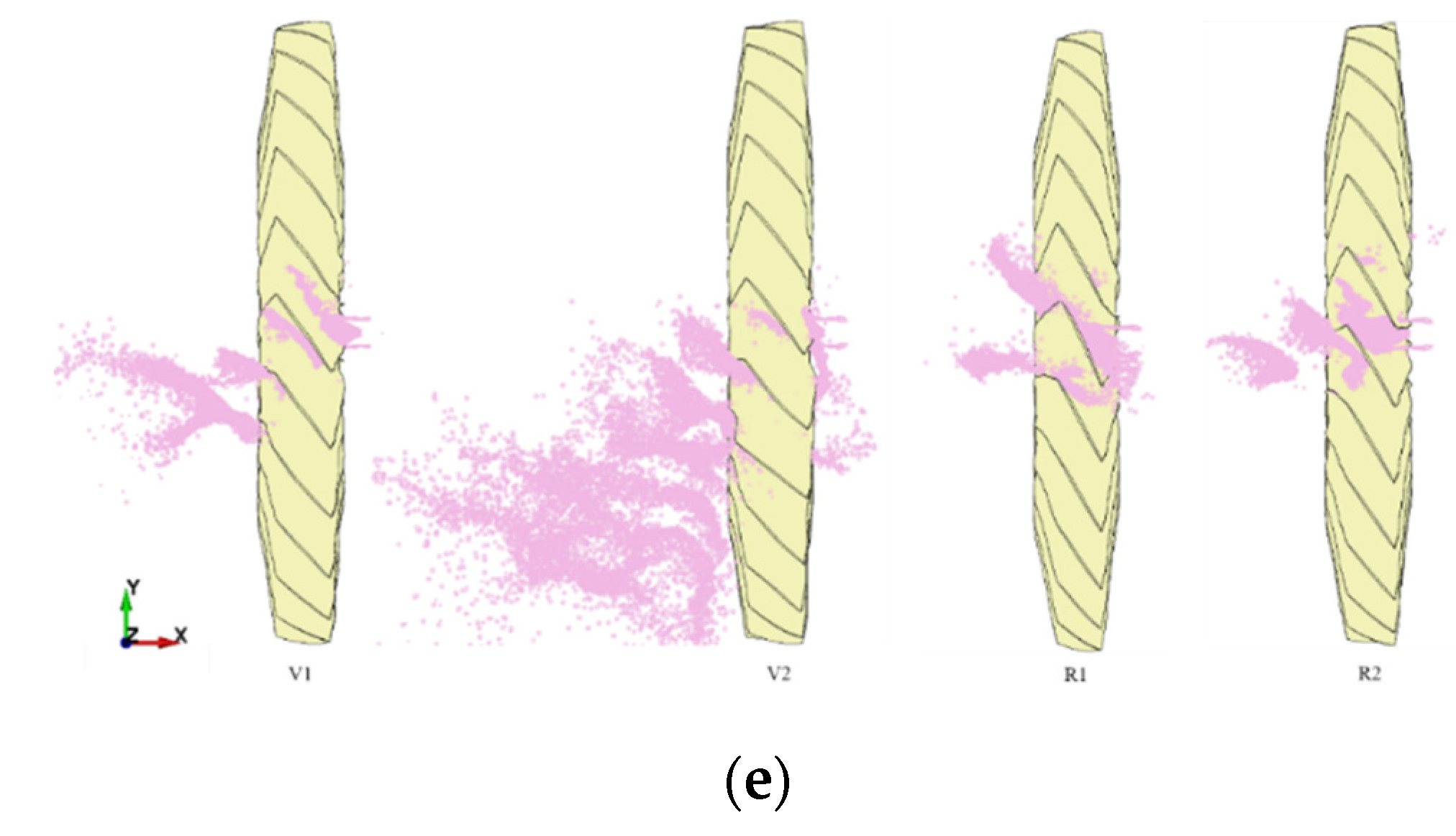
4.2. The Influence of Bird Impact Orientation

Similarly to impact location, it was discovered that bird impact orientation has a significant influence on the response of the fan blades.

Table 6. The change in the kinetic energy of the bird for different bird impact orientations.

Case	G	O1	O2	O3	O4	O5	O6
Initial bird kinetic energy (kJ)	25.59	25.59	25.59	25.59	25.59	25.59	25.59
End bird kinetic energy (kJ)	82.75	82.71	75.53	76.12	90.32	83.79	83.22
Kinetic energy gain (kJ)	57.16	57.12	49.94	50.53	64.73	58.20	57.63

lists the change in the kinetic energy of the bird when impacting from seven different orientations. The most kinetic energy is obtained for the case of O4, reaching 64.73 kJ, while the least kinetic energy is obtained for the case of O2, 49.94 kJ. When the bird strikes the fan from different orientations, the bird is cut into different sizes of blocks, which have different numbers and masses, and strikes the blades in different forms.

Figure 9a,b demonstrates the time variations of the bird’s contact force and bearing force for different impact orientations. The peak forces of cases G, O1, O2, O3, O4, O5 and O6 are 359, 449, 277, 496, 375, 387 and 263 kN. The highest peak impact forces belong to the cases of O3, O1, and O5, as in the noted cases, the bird blocks have the highest masses.

The difference between bearing forces is not significant for different orientations. The maximum bearing forces are 193, 210, 182, 17, 215, 198, and 200 kN, respectively. The trend of variation of bearing forces with time is very similar for all the cases, and the bearing is subjected to the greatest impact in the case of O4.

The distribution of von Mises stress of the blade at t = 2.04 ms for all cases is shown in Figure 9d. As it can be seen, the maximum stress values are greater than the yield stress of the material, which causes the blade to undergo plastic deformation. The maximum blade deformation is visible in the case of O4, which can be attributed to its stress level being the highest among all the cases. Observing the stress distribution in all the cases leads to a similar conclusion. The locations with the highest stress level are usually located at the leading edge or at the root of the blade, which can be considered as the places under the highest chance of failure.

In summary, the bird strike responses of blades are significantly affected by the impact orientations. The fan is more susceptible in the case of O4, while the bird body is cut into large blocks, leading to the production of high impact force and harm.

Zhang and Fei’s simulations showed that impact orientation has a significant influence on the impact force, impact duration, and kinetic energy transfer between the bird and fan [19]. The authors stated that striking from the bottom side results in the highest peak force. This is different from our conclusion. It must be stated that the orientation which generated the maximum impact force in our study was not considered in Zhang and Fei’s study. Nonetheless, for the orientation that was investigated in both studies, the conclusions were similar. Since more impact attitudes were considered in this study, some additional conclusions were made.

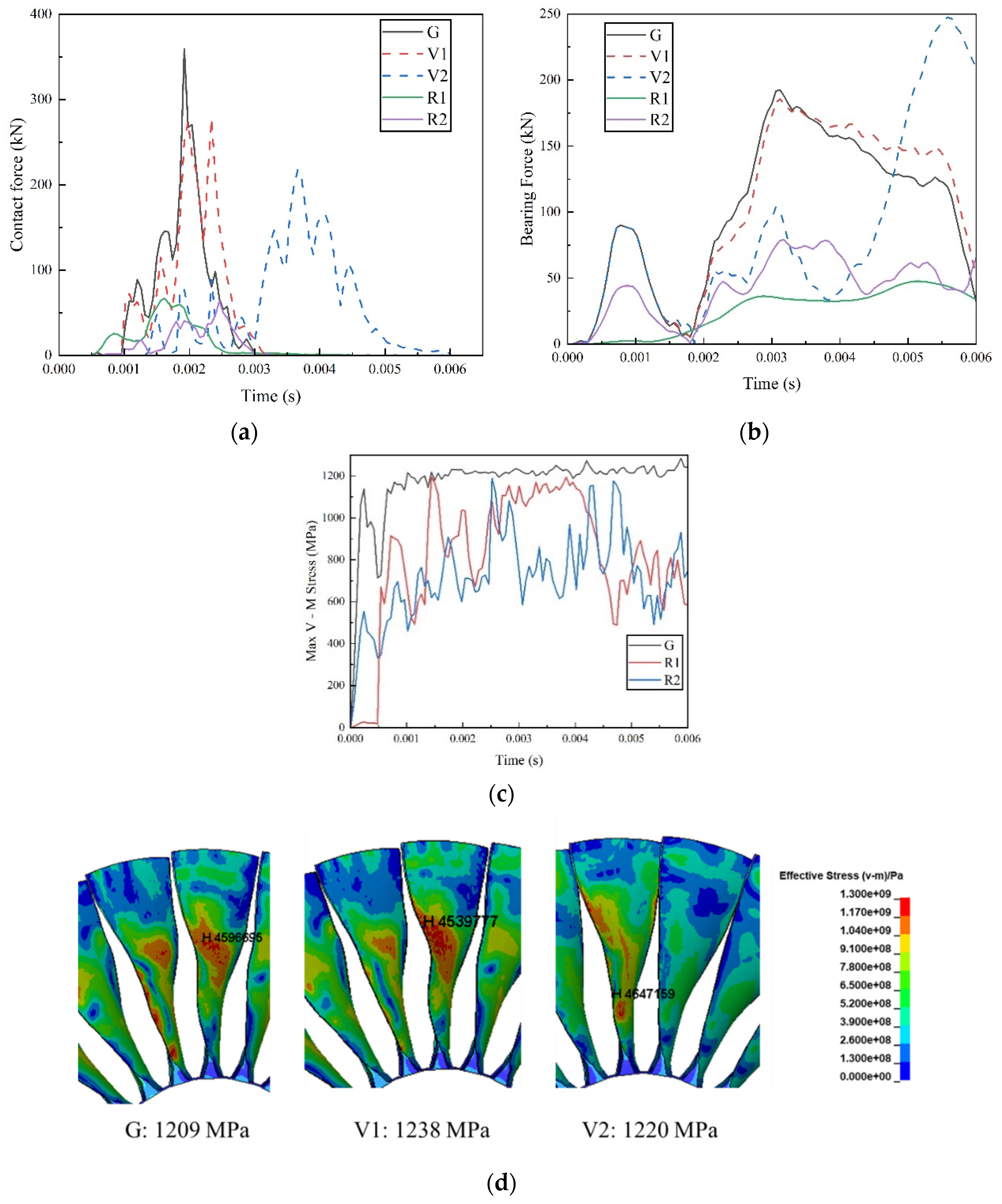
4.3. Bird Initial Velocity and Fan Rotational Speed Influence

The influence of the bird’s initial velocity (three values considered in Welbeck’s experiment) and the fan’s rotational speed (three typical values) on bird strikes was also investigated (Figure 10). According to the curve of bird impact force variation, the peak values of the bird’s impact force decrease with the decrease in the initial velocity (359, 278 and 218 kN for 253, 225, and 116 m/s). The difference in flight velocity leads to different contact duration with the blades as well as different sizes of cut bird blocks, see Figure 10e. The peak force of cases V1 (i.e., 225 m/s) and V2 (i.e., 116 m/s) occur later in the contact force curve as compared to case G (i.e., 253 m/s), and they also have a higher number of peaks (Figure 10a).

Figure 10b shows that decreasing the bird velocity from 253 to 225 m/s has little effect on bearing force. However, reducing the bird’s initial velocity to 116 m/s has a significant effect on the recorded bearing force due to the differences it causes in the number of bird blocks. The case of V2 (i.e., 116 m/s) includes an additional big block of bird impacting the fan at t = 5.5 ms, resulting in a large bearing force of 247 kN, which can easily cause damage to the bearing system. As it can be seen in Figure 10d, there is not much difference in the maximum level of von Mises stress for different initial bird velocities. However, different numbers and sizes of bird blocks have led to different blade deformations.

Comparing the magnitude of bird contact force at the same initial bird velocity but at different fan rotational speeds shows that decreasing the rotational speed of the fan decreases the impact force. The maximum impact force of cases G, R1 and R2 are 359, 66.9 and 63.7 kN, respectively. As compared to the effect of a decrease in the bird’s initial velocity, a decrease in rotational speed has a greater effect on the value of impact force. It can be seen in Figure 10b,c that decreasing the rotational speed has a significant reducing effect on the bearing forces (90.1, 44.1, and 13.9 kN for rotational speeds of 600, 395, and 88 rad/s) and the stress levels (1140, 553, and 281 MPa for rotational speeds of 600, 395, and 88 rad/s). The maximum stress of cases G, R1, R2 were similar after the bird strike, reaching 1280, 1190 and 1191 MPa, beyond the yield stress of the blade. In Figure 10d,e, the von Mises stress maximums are close at different initial bird velocities, but the extents of blade damage and bird deformations are different, the red area of stress at high bird velocities (253 and 225 m/s) is significantly wider than at low bird velocity (116 m/s). Therefore, it can be considered that when the bird’s initial velocity differences are significant, the greater the bird velocity, the more obvious the blade deformation.

The bearing force is mainly determined by the fan’s rotational speed, and the bird’s initial velocity has little influence on it. The kinetic energy change in

Table 7. The change in the kinetic energy for different initial velocities of the bird and different rotational speeds of the fan.

Case	G	V1	V2	R1	R2
Initial bird kinetic energy (kJ)	25.59	20.25	5.38	25.59	25.59
End bird kinetic energy (kJ)	82.75	80.37	74.46	20.30	34.34
Kinetic energy gain (kJ)	57.16	60.12	69.08	−5.29	8.75

shows that the fan blades lose higher levels of kinetic energy as the fan’s rotational speed increases. The bird gains high levels of kinetic energy in the cases of G, V1, and V2 (57.16, 60.12 and 69.08 kJ, respectively). However, the bird only gains 8.75 kJ kinetic energy in the case of R2, and it even loses 5.29 kJ in the case of R1. The engine energy loss has little relationship with the bird velocity (Table 7). Therefore, it can be concluded that the greater the bird’s initial velocity is, the more extensive the blade deformation becomes.

4.4. Support Stiffness and Damping Influence

A bird strike will produce a transient impact on the bearing, and the response of the bearing depends on the stiffnesses and damping of the bearing system, which in turn, influences the bird impact response [22]. It can be seen in Figure 11a,b that the stiffness has a great effect on the bearing force of the rotor. The bearing forces are 193, 139 and 47.3 kN in the cases of G, S1, and S2. It is known that when the bearing stiffness is larger, the resulting bearing force is greater, and the displacement of the shaft center is smaller. The displacements of different stiffness are 1.93, 2.78, and 4.71 mm, respectively, for the cases of G, S1, and S2. Therefore, higher stiffness leads to higher stability in the fan after impact. The damping has less effect on the bird strike, and there is not much difference between the cases of G, D1, and D2. Figure 11a,d show that the stiffness and damping of bearings do not have a substantial influence on the bird strike process and the von Mises stress distribution of the blade. The same conclusion can be drawn from the results in

Table 8. The change in the kinetic energy at different support stiffness and damping.

Case	G	S1	S2	D1	D2
Initial bird kinetic energy (kJ)	25.59	25.59	25.59	25.59	25.59
End bird kinetic energy (kJ)	82.75	82.92	82.99	82.90	82.91
Kinetic energy gain (kJ)	57.16	57.33	57.40	57.31	57.32

. The kinetic energy gain of the bird is very similar for all the cases of G, S1, S2, D1, and D2.

Therefore, it can be concluded that the blade response under bird strike is almost independent of bearing parameters. However, if the stability of the fan during the bird strike is to be improved, the bearing stiffness must be changed. The study of bearing parameters can provide a reference for bearing selection, and it can provide valuable insight into the operation of the bearings after a bird strike.

In Puneeth and JayaPrakash’s study [22], the bearing force excited by bird impact load was taken into account. After comparing the bearing forces under approximate conditions, it was found out that the bearing forces at the fan bearing were not very significant. Therefore, to simplify the calculations, we used discrete elements for the bearings.

4.5. Comparision with Other Studies and Suggessions

Even though many other models are currently used in bird strike studies, and although many of the same conclusions can be taken by comparison, some differences can be found. In future studies, the possible differences in the results obtained from our models on the one hand and other numerical models on the other hand can be explored, and improvements in the models can be made by the help of experimental tests. To sum up, our study presents a comprehensive methodology for evaluating the strength of fan blades in a design procedure.

5. Conclusions

To investigate the effect of a bird’s impact parameters on the aero-engine fan operation and blade damage, an SPH bird model based on a real mallard was used in this paper to simulate the process of bird impact. Six parameters (initial bird velocity, bird orientation, impact location, fan rotational speed, fan hub stiffness, and fan hub damping) have been considered in the simulation. Some conclusions are listed below:

(1)

Decrease in impact height increases stress level and impact force. In other words, the impact on the blade root is more dangerous compared to the impact on the blade tip or the middle part. The bird strike causes plastic deformation in the blade, leading to an increase in the bearing force to values as high as 211 kN. The maximum bird impact force reaches a peak of 390 kN when the bird impacts the blade root.

(2)

The bird impact force, kinetic energy loss of the fan, bearing force, and stress distribution are easily influenced by the impact orientation. Furthermore, the maximum impact force and bearing forces are generated when the bird impacts the fan from the Z-45° orientation, the maximum force reaching 215 kN and the energy loss reaching 64.73 kJ. Therefore, it can be concluded that the orientation where the bird head is tilted 45° horizontally is the most damaging scenario for the bird strike.

(3)

The results show that the bird’s initial velocity affects blade integrity, while the fan’s rotational speed affects rotor stability. Increasing the bearing stiffness enhances the bearing force that can be provided (to values as high as 193 kN,) thus ensuring stable operation of the system in the bird strike event. The value of damping has little effect on the bird strike process.

(4)

It can be predicted that the change in the impact parameters will lead to an obvious variation of stresses, which may cause the stress concentrated area to undergo large deformation and even fracture. The damage to the engine varies greatly with different impact locations and orientations, and the results could guide the design of test conditions. With an understanding of the effects of impact and bearing parameters, the bird strike model can also be used to simulate flocking bird strikes to study bird strike scenarios closer to the actual situation.