A Novel Framework for Online Remaining Useful Life Prediction of an Industrial Slurry Pump
Abstract
:1. Introduction
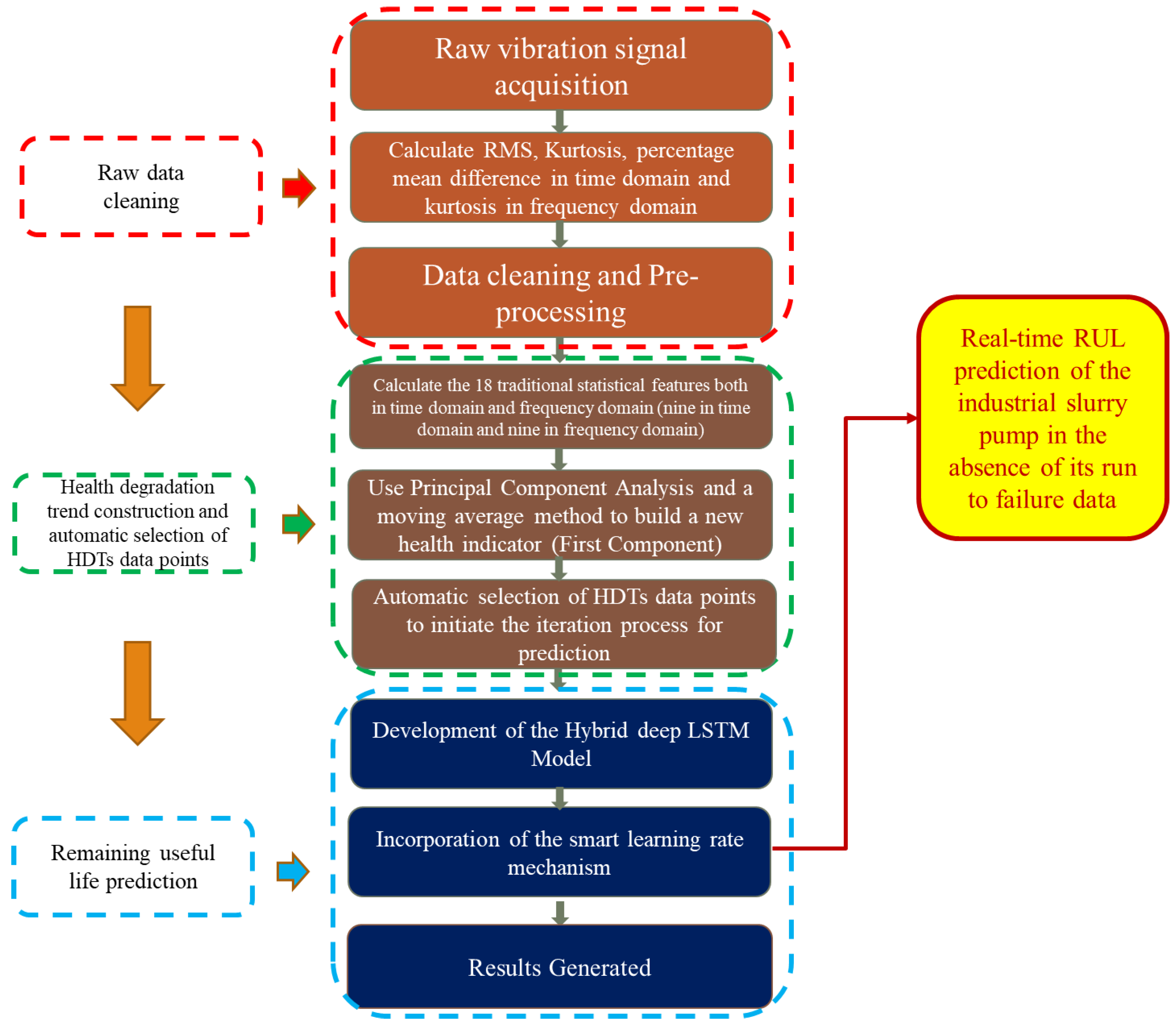
2. Methodology
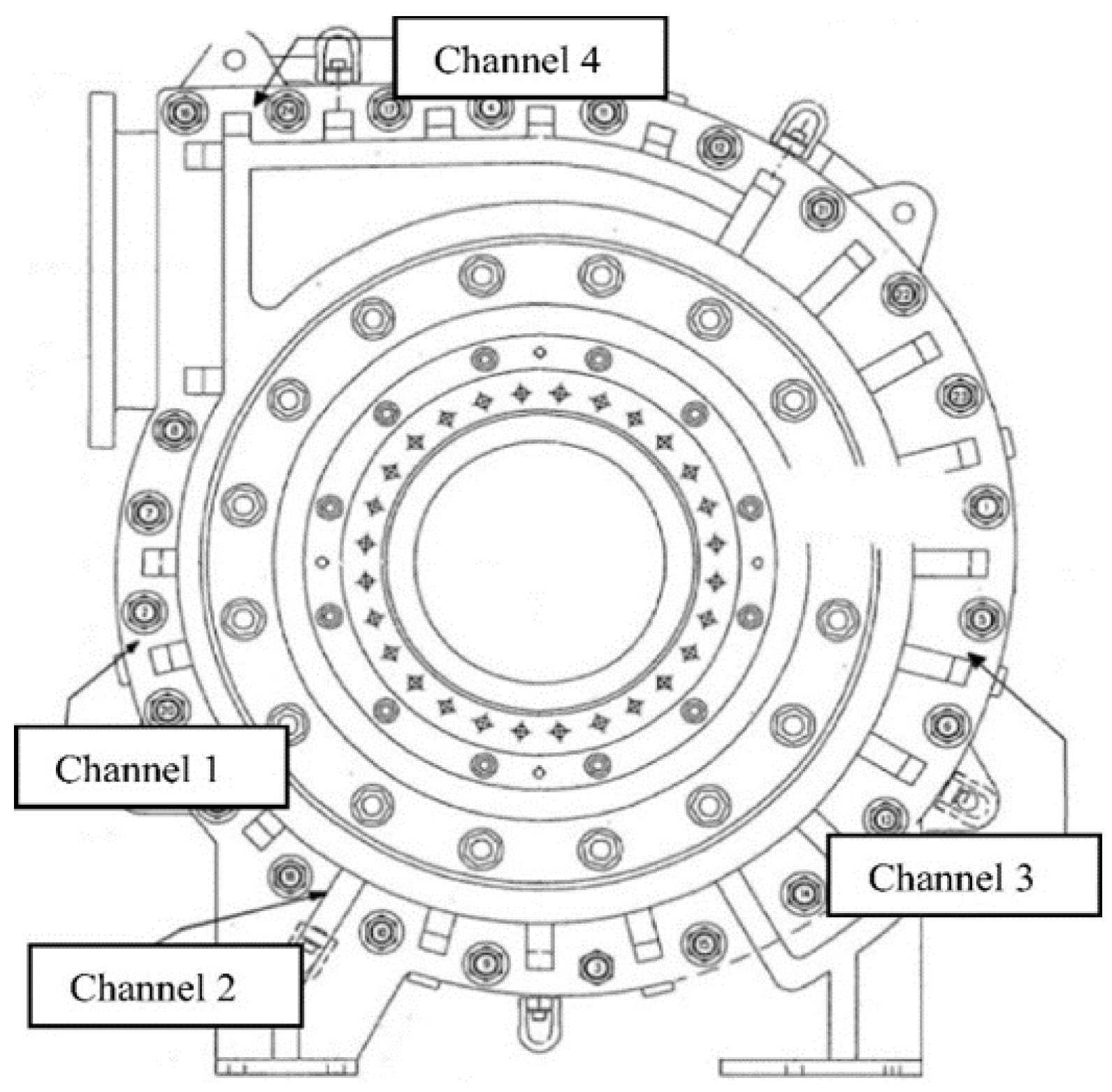
2.1. Data Collection and Its Filtering for Valid Datasets Acquisition
- N = data length of the dataset
- n = selected length of the considered dataset i.e., n = 1, 2, …, N
- Xn = processed vibration signals
- μ = mean of the dataset
- σ = standard deviation of the dataset
- PM = mean of positive values for one particular vibration signal
- MN = mean of negative values for one particular vibration signal
2.2. Development of the Health Degradation Trends
2.2.1. Statistical Feature Extraction
- N = data length of the dataset
- n = selected length of the considered dataset i.e., n = 1,2, …, N
- FLP(t) = the features in the time domain
- FLP(f) = the features in the frequency domain
- LP = low pass filtering
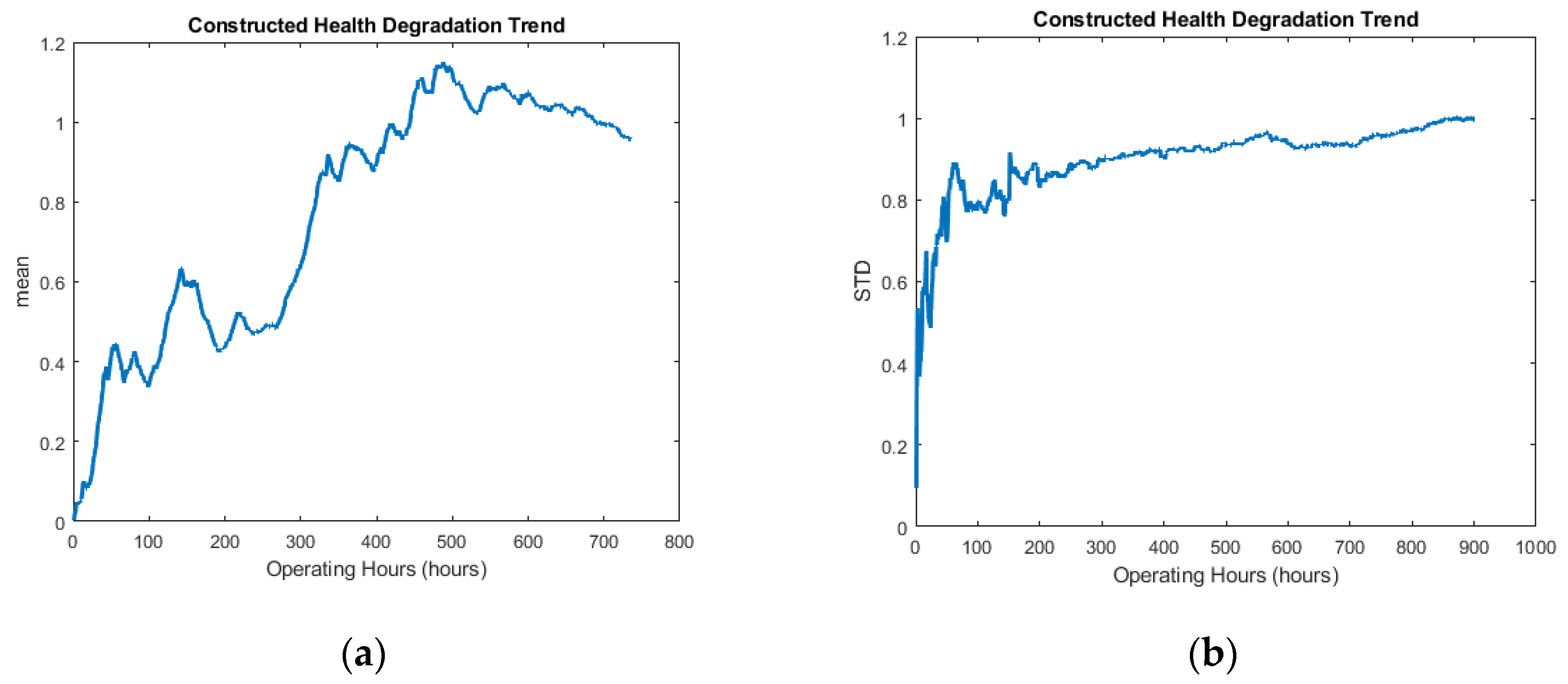
2.2.2. Health Assessment Indicator
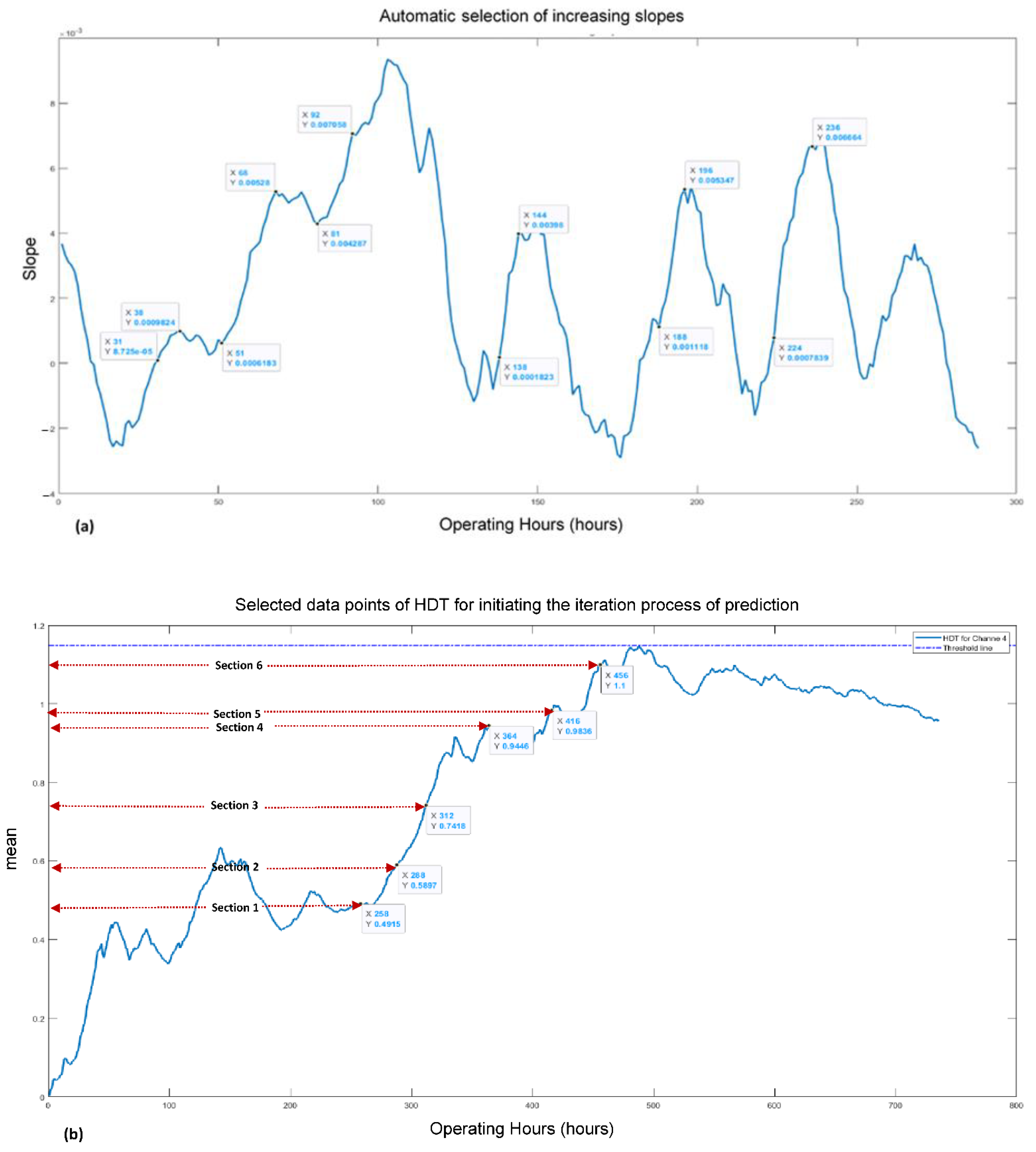
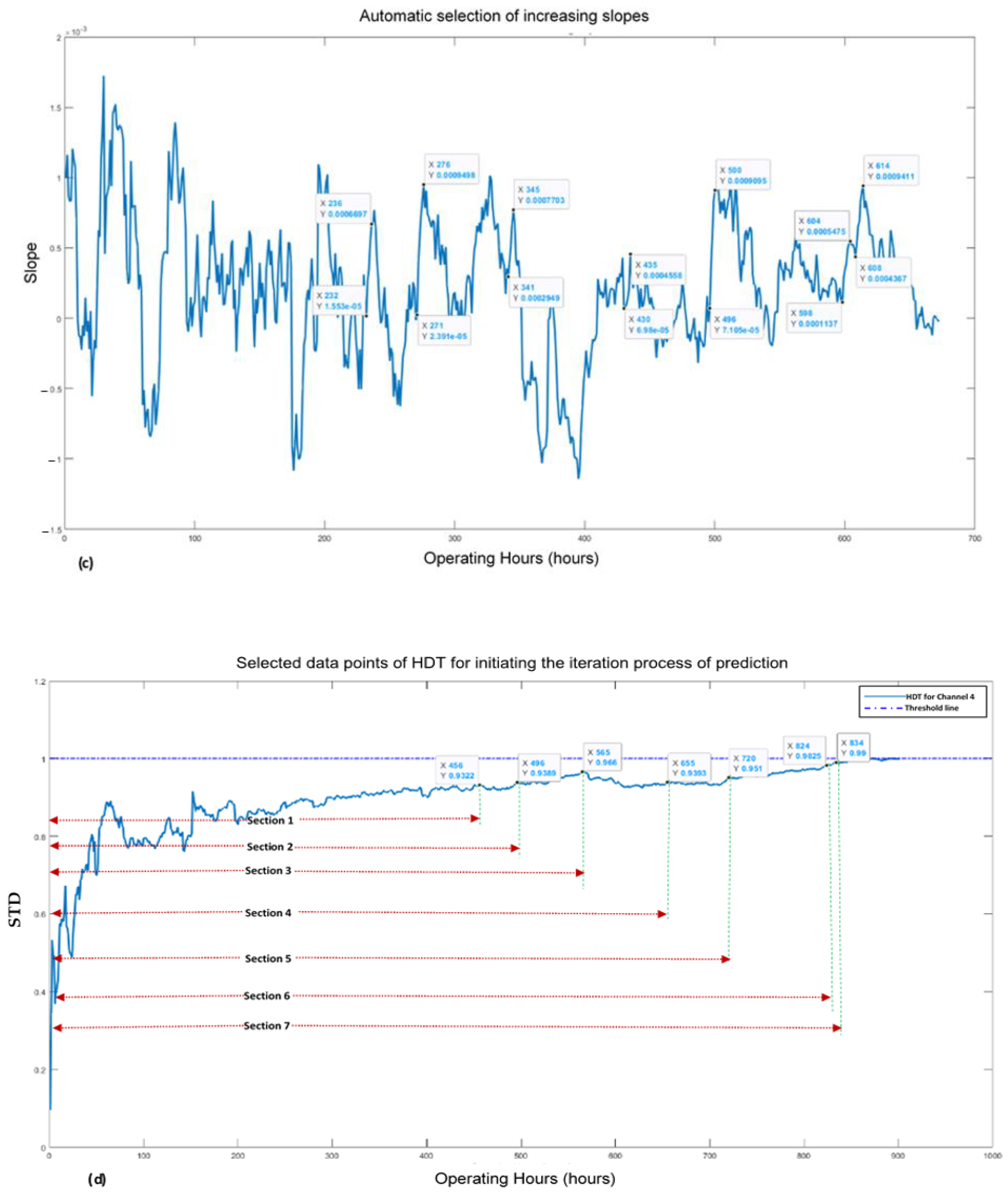
2.3. Automatic Selection of HDTs Data Points for Initiating the Iteration Process of Prediction
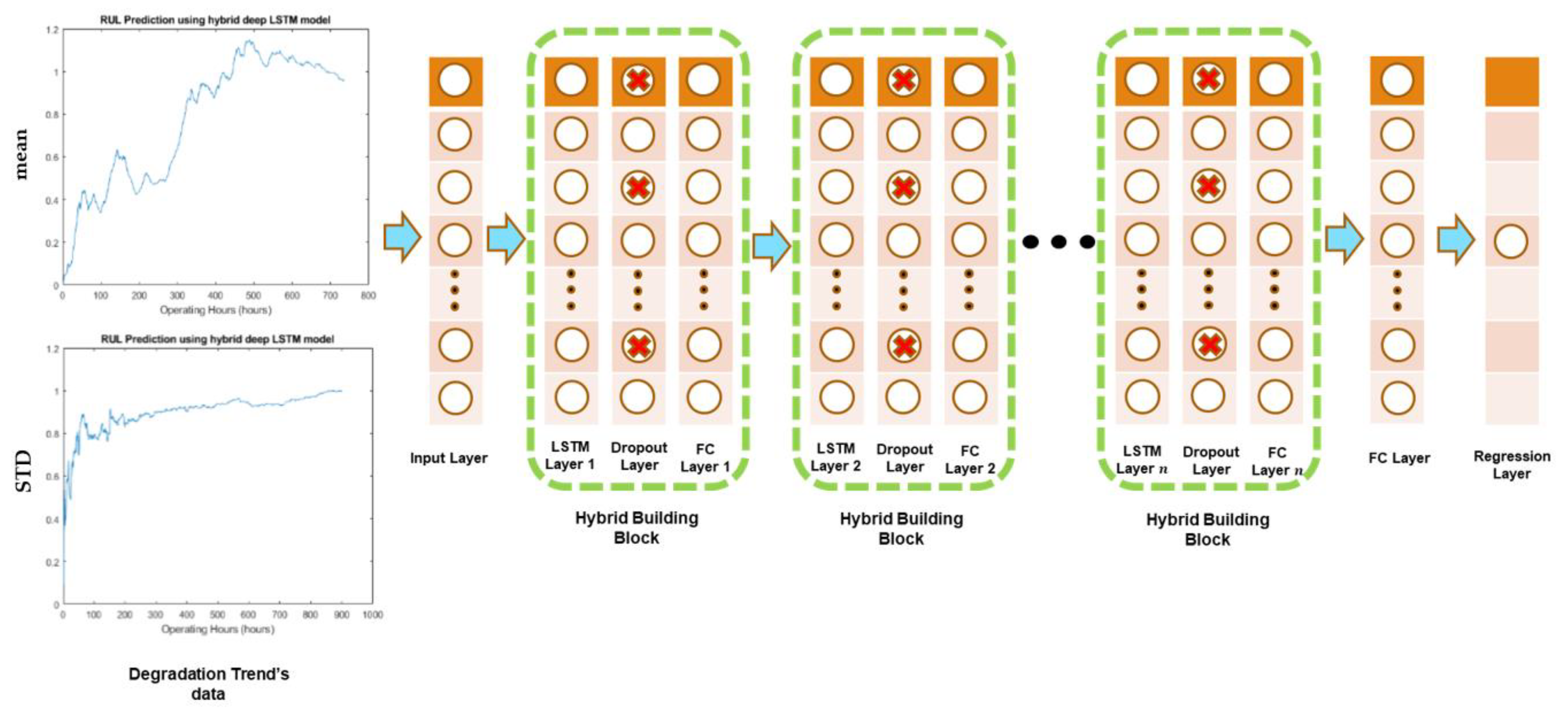
2.4. Development and Design of the Hybrid Deep LSTM Model
Working Mechanism of the Developed Model
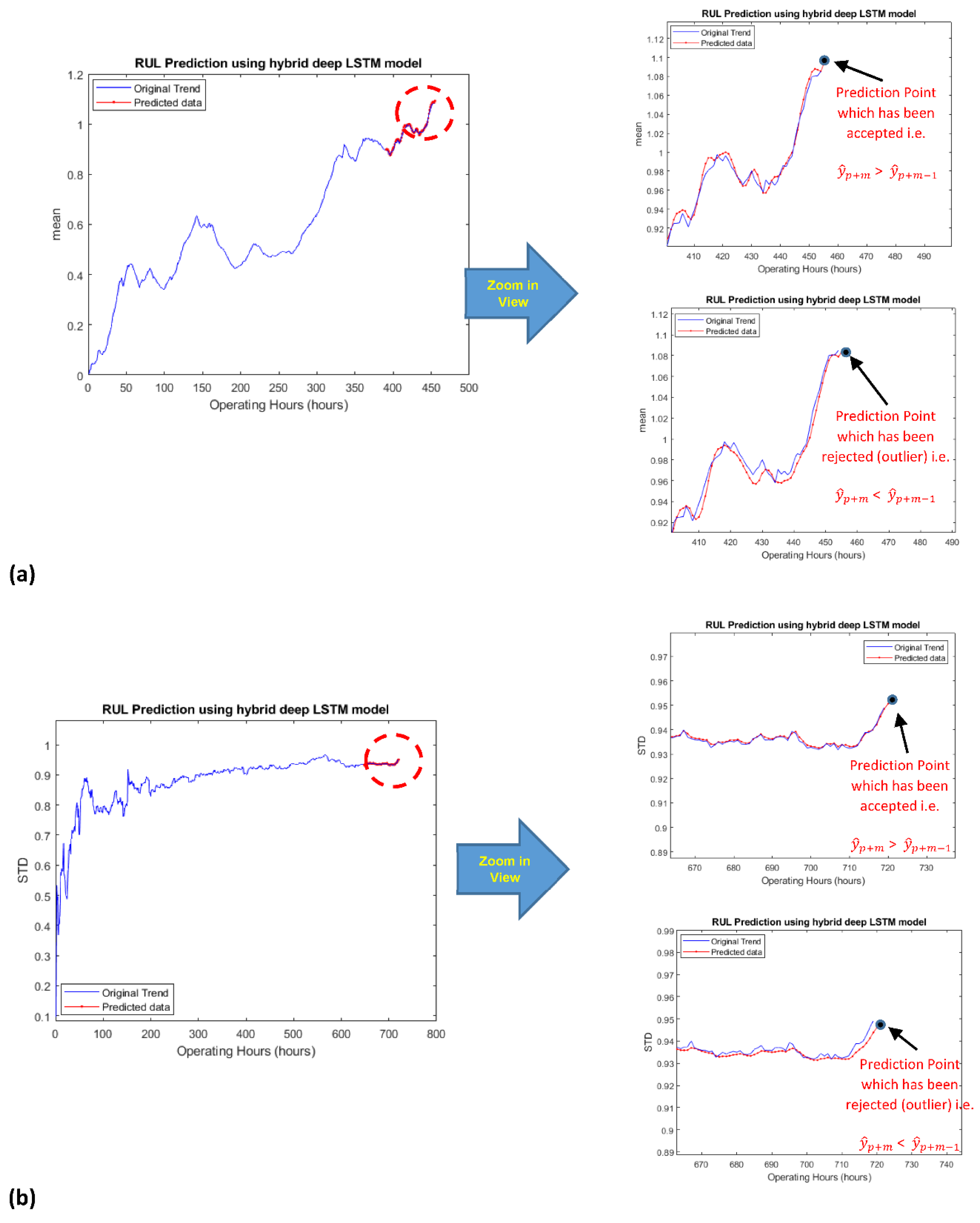
2.5. Development and Incorporation of the Smart Learning Rate Mechanism
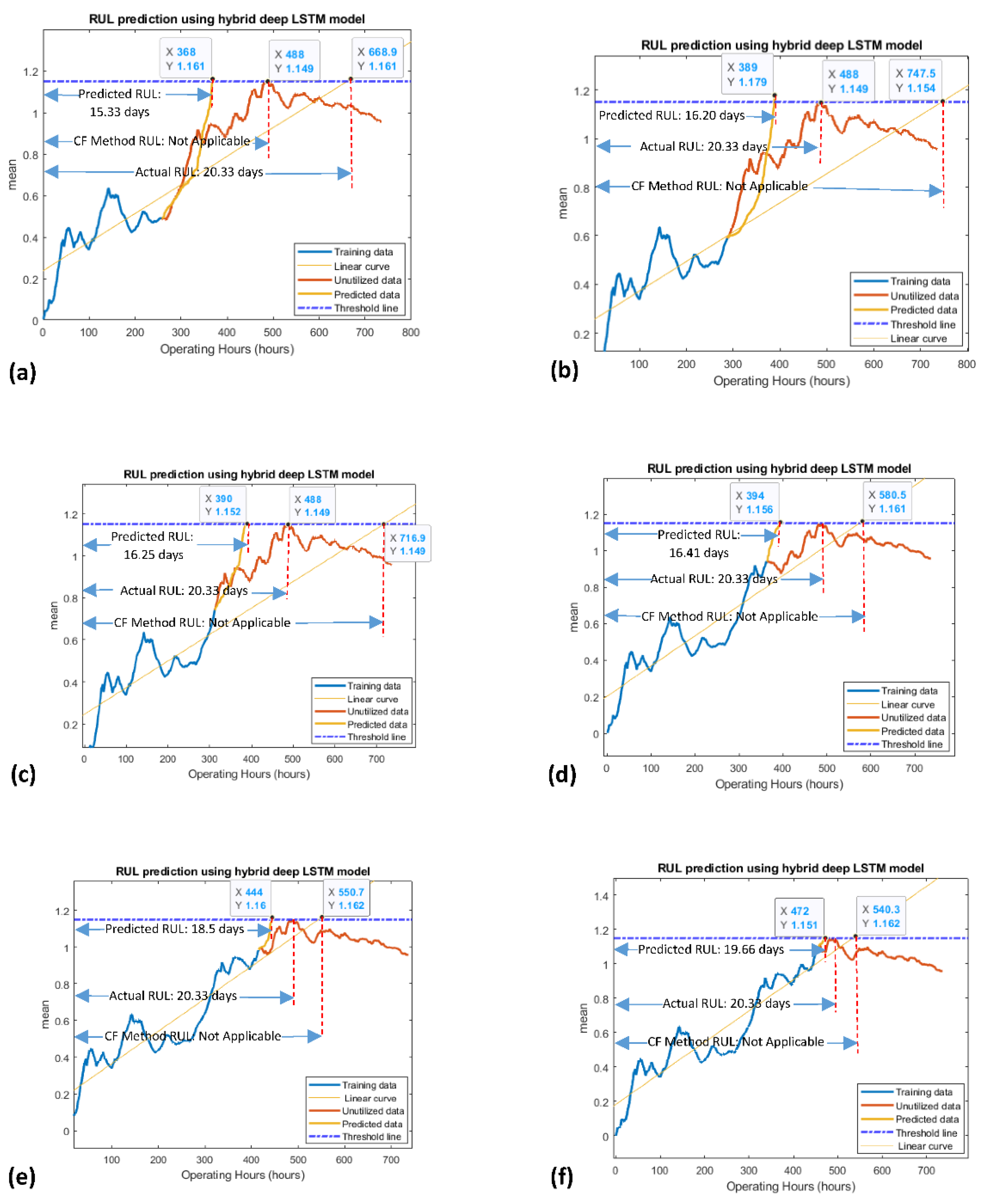
3. Results
Error Analysis
- ωj = weight of particular operation hours
- xj = operation hours
- RULA = actual RUL in terms of weights
4. Conclusions
- It is recommended that the iteration process for prediction should start from particular points of an HDT, which have consecutively increasing slopes. As per [17], it was a research gap that has been attempted to be filled up in this study.
- The developed smart learning rate mechanism incorporated into the hybrid deep LSTM model has worked as a “catalyst” for obtaining the acceptable prediction points. This feature of the proposed method is saving a large extent of time for estimating the online RUL.
- The developed strategy of producing an acceptable prediction point, then appending it into the input vector for another prediction, and so on, has been proved to be a successful alternative to the curve-fitting method. It is suggested that if an HDT is progressing with deep crest- and trough-like structures, then the proposed method should be utilized for estimating the online RUL.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yin, S.; Li, X.; Gao, H.; Kaynak, O. Data-based techniques focused on modern industry: An overview. IEEE Trans. Ind. Electron. 2015, 62, 657–667. [Google Scholar] [CrossRef]
- Xia, M.; Zheng, X.; Imran, M.; Shoaib, M. Data-driven prognosis method using hybrid deep recurrent neural network. Appl. Soft Comput. 2020, 93, 106351. [Google Scholar] [CrossRef]
- Sbarufatti, C.; Corbetta, M.; Giglio, M.; Cadini, F. Adaptive prognosis of lithium-ion batteries based on the combination of particle filters and radial basis function neural networks. J. Power Sources 2017, 344, 128–140. [Google Scholar] [CrossRef]
- Djeziri, M.; Benmoussa, S.; Sanchez, R. Hybrid method for remaining useful life prediction in wind turbine systems. Renew. Energy 2018, 116, 173–187. [Google Scholar] [CrossRef]
- Javed, K.; Gouriveau, R.; Zerhouni, N.; Nectoux, P. Enabling health monitoring approach based on vibration data for accurate prognostics. IEEE Trans. Ind. Electron. 2015, 62, 647–656. [Google Scholar] [CrossRef] [Green Version]
- Ding, N.; Li, H.; Yin, Z.; Zhong, N.; Zhang, L. Journal bearing seizure degradation assessment and remaining useful life prediction based on long short-term memory neural network. Meas. J. Int. Meas. Confed. 2020, 166, 108215. [Google Scholar] [CrossRef]
- Al-Dulaimi, A.; Zabihi, S.; Asif, A.; Mohammadi, A. A multimodal and hybrid deep neural network model for Remaining Useful Life estimation. Comput. Ind. 2019, 108, 186–196. [Google Scholar] [CrossRef]
- Mo, Y.; Wu, Q.; Li, X.; Huang, B. Remaining useful life estimation via transformer encoder enhanced by a gated convolutional unit. J. Intell. Manuf. 2021, 32, 1997–2006. [Google Scholar] [CrossRef]
- Liu, L.; Song, X.; Chen, K.; Hou, B.; Chai, X.; Ning, H. An enhanced encoder–decoder framework for bearing remaining useful life prediction. Meas. J. Int. Meas. Confed. 2020, 170, 108753. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, K.; Kong, X.; Huai, T. A linear mapping method for predicting accurately the RUL of rolling bearing. Meas. J. Int. Meas. Confed. 2021, 176, 109127. [Google Scholar] [CrossRef]
- Sellgren, A.; Addie, G.; Visintainer, R.; Pagalthivarthi, K. Prediction of slurry pump component wear and cost. In Annual Texas A&M Dredging Seminar: 19/06/2005-22/06/2005; Western Dredging Association: Vancouver, WA, USA, 2005; pp. 1–16. [Google Scholar]
- Hu, J.; Tse, P.W. A relevance vector machine-based approach with application to oil sand pump prognostics. Sensors 2013, 13, 12663–12686. [Google Scholar] [CrossRef] [Green Version]
- Tse, Y.L.; Cholette, M.E.; Tse, P.W. A multi-sensor approach to remaining useful life estimation for a slurry pump. Meas. J. Int. Meas. Confed. 2019, 139, 140–151. [Google Scholar] [CrossRef]
- Tse, P.W.; Wang, D. Enhancing the abilities in assessing slurry pumps’ performance degradation and estimating their remaining useful lives by using captured vibration signals. J. Vib. Control. 2015, 23, 1925–1937. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.T. Prognostics of slurry pumps based on a moving-average wear degradation index and a general sequential Monte Carlo method. Mech. Syst. Signal Process. 2015, 56–57, 213–229. [Google Scholar] [CrossRef]
- Sun, S.; Tse, P.W.; Tse, Y.L. An Enhanced Factor Analysis of Performance Degradation Assessment on Slurry Pump Impellers. Shock Vib. 2017, 2017, 1524840. [Google Scholar] [CrossRef]
- Kim, D.; Lee, S.; Kim, D. An applicable predictive maintenance framework for the absence of run-to-failure data. Appl. Sci. 2021, 11, 5180. [Google Scholar] [CrossRef]
- Rakhecha, A. Understanding Learning Rate. 2019. Available online: https://towardsdatascience.com/https-medium-com-dashingaditya-rakhecha-understanding-learning-rate-dd5da26bb6de (accessed on 24 March 2022).
- Abuqaddom, I.; Mahafzah, B.A.; Faris, H. Oriented stochastic loss descent algorithm to train very deep multi-layer neural networks without vanishing gradients. Knowl.-Based Syst. 2021, 230, 107391. [Google Scholar] [CrossRef]
- Khan, M.M.; Tse, P.W.; Trappey, A.J.C. Development of a novel methodology for remaining useful life prediction of industrial slurry pumps in the absence of run to failure data. Sensors 2021, 21, 8420. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, N.; Shen, C. A new data-driven transferable remaining useful life prediction approach for bearing under different working conditions. Mech. Syst. Signal Process. 2020, 139, 106602. [Google Scholar] [CrossRef]
- Hinchi, A.Z.; Tkiouat, M. Rolling element bearing remaining useful life estimation based on a convolutional long-short-Term memory network. Procedia Comput. Sci. 2018, 127, 123–132. [Google Scholar] [CrossRef]
- An, Y.; Wang, X.; Chu, R.; Yue, B.; Wu, L.; Cui, J.; Qu, Z. Event classification for natural gas pipeline safety monitoring based on long short-term memory network and Adam algorithm. Struct. Health Monit. 2020, 19, 1151–1159. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Wu, Y.; Yuan, M.; Dong, S.; Lin, L.; Liu, Y. Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing 2018, 275, 167–179. [Google Scholar] [CrossRef]
- Kisvari, A.; Lin, Z.; Liu, X. Wind power forecasting—A data-driven method along with gated recurrent neural network. Renew. Energy 2021, 163, 1895–1909. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Tang, J.; Li, Y. Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network. Adv. Mech. Eng. 2018, 10, 1687814018817184. [Google Scholar] [CrossRef]
- Fan, Y.; Qian, Y.; Xie, F.; Soong, F.K. TTS synthesis with bidirectional LSTM based Recurrent Neural Networks. Proc. Annu. Conf. Int. Speech Commun. Assoc. Interspeech 2014, 1964–1968. [Google Scholar] [CrossRef]
- Yildirim, Ö. A novel wavelet sequences based on deep bidirectional LSTM network model for ECG signal classification. Comput. Biol. Med. 2018, 96, 189–202. [Google Scholar] [CrossRef]
- Kara, A. A data-driven approach based on deep neural networks for lithium-ion battery prognostics. Neural Comput. Appl. 2021, 33, 13525–13538. [Google Scholar] [CrossRef]
- Esfahani, Z.; Salahshoor, K.; Farsi, B.; Eicker, U. A New Hybrid Model for RUL Prediction through Machine Learning. J. Fail. Anal. Prev. 2021, 21, 1596–1604. [Google Scholar] [CrossRef]
- Gao, S.; Xiong, X.; Zhou, Y.; Zhang, J. Bearing remaining useful life prediction based on a scaled health indicator and a lstm model with attention mechanism. Machines 2021, 9, 238. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, X. Convolutional neural network based on attention mechanism and Bi-LSTM for bearing remaining life prediction. Appl. Intell. 2022, 52, 1076–1091. [Google Scholar] [CrossRef]
- Marei, M.; Li, W. Cutting tool prognostics enabled by hybrid CNN-LSTM with transfer learning. Int. J. Adv. Manuf. Technol. 2022, 118, 817–836. [Google Scholar] [CrossRef]
- Peng, H.; Li, H.; Zhang, Y.; Wang, S.; Gu, K.; Ren, M. Multi-Sensor Vibration Signal Based Three-Stage Fault Prediction for Rotating Mechanical Equipment. Entropy 2022, 24, 164. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Kolekar, T.; Kotecha, K.; Patil, S.; Bongale, A. Performance evaluation for tool wear prediction based on Bi-directional, Encoder–Decoder and Hybrid Long Short-Term Memory models. Int. J. Qual. Reliab. Manag. 2022. [Google Scholar] [CrossRef]
- Yao, J.; Lu, B.; Zhang, J. Tool remaining useful life prediction using deep transfer reinforcement learning based on long short-term memory networks. Int. J. Adv. Manuf. Technol. 2022, 118, 1077–1086. [Google Scholar] [CrossRef]

| Domain | Indicator | Pass Range |
|---|---|---|
| Time Domain | 1. RMS | X > 0.01 |
| 2. Kurtosis | X > 20 | |
| 3. Percentage mean difference | X < 25% | |
| Frequency Domain | 4. Kurtosis | X < 1000 |
| Indicator | Pass Score | Valid | Invalid |
|---|---|---|---|
| 1. RMS (Time domain) | 1 | S ≥ 3 | S < 3 |
| 2. Kurtosis (Time domain) | 1 | ||
| 3. Percentage mean difference (time domain) | 1 | ||
| 4. Kurtosis (Frequency domain) | 1 |
| Channel 2 Datasets | ||||
|---|---|---|---|---|
| No. of Operating Hours (Hours) | Actual RUL with respect to Threshold Point (Days) | Predicted RUL (Days) | Accuracy (%) | |
| Proposed Method | 258 | 20.33 | 15.33 | 75.40 |
| Curve-fitting method | Not Applicable | - | ||
| NARX | Not Applicable | - | ||
| Proposed Method | 288 | 20.33 | 16.20 | 79.60 |
| Curve-fitting method | Not Applicable | - | ||
| NARX | - | |||
| Proposed Method | 312 | 20.33 | 16.25 | 79.93 |
| Curve-fitting method | Not Applicable | - | ||
| NARX | Not Applicable | - | ||
| Proposed Method | 364 | 20.33 | 16.41 | 80.71 |
| Curve-fitting method | Not Applicable | - | ||
| NARX | Not Applicable | - | ||
| Proposed Method | 416 | 20.33 | 18.5 | 90.99 |
| Curve-fitting method | Not Applicable | - | ||
| NARX | Not Applicable | - | ||
| Proposed Method | 456 | 20.33 | 19.66 | 96.70 |
| Curve-fitting method | Not Applicable | - | ||
| NARX | 19.37 | 95.27 | ||
| Channel 4 Datasets | ||||
|---|---|---|---|---|
| No. of Operating Hours (hours) | Actual RUL with respect to Threshold Point (Days) | Predicted RUL (Days) | Accuracy (%) | |
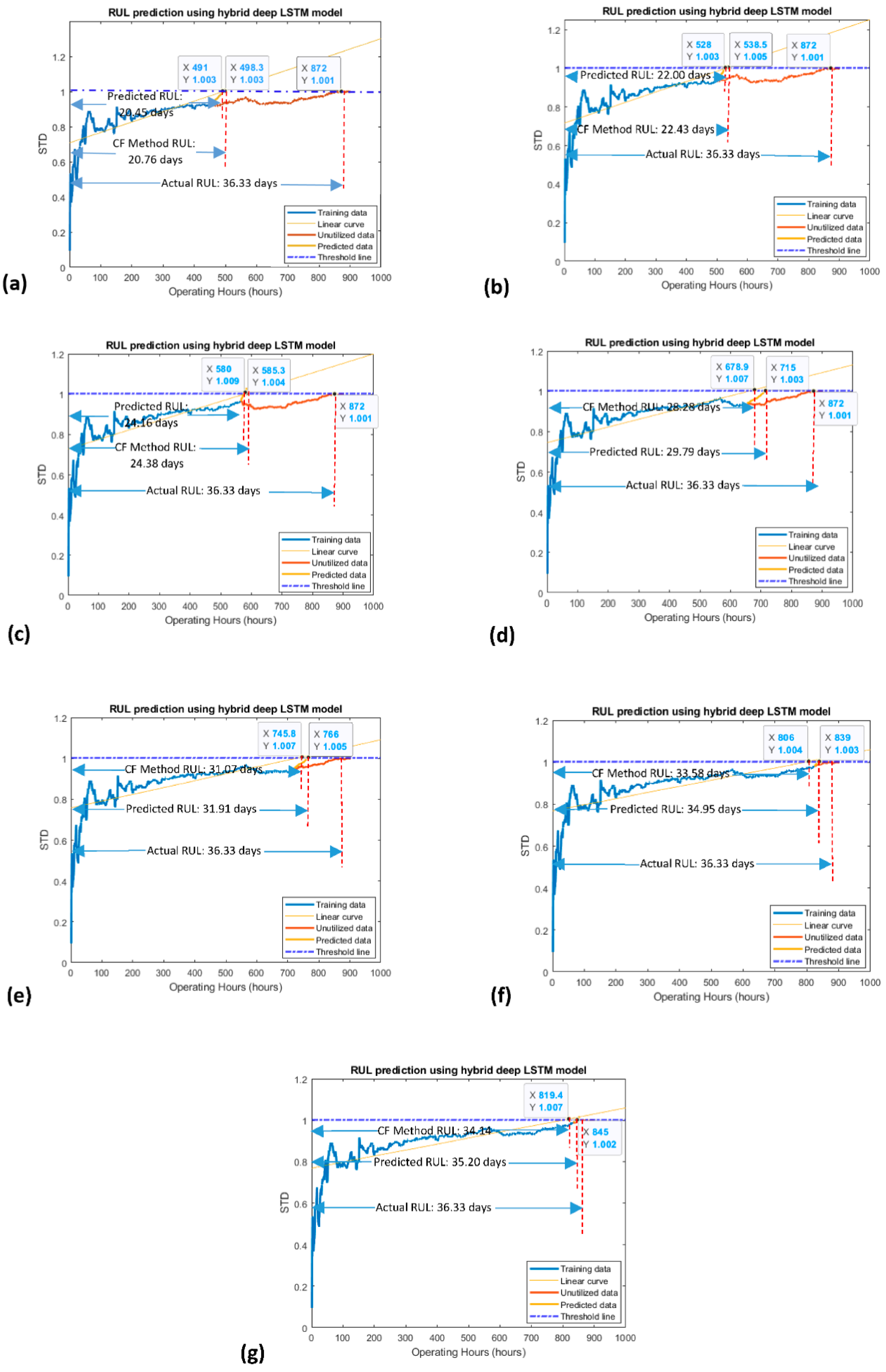
| Proposed Method | 456 | 36.33 | 20.45 | 56.28 |
| Curve-fitting method | 20.76 | 57.14 | ||
| NARX | Not Applicable | - | ||
| Proposed Method | 496 | 36.33 | 22.00 | 60.55 |
| Curve-fitting method | 22.43 | 61.73 | ||
| NARX | Not Applicable | - | ||
| Proposed Method | 565 | 36.33 | 24.16 | 66.50 |
| Curve-fitting method | 24.38 | 67.10 | ||
| NARX | Not Applicable | - | ||
| Proposed Method | 655 | 36.33 | 29.79 | 81.99 |
| Curve-fitting method | 28.28 | 77.84 | ||
| NARX | Not Applicable | - | ||
| Proposed Method | 720 | 36.33 | 31.91 | 87.83 |
| Curve-fitting method | 31.07 | 85.52 | ||
| NARX | Not Applicable | - | ||
| Proposed Method | 824 | 36.33 | 34.95 | 96.20 |
| Curve-fitting method | 33.58 | 92.43 | ||
| NARX | 34.66 | 95.40 | ||
| Proposed Method | 834 | 36.33 | 35.20 | 96.88 |
| Curve-fitting method | 34.14 | 93.97 | ||
| NARX | 35.04 | 96.44 | ||
| Operation Hours | ||||
|---|---|---|---|---|
| Channel 2 Datasets | ||||
| 258 | 9.58 | 4.58 | Not Applicable | Not Applicable |
| 288 | 8.33 | 4.2 | Not Applicable | Not Applicable |
| 312 | 7.33 | 3.25 | Not Applicable | Not Applicable |
| 364 | 5.17 | 1.25 | Not Applicable | Not Applicable |
| 416 | 3 | 1.17 | Not Applicable | Not Applicable |
| 456 | 1.33 | 0.66 | Not Applicable | Not Applicable |
| Channel 4 Datasets | ||||
| 456 | 17.33 | 1.45 | 1.76 | Not Applicable |
| 496 | 15.67 | 1.34 | 1.77 | Not Applicable |
| 565 | 12.79 | 0.62 | 0.84 | Not Applicable |
| 655 | 9.04 | 2.5 | 0.99 | Not Applicable |
| 720 | 6.33 | 1.91 | 1.07 | Not Applicable |
| 824 | 2 | 0.62 | −0.75 | 0.33 |
| 834 | 1.58 | 0.45 | −0.61 | 0.29 |
| Weighted Average Accuracy of Prediction | |||||
|---|---|---|---|---|---|
| Channel 2 Datasets | Channel 4 Datasets | ||||
| Proposed method | Curve-fitting Method | NARX | Proposed method | Curve-fitting Method | NARX |
| 42.15% | Not Applicable | Not Applicable | 22.01% | 7.29% | Not Applicable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.M.; Tse, P.W.; Yang, J. A Novel Framework for Online Remaining Useful Life Prediction of an Industrial Slurry Pump. Appl. Sci. 2022, 12, 4839. https://doi.org/10.3390/app12104839
Khan MM, Tse PW, Yang J. A Novel Framework for Online Remaining Useful Life Prediction of an Industrial Slurry Pump. Applied Sciences. 2022; 12(10):4839. https://doi.org/10.3390/app12104839
Chicago/Turabian StyleKhan, Muhammad Mohsin, Peter W. Tse, and Jinzhao Yang. 2022. "A Novel Framework for Online Remaining Useful Life Prediction of an Industrial Slurry Pump" Applied Sciences 12, no. 10: 4839. https://doi.org/10.3390/app12104839
APA StyleKhan, M. M., Tse, P. W., & Yang, J. (2022). A Novel Framework for Online Remaining Useful Life Prediction of an Industrial Slurry Pump. Applied Sciences, 12(10), 4839. https://doi.org/10.3390/app12104839






