A 3D Fluorescence Classification and Component Prediction Method Based on VGG Convolutional Neural Network and PARAFAC Analysis Method
Abstract
:1. Introduction
2. Materials and Methods
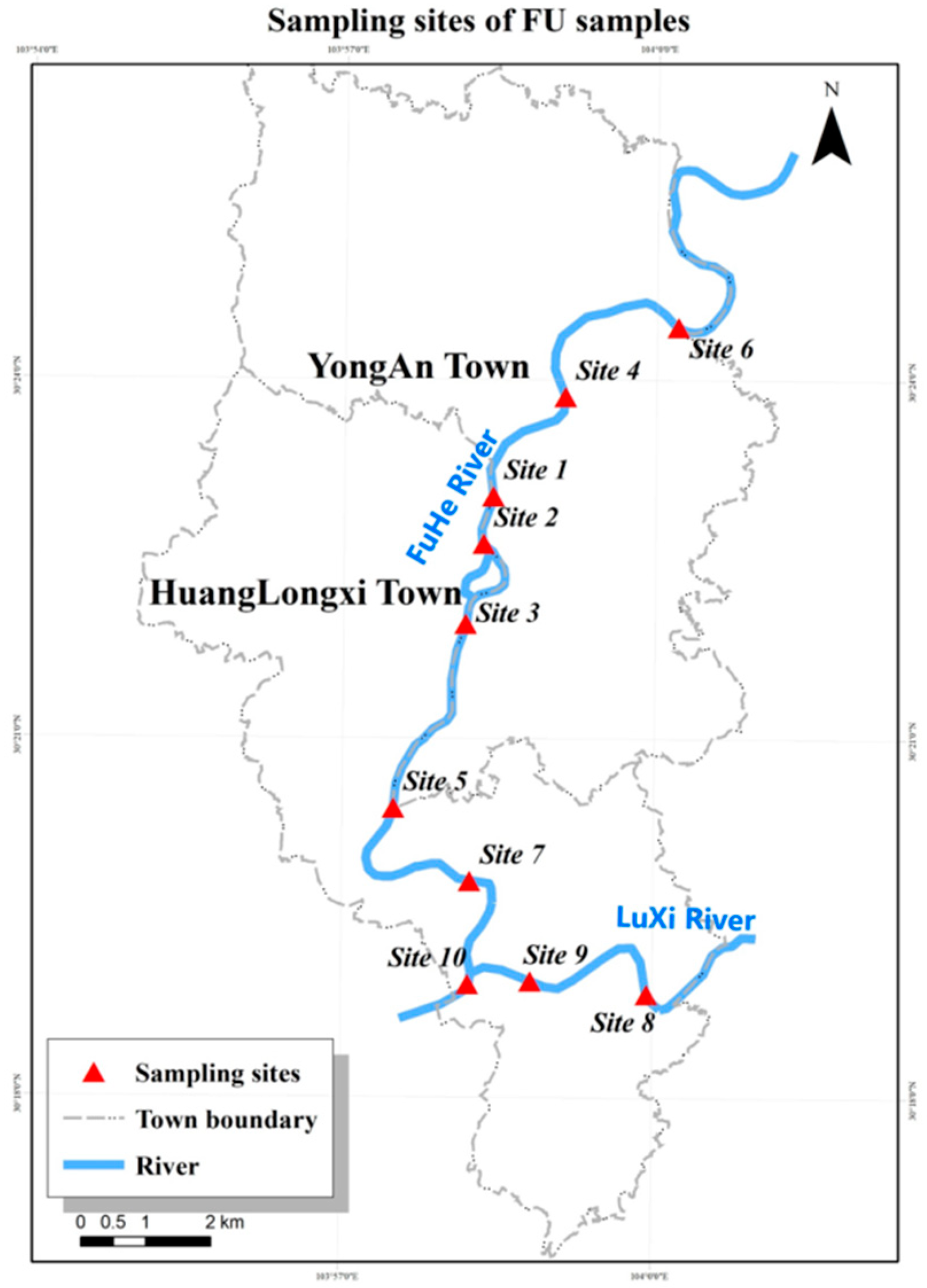
2.1. Samples Collection
2.2. 3D-EEMs Measurement
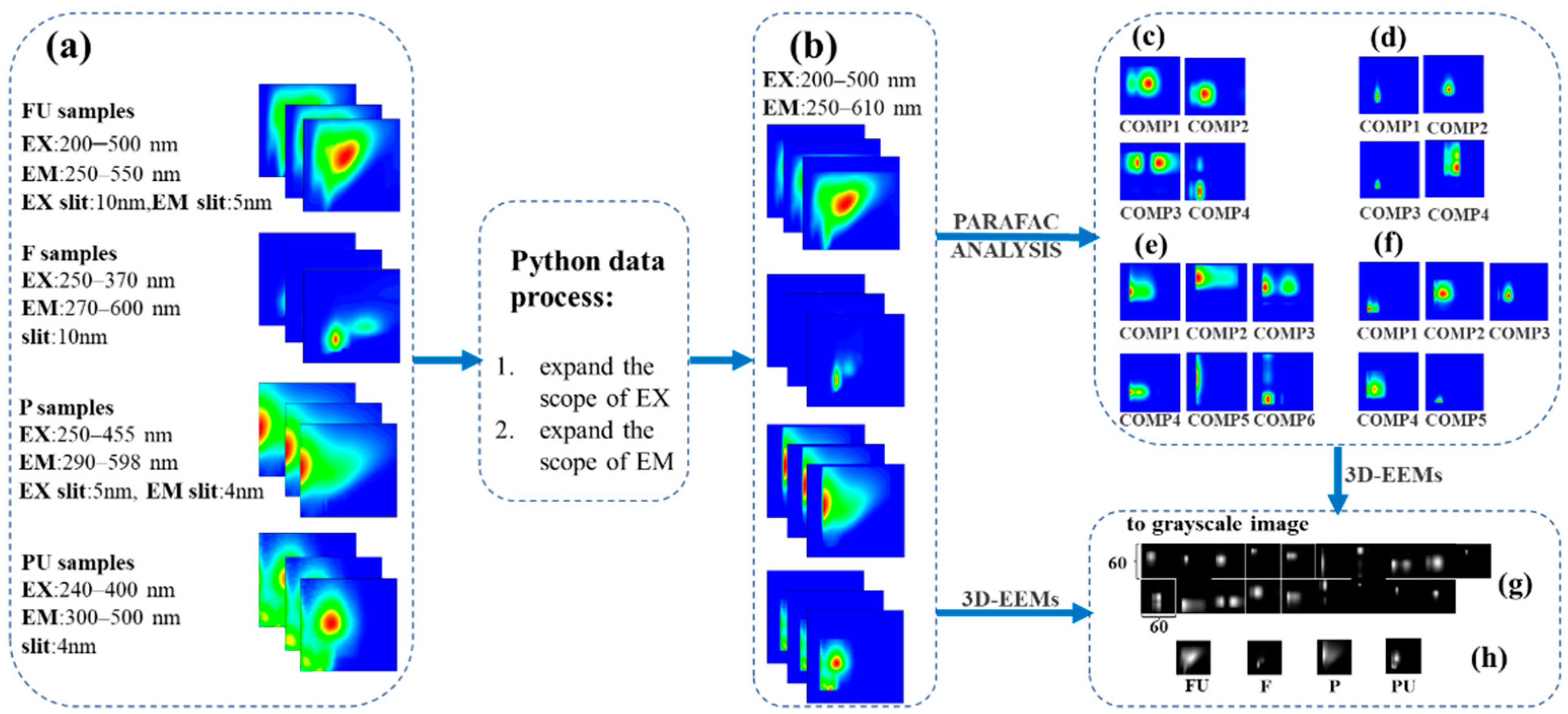
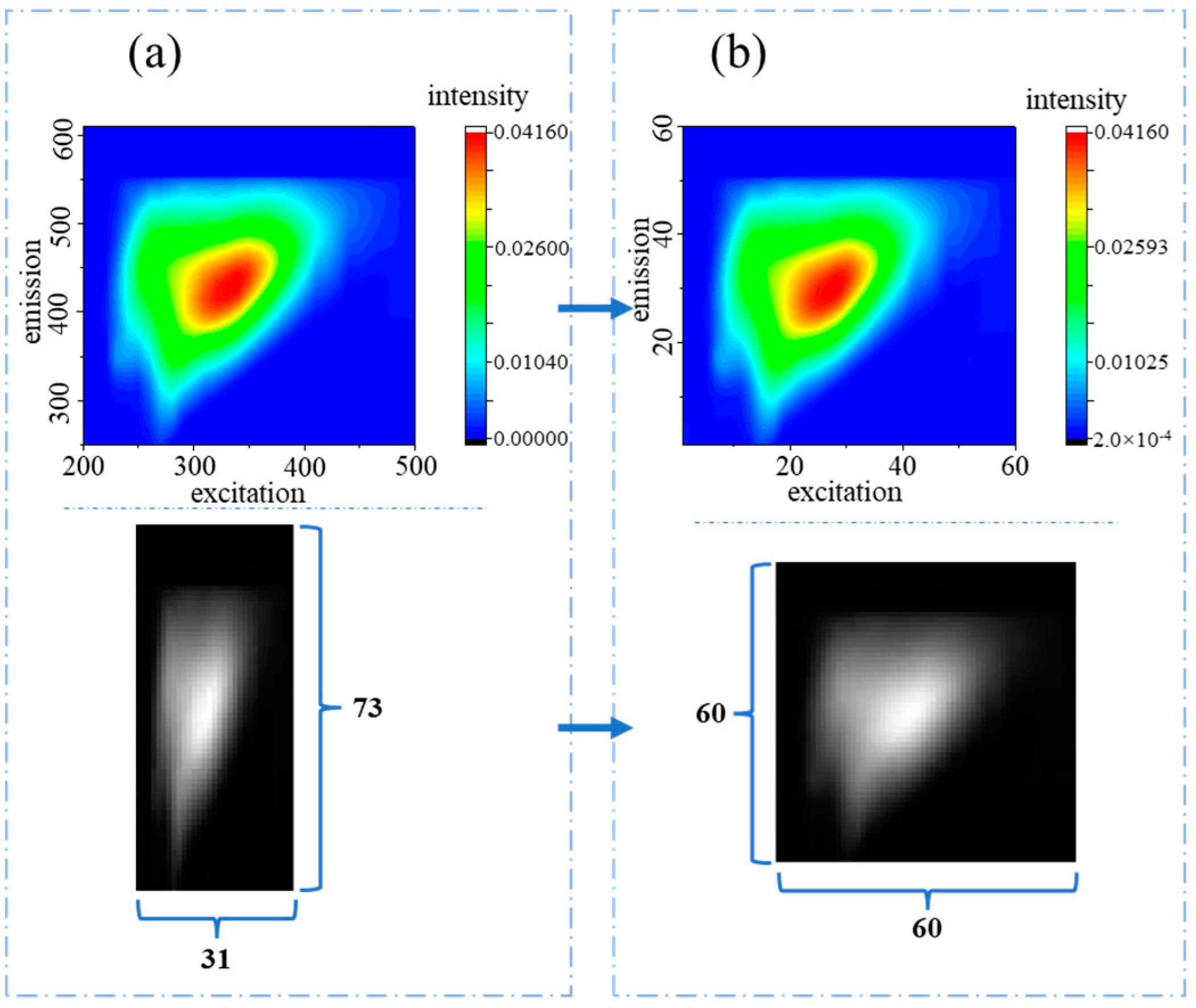
2.3. Data Preprocessing for PARAFAC and CNN
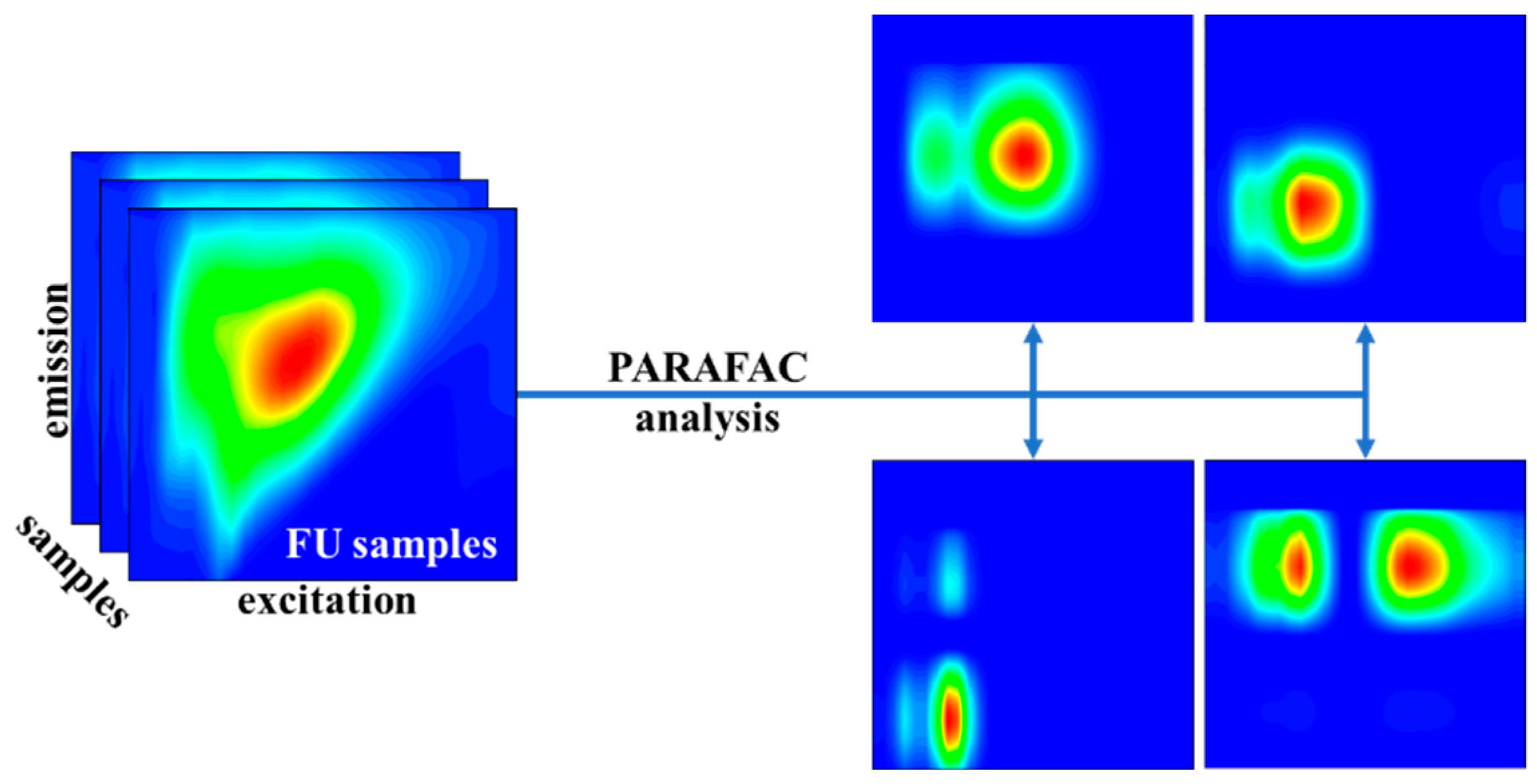
2.4. PARAFAC Method
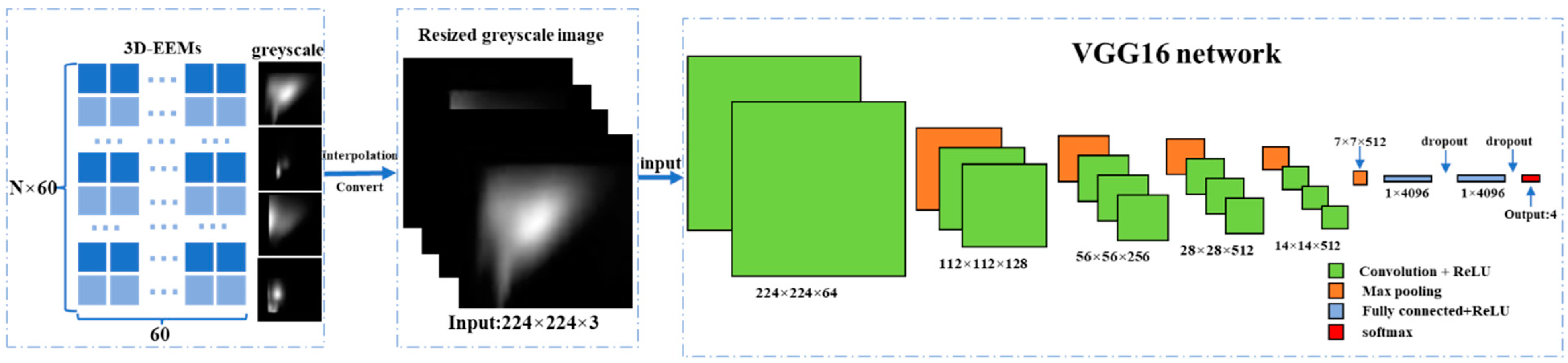
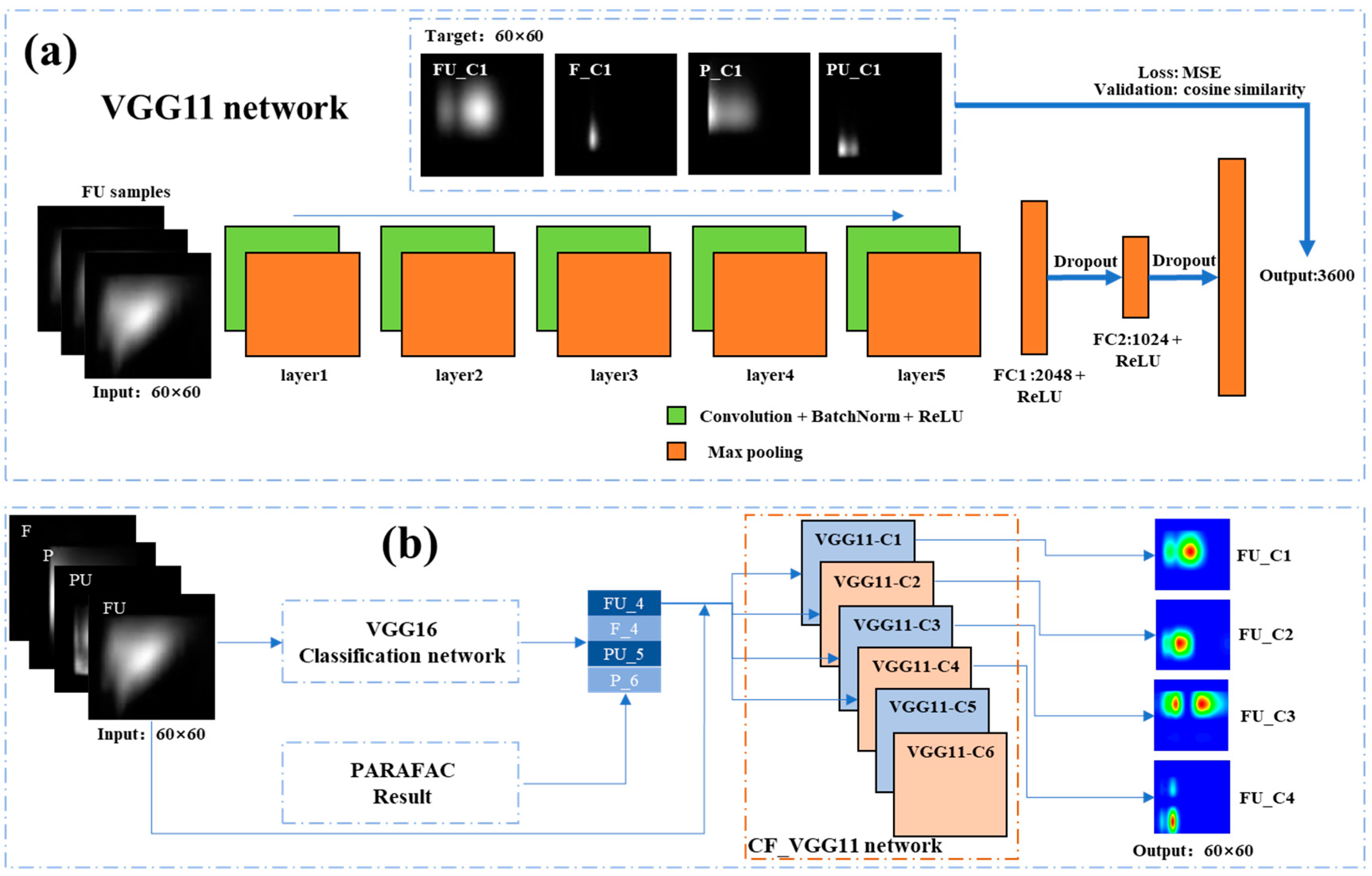
2.5. VGG16 Classification Network
2.6. CF-VGG11 Network
3. Results and Discussion
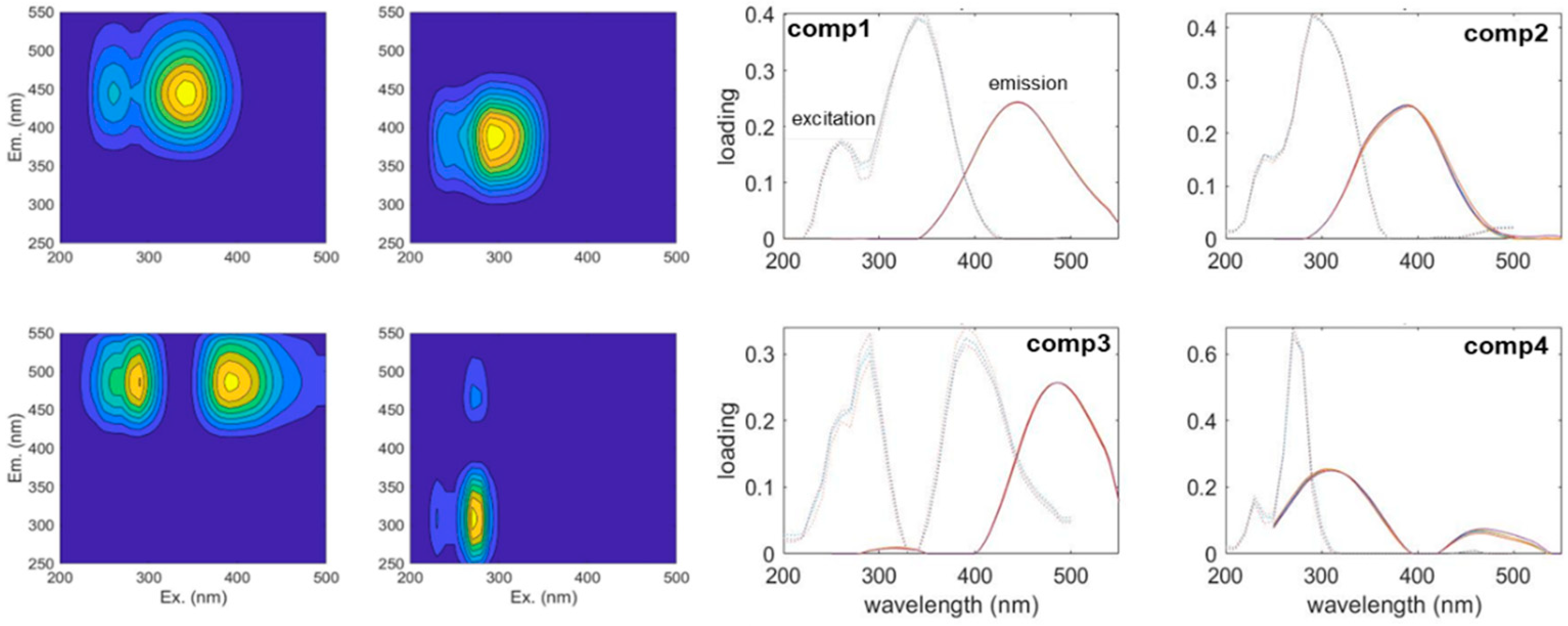
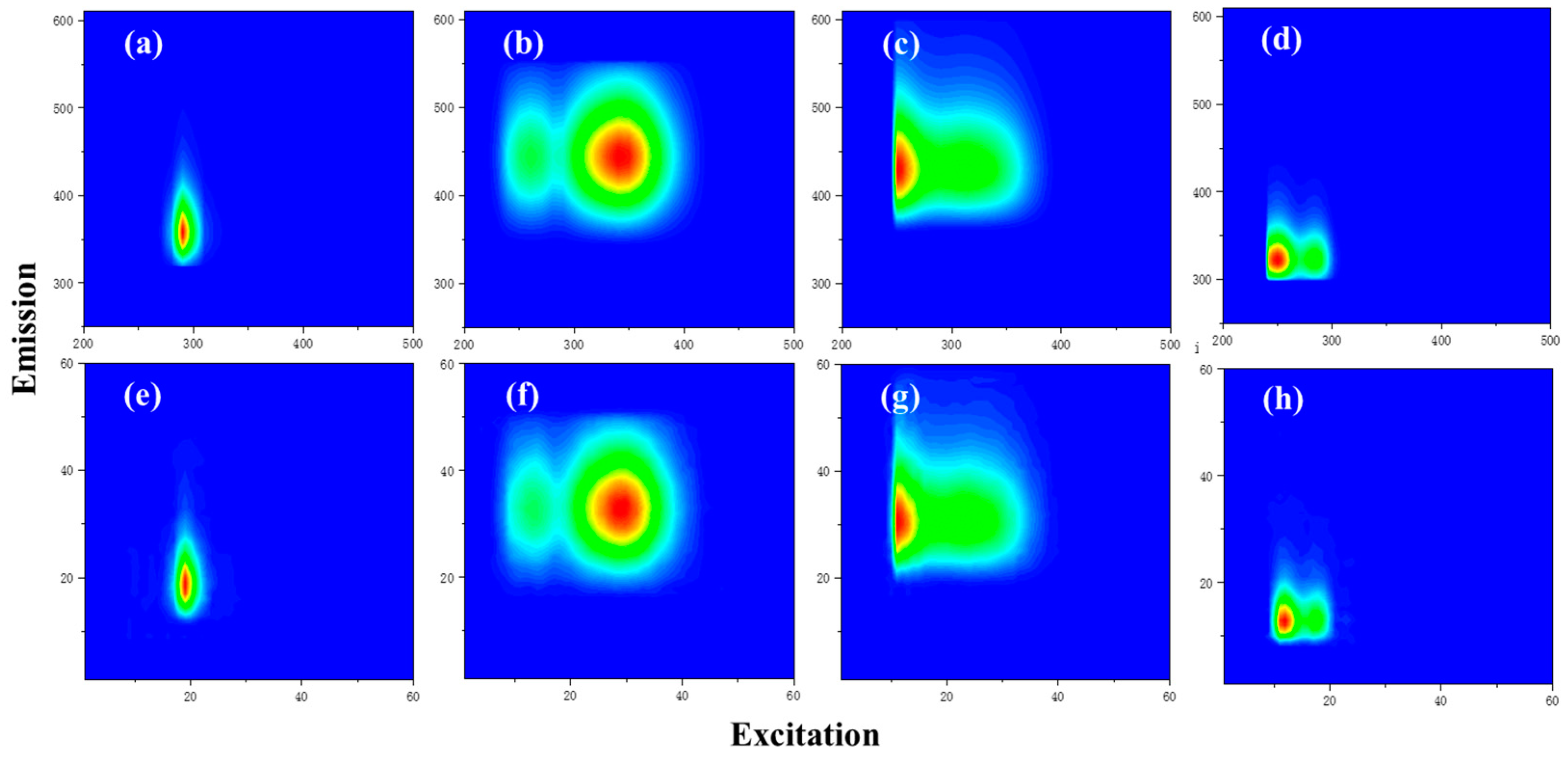
3.1. The Results of the PARAFAC Analysis
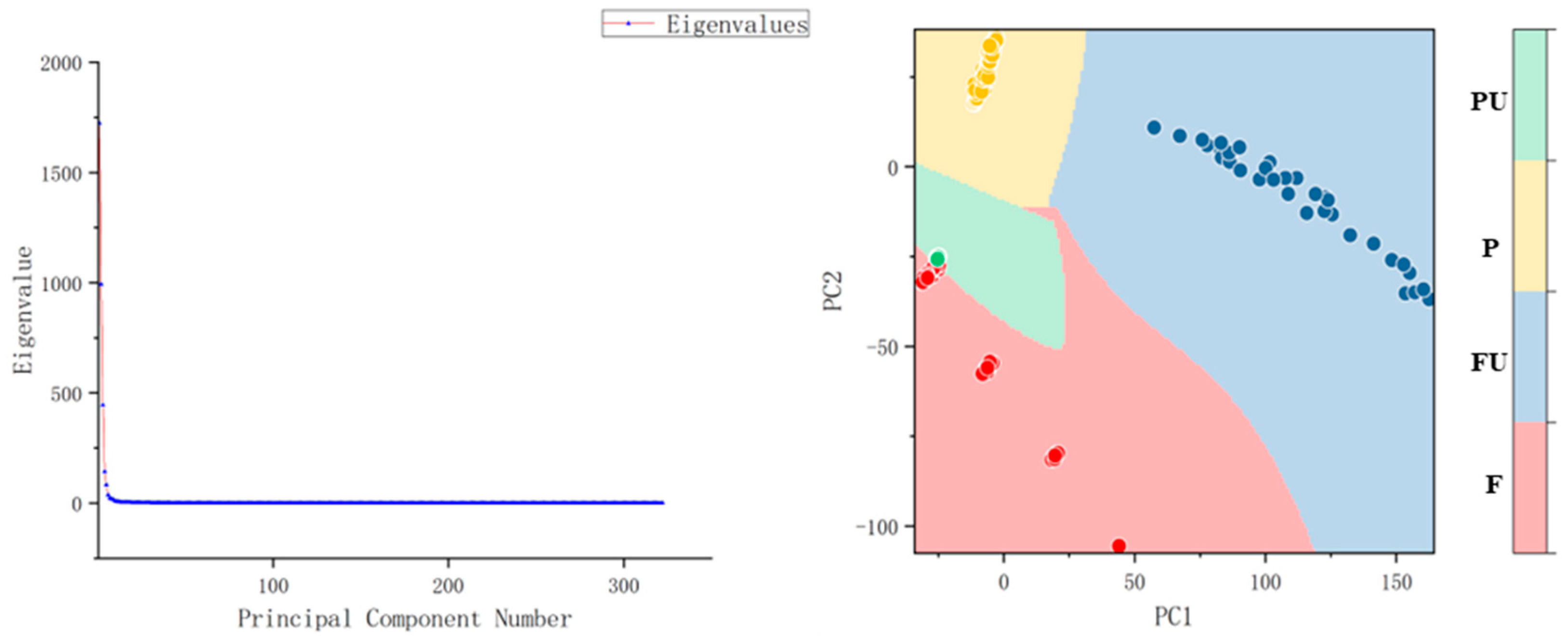
3.2. Training and Validation of the VGG16 Network and the CF-VGG11 Network
3.3. Model Performance
3.4. Comparison between the VGG Network and the PARAFAC Analysis Method
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, B.; Ma, Y.; Wang, N. A novel water pollution monitoring and treatment agent: Ag doped carbon nanoparticles for sensing dichromate, morphological analysis of Cr and sterilization. Microchem. J. 2020, 157, 104855. [Google Scholar] [CrossRef]
- Zhong, R.S.; Zhang, X.H.; Guan, Y.T.; Mao, X.Z. Three-Dimensional Fluorescence Fingerprint for Source Determination of Dissolved Organic Matters in Polluted River. Spectrosc. Spectr. Anal. 2008, 28, 347–351. [Google Scholar]
- Duan, P.; Wei, M.; Yao, L.; Li, M. Relationship between non-point source pollution and fluorescence fingerprint of riverine dissolved organic matter is season dependent. Sci. Total Environ. 2022, 823, 153617. [Google Scholar] [CrossRef] [PubMed]
- Gunnarsdottir, M.J.; Gardarsson, S.M.; Figueras, M.J.; Puigdomènech, C.; Juárez, R.; Saucedo, G. Water safety plan enhancements with improved drinking water quality detection techniques. Sci. Total Environ. 2020, 698, 134185. [Google Scholar] [CrossRef] [PubMed]
- Rizk, R.; Alameraw, M.; Rawash, M.A.; Juzsakova, T.; Domokos, E.; Hedfi, A.; Almalki, M.; Boufahj, F.; Gabriel, P.; Shafik, H.M.; et al. Does the Balaton Lake affected by pollution? Assessment through Surface Water Quality Monitoring by using different assessment methods. Saudi J. Biol. Sci. 2021, 28, 5250–5260. [Google Scholar] [CrossRef]
- Baghoth, S.A.; Sharma, S.K.; Amy, G.L. Tracking natural organic matter (NOM) in a drinking water treatment plant using fluorescence excitation–emission matrices and PARAFAC. Water Res. 2011, 45, 797–809. [Google Scholar] [CrossRef]
- Shi, F. Research on Open-Set Recognition of Organic Pollutants in Water Based on 3D Fluorescence Spectroscopy; Zhejiang University: Zhejiang, China, 2021. [Google Scholar]
- Xu, R.Z.; Cao, J.S.; Feng, G.; Luo, J.Y.; Feng, Q.; Ni, B.J.; Fang, F. Fast identification of fluorescent components in three-dimensional excitation-emission matrix fluorescence spectra via deep learning. Chem. Eng. J. 2022, 430, 132893. [Google Scholar] [CrossRef]
- Xu, R.Y.; Zhu, Z.W.; Hu, Y.J.; Zhang, Y.; Chen, G.Q. The Discrimination of Chinese Strong Aroma Type Liquors with Three-Dimensional Fluorescence Spectroscopy Combined with Principal Component Analysis and Support Vector Matchine. Spectrosc. Spectr. Anal. 2016, 36, 1021–1026. [Google Scholar]
- Zhang, H.; Li, H.; Gao, D.; Yu, H. Source identification of surface water pollution using multivariate statistics combined with physicochemical and socioeconomic parameters. Sci. Total Environ. 2022, 806, 151274. [Google Scholar] [CrossRef]
- Andersen, C.M.; Bro, R. Practical aspects of PARAFAC modeling of fluorescence excitation-emission data. J. Chemom. 2003, 17, 200–215. [Google Scholar] [CrossRef]
- ECarstea, M.; Bridgeman, J.; Baker, A.; Reynolds, D.M. Fluorescence spectroscopy for wastewater monitoring: A review. Water Res. 2016, 95, 205–219. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Liu, Y.; Sun, X.; Miao, S.; Guo, Y.; Li, T. Characterization of fluorescent dissolved organic matter from green macroalgae (Ulva prolifera)-derived biochar by excitation-emission matrix combined with parallel factor and self-organizing maps analyses. Bioresour. Technol. 2019, 287, 121471. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.; Huang, S.; Lei, S.; Yue, J.; Su, Z.; Si, F. Quantity and quality variations of dissolved organic matter (DOM) in column leaching process from agricultural soil: Hydrochemical effects and DOM fractionation. Sci. Total Environ. 2019, 691, 407–416. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.M.; Seo, Y.S.; Hur, J. Investigation of adsorptive fractionation of humic acid on graphene oxide using fluorescence EEM-PARAFAC. Water Res. 2015, 73, 242–251. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wang, Y.; Zhang, W.; Yu, S.; Wang, X.; Gao, N. New advances in fluorescence excitation-emission matrix spectroscopy for the characterization of dissolved organic matter in drinking water treatment: A review. Chem. Eng. J. 2020, 381, 122676. [Google Scholar] [CrossRef]
- Chen, W.; Westerhoff, P.; Leenheer, J.A.; Booksh, K. Fluorescence excitation—Emission matrix regional integration to quantify spectra for dissolved organic matter. Environ. Sci. Technol. 2003, 37, 5701–5710. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, Y.; Jaffé, R. Characterizing the interactions between trace metals and dissolved organic matter using excitation—Emission matrix and parallel factor analysis. Environ. Sci. Technol. 2008, 42, 7374–7379. [Google Scholar] [CrossRef]
- Guimet, F.; Ferré, J.; Boqué, R.; Rius, F.X. Application of unfold principal component analysis and parallel factor analysis to the exploratory analysis of olive oils by means of excitation–emission matrix fluorescence spectroscopy. Anal. Chim. Acta 2004, 515, 75–85. [Google Scholar] [CrossRef]
- Peiris, R.H.; Hallé, C.; Budman, H.; Moresoli, C.; Peldszus, S.; Huck, P.M.; Legge, R.L. Identifying fouling events in a membrane-based drinking water treatment process using principal component analysis of fluorescence excitation-emission matrices. Water Res. 2010, 44, 185–194. [Google Scholar] [CrossRef]
- Cuss, C.W.; McConnell, S.M.; Guéguen, C. Combining parallel factor analysis and machine learning for the classification of dissolved organic matter according to source using fluorescence signatures. Chemosphere 2016, 155, 283–291. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, Z.; Tian, R.; Shang, Z.; Liu, H. Identification and quantification of counterfeit sesame oil by 3D fluorescence spectroscopy and convolutional neural network. Food Chem. 2020, 311, 125882. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Li, J.; Ruan, K.; Sun, M.; Zhang, S.; Liu, T.; Yin, J.; Wang, X.; Chen, H.; Wang, Y.; et al. Deep learning-assisted smartphone-based ratio fluorescence for “on–off-on” sensing of Hg2+ and thiram. Chem. Eng. J. 2022, 435, 134979. [Google Scholar] [CrossRef]
- Liu, T.; Chen, S.; Ruan, K.; Zhang, S.; He, K.; Li, J.; Chen, M.; Yin, J.; Sun, M.; Wang, X.; et al. A handheld multifunctional smartphone platform integrated with 3D printing portable device: On-site evaluation for glutathione and azodicarbonamide with machine learning. J. Hazard. Mater. 2022, 426, 128091. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.R.; Stedmon, C.A.; Graeber, D.; Bro, R. Fluorescence spectroscopy and multi-way techniques. PARAFAC. Anal. Methods 2013, 5, 6557–6566. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.Z.; Peleato, N.M.; Legge, R.L.; Andrews, R.C. Fluorescence excitation emission matrices for rapid detection of polycyclic aromatic hydrocarbons and pesticides in surface waters. Environ. Sci. Water Res. Technol. 2019, 5, 315–324. [Google Scholar] [CrossRef]
- Lawaetz, A.J.; Stedmon, C.A. Fluorescence intensity calibration using the Raman scatter peak of water. Appl. Spectrosc. 2009, 63, 936–940. [Google Scholar] [CrossRef]
- Stedmon, C.A.; Markager, S.; Bro, R. Tracing dissolved organic matter in aquatic environments using a new approach to fluorescence spectroscopy. Mar. Chem. 2003, 82, 239–254. [Google Scholar] [CrossRef]
- Dagar, A.; Nandal, D. High performance Computing Algorithm Applied in Floyd Steinberg Dithering. Int. J. Comput. Appl. 2012, 43, 0975–8887. [Google Scholar]
- Niu, C.; Tan, K.; Jia, X.; Wang, X. Deep learning based regression for optically inactive inland water quality parameter estimation using airborne hyperspectral imagery. Environ. Pollut. 2021, 286, 117534. [Google Scholar] [CrossRef]
- Bro, R. PARAFAC. Tutorial and applications. Chemom. Intell. Lab. Syst. 1997, 38, 149–171. [Google Scholar] [CrossRef]
- Murphy, K.R.; Hambly, A.; Singh, S.; Henderson, R.K.; Baker, A.; Stuetz, R.; Khan, S.J. Organic Matter Fluorescence in Municipal Water Recycling Schemes: Toward a Unified PARAFAC Model. Environ. Sci. Technol. 2011, 45, 2909–2916. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.R.; Stedmon, C.A.; Wenig, P.; Bro, R. Openfluor- an online spectral library of auto-fluorescence by organic compounds in the environment. Anal. Methods 2014, 6, 658–661. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Huang, W.; Ma, S.; Feng, M.; Liu, C.; Gu, X.; Chen, K. Characterization of Chromophoric Dissolved Organic Matter in the Littoral Zones of Eutrophic Lakes Taihu and Hongze during the Algal Bloom Season. Water 2018, 10, 861. [Google Scholar] [CrossRef] [Green Version]
- Kothawala, D.; von Wachenfeldt, E.; Koehler, B.; Tranvik, L. Selective loss and preservation of lake water dissolved organic matter fluorescence during long-term dark incubations. Sci. Total Environ. 2012, 433, 238–246. [Google Scholar] [CrossRef] [PubMed]
- Osburn, C.L.; Wigdahl, C.R.; Fritz, S.C.; Saros, J.E. Dissolved organic matter composition and photoreactivity in prairie lakes of the U.S. Great plains. Limnol. Oceanogr. 2011, 56, 2371–2390. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Chen, L.; Zhang, W.; Huang, Q. Spatiotemporal distribution, sources, and photobleaching imprint of dissolved organic matter in the Yangtze estuary and its adjacent sea using fluorescence and parallel factor analysis. PLoS ONE 2015, 10, e0130852. [Google Scholar] [CrossRef]
- Tang, J.; Wu, J.; Li, Z.; Cheng, C.; Liu, B.; Chai, Y.; Wang, Y. Novel insights into variation of fluorescent dissolved organic matters during antibiotic wastewater treatment by excitation emission matrix coupled with parallel factor analysis and cosine similarity assessment. Chemosphere 2018, 210, 843–848. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.; Chen, Y.; Airiken, M. Estimation of surface water quality parameters based on hyper-spectral and 3D-EEM fluorescence technologies in the Ebinur Lake Watershed, China. Phys. Chem. Earth Parts A/B/C 2020, 118, 118–119. [Google Scholar] [CrossRef]
- Zeng, W.; Qiu, J.; Wang, D.; Wu, Z.; He, L. Ultrafiltration concentrated biogas slurry can reduce the organic pollution of groundwater in fertigation. Sci. Total Environ. 2022, 810, 151294. [Google Scholar] [CrossRef]



| Catalogues | Label | Number |
|---|---|---|
| Fu river | FU | 45 |
| Fish muscle (Andersen et al.) | F | 105 |
| PortSurvey (Murphy et al.) | P | 206 |
| Pure (drEEM Tutorial) | PU | 60 |
| Total | 416 samples | |
| Component | EXmax/Emmax | Description | Number of OpenFluor Matches |
|---|---|---|---|
| C1 | 350 nm/440 nm | terrestrial humic-like, high relative aromaticity and molecular weight [34] | 21 |
| C2 | 300 nm/400 nm | UV-A humic-like, low molecular weight [35] | 14 |
| C3 | 290 nm, 400 nm/480 nm | humic-like [35] | 4 |
| C4 | 280 nm/320 nm | autochthonous protein-like, sensitive to microbial degradation [36,37] | 11 |
| Samples | Number | Train | Validate | Test | Total Samples after Expansion |
|---|---|---|---|---|---|
| FU | 45 | 27 | 9 | 9 | 135 |
| F | 105 | 63 | 21 | 21 | 315 |
| P | 206 | 124 | 41 | 41 | 618 |
| PU | 60 | 36 | 12 | 12 | 180 |
| Total | 416 | 250 | 83 | 83 | 1248 |
| Method | Training Accuracy (%) | Sample Demand | Speed | Operation |
|---|---|---|---|---|
| VGG16 | 99.60 | ≥1 | Fast | Easy |
| PCA + SVM | 99.69 | Many | Slow | Complex |
| Train | Progress | Data | Skills | Integrate to Apps | |
|---|---|---|---|---|---|
| PARAFAC | No | Complex | ≥21 | Yes | Complex |
| VGG16+CF-VGG11 | Yes | Easy | ≥1 | No | Easy |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, K.; Zhao, S.; Jiang, X.; Li, Y.; Fei, J.; Ou, D.; Tang, Q.; Lu, Z.; Liu, T.; Xia, J. A 3D Fluorescence Classification and Component Prediction Method Based on VGG Convolutional Neural Network and PARAFAC Analysis Method. Appl. Sci. 2022, 12, 4886. https://doi.org/10.3390/app12104886
Ruan K, Zhao S, Jiang X, Li Y, Fei J, Ou D, Tang Q, Lu Z, Liu T, Xia J. A 3D Fluorescence Classification and Component Prediction Method Based on VGG Convolutional Neural Network and PARAFAC Analysis Method. Applied Sciences. 2022; 12(10):4886. https://doi.org/10.3390/app12104886
Chicago/Turabian StyleRuan, Kun, Shun Zhao, Xueqin Jiang, Yixuan Li, Jianbo Fei, Dinghua Ou, Qiang Tang, Zhiwei Lu, Tao Liu, and Jianguo Xia. 2022. "A 3D Fluorescence Classification and Component Prediction Method Based on VGG Convolutional Neural Network and PARAFAC Analysis Method" Applied Sciences 12, no. 10: 4886. https://doi.org/10.3390/app12104886
APA StyleRuan, K., Zhao, S., Jiang, X., Li, Y., Fei, J., Ou, D., Tang, Q., Lu, Z., Liu, T., & Xia, J. (2022). A 3D Fluorescence Classification and Component Prediction Method Based on VGG Convolutional Neural Network and PARAFAC Analysis Method. Applied Sciences, 12(10), 4886. https://doi.org/10.3390/app12104886







