Optimization of Pre-Splitting Blasting Hole Network Parameters and Engineering Applications in Open Pit Mine
Abstract
:1. Introduction
2. Theoretical Analysis of Pre-Splitting Blasting
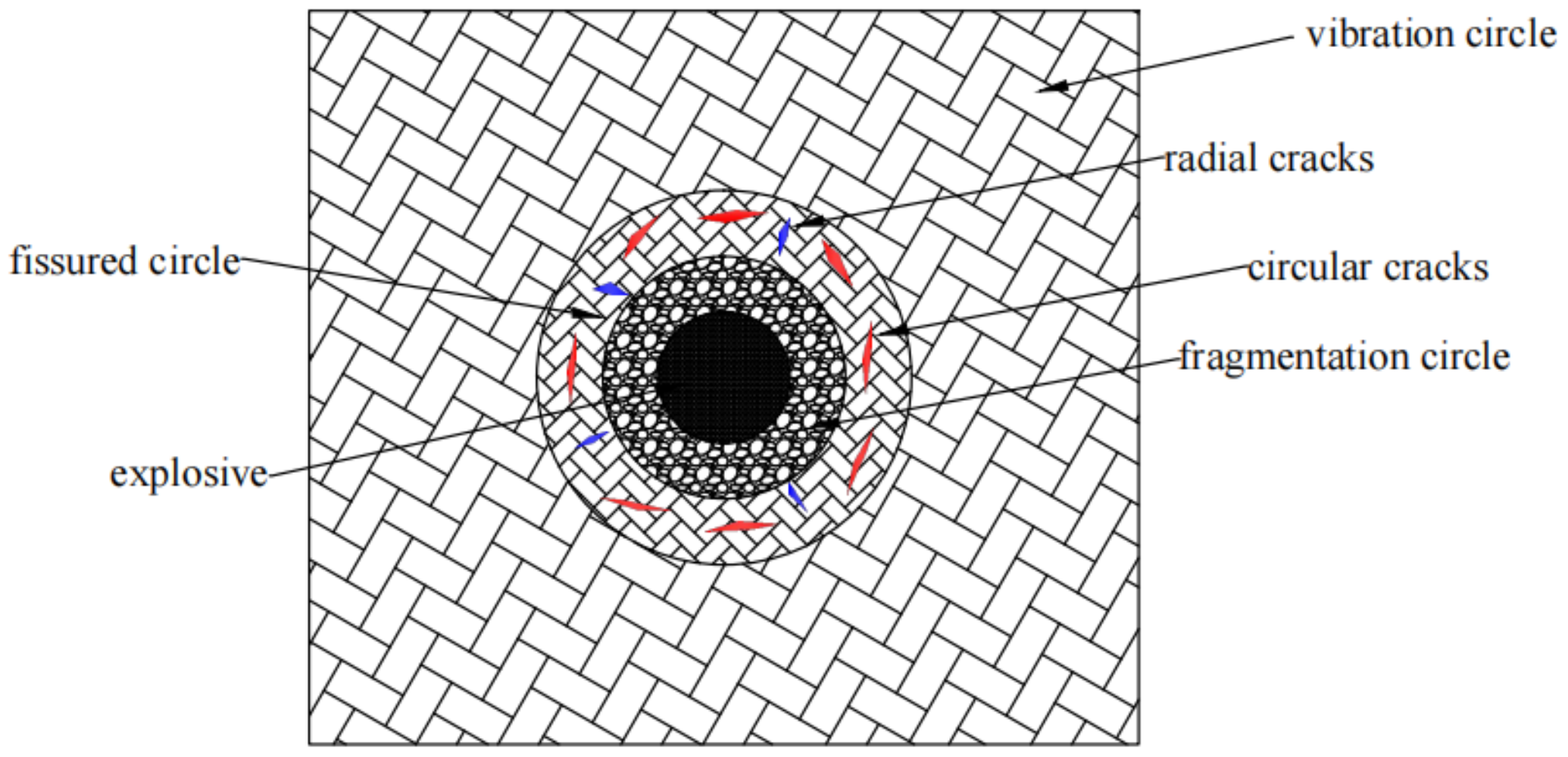
2.1. Rock Blasting Failure Theory
2.2. Propagation Law of Explosion Stress Wave
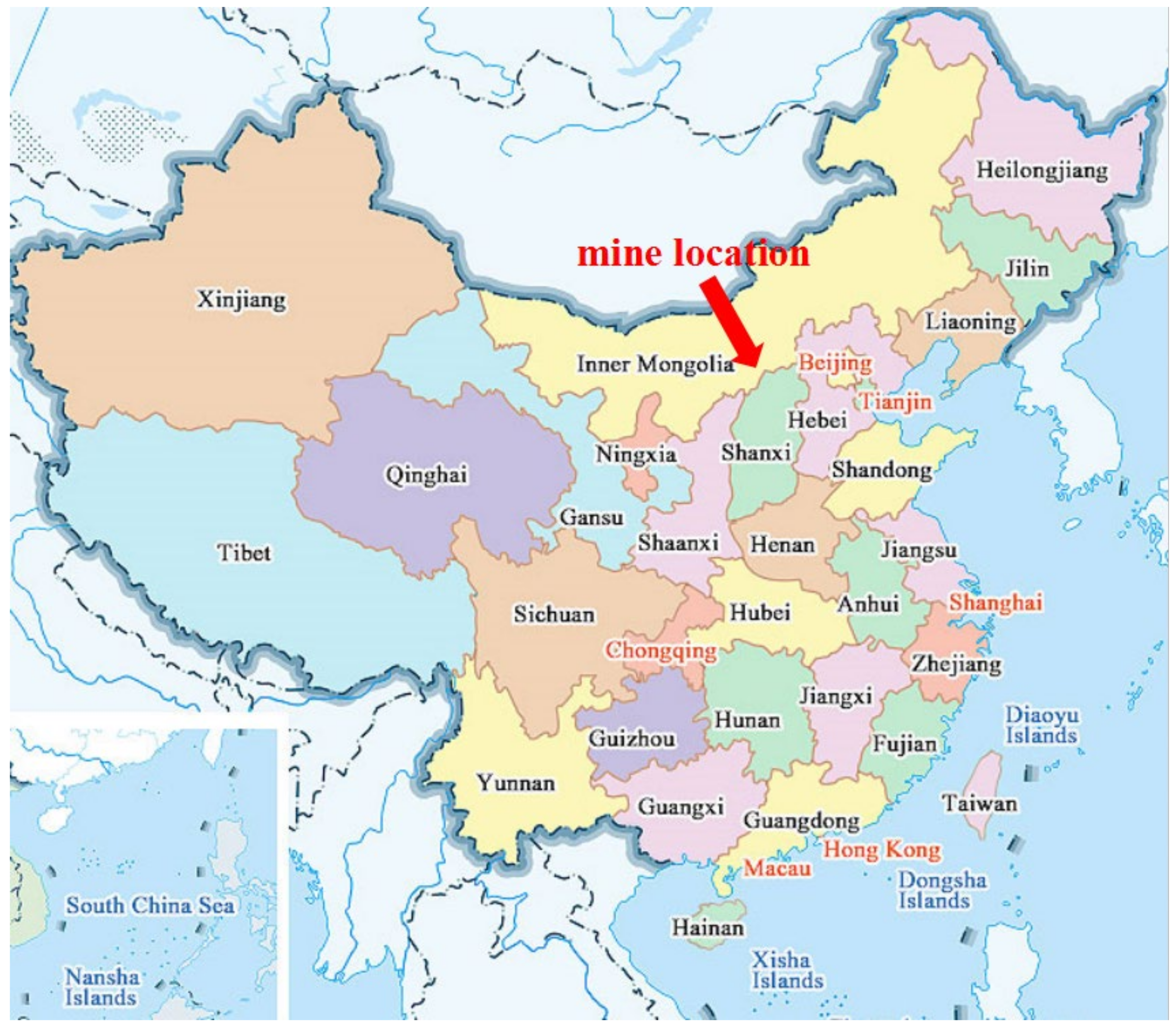
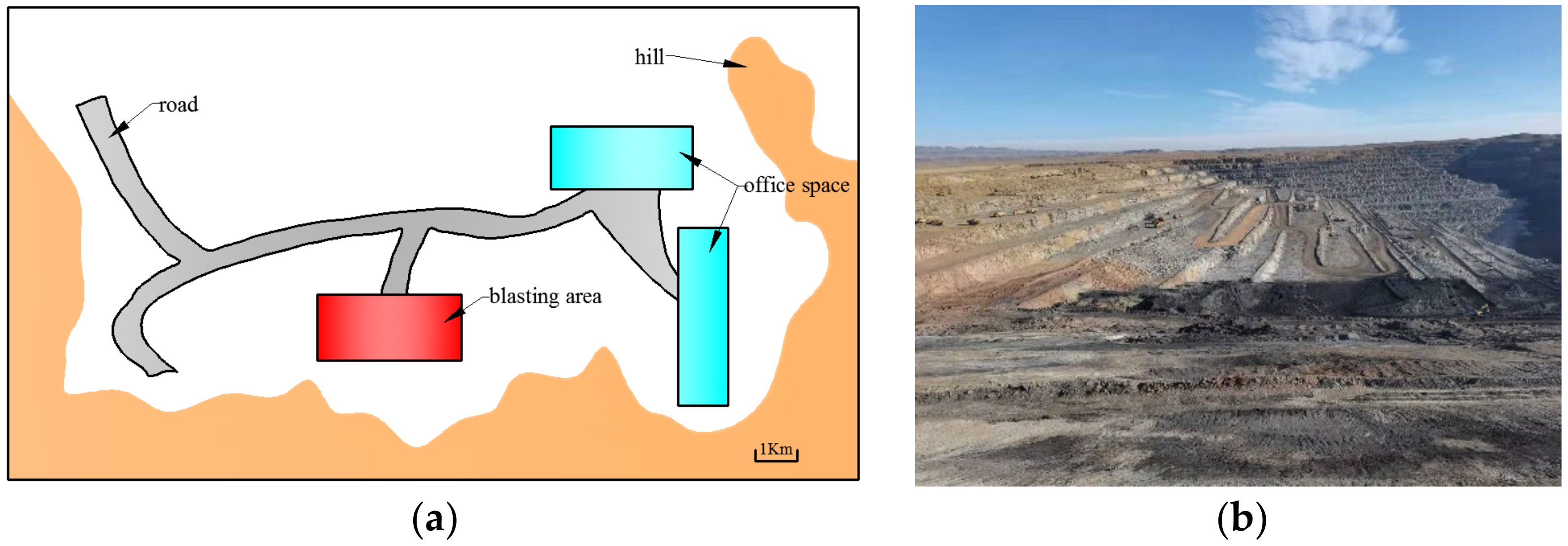
3. Engineering Overview
4. Engineering Practice
4.1. Blasting Parameter Design
4.2. Field Blasting Effect Analysis
5. Numerical Simulation of Blasting Hole Network Parameters
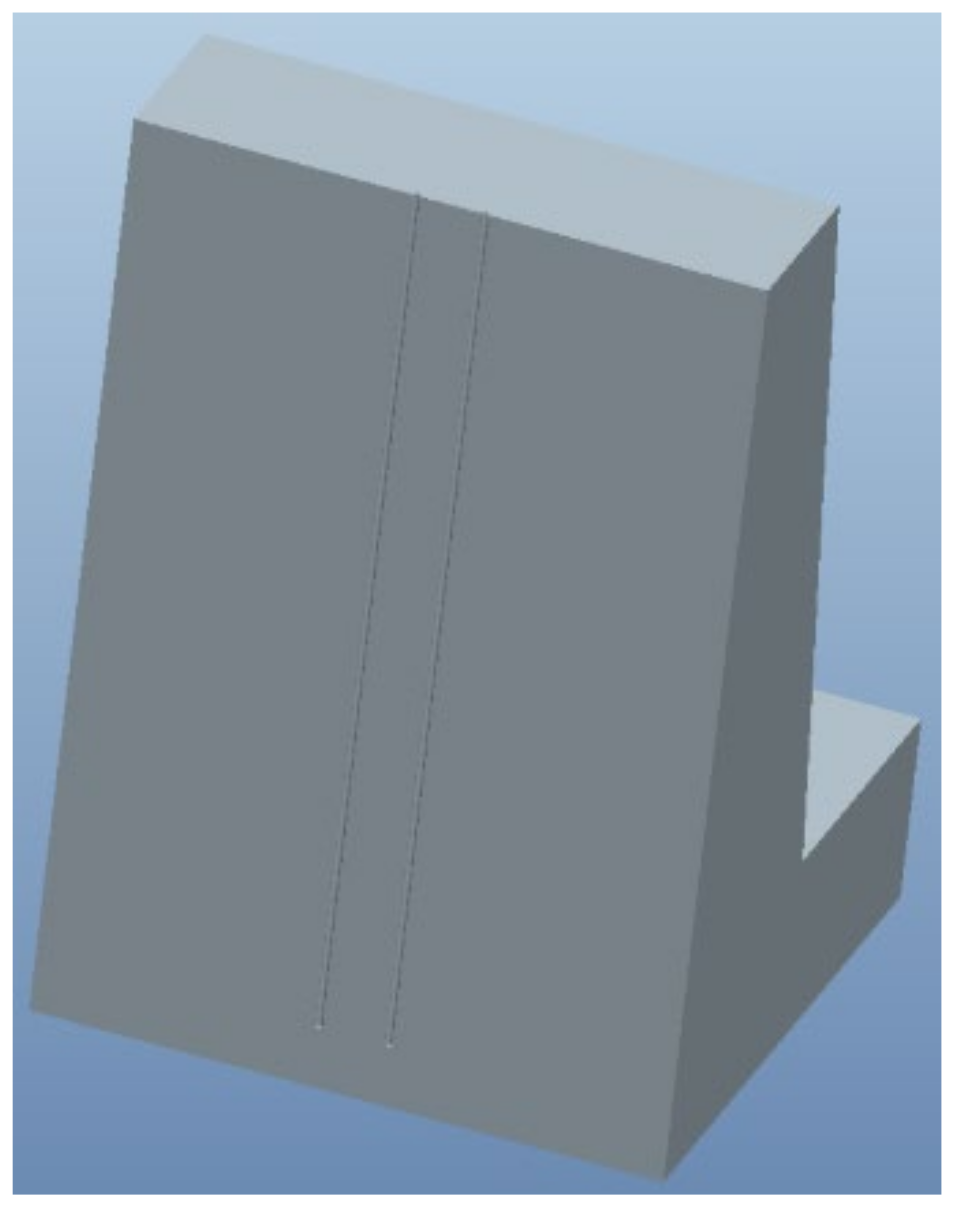
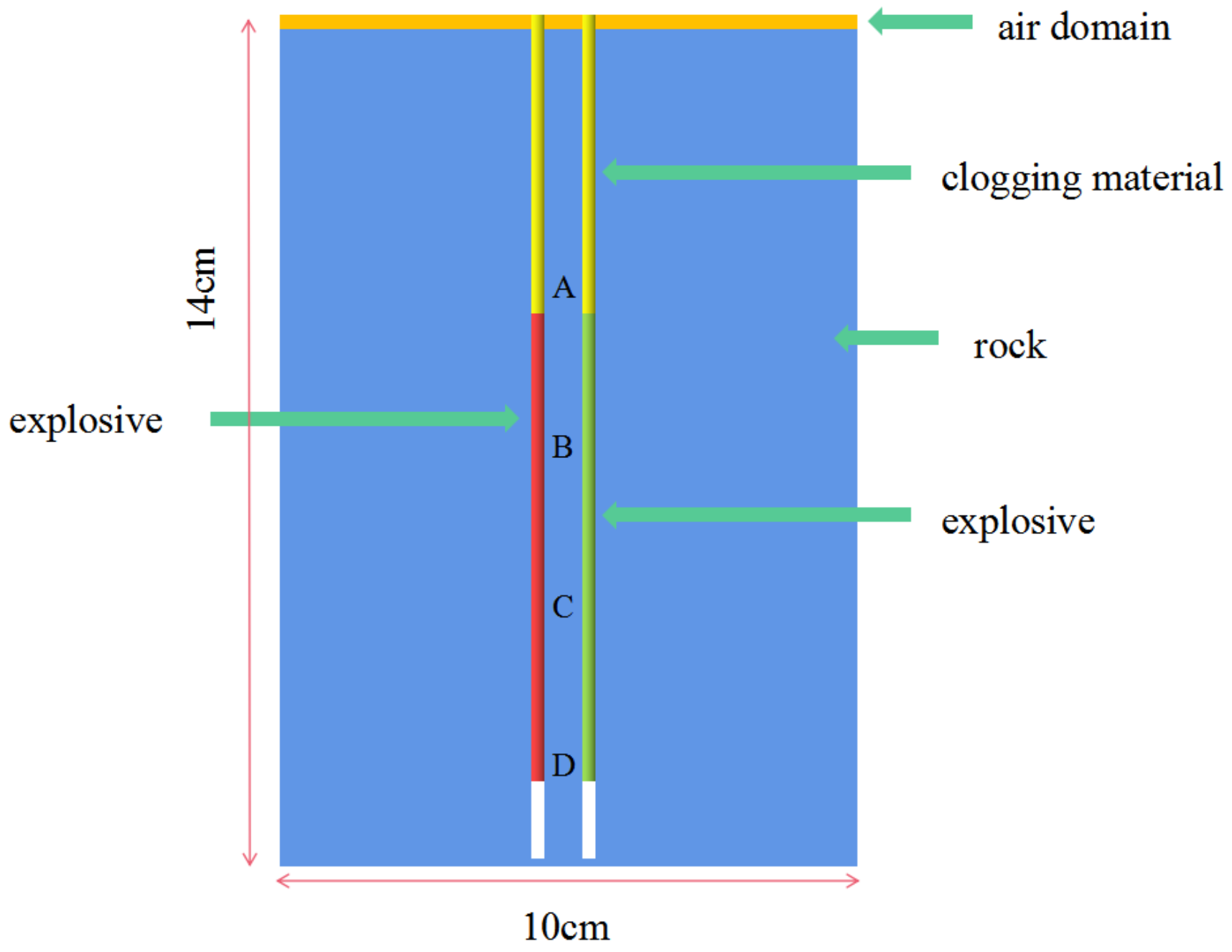
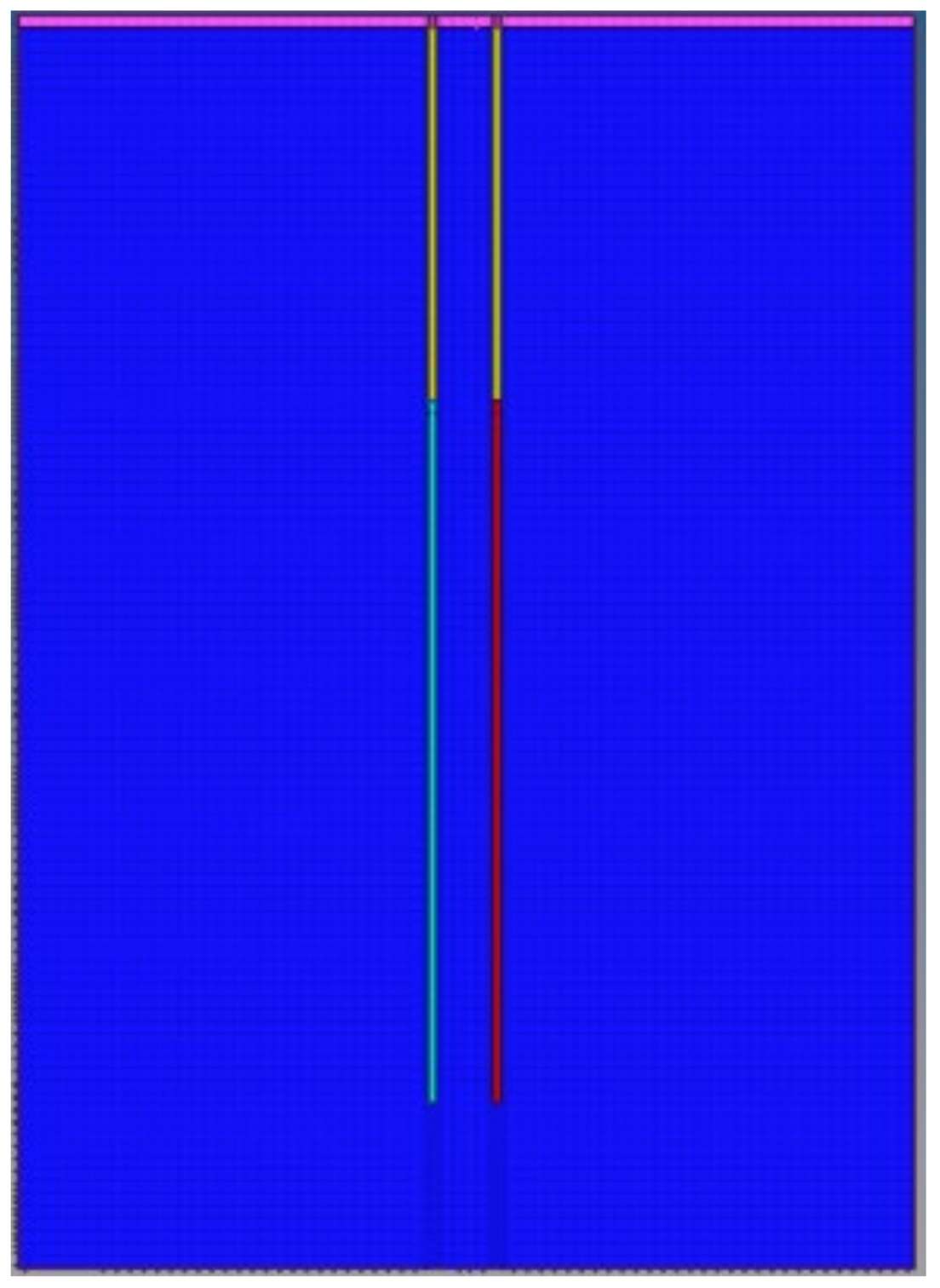
5.1. Model Establishment
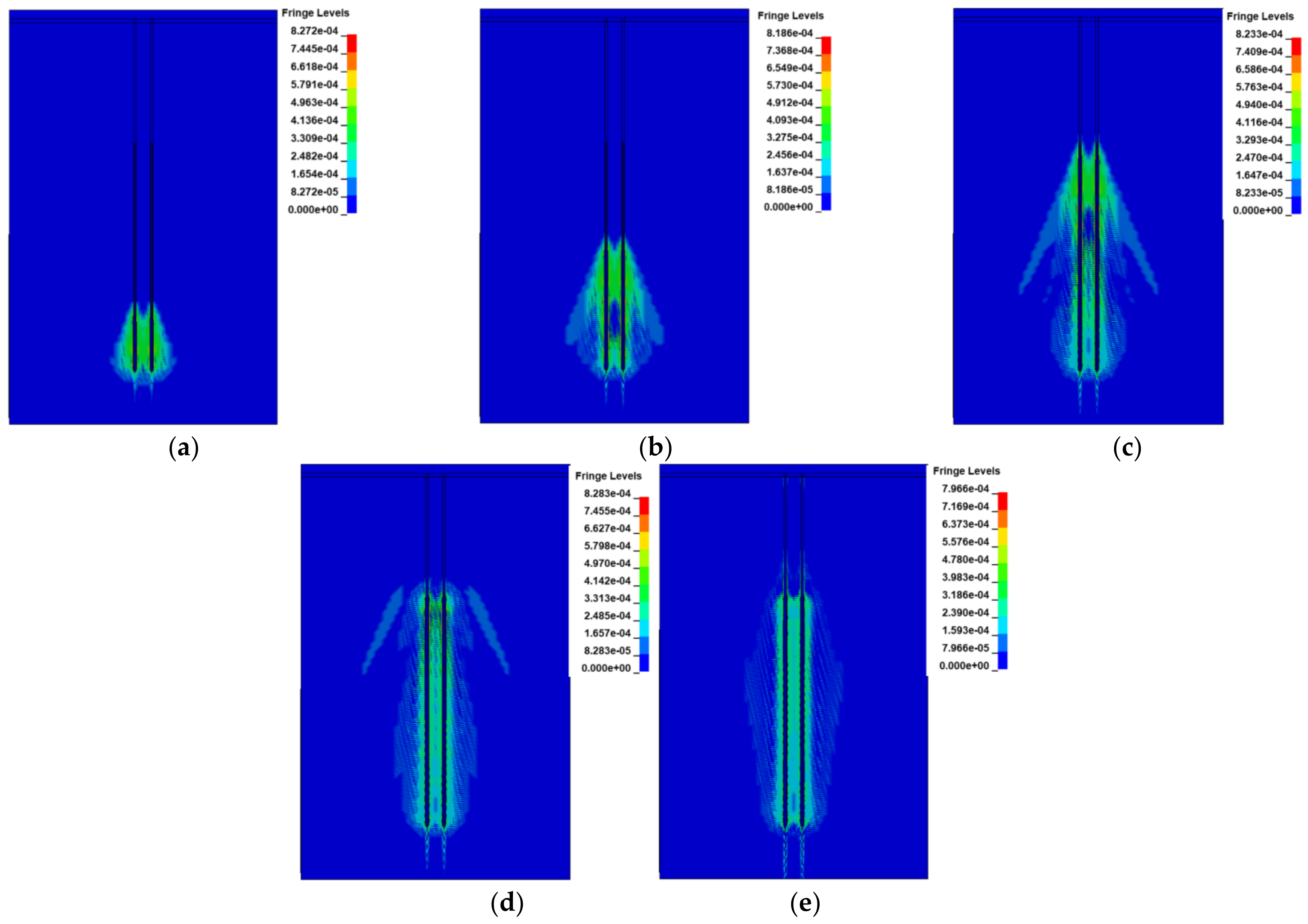
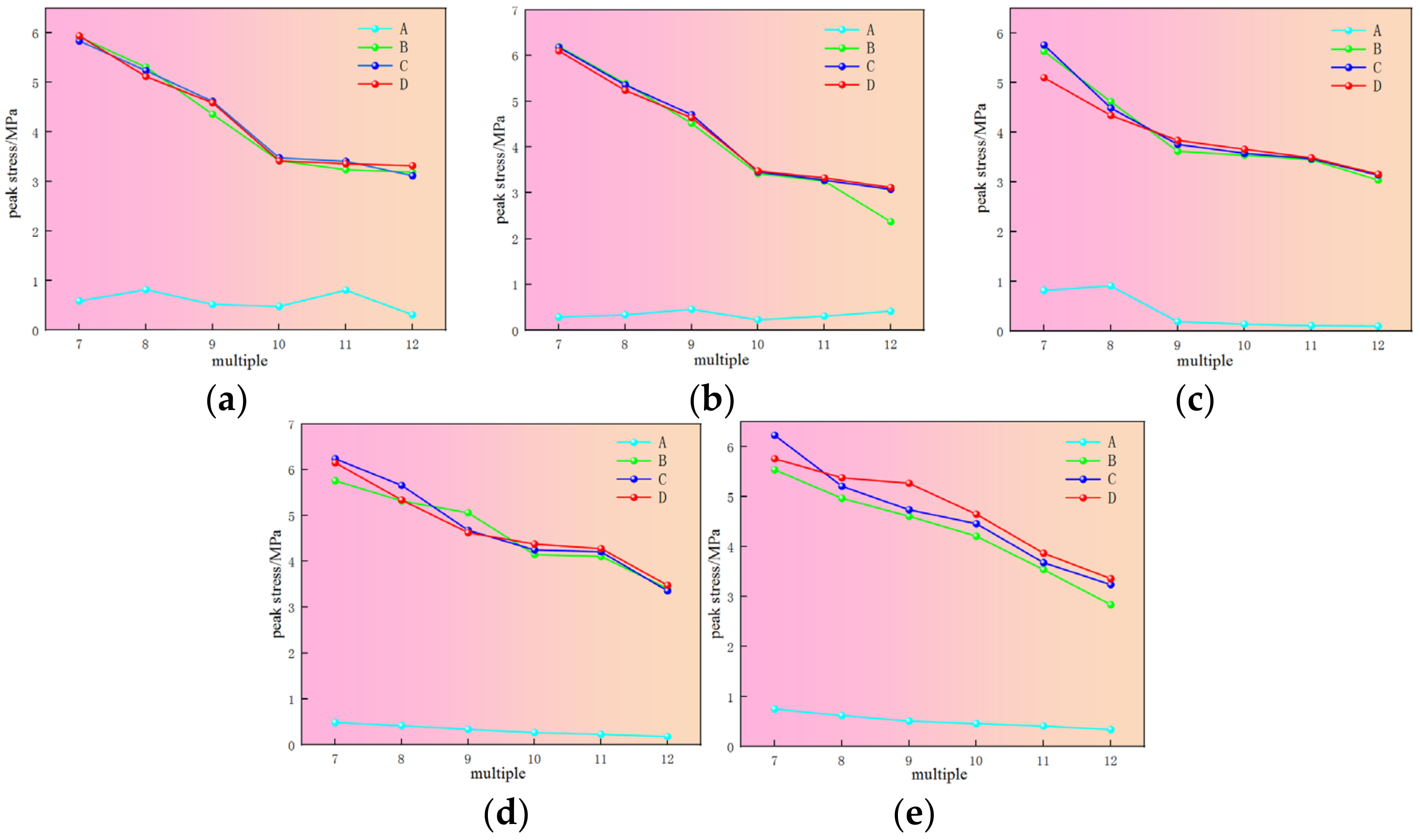
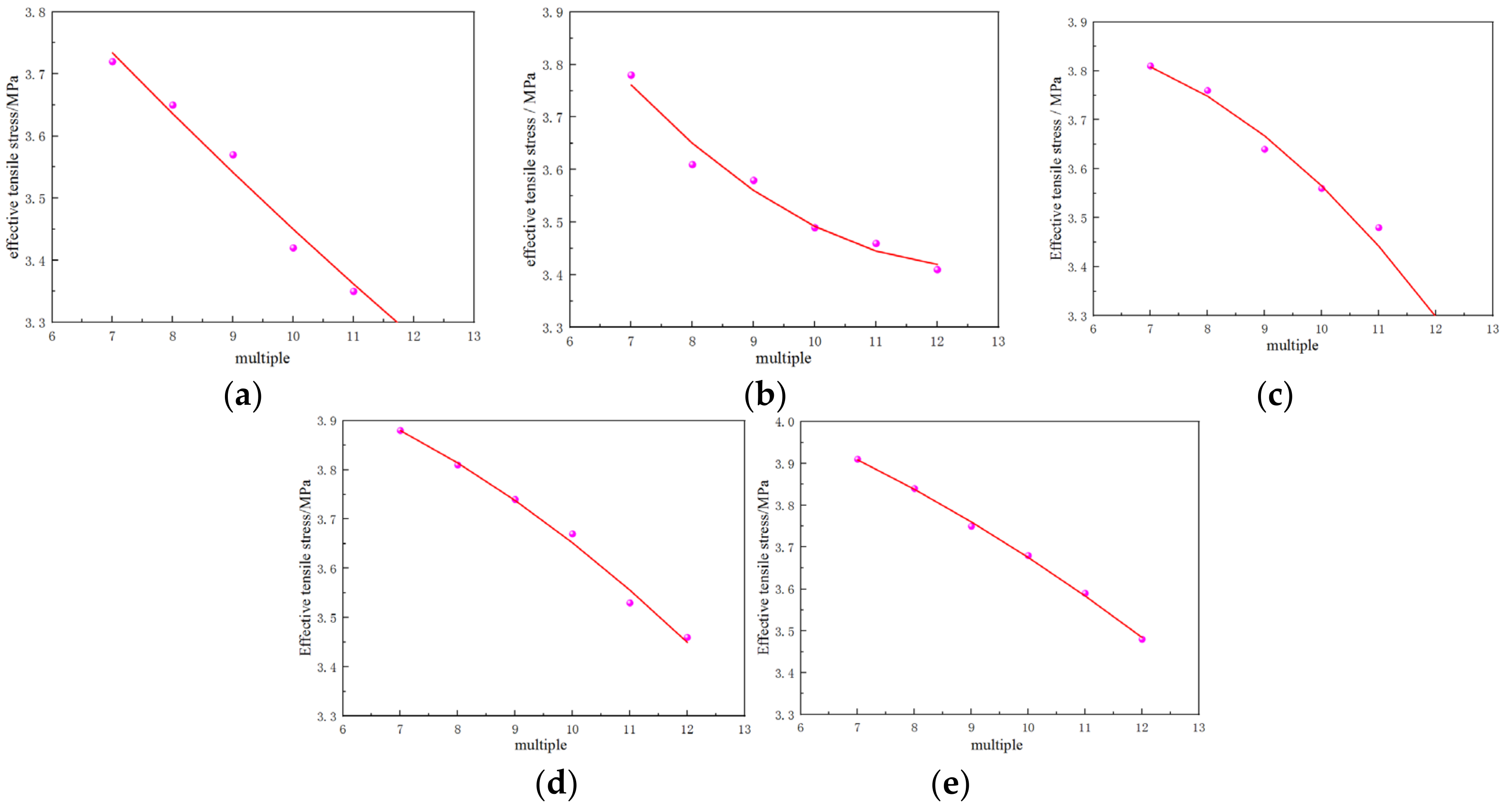
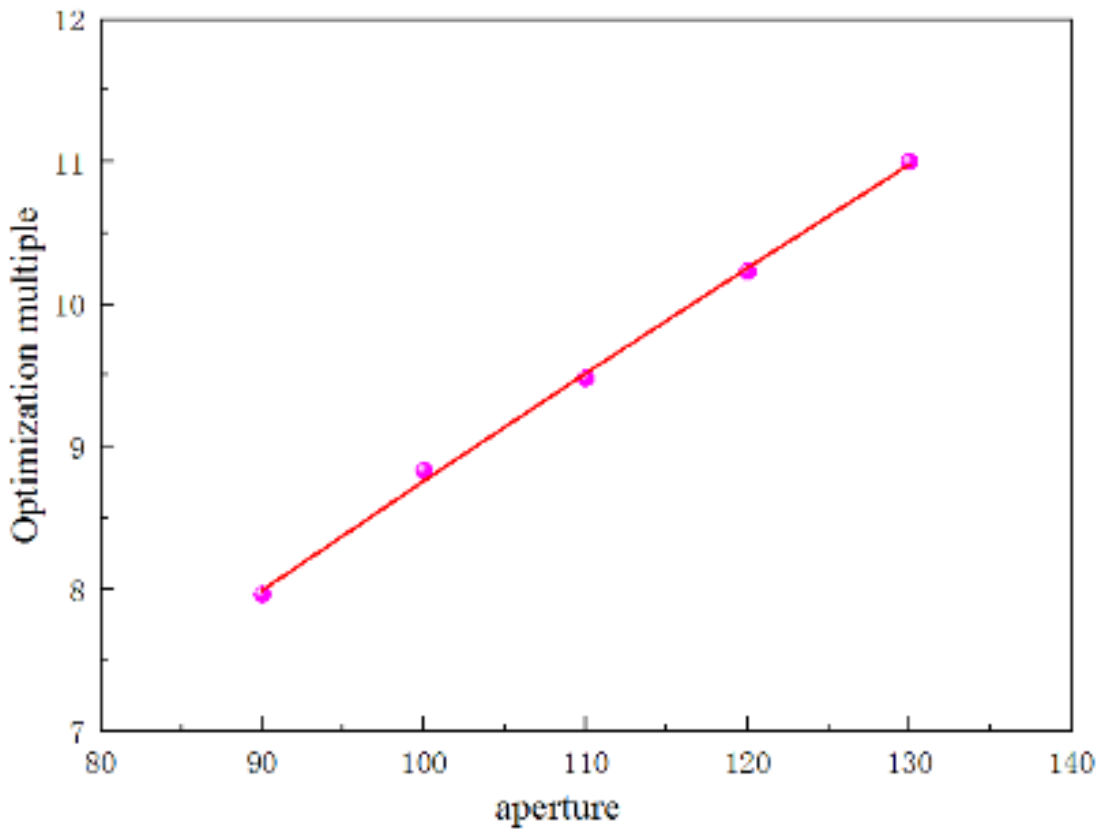
5.2. Numerical Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| Symbol List | |
| Peak stress, MPa | |
| Radial peak stress of rock element, MPa | |
| Distance between rock element and explosion source, m | |
| Attenuation coefficient of stress wave | |
| Density of explosives, g/cm3 | |
| Da | Explosive detonation velocity, cm/us |
| ra, rb | Charge radius and hole radius, mm |
| m | Pressure increase coefficient, generally m = 8~11 |
| W | Coefficient of relationship between tangential tensile stress and peak radial compressive stress |
| u | Poisson ratio |
| Tangential tensile stress, MPa | |
| P0 | Initial stress, MPa |
| K | Adiabatic isentropic index of explosives |
| y | Optimal hole diameter and distance between holes |
| x | Hole diameter, mm |
References
- Wu, T.; Zhou, C.; Jiang, N.; Xia, Y.; Zhang, Y. Stability analysis for high-steep slope subjected to repeated blasting vibration. Arab. J. Geosci. 2020, 13, 828. [Google Scholar] [CrossRef]
- Aliabadian, Z.; Sharafisafa, M. Numerical modeling of presplitting controlled method in continuum rock masses. Arab. J. Geosci. 2014, 22, 5005–5020. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, W.; Chen, M.; Yan, P.; Yang, J. Comparison of Blast-Induced Damage Between Presplit and Smooth Blasting of High Rock Slope. Rock Mech. Rock Eng. 2014, 47, 1307–1320. [Google Scholar] [CrossRef]
- Chen, Y.K.; Xu, J.H.; Wang, J.C. Numerical Simulation of Dynamic Damage and Stability of A Bedding Rock Slope Under Blasting Load. Shock. Vib. 2019, 2019, 9616859. [Google Scholar] [CrossRef] [Green Version]
- Raina, A.K. Influence of Joint Conditions and Blast Design on Pre-split Blasting Using Response Surface Analysis. Rock Mech. Rock Eng. 2019, 52, 4057–4070. [Google Scholar] [CrossRef]
- Cheng, S.; Ma, Z.; Gong, P.; Li, K.; Li, N.; Wang, T. Controlling the Deformation of a Small Coal Pillar Retaining Roadway by Non-Penetrating Directional Pre-Splitting Blasting with a Deep Hole: A Case Study in Wangzhuang Coal Mine. Energies 2020, 13, 3084. [Google Scholar] [CrossRef]
- Paurush, P.; Rai, P.; Sharma, S.K. Selection of Blasting Design Parameters Affecting Peak Particle Velocity-a Case Study. Min. Metall. Explor. 2021, 38, 1435–1447. [Google Scholar] [CrossRef]
- Kabetenov, T.; Yusupov, K.A.; Rustemov, S.T. Rational parameters of blasting, considering action time of explosion-generated pulse. J. Min. Sci. 2015, 51, 261–266. [Google Scholar] [CrossRef]
- Xiang-Long, L.; Qi-Wen, H.; Xue-Bin, M.; Ke-Gang, L.; Jian-Qiang, X. Experimental Research On Presplitting Blasting Of The Final Highwall Of An Opencast Coal Mine. J. Balk. Tribol. Assoc. 2016, 22, 2857–2869. [Google Scholar]
- Yuan, Y.; Yuan, C.F.; Zhu, C.; Liu, H.X.; Wang, S.Z. Study on the disaster reduction mechanism of presplitting blasting and reasonable blasting parameters for shallowly buried remnant pillars. Energy Sci. Eng. 2020, 7, 2884–2894. [Google Scholar] [CrossRef]
- Chen, B.B.; Liu, C.Y.; Yang, J.X. Design and Application of Blasting Parameters for Presplitting Hard Roof with the Aid of Empty-Hole Effect. Shock. Vib. 2018, 2018, 8749415. [Google Scholar] [CrossRef] [Green Version]
- Sharma, S.K.; Rai, P. Establishment of blasting design parameters influencing mean fragment size using state-of-art statistical tools and techniques. Measurement 2017, 1, 34–51. [Google Scholar] [CrossRef]
- Roy, M.P.; Mishra, A.K.; Agrawal, H.; Singh, P.K. Blast vibration dependence on total explosives weight in open-pit blasting. Arab. J. Geosci. 2020, 13, 531. [Google Scholar] [CrossRef]
- Yang, R.S.; Su, H. Experimental study on crack propagation with pre-crack under explosive load. J. China Coal Soc. 2019, 44, 482–489. [Google Scholar]
- Su, H.; Gong, Y.; Yang, R. Influence of pre-split-ting crack width on crack propagation under blast loading. J. China Univ. Min. Technol. 2021, 50, 579–586. [Google Scholar]
- Ma, L.; Li, K.; Xiao, S.; Ding, X.; Chinyanta, S. Research on effects of blast casting vibration and vibration absorption of presplitting blasting in open cast mine. Shock. Vib. 2016, 2016, 4091732. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Wang, J.; Xiao, J.; Tang, L.; Lin, Y. Pre-splitting blasting vibration reduction effect research on weak rock mass. Disaster Adv. 2013, 6, 338–343. [Google Scholar]
- Han, Y.Z.; Liu, H.B. Finite Element Simulation of Medium-Range Blast Loading Using LS-DYNA. Shock. Vib. 2015, 2015, 631493. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Li, H.; Shao, Z.; Chen, S.; Li, X. Investigating the mechanism of rock fracturing induced by high-pressure gas blasting with a hybrid continuum-discontinuum method. Comput. Geotech. 2021, 140, 104445. [Google Scholar] [CrossRef]
- Xu, P.; Yang, R.; Zuo, J.; Ding, C.; Chen, C.; Guo, Y.; Fang, S.; Zhang, Y. Research progress of the fundamental theory and technology of rock blasting. Int. J. Miner. Metall. Mater. 2022, 29, 705–716. [Google Scholar] [CrossRef]
- Banadaki, M.M.D.; Mohanty, B. Numerical simulation of stress wave induced fractures in rock. Int. J. Impact Eng. 2012, 40, 16–25. [Google Scholar] [CrossRef]
- Yi, C.; Johansson, D.; Nyberg, U.; Beyglou, A. Stress Wave Interaction between Two Adjacent Blast Holes. Rock Mech. Rock Eng. 2015, 49, 1803–1812. [Google Scholar] [CrossRef]
- Beijing, X.; Ai, D.; Yang, Y. Crack Detection and Evolution Law for Rock Mass under SHPB Impact Tests. Shock. Vib. 2019, 2019, 3956749. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.H.; Wu, J.; Zhang, Z.H. Blasting Source Equivalent Load on Elastic-Plastic Boundary for Rock Blasting. J. Eng. Mech. 2017, 143, 4017034. [Google Scholar] [CrossRef]







| Slope Location | Petrofabric Types | Structure of Rock Mass | |
|---|---|---|---|
| Earth’s Surface | Deep Part | ||
| northwest side | quartzite | lumpy | lumpy |
| north wall | quartzite | layered-block | layered-block |
| southeastern part | feldspar slate | layered-block | layered-block |
| south slope | feldspar slate | layer-fragmentation | laminarization |
| northeast Gang | mica-schist | thinly bedded | thinly bedded |
| Density ρ g/cm3 | Modulus of Elasticity E/GPa | Poisson’s Ratio v | Yield Strength MPa | Tangent Modulus GPa |
|---|---|---|---|---|
| 2.43 | 156 | 0.26 | 3 | 11.3 |
| Density ρ g/cm3 | Modulus of Elasticity E/GPa | Poisson’s Ratio v | Yield Strength MPa | Tangent Modulus GPa |
|---|---|---|---|---|
| 1.8 | 1.38 | 0.33 | 0.77 | 0.13 |
| Density ρ g/cm3 | Detonation Velocity cm/us | Detonation Pressure Mbar | A | B | R1 | R2 | ω | E Mbar |
|---|---|---|---|---|---|---|---|---|
| 1.25 | 0.35 | 0.04 | 2.144 | 0.00182 | 4.2 | 0.9 | 0.15 | 0.0419 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wu, G.; Zhou, L. Optimization of Pre-Splitting Blasting Hole Network Parameters and Engineering Applications in Open Pit Mine. Appl. Sci. 2022, 12, 4930. https://doi.org/10.3390/app12104930
Wang Z, Wu G, Zhou L. Optimization of Pre-Splitting Blasting Hole Network Parameters and Engineering Applications in Open Pit Mine. Applied Sciences. 2022; 12(10):4930. https://doi.org/10.3390/app12104930
Chicago/Turabian StyleWang, Ziyi, Guiyi Wu, and Lang Zhou. 2022. "Optimization of Pre-Splitting Blasting Hole Network Parameters and Engineering Applications in Open Pit Mine" Applied Sciences 12, no. 10: 4930. https://doi.org/10.3390/app12104930
APA StyleWang, Z., Wu, G., & Zhou, L. (2022). Optimization of Pre-Splitting Blasting Hole Network Parameters and Engineering Applications in Open Pit Mine. Applied Sciences, 12(10), 4930. https://doi.org/10.3390/app12104930






