Improved Ultrasonic Dead Zone Detectability of Work Rolls Using a Convolutional Neural Network
Abstract
:1. Introduction
2. Experimental Procedures
2.1. Specimen
2.2. Experimental Setup
3. Database Implementation
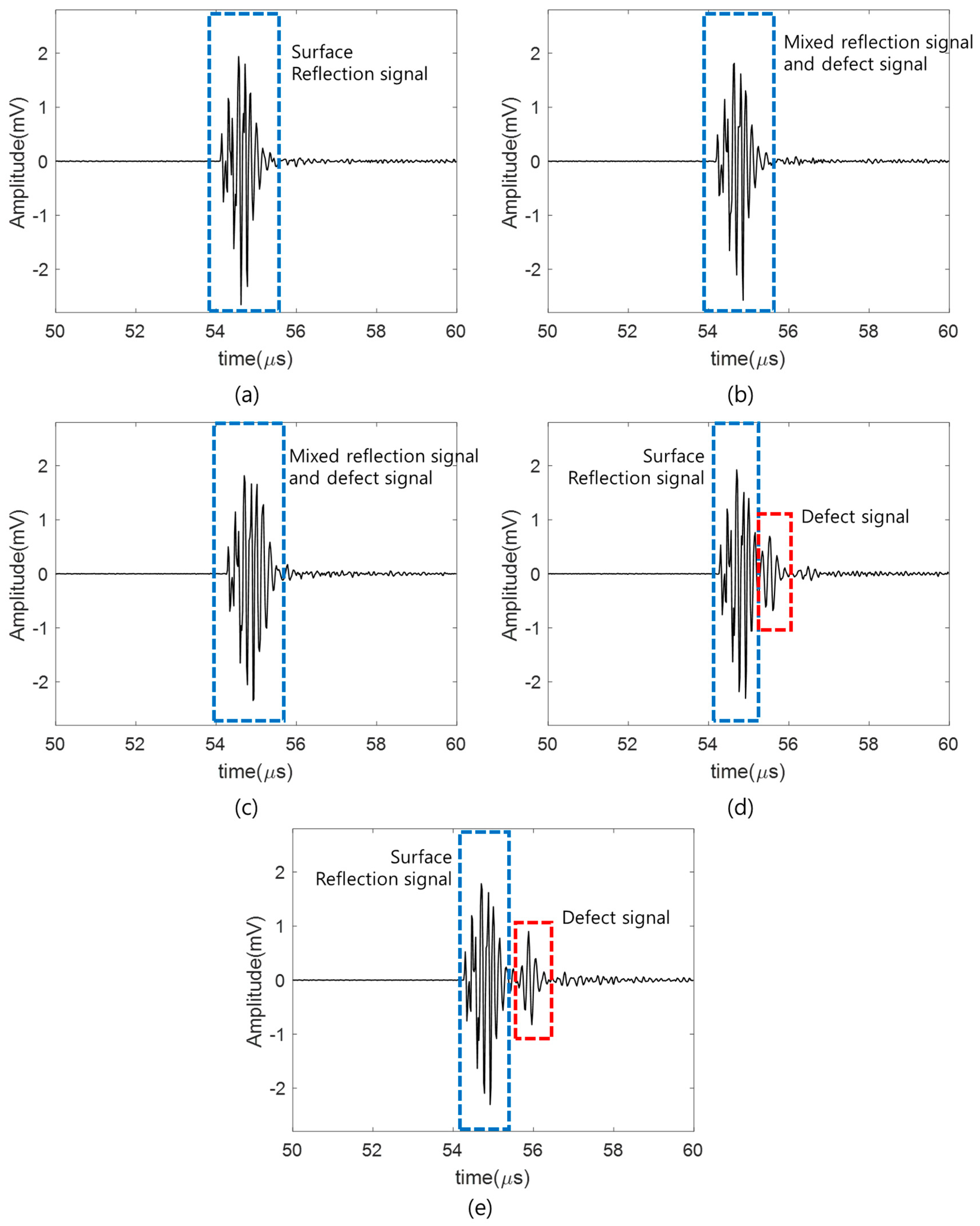
3.1. Ultrasonic Database
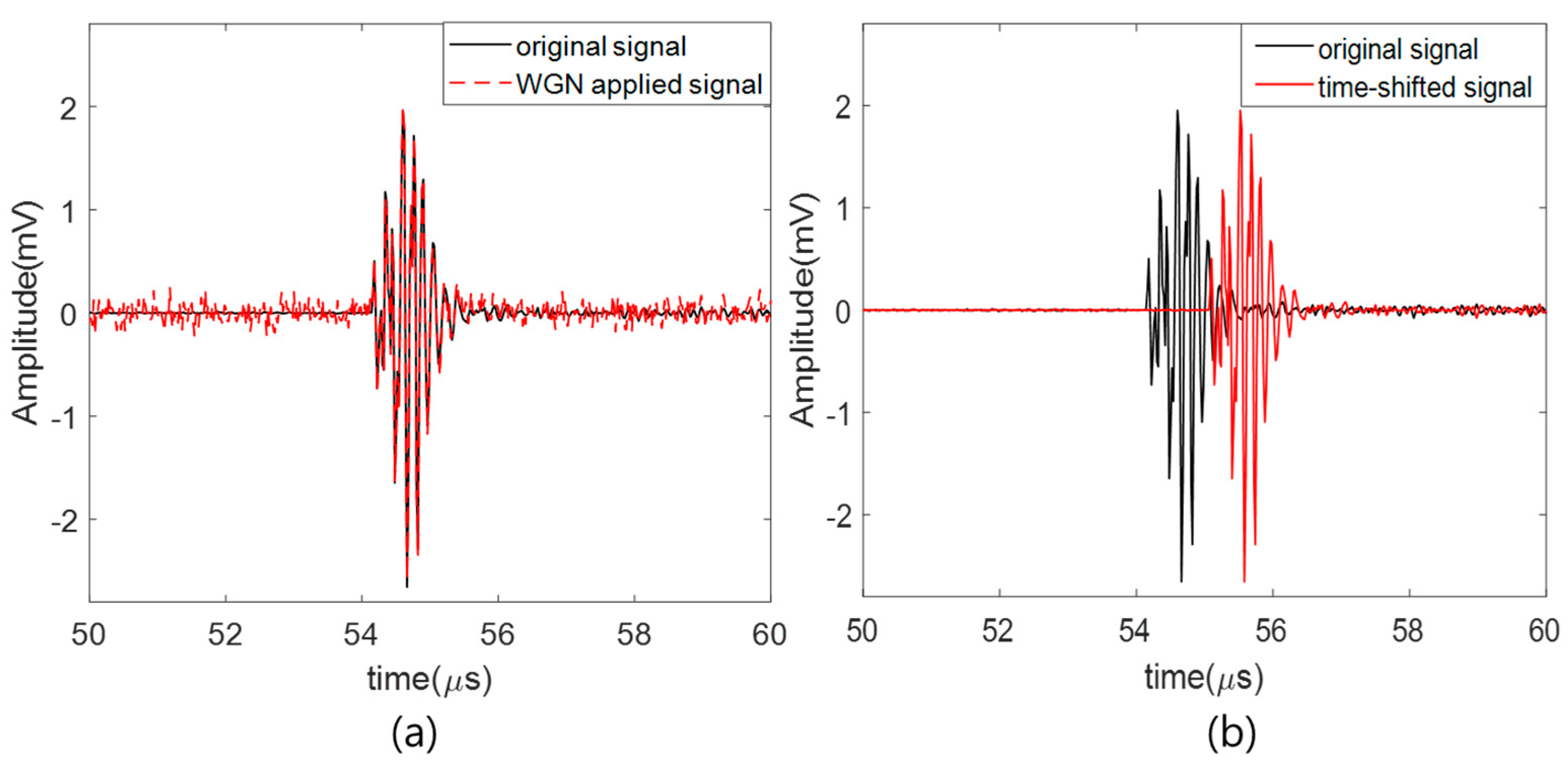
3.2. Database Augmentation
4. Artificial Neural Networks
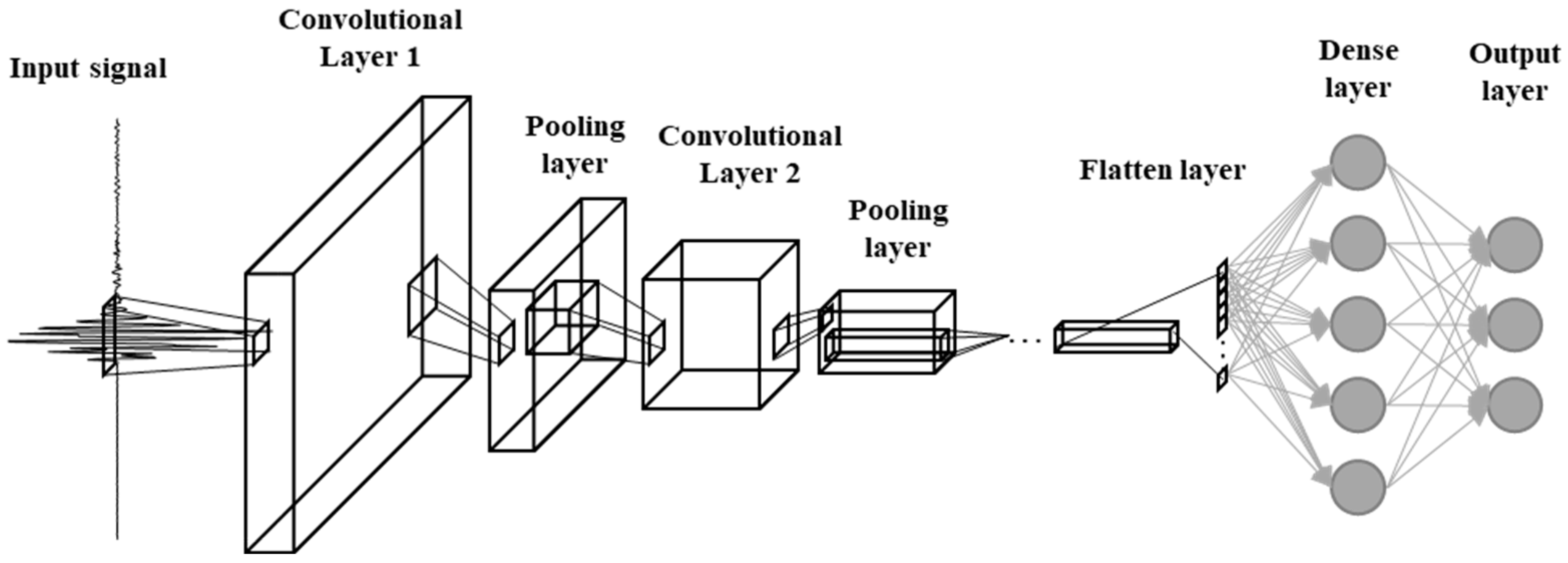
4.1. CNN
4.2. Architecture of the CNN
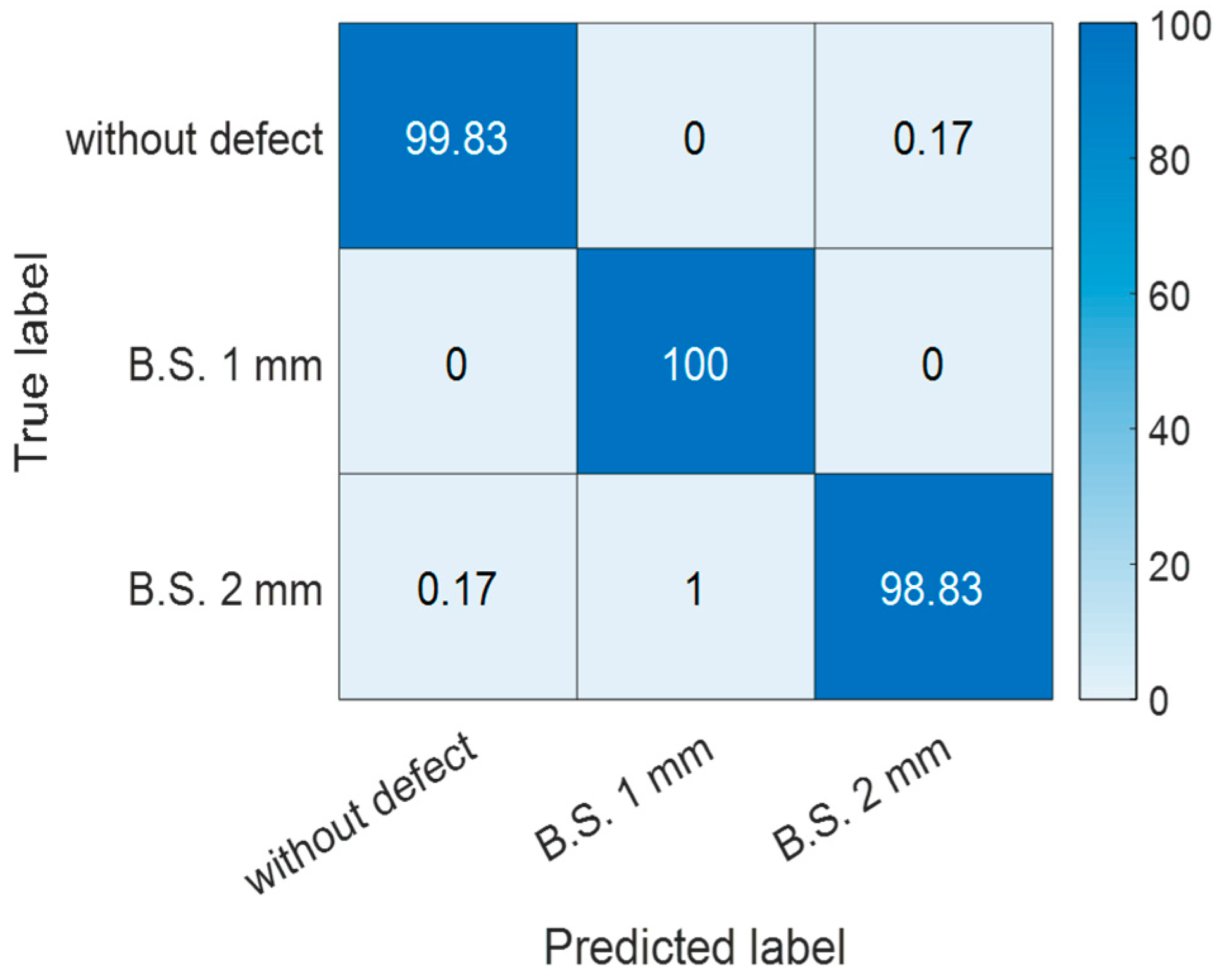
4.3. Performance Evaluation of the CNN
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sinha, P.; Indimath, S.S.; Mukhopadhyay, G.; Bhattacharyya, S. Failure of a work roll of a thin strip rolling mill: A case study. Procedia Eng. 2014, 86, 940–948. [Google Scholar] [CrossRef]
- Carretta, Y.; Hunter, A.K.; Boman, R.; Ponthot, J.-P.; Legrand, N.; Laugier, M.; Dwyer-Joyce, R.S. Ultrasonic roll bite measurements in cold rolling-roll stress and deformation. J. Mater. Process. Technol. 2017, 249, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Singh, K.; Mondal, N.; Mandal, C.; Prasad, R.; Sengupta, P. Application of ultrasonic and eddy current testing for inspection of rolls. NDTnet 2014, 2, 1–9. [Google Scholar]
- Salim, M.; Malek, M.; Sabri, N.; Juni, K. Study on ringing effect in ultrasonic transducer. Sci. Res. Essays 2012, 43, 3682–3689. [Google Scholar]
- Schmerr, L. Fundamentals of Ultrasonic Nondestructive Evaluation: A Modeling Approach, 1st ed.; Plenum Press: New York, NY, USA, 1998; pp. 91–140. ISBN 0-306-45752-0. [Google Scholar]
- Schmerr, L.; Song, S. Ultrasonic Nondestructive Evaluation Systems: Models and Measurements, 1st ed.; Springer: New York, NY, USA, 2010; pp. 127–231. ISBN 978-0-387-49061-8. [Google Scholar]
- Lim, H.; Lee, H.; Kim, B.; Kang, S. Process design for manufacturing 1.5 wt%C ultrahigh carbon workroll: Void closure behavior and bonding strength. Trans. Mater. Process. 2013, 22, 269–274. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Lee, J.; Weon, J.; Lee, W.; Yoon, J.; Park, Y. An improved alloy for forged rolls for cold rolling. Kor. Soc. Technol. Plas. Roll. Symp. 2009, 65–71. [Google Scholar]
- Garza-Montes-de-Oca, N.; Rainforth, W. Wear mechanisms experienced by a work roll grade high speed steel under different environmental conditions. Wear 2009, 267, 441–448. [Google Scholar] [CrossRef]
- Li, C.; Yu, H.; Deng, G.; Liu, X.; Wang, G. Numerical simulation of temperature field and thermal stress field of work roll during hot strip rolling. J. Iron Steel Res. 2007, 14, 18–21. [Google Scholar] [CrossRef]
- Benasciuttia, D.; Brusab, E.; Bazzaro, G. Finite elements prediction of thermal stresses in work roll of hot rolling mills. Procedia Eng. 2010, 2, 707–716. [Google Scholar] [CrossRef] [Green Version]
- Polikar, R.; Udpa, L.; Udpa, S.S.; Taylor, T. Frequency invariant classification of ultrasonic weld inspection signals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 614–625. [Google Scholar] [CrossRef] [PubMed]
- Munir, N.; Kim, H.J.; Park, J.; Song, S.J.; Kang, S.S. Convolutional neural network for ultrasonic weldment flaw classification in noisy conditions. Ultrasonics 2019, 94, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Rimoldi, B. Principles of Digital Communication: A Top-Down Approach; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- McCulloch, W.; Pitts, W. A logical calculus of ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosenblatt, F. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms; Cornell Aeronautical Lab Inc.: Buffalo, NY, USA, 1961; pp. 97–303. [Google Scholar]
- Werbos, P.J. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1975. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; California University San Diego La Jolla Inst for Cognitive Science (ICS-8506): San Diego, CA, USA, 1985. [Google Scholar]
- Géron, A. Hands on Machine Learning with Scikit-Learn and Tensorflow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media Inc.: Newton, MA, USA, 2017. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Nielsen, M.A. Neural Networks and Deep Learning; Determination Press: San Francisco, CA, USA, 2015. [Google Scholar]
- Lecun, Y.; Bottou, L.; Benjio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Fukushima, K. A neural network for visual pattern recognition. Computer 1988, 21, 65–75. [Google Scholar] [CrossRef]
- Meng, M.; Chua, Y.J.; Wouterson, E.; Ong, C.P.K. Ultrasonic signal classification and imaging system for composite materials via deep convolutional neural networks. Neurocomputing 2017, 257, 128–135. [Google Scholar] [CrossRef]
- Munir, N.; Park, J.; Kim, H.J.; Song, S.J.; Kang, S.S. Performance enhancement of convolutional neural network for ultrasonic flaw classification by adopting autoencoder. NDT&E Int. 2020, 111, 102218. [Google Scholar]
- Park, J.; Lee, S.; Kim, H.; Song, S.; Kang, S. System invariant method for ultrasonic flaw classification in weldments using residual neural network. Appl. Sci. 2022, 12, 1477. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. Proc. ICML 2013, 30, 3. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. ACM Commun. 2017, 60, 84–90. [Google Scholar] [CrossRef]





| Label | Training Database | Test Database | ||
|---|---|---|---|---|
| Flaw | No. of Signals | Flaw | No. of Signals | |
| 0 | Without defects | 600 | Without defects | 100 |
| 1 | 1 mm below the surface | 300 | 1 mm below the surface | 50 |
| 2 | 2 mm below the surface | 300 | 2 mm below the surface | 50 |
| Total | 1200 | 200 | ||
| Label | Training Database | Test Database | ||
|---|---|---|---|---|
| Flaw | No. of Signals | Flaw | No. of Signals | |
| 0 | Without defects | 7200 | Without defects | 1200 |
| 1 | 1 mm below the surface | 3600 | 1 mm below the surface | 600 |
| 2 | 2 mm below the surface | 3600 | 2 mm below the surface | 600 |
| Total | 14,400 | 2400 | ||
| Layer Type | Kernel Size/ Stride | Feature Maps | Output Size | |
|---|---|---|---|---|
| 1 | Conv1 | 1 × 16/1 × 8 | 128 | 313 × 128 |
| 2 | Dropout 1 | 0.5 | - | - |
| 3 | Max Pool 1 | 1 × 2/1 × 2 | - | 156 × 128 |
| 4 | Conv2 | 1 × 8/1 × 2 | 32 | 78 × 32 |
| 5 | Dropout 2 | 0.5 | - | |
| 6 | Max Pool 2 | 1 × 2/1 × 2 | 39 × 32 | |
| 7 | Conv 3 | 1 × 8/1 × 2 | 8 | 20 × 8 |
| 8 | Dropout 3 | 0.5 | - | |
| 9 | Max Pool 3 | 1 × 2/1 × 2 | 10 × 8 | |
| 10 | Fully Connected | 300 | - | |
| 11 | Dropout | 0.5 | - | |
| 12 | Softmax with Cross Entropy | 3 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeom, Y.-T.; Kim, H.-H.; Park, J.; Kim, H.-J.; Song, S.-J. Improved Ultrasonic Dead Zone Detectability of Work Rolls Using a Convolutional Neural Network. Appl. Sci. 2022, 12, 5009. https://doi.org/10.3390/app12105009
Yeom Y-T, Kim H-H, Park J, Kim H-J, Song S-J. Improved Ultrasonic Dead Zone Detectability of Work Rolls Using a Convolutional Neural Network. Applied Sciences. 2022; 12(10):5009. https://doi.org/10.3390/app12105009
Chicago/Turabian StyleYeom, Yun-Taek, Hun-Hee Kim, Jinhyun Park, Hak-Joon Kim, and Sung-Jin Song. 2022. "Improved Ultrasonic Dead Zone Detectability of Work Rolls Using a Convolutional Neural Network" Applied Sciences 12, no. 10: 5009. https://doi.org/10.3390/app12105009
APA StyleYeom, Y.-T., Kim, H.-H., Park, J., Kim, H.-J., & Song, S.-J. (2022). Improved Ultrasonic Dead Zone Detectability of Work Rolls Using a Convolutional Neural Network. Applied Sciences, 12(10), 5009. https://doi.org/10.3390/app12105009







