1. Introduction
China has a vast and complex territory, where plateau areas account for about 26% of the total territory, mainly covering the frontier areas of key defense, where the environment is harsh and the airflow is unstable. At present, fixed-wing and rotary-wing UAVs have problems such as low energy utilization, poor mobility, and weak stealth capability, while bionic flapping-wing vehicles can actively adapt to and make use of different airflow environments. It has great development potential in terms of flight efficiency, mobility, and bionic concealment [
1,
2]. It can be used for border patrol, rescue and disaster relief, biodiversity exploration, and so on. As one of the core components of the plateau bionic flapping-wing vehicle, the performance of flapping wings greatly affects the flight properties and determines the flight performance of the vehicles.
For flapping-wing vehicles, different structures and materials of the wings can result in significant variation in the aerodynamic performance of the flapping wings. However, as we are limited by the backwardness of materials, actuators, propulsion systems, etc., directly replicating the kinematics and morphology of biological wings is far from sufficient to manufacture a flapping-wing vehicle with high lift and low power consumption. Therefore, the flapping-wing design, inspired by flying creatures, can only be used as a preliminary conceptual design, and the geometric parameters of the wing need to be further optimized, including wing shape, aspect ratio, root tip ratio, and other parameters.
In the past, most of the research on flapping-wing aircraft have focused on the small and micro scale fields. Although such flapping-wing vehicles have high lift efficiency and can perform missions in confined spaces, they have the limitations of poor load capacity and short flight distance. Therefore, large-scaled flapping-wing vehicles can meet the mission requirements for efficient low-speed cruise flights and far-range long-endurance flights. Among the flapping-wing vehicles with good flight performance that imitate birds of medium and large scale, “Smartbird” of the Festo company in Germany [
3], “RoboRaven” of the University of Maryland [
4,
5], and “HIT-Hawk” of Harbin Institute of Technology [
6] are outstanding. “SmartBird” has a wingspan of 2 m and a weight of 450 g; “RoboRaven” has a wingspan of 1.168 m and a weight of 290 g; and “HIT-Hawk” has a wingspan of 1.1 m and a weight of 455 g. “RoboRaven” adopts a single-stage flexible film flapping wing. The wing material is composed of polyester film and carbon fiber rods. The flapping wing with optimal aerodynamic performance is selected by adjusting the planform and iterating wind tunnel experiments. “HIT-Hawk” still adopts a single-stage flapping wing. The wing is composed of kite cloth and mast. Similarly, through experimental iteration, the wing film material, layout form, and planform of the wing are optimized.
The flapping wing is the main feature that distinguishes flapping-wing vehicles from other types of vehicles. The flapping wing provides all of the thrust and most of the lift of the vehicle. The aerodynamic characteristics of flapping wings determine the performance of the vehicle to a great extent. Although the existing flapping-wing designs and structures vary greatly, the single-stage flexible film flapping wing is adopted by a large number of flapping-wing vehicle prototypes because of its simple structure, light weight, and low requirements for a driving system. Meanwhile, this structural form of flapping wing has been proved to be the most practical configuration through the successful flight of a large number of flapping-wing vehicles. Due to the limitation of the accuracy of theoretical knowledge and the limitations of numerical simulation, the design of flapping-wing vehicles has always been mainly carried out through experimental iteration.
Based on the observation of flying organisms, high altitudes present various physiological challenges to organisms, including respiration, circulation, temperature regulation, and so on. Altshuler and Dudley et al. [
7,
8,
9] pointed out that low-density conditions increase oxygen delivery to flight muscles when organisms fly at high altitudes to compensate for their reduced atmospheric partial pressures. They also stated that the low-density and low-oxygen content of the air will increase metabolic demand as well as create a reduced ability to generate aerodynamic force, limiting the ability to move at high altitudes. During their annual migration, birds select their flight altitudes according to certain criteria, such as minimum energy consumption and favorable wind gusts [
10]. Different altitudes will bring about drastic changes in the aerodynamics and biological behavior of birds. The aerodynamic performance of aircraft depends heavily on the surrounding environment, with the lift and drag coefficient directly proportional to air density [
11]. Air density decreases with an increase in altitude, thus reducing the air drag that impedes the movement of birds and reduces the lift force required for flight. Therefore, some birds can adjust their biological behavior according to the physical properties of the air, varying with altitude [
12,
13]. For example, when birds are in low-density environments at high altitudes, their flapping frequency, amplitude, and speed will increase to provide sufficient lift [
14,
15,
16]. The focus of these experiments was to study the physiological adaptation of birds to altitudes while discarding the aerodynamic changes caused by changes in the physical properties of the air. Even today, measuring the aerodynamic coefficients of birds floating in the air is still a challenge, and the evolution of drag and lift is estimated through theoretical mathematical models and flapping-wing kinematics analysis. Numerical simulation and more accurate computational fluid dynamics (CFD) have been proven to be effective methods for studying the aerodynamics of fixed or flapping wings [
17,
18]. Most of the CFD studies of flapping wings have focused on the geometrical parameters of the wing [
19], others on the influence of the ceiling [
20] or the ground [
21], but few seem to have addressed the influence of altitude on the aerodynamics of a flapping wing.
Sridhar M. et al. [
22] established the design space of the high-altitude fluid-structure coupling effect of flapping wings, with atmospheric density and the stroke plane angle as design variables. The results show that the lift increases with the increment of the stroke plane angle and air density, while the net thrust remains close to zero. The required averaged power decreases with increasing altitude and eventually becomes negative at 3000 m above sea level. They also investigated the influence of vein structures on the fluid-structure interaction of flexible flapping wings at high altitudes [
23]. The paper proposed that the lift and thrust improved with the increment of wing stiffness and stroke plane angle. For a more flexible wing, the force depends on the air density and decreases with an increase in altitude; additionally, the power consumption increases with increasing stiffness. Beaumont F. et al. [
24] studied the aerodynamic effects of flapping amplitude, frequency, and airspeed on rigid Canada geese wings at different altitudes. The results showed that an increase in speed caused higher energy consumption. The 20% increase in amplitude increased the lift-to-drag ratio by about 22%; a 25% increase in frequency increased the lift-to-drag ratio by 158%.
In previous studies, there has been a lack of research on the impact of altitude on flying animals, and the relationship between the flapping-wing design and altitude has not been considered. Wind tunnel experimental techniques, CFD, and flight tests were used to investigate and verify the aerodynamic performance of flapping wings. The wind tunnel experiments were used to optimize the appropriate planform, structural layout, and film material. Backpropagation (BP) neural network models were built to perform the prediction of the trim state. CFD was used to provide recommendations for adjusting flight conditions in high-altitude environments. Flight tests at different altitudes were conducted to verify the performance of the flapping wing. This study broadens the existing knowledge of large-scale flapping-wing designs at high altitudes.
3. Results
The results of the wind tunnel experiments for all the above flapping wings are discussed in this section. In this paper, the key non-dimensional control parameters include the Reynolds number (Re), Strouhal number (St), and angle of attack (AOA).
3.1. Effect of Planforms and the Function of the Additional Materials
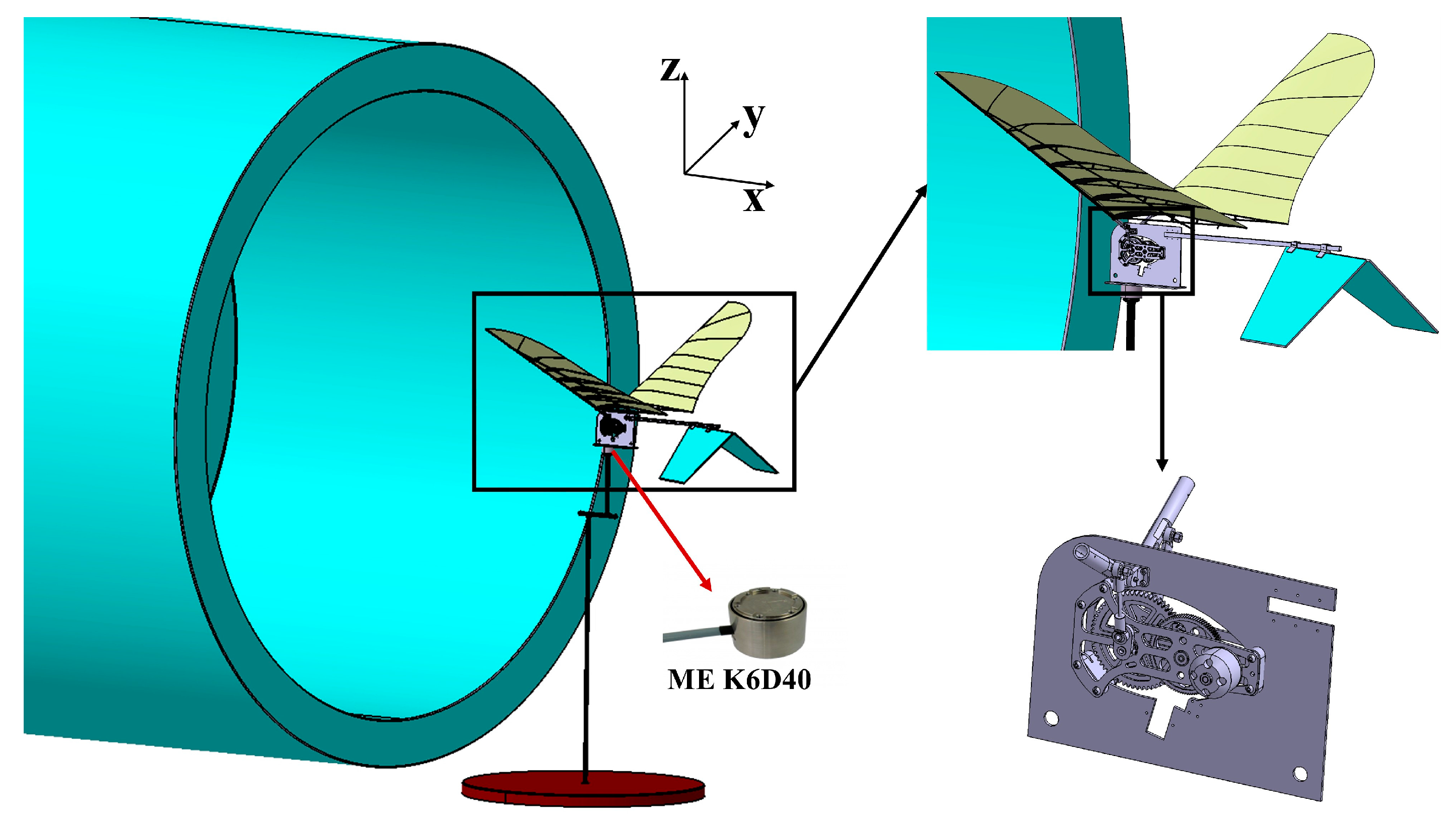
After complicated fabrication, the first to eighth wings in
Table 2 were obtained. The eight wings were installed in the experimental set-up for wind tunnel experiments to investigate the effect of planforms and the effect of the additional materials (
Figure 9).
Figure 10 shows the effect of dimensionless parameters, i.e., the Reynolds number and the Strouhal number, on the force and moment coefficients. The solid and dashed lines each represent the effects of
Re and
St. The five different colors refer to some typical types of flapping wings and allow a clear comparison of the role of the planform and additional materials. A raise in
Re will reduce the lift coefficient, thrust coefficient, and downward pitching moment, which is opposite to the effect of
St. By comparing the curves of different colors, it can be found that the elliptical planform has the best lift coefficients and the minimum downward pitching moment in all
Re and
St ranges, but at the cost of thrust. The attachment of the additional materials also significantly enhances the lift and thrust coefficients in the full
Re and
St ranges.
Figure 11 shows the results of experiments conducted with the first eight wings in
Table 2 under the experimental parameter configurations in
Table 1. The lift increases monotonously with increasing wind speed, angle of attack, and flapping frequency. Additionally, it is found that the thrust decreases with the increment of wind speed and attack of angle, which is opposite to the effect of frequency on thrust production. As for the pitching moment, it decreases with the increment of the above three parameters.
Comparing the force and moment performance of the first to the eighth flapping wings, the lift performance of the sixth and eighth flapping wings is more prominent compared to the other wings, indicating that the elliptical shape and increasing the internal area of the wing contribute to the generation of lift.
For the effect of the planforms of flapping wings on the lift, the elliptical one is slightly better than increasing the internal area of the wing; increasing the external area of the wing with an oblique rod setback, as shown in
Figure 9c, is worse in comparison, and the planform shown in
Figure 9b has the worst lift performance. The internal area of the flapping wing is mainly related to the generation of lift, so it is necessary to ensure that it has sufficient area, while the chord torsional stiffness of the wing needs to be moderate. Considering the function of the additional materials, as shown in
Figure 11a,d,g, it is obvious that the lift of the solid line is always higher than that of the dashed line, which indicates that the periodic-averaged lift of the flapping wing is generally improved substantially when additional materials are attached. To be specific, the lift increases by at least 50%.
In terms of thrust, the first, sixth, and seventh wings perform significantly better than the other wings. The positive contribution of increasing the internal area of the wing to thrust is greater than the other two types of increasing the external area of the wing. It is worth noting that the elliptical planform of the flapping wing can only produce less thrust. According to the theory of fixed wings, the reduction of the induced drag of elliptical wings is not enough to compensate for the increment brought by the high lift coefficient. Through the comparison of solid and dashed lines, it can be found that the additional materials can have a beneficial impact on thrust. Numerically, the thrust increases by at least 20%.
The pitching moment at the root of the wing is shown in
Figure 11c,f,i. Among these eight flapping wings, the elliptical planform results in the largest downward force moment. The downward force moment of the external area of the wing that is increased with an oblique rod setback is higher than that of the wing without an oblique rod setback, and the planform of increasing the internal area of the wing is lower. It can also be concluded that the attachment of additional materials can reduce the downward force moment to some extent.
Considering the influence of the above planform and additional materials on the lift, thrust, and pitching moment of the flapping wings (i.e.,
Figure 9d), increasing the internal area of the wing and attaching additional materials (weighing 163 g) are chosen for subsequent study.
3.2. Effect of Film Materials and Number of the Ribs
The takeoff weight is critical for the vehicle, so it is necessary to reduce the weight of the flapping wing. Therefore, on the basis of increasing the internal area of the wing, as determined above, the film material and the number of wing ribs will be discussed.
The planform of the wing, the position of the oblique rod, and the airfoil are guaranteed to be consistent. Without additional materials, six or seven wing ribs are combined with polyester or linen wing film material, respectively. The weight of all four wings in
Figure 12 is around 120 g.
From
Figure 13, it can be concluded that the solid and dashed lines show opposite trends for the flapping wing aerodynamic performance in the range of
Re and
St studied in this paper. The reduction in the number of wing ribs results in a significant increase in the lift coefficient and a slight decrease in the thrust coefficient. The wing membrane material affects the aerodynamic performance to a small extent, but the linen material creates a slight increase in the downward pitching moment.
Figure 14 shows the lift, thrust, and pitching moment of the last four wings for different wind speeds, attack angles, and flapping frequencies. The solid black line indicates the 163 g wing before weight reduction.
In terms of lift, the performance of all four wings deteriorates after weight reduction. Comparing these four wings, the flapping wings with six wing ribs are better than those with seven wing ribs. While the material of the wing film has little influence on the lift, the flapping wings of linen material produce greater lift than that of polyester film. For flapping wings, lift generation is mainly related to wind speed and an effective angle of attack. In comparison, the increment of flapping frequency does not significantly improve the lift, if any, probably due to the flexible deformation of the wing, caused by high frequency, thus changing the effective angle of attack.
For thrust, it is obvious that the wing before weight reduction still performs better. In contrast to the effect of the number of wing ribs on lift, the reduction has a slight detrimental effect on thrust. The two materials of the wing film do not play a significant role in thrust. The main factor affecting thrust, while keeping the amplitude constant, is flapping frequency. Increasing the flapping frequency will effectively improve thrust at the cost of power consumption.
When referring to the pitching moment, it can be found that the wing after weight reduction is weakened in absolute values. The combination of seven wing ribs and linen film creates the minimum downward force moment.
Linen is about 2.6 g heavier than the polyester film material, which has a slight lift improvement and a certain degree of thrust increment at high speeds. The six ribs are about 7.1 g lighter compared to the seven ribs, with a significant lift and a slight decrease in thrust. The slow-motion video of the flapping motion shows that the six wing ribs are stiffer than the seven wing ribs in the chord direction of the wingtip, and the former deformation is not as pronounced as the latter. During stroke reversal, the chordwise twist of the wing with seven ribs is faster, which results in a greater chordwise twist angle at the wingtip at the initial moment of the downstroke. The greater downward chordwise twist angle during downstroke results in stronger thrust, while the higher speed during stroke reversal can reduce the downward fluid mass, resulting in less lift. The result is that for a single-stage flapping wing, the flapping motion should match the passive twisting motion in the chord direction, which benefits from the excellent stiffness design.
3.3. Periodic-Averaged Aerodynamic Performance Trim of Flapping Wings
The parameters of the trim state are so critical to the vehicle that it is necessary to use the available data for trim predictions. For the trim of flexible flapping wings, it is more accurate to use the data from wind tunnel experiments to establish the model. However, since the experimental state of the wind tunnel is discrete and not conducive to the solution of the leveling state, the neural network toolbox in Matlab needs to be used for interpolation first. The BP neural network is a multi-layer feed-forward neural network trained according to the error backpropagation algorithm, and it is one of the most widely used neural network models.
The wind tunnel experimental data of full state points were imported into Matlab for collation, and the correspondence between the independent variables (
V,
AOA,
f) and the dependent variables (
L,
T,
My) was established by using the Neural Network Fitting app. The percentages of training, validation, and testing samples are 70%, 15%, and 15%, respectively. The topology of the BP is further defined, where the number of hidden neuron layers is 10 and the number of output layers is 2. Levenberg-Marquardt was chosen as a training algorithm. As shown in
Figure 15, the regression coefficients R between the output values and the target values are all close to 1, indicating that the predictions of the BP neural network model are relatively accurate.
The input values of the above neural network prediction model are then interpolated to traverse as many state points as possible. The condition that the lift force is equal to the gravity, i.e., 1300 g, the thrust force is balanced with the drag force, and the pitch moment value of 0 is used to end the traversal of the state points. The output value of the neural network model is constrained to obtain the value of the independent variables that satisfy the trim states in
Table 5.
.
The prediction of the trim state can provide guidance for the flight of the vehicle in the cruise status. By comparing the speed, angle of attack, and flapping frequency of the four wings in cruise mode, it can be found that the wing film material has almost no effect on the flapping frequency in cruise mode, while the linen material reduces the angle of attack in this condition. The reduction in the number of wing ribs effectively weakens the cruising speed and flapping frequency. After comparing the performance of the four wings, a combination of six wing ribs and linen film material was selected for the prototype assembly.
3.4. Numerical Simulation of Large-Scaled Rigid Wings at High Altitudes
Before the flight test, it is necessary to numerically simulate the flapping wing at different altitudes and adjust the flight state at high altitudes. The numerical method is mainly used to predict the effect of altitude on the trim state and power consumption. This section aims to give guidance for subsequent flight tests.
The states of the flight parameters shown in
Table 6 were selected for numerical calculation. The effects of altitude, flight speed, angle of attack, and flapping frequency on lift and drag were studied by intercomparison.
Table 7 shows the time-averaged aerodynamic performance results for the calculated cases presented in
Table 6. In order to visually compare the differences between the eight cases, the results of the second to eighth cases are expressed as percentages of the corresponding parameters compared to the first case, i.e., the plain environment.
Figure 16a,b indicate that altitude plays a significant role in the transient force during downstrokes. As the altitude increases, the peak positive lift in the middle of the downstroke decreases considerably, while the peak negative lift in the upstroke becomes slightly larger. The drag force shows the same trend as altitude. It is also known from the periodic-averaged aerodynamic performance in
Table 7 that the increment of altitude leads to a slight decrease in the lift coefficient. The absolute values of the time-averaged lift, drag, and pitching moment all decrease remarkably with increasing altitude. Specifically, when the altitude increased from 0 to 4000 m, the
Re was subsequently reduced by 27.98%, and the time-averaged lift, drag, and pitching moment decreased by 33.31%, 33.08%, and 33.33%, respectively. However, the lift coefficient decreased by only 0.25%, the drag coefficient increased by only 0.10%, and the pitching moment decreased by only 0.28%. The lack of lift will be one of the most serious problems for the vehicle at high altitudes if the flight state is kept constant.
The legend of
Figure 16c,d, for example, V7AOA10f4, represents the calculated case, with a wind speed of 7 m/s, an angle of attack of 10°, and a flapping frequency of 4 Hz. As can be seen from
Figure 16c,d, the increment in the angle of attack can boost the transient lift throughout the cycle, but this is at the cost of increased drag and a tendency to stall. The angle of attack affects the drag mainly in the downstroke, and the trend of the transient drag can be found in the fact that when the angle of attack increases from 10° to 15°, the sudden drop at the beginning of the downstroke is eliminated. The same problem is presented in terms of the time-averaged value in
Table 7, and the increase in the absolute value of the pitching moment implies an increase in power consumption. A 1/3 reduction in the angle of attack results in a 27.19%, 62.34%, and 26.56% reduction in lift, drag, and pitching moment coefficients, respectively. The increase in flight speed will significantly increase the peak positive lift during the downstroke, when the peak value of drag also increases sharply. The change in flight speed, on the contrary, has less effect during the upstroke. From the time-averaged value, the absolute values of force and pitching moment coefficients are reduced. After dimensioning, the absolute values of force, moment, and consumed power increase obviously.
In order to compensate for the decrease in thrust performance due to the reduced density, the flapping frequency of the wings needs to be increased. The adjustment of the frequency brings about a larger absolute magnitude of the peak value in the cycle. The time-averaged results obtained for the two selected frequencies (i.e., 4 and 5 Hz) are presented for comparison in
Table 7. It appears that a 25% increase in frequency and the Strouhal number produce an 11.38% increase in the averaged lift coefficient and a 9.53% decrease in the averaged drag coefficient. At the same time, the pitching moment coefficient increases by 12.31%.
In general, when flapping-wing vehicles with the same weight fly at high altitudes, it is necessary to improve the flapping frequency to realize trim flight at higher flight speeds. In addition, it is worth noting that compared with sea level, the increase in flapping frequency at high altitudes will increase power consumption, so how to adjust its abnormal state at high altitudes needs further flight tests. This paper does not consider the flexible deformation of real flapping wings and the gap between the numerical model and the real model, which will affect the aerodynamic force and power consumption in forward flights to a certain extent.
3.5. Test Flight at High Altitudes
The flight test of the assembled aircraft was carried out at different altitudes. On one hand, it is to verify whether the designed wing is suitable for different altitudes; on the other hand, it is to explore the influence of altitude.
The 163 g flapping wing before weight reduction (
Figure 9d) was assembled with the prototype vehicle, and flight tests were conducted at different altitudes. The lower altitude area refers to Xi’an, Shaanxi Province, where the altitude is about 500 m (
Figure 17a), while the higher altitude area is Lhasa, Tibet Autonomous Region, where the altitude is about 4500 m (
Figure 17b).
The flight tests of the vehicle’s load capacity and endurance were carried out in the Xi’an area. The vehicle was equipped with an inverted T-tail and the same drive method as the wind tunnel experiment mechanism. As shown in
Table 8, the assembled vehicle had an empty load of ~1150 g and a maximum takeoff weight of ~1300 g. A total of approximately one hour of flight testing was successfully completed, where the capacity of the battery was 106 Wh. The environmental conditions at this time were a temperature of approximately 20 °C and a wind speed rating of 1 level.
Subsequently, the flight tests were conducted in Lhasa, with an empty load of 1100 g and the same maximum takeoff weight. The flight time was reduced by 25% to 45 min compared to the altitude of 500 m, where the temperature was 13 °C and the wind speed was level 3.
After flight tests at two altitudes, the designed flapping wing was verified to possess excellent aerodynamic performance, capable of withstanding considerable loads and endurance.
4. Conclusions
In this paper, several flapping wings have been fabricated, including four planforms (basic shape, increasing the external area of the wing, and elliptical shape), whether to attach additional materials, two numbers of wing ribs (six and seven wig ribs), and two different materials of wing film (polyester and linen materials). Wind tunnel experiments were conducted on a total of twelve wings; then, a BP neural network model was built to predict the trim state of the flapping wings. Taking into account their weight and aerodynamic performance, the most outstanding flapping wing was eventually selected, which was the one with six wing ribs, linen film material, and the planform of increasing the internal area of the wing. In addition to the above study, a transient numerical method based on the overset mesh technique was used to investigate the influence of different altitudes and different states. Finally, the flight tests of the vehicle’s load capacity and endurance were carried out in the Xi’an area and Lhasa, respectively, to verify the performance of the flapping wing.
According to the wind tunnel experimental results, the lift is mainly affected by wind speed and the angle of attack. In contrast, the major factor in changing thrust is the flapping frequency. Regardless of the planform, the lift and thrust of the flapping wings show a significant upward trend after attaching additional materials, which is at the cost of increased pitching moment and power consumption. As for the effect of the planform, the elliptical flapping wing had the greatest lift performance but also the worst thrust performance, which is the reason for not continuing the follow-up study on it. Taking all factors into account, increasing the external area of the wing had the most superior aerodynamic performance.
The design of the vehicle has demanding weight requirements, so subsequent research is necessary to reduce the weight of the flapping wing as much as possible for less loss of aerodynamic performance. For the planform of increasing the external area of the wing, the influence of the number of wing ribs and the materials of wing film were explored. The results indicated that linen film plays a slight role in lift compared to the polyester one, and the thrust at high speed is also improved. The wings with six wing ribs have noticeably better lift performance than the wings with seven wing ribs, with a slight reduction in thrust.
The trim state is predicted by the BP neural network model, and the flight parameters under the trim state of different wings are compared. The wing with an increased internal area of the wing, six wing ribs, and linen film material is the wing that makes it easier to achieve the trim state.
Flight tests were conducted at low and high altitudes, respectively, to check out the performance of the flapping wings. The results show that the flapping wings with careful parameter design can meet the requirements of load capacity and flight time and have excellent flight ability.