Performance Prediction of Composite Marine Propeller in Non-Cavitating and Cavitating Flow
Abstract
:1. Introduction
2. Methodology and Results
2.1. Test Model
2.2. Flow Simulation
2.2.1. Governing Equation and Boundary Condition
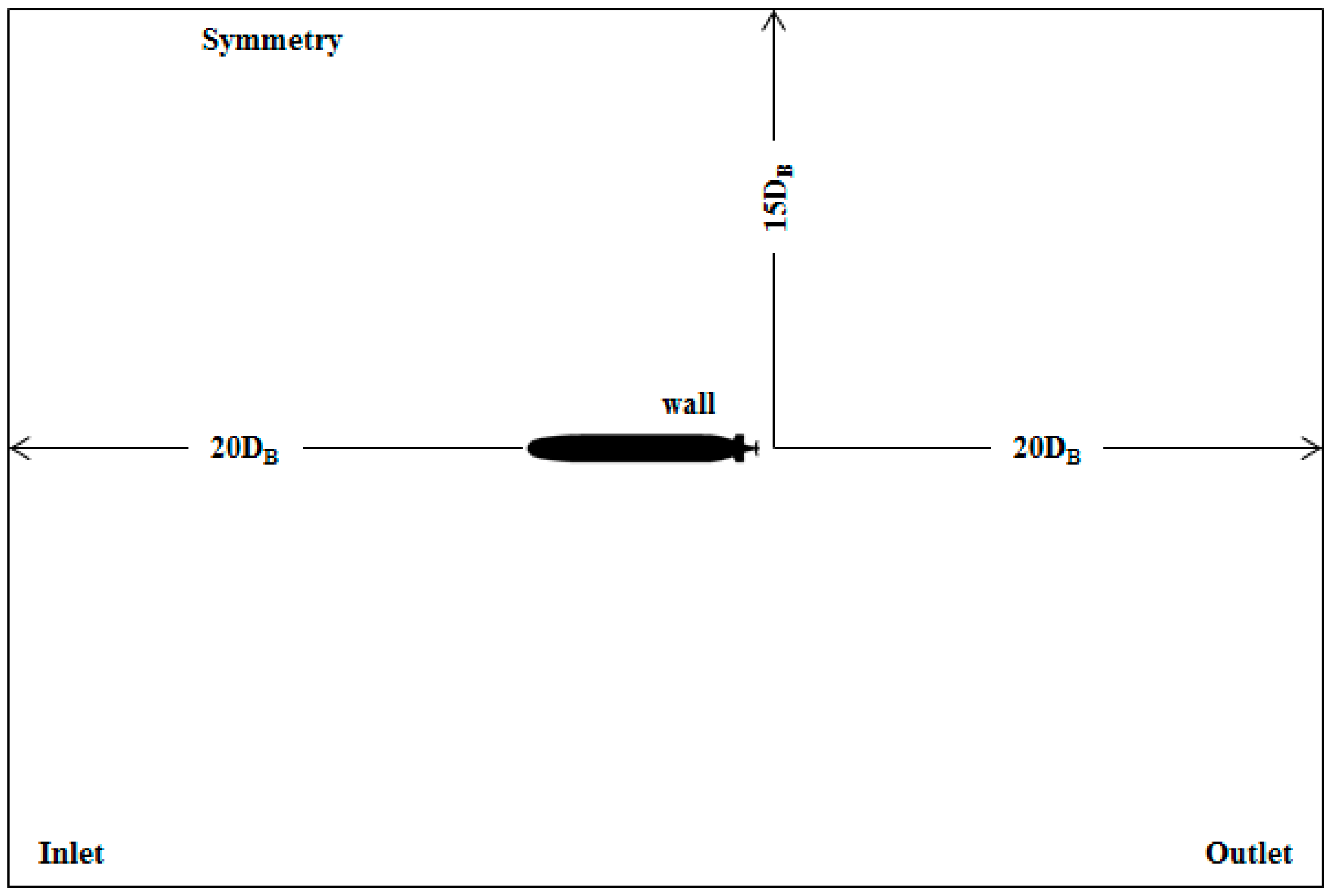
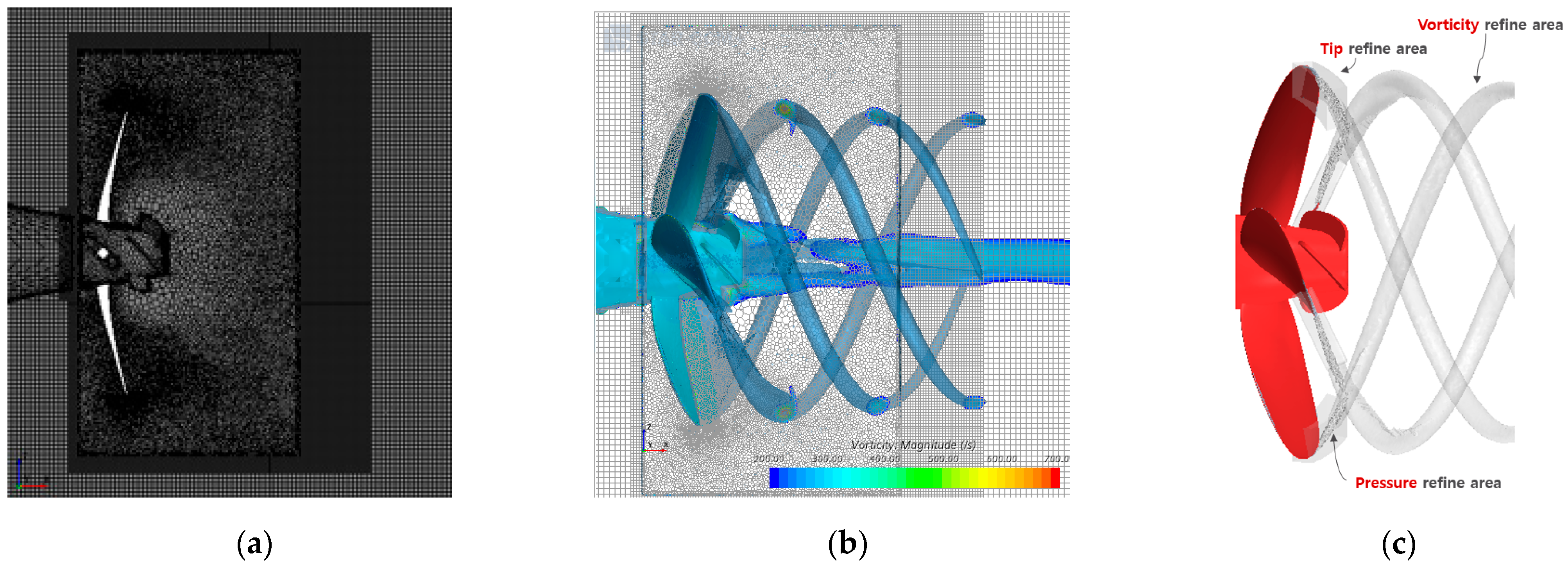
2.2.2. Simulation Set-Up
2.3. Structural Modeling
2.3.1. Governing Equation
2.3.2. Material Properties
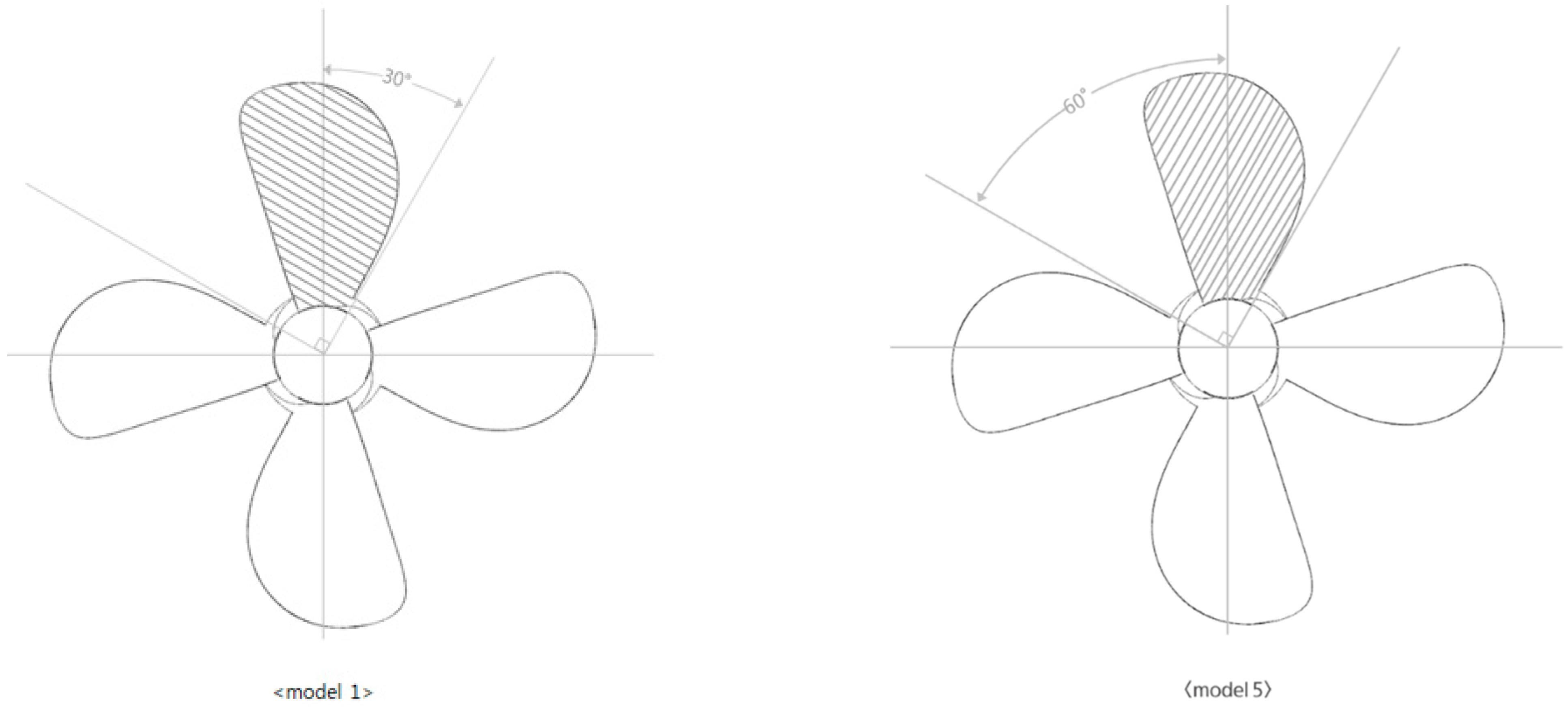
2.3.3. Stacking Method
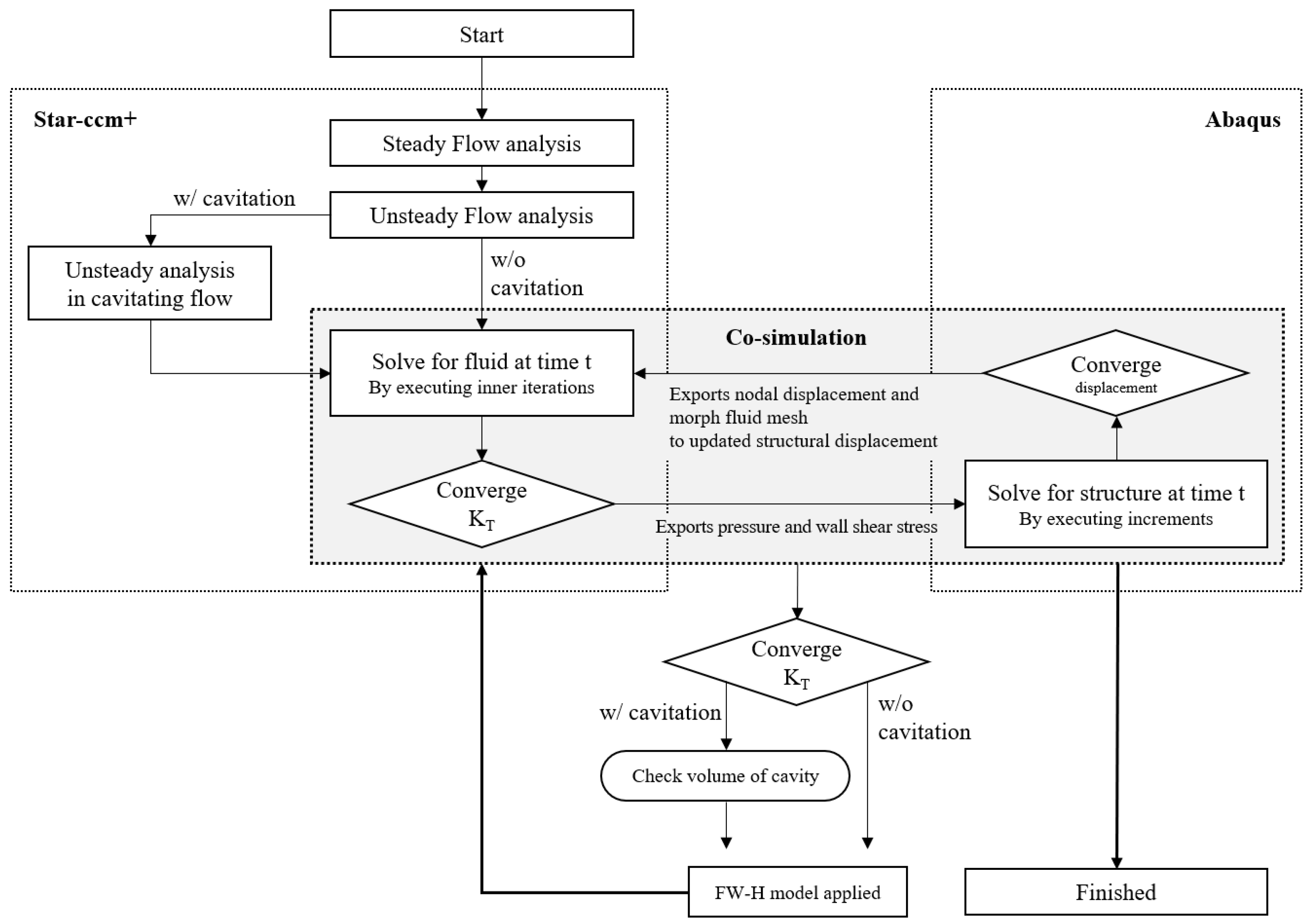
2.4. Coupled CFD-FEM FSI Analysis
2.4.1. Non-Cavitating Flow
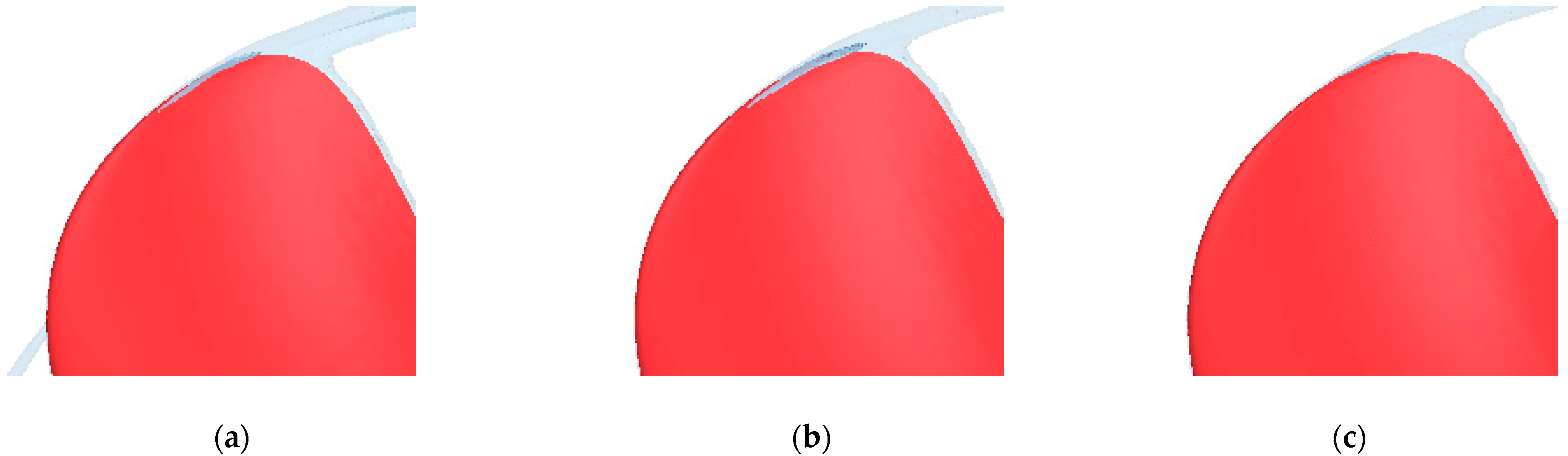
2.4.2. Cavitating Flow
3. Discussion
4. Conclusions
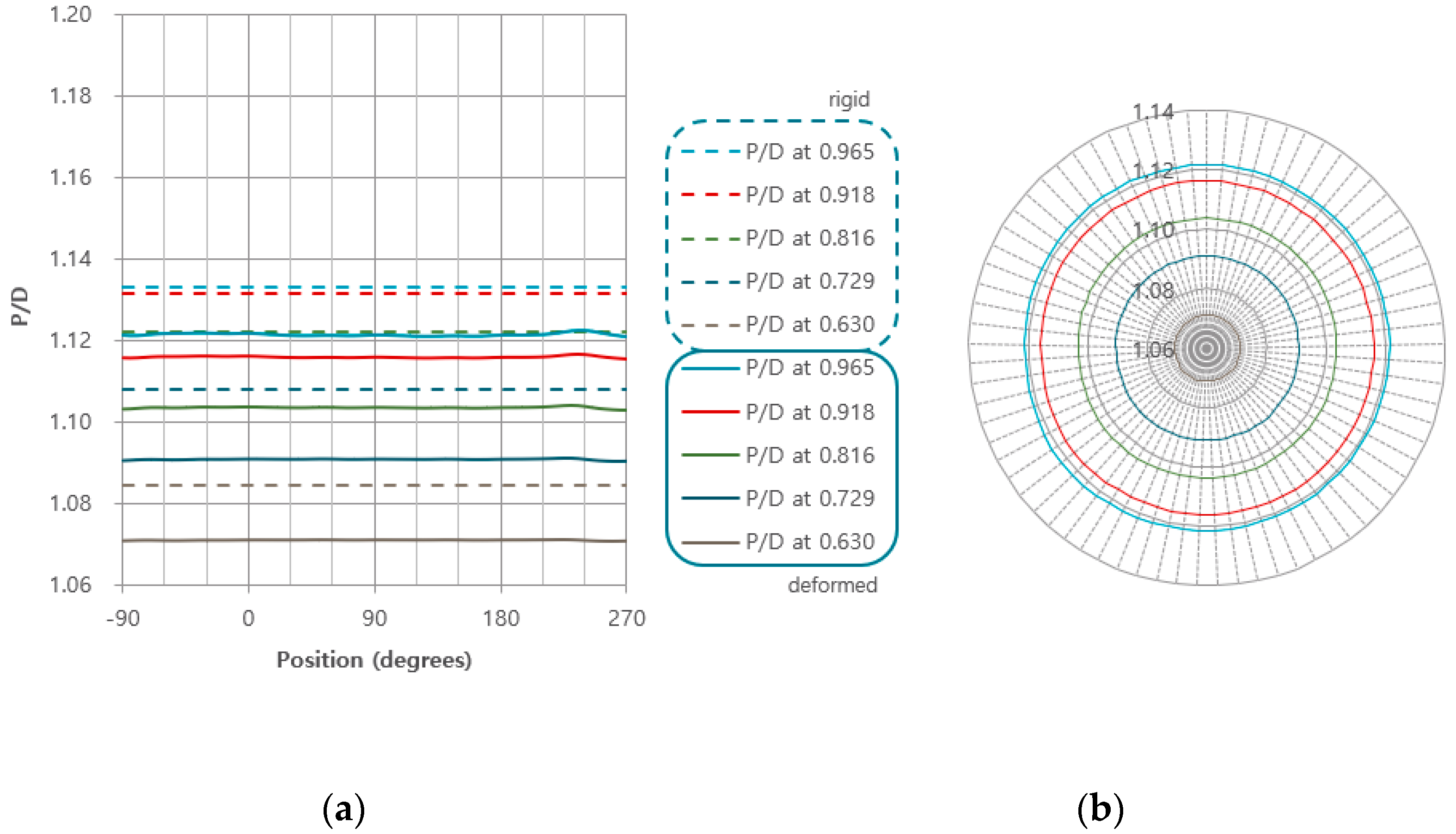
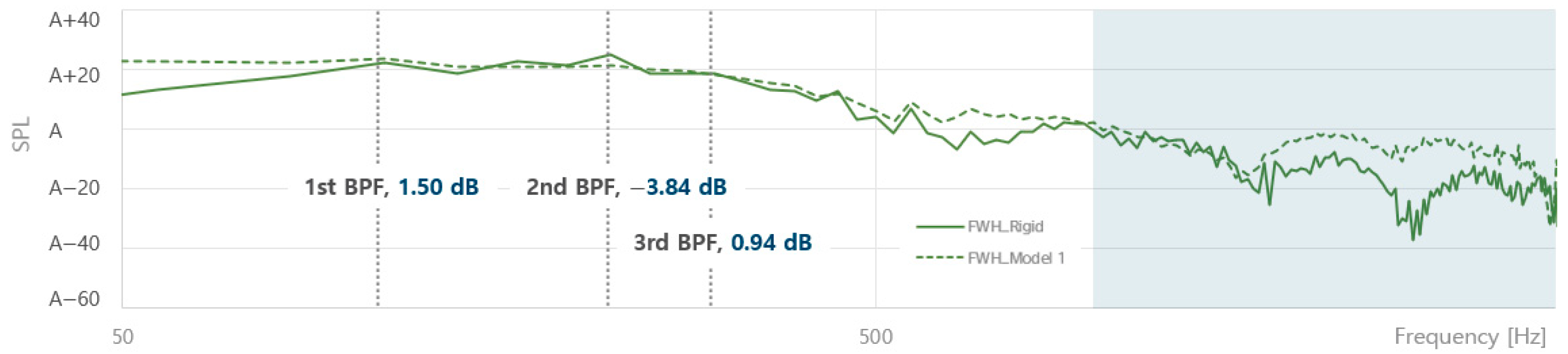
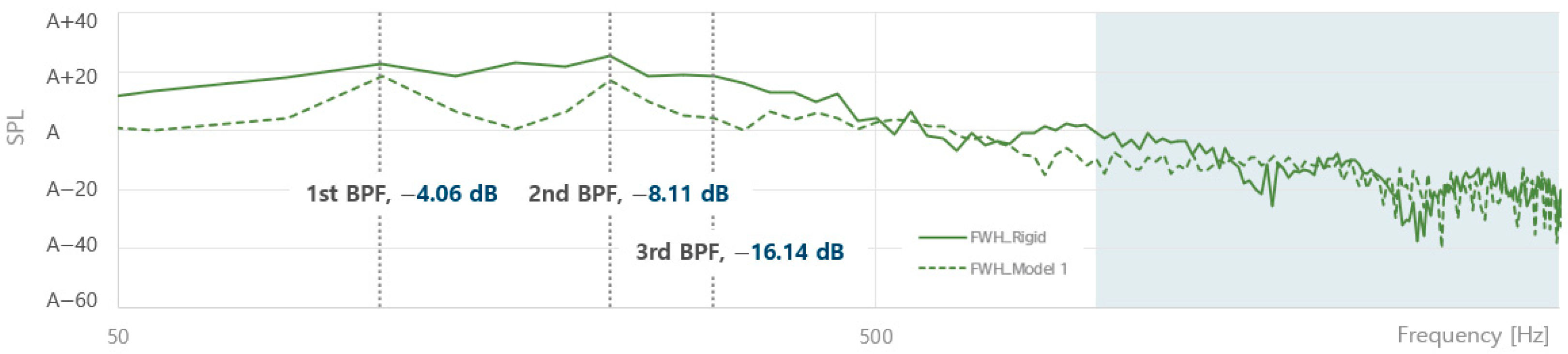
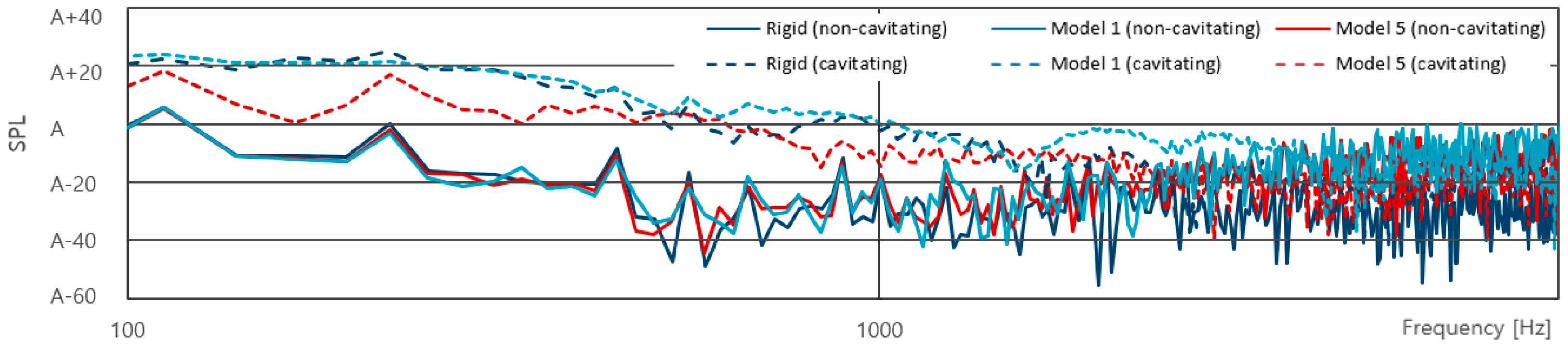
- Some deformed parameters of the propeller, such as the pitch and rake, affected the performance of the propeller. In particular, it was confirmed that the deformation pattern of the pitch is directly related to the change in the strength of the vortical flow near the tip region.
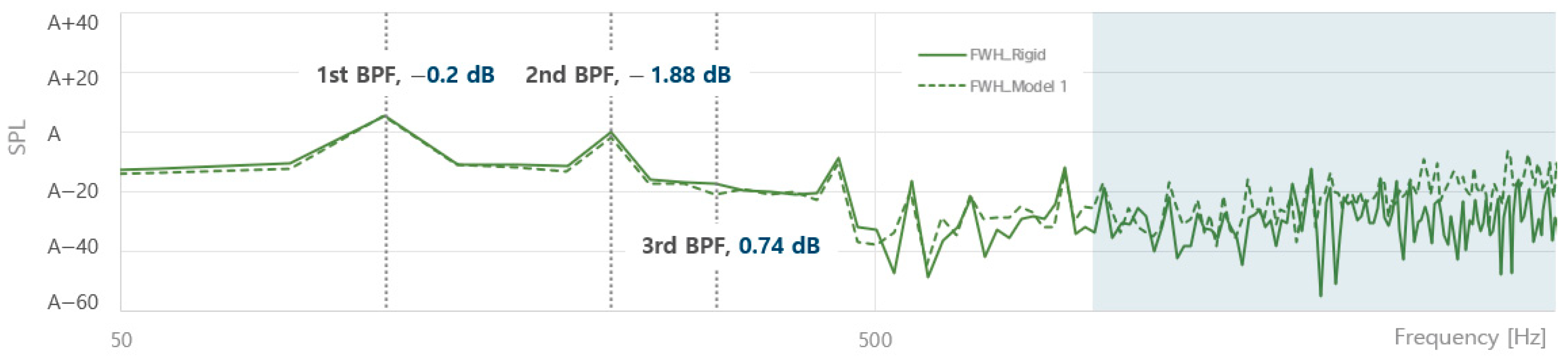
- The deformation of the composite propeller itself did not have a significant effect on the sound pressure level, but the volume change of cavitation caused by the pitch change had a decisive effect on the variation of sound pressure level radiated from the composite propeller.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mouritz, A.P.; Gellert, E.; Burchill, P.; Challis, K. Review of advanced composite structures for naval ships and submarines. Compos. Struct. 2001, 53, 21–42. [Google Scholar] [CrossRef]
- Chen, B.; Neely, S.; Michael, T.; Gowing, S.; Szwerc, R.; Buchler, D.; Schul, R. Design, fabrication and testing of pitch-adapting (flexible) composite propellers. In Proceedings of the Propeller/Shafting 2006 Symposium, Williamsburg, VA, USA, 12 September 2006. [Google Scholar]
- Young, Y.L. Fluid-structure interaction analysis of flexible composite marine propeller. J. Fluids Struct. 2008, 24, 799–818. [Google Scholar] [CrossRef]
- Motley, M.R.; Liu, Z.; Young, Y.L. Utilizing fluid-structure interactions to improve energy efficiency of composite marine propellers in spatially varying wake. Compos. Struct. 2009, 90, 304–313. [Google Scholar] [CrossRef]
- Motley, M.R.; Young, Y.L. Performance-based design and analysis of flexible composite propulsors. J. Fluids Struct. 2011, 27, 1310–1325. [Google Scholar] [CrossRef]
- Paul, A.; Schmidt, A.; Wolf, E. Acoustically optimized propeller made from composite materials. ThyssenKrupp Techforum 2011, 1, 58–63. [Google Scholar]
- Lee, S.G.; Hwang, J.O.; Byun, J.H. Material & Structural Characteristics of Composite Material Flexible Propeller. J. Soc. Nav. Archit. Korea 2009, 46, 203–217. [Google Scholar]
- Lee, S.G.; Nam, J.H.; Hyun, B.S.; Paik, B.G.; Lee, C.S.; Jang, H.G.; Nho, I.S. Enhanced manufacturing and performance analysis of flexible composite propeller. J. Soc. Nav. Archit. Korea 2012, 49, 521–527. [Google Scholar] [CrossRef]
- Jang, H.G.; Nho, I.S.; Hong, C.H.; Lee, C.S. Design algorithm of flexible propeller by fluid-structure interactive analysis. J. Soc. Nav. Archit. Korea 2012, 49, 528–533. [Google Scholar] [CrossRef] [Green Version]
- Jang, H.G.; Nho, I.S.; Hong, C.H.; Lee, C.S. Natural frequency analysis of cantilever plates with added mass. J. Soc. Nav. Archit. Korea 2013, 50, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Nakashima Propeller Co., Ltd. Benefits of Carbon Composite Marine Propeller. Available online: https://www.classnk.or.jp/classnk-rd/assets/pdf/katsudou201511_D.pdf (accessed on 12 May 2022).
- Lee, H.; Song, M.C.; Suh, J.C.; Kim, Y.J.; Chang, B.J. Hydro-elastic analysis of marine propellers based on a BEM-FEM coupled FSI algorithm. Int. J. Nav. Arch. Ocean 2014, 6, 562–577. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Song, M.C.; Suh, J.C.; Cha, M.C.; Chang, B.J. A numerical study on the hydro-elastic behavior of composite marine propeller. In Proceedings of the 4th International Symposium on Marine Propulsors, Austin, TX, USA, 31 May 2015. [Google Scholar]
- Lee, H.; Song, M.C.; Han, S.H.; Chang, B.J.; Suh, J.C. Hydro-elastic aspects of a composite marine propeller in accordance with ply lamination methods. J. Mar. Sci. Technol. 2017, 22, 479–493. [Google Scholar] [CrossRef]
- Kim, J.H.; Ahn, B.K.; Lee, C.S.; Kim, G.D. Numerical prediction of hydroelastic performance of the flexible propeller. Int. J. Offshore Polar Eng. 2019, 29, 339–346. [Google Scholar] [CrossRef]
- Kim, J.H.; Ahn, B.K.; Kim, G.D. Design of Flexible Composite Propellers considering Fluid-structure Interaction. J. Soc. Nav. Archit. Korea 2020, 57, 61–69. [Google Scholar] [CrossRef]
- Mccormick, B.W. On Cavitation Produced by a Vortex Trailing From a Lifting Surface. J. Basic Eng. 1962, 83, 369–379. [Google Scholar] [CrossRef]
- Kuiper, G. Cavitation Inception on Ship Propeller Models. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1981. [Google Scholar]
- Sezen, S.; Atlar, M.; Fitzsimmons, P. Prediction of cavitating propeller underwater radiated noise using RANS & DES-based hybrid method. Ships Offshore Struct. 2021, 16, 93–105. [Google Scholar]
- Schnerr, G.H.; Sauer, J. Physical and Numerical Modeling of Unsteady Cavitation Dynamics. In Proceedings of the 4th International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May 2001. [Google Scholar]
- Kroger, H.; Frohlingsdorf, W. Simulation-based optimization of the manufacturing process for a composite marine propeller. In Proceedings of the CFK-Valley Stade Convention, Stade, Germany, 12 June 2012. [Google Scholar]
- Motley, M.R.; Kramer, M.R.; Young, Y.L. Free surface and solid boundary effects on the free vibration of cantilevered composite plates. Compos. Struct. 2013, 96, 365–375. [Google Scholar] [CrossRef]
- Suh, S.B.; Park, I.R. Numerical Simulation of the Flow Around the SUBOFF Submarine Model Using a DES Method. J. Soc. Nav. Archit. Korea 2021, 58, 73–83. [Google Scholar] [CrossRef]
- Ffowcs Williams, J.; Hawkings, D. Sound generation by turbulence and surface in arbitrary motion. Philosophical. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Lighthill, M. On sound generated aerodynamically Ⅰ. General theory. Proc. R. Soc. Lond. A Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar]
- Farassat, F. Derivation of Formulations 1 and 1A of Farassat; Technical Memorandum TM-2007-214853; NASA, Langley Research Center USA: Hampton, VA, USA, 2007. [Google Scholar]
- Kuiper, G. New developments around sheet and tip vortex cavitation on ships. In Proceedings of the 4th International Symposium on Cavitation, Pasadena, CA, USA, 20 June 2001. [Google Scholar]
- Lee, J.H.; Seo, J.S. Application of spectral kurtosis to the detection of tip vortex cavitation noise in marine propeller. Mech. Syst. Signal Process. 2013, 40, 222–236. [Google Scholar] [CrossRef]
- Seol, H.S.; Kim, S.Y. Study on the analysis of model propeller tip vortex cavitation inception. J. Acoust. Soc. Korea 2018, 37, 387–395. [Google Scholar]
- Wu, Q.; Huang, B.; Wang, G.; Cao, S.; Zhu, M. Numerical modelling of unsteady cavitation and induced noise around a marine propeller. Ocean Eng. 2018, 160, 143–155. [Google Scholar] [CrossRef]

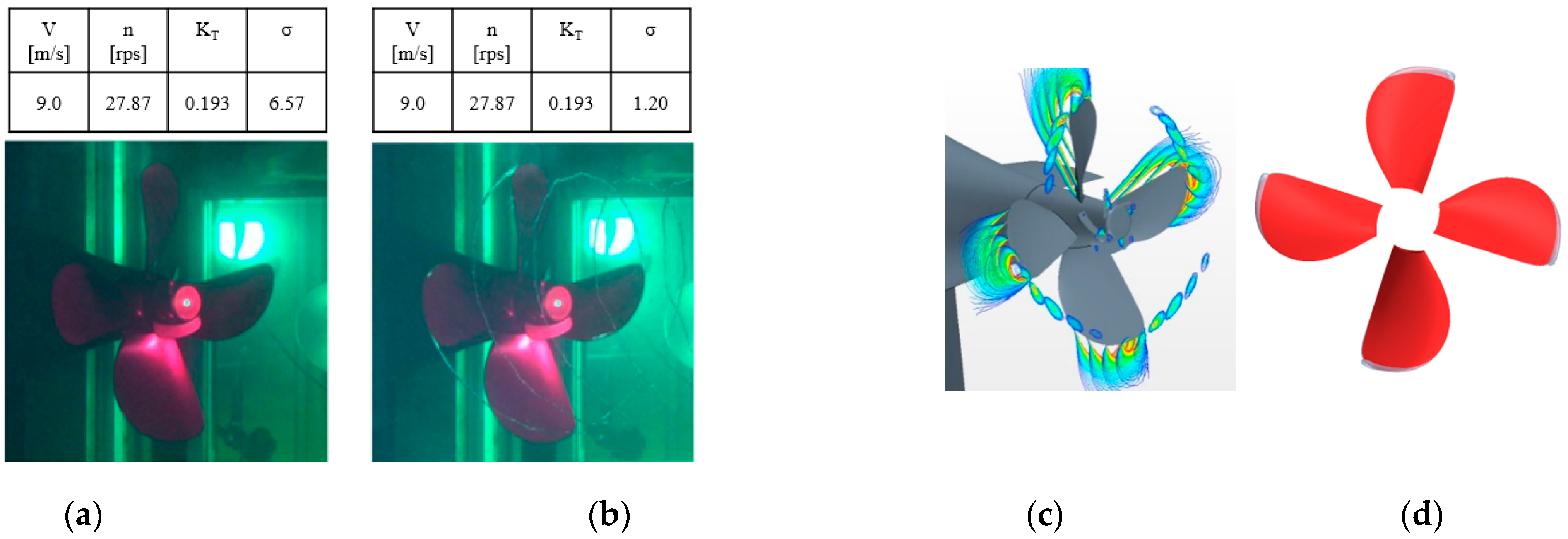








| Parameters | Value |
|---|---|
| Diameter, D [m] | 0.2882 |
| Hub ratio | 0.2233 |
| Pitch ratio at r/R = 0.7, (P/D)r/R=0.7 | 1.1018 |
| Mean pitch ratio, (P/D)mean | 1.0777 |
| Expanded area ratio | 0.4959 |
| Number of blades, Z | 4 |
| Tip skew angle [°] | 7.5000 |
| Tip rake [mm] | 0.0252 |
| No. of Grids | Thrust [N] | KT | |
|---|---|---|---|
| Coarse | Approx. 6.7 million | 942.19 | 0.1761 |
| Medium | Approx. 14.3 million | 977.99 | 0.1828 |
| Fine | Approx. 23.2 million | 996.03 | 0.1862 |
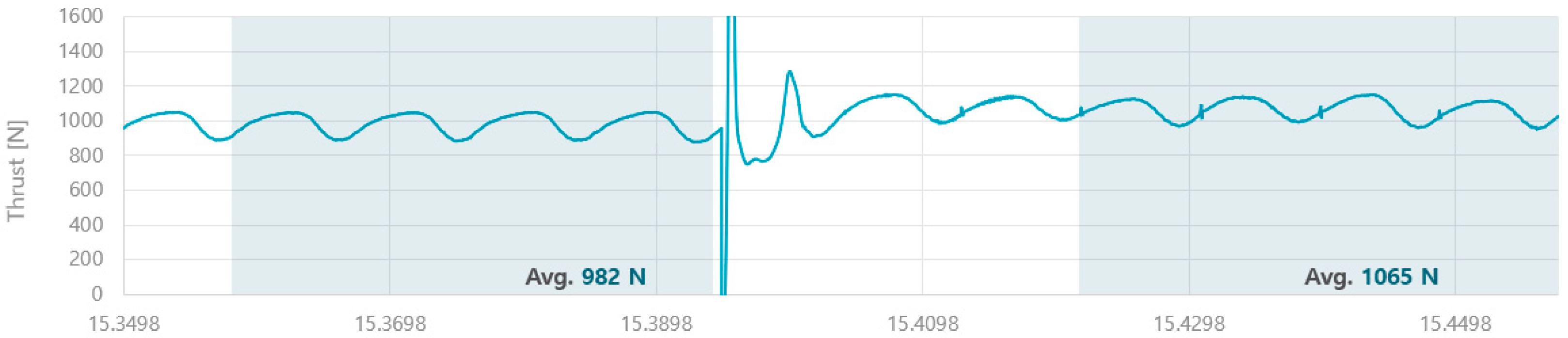
| Velocity, V [m/s] | 9.00 |
| Propeller rotating speed, n [rps] | 27.87 |
| Thrust coefficient, KT | 0.193 |
| Cavitation number at the center of propeller shaft, σn,center | 6.57 |
| Pressure, P [Pa] | 212,500 |
| Remarks | Non-cavitation condition |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-H.; Lee, H.; Kim, S.-H.; Choi, H.-Y.; Hah, Z.-H.; Seol, H.-S. Performance Prediction of Composite Marine Propeller in Non-Cavitating and Cavitating Flow. Appl. Sci. 2022, 12, 5170. https://doi.org/10.3390/app12105170
Kim J-H, Lee H, Kim S-H, Choi H-Y, Hah Z-H, Seol H-S. Performance Prediction of Composite Marine Propeller in Non-Cavitating and Cavitating Flow. Applied Sciences. 2022; 12(10):5170. https://doi.org/10.3390/app12105170
Chicago/Turabian StyleKim, Ji-Hye, Hyoungsuk Lee, Sung-Hoon Kim, Hee-Young Choi, Zoo-Hwan Hah, and Han-Shin Seol. 2022. "Performance Prediction of Composite Marine Propeller in Non-Cavitating and Cavitating Flow" Applied Sciences 12, no. 10: 5170. https://doi.org/10.3390/app12105170
APA StyleKim, J.-H., Lee, H., Kim, S.-H., Choi, H.-Y., Hah, Z.-H., & Seol, H.-S. (2022). Performance Prediction of Composite Marine Propeller in Non-Cavitating and Cavitating Flow. Applied Sciences, 12(10), 5170. https://doi.org/10.3390/app12105170








