Mathematical Modeling and Optimal Control for a Class of Dynamic Supply Chain: A Systems Theory Approach
Abstract
:Featured Application
Abstract
1. Introduction
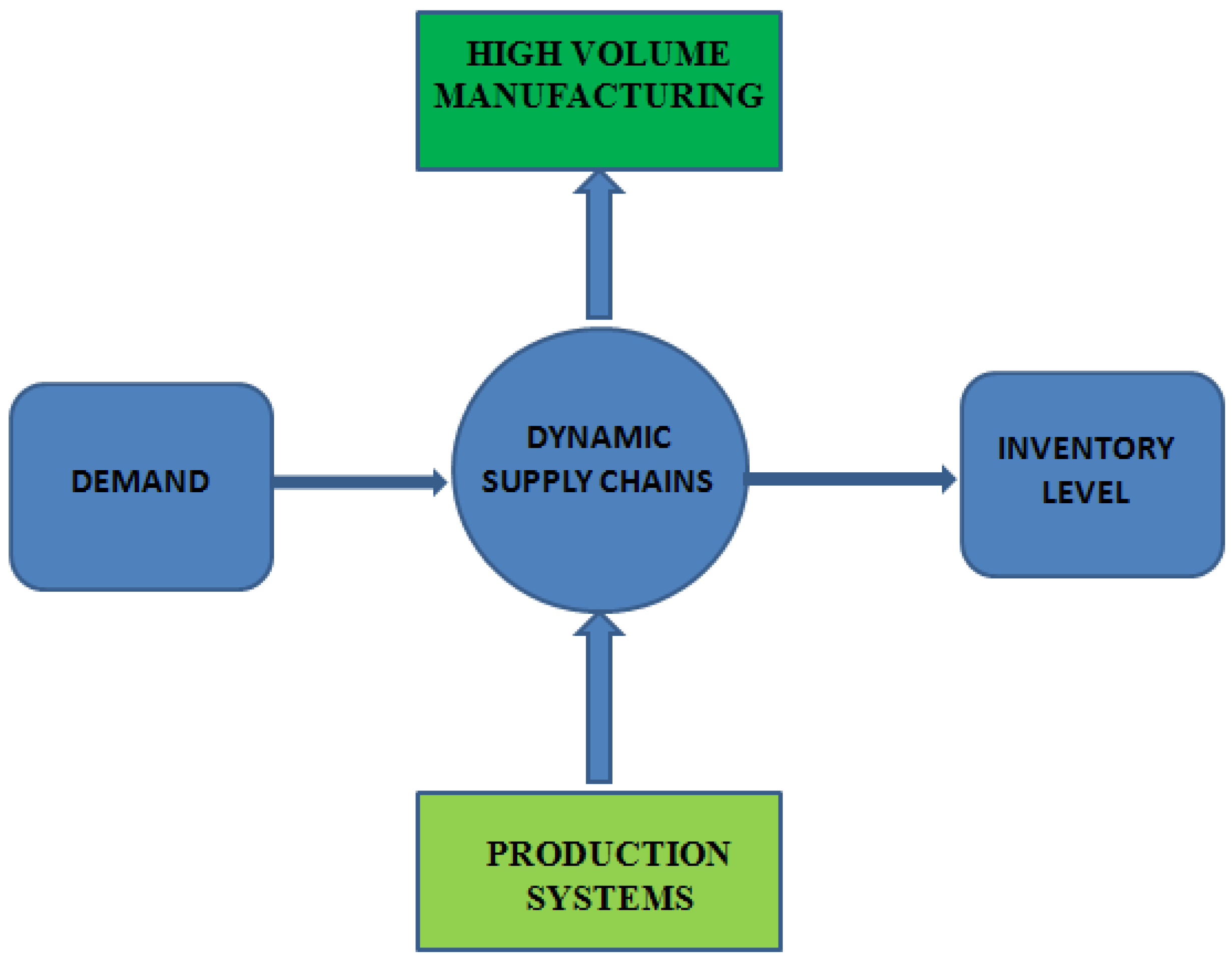
2. Dynamic Supply Chains
2.1. High-Volume Manufacturing
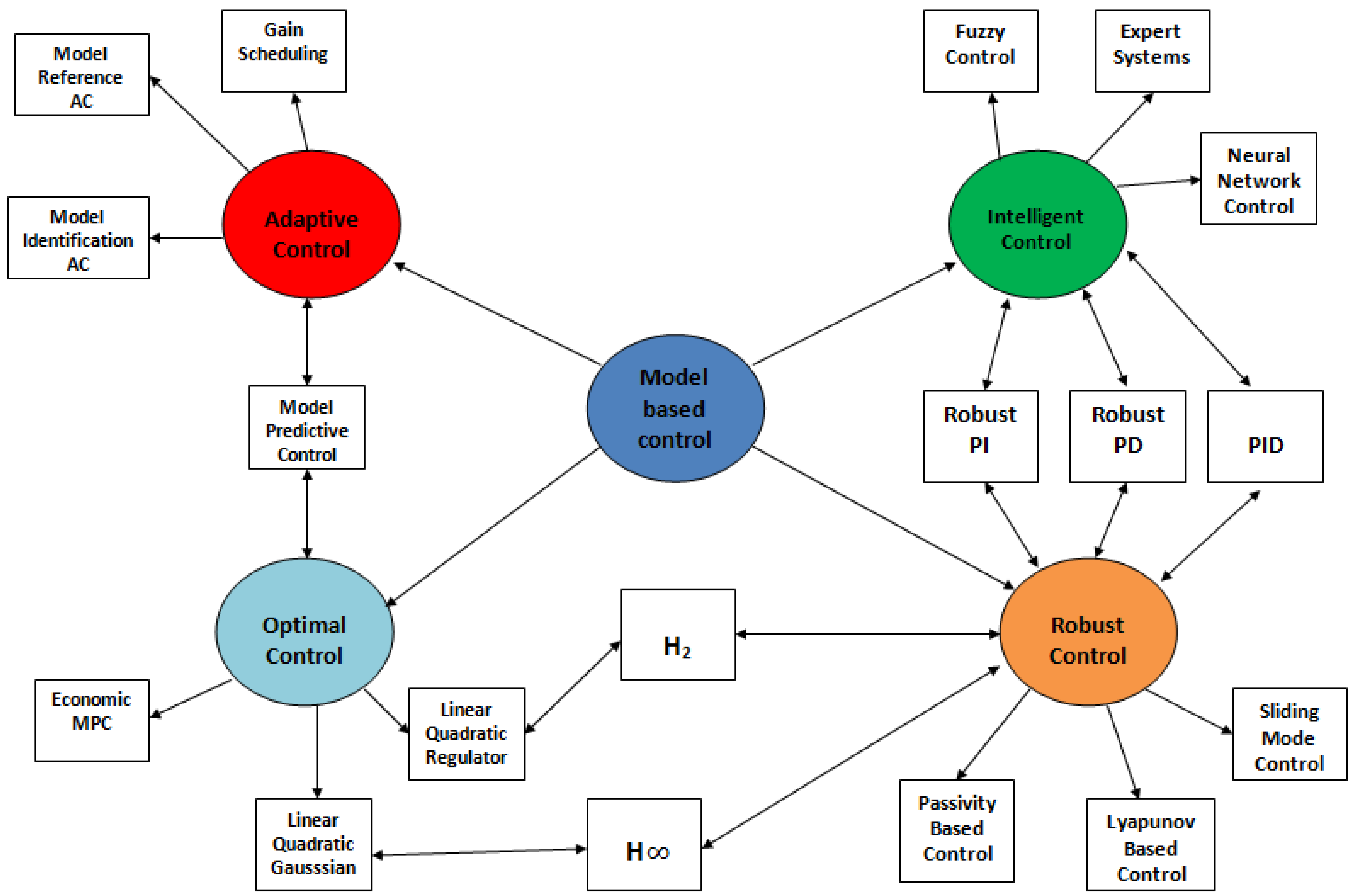
2.2. Optimal Control Theory in Supply Chains
3. The Mixing Problem and Notation
4. Mathematical Modeling
4.1. System Dynamics
4.2. System Dynamics with Lead Time
4.3. Sensitivity Analysis
4.4. Stability Analysis
5. Results
5.1. Optimal Control
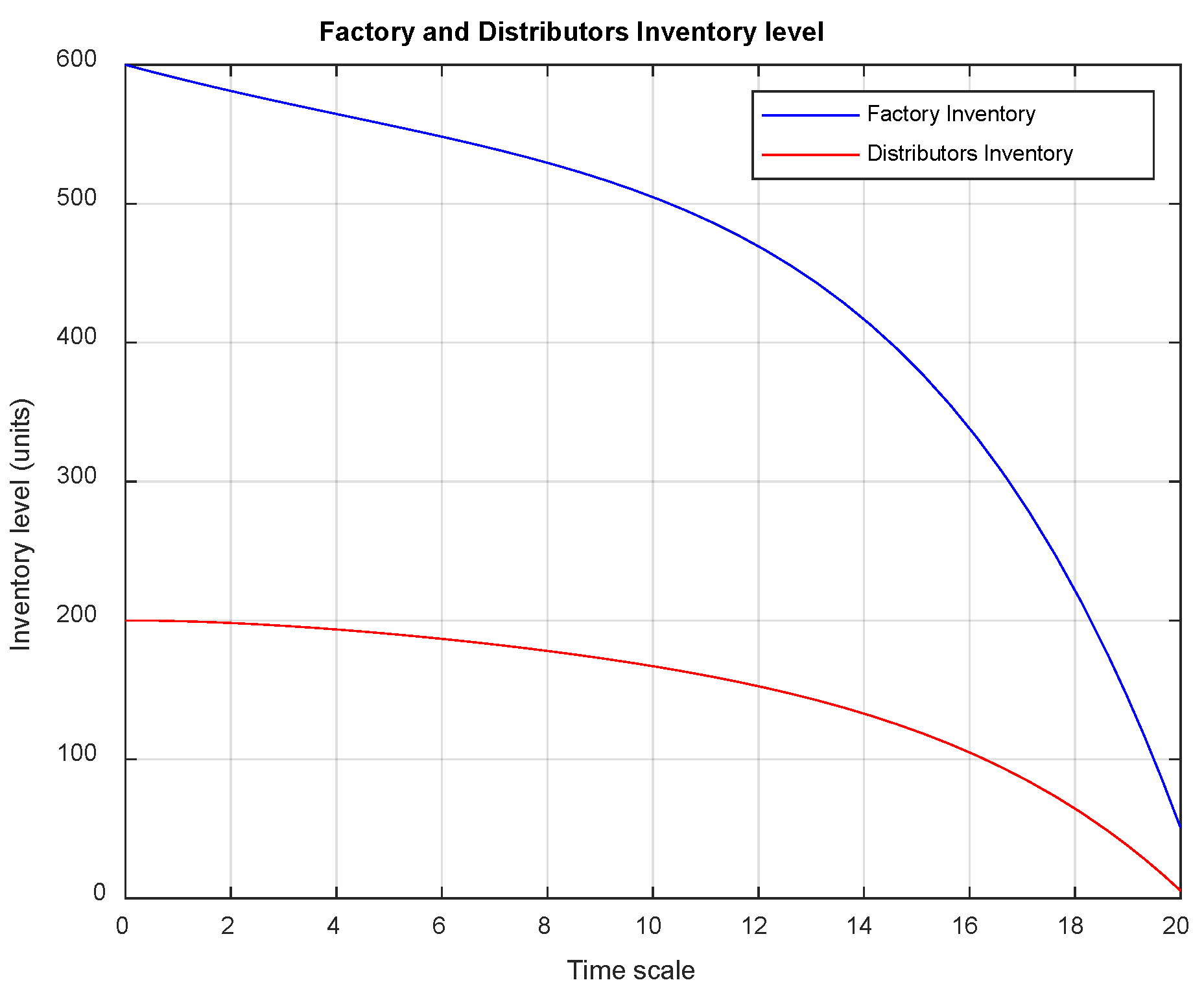
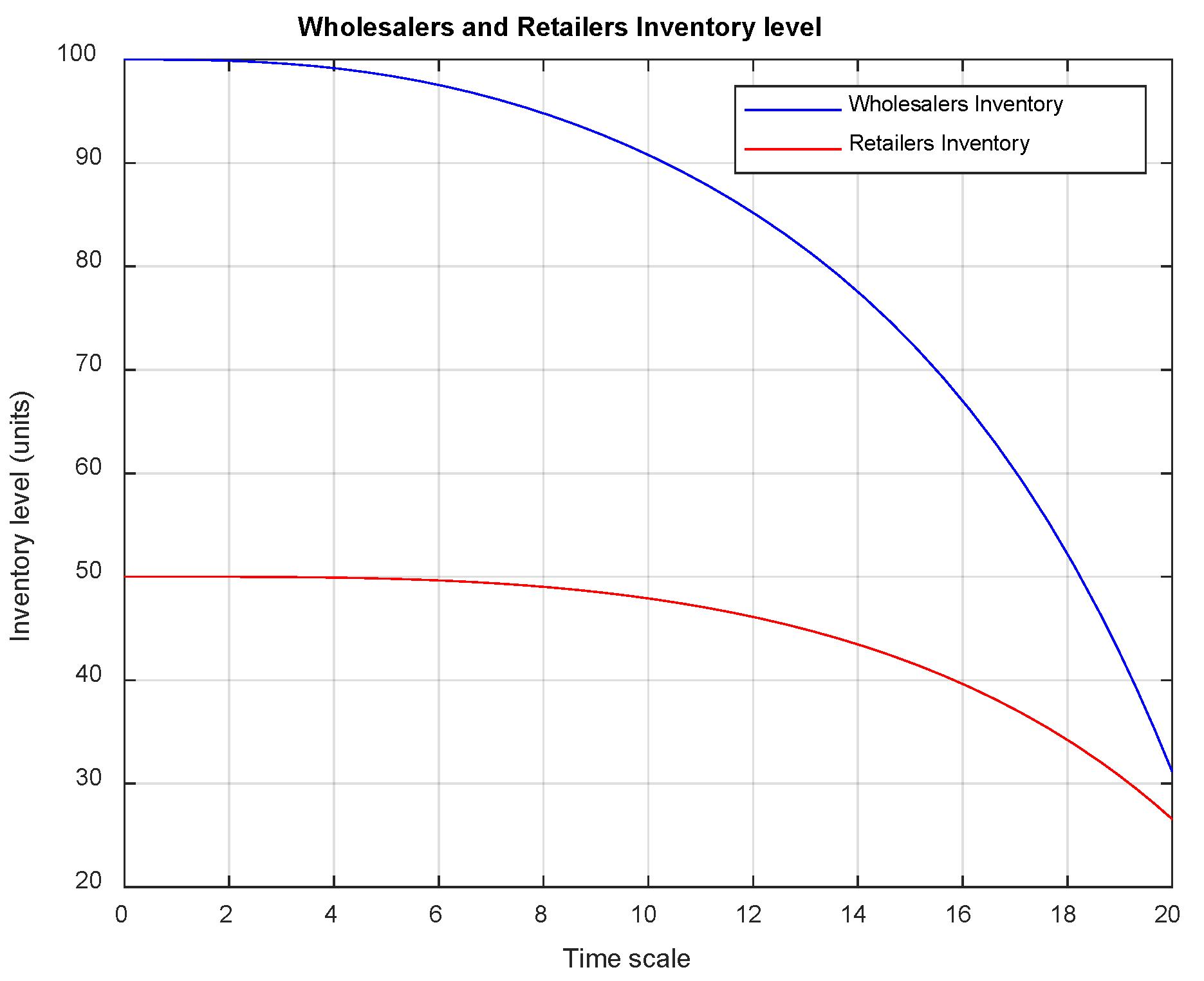
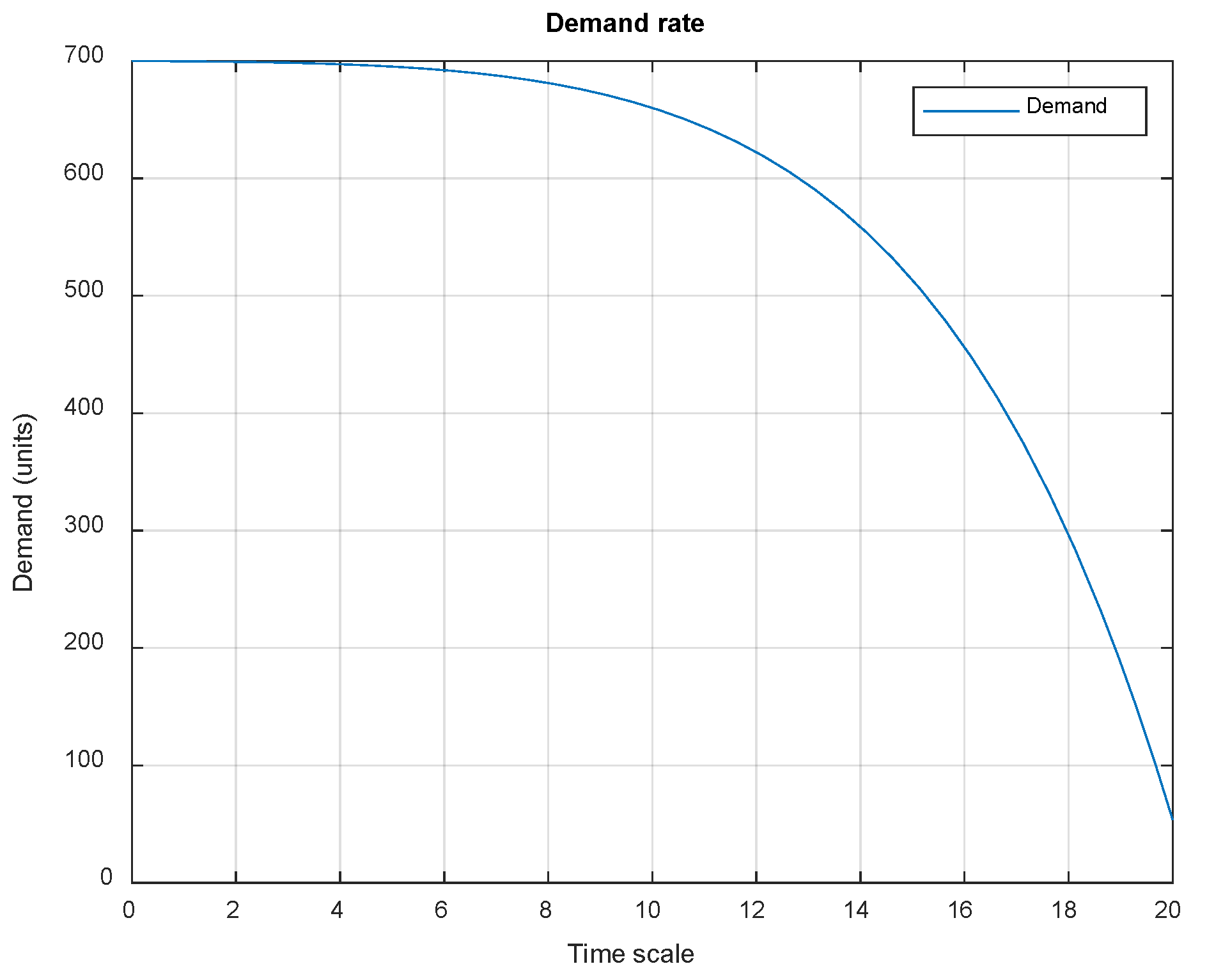
5.2. Simulations
5.3. Sensitivity Analysis of R0
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kappelman, A.C.; Sinha, A.K. Optimal control in dynamic food supply chains using big data. Comput. Oper. Res. 2021, 126, 105117. [Google Scholar] [CrossRef]
- Chen, P. The investment strategies for a dynamic supply chain under stochastic demands. Int. J. Prod. Econ. 2012, 39, 80–89. [Google Scholar] [CrossRef]
- Jain, V.; Deshmukh, S.G. Dynamic supply chain modeling using a new fuzzy hybrid negotiation mechanism. Int. J. Prod. Econ. 2009, 122, 319–328. [Google Scholar] [CrossRef]
- Jain, V.; Wadhwa, S.; Deshmukh, S.G. Revisiting information systems to support a dynamic supply chain: Issues and perspectives. Prod. Plan. Control Manag. Oper. 2009, 20, 17–29. [Google Scholar] [CrossRef]
- Umble, M.M. Analyzing manufacturing problems using V-A-T analysis. Prod. Inventory Manag. J. 1992, 33, 55–60. [Google Scholar]
- Eyers, D. Control architectures for industrial additive manufacturing systems. Proc. I MechE Part B J Eng. Manuf. 2018, 232, 1767–1777. [Google Scholar] [CrossRef]
- Orji, I.J.; Liu, S. A dynamic perspective on the key drivers of innovation-led lean approaches to achieve sustainability in manufacturing supply chain. Int. J. Prod. Econ. 2020, 219, 480–496. [Google Scholar] [CrossRef]
- Akyuz, G.A.; Erkan, T.E. Supply chain performance measurement: A literature review. Int. J. Prod. Res. 2018, 48, 5137–5155. [Google Scholar] [CrossRef]
- Singha, D.; Verma, A. Inventory management in supply chain. Mater. Today Proc. 2018, 5, 3867–3872. [Google Scholar] [CrossRef]
- De Vries, J. Diagnosing inventory management systems: An empirical evaluation of a conceptual approach. Int. J. Prod. Econ. 2007, 108, 63–73. [Google Scholar] [CrossRef]
- Fiestras-Janeiro, M.G.; García-Jurado, I.; Meca, A.; Mosquera, M.A. Cooperative game theory and inventory management. Eur. J. Oper. Res. 2011, 210, 459–466. [Google Scholar] [CrossRef]
- Bieniek, N. The ubiquitous nature of inventory: Vendor Managed Consignment Inventory in adverse market conditions. Eur. J. Oper. Res. 2019, 291, 411–420. [Google Scholar] [CrossRef]
- Duan, L.; Ventura, J.A. A dynamic Supplier Selection and Inventory Management Model for a Serial Supply Chain with a Novel Supplier Price Break Scheme and Flexible Time Periods. Eur. J. Oper. Res. 2019, 272, 979–998. [Google Scholar] [CrossRef]
- Giannoccaro, I.; Pontrandolfo, P.; Scozzi, B. A fuzzy echelon approach for inventory management in supply chains. Eur. J. Oper. Res. 2003, 149, 185–196. [Google Scholar] [CrossRef]
- Giannoccaro, I.; Pontrandolfo, P. Inventory management in supply chains: A reinforcement learning approach. Int. J. Prod. Econ. 2002, 78, 153–161. [Google Scholar] [CrossRef]
- Lieberman, M.B.; Helper, S.; Demeester, L. The empirical determinants of inventory levels in high-volume manufacturing. Prod. Oper. Manag. 1999, 8, 44–55. [Google Scholar] [CrossRef]
- Wiener, N. Cybernetics or Control and Communications in the Animal and the Machines; The MIT Press: Cambridge, MA, USA, 1948. [Google Scholar]
- Davizon, Y.A. Mathematical Modeling, Optimal Control and Stability Analysis for Dynamic Supply Chains. Ph.D. Thesis, The University of Texas at El Paso, El Paso, TX, USA, 2020. [Google Scholar]
- Song, D.P. Optimal integrated ordering and production policy in a supply chain with stochastic lead-time, processing-time, and demand. IEEE Trans. Autom. Control. 2009, 54, 2027–2041. [Google Scholar] [CrossRef]
- Kogan, K.; Lou, S.; Tapiero, C.S.; Shnaiderman, M. Supply chain with inventory review and dependent demand distributions: Dynamic inventory outsourcing. IEEE Trans. Autom. Sci. Eng. 2010, 7, 197–207. [Google Scholar] [CrossRef]
- Ignaciuk, P.; Bartoszewicz, A.A. Linear–quadratic optimal control strategy for periodic-review inventory systems. Automatica 2010, 46, 1982–1993. [Google Scholar] [CrossRef]
- Ignaciuk, P.; Bartoszewicz, A. Linear-Quadratic optimal control of periodic-review Perishable inventory systems. IEEE Trans. Control Syst. Technol. 2012, 20, 1400–1407. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A.; Sokolov, B. Applicability of optimal control theory to adaptive supply chain planning and scheduling. Annu. Rev. Control 2012, 36, 73–84. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A.; Sokolov, B. Robust dynamic schedule coordination control in the supply chain. Comput. Ind. Eng. 2016, 94, 18–31. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, D.; Sethi, S.; Dolgui, A.; Sokolov, B. A survey on control theory applications to operational systems, supply chain management, and Industry 4.0. Annu. Rev. Control 2018, 46, 134–147. [Google Scholar] [CrossRef]
- Dolgui, A.; Ivanov, D.; Sethi, S.P.; Sokolov, B. Scheduling in production, supply chain and Industry 4.0 systems by optimal control: Fundamentals, state-of-the-art and applications. Int. J. Prod. Res. 2018, 57, 411–422. [Google Scholar] [CrossRef]
- Zu, Y.; Chen, L.; He, S. Inter-Organizational control of low-carbon production in a supply chain. IEEE Access 2019, 7, 170322–170332. [Google Scholar] [CrossRef]
- Wu, Z. Optimal control approach to advertising strategies of a supply chain under consignment contract. IEEE Access 2019, 7, 41454–41462. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, D. New optimal-control-based advertising strategies and coordination of a supply chain with differentiated products under consignment contract. IEEE Access 2019, 7, 170703–170714. [Google Scholar] [CrossRef]
- Yu, H.; Bai, S.; Chen, D. An optimal control model of the low-carbon supply chain: Joint emission reduction, pricing strategies, and new coordination contract design. IEEE Access 2020, 8, 106273–106283. [Google Scholar] [CrossRef]
- Rarità, L.; Stamova, I.; Tomasiello, S. Numerical schemes and genetic algorithms for the optimal control of a continuous model of supply chains. Appl. Math. Comput. 2021, 388, 125464. [Google Scholar] [CrossRef]
- He, Y.; Zheng, S.; Yuan, L. Dynamics of Fractional-Order Digital Manufacturing Supply Chain System and Its Control and Synchronization. Fractal Fract. 2021, 5, 128. [Google Scholar] [CrossRef]
- Kegenbekov, Z.; Jackson, I. Adaptive Supply Chain: Demand–Supply Synchronization Using Deep Reinforcement Learning. Algorithms 2021, 14, 240. [Google Scholar] [CrossRef]
- Badillo, I.; Tejeida, R.; Morales, O.; Flores, M. Supply Chain Management from a Systems Science Perspective, Supply Chain Management—New Perspectives; Intech.: London, UK, 2011. [Google Scholar]
- Zill, D.G. Advanced Engineering Mathematics, 6th ed.; Jones & Bartlett Learning: Burlington, MA, USA, 2017. [Google Scholar]
- Herty, M.; Ringhofer, C. Feedback controls for continuous priority models in supply chain management. Comput. Methods Appl. Math. 2011, 11, 206–213. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Luaces, V. Square Matrices Associated to Mixing Problems ODE Systems. Matrix Theory—Applications and Theorems; Hassan, A.Y., Ed.; Intech.: London, UK, 2018. [Google Scholar]
- Bassingthwaighte, J.B.; Butterworth, E.; Jardine, B.; Raymond, G.M. Compartmental Modeling in the Analysis of Biological Systems. In Toxicology: Volume I, Methods in Molecular Biology; Springer: Berlin/Heidelberg, Germany, 2012; Volume 929. [Google Scholar]
- Rahimian, E.; Zabihi, S.; Mahmood Amiri, M.; Linares-Barranco, B. Digital implementation of the two-compartmental Pinsky–Rinzel pyramidal neuron model. IEEE Trans. Biomed. Circuits Syst. 2018, 1, 47–57. [Google Scholar] [CrossRef] [PubMed]
- Fogarty, D.W.; Blackstone, J.H.; Hoffmann, T.R. Production & Inventory Management; South-Western Publishing Company: Nashville, TN, USA, 1991. [Google Scholar]

| Manuscript | Contribution | Control Approach |
|---|---|---|
| Ivanov, et al., 2016, [24] | This paper addresses the problem of supply chain coordination with a robust schedule coordination approach, applying optimal control theory. | Optimal control |
| Ivanov, et al., 2018, [25] | This research work extends a previous survey by identifying two new directions for control theory applications and digital technology use in control-theoretic models. | Optimal control |
| Dolgui, et al., 2018, [26] | A survey on optimal control applications regarding scheduling in production, supply chain, and Industry 4.0 systems via deterministic maximum principle. | Optimal control |
| Zu, et al., 2019, [27] | This paper presents a method to study the Stackelberg differential game between a manufacturer and a supplier. | Differential game |
| Wu, 2019, [28] | This paper presents a differential game for a single manufacturer and a single retailer in a supply chain under a consignment contract. | Optimal control |
| Wu and Chen, 2019, [29] | The cooperative advertising problem is addressed, applying optimal control theory for a supply chain under a consignment contract in a competitive environment. | Optimal control |
| Yu, et al., 2020, [30] | An optimal control model is presented for a class of low-carbon supply chain system. A linear differential equation describes the dynamics of emission reduction level. | Optimal control |
| Rarita, et al., 2021, [31] | This paper considers supply chains modeled by partial and ordinary differential equations. | Optimal control |
| He, et al., 2021, [32] | In this paper, a fractional-order digital manufacturing supply chain system is proposed with feedback controllers to control the chaotic supply chain system. | Fractional order control |
| Kegenbekov and Jackson, 2021, [33] | This paper shows how a deep reinforcement learning-based optimization algorithm can synchronize inbound and outbound flows to support a business operating in the stochastic environment. | Deep reinforcement learning |
| Parameter | Value | Sensitivity Index |
|---|---|---|
| Φ1 | 10 | 0.001 |
| Φ2 | 10 | 0.001 |
| Φ3 | 10 | 0.001 |
| Φ4 | 10 | 0.001 |
| C1 | 100 | −0.001 |
| C2 | 100 | −0.001 |
| C3 | 100 | −0.001 |
| C4 | 100 | −0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taboada, H.; Davizón, Y.A.; Espíritu, J.F.; Sánchez-Leal, J. Mathematical Modeling and Optimal Control for a Class of Dynamic Supply Chain: A Systems Theory Approach. Appl. Sci. 2022, 12, 5347. https://doi.org/10.3390/app12115347
Taboada H, Davizón YA, Espíritu JF, Sánchez-Leal J. Mathematical Modeling and Optimal Control for a Class of Dynamic Supply Chain: A Systems Theory Approach. Applied Sciences. 2022; 12(11):5347. https://doi.org/10.3390/app12115347
Chicago/Turabian StyleTaboada, Heidi, Yasser A. Davizón, José F. Espíritu, and Jaime Sánchez-Leal. 2022. "Mathematical Modeling and Optimal Control for a Class of Dynamic Supply Chain: A Systems Theory Approach" Applied Sciences 12, no. 11: 5347. https://doi.org/10.3390/app12115347
APA StyleTaboada, H., Davizón, Y. A., Espíritu, J. F., & Sánchez-Leal, J. (2022). Mathematical Modeling and Optimal Control for a Class of Dynamic Supply Chain: A Systems Theory Approach. Applied Sciences, 12(11), 5347. https://doi.org/10.3390/app12115347





