On the Sum of α-μ/Inverse Gamma Variates with Applications to Diversity Receivers
Abstract
:1. Introduction
2. Statistical Characteristics of α-μ/IGA Distribution
2.1. Univariate Case
2.2. Bivariate Case
3. Statistical Characteristics of the Sum of α-μ/IGA RVs
3.1. Exact Statistics of the Sum of the Independent RVs
3.2. Approximated Statistics of the Sum of the Independent RVs
3.3. Statistics of the Two Correlated RVs
4. Performance Analysis
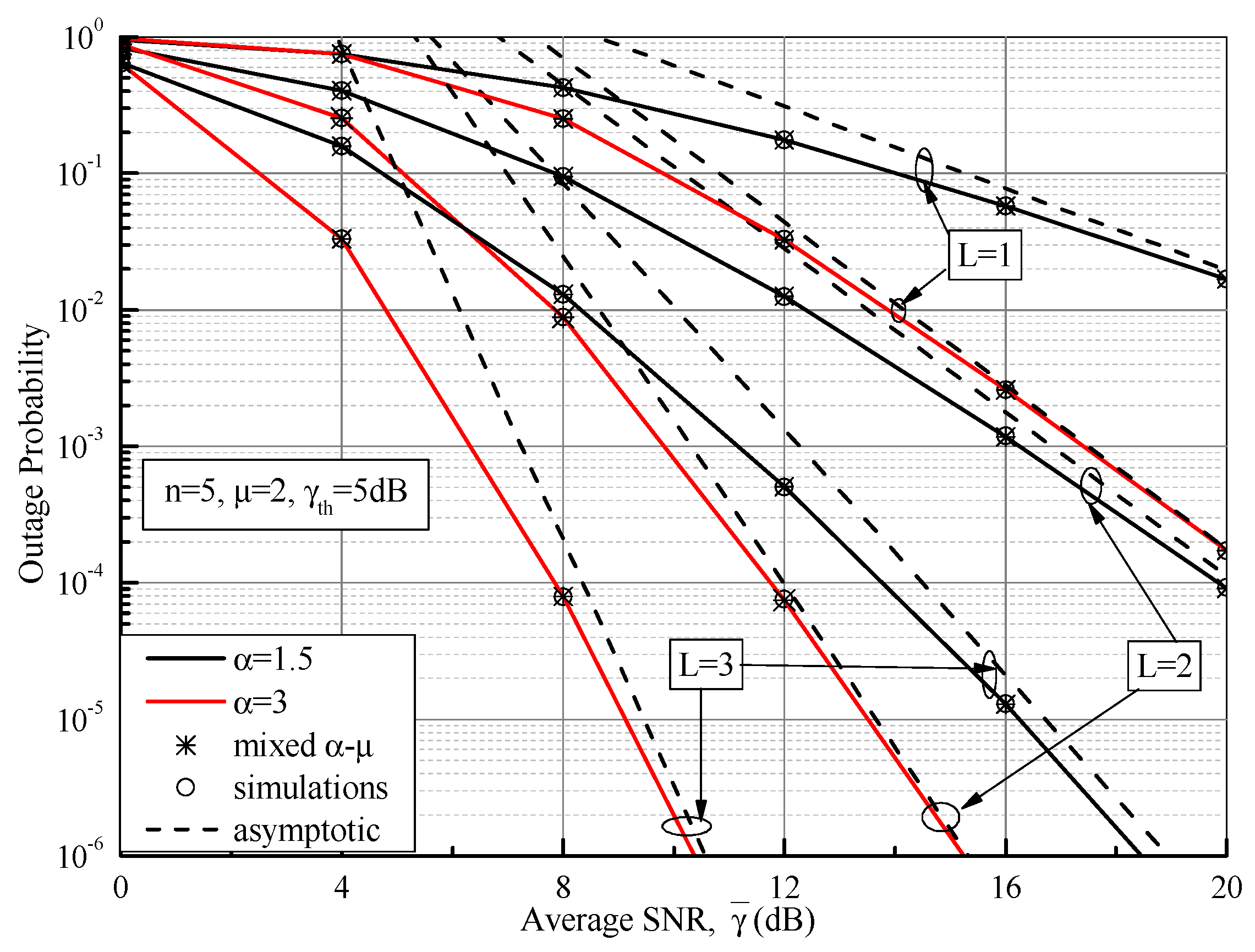
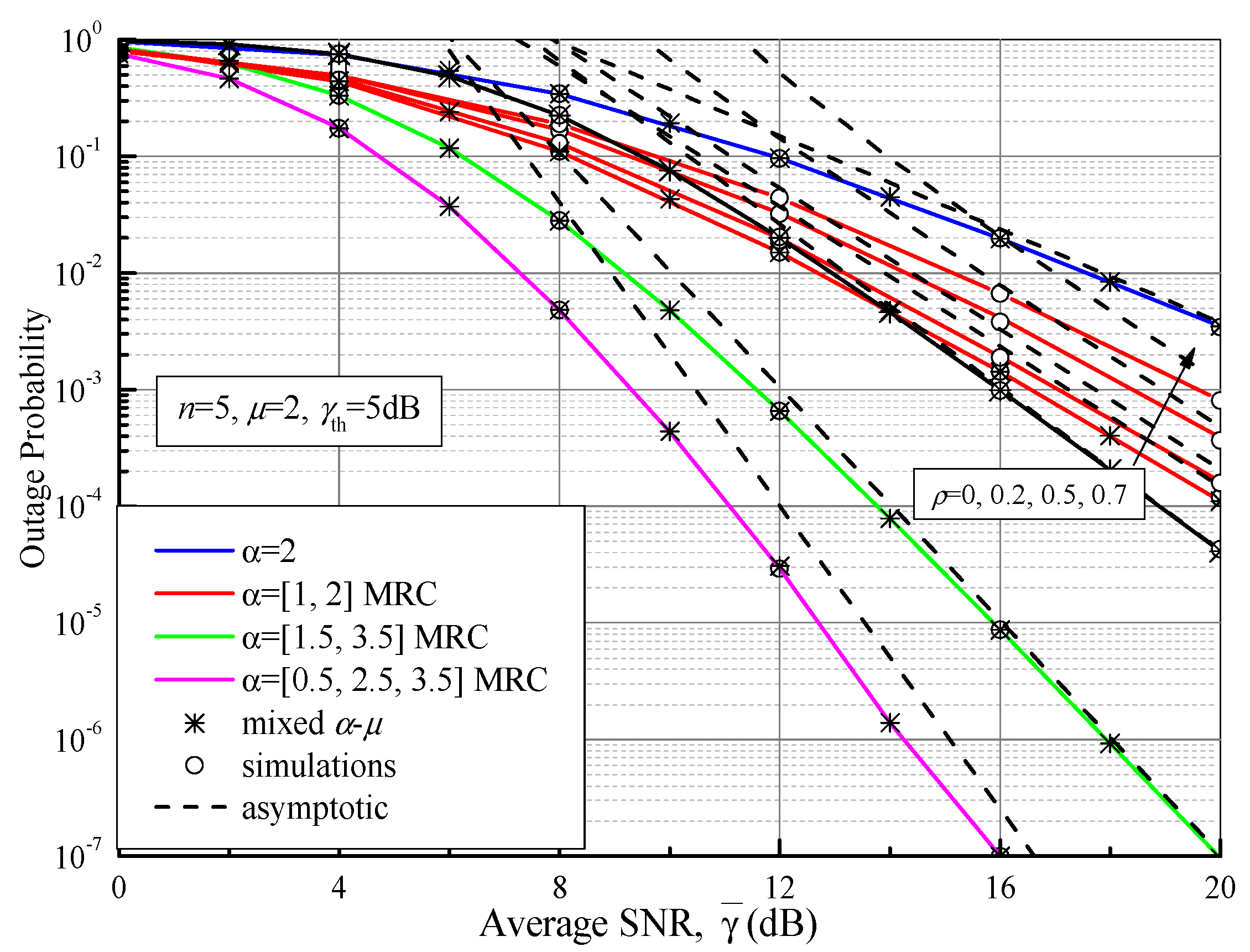
4.1. Outage Probability
4.2. Average BEP/SEP
4.2.1. ABEP/ASEP in the Exponential Form
4.2.2. ABEP/ASEP in the Erfc Function Form
A. Single-Link System
B. MRC System
4.3. Average Channel Capacity
4.3.1. Single-Link System
4.3.2. MRC System
4.4. Effective Capacity
4.4.1. Single-Link System
4.4.2. MRC System
5. Asymptotic Analysis
5.1. Single-Link System
5.2. MRC System
6. Numerical and Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Simon, M.K.; Alouini, M.S. Digital Communication over Fading Channels, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Moualeu, J.M.; da Costa, D.B.; Lopez-Martinez, F.J.; de Souza, R.A.A. On the performance of α-η-κ-μ fading channels. IEEE Commun. Lett. 2019, 23, 967–970. [Google Scholar] [CrossRef]
- Abdi, A.; Kaveh, M. K distribution: An appropriate substitute for Rayleigh-lognormal distribution in fading-shadowing wireless channels. Electron. Lett. 1998, 34, 851–852. [Google Scholar] [CrossRef] [Green Version]
- Eltoft, T. The Rician inverse Gaussian distribution: A new model for non-Rayleigh signal amplitude statistics. IEEE Trans. Image Process. 2005, 14, 1722–1735. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, M.; Soni, S.K. A unified performance analysis of energy detector over α-η-μ/lognormal and α-κ-μ/lognormal composite fading channels with diversity and cooperative spectrum sensing. Int. J. Electron. Commun. (AEÜ) 2018, 94, 367–376. [Google Scholar] [CrossRef]
- Al-Hmood, H.; Al-Raweshidy, H.S. Unified modeling of composite κ-μ/gamma, η-μ/gamma, and α-μ/gamma fading channels using a mixture gamma distribution with applications to energy detection. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 104–108. [Google Scholar] [CrossRef]
- Chauhan, P.S.; Soni, S.K. Average SEP and channel capacity analysis over Generic/IG composite fading channels: A unified approach. Phys. Commun. 2019, 34, 9–18. [Google Scholar] [CrossRef]
- Paris, J.F. Statistical characterization of κ-μ shadowed fading. IEEE Trans. Veh. Technol. 2014, 63, 518–526. [Google Scholar] [CrossRef] [Green Version]
- Simmons, N.; da Silva, C.R.N.; Cotton, S.L.; Sofotasios, P.C.; Yacoub, M.D. Double shadowing the Rician fading model. IEEE Wirel. Commun. Lett. 2019, 8, 344–347. [Google Scholar] [CrossRef]
- Simmons, N.; Da Silva, C.R.N.; Cotton, S.L.; Sofotasios, P.C.; Yoo, S.K.; Yacoub, M.D. On shadowing the κ-μ fading model. IEEE Access 2020, 8, 120513–120536. [Google Scholar] [CrossRef]
- Leonardo, E.J.; Yacoub, M.D. The product of two α-μ variates and the composite α-μ multipathshadowing model. IEEE Trans. Veh. Technol 2015, 64, 2720–2725. [Google Scholar] [CrossRef]
- Badarneh, O.S. The α-μ/α-μ composite multipath-shadowing distribution and its connection with the extended generalized-K distribution. AEU-Int. J. Elect. Commun. 2016, 70, 1211–1218. [Google Scholar] [CrossRef]
- Yoo, S.; Cotton, S.; Zhang, L.; Sofotasios, P. The inverse Gamma distribution: A new shadowing model. In Proceedings of the 8th Asia-Pacific Conference on Antennas and Propagation, Incheon, Korea, 4–7 August 2019; pp. 475–476. [Google Scholar] [CrossRef]
- Ramırez-Espinosa, P.; Lopez-Martınez, F.J. On the utility of the inverse gamma distribution in modeling composite fading channels. In Proceedings of the IEEE Global Communications Conference, Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Ramírez-Espinosa, P.; López-Martínez, F.J. Composite fading models based on inverse Gamma shadowing: Theory and validation. IEEE Trans. Wirel. Commun. 2021, 20, 5034–5045. [Google Scholar] [CrossRef]
- Bithas, P.; Nikolaidis, V.; Kanatas, A.G.; Karagiannidis, G.K. UAV-to-ground communications: Channel modeling and UAV selection. IEEE Trans. Commun. 2020, 68, 5135–5144. [Google Scholar] [CrossRef]
- Yoo, S.K.; Cotton, S.L.; Sofotasios, P.C.; Matthaiou, M.; Valkama, M.; Karagiannidis, G.K. The κ-μ/inverse gamma fading model. In Proceedings of the IEEE PIMRC, Hong Kong, China, 30 August–2 September 2015; pp. 425–429. [Google Scholar]
- Yoo, S.K.; Sofotasios, P.C.; Cotton, S.L.; Matthaiou, M.; Valkama, M.; Karagiannidis, G.K. The η-μ/inverse gamma composite fading model. In Proceedings of the IEEE PIMRC, Hong Kong, China, 30 August–2 September 2015; pp. 166–170. [Google Scholar]
- Yoo, S.K.; Bhargav, N.; Cotton, S.L.; Sofotasios, P.C.; Matthaiou, M.; Valkama, M.; Karagiannidis, G.K. The κ-μ/inverse gamma and η-μ/inverse gamma composite fading models: Fundamental statistics and empirical validation. IEEE Trans. Commun. 2017, 69, 5514–5530. [Google Scholar] [CrossRef]
- Yoo, S.K.; Cotton, S.L.; Sofotasios, P.C.; Muhaidat, S.; Karagiannidis, G.K. Effective capacity analysis over generalized composite fading channels. IEEE Access 2020, 8, 123756–123764. [Google Scholar] [CrossRef]
- Pant, D.; Chauhan, P.S.; Soni, S.K.; Naithani, S. BER and channel capacity analysis of wireless system over κ-μ/inverse gamma and η-μ/inverse gamma composite fading model. Wirel. Netw. 2021, 27, 1251–1267. [Google Scholar] [CrossRef]
- Pant, D.; Chauhan, P.S.; Soni, S.K. Error probability and channel capacity analysis of wireless system over inverse gamma shadowed fading channel with selection diversity. Int. J. Commun. Syst. 2019, 32, e4083. [Google Scholar] [CrossRef]
- Upaddhyay, V.K.; Chauhan, P.S.; Soni, S.K. Effective capacity analysis of SIMO system with MRC and SC over Inverse-Gamma shadowing. Int. J. Electron. 2021, 109, 181–199. [Google Scholar] [CrossRef]
- Cheng, W.J.; Wang, X.T.; Xu, X.M. On the performance analysis of wireless transmission over α-μ/inverse gamma composite fading channels. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC Workshops), Chongqing, China, 9–11 August 2020; pp. 64–69. [Google Scholar] [CrossRef]
- Maurya, R.; Chauhan, P.S.; Srivastava, S.; Soni, S.K.; Mishra, B. Energy detection investigation over composite α-μ/inverse-Gamma wireless channel. Int. J. Electron. Commun. 2020, 130, 153556. [Google Scholar] [CrossRef]
- Upaddhyay, V.K.; Soni, S.K.; Chauhan, P.S. An approximate statistical analysis of wireless channel over α-μ shadowed fading channel. Int. J. Commun. Syst. 2021, 34, e4884. [Google Scholar] [CrossRef]
- Goswami, A.; Kumar, A. Statistical Characterization and Performance Evaluation of α−η−μ/Inverse Gamma and α−κ−μ/Inverse Gamma Channels. Wirel. Pers. Commun. 2022, 124, 2313–2333. [Google Scholar] [CrossRef]
- Yoo, S.K.; Cotton, S.L.; Sofotasios, P.C.; Matthaiou, M.; Valkama, M.; Karagiannidis, G.K. The Fisher-Snedecor distribution: A simple and accurate composite fading model. IEEE Commun. Lett. 2017, 21, 1661–1664. [Google Scholar] [CrossRef] [Green Version]
- Cheng, W.J.; Wang, X.T. Bivariate Fisher–Snedecor distribution and its applications in wireless communication systems. IEEE Access 2020, 8, 146342–146360. [Google Scholar] [CrossRef]
- Cheng, W.J.; Wang, X.T.; Ma, T.F.; Wang, G. On the performance analysis of switched diversity combining receivers over Fisher–Snedecor composite fading channels. Sensors 2021, 21, 3014. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Du, H.Y.; Sun, Q.; Ai, B.; Ng, D.W.K. Physical layer security enhancement with reconfigurable intelligent surface-aided networks. IEEE Trans. Inf. Forensics Secur. 2021, 16, 3480–3495. [Google Scholar] [CrossRef]
- Badarneh, O.S. The α- composite fading distribution: Statistical characterization and applications. IEEE Trans. Veh. Technol. 2020, 69, 8097–8106. [Google Scholar] [CrossRef]
- Badarneh, O.S. The α-η- and α-κ- composite fading distributions. IEEE Commun. Lett. 2020, 24, 1924–1928. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Muhaidat, S.; Costa, D.B.D. The α-η-κ- composite fading distribution. IEEE Wirel. Commun. Lett. 2020, 9, 2182–2186. [Google Scholar] [CrossRef]
- Treanta, S. Optimization on the distribution of population densities and the arrangement of urban activities. Stat. Optim. Inf. Comput. 2018, 6, 208–218. [Google Scholar] [CrossRef]
- Yacoub, M.D. The α-μ distribution: A physical fading model for the stacy distribution. IEEE Trans. Veh. Technol. 2007, 56, 27–34. [Google Scholar] [CrossRef]
- Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series, and Products, 7th ed.; Academic: New York, NY, USA, 2007. [Google Scholar]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Aldalgamouni, T.; Ilter, M.C.; Badarneh, O.S.; Yanikomeroglu, H. Performance analysis of fisher-snedecor composite fading channels. In Proceedings of the IEEE Middle East and North Africa Communications Conference, Jounieh, Lebanon, 18–20 April 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Al-Hmood, H.; Al-Raweshidy, H.S. Selection combining scheme over non-identically distributed Fisher-Snedecor fading channels. IEEE Wirel. Commun. Lett. 2021, 10, 840–843. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Costa, D.B.D.; Sofotasios, P.C.; Muhaidat, S.; Cotton, S.L. On the sum of Fisher-Snedecor variates and its application to maximal-ratio combining. IEEE Wirel. Commun. Lett. 2018, 7, 966–969. [Google Scholar] [CrossRef] [Green Version]
- Atapattu, S.; Tellambura, C.; Jiang, H. A mixture gamma distribution to model the SNR of wireless channels. IEEE Trans. Wirel. Commun. 2011, 10, 4193–4203. [Google Scholar] [CrossRef]
- Ramirez-Espinosa, P.; Moualeu, J.M.; da Costa, D.B.; Lopez-Martinez, F.J. The α-κ-μ shadowed fading distribution: Statistical characterization and applications. In Proceedings of the IEEE Global Communications Conference, Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Bithas, P.S.; Kanatas, A.G.; Matolak, D.W. Exploiting shadowing stationarity for antenna selection in V2V communications. IEEE Trans. Veh. Technol. 2018, 68, 1607–1615. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series (More Special Functions); Gordon and Breach: Philadelphia, PA, USA, 1992; Volume 3. [Google Scholar]
- Kilbas, A.A.; Saigo, M. H-Transforms: Theory and Applications (Analytical Method and Special Function), 1st ed.; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar] [CrossRef]
- Mittal, P.K.; Gupta, K.C. An integral involving generalized function of two variables. Proc. Indian Acad. Sci.-Sect. A 1972, 75, 117–123. [Google Scholar] [CrossRef]
- Rahama, Y.A.; Ismail, M.H.; Hassan, M. On the sum of independent Fox’s H-Function variates with applications. IEEE Trans. Veh. Technol. 2018, 67, 6752–6760. [Google Scholar] [CrossRef]
- Du, H.Y.; Zhang, J.Y.; Cheng, J.L.; Ai, B. Sum of Fisher-Snedecor random variables and its applications. IEEE Open J. Commun. Soc. 2020, 1, 342–356. [Google Scholar] [CrossRef]
- Hamdi, K.A. Capacity of MRC on correlated rician fading channels. IEEE Trans. Commun. 2008, 56, 708–711. [Google Scholar] [CrossRef] [Green Version]
- Ji, Z.; Dong, C.; Wang, Y.; Lu, J. On the analysis of effective capacity over generalized fading channels. In Proceedings of the IEEE International Conference on Communications, Sydney, Australia, 10–14 June 2014; pp. 1977–1983. [Google Scholar] [CrossRef]
- Alhennawi, H.R.; El Ayadi, M.M.; Ismail, M.H.; Mourad, H.A.M. Closed-form exact and asymptotic expressions for the symbol error rate and capacity of the H-function fading channel. IEEE Trans. Veh. Technol. 2016, 65, 1957–1974. [Google Scholar] [CrossRef]
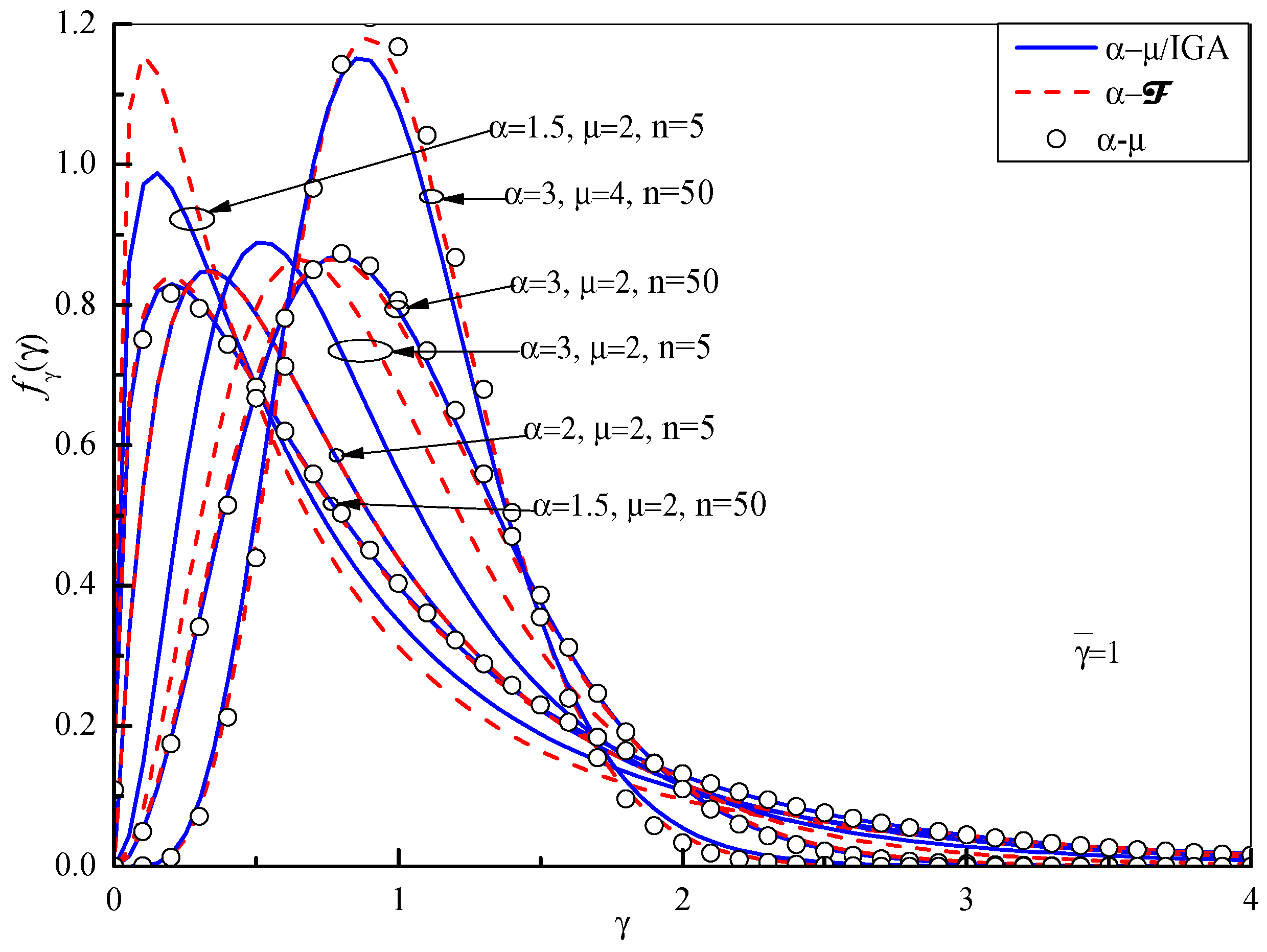
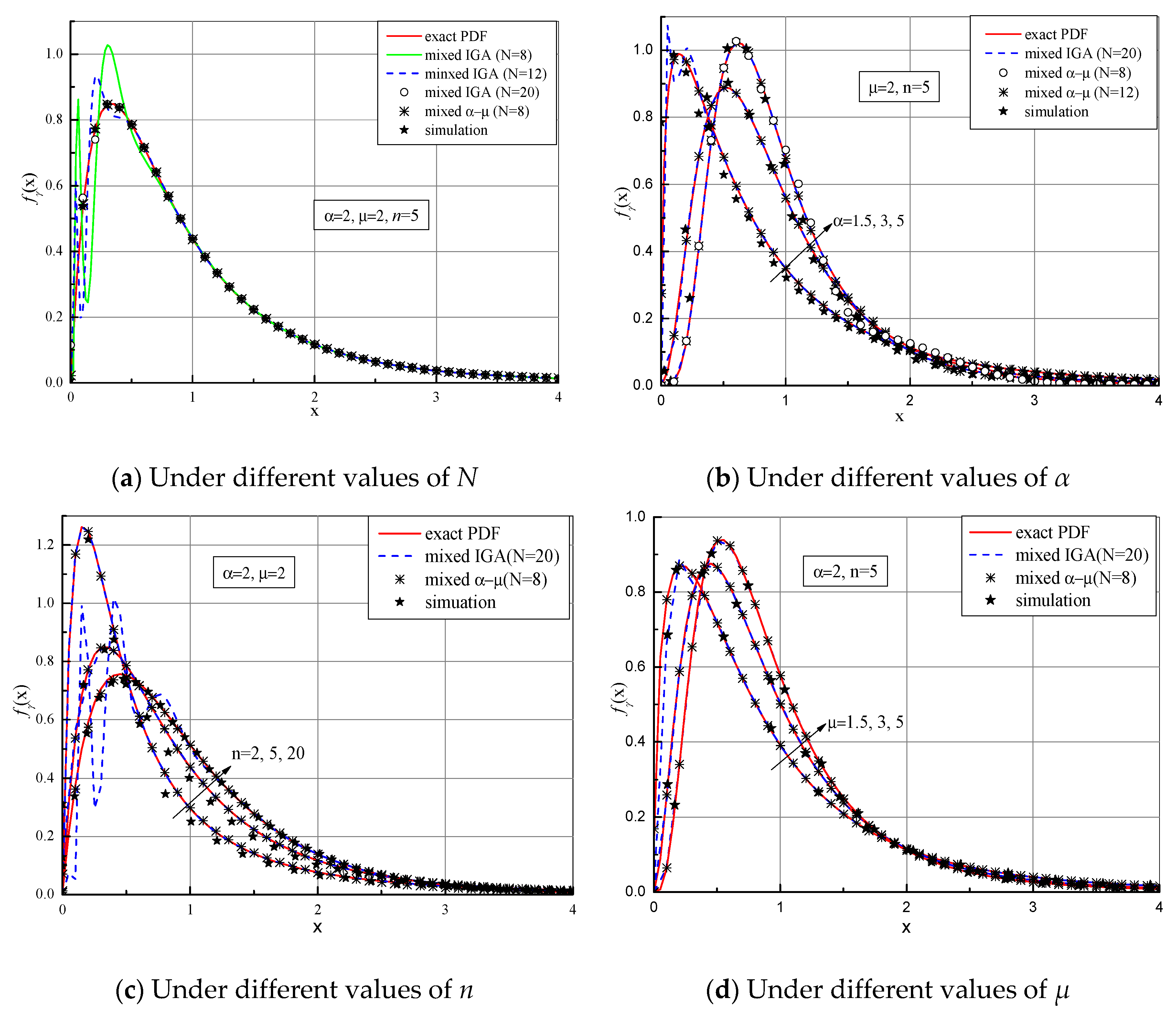
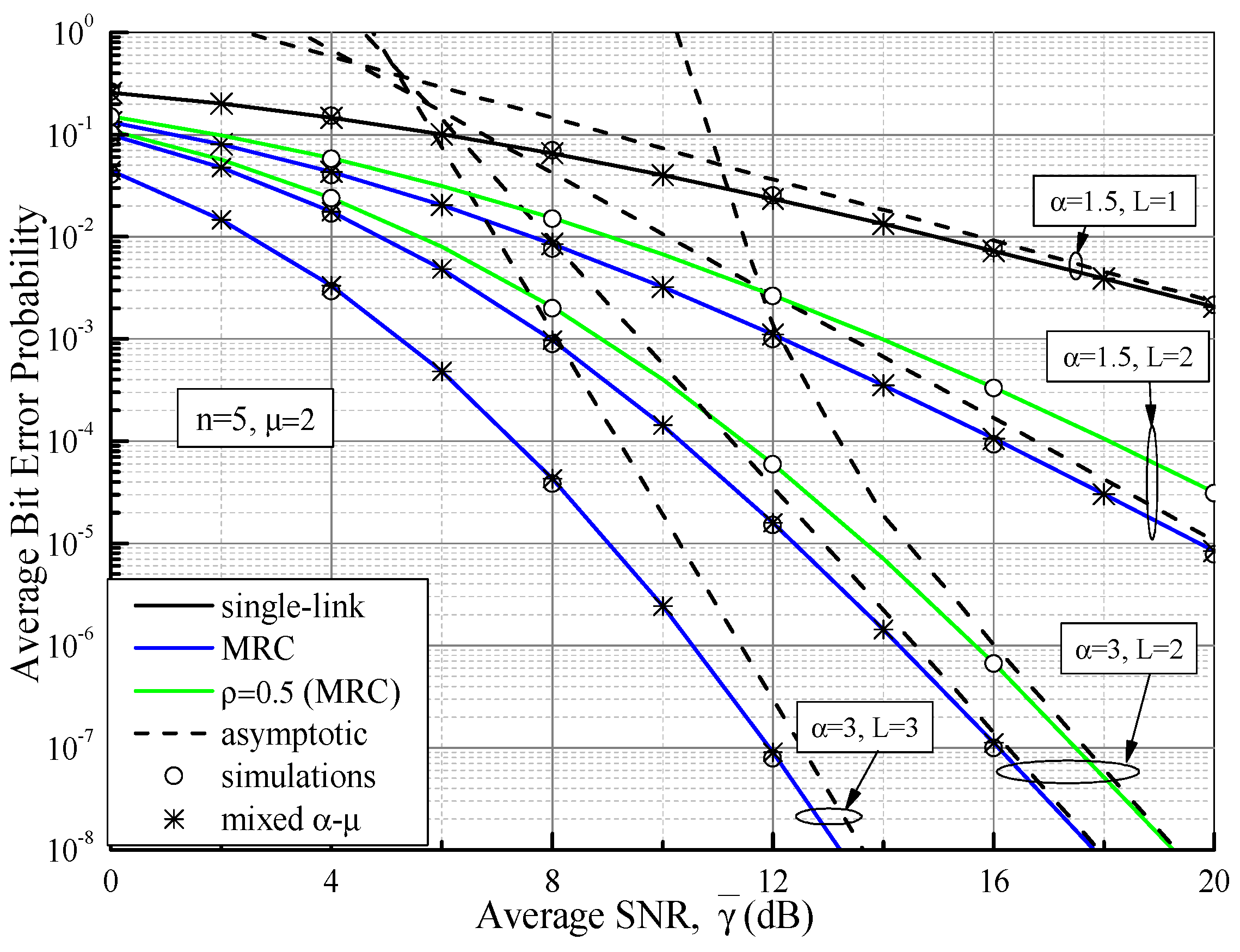
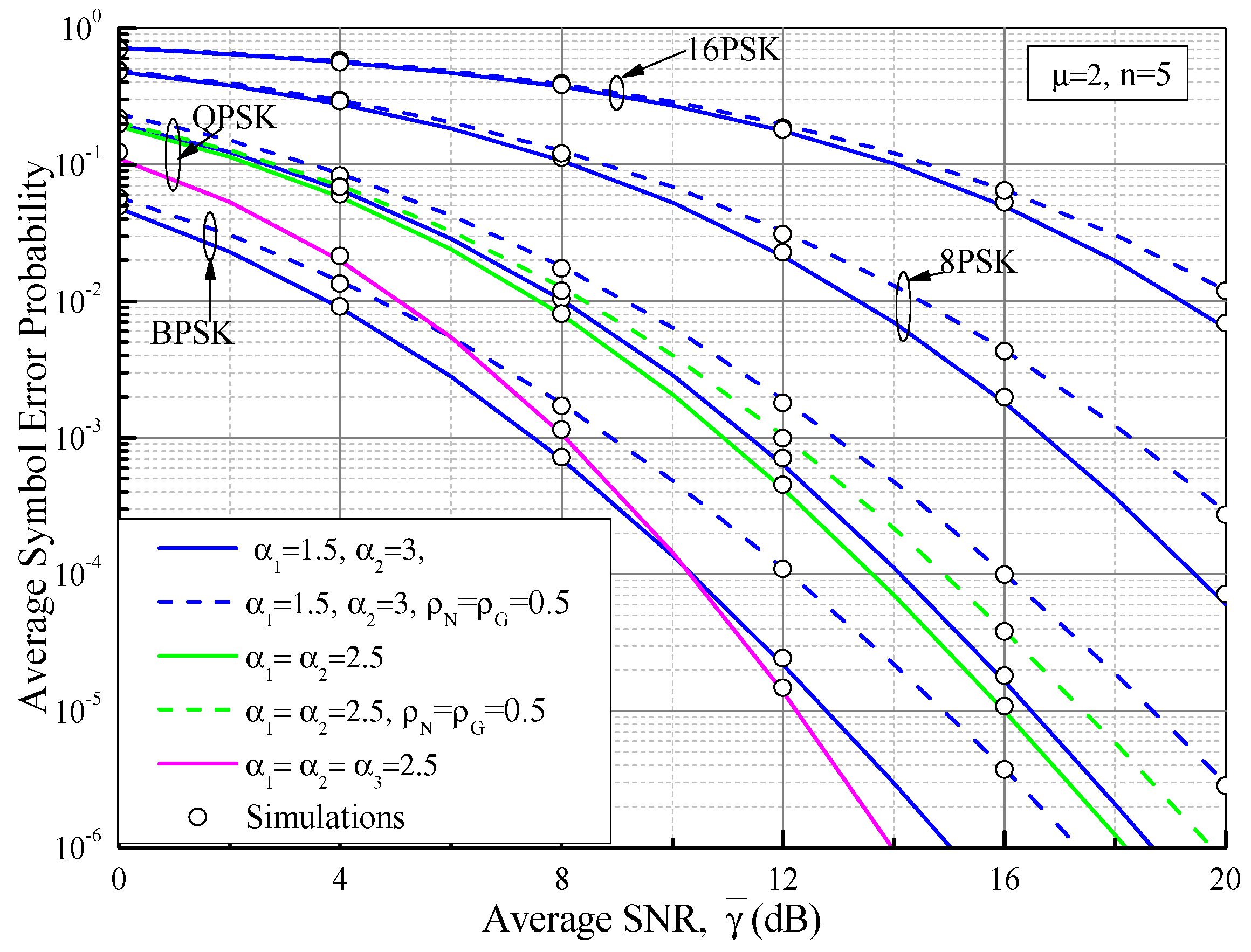
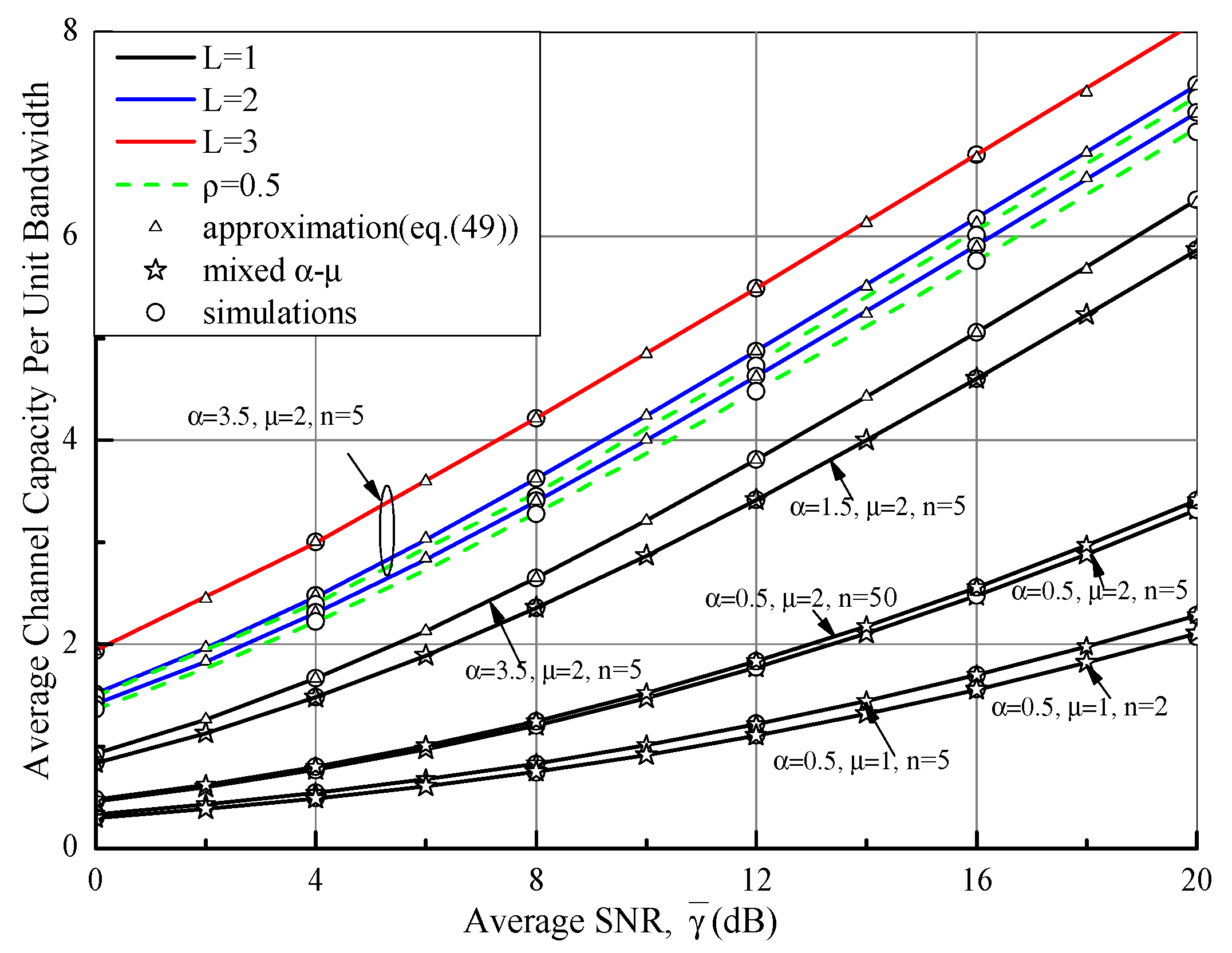
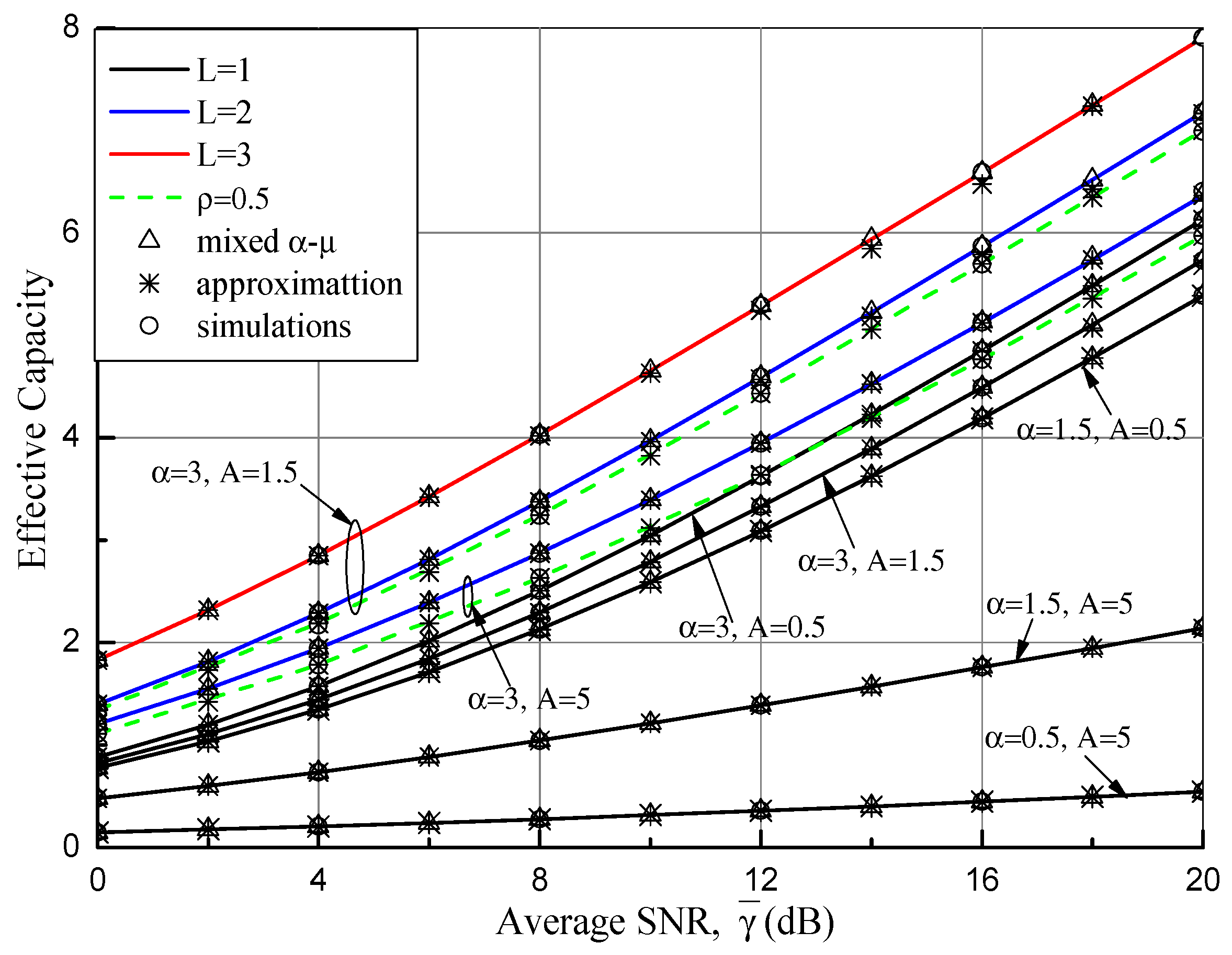
| Channel Parameters | N = 8 | N = 20 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mixed IGA | Mixed α-μ | Mixed IGA | Mixed α-μ | ||||||
| MSE | KLD | MSE | KLD | MSE | KLD | MSE | KLD | ||
| α = 2, μ = 2 | n = 2 | 0.001158 | 0.007285 | 1.148 × 10−5 | 0.009336 | 9.947 × 10−5 | 0.001056 | 3.008 × 10−8 | 6.149 × 10−4 |
| n = 20 | 0.03936 | 0.4076 | 2.766 × 10−5 | 0.009583 | 0.008485 | 0.09145 | 2.933 × 10−19 | 1.816 × 10−9 | |
| α = 2, n = 5 | μ = 1 | 0.05102 | 1.5389 | 4.759 × 10−11 | 2.399 × 10−5 | 0.02487 | 0.5276 | 9.694 × 10−20 | 8.243 × 10−10 |
| μ = 5 | 1.491 × 10−5 | 2.3875 × 10−4 | 1.258 × 10−6 | 4.8473 × 10−4 | 1.886 × 10−8 | 3.608 × 10−6 | 1.047 × 10−10 | 1.048 × 10−5 | |
| α = 2, n = 5 | α = 1 | 0.1449 | 0.3154 | 2.345 × 10−12 | 5.906 × 10−6 | 0.03569 | 0.08006 | 2.536 × 10−17 | 2.433 × 10−8 |
| α = 5 | 2.526 × 10−5 | 8.651 × 10−4 | 2.366 × 10−4 | 0.007668 | 1.012 × 10−6 | 1.378 × 10−4 | 8.094 × 10−7 | 4.4059 × 10−4 | |
| Modulation Scheme | Parameter Values | |
|---|---|---|
| DPSK | ||
| Coherent BPSK | ||
| MPSK | ||
| Square MQAM | , |
| Communication Systems | ABEP (Pe) |
|---|---|
| Single-link system by using (9) | |
| Single-link system by using (12) | |
| L-branch MRC system by using (A1) | |
| L-branch MRC system by using (23) | |
| Two-branch MRC system by using (32) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, W.; Ma, T.; Wang, G. On the Sum of α-μ/Inverse Gamma Variates with Applications to Diversity Receivers. Appl. Sci. 2022, 12, 5375. https://doi.org/10.3390/app12115375
Cheng W, Ma T, Wang G. On the Sum of α-μ/Inverse Gamma Variates with Applications to Diversity Receivers. Applied Sciences. 2022; 12(11):5375. https://doi.org/10.3390/app12115375
Chicago/Turabian StyleCheng, Weijun, Tengfei Ma, and Gang Wang. 2022. "On the Sum of α-μ/Inverse Gamma Variates with Applications to Diversity Receivers" Applied Sciences 12, no. 11: 5375. https://doi.org/10.3390/app12115375







