Infrared Dim and Small Target Detection Based on the Improved Tensor Nuclear Norm
Abstract
:1. Introduction
2. Singular Value Decomposition of a Tensor
| Algorithm 1: T-SVD for tensor . |
Input |
1. Compute |
2. compute each frontal slice of , and from as follows: |
For do |
end for |
3. Compute |
4. Compute |
5. Compute |
Output T-SVD components , , and of |
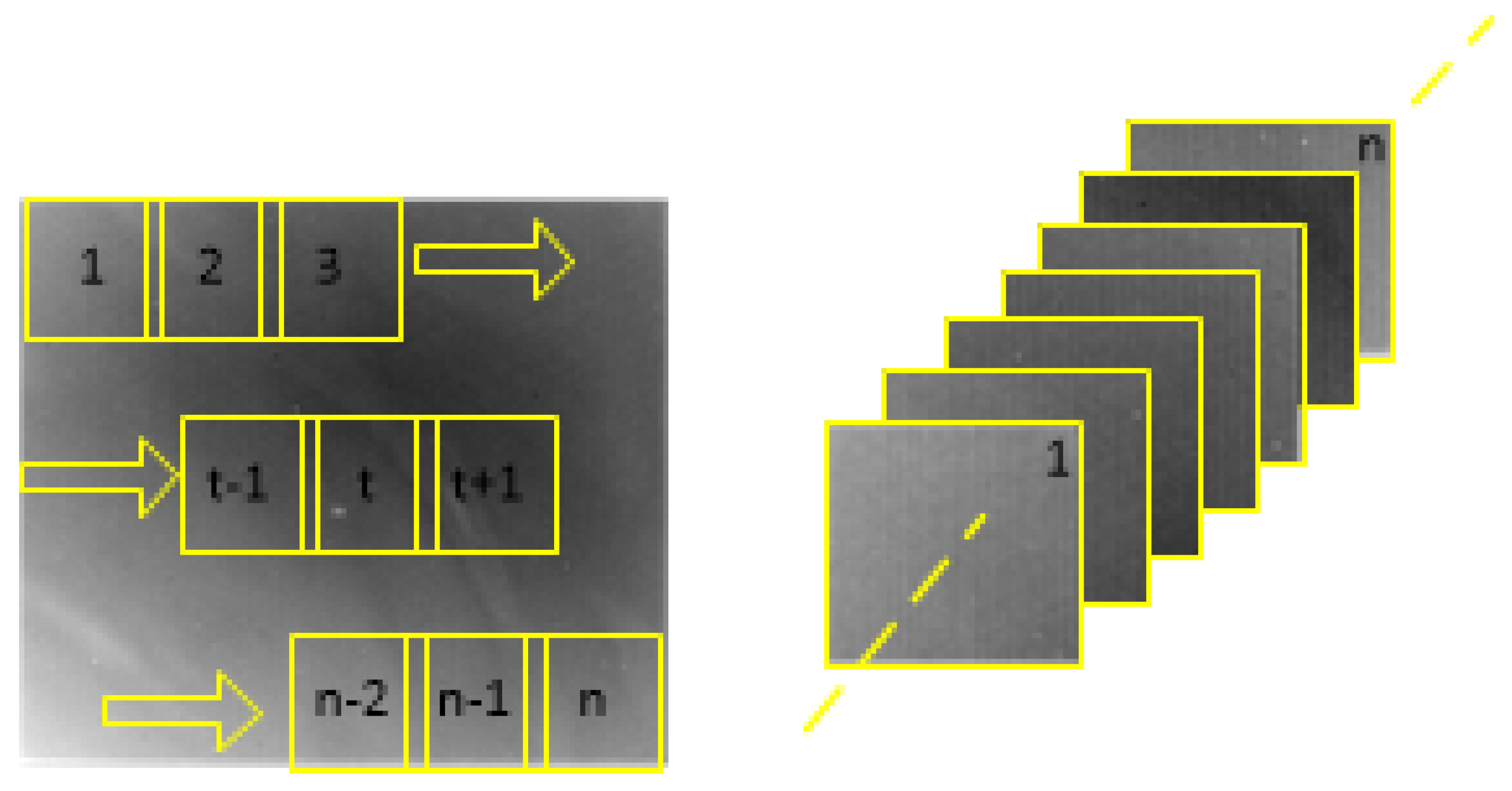
3. Infrared Patch Tensor (IPT) Model
3.1. Model Construction Method
3.2. Structural Tensor Description
3.3. A Priori Model Construction Based on the Structural Tensor
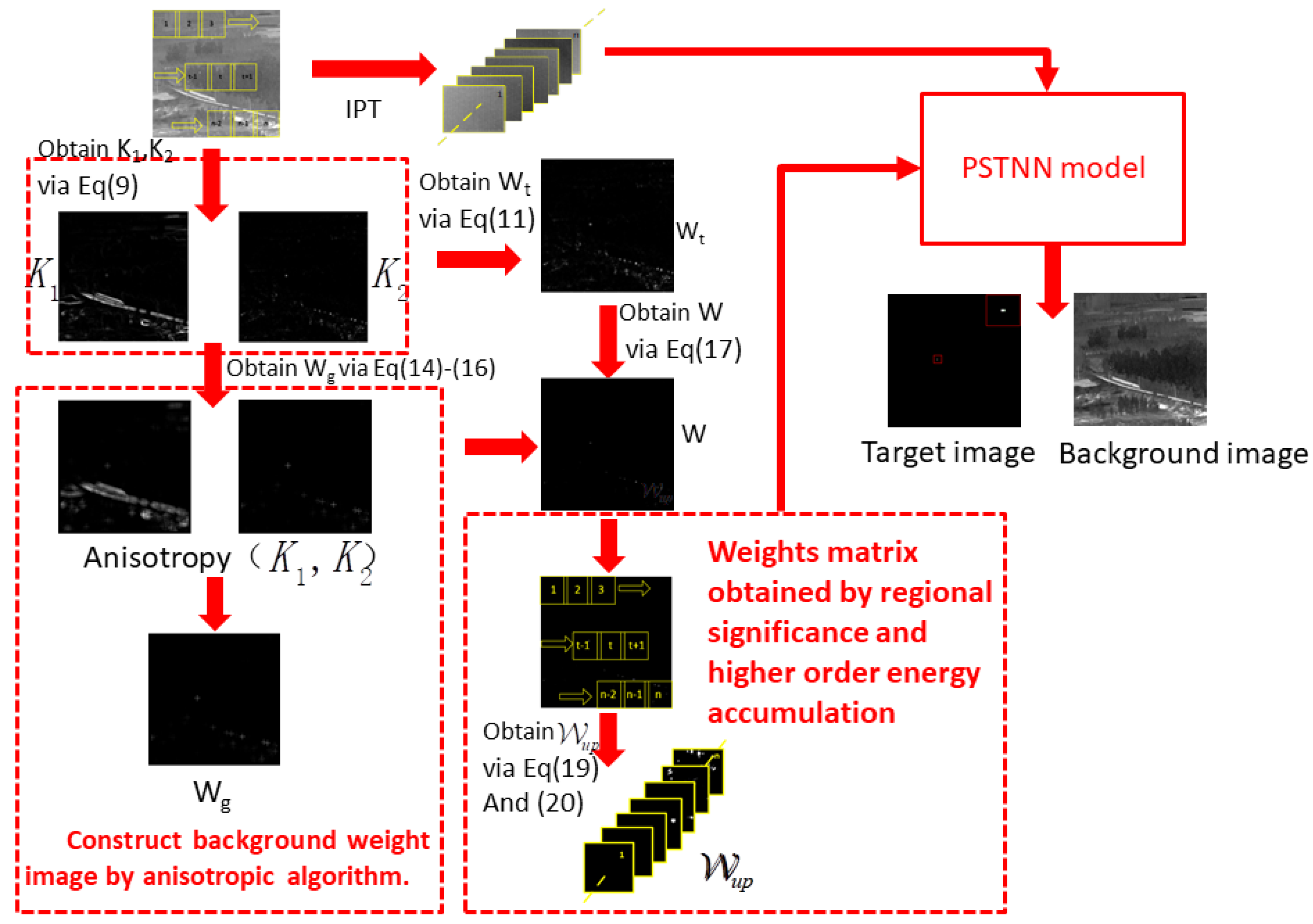
4. Construction of the a Priori Model in This Paper
5. Construction and Solution of the Infrared Dim and Small Target Detection Model
5.1. Construction of the Model
5.2. Solving the Model
| Algorithm 2: Flow chart of the algorithm solution. ADMM solver to the proposed model. |
Initialization: |
while not converge do |
1. update by |
2. Update by |
3. Update by |
4. Fix the others and update by Equations (20) and (21): |
5. Update by |
6. Check the convergence conditions: or |
7. Update |
end while |
Output |
6. Results and Analysis
6.1. Evaluation Indicators
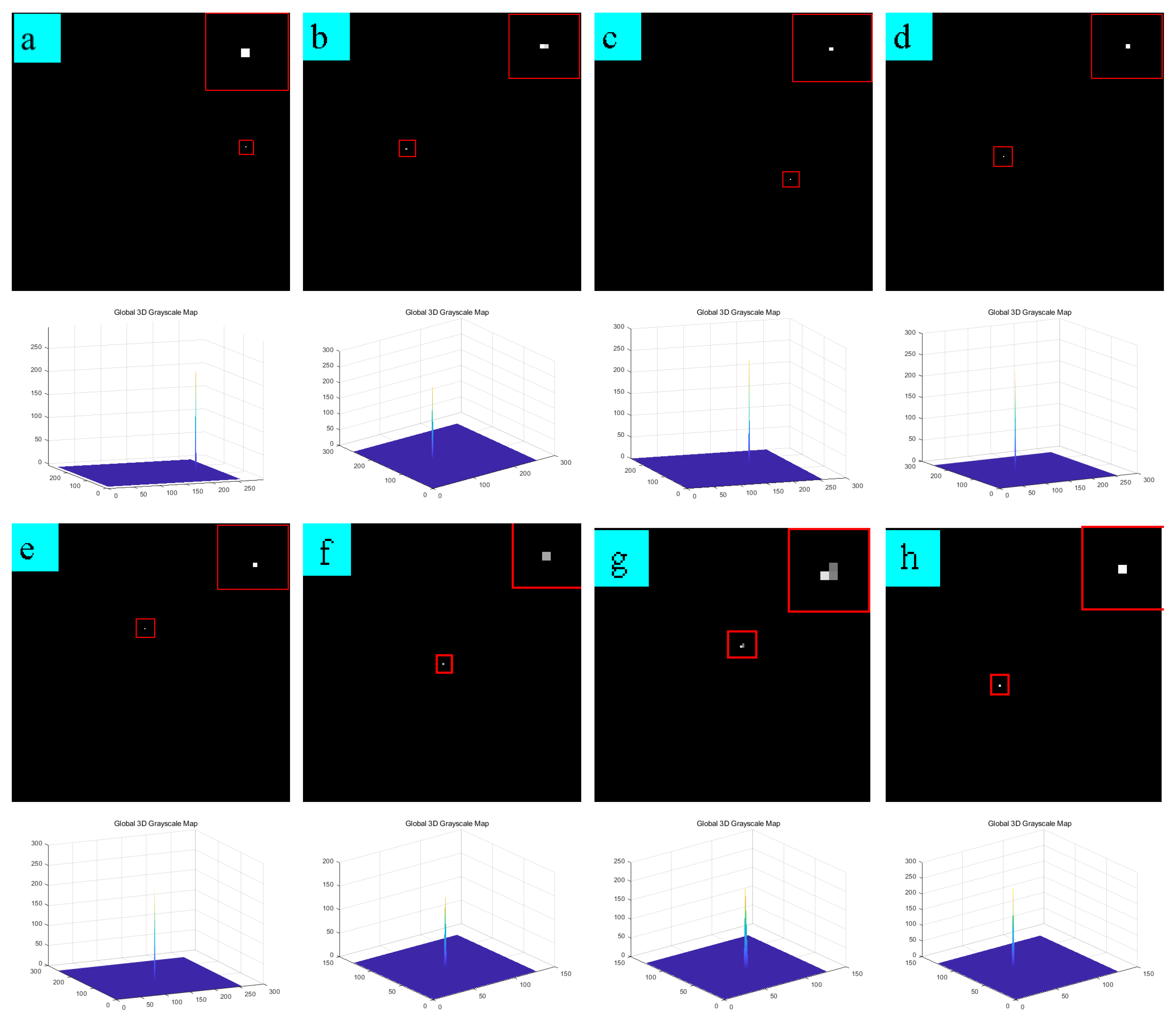
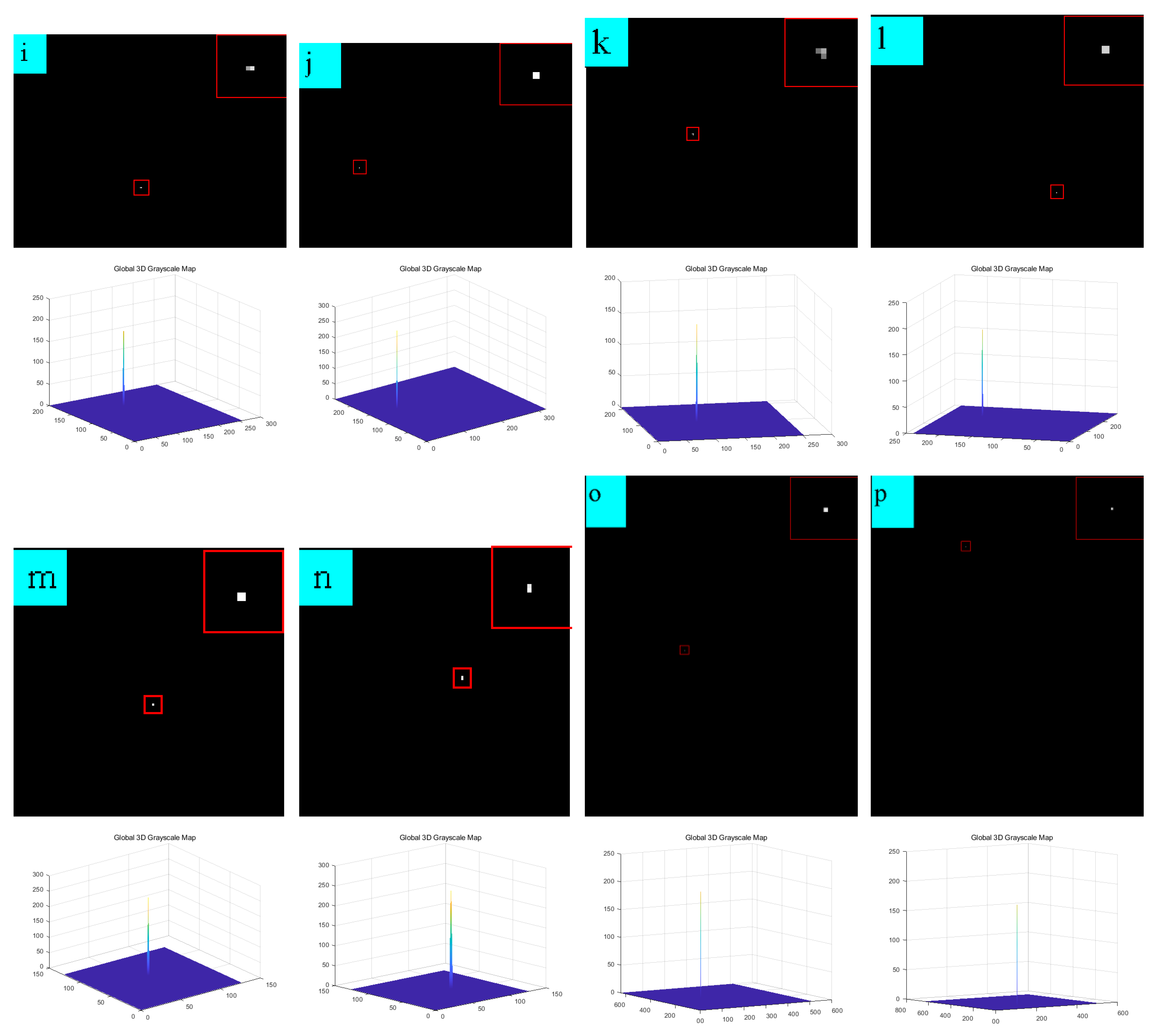
6.2. Analysis of Single-Frame Detection Results
6.3. Sequence Image Detection Experiments
7. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Aadcdd | absolute average difference weighted by cumulative directional derivatives |
| GST | Generalized-structure-tensor |
| VNTFR | via non-convex tensor fibered rank |
| FKRW | facet kernel and random walker |
| MPCM | multiscale patch-based contrast measure |
| SRWS | self-regularized weighted sparse |
| PSTNN | partial sum of the tensor nuclear norm |
References
- Bo, L.; Bo, W.; Sun, G.; Yin, X.; Pu, H.; Liu, C.; Song, Y. A fast detection method for small weak infrared target in complex background. Proc. Spie 2016, 30, 100301V. [Google Scholar]
- Bai, X.; Zhou, F. Analysis of new top-hat transformation and the application for infrared dim small target detection. Pattern Recognit. 2010, 43, 2145–2156. [Google Scholar] [CrossRef]
- Deng, L.; Zhang, J.; Xu, G.; Zhu, H. Infrared small target detection via adaptive M-estimator ring top-hat transformation. Pattern Recognit. 2020, 112, 107729. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, R.M.; Yang, J. Small Target Detection Using Two-Dimensional Least Mean Square (TDLMS) Filter Based on Neighborhood Analysis. Int. J. Infrared Millim. Waves 2008, 29, 188–200. [Google Scholar] [CrossRef]
- Li, H.; Wang, Q.; Wang, H.; Yang, W.K. Infrared small target detection using tensor based least mean square. Comput. Electr. Eng. 2021, 91, 106994. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Z.; Zhang, J.; Huang, Y.; Peng, Z. Dim small targets detection based on self-adaptive caliber temporal-spatial filtering. Infrared Phys. Technol. 2017, 85, 465–477. [Google Scholar] [CrossRef]
- Li, J.; Fan, X.; Chen, H.; Li, B.; Min, L.; Xu, Z. Dim and Small Target Detection Based on Improved Spatio-Temporal Filtering. IEEE Photonics J. 2022, 14, 1–11. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, C.; Fu, Q.; Han, Z. A Novel Pattern for Infrared Small Target Detection with Generative Adversarial Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4481–4492. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, H.; Qin, H.; Rong, S.; Zhao, D.; Du, J. Guided filter and convolutional network based tracking for infrared dim moving target. Infrared Phys. Technol. 2017, 85, 431–442. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared Patch-Image Model for Small Target Detection in a Single Image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Zhang, P.; He, Y. Infrared Small Target Detection via Nonnegativity-Constrained Variational Mode Decomposition. IEEE Geoence Remote Sens. Lett. 2017, 14, 1700–1704. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Kong, D.; Zhang, P.; He, Y. Infrared dim target detection based on total variation regularization and principal component pursuit. Image Vis. Comput. 2017, 63, 1–9. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, L.; Zhang, T.; Cao, S.; Peng, Z. Infrared Small Target Detection via Non-Convex Rank Approximation Minimization Joint l2,1 Norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Wu, H.; Liu, Y.; Peng, L.; Yang, C.; Peng, Z. Infrared Small Target Detection Based on Non-Convex Optimization with Lp-Norm Constraint. Remote Sens. 2019, 11, 559. [Google Scholar] [CrossRef] [Green Version]
- Wu, A.; Fan, X.; Chen, H.; Min, L.; Xu, Z. Infrared Dim and Small Target Detection Algorithm Combining Multiway Gradient Regularized Principal Component Decomposition Model. IEEE Access 2022, 10, 36057–36072. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y. Reweighted Infrared Patch-Tensor Model With Both Nonlocal and Local Priors for Single-Frame Small Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3752–3767. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Peng, Z. Infrared Small Target Detection Based on Partial Sum of the Tensor Nuclear Norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Qu, Y.; Tao, D.; Wu, W.; Yuan, Q.; Zhang, W. Hyperspectral Image Restoration via Iteratively Regularized Weighted Schatten p-Norm Minimization. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4642–4659. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, J.; Li, M.; An, W. Infrared Small Target Detection via Spatial-Temporal Infrared Patch-Tensor Model and Weighted Schatten p-norm Minimization. Infrared Phys. Technol. 2019, 102, 103050. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, J.; An, W. Infrared Dim and Small Target Detection via Multiple Subspace Learning and Spatial-Temporal Patch-Tensor Model. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3737–3752. [Google Scholar] [CrossRef]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Gao, J.; Guo, Y.; Lin, Z.; Wei, A.; Li, J. Robust Infrared Small Target Detection Using Multiscale Gray and Variance Difference Measures. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 5039–5052. [Google Scholar] [CrossRef]
- Deng, H.; Liu, J.; Chen, Z. Infrared small target detection based on modified local entropy and EMD. Chin. Opt. Lett. 2010, 8, 24–28. [Google Scholar] [CrossRef] [Green Version]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2005), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Fan, X.; Xu, Z.; Zhang, J.; Huang, Y.; Peng, Z.; Wei, Z.; Guo, H. Dim small target detection based on high-order cumulant of motion estimation. Infrared Phys. Technol. 2019, 99, 86–101. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Hui, B.W.; Song, Z.Y.; Fan, H.Q. A dataset for infrared image dim-small aircraft target detection and tracking under ground/air background. Sci. Data Bank 2019. [Google Scholar] [CrossRef]
- Aghaziyarati, S.; Moradi, S.; Talebi, H. Small infrared target detection using absolute average difference weighted by cumulative directional derivatives. Infrared Phys. Technol. 2019, 101, 78–87. [Google Scholar] [CrossRef]
- Gao, C.Q.; Tian, J.W.; Wang, P. Generalised-structure-tensor-based infrared small target detection. Electron. Lett. 2008, 44, 1349–1351. [Google Scholar] [CrossRef]
- Kong, X.; Yang, C.; Cao, S.; Li, C.; Peng, Z. Infrared Small Target Detection via Nonconvex Tensor Fibered Rank Approximation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–21. [Google Scholar] [CrossRef]
- Qin, Y.; Bruzzone, L.; Gao, C.; Li, B. Infrared Small Target Detection Based on Facet Kernel and Random Walker. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7104–7118. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 12, 629–639. [Google Scholar] [CrossRef] [Green Version]
- Tz, A.; Zp, A.; Hao, W.A.; Yh, A.; Cl, B.; Cy, A. Infrared small target detection via self-regularized weighted sparse model. Neurocomputing 2021, 420, 124–148. [Google Scholar]






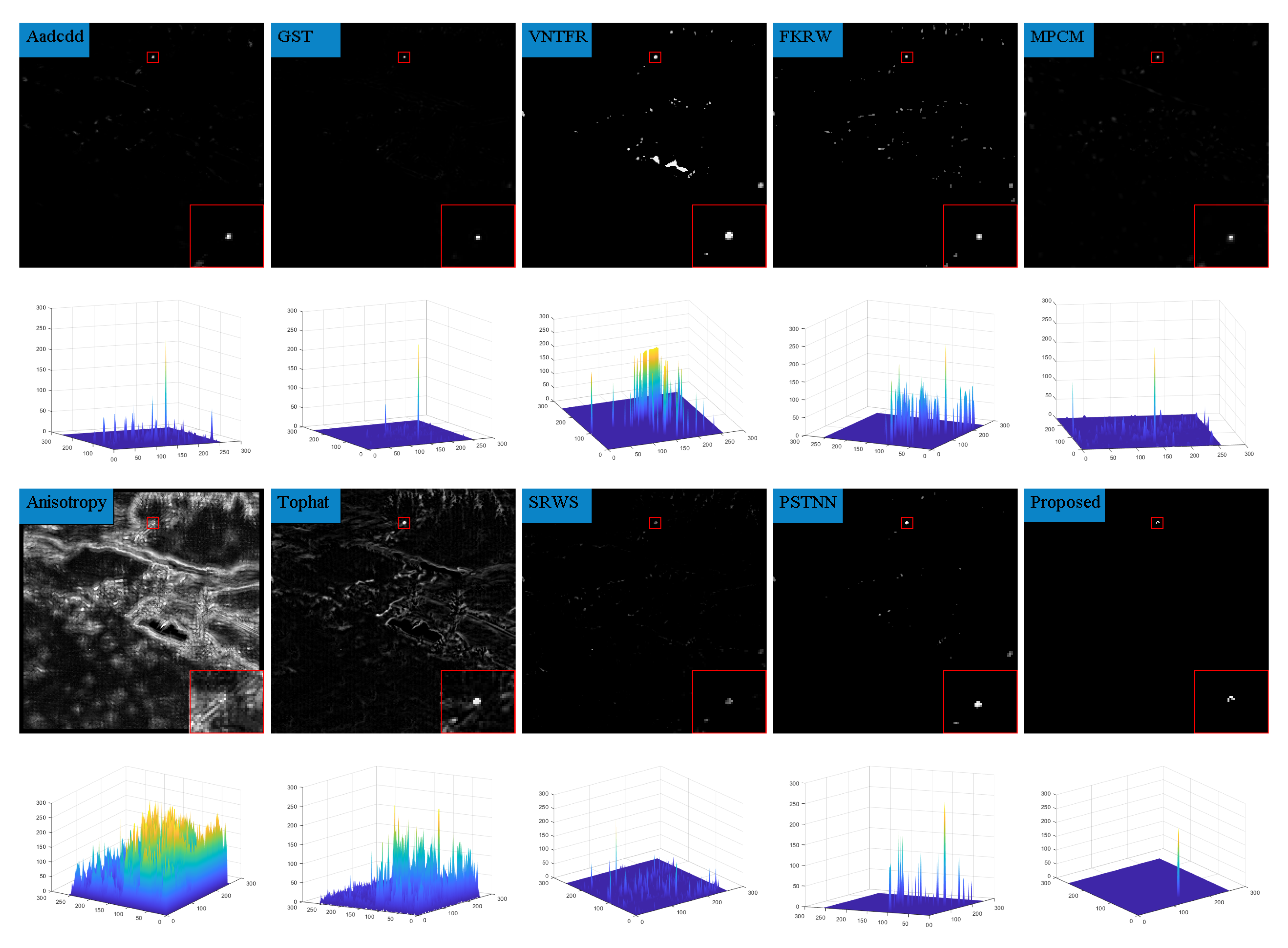
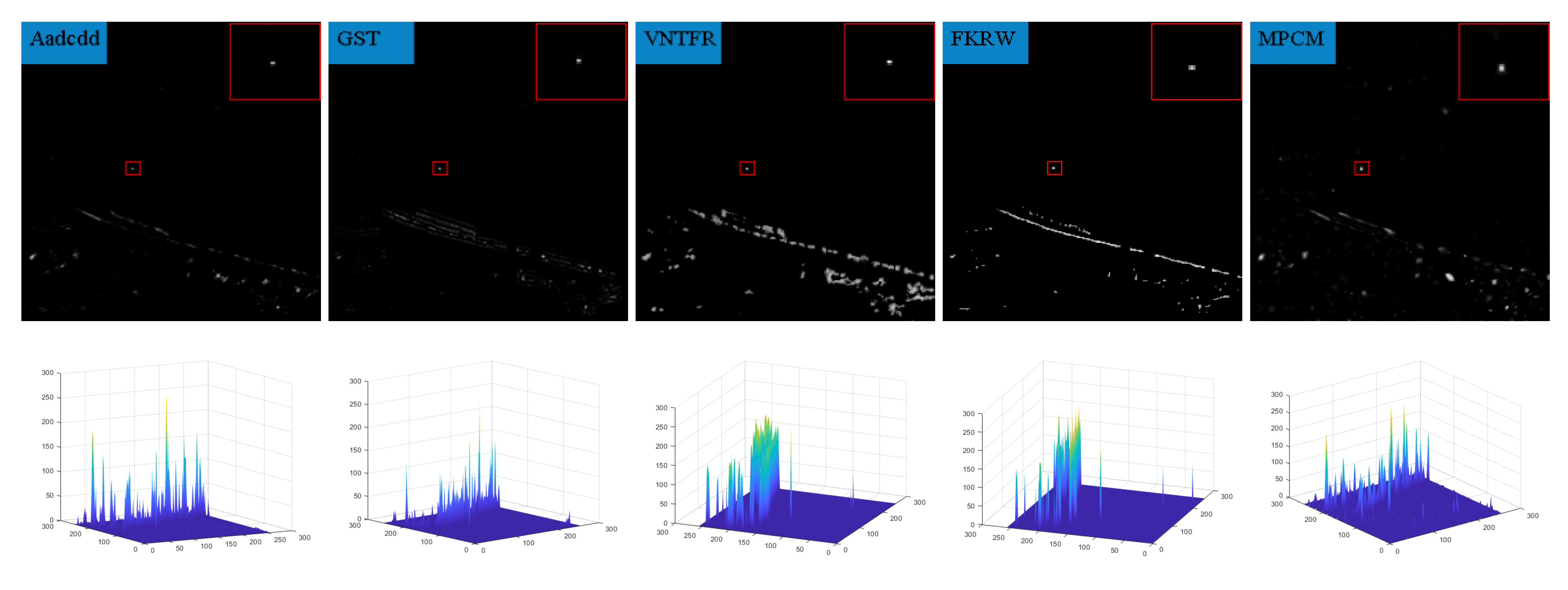
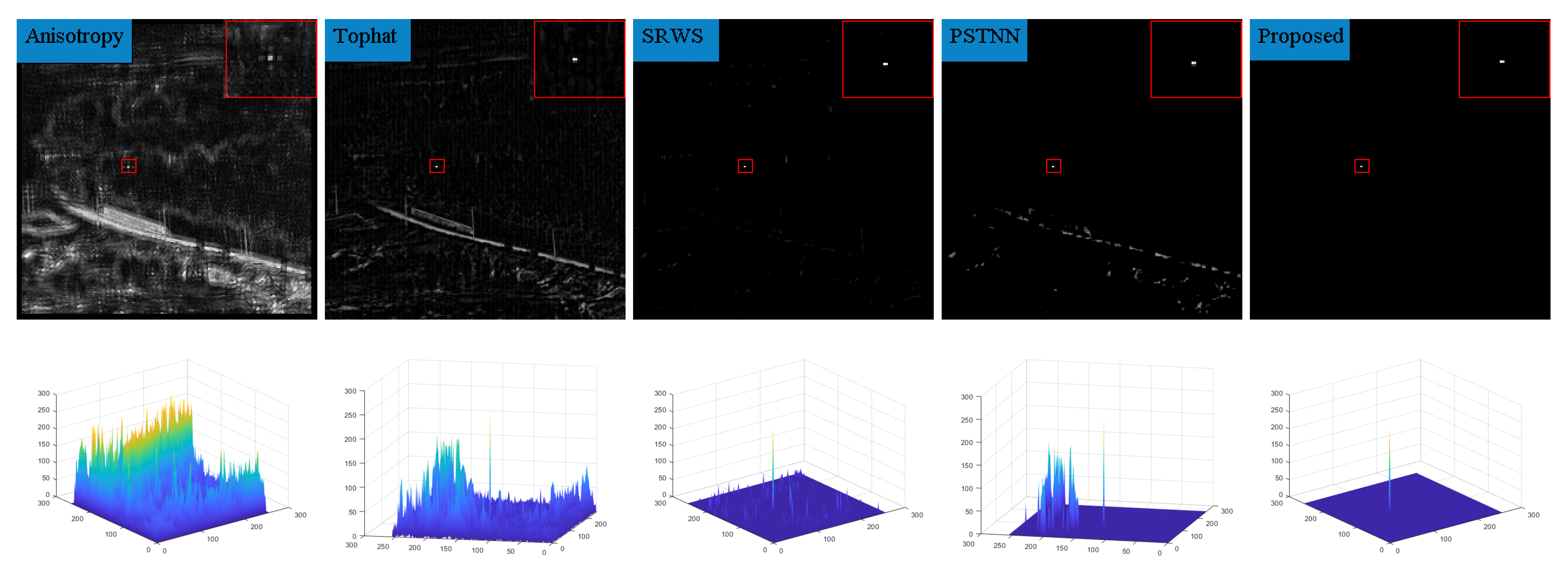


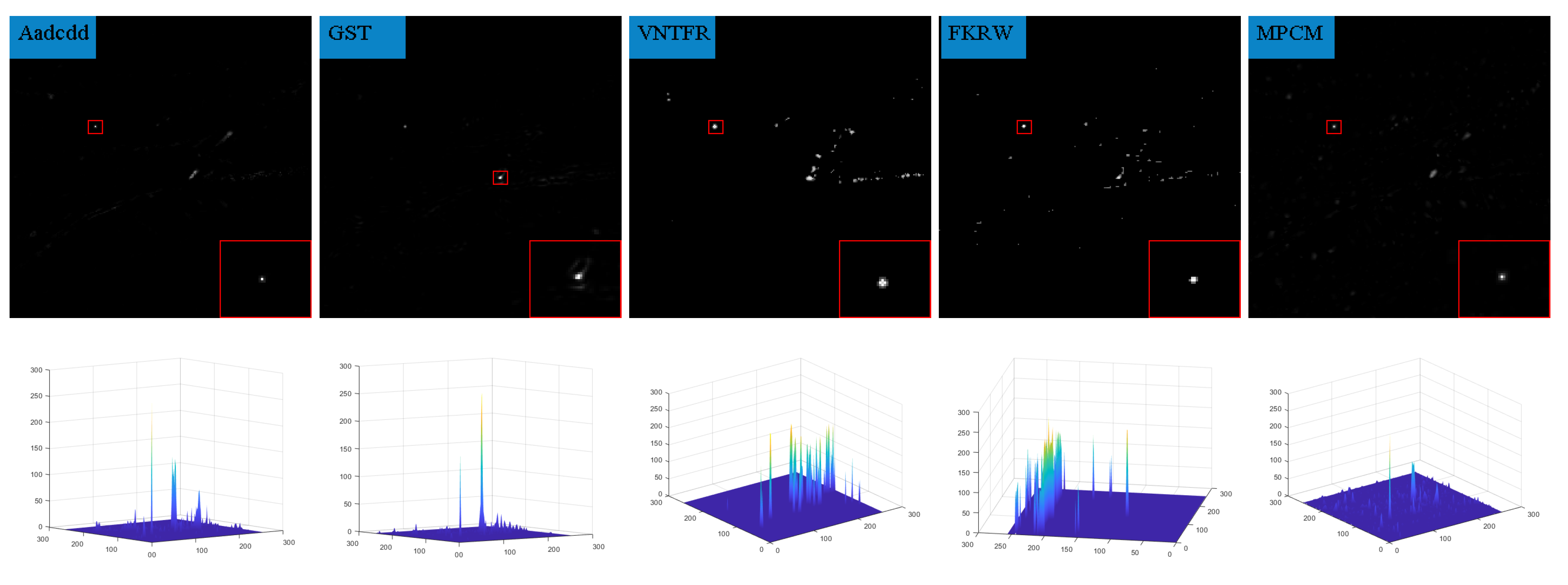
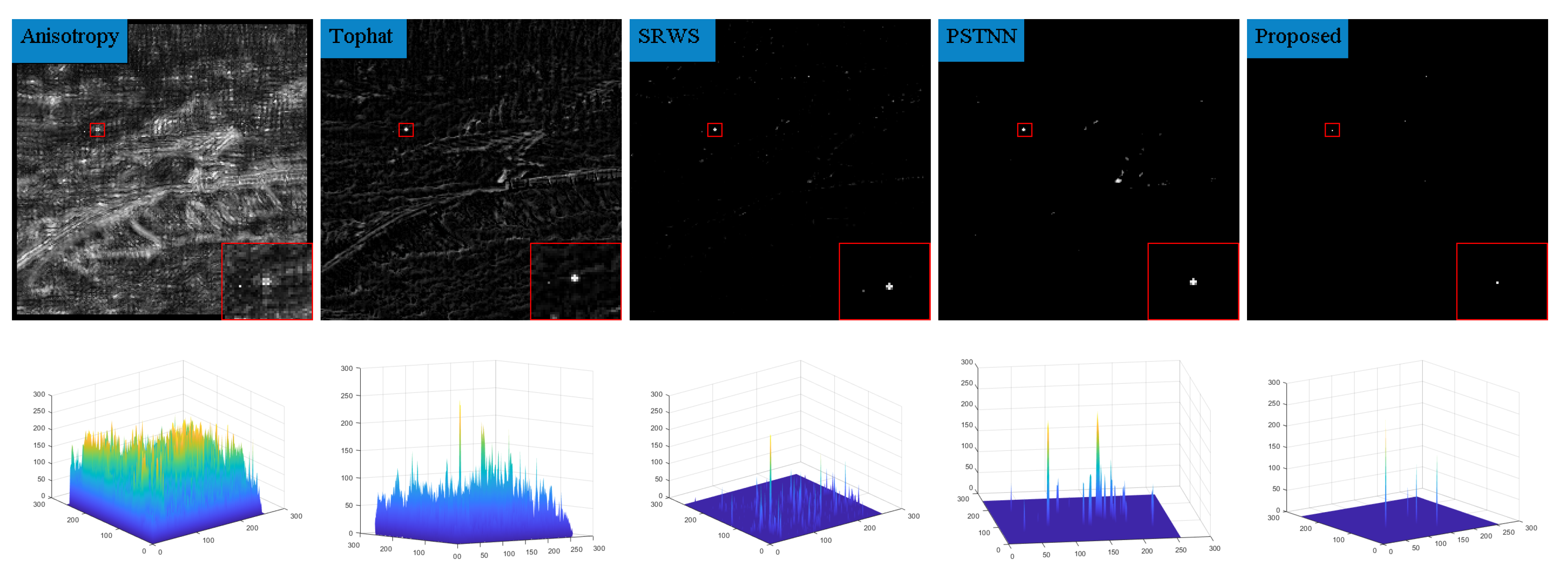
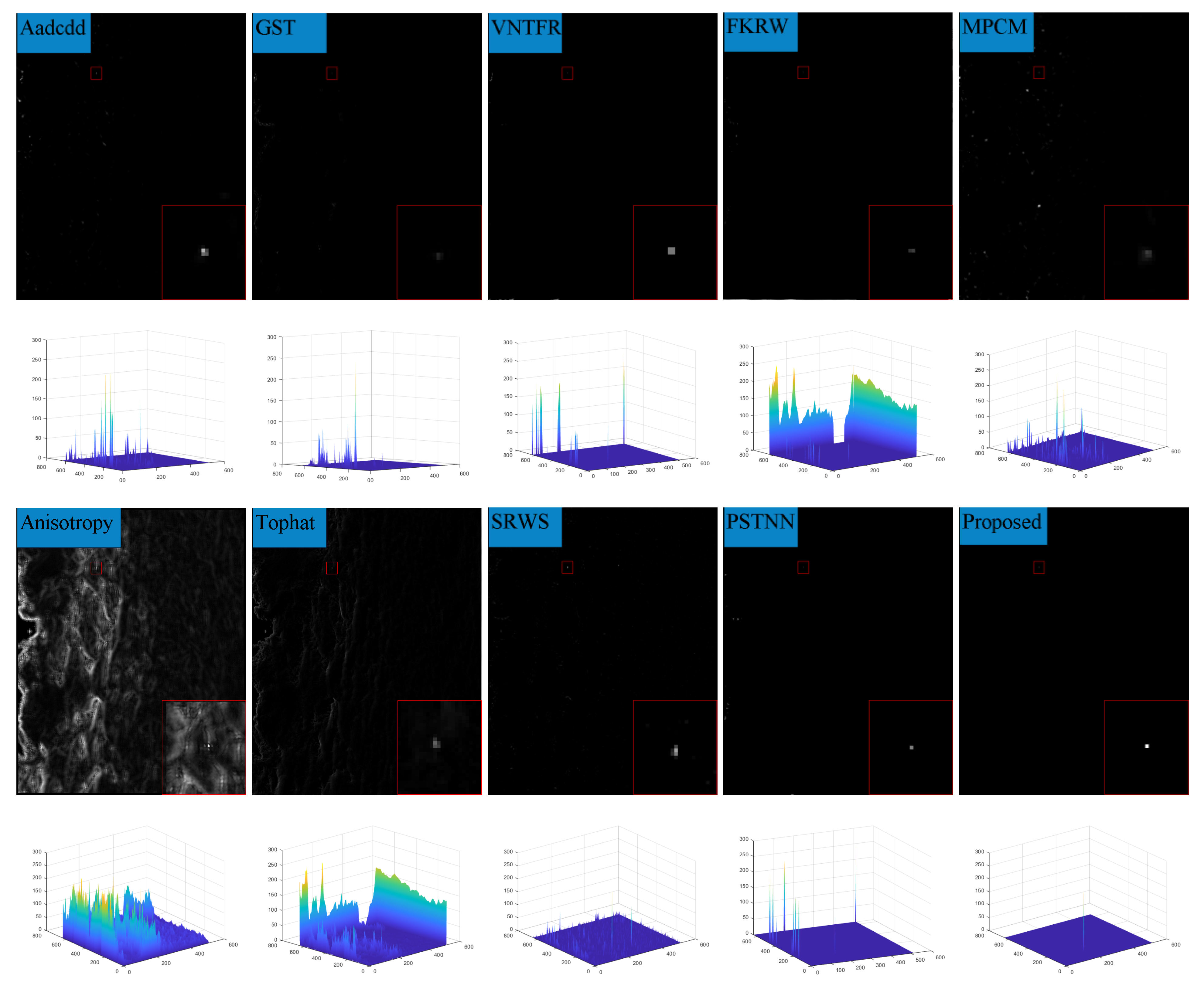

| Method | Scene 1 | Scene 2 | Scene 3 | |||
|---|---|---|---|---|---|---|
| Bsf | SNR | Bsf | SNR | Bsf | SNR | |
| Anisotropy | 24.79 | 2.17 | 16.87 | 2.15 | 29.45 | 2.94 |
| Top_hat | 67.26 | 8.84 | 39.13 | 6.14 | 76.07 | 6.92 |
| mpcm | 424.01 | 13.94 | 75.83 | 11.64 | 316.09 | 14.07 |
| GST | 640.39 | 15.30 | 124.10 | 10.46 | 217.61 | 10.21 |
| VATF | 92.30 | 10.54 | 35.83 | 6.24 | 78.51 | 6.26 |
| FKWR | 187.01 | 11.39 | 46.23 | 7.06 | 73.58 | 7.24 |
| SRWS | 1.43 | 11.95 | 1.04 | 13.92 | 1.91 | 14.51 |
| Aadcdd | 428.21 | 14.49 | 113.59 | 9.05 | 246.90 | 11.21 |
| PSTNN | 307.94 | 15.07 | 87.53 | 9.62 | 186.54 | 10.65 |
| Proposed | 744.35 | 16.92 | 469.04 | 16.03 | 827.34 | 14.54 |
| Method | Scene 4 | Scene 5 | Scene 6 | |||
|---|---|---|---|---|---|---|
| Bsf | SNR | Bsf | SNR | Bsf | SNR | |
| Anisotropy | 31.93 | 5.92 | 23.65 | 3.17 | 29.73 | 5.93 |
| Top_hat | 80.27 | 8.86 | 57.09 | 8.93 | 80.31 | 5.92 |
| mpcm | 365.00 | 15.77 | 334.98 | 14.35 | 261.97 | 9.75 |
| GST | 473.14 | 14.38 | 407.67 | 12.63 | 489.30 | 8.76 |
| VATF | 53.78 | 6.85 | 132.99 | 13.46 | 369.76 | 7.92 |
| FKWR | 103.34 | 10.44 | 173.07 | 12.27 | 87.48 | 1.20 |
| SRWS | 1.68 | 15.23 | 1.04 | 15.17 | 1.70 | 16.68 |
| Aadcdd | 574.57 | 15.28 | 403.66 | 12.87 | 347.99 | 13.71 |
| PSTNN | 223.49 | 12.59 | 221.20 | 14.92 | 408.40 | 8.68 |
| Proposed | 513.87 | 16.22 | 424.06 | 16.13 | 1753.70 | 18.04 |
| Sequence | Size/Pixels | Length/Frames | Description of Sequence |
|---|---|---|---|
| Seq. 1 | 256 × 256 | 100 | The target is in the shape of a dot, and the background of the picture is grass. |
| Seq. 2 | 256 × 256 | 59 | The target is in the shape of a dot, and the background of the picture is a tree and a bright road. |
| Seq. 3 | 256 × 256 | 100 | The target is in the shape of a dot with a bright building in the background of the picture. |
| Seq. 4 | 256 × 256 | 100 | The target is in the shape of a dot with a dark mountain and bright buildings in the background. |
| Seq. 5 | 256 × 256 | 100 | The target is in the shape of a dot; the background of the picture is a forest and a bright bare field. |
| Seq. 6 | 513 × 641 | 55 | The target is in the shape of a dot; the background of the picture is a large cloud layer and the target is submerged in the cloud layer. |
| Method | Scene 1 | Scene 2 | Scene 3 | Scene 4 | Scene 5 | Scene 6 |
|---|---|---|---|---|---|---|
| Anisotropy | 0.030574 | 0.02761 | 0.027462 | 0.027965 | 0.026676 | 0.055889 |
| Top_hat | 0.076485 | 0.078233 | 0.07718 | 0.07832 | 0.078751 | 0.219467 |
| mpcm | 0.233488 | 0.237644 | 0.234299 | 0.260856 | 0.229161 | 1.204722 |
| GST | 0.013985 | 0.013881 | 0.013755 | 0.013982 | 0.015546 | 0.030258 |
| VATF | 1.266642 | 1.231002 | 1.223736 | 1.258206 | 1.365244 | 5.830361 |
| FKWR | 0.210284 | 0.178647 | 0.203463 | 0.225881 | 0.121728 | 0.572601 |
| SRWS | 2.709106 | 2.65044 | 2.66639 | 3.104156 | 2.903653 | 377.7915 |
| Aadcdd | 0.025507 | 0.036414 | 0.036629 | 0.033213 | 0.038618 | 0.151683 |
| PSTNN | 0.3873 | 0.404629 | 0.414345 | 0.407923 | 0.325582 | 1.659501 |
| Proposed | 0.253116 | 0.221659 | 0.224719 | 0.221864 | 0.204717 | 1.146247 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Wu, A.; Chen, H.; Huang, Q.; Xu, Z. Infrared Dim and Small Target Detection Based on the Improved Tensor Nuclear Norm. Appl. Sci. 2022, 12, 5570. https://doi.org/10.3390/app12115570
Fan X, Wu A, Chen H, Huang Q, Xu Z. Infrared Dim and Small Target Detection Based on the Improved Tensor Nuclear Norm. Applied Sciences. 2022; 12(11):5570. https://doi.org/10.3390/app12115570
Chicago/Turabian StyleFan, Xiangsuo, Anqing Wu, Huajin Chen, Qingnan Huang, and Zhiyong Xu. 2022. "Infrared Dim and Small Target Detection Based on the Improved Tensor Nuclear Norm" Applied Sciences 12, no. 11: 5570. https://doi.org/10.3390/app12115570
APA StyleFan, X., Wu, A., Chen, H., Huang, Q., & Xu, Z. (2022). Infrared Dim and Small Target Detection Based on the Improved Tensor Nuclear Norm. Applied Sciences, 12(11), 5570. https://doi.org/10.3390/app12115570





