Experimental Investigation into Failure Modes of Low-Yield-Point Steel Plate Shear Walls
Abstract
:1. Introduction
2. Horizontal Cyclic Loading Test
2.1. Test Scheme
2.1.1. Design of Specimen 1
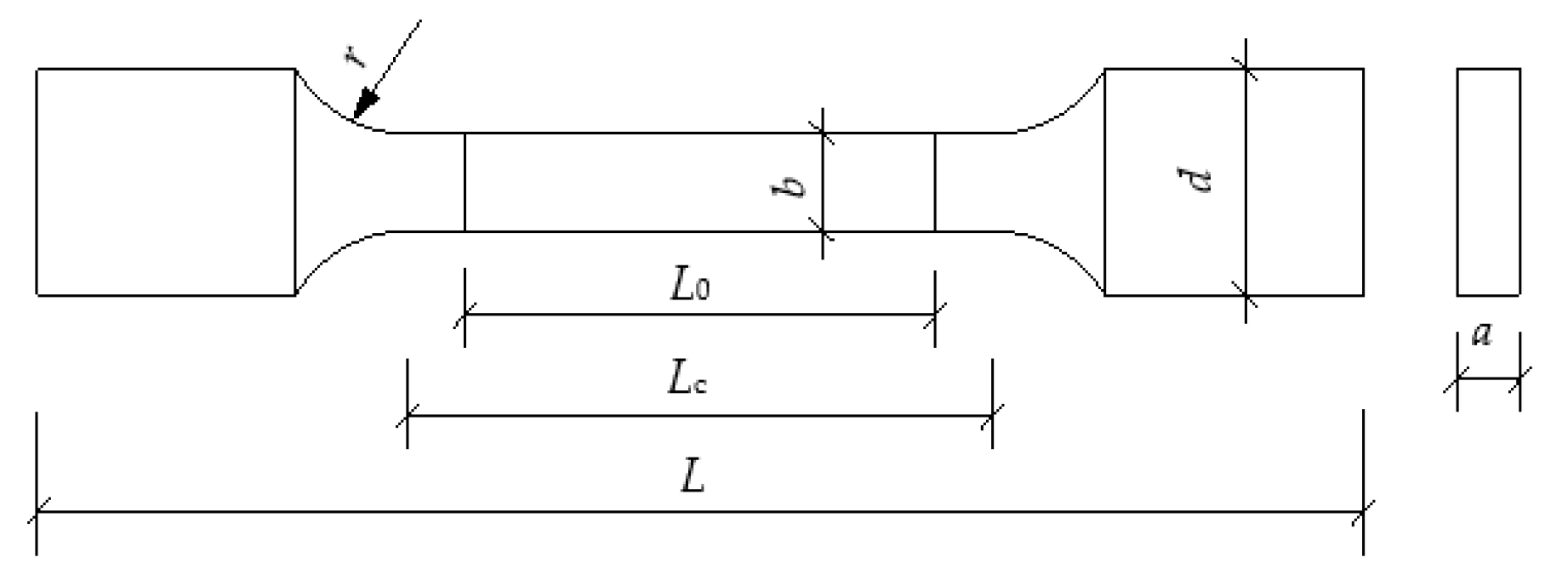
2.1.2. Material Property Test
2.1.3. Experimental Device
2.1.4. Loading Scheme
2.2. Experimental Results
2.2.1. Description of Failure Phenomenon
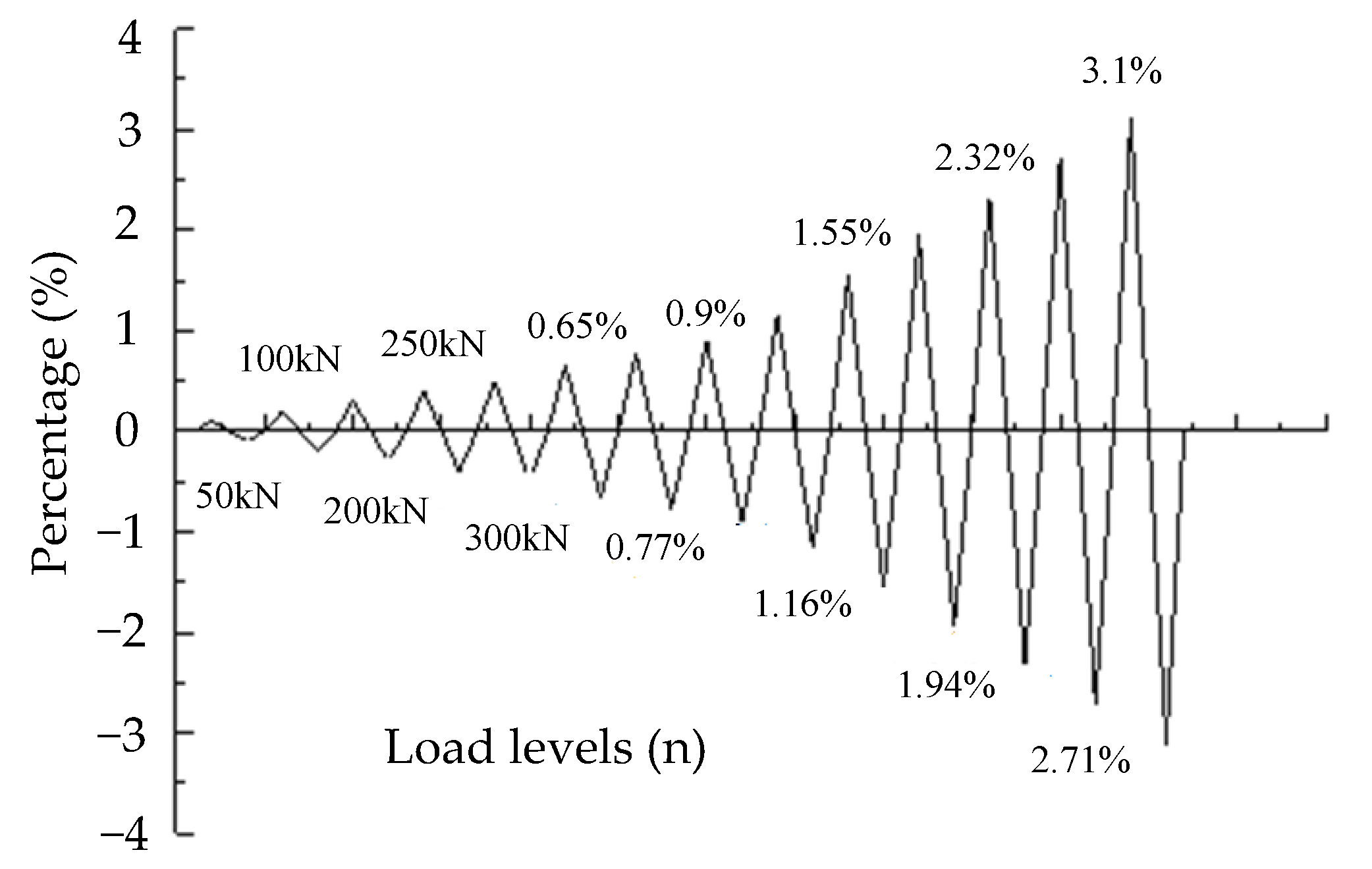
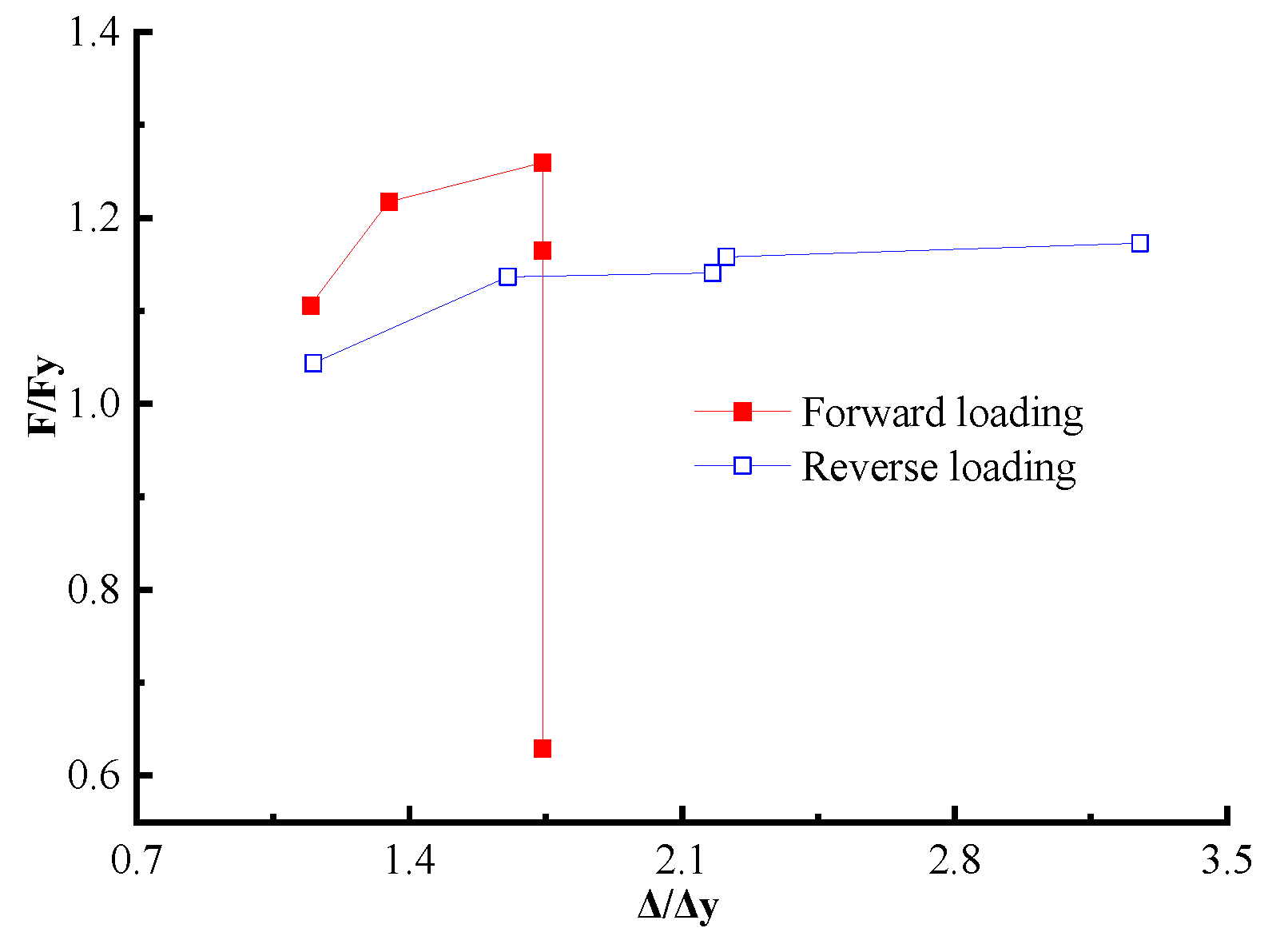
2.2.2. Change in Bearing Capacity after Yielding
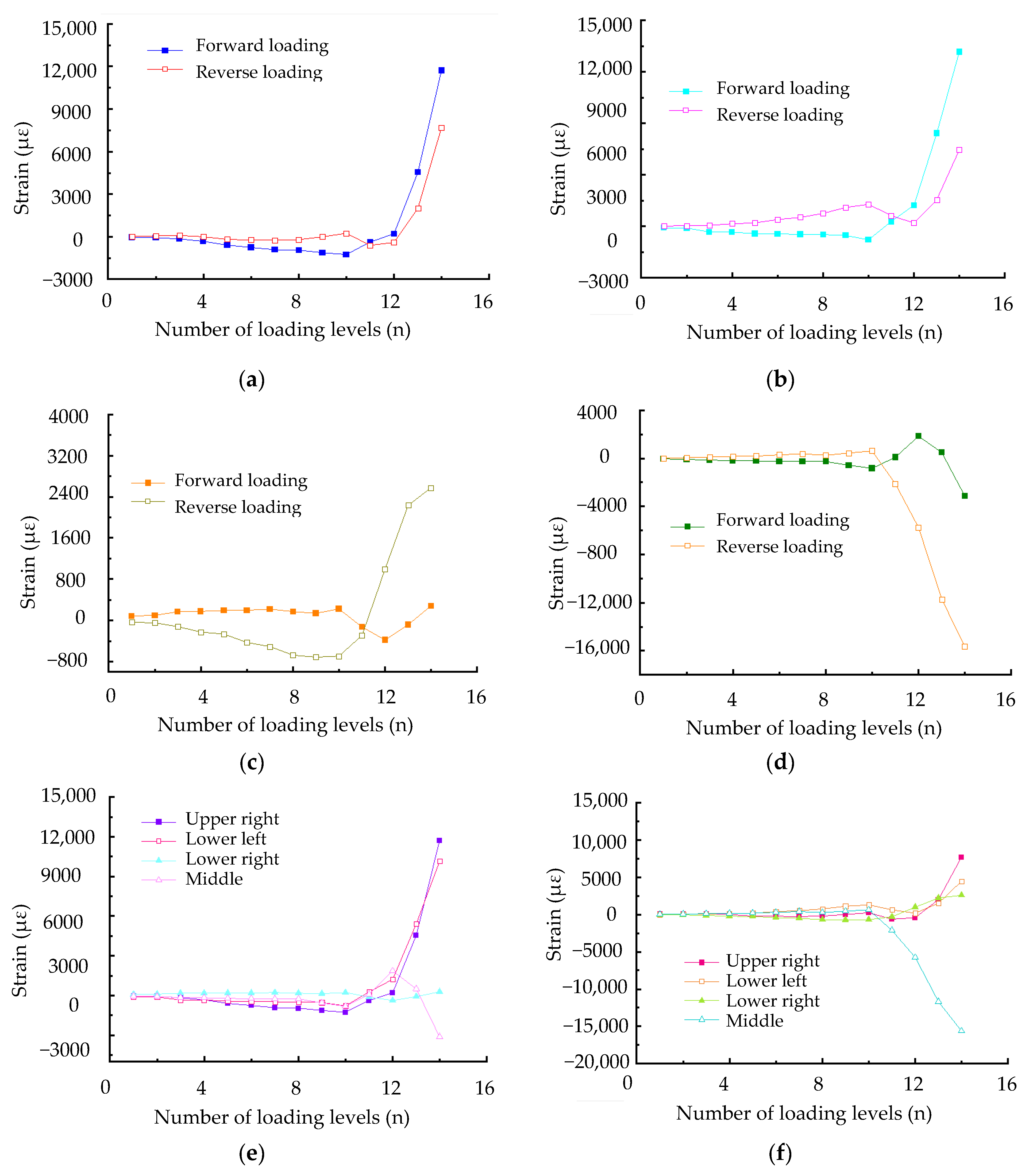
2.2.3. Strain
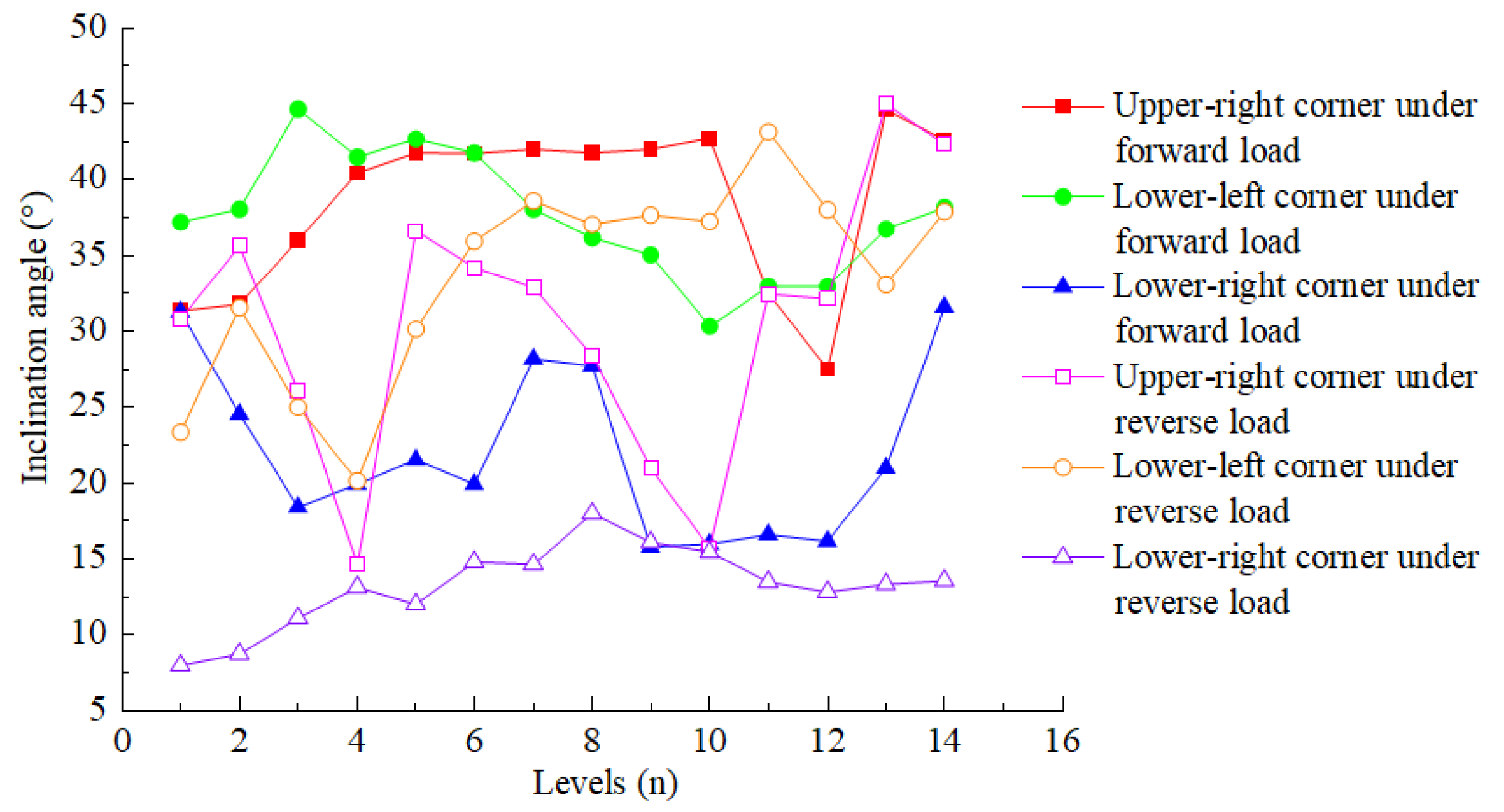
2.2.4. First Principal Stress Inclination of Wall Panel
3. Vertical Loading Test
3.1. Test Scheme
3.1.1. Design of Specimen 2
3.1.2. Experimental Device
3.1.3. Loading Scheme
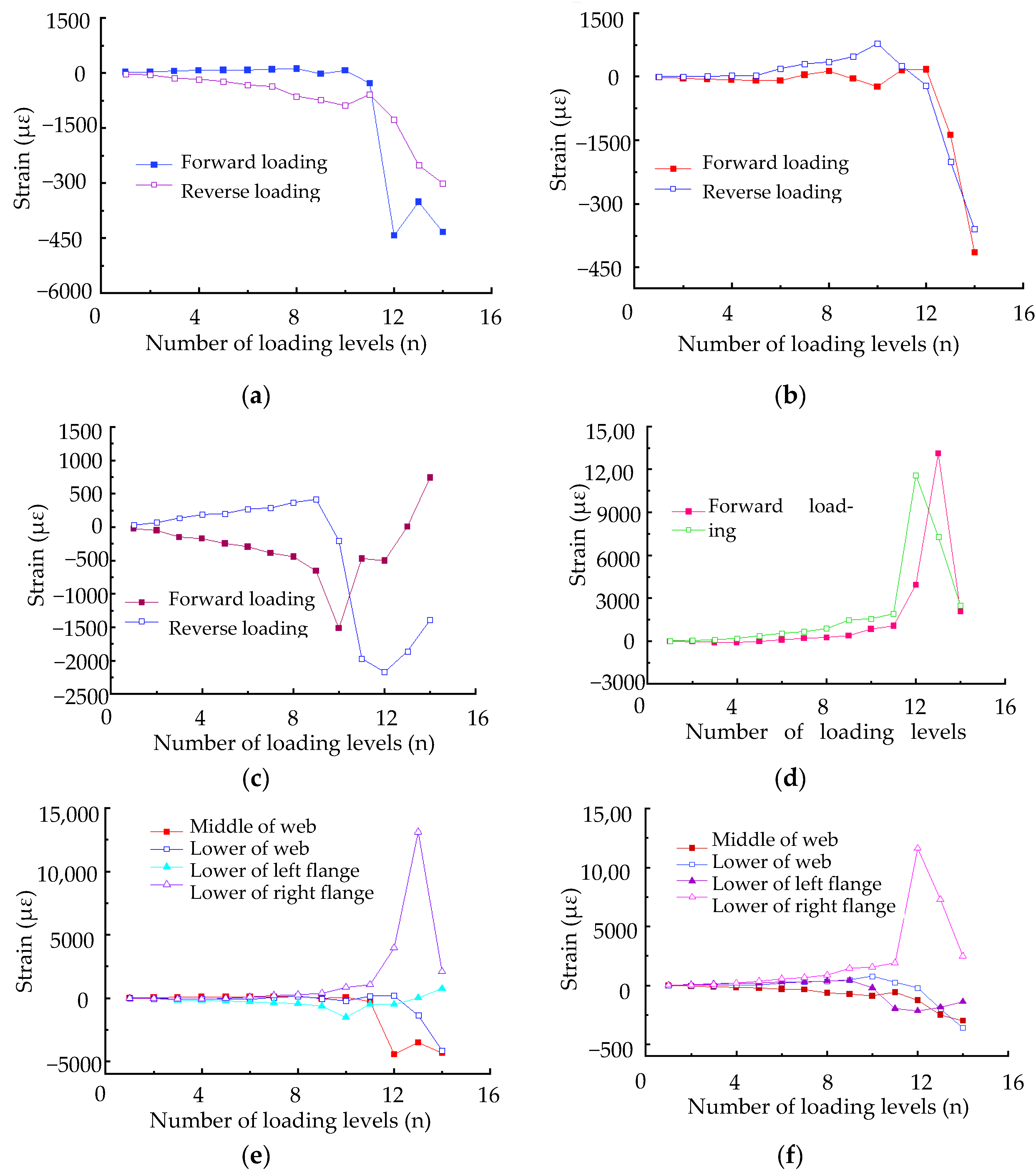
3.2. Experimental Results
Description of Failure Phenomenon
4. Conclusions
- (1)
- Specimen 1 was loaded with a mixed force-displacement system. The infill panel entered the yielding state at the end of the first five loading levels with the maximum out-of-plane displacement of 0.14 mm, and then the infill panel started to appear with a slight bulge at the eleventh loading level and the maximum out-of-plane displacement of 3.7 mm. The infill panel severely bulged and the column base was significantly distorted up to the fourteenth loading level. The maximum out-of-plane displacement at the center of the infill panel reached 31.8 mm.
- (2)
- Specimen 1 was further loaded by applying the controlled displacement that increased from 1.74 to 3.28 times the yield displacement after yielding. The structural bearing capacity decreased extremely slowly and the specimen still possessed a relatively high strength, which indicated that the ductility of this structure was excellent.
- (3)
- The overall strains of the infill panel and frame columns continued to grow smoothly with the increasing forward and reverse loading levels. The increasing rate of strain developed rapidly until the fourteenth loading level, and the measured maximum strains respectively reached 11,735 με for the infill plate and 13,117 με for the frame column, which was significantly higher than the yielding strains of 470.4 με and 1174 με derived from the material tests of LYP steel and ordinary Q235 steel.
- (4)
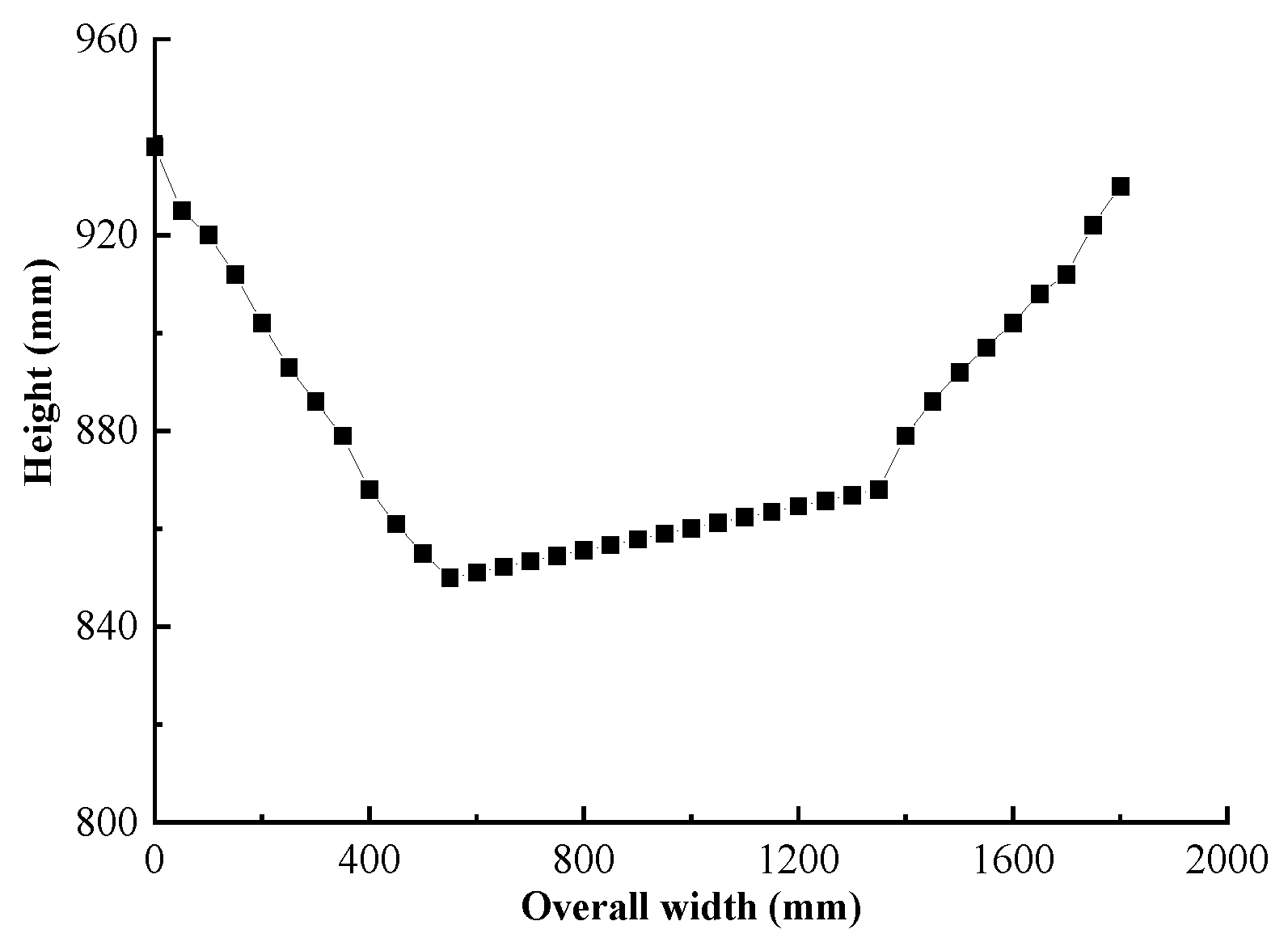
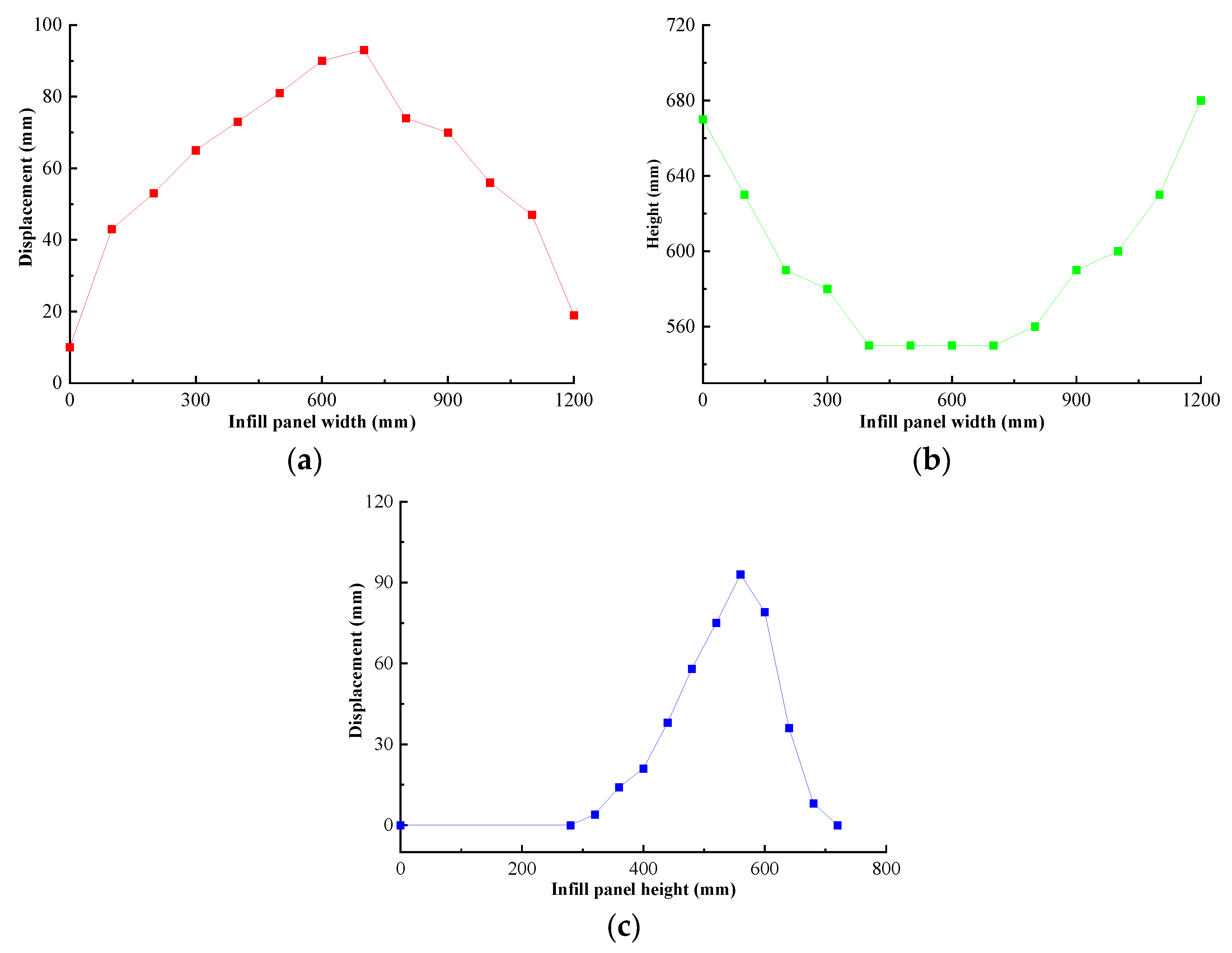
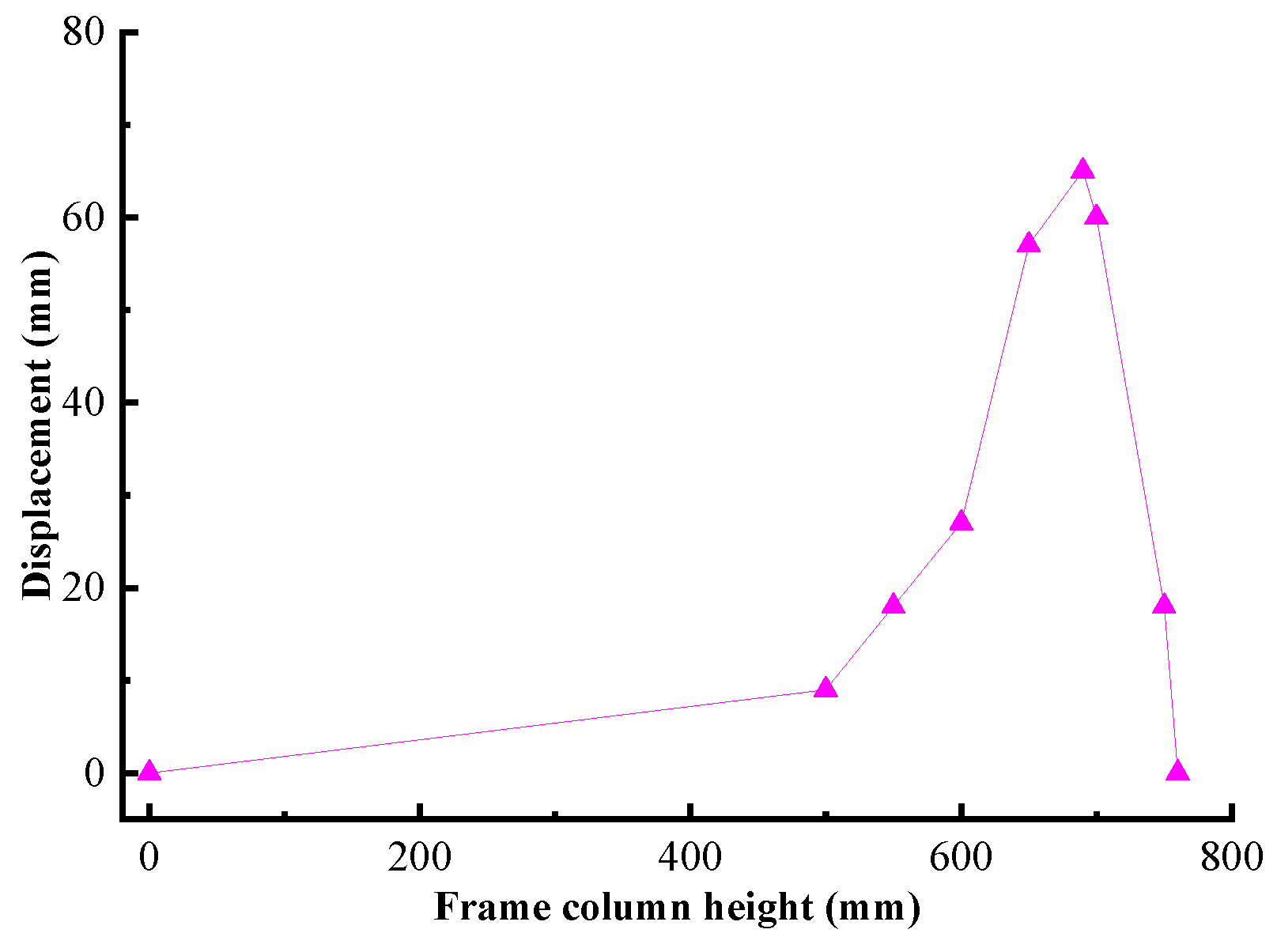
- The results obtained by the vertical loading experiment for specimen 2 indicated that the maximum deformation of both infill panel and frame columns occurred at the middle-upper part of members. The dramatic out-of-plane bulging phenomenon developed along the width of the infill plate under the vertical load, whereas the seriously torsional deformation occurred at the frame column. The maximum out-of-plane deformations were 95 mm at the center of the infill panel and 70 mm at the flange of the frame column, respectively.
- (5)
- The inclination angle of the first principal stress in the wall panel was analyzed, and in overall terms, the inclination angle of the shear panel varied from 8° to 45°.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bypour, M.; Kioumarsi, M.; Yekrangnia, M. Shear capacity prediction of stiffened steel plate shear walls (SSPSW) with openings using response surface method. Eng. Struct. 2021, 226, 111340. [Google Scholar] [CrossRef]
- Bypour, M.; Kioumarsi, B.; Kioumarsi, M. Investigation of Failure Mechanism of Thin Steel Plate Shear Wall in RC Frame. Key Eng. Mater. 2019, 803, 314–321. [Google Scholar] [CrossRef]
- Bypour, M.; Gholhaki, M.; Kioumarsi, M.; Kiousmarsi, B. Nonlinear analysis to investigate effect of connection type on behavior of steel plate shear wall in RC frame. Eng. Struct. 2019, 179, 611–624. [Google Scholar] [CrossRef]
- Moammer, O.; Deylami, A.; Jafari, K.; Raisszadeh, A.H. Numerical investigation of influence of plate yield point on performance of steel plate shear wall. Ce/Papers 2017, 1, 3165–3172. [Google Scholar] [CrossRef]
- Munesi, A.; Gholhaki, M.; Sharbatdar, M. Numerical study on seismic behaviour of buckling-restrained steel plate shear walls. Proc.Inst. Civ. Eng. Struct. Build. 2021. [Google Scholar] [CrossRef]
- Hamed, A.A.; Asl, R.B.; Rahimzadeh, H. Experimental and numerical study on the structural performance of auxetic-shaped, ring-shaped and unstiffened steel plate shear walls. J. Build. Eng. 2021, 34, 101939. [Google Scholar] [CrossRef]
- Mu, Z.G.; Yang, Y.Q. Experimental and numerical study on seismic behavior of obliquely stiffened steel plate shear walls with openings. Thin-Walled Struct. 2020, 146, 106457. [Google Scholar] [CrossRef]
- Paslar, N.; Farzampour, A.; Hatami, F. Infill plate interconnection effects on the structural behavior of steel plate shear walls. Thin-Walled Struct. 2020, 149, 106621. [Google Scholar] [CrossRef]
- Meghdadaian, M.; Ghalehnovi, M. Improving seismic performance of composite steel plate shear walls containing openings. J. Build. Eng. 2019, 21, 336–342. [Google Scholar] [CrossRef]
- Xu, T.; Shao, J.H.; Zhang, J.Y.; Kaewunruen, S. Experimental Performance Evaluation of Multi-Storey Steel Plate Shear Walls Designed by Different Methods. Int. J. Civ. Eng. 2019, 17, 1145–1154. [Google Scholar] [CrossRef]
- Wang, T.T.; Shao, J.H.; Xu, T.; Wang, Z.G. Study on Axial Compression Properties of Aluminum Foam-filled Steel Tube Members after High Temperature. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 883–900. [Google Scholar] [CrossRef]
- Wang, Z.G.; Wang, Y.; Pan, C.R.; Li, J. Research on the Torsional Properties of Aluminum Foam-filled Steel Tube after Fire. J. Asian Archit. Build. Eng. 2018, 17, 525–531. [Google Scholar] [CrossRef] [Green Version]
- Shao, J.H.; Wang, K.; Kaewunruen, S.; Cai, W.H.; Wang, Z.G. Experimental Investigations into Earthquake Resistance of Steel Frame Retrofitted by Low-Yield-Point Steel Energy Absorbers. Appl. Sci. 2019, 9, 3299. [Google Scholar] [CrossRef] [Green Version]
- Mou, B.; Li, Y.Z.; Qiao, Q.Y. Connection behavior of CFST column-to-beam joint implanted by steel rebars under cyclic loading. Eng. Struct. 2021, 246, 113036. [Google Scholar] [CrossRef]
- Wang, T.T.; Shao, J.H.; Zhao, C.; Liu, W.J.; Wang, Z.G. Shaking Table Test for Evaluating the Seismic Performance of Steel Frame Retrofitted by Buckling-Restrained Braces. Shock. Vib. 2021, 2021, 6654201. [Google Scholar] [CrossRef]
- Mou, B.; Zhou, W.Q.; Qiao, Q.Y.; Feng, P.; Wu, C.L. Column base joint made with ultrahigh-strength steel bars and steel tubular: An experimental study. Eng. Struct. 2021, 228, 111483. [Google Scholar] [CrossRef]
- Mou, B.; Liu, X.; Sun, Z. Seismic behavior of a novel beam to reinforced concrete-filled steel tube column joint. J. Constr. Steel Res. 2021, 187, 106931. [Google Scholar] [CrossRef]
- Abebe, D.Y.; Jeong, S.J.; Getahune, B.M.; Segu, D.Z.; Choi, J.H. Hysteretic characteristics of shear panel damper made of low yield point steel. Mater. Res. Innov. 2015, 19, S5–S902. [Google Scholar] [CrossRef]
- Abebe, D.Y.; Choi, J.H.; Jeong, S.J. Effect of Width-to-Thickness Ratio on Large Deformation in Shear Panel Hysteresis Damper Using Low Yield Point Steel. Appl. Mech. Mater. 2013, 446–447, 1460–1465. [Google Scholar] [CrossRef]
- Abebe, D.Y. Analytical Study on Large Deformation in Shear Panel Hysteresis Damper Using low-yield-point Steel. In Proceedings of the 2013 NZSEE Conference, Wellington, New Zealand, 26 April 2013; Graduate School of Architectural Engineering, University of Chosun: Gwangju, Korea, 2013. [Google Scholar]
- Jebelli, H.; Mofid, M. Effects of using low yield point steel in steel plate shear walls. IES J. Part A Civ. Struct. Eng. 2014, 7, 51–56. [Google Scholar] [CrossRef]
- Shahi, N.; Adibrad, M.H. Finite-element analysis of steel shear walls with low-yield-point steel web plates. Proc. Inst. Civ. Eng. Struct. Build. 2018, 171, 326–337. [Google Scholar] [CrossRef]
- Togo, T.; HE, L.S.; Hayashi, K.; Kurata, M.; Nakashima, M. Seismic behavior and design of assembled slit shear walls using low-yield-point steel. J. Struct. Constr. Eng. (Trans. AIJ) 2016, 81, 335–343. [Google Scholar] [CrossRef] [Green Version]
- Bahrebar, M.; Lim, J.B.P.; Clifton, G.C.; Zirakian, T.; Shahmohammadi, A.; Hajsadeghi, M. Response assessment and prediction of low yield point steel plate shear walls with curved corrugated web plates and reduced beam sections. Structures 2020, 28, 1729–1745. [Google Scholar] [CrossRef]
- He, L.S.; Togo, T.; Hayashi, K.; Kurata, M.; Nakashima, M. Cyclic Behavior of Multirow Slit Shear Walls Made from Low-Yield-Point Steel. J. Struct. Eng. 2016, 142, 4016094. [Google Scholar] [CrossRef]
- Zirakian, T.; Zhang, J. Structural performance of unstiffened low yield point steel plate shear walls. J. Constr. Steel Res. 2015, 112, 40–53. [Google Scholar] [CrossRef]
- Shariati, M.; Faegh, S.S.; Mehrabi, P.; Bahavarnia, S.; Zandi, Y.; Masoom, D.R.; Toghroli, A.; Trung, N.T.; Salih, M.N.A. Numerical study on the structural performance of corrugated low yield point steel plate shear walls with circular openings. Steel Compos. Struct. 2019, 33, 569–581. [Google Scholar] [CrossRef]
- Zirakian, T.; Zhang, J. Seismic design and behavior of low yield point steel plate shear walls. Int. J. Steel Struct. 2015, 15, 135–151. [Google Scholar] [CrossRef]
- Khoeilar, A.R.; Zirakian, T.; Boyajian, D.; Maalouf, S.; Dermendjian, N. Case Study on Retrofit of Steel Plate Shear Walls Using low-yield-point Steel Infill Plates. J. Steel Struct. Constr. 2016, 2, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Azandariani, M.G.; Gholhaki, M.; Kafi, M.A. Experimental and numerical investigation of low-yield-strength (LYS) steel plate shear walls under cyclic loading. Eng. Struct. 2020, 203, 109866. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, X.K.; Yang, L.; Yang, W.G. Cyclic performance for low-yield point steel plate shear walls with diagonal T-shaped-stiffener. J. Constr. Steel Res. 2020, 171, 106163. [Google Scholar] [CrossRef]

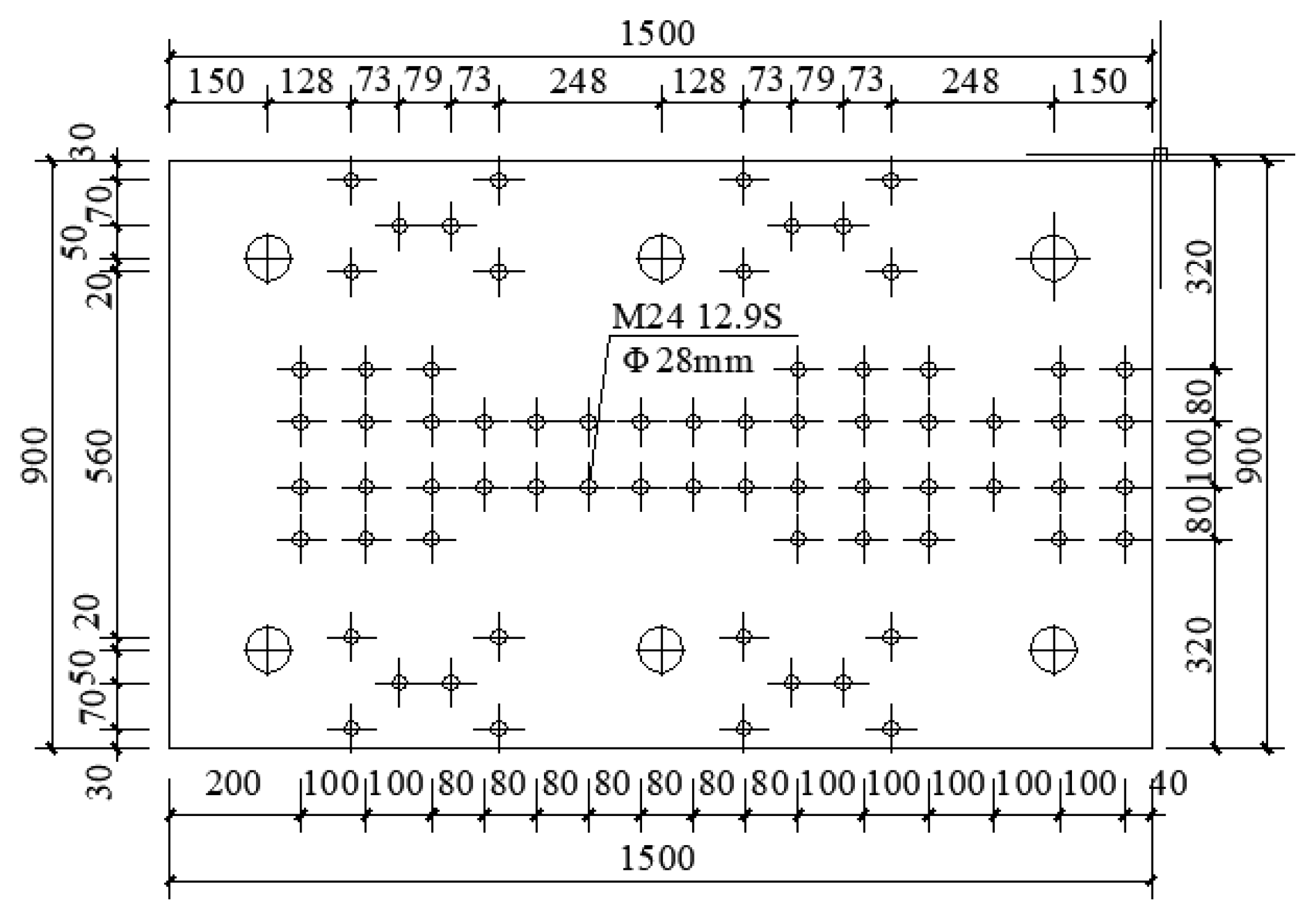





















| Member | Specimen 1 |
|---|---|
| Frame column | H125 × 125 × 6.5 × 9 |
| Frame beam | H150 × 150 × 7 × 10 |
| Infill panel | −650 × 650 × 8 |
| Parameters | Thickness a | Gauge Width b | Gauge Length L0 | Parallel Length Lc | Transition Arc Length r | Clamp d | Overall Length L |
|---|---|---|---|---|---|---|---|
| Sizes | 8 | 25 | 80 | 110 | 25 | 45 | 310 |
| Specimen | Maximum Load F (kN) | Yield Strength fy (MPa) | Tensile Strength fu (MPa) | Modulus of Elasticity E (MPa) | Elongation (%) | Yield Ratio fy/fu | |
|---|---|---|---|---|---|---|---|
| Material | Number | ||||||
| Low-yield-point steel | M1 | 47.42 | 100.59 | 250.68 | 198,639 | 46.36 | 0.40 |
| M2 | 47.13 | 94.74 | 248.96 | 208,734 | 48.18 | 0.38 | |
| M3 | 47.04 | 90.76 | 248.76 | 200,974 | 48.18 | 0.36 | |
| Ordinary steel (Q235) | 74.26 | 234.91 | 391.21 | 200,152 | 35.10 | 0.60 | |
| Levels | Load (kN) | Displacement (mm) | |
|---|---|---|---|
| Forward | Reverse | ||
| 1 | 50 | 0.17 | 0.17 |
| 2 | 100 | 0.48 | 0.46 |
| 3 | 200 | 1.3 | 1.1 |
| 4 | 250 | 1.8 | 1.5 |
| 5 | 300 | 2.4 | 1.8 |
| Levels | Infill Panel | Left Column | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Upper Right | Lower Left | Lower Right | Middle | Middle of Web | Lower of Web | Lower of Left Flange | Lower of Right Flange | |||||||||
| F | R | F | R | F | R | F | R | F | R | F | R | F | R | F | R | |
| 1 | −35 | 29 | −86 | 17 | 89 | −36 | −39 | 30 | 19 | −26 | −17 | 3 | −26 | 29 | −20 | 15 |
| 2 | −69 | 61 | −110 | 34 | 103 | −43 | −76 | 59 | 30 | −57 | −40 | 4 | −49 | 68 | −38 | 34 |
| 3 | −169 | 92 | −330 | 62 | 170 | −116 | −150 | 110 | 56 | −139 | −59 | 8 | −148 | 137 | −80 | 78 |
| 4 | −325 | −2 | −338 | 147 | 179 | −225 | −163 | 166 | 74 | −172 | −70 | 25 | −173 | 187 | −96 | 195 |
| 5 | −588 | −199 | −427 | 197 | 197 | −261 | −213 | 197 | 78 | −232 | −93 | 26 | −244 | 203 | −29 | 355 |
| 6 | −758 | −235 | −446 | 392 | 200 | −426 | −244 | 297 | 77 | −328 | −94 | 192 | −294 | 273 | 91 | 554 |
| 7 | −925 | −261 | −473 | 526 | 222 | −507 | −256 | 386 | 102 | −370 | 48 | 303 | −390 | 288 | 187 | 655 |
| 8 | −948 | −203 | −477 | 751 | 176 | −673 | −258 | 281 | 120 | −634 | 131 | 349 | −442 | 369 | 259 | 871 |
| 9 | −1130 | −4 | −528 | 1100 | 139 | −715 | −569 | 447 | −24 | −746 | −46 | 473 | −657 | 418 | 374 | 1458 |
| 10 | −1257 | 232 | −790 | 1279 | 227 | −692 | −826 | 632 | 70 | −888 | −232 | 780 | −1516 | −204 | 834 | 1561 |
| 11 | −379 | −613 | 282 | 626 | −124 | −288 | 92 | −2114 | −279 | −581 | 160 | 254 | −472 | −1969 | 1055 | 1901 |
| 12 | 210 | −414 | 1228 | 190 | −379 | 998 | 1859 | −5744 | −4430 | −1269 | 176 | −202 | −503 | −2170 | 3944 | 11,609 |
| 13 | 4548 | 2005 | 5425 | 1546 | −83 | 2235 | 500 | −11,696 | −3511 | −2511 | −1375 | −2005 | 8 | −1858 | 13,117 | 7285 |
| 14 | 11,735 | 7708 | 10,157 | 4461 | 284 | 2576 | −3128 | −15,625 | −4336 | −3013 | −4155 | −3600 | 741 | −1393 | 2077 | 2480 |
| Direction of Strain Rosette | Calculating Equations of Axial Strain εx, εy and Shear Strain γxy |
|---|---|
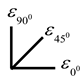 | , , |
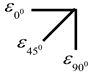 | , , |
 | , , |
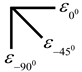 | , , |
| Infill Panel | Upper Right | Lower Left | Lower Right | ||||
|---|---|---|---|---|---|---|---|
| Levels | Forward | Reverse | Forward | Reverse | Forward | Reverse | |
| 1 | 31.33 | 30.78 | 37.20 | 23.34 | 31.29 | 7.97 | |
| 2 | 31.81 | 35.63 | 38.06 | 31.57 | 24.54 | 8.75 | |
| 3 | 36.01 | 26.04 | 44.65 | 25.00 | 18.41 | 11.09 | |
| 4 | 40.42 | 14.69 | 41.49 | 20.15 | 19.93 | 13.13 | |
| 5 | 41.74 | 36.61 | 42.67 | 30.13 | 21.53 | 12.01 | |
| 6 | 41.70 | 34.20 | 41.76 | 35.94 | 19.91 | 14.80 | |
| 7 | 41.98 | 32.88 | 38.06 | 38.59 | 28.19 | 14.65 | |
| 8 | 41.74 | 28.42 | 36.16 | 37.06 | 27.70 | 17.98 | |
| 9 | 42.00 | 21.00 | 35.02 | 37.65 | 15.80 | 16.10 | |
| 10 | 42.73 | 15.69 | 30.35 | 37.22 | 16.00 | 15.46 | |
| 11 | 32.49 | 32.44 | 32.94 | 43.14 | 16.62 | 13.50 | |
| 12 | 27.53 | 32.13 | 32.95 | 38.00 | 16.18 | 12.83 | |
| 13 | 44.59 | 44.99 | 36.74 | 33.06 | 21.00 | 13.32 | |
| 14 | 42.59 | 42.29 | 38.16 | 37.90 | 31.60 | 13.57 | |
| Member | Specimen 2 |
|---|---|
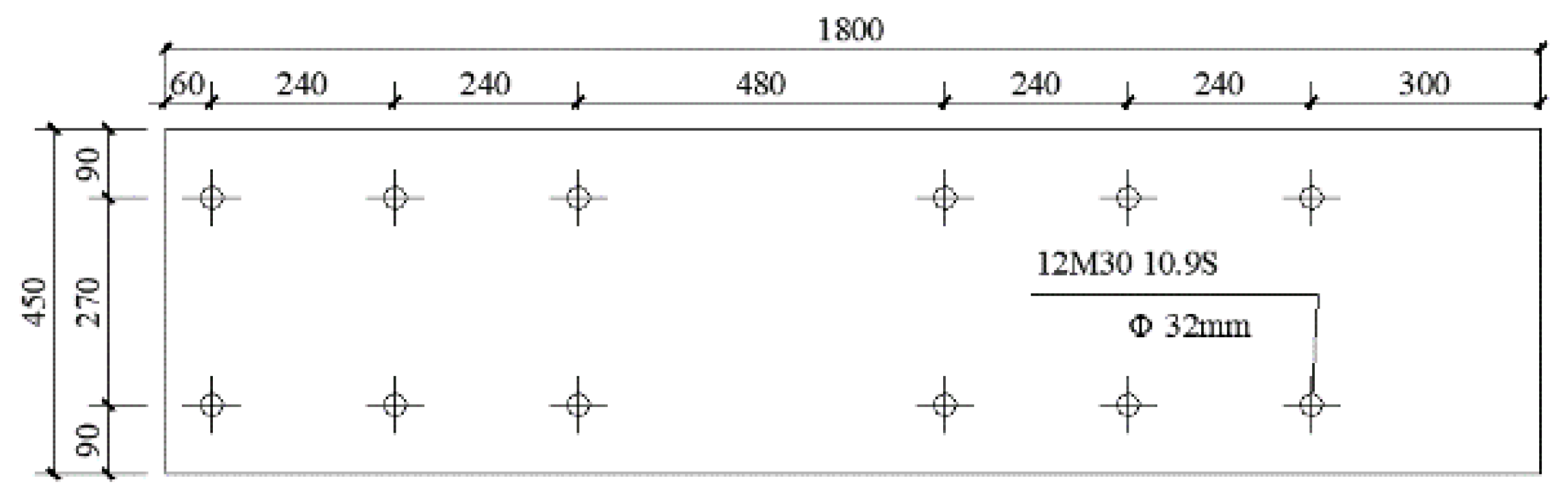
| Frame column | H150 × 150 × 7 ×1 0 |
| Infill panel | −1200 × 800 × 8 |
| Top plate | −1800 × 450 × 60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Shao, J.; Tang, B.; Wang, Z. Experimental Investigation into Failure Modes of Low-Yield-Point Steel Plate Shear Walls. Appl. Sci. 2022, 12, 5632. https://doi.org/10.3390/app12115632
Liu Q, Shao J, Tang B, Wang Z. Experimental Investigation into Failure Modes of Low-Yield-Point Steel Plate Shear Walls. Applied Sciences. 2022; 12(11):5632. https://doi.org/10.3390/app12115632
Chicago/Turabian StyleLiu, Qinglan, Jianhua Shao, Baijie Tang, and Zhanguang Wang. 2022. "Experimental Investigation into Failure Modes of Low-Yield-Point Steel Plate Shear Walls" Applied Sciences 12, no. 11: 5632. https://doi.org/10.3390/app12115632
APA StyleLiu, Q., Shao, J., Tang, B., & Wang, Z. (2022). Experimental Investigation into Failure Modes of Low-Yield-Point Steel Plate Shear Walls. Applied Sciences, 12(11), 5632. https://doi.org/10.3390/app12115632





