Electronic Band Structures of the Possible Topological Insulator Pb2BiBrO6 and Pb2SeTeO6 Double Perovskite: An Ab Initio Study
Abstract
:Featured Application
Abstract
1. Introduction
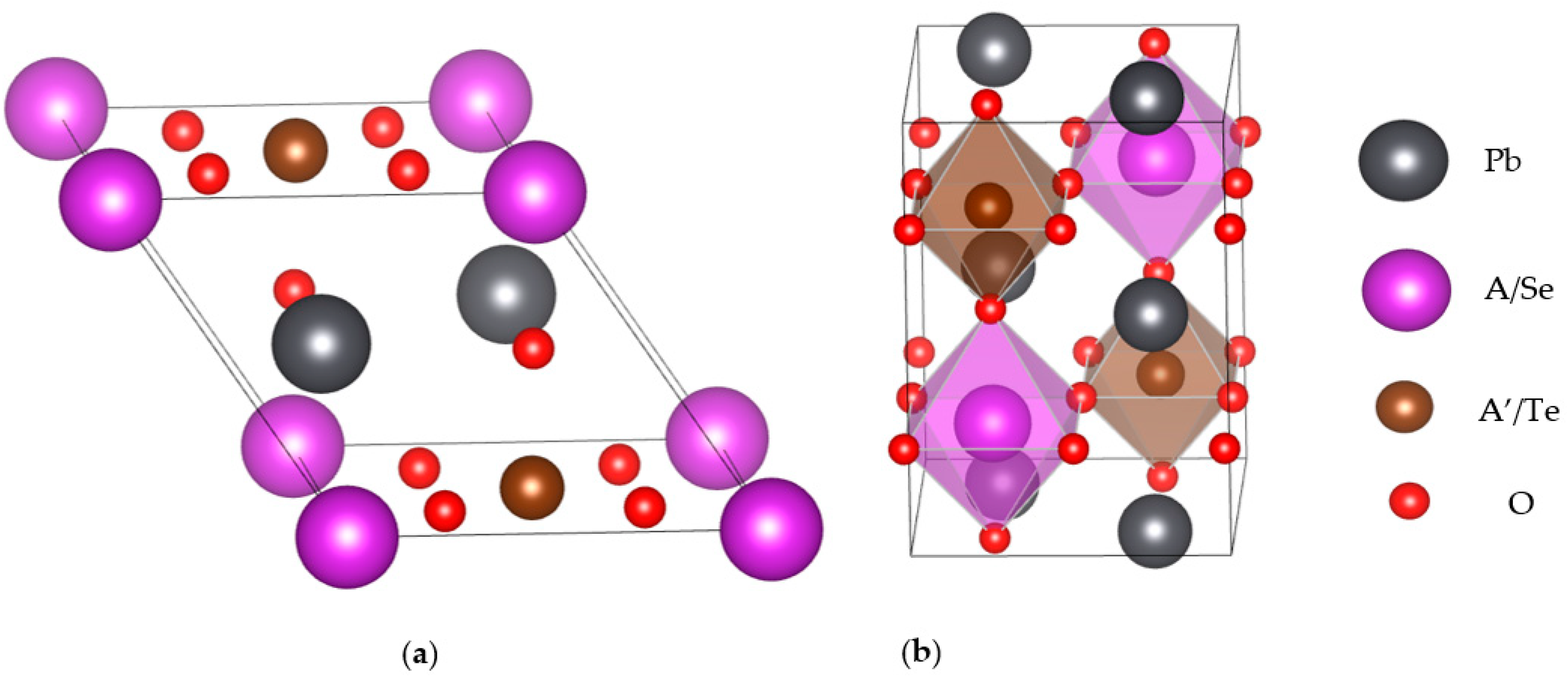
2. Structures and Computational Methods
3. Results and Discussion
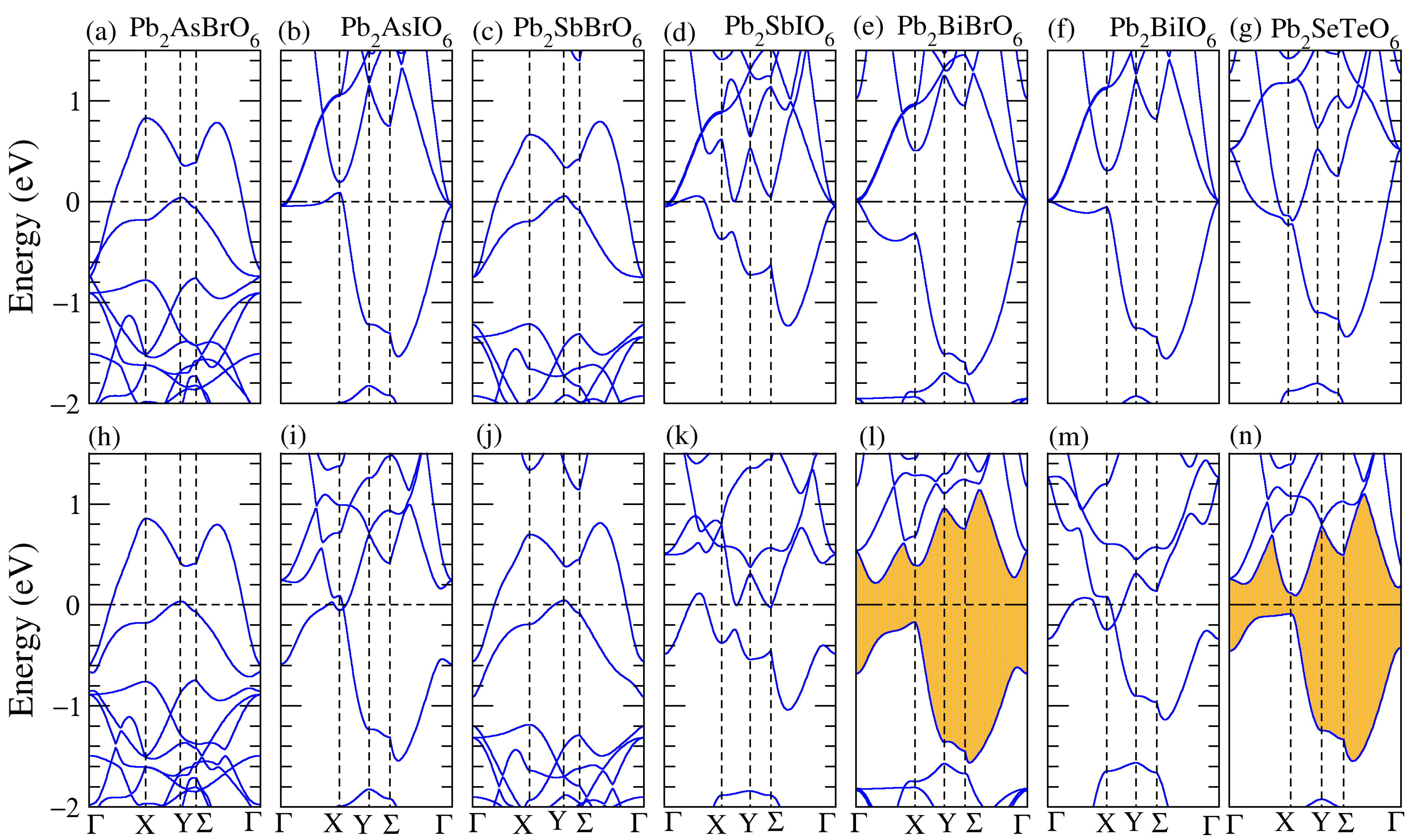
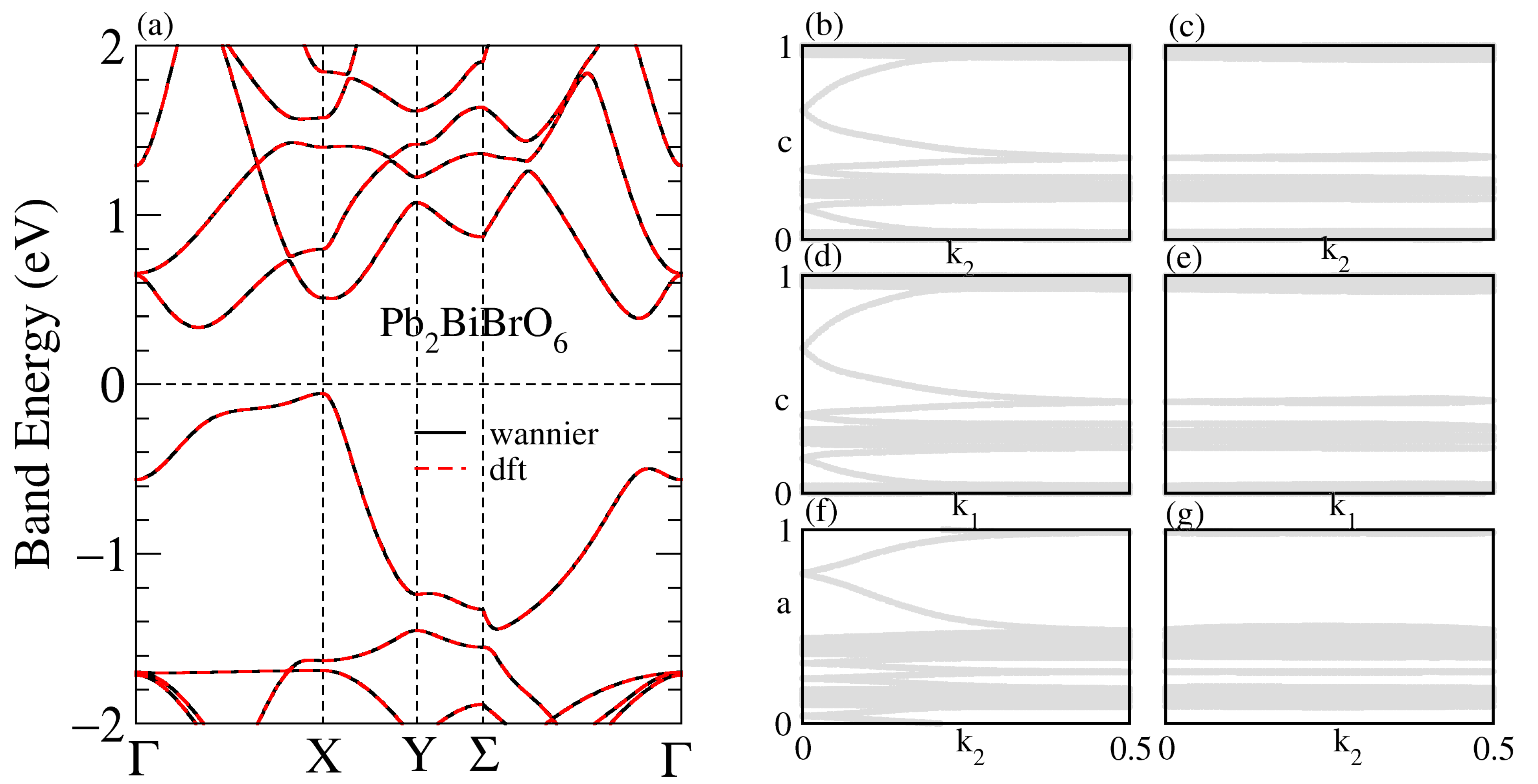
3.1. Structural, and Electronic Band Structure
3.2. Mechanical Properties
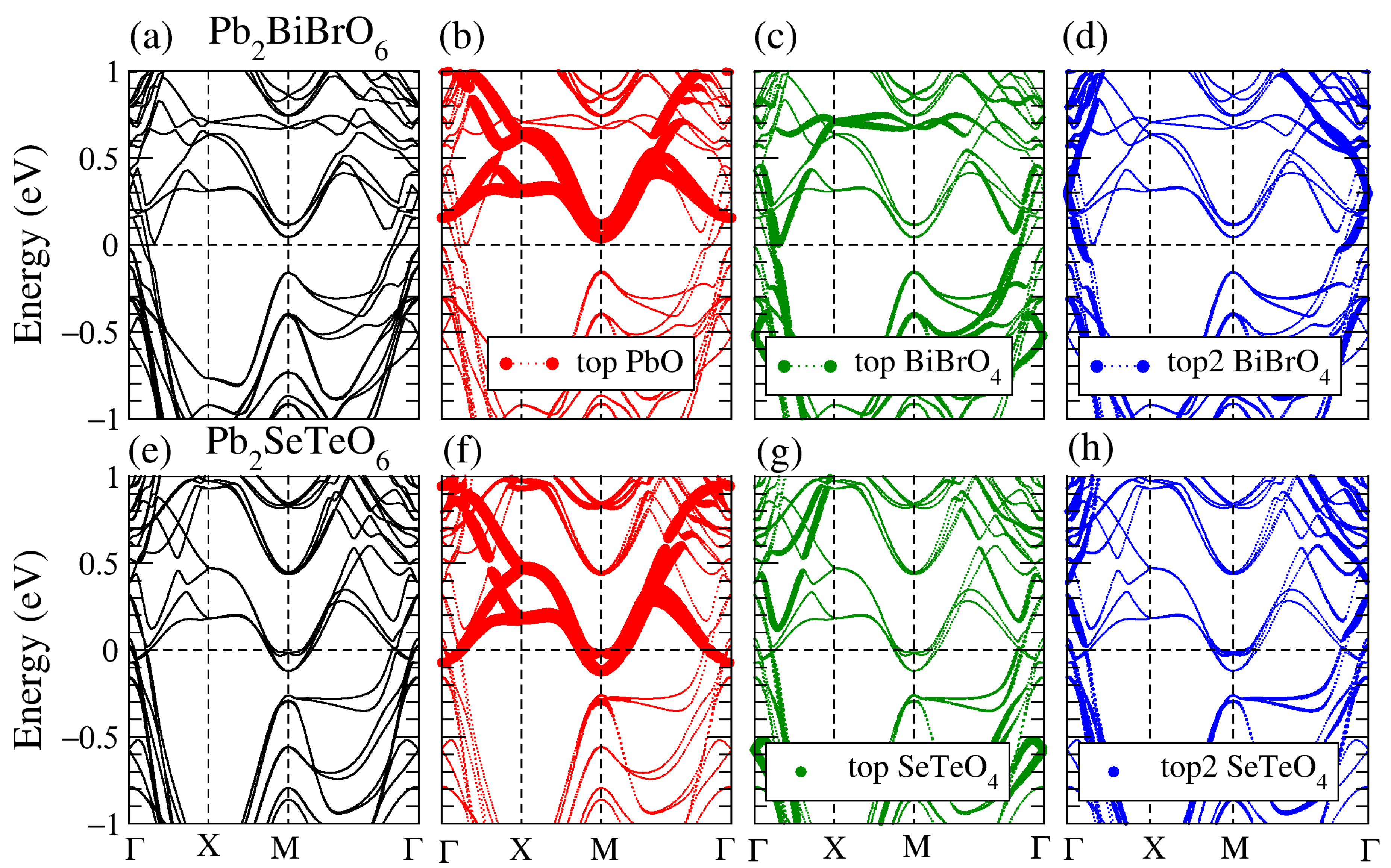
3.3. Band Structure of the Supercell
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ando, Y. Topological insulator materials. J. Phys. Soc. Jpn. 2013, 82, 102001. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef] [Green Version]
- Von Klitzing, K.; Dorda, G.; Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys. Rev. Lett. 1980, 45, 494. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.D.M. Model for a quantum hall effect without landau levels: Condensed-matter realization of the “parity anomaly”. Phys. Rev. Lett. 1988, 61, 2015. [Google Scholar] [CrossRef] [PubMed]
- Kane, C.L.; Mele, E.J. Quantum spin hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernevig, B.A.; Zhang, S.-C. Quantum spin hall effect. Phys. Rev. Lett. 2006, 96, 106802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum spin hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757. [Google Scholar] [CrossRef] [Green Version]
- Oka, T.; Aoki, H. Photovoltaic hall effect in graphene. Phys. Rev. B 2009, 79, 081406. [Google Scholar] [CrossRef] [Green Version]
- Linder, N.H.; Refael, G.; Galitski, V. Floquet topological insulator in semiconductor quantum wells. Nat. Phys. 2011, 7, 490. [Google Scholar] [CrossRef] [Green Version]
- Shvets, I.A.; Klimovskikh, I.I.; Aliev, Z.S.; Babanly, M.B.; Zuniga, F.J.; Sanchez-Barriga, J.; Krivenkov, M.; Shikin, A.M.; Chulkov, E.V. Surface electronic structure of the wide band gap topological insulator PbBi4Te4Se3. Phys. Rev. B 2019, 100, 195125. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Kane, C.L.; Mele, E.J. Surface states of topological insulators. Phys. Rev. B 2012, 86, 081303. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.J.; Liu, C.-X.; Qi, X.-L.; Dai, X.; Fang, Z.; Zhang, S.-C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438. [Google Scholar] [CrossRef]
- Xia, Y.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, D.; Xia, Y.; Qian, D.; Wray, L.; Meier, F.; Dil, J.H.; Osterwalder, J.; Patthey, L.; Fedorov, A.V.; Bansil, A.; et al. Observation of time-reversal-protected single-dirac-cone topological-insulator states in Bi2Te3 and Sb2Te3. Phys. Rev. Lett. 2009, 103, 146401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuroda, K.; Arita, M.; Miyamoto, K.; Ye, M.; Jiang, J.; Kimura, A.; Krasovskii, E.E.; Chulkov, E.V.; Iwasawa, H.; Okuda, T.; et al. Hexagonally deformed fermi surface of the 3D topological insulator Bi2Se3. Phys. Rev. Lett. 2010, 105, 076802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 2011, 106, 106802. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Weng, H.; Wu, Q.; Dai, X.; Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys. Rev. B 2013, 88, 125427. [Google Scholar] [CrossRef] [Green Version]
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.-C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, K.I.; Kimura, T.; Sawada, H.; Terakura, K.; Tokura, Y. Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure. Nature 1998, 395, 677. [Google Scholar] [CrossRef]
- Paul, A.K.; Jansen, M.; Yan, B.; Felser, C.; Reehuis, M.; Abdala, P.M. Synthesis, crystal structure, and physical properties of Sr2FeOsO6. Inorg. Chem. 2013, 52, 6713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Samanta, K.; Sanyal, P.; Saha-Dasgupta, T. Half-metallic behavior in doped Sr2CrOsO6 double perovskite with high transition temperature. Sci. Rep. 2015, 5, 15010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivanov, S.A.; Nordblad, P.; Mathieu, R.; Tellgren, R.; Ritter, C. Structural and magnetic properties of the ordered perovskite Pb2CoTeO6. Dalton Trans. 2010, 39, 11136. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Ivanov, S.; Mathieu, R.; Weil, M.; Li, X.; Lazor, P. Pressure tuning of octahedral tilt in the ordered double perovskite Pb2CoTeO6. J. Alloys Compd. 2019, 801, 310. [Google Scholar] [CrossRef]
- Dai, J.; West, D.; Wang, X.; Wang, Y.; Kwok, D.; Cheong, S.-W.; Zhang, S.B.; Wu, W. Toward the intrinsic limit of the topological insulator Bi2Se3. Phys. Rev. Lett. 2016, 117, 106401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin hall phase. Nature 2008, 452, 970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, S.; Kim, Y.; Tan, L.-Z.; Rappe, A.-M. Strain-induced ferroelectric topological insulator. Nano Lett. 2016, 16, 1663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tung, J.-C.; Hsieh, Y.-H.; Liu, P.-L. Strain induced topological insulator phase in CsPbBrxI3−x (x = 0, 1, 2, and 3) Perovskite: A theoretical study. Appl. Sci. 2021, 11, 5353. [Google Scholar] [CrossRef]
- Felser, C.; Qi, X.-L. Topological insulators. MRS Bull. 2014, 39, 843. [Google Scholar] [CrossRef] [Green Version]
- Pi, S.-T.; Wang, H.; Kim, J.; Wu, R.; Wang, Y.-K.; Lu, C.-K. New class of 3D topological insulator in double perovskite. J. Phys. Chem. Lett. 2017, 8, 332. [Google Scholar] [CrossRef] [Green Version]
- Lee, P.-H.; Zhou, J.; Pi, S.-T.; Wang, Y.-K. Topological insulators double perovskites: A2TePoO6 (A = Ca, Sr, Ba). J. Appl. Phys. 2017, 122, 224902. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.-L. Topological insulators in three dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüllerr, J. Ultrasoft pseudopotentials applied to magnetic Fe, Co, and Ni: From atoms to solids. Comput. Mater. Sci. 1996, 6, 15. [Google Scholar] [CrossRef]
- Wang, Y.; Perdew, J.-P. Correlation hole of the spin-polarized electron gas, with exact small-wave-vector and high-density scaling. Phys. Rev. B 1991, 44, 13298. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Perdew, J.-P. Erratum: Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar]
- Mostofi, A.A.; Yates, J.R.; Pizzi, G.; Lee, Y.S.; Souza, I.; Vanderbilt, D.; Marzari, N. An updated version of wannier90: A tool for obtaining maximally-localised wannier functions. Comput. Phys. Commun. 2014, 185, 2309. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.S.; Zhang, S.N.; Song, H.-F.; Troyer, M.; Soluyanov, A.A. WannierTools: An open-source software package for novel topological materials. Comput. Phys. Commun. 2018, 224, 405. [Google Scholar] [CrossRef] [Green Version]
- Weng, H.; Dai, X.; Fang, Z. Exploration and prediction of topological electronic materials based on first-principles calculations. MRS Bull. 2014, 39, 849. [Google Scholar] [CrossRef] [Green Version]
- Gresch, D.; Autes, G.; Yazyev, O.V.; Troyer, M.; Vanderbilt, D.; Bernevig, B.A.; Soluyanov, A.A. Z2Pack: Numerical implementation of hybrid Wannier centers for identifying topological materials. Phys. Rev. B 2017, 95, 075146. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.-J.; Zhao, E.-J.; Xiang, H.-P.; Hao, X.-J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pugh, S.F. XCII relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 7, 823–843. [Google Scholar] [CrossRef]


| a = b | c/a | V0 | O1z | O2x | O2y | Bandgap (eV) | |
|---|---|---|---|---|---|---|---|
| Pb2AsBrO6 | 6.003 | 1.282 | 138.69 | 0.4371 | 0.2529 | 0.2185 | 0 (0) |
| Pb2AsIO6 | 5.905 | 1.413 | 145.50 | 0.4942 | 0.2473 | 0.2471 | 0 (0) |
| Pb2SbBrO6 | 6.151 | 1.286 | 149.61 | 0.4599 | 0.2586 | 0.2299 | 0 (0) |
| Pb2SbIO6 | 6.059 | 1.413 | 157.15 | 0.4981 | 0.2512 | 0.2510 | 0 (0) |
| Pb2BiBrO6 | 6.011 | 1.413 | 153.48 | 0.4715 | 0.2644 | 0.2642 | 0 (0.390) |
| Pb2BiIO6 | 6.165 | 1.413 | 165.63 | 0.4775 | 0.2612 | 0.2612 | 0 (0) |
| Pb2SeTeO6 | 5.894 | 1.413 | 144.70 | 0.4904 | 0.2451 | 0.2452 | 0 (0.181) |
| Pb2AA’O6 | |||||||
|---|---|---|---|---|---|---|---|
| AA’ = AsBr | AsI | SbBr | SbI | BiBr | BiI | SeTe | |
| C11 (GPa) | 185.28 | 188.62 | 176.62 | 160.63 | 180.21 | 166.60 | 199.12 |
| C12 (GPa) | 90.70 | 106.72 | 101.72 | 105.93 | 103.57 | 112.36 | 109.61 |
| C13 (GPa) | 71.75 | 97.33 | 62.39 | 85.14 | 73.44 | 65.18 | 96.05 |
| C33 (GPa) | 236.41 | 199.08 | 254.26 | 186.08 | 211.17 | 214.27 | 214.78 |
| C44 (GPa) | 45.56 | 48.74 | 44.39 | 47.43 | 67.98 | 74.31 | 56.89 |
| C66 (GPa) | 47.11 | 41.39 | 36.53 | 27.50 | 38.17 | 26.98 | 44.81 |
| BR (GPa) | 118.99 | 131.01 | 117.23 | 117.74 | 119.16 | 114.77 | 135.15 |
| BV (GPa) | 119.48 | 131.01 | 117.83 | 117.75 | 119.16 | 114.77 | 135.16 |
| B (GPa) | 119.24 | 131.01 | 117.53 | 117.74 | 119.16 | 114.77 | 135.16 |
| GR (GPa) | 50.71 | 44.26 | 43.40 | 32.22 | 46.40 | 36.26 | 49.26 |
| GV (GPa) | 52.81 | 44.63 | 48.89 | 35.89 | 50.27 | 45.97 | 50.06 |
| G (GPa) | 51.76 | 44.45 | 46.15 | 34.56 | 48.34 | 41.12 | 49.66 |
| E (GPa) | 135.65 | 119.79 | 122.42 | 94.43 | 127.73 | 110.19 | 132.72 |
| 0.31 | 0.35 | 0.33 | 0.37 | 0.32 | 0.34 | 0.34 | |
| 0.21 | 0.04 | 0.64 | 0.40 | 0.42 | 1.34 | 0.08 | |
| B/G | 2.30 | 2.95 | 2.54 | 3.41 | 2.47 | 2.79 | 2.72 |
| Pb2AA’O6 | |||||||
|---|---|---|---|---|---|---|---|
| AA’ = AsBr | AsI | SbBr | SbI | BiBr | BiI | SeTe | |
| 7.96 | 8.13 | 7.94 | 8.02 | 8.65 | 8.48 | 8.23 | |
| 4861.57 | 4838.29 | 4759.84 | 4519.42 | 4607.82 | 4470.86 | 4947.25 | |
| 2549.19 | 2338.39 | 2416.37 | 2075.70 | 2364.18 | 2201.39 | 2456.78 | |
| 2851.17 | 2628.24 | 2708.24 | 2338.91 | 2647.99 | 2471.74 | 2757.15 | |
| 353 | 321 | 327 | 278 | 317 | 289 | 337 | |
| 1264 | 935 | 1265 | 1115 | 1211 | 1175 | 1273 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tung, J.-C.; Lee, C.-H.; Liu, P.-L.; Wang, Y.-K. Electronic Band Structures of the Possible Topological Insulator Pb2BiBrO6 and Pb2SeTeO6 Double Perovskite: An Ab Initio Study. Appl. Sci. 2022, 12, 5913. https://doi.org/10.3390/app12125913
Tung J-C, Lee C-H, Liu P-L, Wang Y-K. Electronic Band Structures of the Possible Topological Insulator Pb2BiBrO6 and Pb2SeTeO6 Double Perovskite: An Ab Initio Study. Applied Sciences. 2022; 12(12):5913. https://doi.org/10.3390/app12125913
Chicago/Turabian StyleTung, Jen-Chuan, Chi-Hsuan Lee, Po-Liang Liu, and Yin-Kuo Wang. 2022. "Electronic Band Structures of the Possible Topological Insulator Pb2BiBrO6 and Pb2SeTeO6 Double Perovskite: An Ab Initio Study" Applied Sciences 12, no. 12: 5913. https://doi.org/10.3390/app12125913
APA StyleTung, J.-C., Lee, C.-H., Liu, P.-L., & Wang, Y.-K. (2022). Electronic Band Structures of the Possible Topological Insulator Pb2BiBrO6 and Pb2SeTeO6 Double Perovskite: An Ab Initio Study. Applied Sciences, 12(12), 5913. https://doi.org/10.3390/app12125913








