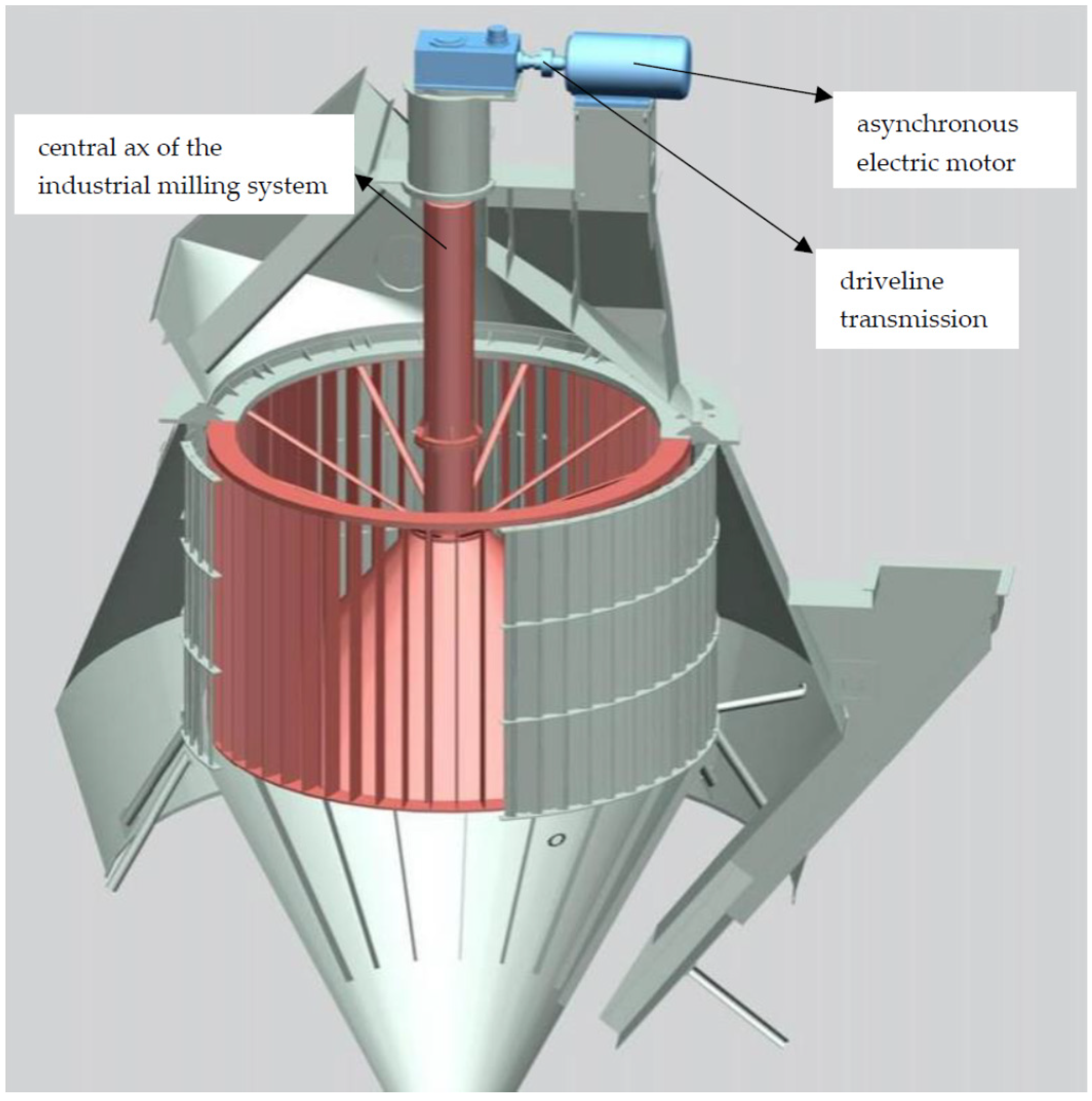
1. Introduction
The double tripod industrial driveshafts (DTID) are used in the cement industry plant, food industry, and agriculture industry to link the power supplier with the industrial mill. In most cases, the power supplier is the asynchronous electric motors, and the link to a moderate heavy-duty mill is DTID, the industrial system presented in
Figure 1. Generally, in heavy-duty use, a drivetrain line from the electric motor to the mill is covered by a double cardan driveshaft, see
Figure 2, but this type of driveshaft, having two Hooke’s joints, induces a nonuniformity that must be avoided [
1] (pp. 5–9).
For a moderate heavy-duty industrial milling system, to avoid the non-uniformity of Hooke’s joints, a double tripod industrial driveshaft (DTID) is used in the driveline transmission because this type of driveshaft has two constant velocity joints (CVJ) [
1] (pp. 52–79). The DTIDs are, in fact, quasi-homokinetic driveshafts, as proven by Dudita et al. [
1] (p. 78), in [
2], and mentioned in [
3]. This is the type of DTID that the present work deals with, and the first effect considered is the kinematic nonuniformity already studied in detail by the papers [
2,
3]. Qiu et al. developed [
4] a double roller tripod joint to obtain a better constant velocity. The excitation torque load, an input of the asynchronous electric motor, can be considered harmonic type, as mentioned by Miljkovic in the paper [
5]. The present work investigates nonstationary forced torsional vibrations (NFTV) of DTID using designed methods that certify the possible chaotic deterministic or ergodic dynamic behavior. In [
6], Rossi et al. developed a torsional model with two degrees of freedom (2 DOF) to investigate the damping of torsional vibrations in variable speed drive, particularly the torsional mode excitations. Xu et al. studied [
7] the amplitude-frequency characteristics for torsional vibration in an automotive powertrain using a model with 29 DOF. In his doctoral thesis [
8] (pp. 6–100), Yao investigated the modeling of nonlinear driveshaft systems with double U-joints, observing the passage effect and the Sommerfeld effect for both 2 DOF and 3 DOF models. Based on findings in the literature [
6,
7,
8], it is evident, in opposition to the models in [
9], that the modified physically consistent model (MPCM) for FTV of DTID is a better approach to industrial realities. The next paragraph will discuss the MPCM for FTV of DTID that considers the following aspects: double tripod of the joints for ID, geometric and kinematic nonuniformity of CVJs, and harmonic excitation of torsional torque load due to the use of an asynchronous electric motor for the moderate heavy-duty industrial milling system as well as the reactive harmonic torque induced by the mill. In their paper, Mazzei and Scott remarked for the first time using numerical data [
10] that the most critical resonance for a driveshaft with a universal joint is the principal parametric resonance. SoltanRezzaee et al. in the article [
11], investigated the parametric instability of driveshafts with U-joints using the monodromy matrix method. Another study [
12] investigated the dynamic instability of a double cardan joint using the FEM (finite element method) coupled with the monodromy matrix method. As suggested in the literature [
10,
11,
12], the most crucial resonant case of a driveshaft is the principal parametric resonance; therefore, the present work is dedicated to investigating the nonstationary dynamic instability of FTV for DTID in the principal parametric resonance region (PPRR). Loginovskikh et al. [
13] investigated the values of tangential stress for a pumping unit shaft in the resonant case, confirming the need for avoiding such a torsional resonance region. The paper [
14] studied the designing needs of models for torsional vibrations of shafts of mechanical systems to control the dynamic behavior in torsion, by vibration dampers and equivalent stiffness of double-mass oscillating systems. Zhai et al. [
15] investigated the vibration characteristics of the shaft systems for dredging pumps using the FEM to determine the upper and the lower limits for critical speeds of torsional vibration. It was observed that the rated speed of the dredging pump was far less than the predicted critical speed. Therefore, FEM offers only some reference value on the stability analysis of the shaft system. Experimental investigations and finite element analysis were carried out in the literature [
16] to determine the natural frequencies and the mode shapes for steel and CFRP (carbon fiber reinforced plastic) driveshafts. This interest in CFRP is due to the advantages afforded to the industry when using CFRP instead of steel. Mazzei and Scott demonstrated through [
17] that a method of avoiding parametric resonances of the universal joint driveline is accelerating through these regions. As identified in the literature [
13,
14,
15,
16,
17], it is necessary to investigate the PPRR locally and globally in close detail. Steinwede, in his Ph.D. thesis [
18] (pp. 88–94), experimentally found the pitting and the microcracks on the tripod of the driveshaft. He explained that the driveshaft joints have similar dynamic behavior as the geared system transmission [
18] (p. 117). Additionally, he stated that the bending and torsion vibrations manifest a “strange beating behavior” [
18] (pp. 138–139) that is generated by the engine excitation, geometric and mass nonuniformities, and kinematic nonuniformity of joints. In the literature, the investigation of the chaotic behavior of the geared system transmission was performed in [
19] (pp. 102–103, 127–131), and it was found that geared systems may have a deterministic chaos vibration that conducts in time to phenomena as pitting and microcracks. These aspects mentioned before must be investigated. One of the present paper’s goals is to investigate possible chaotic dynamic behavior for the NFTV in transition through PPRR. Kecik and Warminski [
20] investigated the chaotic motion of an auto-parametric system by simulations using the maximal Lyapunov exponent method (MLEM) and laboratory experiments. In [
21], Chang studied the control over chaotic behavior of an active magnetic bearing system by MLEM, Poincaré Maps, and phase portraits. Bavi et al. investigated the simultaneous resonance and stability analysis of unbalanced asymmetric thin-walled composite shafts in [
22] using the multiple-scale approach (MSA) and the phase portrait graphs. As identified in [
20,
21,
22], the methods of investigating the chaotic dynamic behavior are the MLEM (quantitative method) and the Poincaré Maps method (qualitative method), and for the computation of dynamic instability frontiers regions the perturbation approach MSA is used. The present paper will use time–history analysis to detect the dynamic chaotic behavior using the phase portrait graphs of the NFTV for DTID. The chaos will be investigated using a robust designed method given by the modified Lyapunov exponent’s method (MLEM) coupled with Poincaré Maps (PM), that is, Lyapunov Exponents Approach-Poincaré Map (LEA–PM), of the NFTV for DTID in transition through PPRR. These are the novel aspects of the new method: detection of chaos by analysis of time–history and investigation of chaos by employing LEA–PM. Why is this new and “mathematical affordable” method used by the designers of DTID? As mentioned before, most researchers, such as in [
21], use MLEM directly without detecting chaos before. The new robust method detects possible chaotic behavior. Additionally, the MLEM is not sufficient for deterministic chaotic behavior, as mentioned in [
23], and for this reason, MLEM was modified in a more complex new method, LEA. All the research on chaos manifestations needed a second confirmation for the deterministic chaos (the manifestation of
strange attractors) due to the complexity of the dynamic phenomena when chaos occurs. Accordingly, the new method involves using a qualitative second method, the PM. Therefore, the new method LEA–PM becomes a robust method of investigating chaos. The new method is an equivalent method to investigate the chaos of dynamical systems in the simplest Riemannian spaces (spaces with Euclidian metrics). In contrast, the KCC method [
24] is the newest method of investigating chaos for the higher-order dynamical systems in Finsler spaces. The KCC method is not a “mathematical affordable” method, such as LEA–PM, for the designers because it involves the management of spaces with two different metrics as Finsler spaces (the problem of curvature properties of homogeneous Finsler spaces with
-metrics is one of the central problems in Riemann–Finsler geometry) and the Jacobi stability analysis using KCC. In conclusion, the novelty of this work consists in introducing a new robust method with two-step detection and certification of the deterministic chaos for NFTV of DTID based on an MPCM of FTV that considers the following phenomena: nonuniformity of geometric and mass characteristics of the DTID, the kinematic nonuniformity of the DTID’s homokinetic joints, and the multiple harmonic excitations induced by the asynchronous electric motor and the milling system. The present research challenges are the investigation of NFTV of DTID using time–history analysis, phase portraits for possible chaos detection, and LEA–PM for deterministic chaos or nonstationary dynamic ergodic behavior of DTID in PPRR. This goal of the present work is the theoretical investigation of the pitting manifestation for the homokinetic transmissions, particularly the DTID mentioned by Steinwede [
18] (pp. 138–139) for the automotive driveshaft and explained by the similarity with chaotic manifestations of the geared systems transmission [
19] (pp. 102–103, 127–131) for which pitting and microcracks are common manifestations. Therefore, the aim of the work is the design of a new robust method to detect and confirm, without any doubt, the existence or not of deterministic chaos for the nonstationary FTV of a double tripod industrial driveshaft in the principal parametric resonance region. The novelty of this new method consists of using time–history analysis (THA represents the analysis of the phase portraits) as a detection method of possible chaos manifestation coupled with a new method, LEA–PM, to certify the existence of deterministic chaos. The LEA–PM has certain advantages because it is based not only on the MLEM (maximal Lyapunov exponent method) and using on the Poincaré Maps Method to reconfirm the deterministic chaos. The novelty of the present work is the design of the new robust method THA–LEA–PM that detects and certifies the deterministic chaos for NFTV of DTID’s elements in transition through PPRR. Additionally, the new LEA (Lyapunov exponent approach) combines the classic MLEM with a new criterion (the sum of Lyapunov exponents must be negative), as mentioned in [
23]. In the meantime, THA–LEA–PM is much simpler to use, from a mathematical point of view, than KCC, as mentioned above.
2. The Modified Physically Consistent Model of FTV for Double Tripod Industrial Driveshaft
A DTID is a driveline transmission from an electric motor to a milling system composed of three elements: driven input element (DIE1), driving midshaft part (DME2), and driving output element (DOE3), as presented in
Figure 3. The tripod joint is shown in detail in
Figure 4. The DTID is rigidly fixed in the gearbox of the asynchronous electric motor through a spline assembly of the DIE1, see
Figure 4, and is linked to the milling system through a similar spline assembly (see
Figure 4).
As shown in
Figure 4, both tripods are fixed through splines on the DME2 at both ends of the midshaft and can plunge inside the bells of DIE1 and DOE3.
Figure 5 is a tripod with three trunnion shafts with a distance of 120° between them, fixed on a tubular element with internal splines, and a needle-bearing roller is fixed on each trunnion shaft.
Figure 6 shows a picture of a DTID’s DIE1 or DOE3 with a section on the bell to show the trunnion shaft and a needle-bearing roller.
As seen in
Figure 3,
Figure 4,
Figure 5 and
Figure 6, the DTID is a multi-body system. Each element is attached to a cartesian system, as shown in
Figure 7, and it is considered that the parts DIE1 and DOE3 have rigid twisting body motions along the longitudinal axes. In contrast, the element DME2 has an elastic continuous twisting motion along the longitudinal axis
. The axes
are parallel, therefore the planes
, and
are coplanar. The angles
are due to the misalignments between the output axis of the electric motor’s gearbox and the ax of the milling system being in the range of 0–9°.
The inertial characteristics for each element of the DTID are reduced to the longitudinal axis
(see
Figure 7). All the axial geometric and the axial mass moments of inertia (AGMI and AMMI) for DIE1, DME2, and DOE3 are presented in
Appendix A. The significance of the AGMI and AMMI expressed in
Appendix A is:
,
are the axial geometric and the axial mass moments of inertia (AGMI and AMMI) for DIE1,
,
are the AGMI and the AMMI for DME2,
,
are the same inertial characteristics for DOE3,
,
are the AGMI for DIE1’s axis and bell,
,
are AGMI for DOE3’s ax and bell,
,
are the geometric nonuniformities for DIE1 and DOE3,
,
are the principal AGMI for DIE1’s bell,
,
are the principal AGMI for DOE3’s bell,
,
are the positions from mass center of the bells for DIE1 and DOE3 to the centroid of conjugated tripods,
are the diameters of the DIE1’s ax and DOE3’s ax,
are the lengths of ax and bell for DIE1,
are the lengths of ax and bell for DOE3,
are the principal AGMI for tripod TJ1,
are the principal AGMI for tripod TJ2,
is the diameter of DME2,
are the areas cross-section of the DIE1 and DOE3, and
is the mass volume density for the isotropic material of DTID. Thus, all the inertial characteristics for the DTID’s elements are parametric functions of the variables’ angles
, expressing the geometric nonuniformity of a driveline transmission. The rigidity and the damping of the DTID’s elements are like those presented in [
9] because the DTID also has three elements, DIE1, DME2, and DOE3, as illustrated in
Figure 8, linked through the joints TJ1 (tripod joint 1) and TJ2 (tripod joint 2), with dynamic torsional characteristics expressed as follows:
The first DTID element is DIE1 (see
Figure 7 and
Figure 8), which has the torsion rigidity and the torsion damping coefficient given by the equations:
where G is the steel shear modulus,
are the stiffness and the damping coefficient in torsion of DIE1, and
is the damping ratio of the DIE1’s material, steel, having the value range 0.0016–0.0318 [
9];
- 2.
The TJ1 is the tripod that links DIE1 and DME2 (see
Figure 7 and
Figure 8), having the torsion stiffness
and the coefficient of torsion damping
;
- 3.
The second DTID element is DME2 (see
Figure 7 and
Figure 8), which has a continuous elastic behavior in torsion and has fixed through splines at both ends of the tripods with the inertial characteristics in torsion
where
are the axial mass moment of inertia of the tripods with the DME2’s axis included,
has the same signification for DME2,
are the lengths of the tripods, and
is the diameter of the DTID’s element DME2;
- 4.
The TJ2 is the tripod that links DME2 and DOE3 (see
Figure 7 and
Figure 8), having the torsion stiffness
and the coefficient of torsion damping
;
- 5.
The third DTID element is DOE3 (see
Figure 7 and
Figure 8), which has the torsion rigidity and the torsion damping coefficient given by the equations:
where
are the stiffness and the damping coefficient in torsion of DOE3. The equation gives the load torque received by DTID from the asynchronous electric motor (see
Figure 7 and
Figure 8) [
25,
26]:
where
is the nonuniformity of the asynchronous electric motor torque, having the value in the field 0.01–0.07 [
25],
is the amplitude of the engine torque in Nm, and
is the output velocity angle of the asynchronous electric motor in rot/min. As mentioned in [
25], due to the manifested nonuniformity instantaneous electromagnetic torque components in the range of −0.1–0.1 (manifestation that exists even for synchronous motor [
26]), the active and reactive electric power has a nonuniformity in the range ±0.07 [
25,
26]. Therefore, the output torque has the same nonuniformity. Usually, these nonuniformities have a harmonic variation given by the equation [
25]:
A reactive torque charges the output element DOE3 of DTID due to the milling system (see
Figure 7 and
Figure 8), having a similar harmonic variation due to the variable granulation of the substance to mill as the input torque
, given by the equation:
where
is the amplitude of reactive torque of the milling system and
is a moderate nonuniformity due to the granulation of the material milled in the system, having a value in the range 0–0.17 [
27] (pp. 319–348). Analyzing the Equations (1)–(9) and the
Figure 3,
Figure 4,
Figure 6,
Figure 7 and
Figure 8, it can be remarked that the PCM for FTV of the automotive driveshaft, presented in [
9], was modified to overcome the reality, so for DTID, the new MPCM has two tripod joints instead of one, with different geometric characteristics and different inertia manifestation. Additionally, the new MPCM for FTV has multiple harmonic excitations terms, which is a generalization of double excitations terms as in [
28,
29] (p. 14), this being another novel aspect that this work has improved. This aspect of multiple excitation terms is a consequence of using an asynchronous electric motor as a power supplier (the best economic choice) and the various granulations of the milling substance.
4. Detection of Chaotic Manifestation for Nonstationary FTV of Double Tripod Industrial Driveshaft in Principal Parametric Resonance Region
To detect chaotic manifestation for NFTV of DTID in PPRR, the Equations (20) and (21) are used to compute the phase portrait graphs
for DIE1 and DOE3 in PPRR. The DTID’s elements DIE1 and DOE3 considered to have the characteristics of the DTID’s material, the geometry characteristics such as the AGMIs, and their nonuniformity, are presented in
Table 1 and
Table 2. These given geometric features are in agreement with those considered by Steinwede [
18] (p. 111).
Based on AUTOCAD,
were calculated using the generic dimensions of the DTID’s DIE1 and DOE3. MATLAB software determined the variation graph of the functions
, representing the NPs of DIE1 and DOE3 as presented in
Figure 9 and
Figure 10.
The values obtained for NPs of DIE1 and DOE3, shown in the graphs presented in
Figure 9 and
Figure 10, agree with the values mentioned in [
18] (pp. 119–139). Therefore, the MPCM of NFTV for DTID, which is a novelty of the present work, represents a model that agrees with the data in the literature [
18].
Table 3 presents the free natural frequencies for the torsional vibrations of DME2 based on the Equation (17), yielding:
The last terms in Equations (20) and (21) are neglected because the excitation frequency in PPRR for DIE1 (see
Figure 9) and for DOE3 (see
Figure 10) is not in the range of free natural frequencies for torsional vibrations of DME2 (see
Table 3) yielding the equations:
The characteristics of external excitations of DTID are presented in
Table 4.
The expressions must define the excitation frequencies
of DTID’s DIE1 and DOE3 in the PPRR:
To calculate the time–history graphs for DIE1 and for DOE3, the Equations (25) and (26) were numerically integrated using MATLAB software based on function ode 45 (Runge–Kutta integration method of fifth-order). The graphs represent the phase portraits of NFTV for DIE1 and DOE3, being the detection method of possible chaotic dynamic behavior. To certify the chaotic dynamic behavior of NFTV, the new robust method LEA–PM, described in the next paragraph, is used.
6. Results and Discussions
Figure 11,
Figure 12 and
Figure 13 illustrate the graphs of time–history to analyze the dynamic instability of NFTV for DTID’s DIE1 in transition through PPRR
(see Equation (27),
Figure 9, and
Table 1), considering the worst misalignment for DIE1
,
(see Equation (22),
Table 1),
, and the damping ratio
. MATLAB software was developed based on Equation (25) for NFTV of DIE1 to calculate the time–history
.
In
Figure 11a–c,
Figure 12a–c and
Figure 13a–c, it is remarked that the nonstationary
,
for NFTV of DIE1 manifests the “beatings” effects and a rapid decrease of the extreme values with the damping’s increases in the range
.
Figure 11d,
Figure 12d and
Figure 13d illustrate that the phase portraits represent the chaotic manifestation of a
strange attractor for
and
, multiple limit cycles and “turning points”, respectively, while for
only a limit cycle is manifested meaning that the nonstationary dynamic behavior for DIE1 has an ergodic manifestation starting from the value of the damping ratio.
The results obtained in
Figure 11d,
Figure 12d and
Figure 13d show the similarity of the phase portrait pictures when compared with data in the literature [
33]. It is noted that “pictures” in
Figure 11d and
Figure 12d are like those specific to a
strange attractor. In this way, the aim of using time–history analysis (THA) for NFTV of DIE1 was reached, THA being thus a detection method for chaos manifestation of NFTV for the elements of DTID. For the cases when the damping ratio is in the vicinity range
, the deterministic chaos of NFTV for DIE1 needs to be certified using the new robust method LEA–PM.
Figure 14,
Figure 15 and
Figure 16 illustrate the graphs of time–history to analyze the dynamic instability of NFTV for DTID’s DOE3 in transition through PPRR
(see Equation (28),
Figure 10, and
Table 2), considering the worst misalignment for DOE3
(see Equation (23) and
Table 2),
and the damping ratio
. MATLAB software was developed based on Equation (26) for NFTV of DOE3 to calculate the time–history
.
In
Figure 14a–c,
Figure 15a–c and
Figure 16a–c, it is remarked that the nonstationary
,
for NFTV of DOE3 manifests the same “beatings” effects and a rapid decrease of the extreme values with the damping’s increases in the range
as for DIE1 (see
Figure 11a–c,
Figure 12a–c and
Figure 13a–c). The graphs illustrated in
Figure 14d,
Figure 15d and
Figure 16d show that the phase portraits represent the chaotic manifestation of a
strange attractor for
and
, multiple limit cycles and “turning points”, respectively, while for
only a limit cycle is manifested meaning that the nonstationary dynamic behavior for DOE3 has an ergodic manifestation starting from this value of the damping ratio.
The similarity of the phase portrait pictures is shown when comparing the results obtained in
Figure 14d,
Figure 15d and
Figure 16d with data in the literature [
33]. It is noted that “pictures” in
Figure 14d and
Figure 15d are like those specific to a
strange attractor. In this way, the aim of using THA for NFTV of DOE3 was reached, THA being thus a detection method for chaos manifestation of NFTV for the elements of DTID. For the cases when the damping ratio is in the vicinity range
the deterministic chaos of NFTV for DIE1 needs to be certified using the new robust method LEA–PM.
As can be seen from
Figure 11,
Figure 12,
Figure 13,
Figure 14,
Figure 15 and
Figure 16, the THA (phases portraits, all the d. figures) was used as
a detection method for possible chaotic dynamic manifestations of the DTID’s elements (DIE1 and DOE3). Amer et al. [
34], had used time–history analysis to study the steady-state nonlinear motion of a damped spring pendulum with an attached linear damped transverse absorber near resonance (primary external and internal resonance) and to investigate the stability of fixed points. Based on this kind of investigation, the above-mentioned dynamic system found that the motion is free of chaos motion [
34] (p. 32). Liu et al. [
35] use the THA to investigate the stability of nonlinear behavior of a spur gear pair transmission system with backlash, finding the trends in the unstable conditions of these systems. Azimi [
36], after employing the Pitchfork and Hops Bifurcations to investigate the geared systems in permanent contact, used THA coupled with the Poincaré Map Method to detect the creation of limit cycles (new equilibria) in the case of nonlinear softening behavior of geared systems transmission. Zhang et al. [
37] investigated the mechanism and the characteristics of the varying global compliance (VC) parametric resonances in ball bearings using time–history analysis, phases orbits analysis, Poincaré Map Method, and frequency spectra. Thus, the chaotic motions were detected and certified. Rysak and Gregorczyk [
38], calibrated the order of integration of the differential transform method (DTM) using THA for the fractional chaotic Rössler system.
The new method presented in paragraph 5 uses LEA–PM to certify the deterministic chaos. Based on Equations (31)–(33), developing specific MATLAB software, the Lyapunov exponents for the DSOE (29) of NFTV were computed for DIE1 in transition through PPRR. The results are illustrated in
Figure 17,
Figure 18,
Figure 19 and
Figure 20 for the characteristic values of DIE1, such as excitation frequency in the vicinity of
Hz (see Equation (27),
Figure 9, and
Table 1),
,
(see Equation (22),
Table 1),
, and the damping ratio in the range
.
As can be seen from the
Figure 17,
Figure 18,
Figure 19 and
Figure 20 in (a) is presented the graph variation of the Lyapunov exponent
(see Equation (31), to verify the criteria (37)), in (b) is illustrated the graph variation of the Lyapunov exponent
( see Equation (32), to verify the criteria (37)), in (c) is shown the graph variation of the Lyapunov exponent
( see Equation (33), to verify the criteria (37)), and in (d) is presented the graph variation of
the sum of Lyapunov exponents (in order to apply the criteria (39)), for the nonstationary FTV of DIE1 in transition through the PPRR, namely for excitation frequency in the range [2950,3200] Hz.
Through the analysis of the graphs illustrated in
Figure 17, it can be concluded that the conditions imposed by Equations (37)–(39), as mentioned in [
23,
31], are fulfilled and, therefore, in the excitation frequency’s range of 2950–3200 Hz, the range of PPRR for FTV of DIE1, for
the deterministic chaos (strange attractor) is manifested. For certification of this manifestation, the last part of the new robust method LEA–PM, the qualitative PMM, will be used.
Through the analysis of the graphs illustrated in
Figure 18, it can be concluded that the conditions imposed by Equations (37)–(39), as mentioned in [
23,
31], are fulfilled and, therefore, in the excitation frequency’s range of 2950–3200 Hz, the range of PPRR for FTV of DIE1, for
the deterministic chaos (strange attractor) is manifested. For certification of this manifestation, the last part of the new robust method LEA–PM, the qualitative PMM, will be used.
Through the analysis of the graphs illustrated in
Figure 19, it can be concluded that the conditions imposed by Equations (37)–(39), as mentioned in [
23,
31], are fulfilled and, therefore, in the excitation frequency’s range of 2950–3200 Hz, the range of PPRR for FTV of DIE1, for
the deterministic chaos (strange attractor) is manifested. For certification of this manifestation, the last part of the new robust method LEA–PM, the qualitative PMM, will be used.
Through the analysis of the graphs illustrated in
Figure 20, it can be concluded that the conditions imposed by Equations (37)–(39), as mentioned in [
23,
31], are not fulfilled and, therefore, in the excitation frequency’s range of 2950–3105 Hz, the range of PPRR for FTV of DIE1, for
the deterministic chaos (strange attractor) is not possible. Using LEA–PM, it is certified by the conditions imposed (37)–(39) that for damping ratio in the range
the NFTV of DIE1 in transition through PPRR is an ergodic dynamic behavior representing a transition to chaos, as mentioned in [
23].
Based on Equations (34)–(36), developing specific MATLAB software, the Lyapunov exponents for the DSOE (30) of NFTV were computed for DOE3 in transition through PPRR. The results are illustrated in
Figure 21,
Figure 22,
Figure 23 and
Figure 24 for the characteristic values of DOE3, such as excitation frequency in the vicinity of
(see Equation (28),
Figure 10, and
Table 2),
,
(see Equation (23) and
Table 2),
, and the damping ratio in the range
.
As can be seen from the
Figure 21,
Figure 22,
Figure 23 and
Figure 24 in (a) is presented the graph variation of the Lyapunov exponent
(see Equation (34), to verify the criteria (37)), in (b) is illustrated the graph variation of the Lyapunov exponent
( see Equation (35), to verify the criteria (37)), in (c) is shown the graph variation of the Lyapunov exponent
( see Equation (36), to verify the criteria (37)), and in (d) is presented the graph variation of
the sum of Lyapunov exponents (in order to apply the criteria (39)), for the nonstationary FTV of DOE3 in transition through the PPRR, namely for excitation frequency in the range [2650,2950] Hz.
Through the analysis of the graphs illustrated in
Figure 21, it can be concluded that the conditions imposed by Equations (37)–(39), as mentioned in [
23,
31], are fulfilled and, therefore, in the excitation frequency’s range of 2650–2950 Hz, the range of PPRR for FTV of DOE3, for
the deterministic chaos (strange attractor) is manifested. For certification of this manifestation, the last part of the new robust method LEA–PM, the qualitative PMM, will be used.
Through the analysis of the graphs illustrated in
Figure 22, it can be concluded that the conditions imposed by Equations (37)–(39), as mentioned in [
23,
31], are fulfilled and, therefore, in the excitation frequency’s range of 2650–2950 Hz, the range of PPRR for FTV of DOE3, for
the deterministic chaos (strange attractor) is manifested. For certification of this manifestation, the last part of the new robust method LEA–PM respectively, the qualitative PMM, will be used.
Through the analysis of the graphs illustrated in
Figure 23, it can be concluded that the conditions imposed by Equations (37)–(39), as mentioned in [
23,
31], are fulfilled and, therefore, in the excitation frequency’s range of 2700–2925 Hz, the range of PPRR for FTV of DOE3, for
the deterministic chaos (strange attractor) is manifested. For certification of this manifestation, the last part of the new robust method LEA–PM respectively, the qualitative PMM, will be used.
Through the analysis of the graphs illustrated in
Figure 24, it can be concluded that the conditions imposed by Equations (37)–(39), as mentioned in [
23,
31], are not fulfilled and, therefore, in the excitation frequency’s range of 2670–2925 Hz, the range of PPRR for FTV of DOE3, for
the deterministic chaos (strange attractor) is not possible. Using LEA–PM, it is certified by the conditions imposed (37)–(39) that for damping ratio in the range
the NFTV of DOE3 in transition through PPRR is an ergodic dynamic behavior representing a transition to chaos, as mentioned in [
23]. Asokanthan and Meehan [
39], investigated the nonlinear vibration of a basic torsional system driven by a Hooke’s joint using time–history analysis (THA) and the bifurcation analysis, and the quasi-periodic and chaotic motion were revealed. Asokanthan and Wang [
40] studied the torsional instabilities in a Hooke’s joint-driven system via maximal Lyapunov’s exponents (the well-known MLEM). They found a direct link between the maximal Lyapunov exponents and the instability regions for subharmonic and combination resonances.
To certify using a qualitative method that the DIE1 and DOE3 have NFTV in the PPRR of chaotic type, MATLAB software was developed based on DSOE (29) for DIE1 and on DSOE (30) for DOE3, to represent the Poincaré Maps that represents the intersection of the orbits in the phase portraits with an orthogonal surface at equal periods (N number of points), using the mathematical procedure presented in [
32] (p. 194). The Poincaré map represents saddle points or saddle separatrices images if the vibration motion is periodic or quasi-periodic.
Figure 25 is presented the PM for DIE1 when
,
(see Equation (27),
Figure 9, and
Table 1),
using 50,000, 15,000, 10,000, and 1000 sections of orthogonal surface to the orbits in the phase portrait
From the phase portraits illustrated in
Figure 25, the properties of PM can be noted in the case of strange attractor:
diffuse structure of points having a different density of pixels per unit area of the surface and
auto-similarity of the image.
Figure 26 and
Figure 27 present the PM for DIE1 when
and
using 15,000 to 1000 sections of orthogonal surface to the orbits in the phase portrait
Images illustrated in
Figure 26 have the aspects of a strange attractor.
The aspect of the image in
Figure 26 has a chaotic manifestation specific to deterministic chaos (strange attractor), and the aspect of the images of both
Figure 26 and
Figure 27 are like those presented in
Figure 25.
Comparing the images presented in
Figure 26 with those illustrated in
Figure 27, it can be concluded that the strange attractor started to vanish because we were close to the condition
when it is manifested in the ergodic dynamic process of DIE1 (see
Figure 24). The pictures illustrated in
Figure 25,
Figure 26 and
Figure 27 represent the final confirmation for the occurrence of deterministic chaos (strange attractor) (see
Figure 17,
Figure 18 and
Figure 19) for the NFTV of DIE1 in PPRR for
and damping ratio in the range
.
Figure 28,
Figure 29 and
Figure 30 present the PM for DOE3 when
(see Equation (28),
Figure 10, and
Table 2)
using 50,000 to 5000 sections of orthogonal surface to the orbits in the phase portrait
The pictures illustrated in
Figure 28,
Figure 29 and
Figure 30 demonstrate the properties of PM in the case of the strange attractor:
diffuse structure of points having a different density of pixels per unit area of the surface and
auto-similarity of the image. For N = 50,000, it is obvious the similarity between the strange attractor of the chaotic dynamic behavior of DIE1 and DOE3, but for
, differences can be noted. In the same way as DIE1 for
, DOE3 has a semblance of chaotic dynamic behavior for
. A comparison of the images presented in
Figure 28 with those illustrated in
Figure 30 demonstrate that the strange attractor started to vanish because we are close to the condition
when it was manifested in the ergodic dynamic process of DOE3 (see
Figure 24). This is the value of the damping ratio starting from which the dynamic behavior of DOE3 becomes an ergodic process. The pictures illustrated in
Figure 28,
Figure 29 and
Figure 30 represent the final confirmation for the occurrence of deterministic chaos (strange attractor) (see
Figure 21,
Figure 22 and
Figure 23) for the NFTV of DOE3 in PPRR for
and damping ratio in the range
. This may explain the experimental data mentioned by Steinwede in [
18] (pp. 88–94), where pitting and microcracks occurred on the interior side of the bels for the DIE1 and DOE3, respectively, as well as manifestations of cracks on the trunnion tripod axes. Steinwede explains these phenomena by the approach of the dynamic behavior in forced torsional vibrations of automotive driveshafts to the dynamic behavior of feared systems. These phenomena appear because of chaotic dynamic behavior, as mentioned in [
19,
23]. In [
19] (p. 104), pitting is due to chaotic dynamic behavior, while the cracks and microcracks result from ergodic dynamic processes for the geared systems. A similar mechanism of inducing such phenomena is manifested for the NFTV of DTID. For a similar dynamic system, the double u-joint driveshaft, Yao and DeSmidt investigated [
41] the nonlinear coupled torsional and lateral vibration and the Sommerfeld behavior using the THA. The Sommerfeld effect is a nonlinear phenomenon observed in some rotor systems being driven through a resonance regime when there is not enough power to accelerate the rotor through resonance. Yao and DeSmidt found that this phenomenon is a function of driveline misalignment. Awrejcewicz and Ludwicki [
42] investigated the dynamics of a similar system that is the spatial (3D) physical pendulums with nonautonomous systems universal joints. To analyze the dynamic behavior of such a system, Awrejcewicz and Ludwick used THA and the Poincaré Map Method.
The novelty of the methods detailed in the present work is detecting chaotic dynamic behavior for NFTV of DTID using THA coupled with the robust method LEA–PM that certifies the deterministic chaos. These new methods must be a part of the design systems of DTID to prevent excessive pitting, microcracks, or even failure as a result of cracks for DTID. The dynamic instability investigation demonstrates that the increase of the damping ratio has a benefic effect. Still, this aspect induces thermo-stress concentrators. Therefore, the growth of the damping ratio of the material for DTID involves the unique design of cooling mechanisms for DTID, engaging chemical composition for the greases used. The new robust THA–LEA–PM method allows the investigation of chaotic manifestation for NFTV of the DTID and has two significant steps, one for detecting chaos manifestation and the second for certifying the deterministic chaos (strange attractor occurrence). For the first step, the THA (based on Equations (25) and (26)) is used while for the second step LEA–PM (based on the four criteria that embed the conditions (37)–(39) and PM) is used. Another novelty of the method is the modification of MLEM (see [
23,
31]), transforming it into LEA (based on conditions (37)–(39)) and coupling it with PM. This new robust method to investigate the chaos manifestation for NFTV of DTID in PPRR can be named THA–LEA–PM.
7. Conclusions
This study deals with the dynamic instability analysis for the DTID in transition through PPRR. To achieve the goals, an existent model for FTV of AD was modified by designing an MPCM for FTV of a DTID that included the nonuniformity of AGMI, the nonuniformity of AMMI (
new aspects of the nonuniformities of AGMI and AMMI for DTID’s elements that were considered till now linked through CVJ, see Appendix A Equations (A1)–(A12)), the quasi-homokinetic TJs of the DTID
(new aspects, see Equations (1) and (5)), the external harmonic excitations induced by the asynchronous electric motor (
new aspects considering higher-order components of the nonuniformity of the torque load, see Equations (6) and (7)) and the nonuniformity of the reactive torque of the milling system(
new aspects considering higher-order components of the nonuniformity of the reactive torque, see Equations (8) and (9)). For the investigation of nonstationary dynamic instability of FTV for DTID’s elements in the PPRR, the THA was designed for the detection of chaotic dynamic behavior based on the Equations (25) and (26), generating the phase portraits that represent the detection of possible chaos manifestation through PPRR of the DTID’s elements. Based on THA, the chaos manifestation for DIE1 was detected through the phase portraits when
, the damping ratio was in the vicinity range
in the PPRR the excitation frequency being in the vicinity of the value
(see
Figure 11d and
Figure 12d), while for
, and the damping ratio
the phase portrait indicated a limit cycle (see
Figure 13d). Using THA, the chaos manifestation for DOE3 was detected through the phase portraits when
, the damping ratio was in the vicinity range
in the PPRR the excitation frequency being in the vicinity of the value
(see
Figure 14d and
Figure 15d), while for
, and the damping ratio
the phase portrait indicated a limit cycle (see
Figure 16d).
A crucial contribution was the computation of the ranges of the principal parametric resonances that vary with the misalignment angles and with the nonuniformities of DTID’s AMMIs (see Equations (22) and (23)).
Another significant contribution of this study is the development of a new robust method to certify and confirm the deterministic chaos, namely LEA–PM (see the DSOE (29) and (30)). The Lyapunov exponents were computed using Equations (31)–(33) for DIE1 (see
Figure 17,
Figure 18,
Figure 19 and
Figure 20) and Equations (34)–(36) for DOE3 (see
Figure 21,
Figure 22,
Figure 23 and
Figure 24) and were verified by the conditions (37)–(39) of LEA. Using LEA for DIE1 when
, the damping ratio is in the vicinity range
, and the frequency’s excitation is in the range
the nonstationary FTV is chaotic (see
Figure 17,
Figure 18 and
Figure 19). Using, for DOE3, LEA when
, the damping ratio is in the vicinity range
and the frequency’s excitation is in the range
the nonstationary FTV is chaotic (see
Figure 21 and
Figure 22). The same manifestation is obtained for DOE3 when
, the damping ratio is in the vicinity range
but the frequency’s excitation is in the range
, and therefore, the nonstationary FTV is chaotic (see
Figure 23).The images determined using the Poincaré Map method for NFTV of DIE1 (see
Figure 25,
Figure 26 and
Figure 27) and DOE3 (see
Figure 28,
Figure 29 and
Figure 30) reconfirmed the chaos manifestation of the DTID’s elements. From the literature survey [
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42], it was noted that all the research data are based on one method (THA, MLEM, PMM) or two methods (THA–MLEM, THA–PMM) for analyzing the chaotic dynamic behavior of the systems. For the first time, three methods are used to study the chaotic behavior of the DTID through the PPRR: THA for detection of the chaos, LEA (a modified MLEM) to certify the existence of deterministic chaos (
strange attractors), and PM to reconfirm deterministic chaos.
The innovations and contributions of the present work can be summarized as follows:
- 1.
The design of a modified physically consistent model (MPCM) of the FTV for a double tripod industrial driveshaft (DTID) considering the following phenomena:
- –
the nonuniformity of axial mass moments of inertia (AMMI) and axial geometric moments of inertia (AGMI) of the DTID’s elements: driving input element 1 (DIE1) and driven output element 3 (DOE3),
- –
the geometric inertia nonuniformity of the tripod joints (TJ1 and TJ2) of the DTID,
- –
the geometric and kinematic nonuniformity of the quasi-constant velocity joints (quasi-CVJ),
- –
the nonuniformity of the torque load’s higher order received by DTID from the asynchronous electric motor,
- –
the nonuniformity of the reactive torque’s higher order of the milling system;
- 2.
The computation of the free natural frequencies of the DTID’s elements as functions of the misalignment angles of the DTID’s elements , the AMMI and the AGMI of the DTID’s elements;
- 3.
The use of time–history analysis (THA-phase portraits) to detect the chaotic manifestation of nonstationary FTV for DTID’s elements in transition through principal parametric resonance region (PPRR);
- 4.
The design of a quantitative method to certify the occurrence of deterministic chaos (strange attractors) LEA (Lyapunov exponents approach), that is a modified MLEM (maximal Lyapunov exponent method) coupled with a new criterion, the sum of all Lyapunov’s exponents is negative, for the nonstationary FTV for DTID’s elements in transition through principal parametric resonance region (PPRR);
- 5.
The use of Poincaré Maps (PM) to reconfirm the occurrence of deterministic chaos (strange attractors) for the nonstationary FTV for DTID’s elements in transition through principal parametric resonance region (PPRR);
- 6.
The determination of the range for damping ratio, using THA–LEA–PM, where the deterministic chaos occurs (strange attractor) for the nonstationary FTV for DTID’s DIE1 in transition through principal parametric resonance region (PPRR) and worst misalignment , respectively ;
- 7.
The determination of the range for damping ratio, using THA–LEA–PM, where the deterministic chaos occurs for the nonstationary FTV for DTID’s DOE3 in transition through principal parametric resonance region (PPRR) and worst misalignment , ;
- 8.
For the first time, through the chaotic dynamic behavior for the nonstationary FTV for DTID’s elements in transition through the principal parametric resonance region (PPRR), it was revealed theoretically the manifestation of pitting, microcracks, and cracks and the similarity between the phenomena of homokinetic transmission with the phenomena of geared systems transmission.
In conclusion, the robust method THA–LEA–PM, along with the advantages highlighted earlier, also has the considerable advantage of being “mathematical affordable” for designers. This advantage results from the fact that the investigation is possible in the simplest Riemannian space (the space the Euclidian metric), while the newest method of investigating the chaos KCC method, as mentioned in [
24], allows this investigation in Finsler spaces (involving the problem of curvature properties of homogeneous Finsler spaces with
-metrics which is one of the central problems in Riemann–Finsler geometry) as well as the management of Jacobi stability analysis for Berwald curvature. In the DTID’s design stage, this new robust method THA–LEA–PM prevents the excessive pitting, microcracks, or even failure by cracks for DTID’s elements DIE1, DOE3, and trunnion tripods axes of the DTID’s joints. Future research will enhance the investigation of chaotic dynamic instability of DTID’s NFTV in transition through superharmonic resonances, subharmonic resonances, combination resonances, and internal resonances.