Vibration Prediction of Space Large-Scale Membranes Using Energy Flow Analysis
Abstract
:1. Introduction
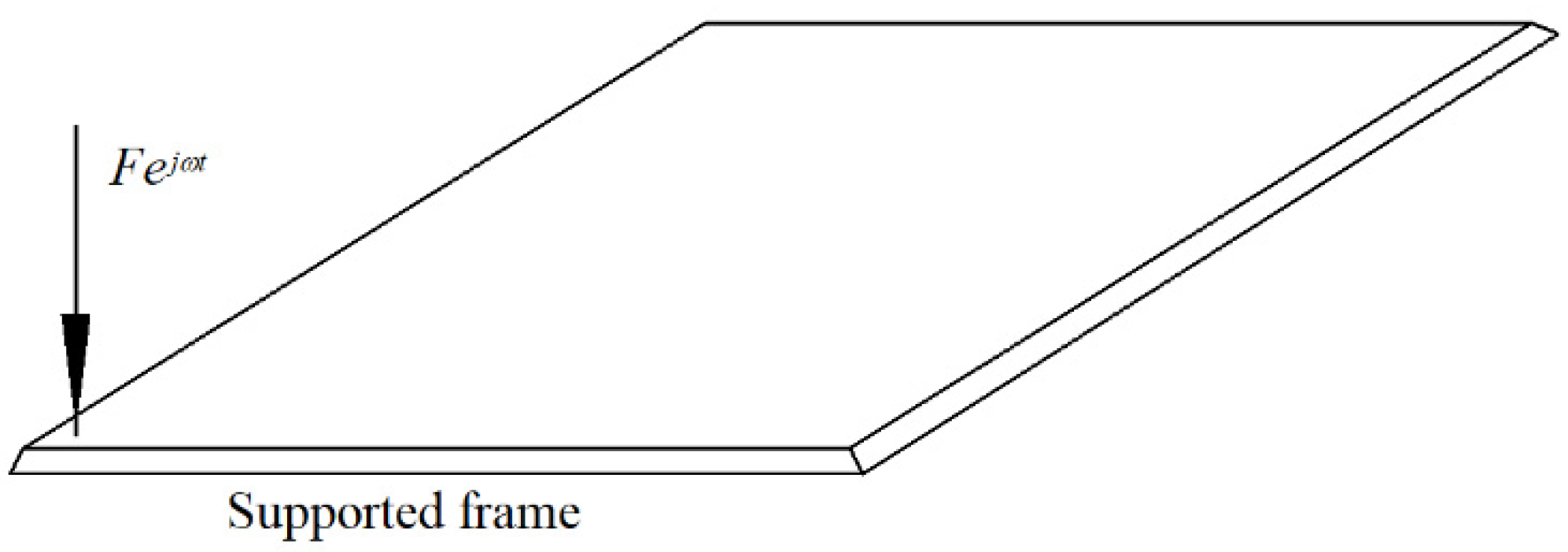
2. Materials and Methods
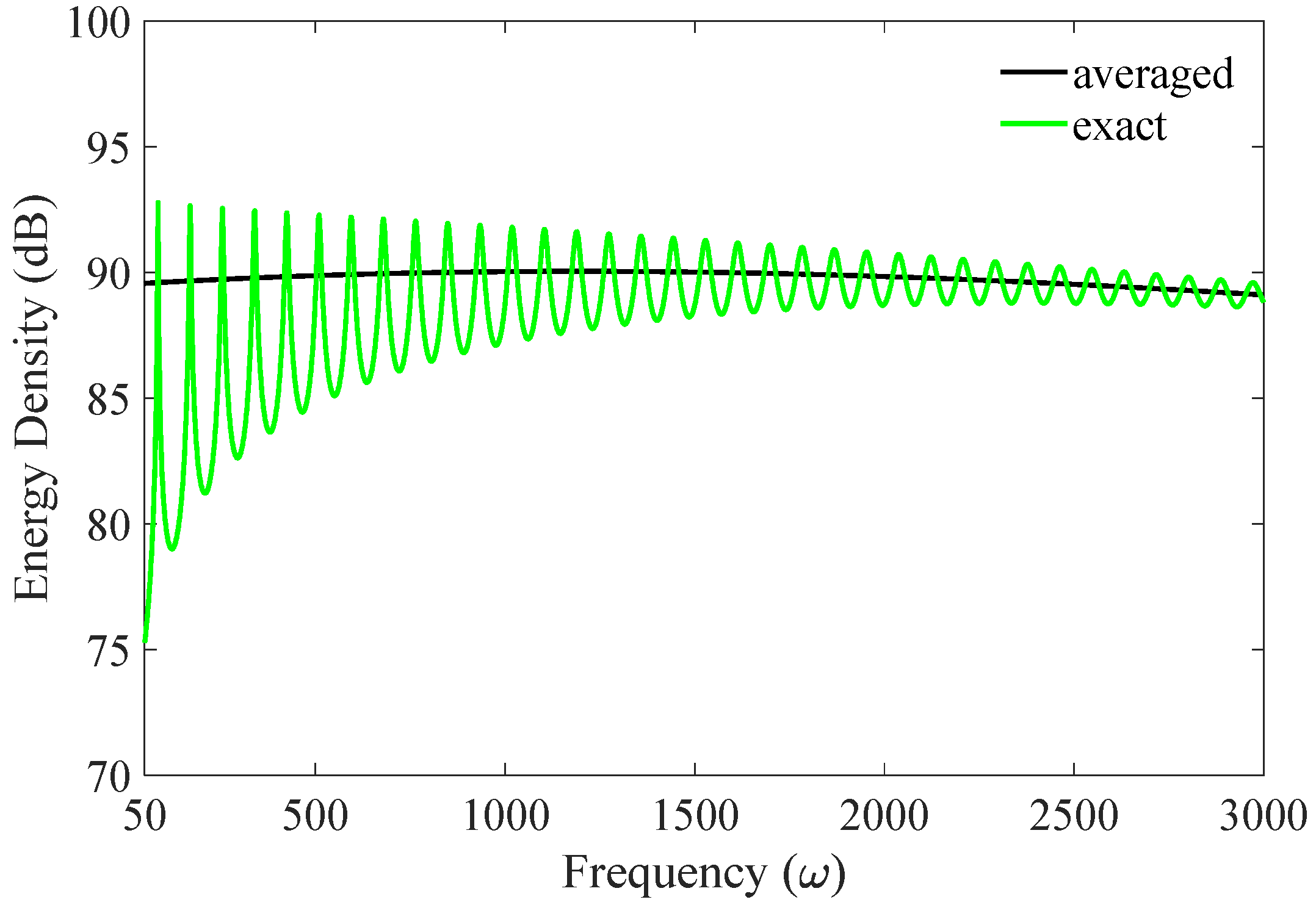
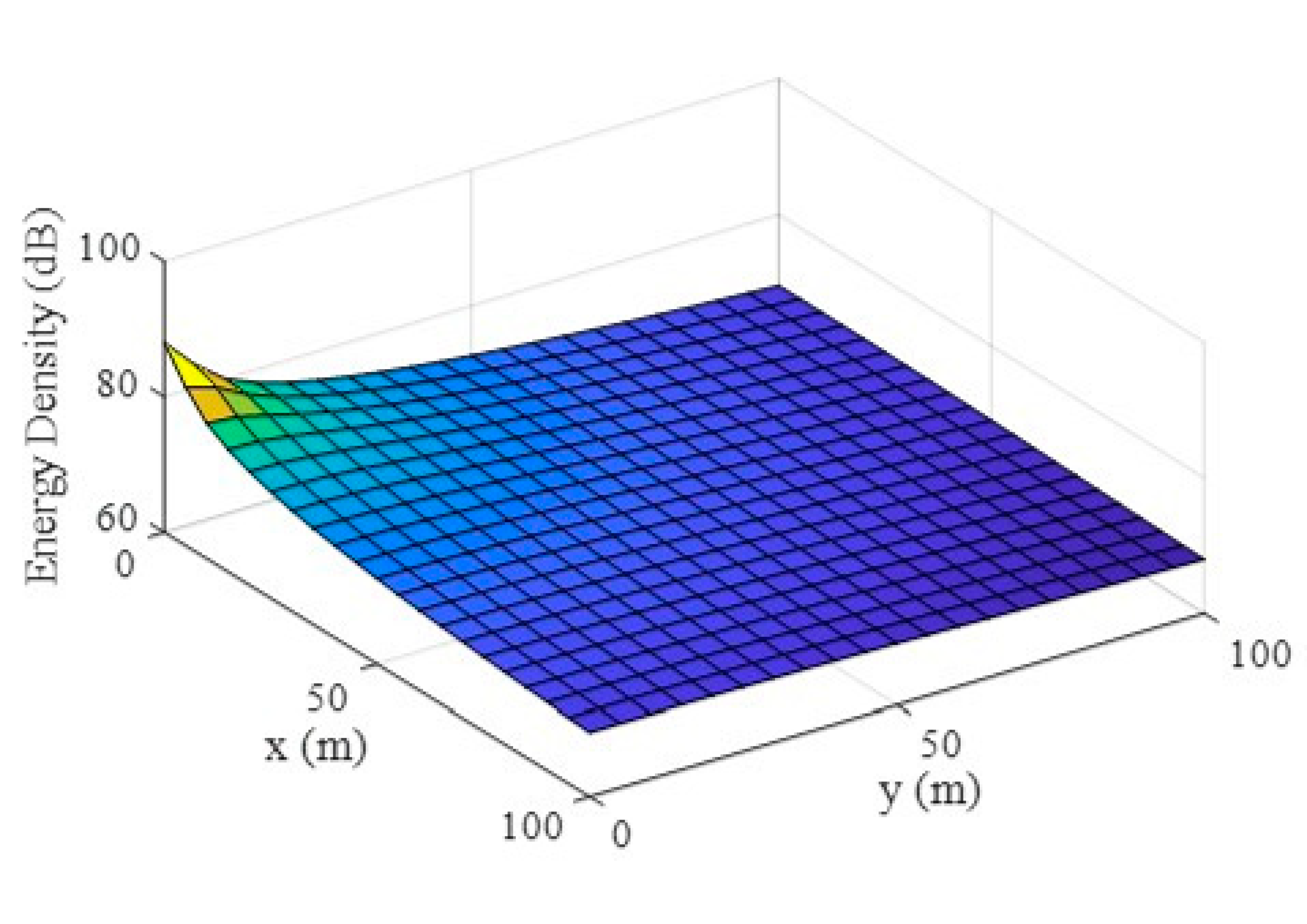
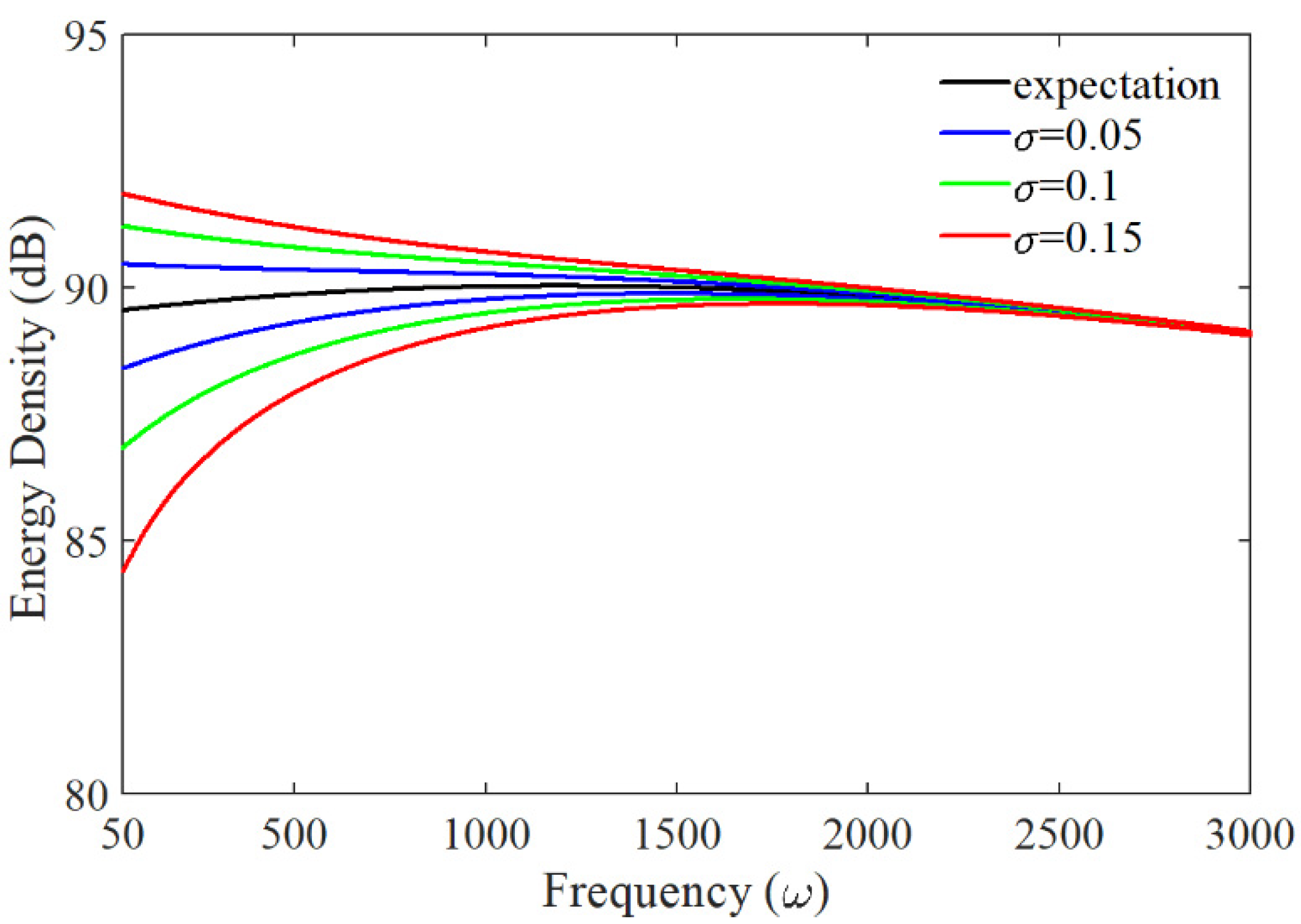
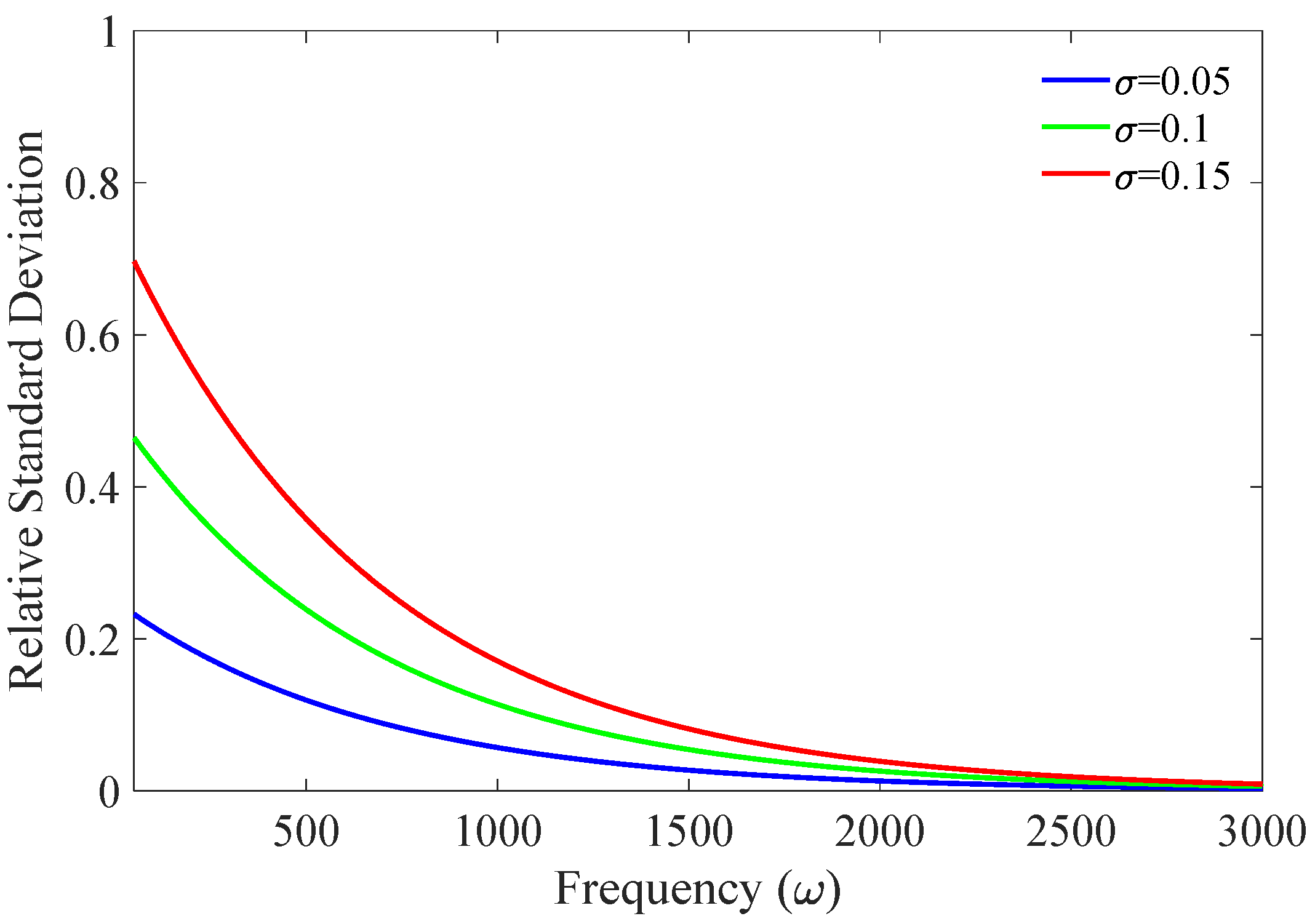
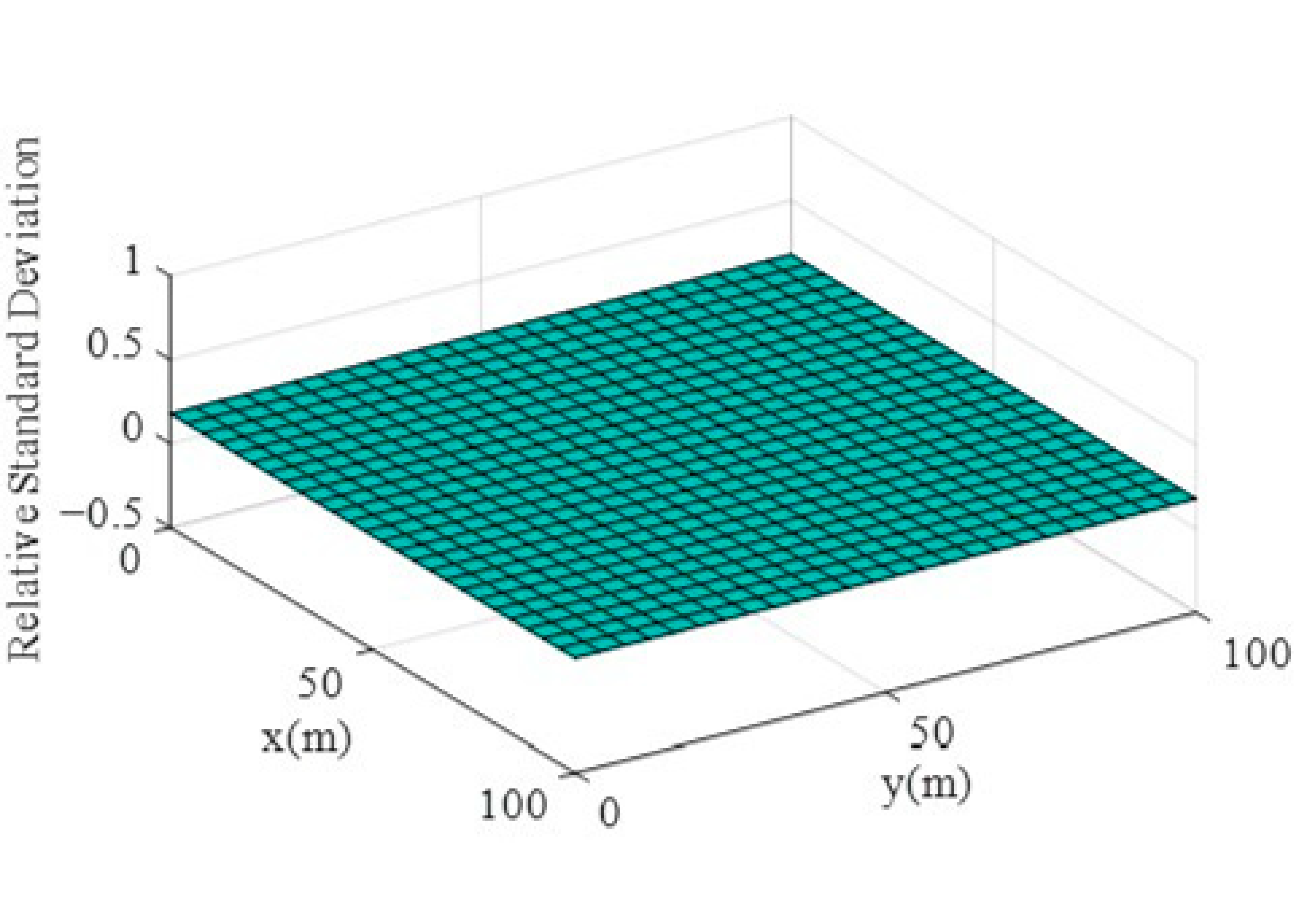
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lane, S.A.; Murphey, T.W.; Zatman, M. Overview of the innovative space-based radar antenna technology program. J. Spacecr. Rocket. 2012, 48, 135–145. [Google Scholar] [CrossRef]
- Cheng, Z.A.; Hou, X.B.; Zhang, X.H.; Zhou, L.; Guo, J.; Song, C. In-orbit assembly mission for the space solar power station. Acta Astronaut. 2016, 129, 299–308. [Google Scholar] [CrossRef]
- Liu, J.F.; Cui, N.G.; Shen, F.; Rong, S.Y. Nonlinear static analysis-based thrust for solar sail. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2015, 229, 149–162. [Google Scholar] [CrossRef]
- Liu, J.F.; Chen, L.Q.; Cui, N.G. Solar sail chaotic pitch dynamics and its control in Earth orbits. Nonlinear Dyn. 2017, 90, 1755–1770. [Google Scholar] [CrossRef]
- Firuzi, S.; Gong, S.P. Refractive sail and its applications in solar sailing. Aerosp. Sci. Technol. 2018, 77, 362–372. [Google Scholar] [CrossRef]
- Song, Y.; Gong, S.P. Solar-sail trajectory design for multiple near-Eath asteroid exploration based on deep neural networks. Aerosp. Sci. Technol. 2019, 91, 28–40. [Google Scholar] [CrossRef] [Green Version]
- Gong, S.P.; Macdonald, M. Review on solar sail technology. Astrodynamics 2019, 3, 93–125. [Google Scholar] [CrossRef]
- Matsushita, M.; Okuizumi, N.; Satou, Y.; Mori, O.; Iwasa, T.; Matunaga, S. Influence of thin-film device with curvature on natural frequency of rectangle membrane under uniaxial tension. Astrodynamics 2019, 3, 257–272. [Google Scholar] [CrossRef]
- Takao, Y.; Mori, O.; Kawaguchi, J. Self-excited oscillation of spinning solar sails utilizing solar radiation pressure. Astrodynamics 2020, 4, 177–192. [Google Scholar] [CrossRef]
- Zhao, C.; Huo, M.; Qi, J.; Cao, S.; Zhu, D.; Sun, L.; Sun, H.; Qi, N. Coupled attitude-vibration analysis of an E-sail using absolute nodal coordinate formulation. Astrodynamics 2020, 4, 249–263. [Google Scholar] [CrossRef]
- Kukathasan, S.; Pellegrino, S. Vibration of prestressed membrane structures in air. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 22–25 April 2002. [Google Scholar]
- Alexander, T.; David, S.W.; John, T.W. Nonlinear shell modeling of thin membranes with emphasis on structural wrinkling. In Proceedings of the 44rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar]
- Shen, Y.; Zheng, W.P.; Wang, X.Y. Dynamic and vibration analysis of a SAR membrane antenna. In Proceedings of the ASME 2007 International Mechanical Engineering Congress and Exposition, Seattle, WA, USA, 11–15 November 2007. [Google Scholar]
- Houmat, A. Free vibration analysis of arbitrarily shaped membranes using the trigonometric p-version of the finite-element method. Thin-Wall Struct. 2006, 44, 943–951. [Google Scholar] [CrossRef]
- Lyon, R.H. Random vibration of connected structure. J. Acoust. Soc. Am. 1964, 36, 1344–1354. [Google Scholar] [CrossRef]
- Lyon, R.H. Statistical Energy analysis of dynamical systems. In Theory and Applications; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Chen, S.M.; Wang, D.F. Interior noise prediction of the automobile based on hybrid FE-SEA method. Math. Probl. Eng. 2011, 2011, 34–35. [Google Scholar] [CrossRef]
- Liu, Q.; Thompson, D.J.; Xu, P.; Feng, Q.; Li, X. Investigation of train-induced vibration and noise from a steel-concrete composite railway bridge using a hybrid finite element-statistical energy analysis method. J. Sound Vib. 2020, 471, 115197. [Google Scholar] [CrossRef]
- Kim, T.M.; Kim, J.T.; Kim, J.S. SEA-FEM hybrid analysis for predicting inter-floor impact noise. Appl. Acoust. 2018, 29, 397–407. [Google Scholar] [CrossRef]
- Fazzolari, F.A.; Tan, P. A hybrid finite element-statistical energy analysis approach for the dynamic response of built-up systems with nonlinear joints. J. Sound Vib. 2020, 489, 115696. [Google Scholar] [CrossRef]
- Nefske, D.J.; Sung, S.H. Power flow finite element analysis of dynamics systems: Basic theory and application to beams. J. Vib. Acoust. 1989, 111, 94–100. [Google Scholar] [CrossRef]
- Wohlever, J.C.; Bernhard, R.J. Energy distributions in rods and beams. In Proceedings of the AIAA 12th Aeroacoustics Conference, San Antonio, TX, USA, 10–12 April 1989. [Google Scholar]
- Bouthier, O.M.; Bernhard, R.J. Simple models of the energetics of transversely vibrating plates. J. Sound Vib. 1995, 182, 149–164. [Google Scholar] [CrossRef]
- Bouthier, O.M. Energetics of Vibrating System. Doctoral Thesis, Purdue University, West Lafayette, IN, USA, 1992. [Google Scholar]
- Cho, P.E. Energy Flow Analysis of Coupled Structures. Doctoral Thesis, Purdue University, West Lafayette, IN, USA, 1993. [Google Scholar]
- Bouthier, O.M.; Bernhard, R.J. Simple models of energy flow in vibrating membranes. J. Sound Vib. 1995, 182, 129–147. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, A.; Vlahopoulos, N.; Wu, K. High-frequency vibration analysis of thin elastic plates under heavy fluid loading by an energy finite element formulation. J. Sound Vib. 2003, 263, 21–46. [Google Scholar] [CrossRef]
- Vlahopoulos, N.; Wu, K.; Medyanik, S. Energy finite element analysis for structural-acoustic design of naval vehicles. J. Ship Prod. Des. 2012, 28, 42–48. [Google Scholar] [CrossRef]
- Kwon, H.W.; Hong, S.Y.; Song, J.H. Vibrational energy flow analysis of coupled cylindrical thin shell structures. J. Mech. Sci. Technol. 2016, 30, 4049–4062. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, X.; Zhang, B. Application of the energy finite element analysis to vibration of beams with stepped thickness and variable cross-section. J. Mech. Sci. Technol. 2018, 20, 2237–2252. [Google Scholar]
- Chen, Z.; Yang, Z.; Guo, N.; Zhang, G. An energy finite element method for high frequency vibration analysis of beams with axial force. Appl. Math. Model. 2018, 61, 521–539. [Google Scholar] [CrossRef]
- Shinozuka, M. Monte Carlo solution of structural dynamics. Comput. Struct. 1972, 2, 855–874. [Google Scholar] [CrossRef]
- Wu, F.; Yao, L.; He, Z.; Hu, M. Development of a novel deterministic-statistical approach for vibro-acoustic problems in mid-frequency based on modified integration rule. Int. J. Comput. Methods 2020, 17, 1850142. [Google Scholar] [CrossRef]
- Ezvan, O.; Batou, A.; Soize, C.; Gagliardini, L. Multilevel model reduction for uncertainty quantification in computational structural dynamics. Comput. Mech. 2017, 59, 219–246. [Google Scholar] [CrossRef] [Green Version]
- Li, J.W.; Ni, B.Y.; Jiang, C.; Fang, T. Dynamic response bound analysis for elastic beams under uncertain excitations. J. Sound Vib. 2018, 422, 471–489. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, Z.; Li, Y. Hybrid uncertainty propagation of coupled structural-acoustic system with large fuzzy and interval parameters. Appl. Acoust. 2015, 102, 62–70. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Zhang, Q.; Liu, J. Vibration Prediction of Space Large-Scale Membranes Using Energy Flow Analysis. Appl. Sci. 2022, 12, 6238. https://doi.org/10.3390/app12126238
Wang K, Zhang Q, Liu J. Vibration Prediction of Space Large-Scale Membranes Using Energy Flow Analysis. Applied Sciences. 2022; 12(12):6238. https://doi.org/10.3390/app12126238
Chicago/Turabian StyleWang, Kun, Qi Zhang, and Jiafu Liu. 2022. "Vibration Prediction of Space Large-Scale Membranes Using Energy Flow Analysis" Applied Sciences 12, no. 12: 6238. https://doi.org/10.3390/app12126238




