Seismic Response of Loess-Mudstone Slope with High Anti-Dip Angle Fault Zone
Abstract
:1. Introduction
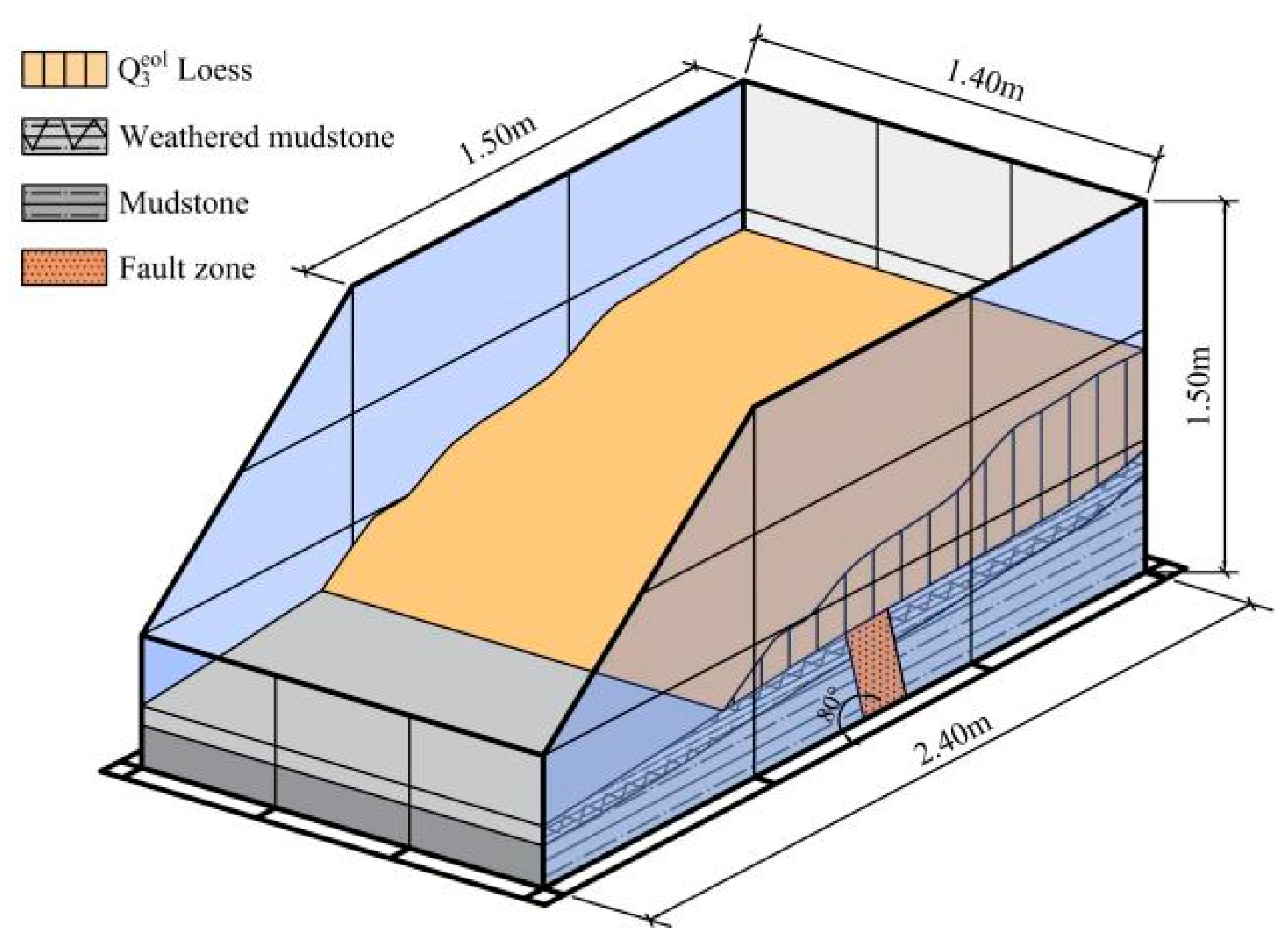
2. Shaking Table Test Programme
2.1. Shaking Table Equipment
2.2. Similarity Design of the Shaking Table Test
2.3. Selection of Similarity Materials
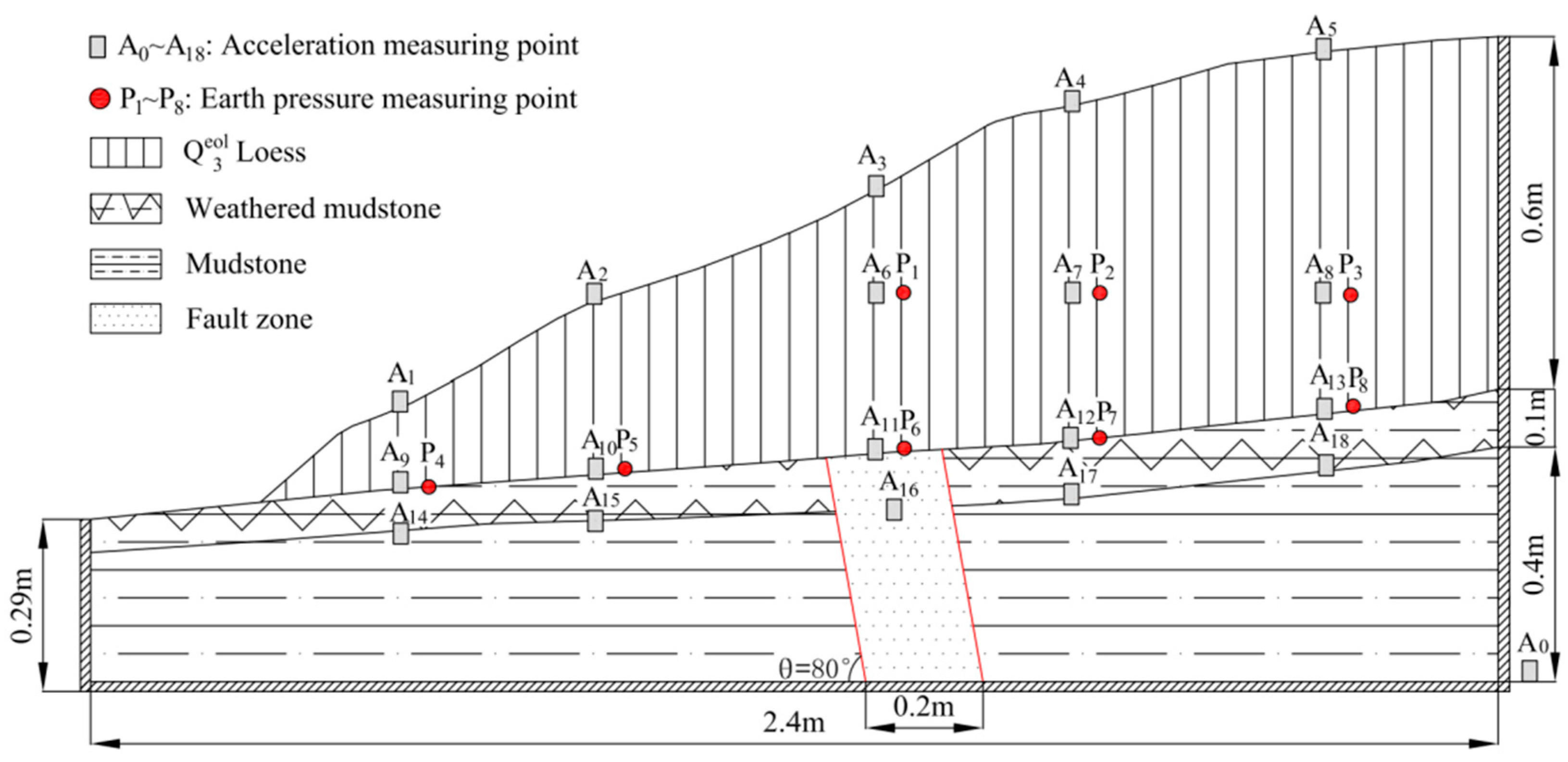
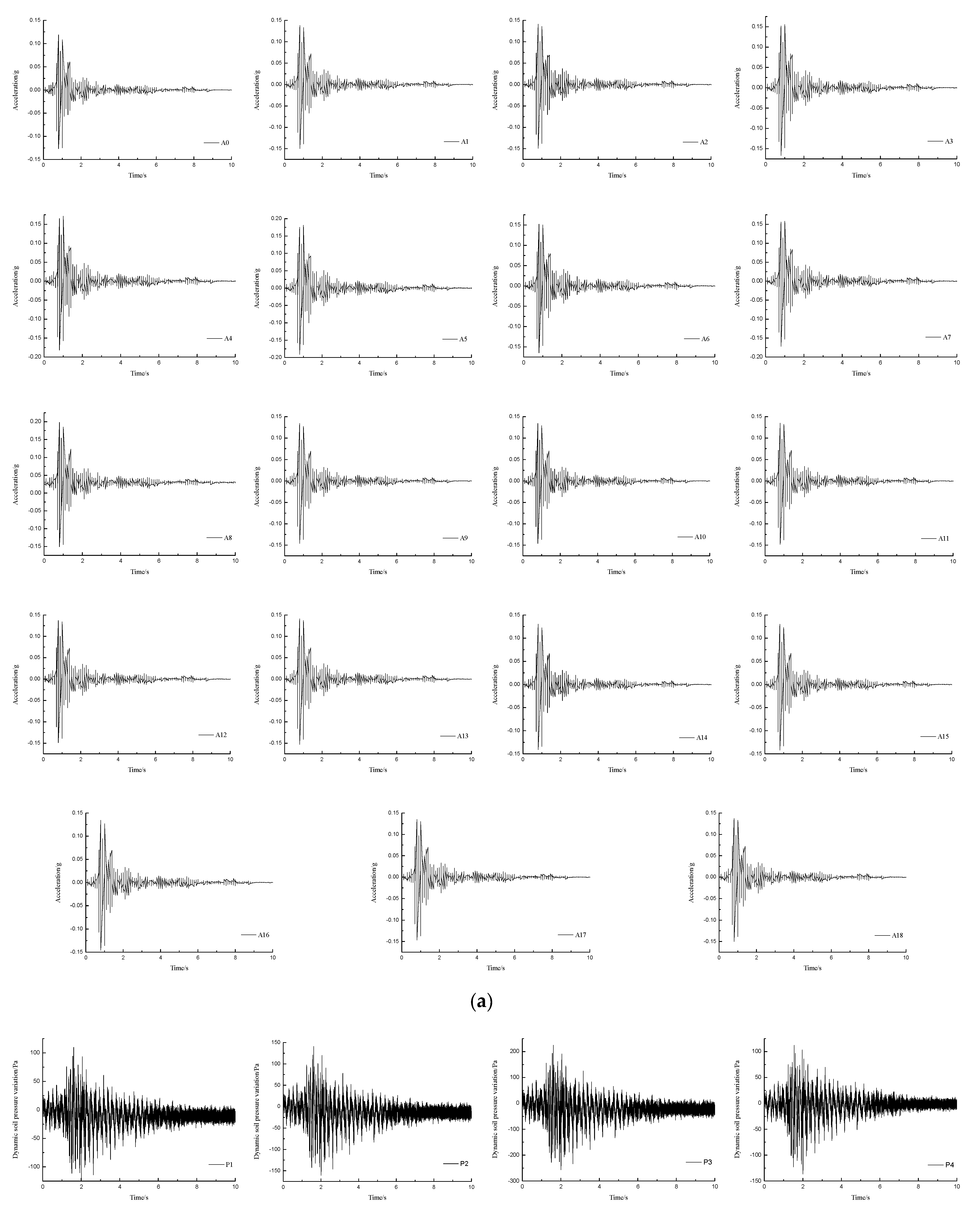
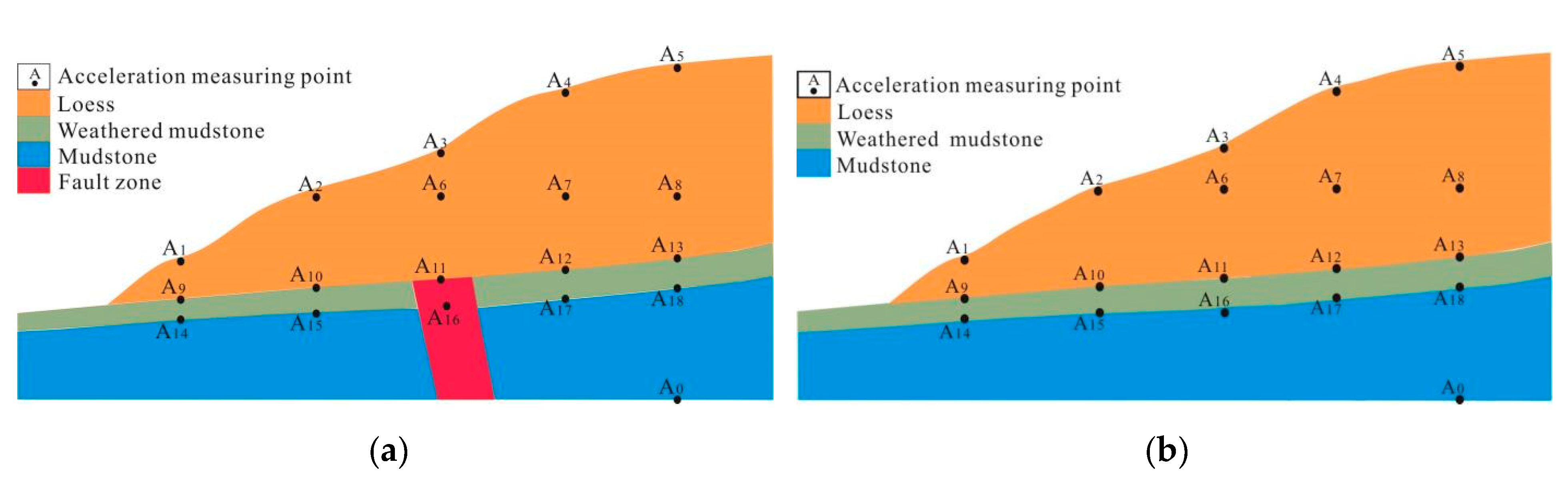
2.4. Sensors in the Test
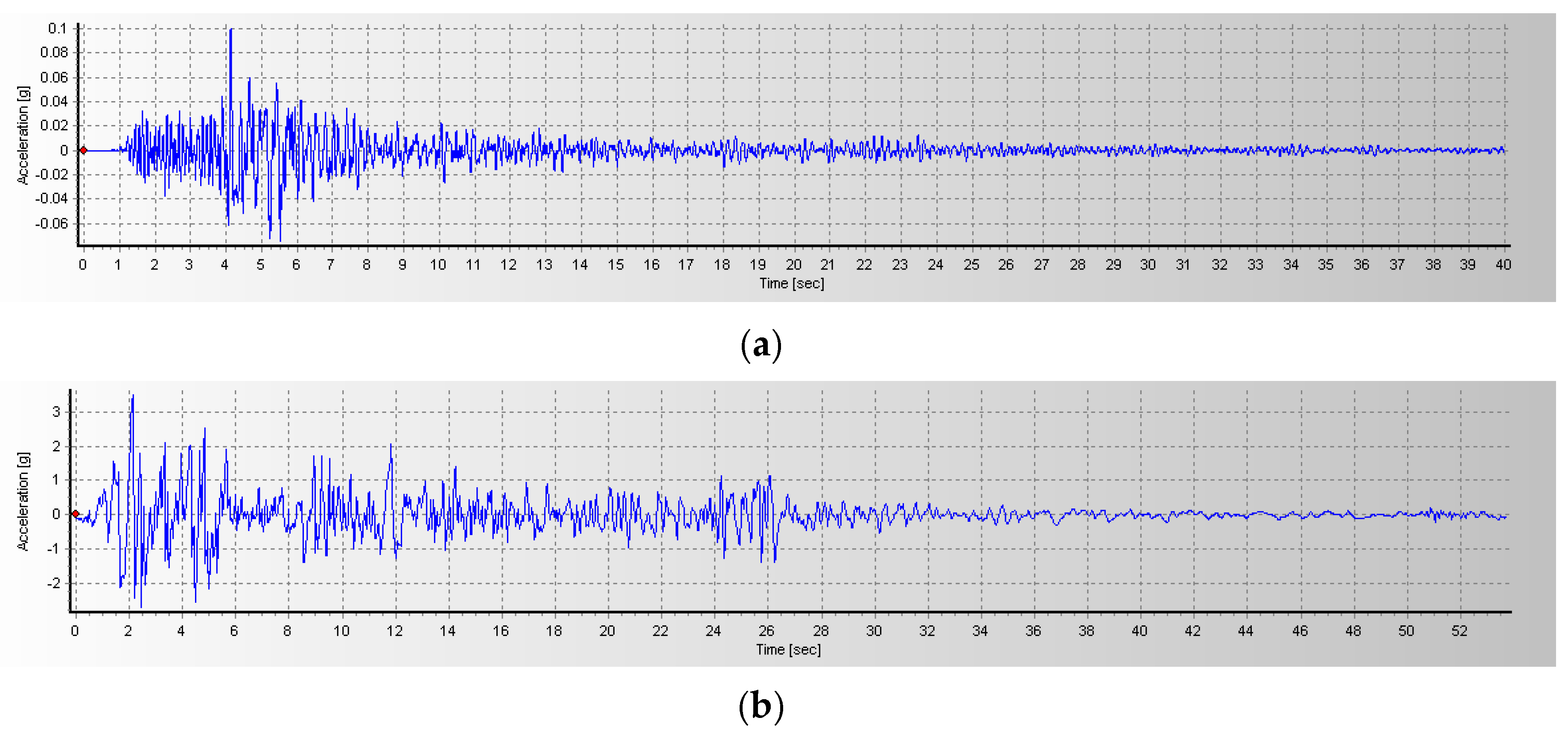
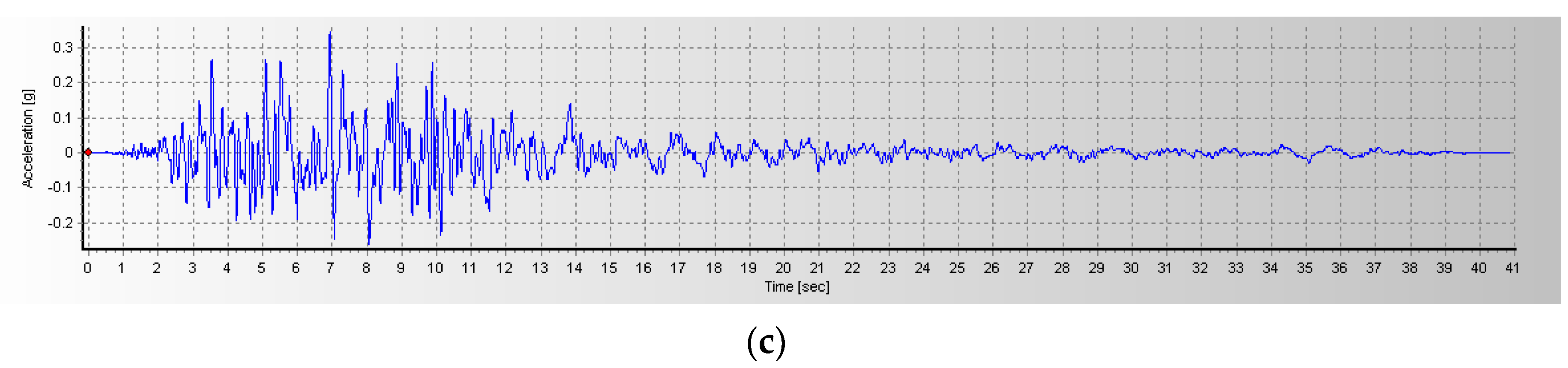
2.5. Loading Sequence of Earthquake Waves
3. Results of the Test and Analysis
3.1. Acceleration Response Characteristics along the Slope Surface
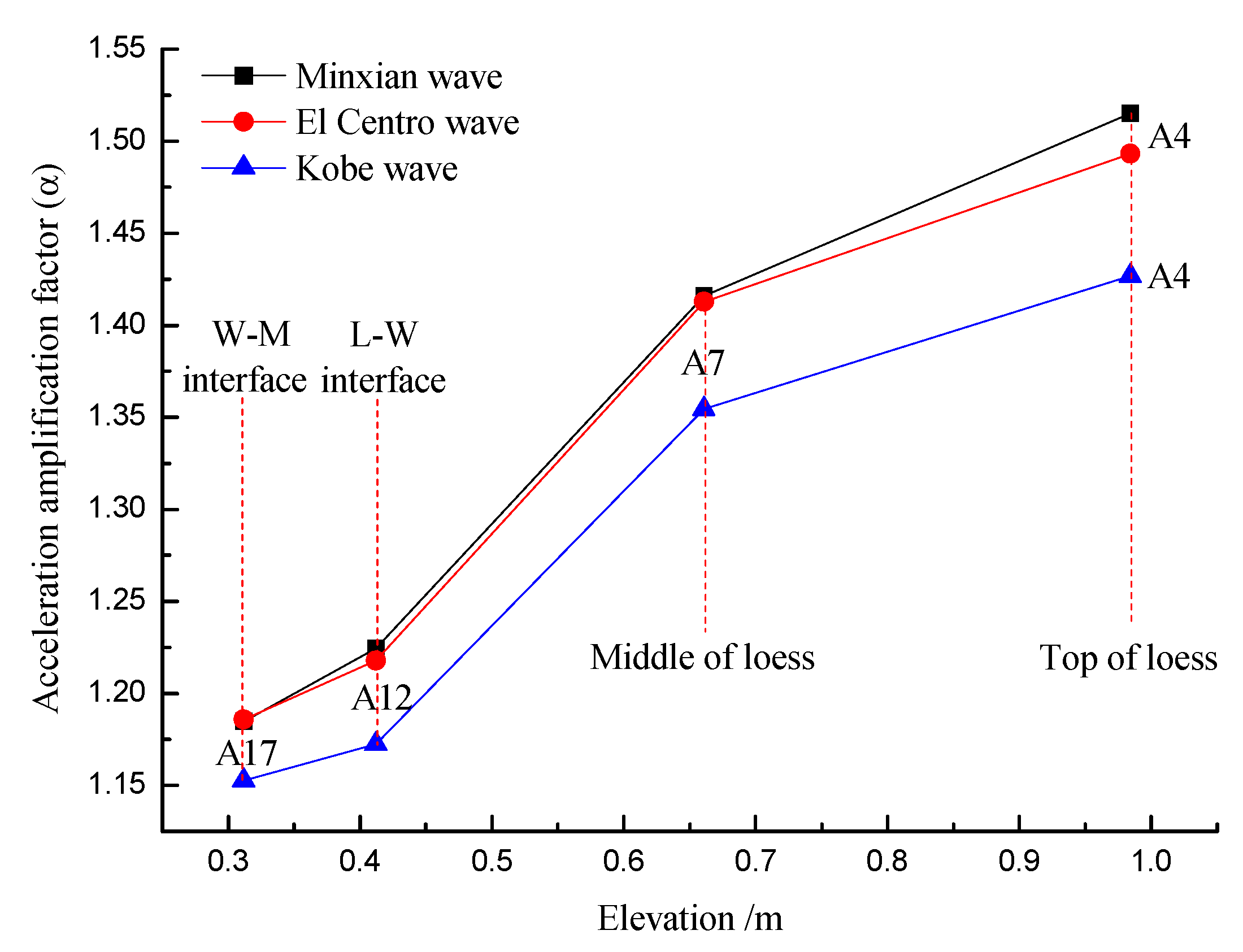
3.2. Acceleration Response Characteristics in Loess Stratum
3.3. Acceleration Response Characteristics at Different Lithological Interfaces
3.4. Acceleration Response Characteristics along the Vertical Section
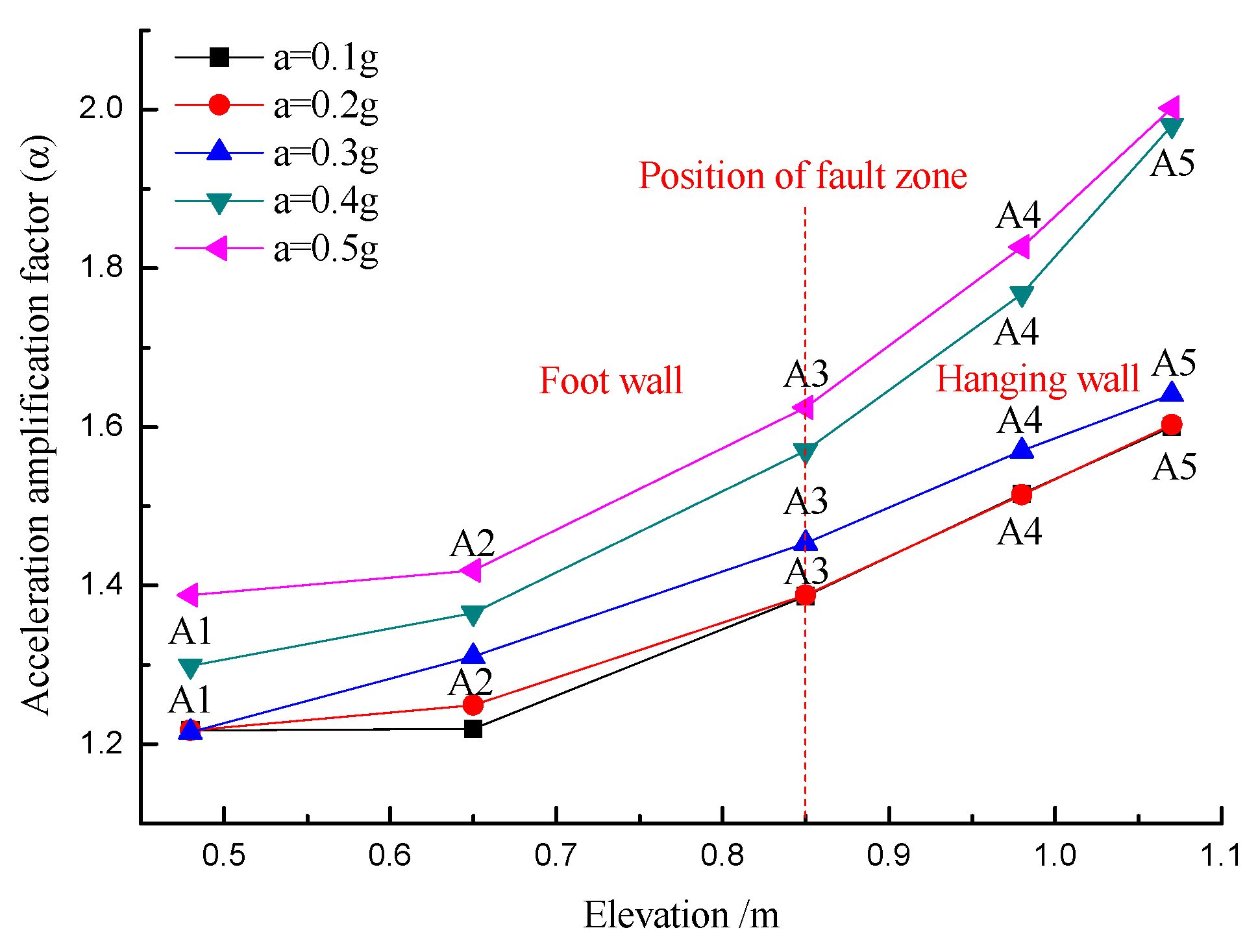
3.5. Influence of Different Input PGA Values on Dynamic Response of Slope Surface
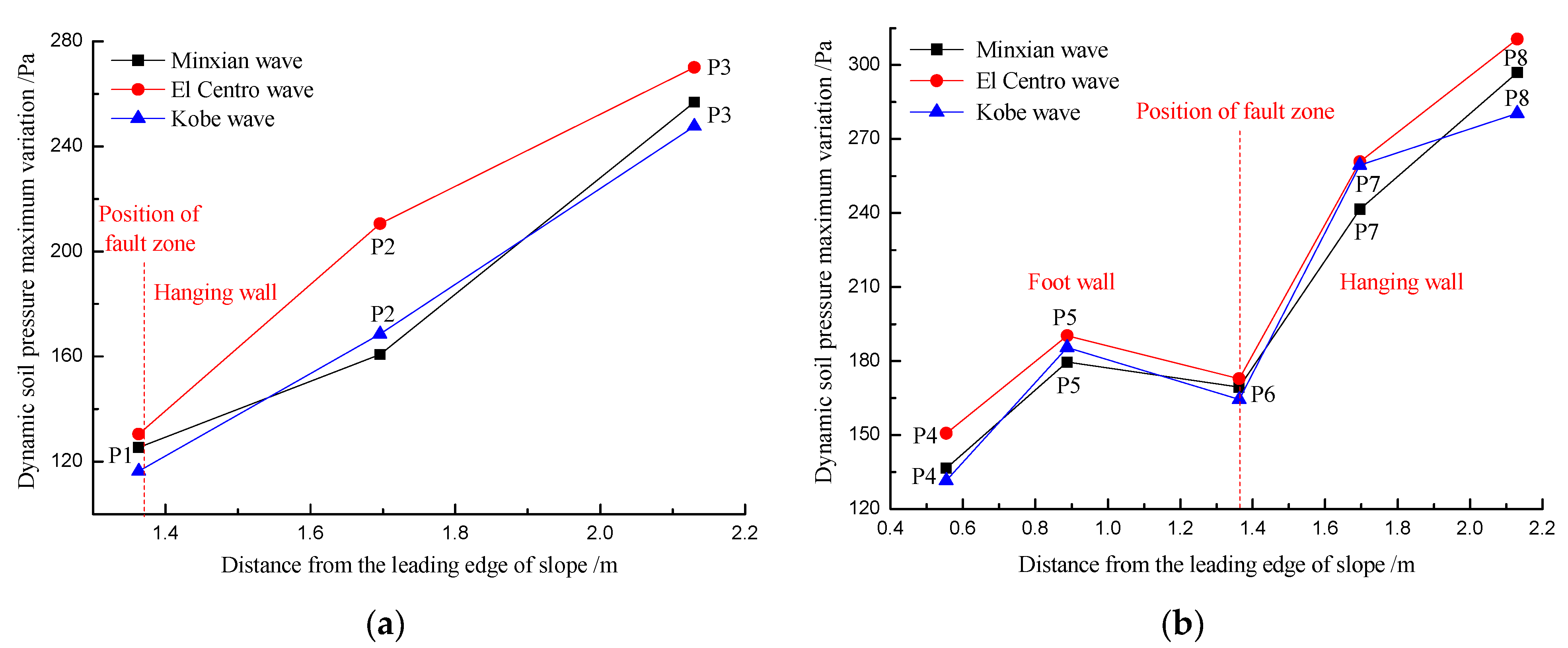
3.6. Seismic Response Rules of Soil Pressure in Loess Stratum
3.7. Seismic Response Rules of Soil Pressure at L–W Interface
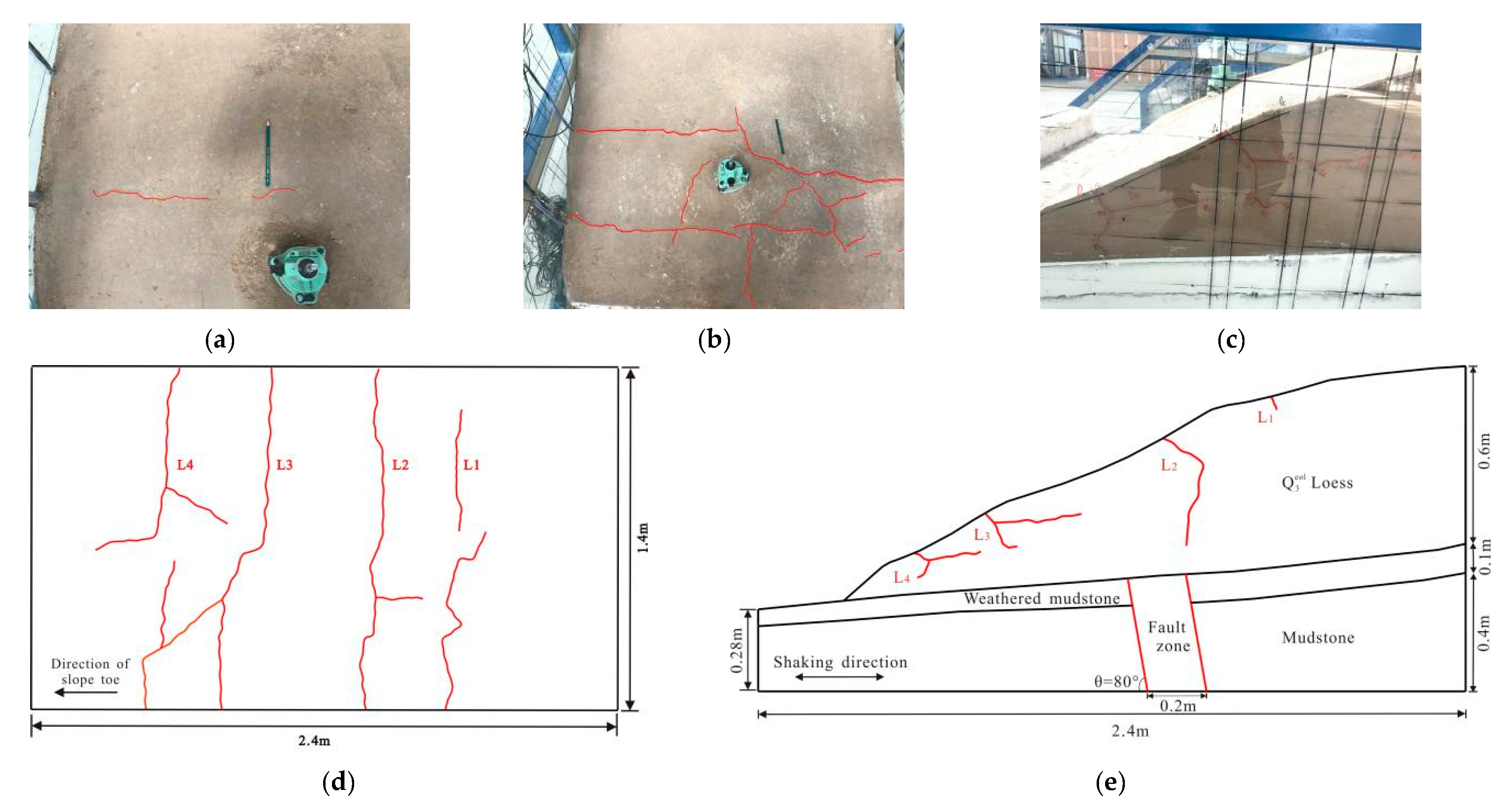
3.8. Dynamic Deformation Characteristics of Slope
4. Results of the Numerical Simulation and Analysis
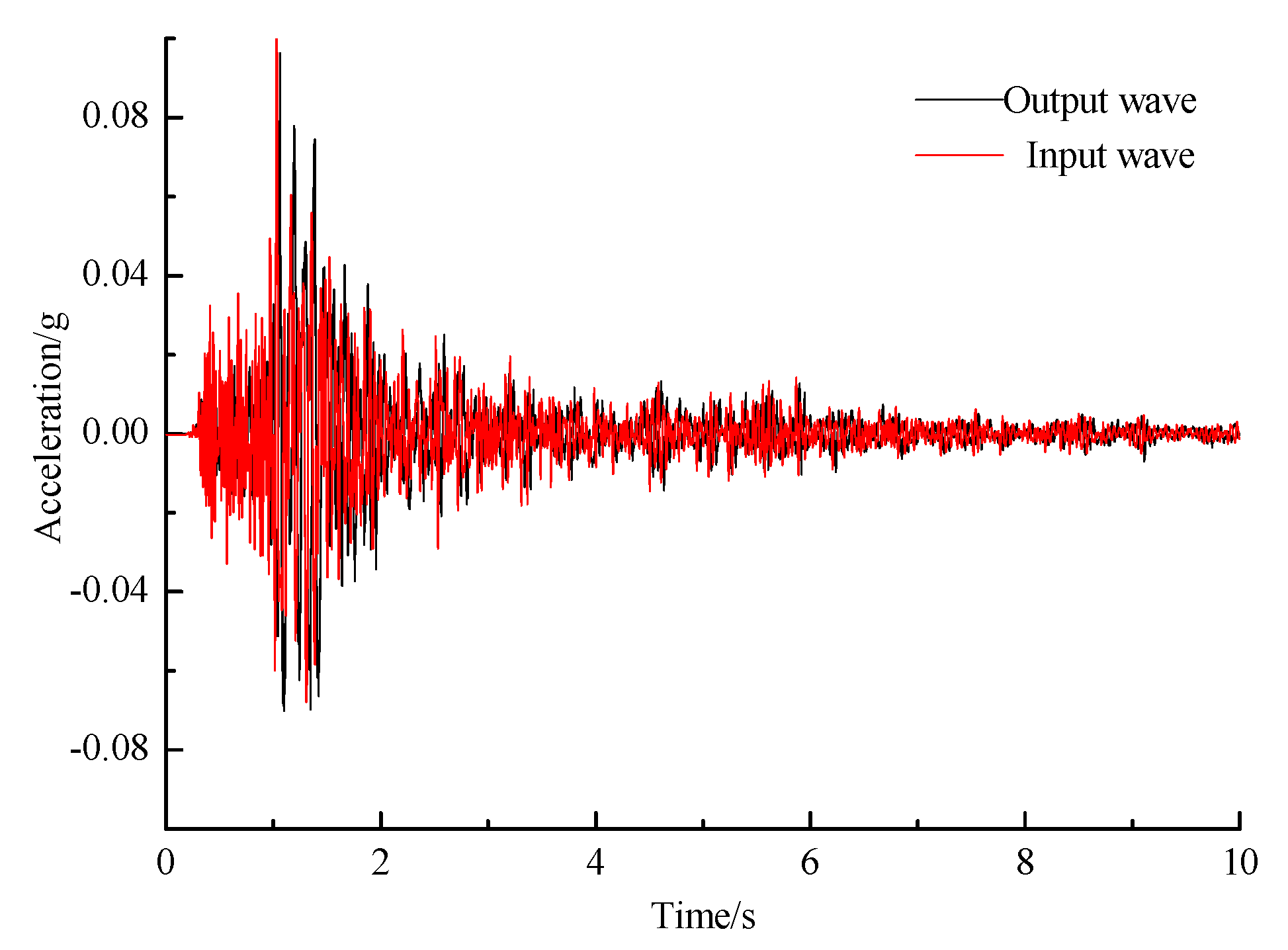
4.1. Comparison of Acceleration Dynamic Response
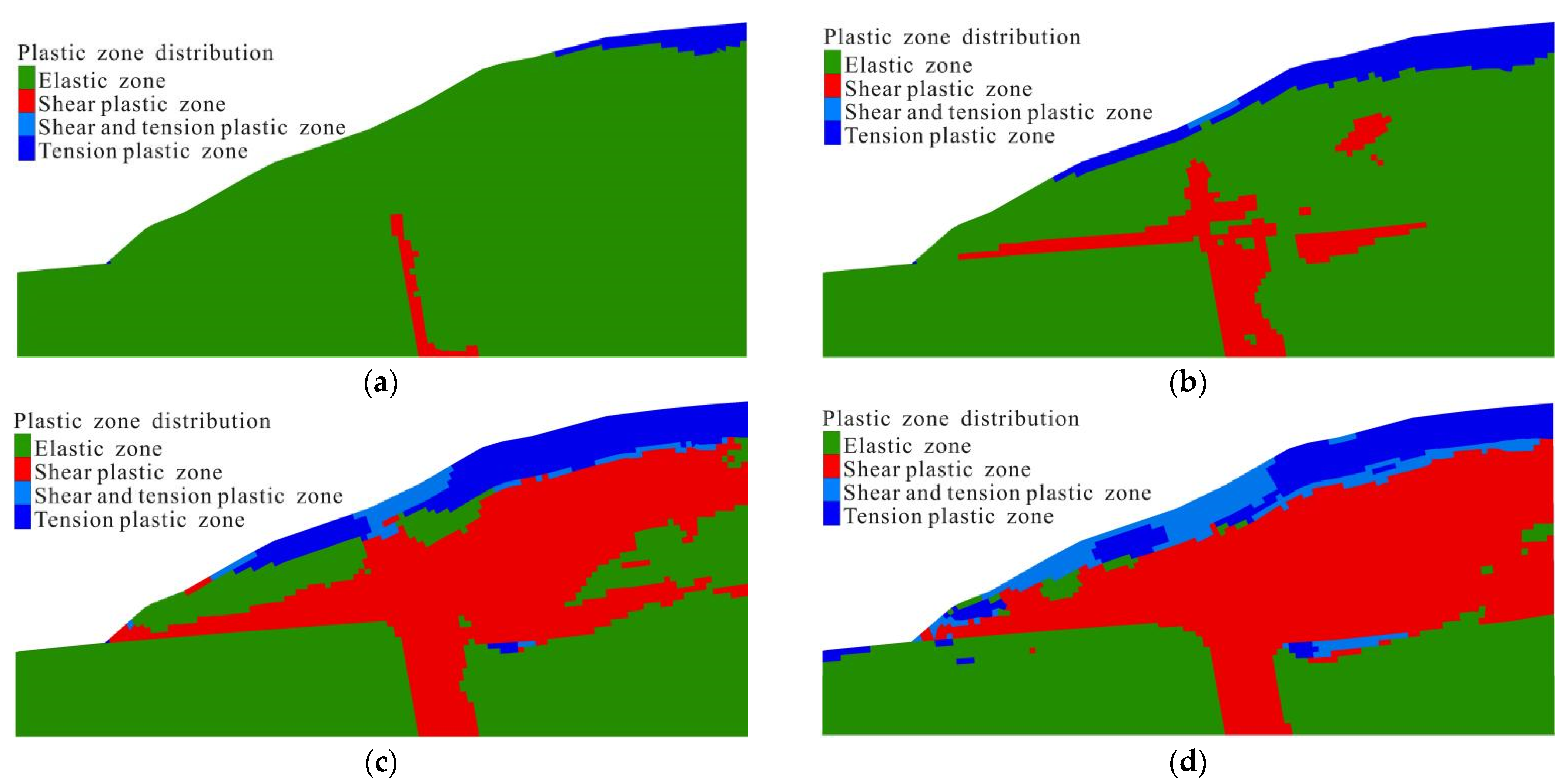
4.2. Distribution of Plastic Zone in Model Slopes
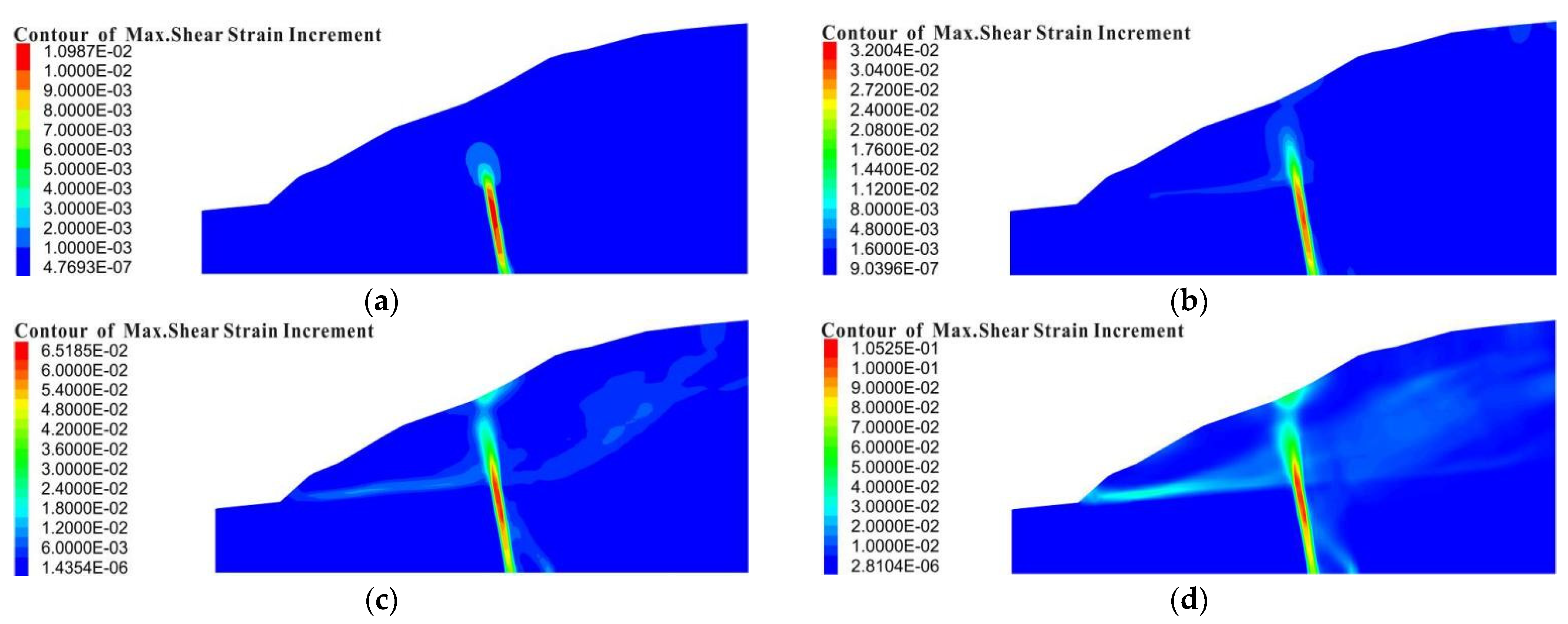
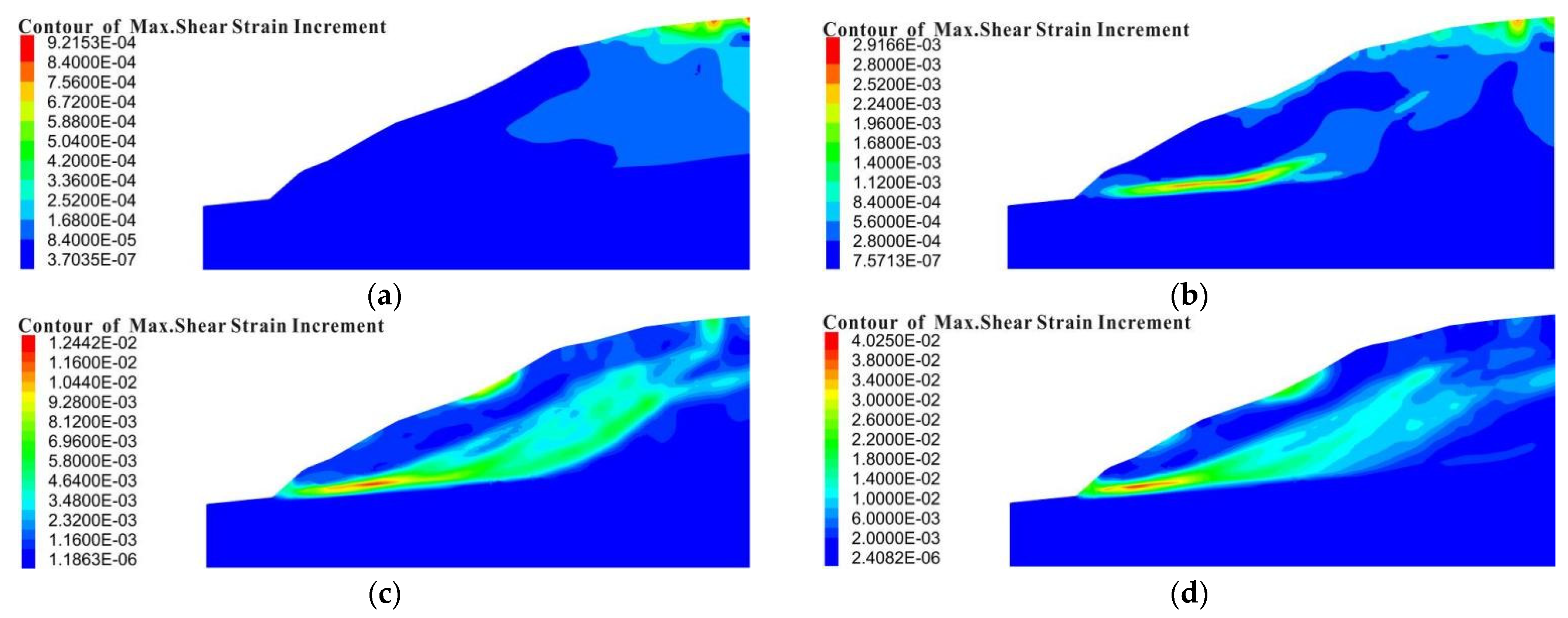
4.3. Distribution of Shear Strain in Model Slopes
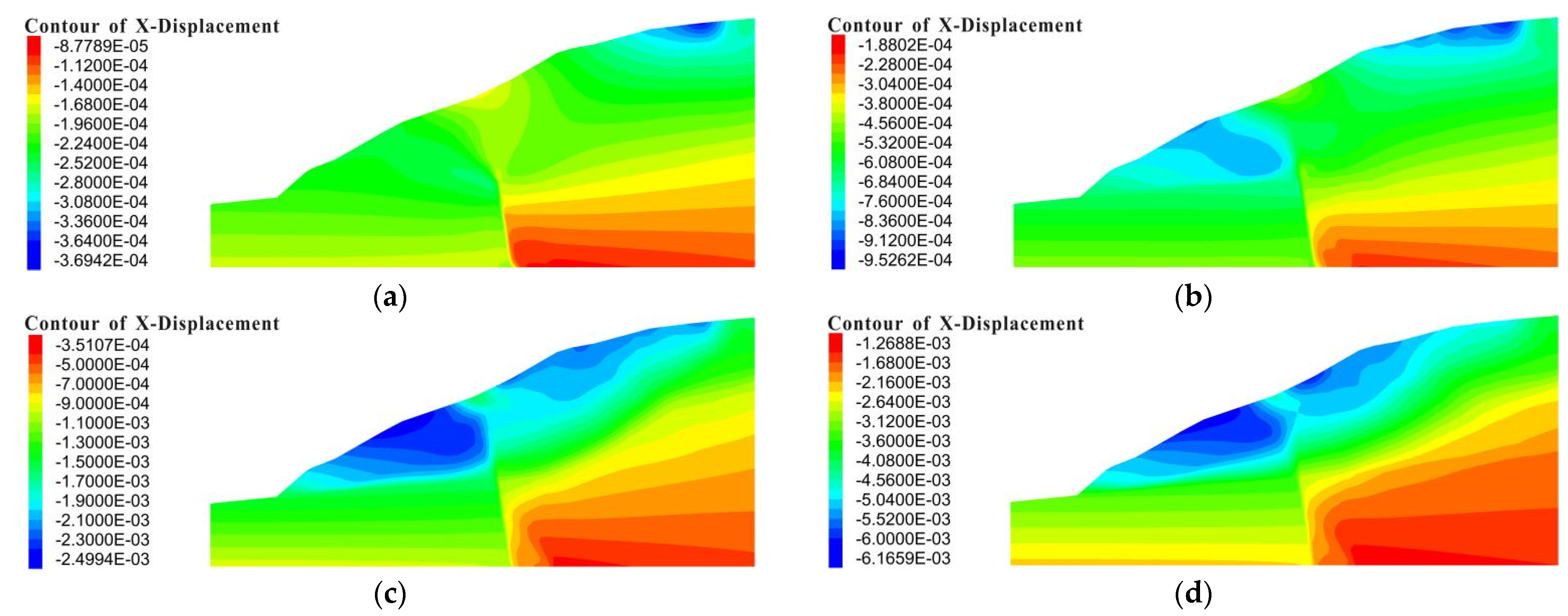
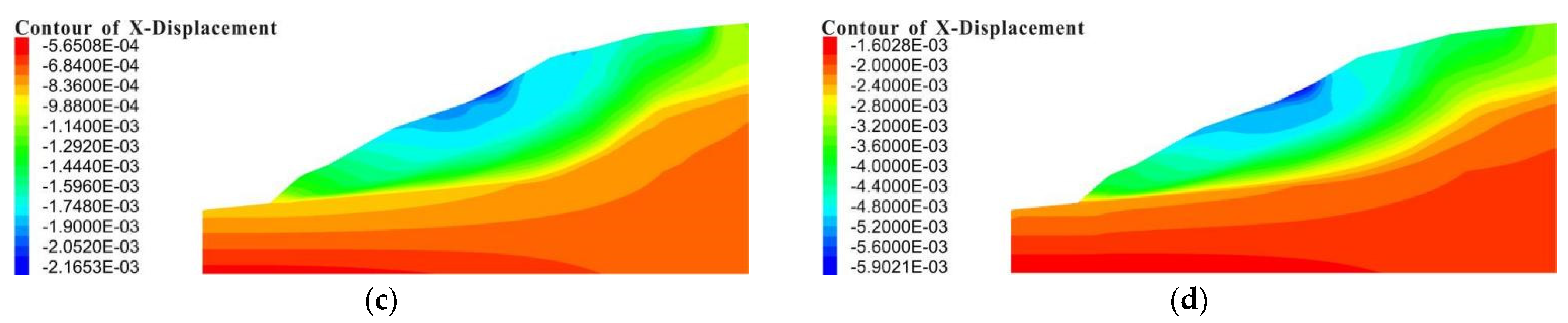
4.4. Features of the Permanent Displacement in Model Slopes
5. Conclusions
- (1)
- The acceleration dynamic response of the LMS with an HADAFZ had a top surface amplification effect on the slope surface, an accelerated increase effect on the slope-surface hanging wall, an amplification effect away from the free slope face in the loess stratum, and a combination of elevation and lithology effects in the vertical section. In addition, at the L–W and W–M interfaces, the amplification response of the hanging wall was the largest, the fault zone was the second, and the foot wall was the smallest.
- (2)
- The key value of input PGA for the dynamic response of the LMS with an HADAFZ was a = 0.3 g. When a > 0.3 g, the hanging wall amplification effect became more apparent, showing that the AAFs on the slope-surface hanging wall increased significantly and that cracks began to appear on the slope surface.
- (3)
- The seismic response of soil pressure had a positive correlation with the thickness of the overlying strata in the loess stratum and the L–W interface, simultaneously, influenced by the hanging wall amplification effect. Meanwhile, the DSPMV in both sides of the fault zone was larger than that in the fault zone, which showed that the loose and weak fault zone can weaken or reduce the dynamic earth pressure.
- (4)
- The deformation and failure of the LMS with an HADAFZ under the earthquake action showed cracking failure rather than overall sliding and the HADAFZ in LMS was equivalent to a damping boundary, which hindered the integral connection of the potential sliding surface and restricted the overall sliding failure of the slope, and it was thus beneficial to the dynamic stability of slope to a certain extent.
- (5)
- The AAFs of the shaking table test and numerical simulation showed consistency. In addition, the results of the distribution of the plastic zone and shear strain and the features of the permanent displacement in the numerical simulation all showed that the slope with an HADAFZ is relatively more stable than the slope without a fault zone.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- You, Z.; Feng, Z.M.; Yang, G.G.; Yang, Y.Z. Seismic risk assessment based on information diffusion theory in the western China. Sci. Geogr. Sin. 2011, 31, 1125–1130. (In Chinese) [Google Scholar]
- Gao, G.R. The distribution and geotechnical properties of loess soils, lateritic soils and clayey soils in china. Eng. Geol. 1996, 42, 95–104. [Google Scholar] [CrossRef]
- Tian, Y.Y.; Xu, C.; Chen, J.; Zhou, Q.; Shen, L.L. Geometrical characteristics of earthquake-induced landslides and correlations with control factors: A case study of the 2013 Minxian, Gansu, China, Mw 5.9 event. Landslides 2017, 14, 1915–1927. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Shyu, J.B.; Zheng, W.; Min, W. Landslides triggered by the 22 July 2013 Minxian–Zhangxian, China, Mw 5.9 earthquake: Inventory compiling and spatial distribution analysis. J. Asian Earth Sci. 2014, 92, 125–142. [Google Scholar] [CrossRef]
- Xu, C.; Shen, L.L.; Wang, G.L. Soft computing in assessment of earthquake-triggered landslide susceptibility. Environ. Earth Sci. 2016, 75, 767. [Google Scholar] [CrossRef]
- Huang, Q.B.; Jia, X.N.; Peng, J.B.; Liu, Y.; Wang, T. Seismic response of loess-mudstone slope with bedding fault zone. Soil Dyn. Earthq. Eng. 2019, 123, 371–380. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; John Wiley: New York, NY, USA, 1948. [Google Scholar]
- Sladen, J.A.D.; Hollander, R.D.; Krahn, J.; Mitchell, D.E. Back analysis of the Nerlerk berm liquefaction slides. Can. Geotech. J. 1985, 22, 579–588. [Google Scholar] [CrossRef]
- Lade, P.V. Static instability and liquefaction of loose fine sandy slopes. Am. Soc. Civ. Eng. J. Geotech. Eng. 1992, 118, 51–71. [Google Scholar] [CrossRef]
- Puri, V.K. Liquefaction Behavior and Dynamic Properties of Loessial (Silty) Soils. Ph.D. Thesis, University of Missouri-Rolla, Rolla, MO, USA, 1984. [Google Scholar]
- Sandoval-Shannon, J.A. Liquefaction and Settlement Characteristics of Silt Soils. Ph.D. Thesis, University of Missouri-Rolla, Rolla, MO, USA, 1989. [Google Scholar]
- Ishihara, K.; Okusa, S.; Oyagi, N.; Ischuk, A. Liquefaction-induced flow slide in the collapsible loess deposit in Soviet Tajik. Soils Found. 1990, 30, 73–89. [Google Scholar] [CrossRef] [Green Version]
- Prakash, S.; Sandoval, J.A. Liquefaction of low plasticity silts. Soil Dyn. Earthq. Eng. 1992, 11, 373–379. [Google Scholar] [CrossRef]
- Guo, T.; Prakash, S. Liquefaction of silts and silt-clay mixtures. J. Geotech. Geoenviron. Eng. 1999, 125, 706–710. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of earthquakes on dams and embankments. Geotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef] [Green Version]
- Goodman, R.E.; Seed, H.B. Earthquake-induced displacements in sand embankments. Am. Soc. Civ. Eng. J. Soil Mech. Found. 1966, 92, 125–146. [Google Scholar] [CrossRef]
- Wilson, R.C.; Keefer, D.K. Dynamic analysis of a slope failure from the 6 August 1979 Coyote Lake, California, earthquake. Bull. Seismol. Soc. Am. 1983, 73, 863–877. [Google Scholar] [CrossRef]
- Sarma, S.K. Seismic stability of earth dams and embankments. Geotechnique 1975, 25, 743–761. [Google Scholar] [CrossRef]
- Franklin, A.G.; Chang, F.K. Earthquake Resistance of Earth and Rock-Fill Dams: Report 5, Permanent Displacements of Earth Embankments by Newmark Sliding Block Analysis; Department of Defense, Department of the Army, Corps of Engineers, Waterways Experiment Station, Soils and Pavements Laboratory: Vicksburg, MI, USA, 1977. [Google Scholar]
- Constantinou, M.C.; Gazetas, G.; Tadjbakhsh, I. Stochastic seismic sliding of rigid mass supported through non-symmetric friction. Earthq. Eng. Struct. Dyn. 1984, 12, 777–794. [Google Scholar] [CrossRef]
- Bo, J.S.; Xu, G.D.; Jing, L.P. Seismic response and dynamic stability analysis of soil slopes. Earthq. Eng. Eng. Vib. 2001, 21, 116–120. (In Chinese) [Google Scholar]
- Davis, L.L.; West, L.R. Observed effects of topography on ground motion. Bull. Seismol. Soc. Am. 1973, 63, 283–298. [Google Scholar] [CrossRef]
- Hartzell, S.H.; Carver, D.L.; King, K.W. Initial investigation of site and topographic effects at Robinwood Ridge, California. Bull. Seismol. Soc. Am. 1994, 84, 1336–1349. [Google Scholar] [CrossRef]
- Ashford, S.A.; Sitar, N.; Lysmer, J.; Deng, N. Topographic effects on the seismic response of steep slopes. Bull. Seismol. Soc. Am. 1997, 87, 701–709. [Google Scholar]
- Qi, S.W.; Wu, F.Q.; Liu, C.L.; Ding, Y.H. Engineering geology analysis on stability of slope under earthquake. Chin. J. Rock Mech. Eng. 2004, 23, 2792. (In Chinese) [Google Scholar]
- Zhang, Z.Z.; Wu, Z.J.; Wang, P.; Yan, W.J. Influencing factors analysis and zonation model research of landslides in loess region. Adv. Mater. Res. 2012, 594–597, 167–174. [Google Scholar] [CrossRef]
- Zhang, D.X.; Wang, G.H. Study of the 1920 Haiyuan earthquake-induced landslides in loess (China). Eng. Geol. 2007, 94, 76–88. [Google Scholar] [CrossRef]
- Evans, S.G.; Roberts, N.J.; Ischuk, A.; Delaney, K.B.; Morozova, G.S.; Tutubalina, O. Landslides triggered by the 1949 Khait earthquake, Tajikistan, and associated loss of life. Eng. Geol. 2009, 109, 195–212. [Google Scholar] [CrossRef]
- Wang, N.; Wang, L.M.; Yuan, Z.X.; Wang, Q. Characteristic and stability analysis for loess seismic landslide in valley city. Adv. Mater. Res. 2012, 594–597, 1856–2863. [Google Scholar]
- Wang, G.H.; Zhang, D.X.; Furuya, G.; Yang, J. Pore-pressure generation and fluidization in a loess landslide triggered by the 1920 Haiyuan earthquake, China: A case study. Eng. Geol. 2014, 174, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.J.; Sun, J.J.; Chen, Y.J.; Wang, Q.; Zha, W.C. Analysis of disaster-causing mechanism of loess landslides induced by the Minxian-Zhangxian Ms6.6 earthquake, China. Jpn. Geotech. Soc. Spec. Publ. 2015, 1, 40–45. [Google Scholar] [CrossRef] [Green Version]
- Jia, X.N.; Huang, Q.B.; Wang, T.; Zhang, N.; Jiang, Z.K. Shaking table test of dynamic response of loess-mudstone slopes with a steep dip bedding fault zone. Chin. J. Rock Mech. Eng. 2018, 37, 2721–2732. (In Chinese) [Google Scholar]
- Song, D.; Chen, Z.; Ke, Y.; Nie, W. Seismic response analysis of a bedding rock slope based on the time-frequency joint analysis method: A case study from the middle reach of the Jinsha River, China. Eng. Geol. 2020, 274, 105731. [Google Scholar] [CrossRef]
- Huang, Y.; Han, X.; Zhao, L. Recurrent neural networks for complicated seismic dynamic response prediction of a slope system. Eng. Geol. 2021, 289, 106198. [Google Scholar] [CrossRef]
- Zhu, C.; Cheng, H.; Bao, Y.; Chen, Z.; Huang, Y. Shaking table tests on the seismic response of slopes to near-fault ground motion. Geomech. Eng. 2022, 29, 133–143. [Google Scholar]








| Name | Parameter | Name | Parameter |
|---|---|---|---|
| Table size | 4 m × 4 m | Max acceleration | X direction: ±1.5 g |
| Frequency | 0.1~50 HZ | Y direction: ±1.0 g | |
| Max loading | 30 t | Z direction: ±1.0 g | |
| Max overturning moment | 80 t·m | Max displacement | X direction: ±15 cm |
| Max eccentric torque | 30 t·m | Y direction: ±25 cm | |
| Shaking direction | X,Y,Z | Z direction: ±10 cm |
| Physical Quantities | Similar Constants | Similarity Ratio (Prototype/Model) |
|---|---|---|
| Length (l) (controlled quantity) | 20.0 | |
| Density (ρ) (controlled quantity) | 1.0 | |
| Elastic modulus (E) (controlled quantity) | 20.0 | |
| Cohesion (c) | 20.0 | |
| Internal friction angle (φ) | 1.0 | |
| Stress (σ) | 20.0 | |
| Strain (ε) | 1.0 | |
| Shaking time (t) | 4.472 | |
| Frequency (f) | 0.224 | |
| Acceleration (a) | 1.0 | |
| Velocity (v) | 4.472 | |
| Displacement (u) | 20.0 |
| Material (%) | Prototype Loess | Sand | Barite Powder | Quartz Sand | Gypsum | Glycerin | Water |
|---|---|---|---|---|---|---|---|
| Loess | 47.6 | 14.3 | 33.3 | 0.0 | 0.0 | 0.0 | 4.8 |
| Weathered mudstone | 0.0 | 0.0 | 33.0 | 55.0 | 2.0 | 2.5 | 7.5 |
| Mudstone | 0.0 | 0.0 | 33.5 | 55.5 | 2.3 | 2.2 | 6.5 |
| Fault zone | 0.0 | 0.0 | 33.5 | 55.5 | 2.0 | 2.5 | 6.5 |
| Soil | Type | Unit Weight (γ)/(kN·m−3) | Cohesion (c)/kPa | Internal Friction Angle (φ)/(°) | Elastic Modulus (E)/MPa | Poisson’s Ratio (μ) |
|---|---|---|---|---|---|---|
| Loess | Prototype | 18 | 5.0~10.0 | 18~22 | 6.00~9.00 | 0.33~0.38 |
| Model | 18 | 0.4 | 20 | 0.41 | 0.36 | |
| Weathered mudstone | Prototype | 18.5 | 15.0~20.0 | 22~28 | 70~100 | 0.28~0.31 |
| Model | 18.5 | 0.9 | 26 | 4 | 0.30 | |
| Mudstone | Prototype | 21 | 35~43 | 26~32 | 196.00~220.00 | 0.27~0.33 |
| Model | 21 | 2 | 30 | 10.59 | 0.32 | |
| Fault zone | Prototype | 20 | 15~22 | 18~23 | 98.00~109.00 | 0.29~0.34 |
| Model | 20 | 1 | 20 | 5.29 | 0.32 |
| Test Content | The ID of Condition | The Type of Inputting Wave | Inputting Peak Acceleration/g |
|---|---|---|---|
| The first sweep frequency test | S-W1 | White noise | 0.03 |
| The loading as first level | S-M1 | Minxian wave | 0.1 |
| S-E1 | El Centro wave | 0.1 | |
| S-K1 | Kobe wave | 0.1 | |
| The second sweep frequency test | S-W2 | White noise | 0.03 |
| The loading as second level | S-M2 | Minxian wave | 0.2 |
| S-E2 | El Centro wave | 0.2 | |
| S-K2 | Kobe wave | 0.2 | |
| The third sweep frequency test | S-W3 | White noise | 0.03 |
| The loading as third level | S-M3 | Minxian wave | 0.3 |
| S-E3 | El Centro wave | 0.3 | |
| S-K3 | Kobe wave | 0.3 | |
| The fourth sweep frequency test | S-W4 | White noise | 0.03 |
| The loading as fourth level | S-M4 | Minxian wave | 0.4 |
| S-E4 | El Centro wave | 0.4 | |
| S-K4 | Kobe wave | 0.4 | |
| The fifth sweep frequency test | S-W5 | White noise | 0.03 |
| The loading as fifth level | S-M5 | Minxian wave | 0.5 |
| S-E5 | El Centro wave | 0.5 | |
| S-K5 | Kobe wave | 0.5 | |
| The sixth sweep frequency test | S-W6 | White noise | 0.03 |
| The loading as sixth level | S-M6 | Minxian wave | 0.6 |
| S-E6 | El Centro wave | 0.6 | |
| S-K6 | Kobe wave | 0.6 | |
| The seventh sweep frequency test | S-W7 | White noise | 0.03 |
| The loading as seventh level | S-M7 | Minxian wave | 0.8 |
| S-E7 | El Centro wave | 0.8 | |
| S-K7 | Kobe wave | 0.8 | |
| The eighth sweep frequency test | S-W8 | White noise | 0.03 |
| Soil | Density/(kg·m−3) | Bulk Modulus/MPa | Shear Modulus/MPa | Cohesion/kPa | Internal Friction Angle/° |
|---|---|---|---|---|---|
| Loess | 1800 | 0.49 | 0.15 | 0.4 | 20 |
| Weathered mudstone | 1850 | 3.33 | 1.54 | 0.9 | 26 |
| Mudstone | 2100 | 9.81 | 4.01 | 2.0 | 30 |
| Fault zone | 2000 | 4.90 | 2.00 | 1.0 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Huang, Q.; Peng, J.; Lan, H.; Liu, Y. Seismic Response of Loess-Mudstone Slope with High Anti-Dip Angle Fault Zone. Appl. Sci. 2022, 12, 6353. https://doi.org/10.3390/app12136353
Jia X, Huang Q, Peng J, Lan H, Liu Y. Seismic Response of Loess-Mudstone Slope with High Anti-Dip Angle Fault Zone. Applied Sciences. 2022; 12(13):6353. https://doi.org/10.3390/app12136353
Chicago/Turabian StyleJia, Xiangning, Qiangbing Huang, Jianbing Peng, Hengxing Lan, and Yue Liu. 2022. "Seismic Response of Loess-Mudstone Slope with High Anti-Dip Angle Fault Zone" Applied Sciences 12, no. 13: 6353. https://doi.org/10.3390/app12136353
APA StyleJia, X., Huang, Q., Peng, J., Lan, H., & Liu, Y. (2022). Seismic Response of Loess-Mudstone Slope with High Anti-Dip Angle Fault Zone. Applied Sciences, 12(13), 6353. https://doi.org/10.3390/app12136353





