Multifilters-Based Unsupervised Method for Retinal Blood Vessel Segmentation
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
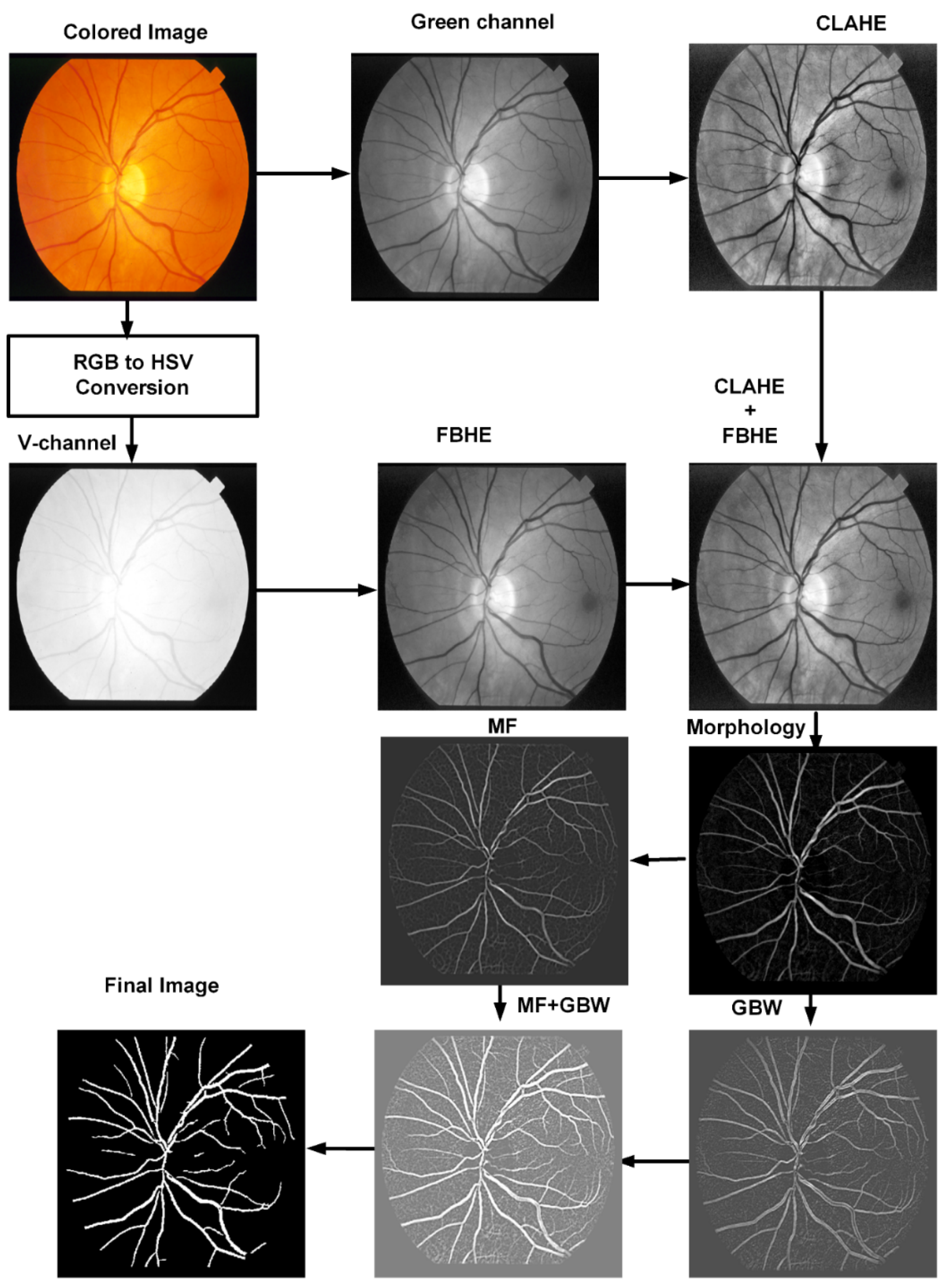
3.1. Preprocessing
3.2. Morphological Filter
3.3. Matched Filter
3.4. Gabor Wavelet
3.5. Human Visual System Based Binarization
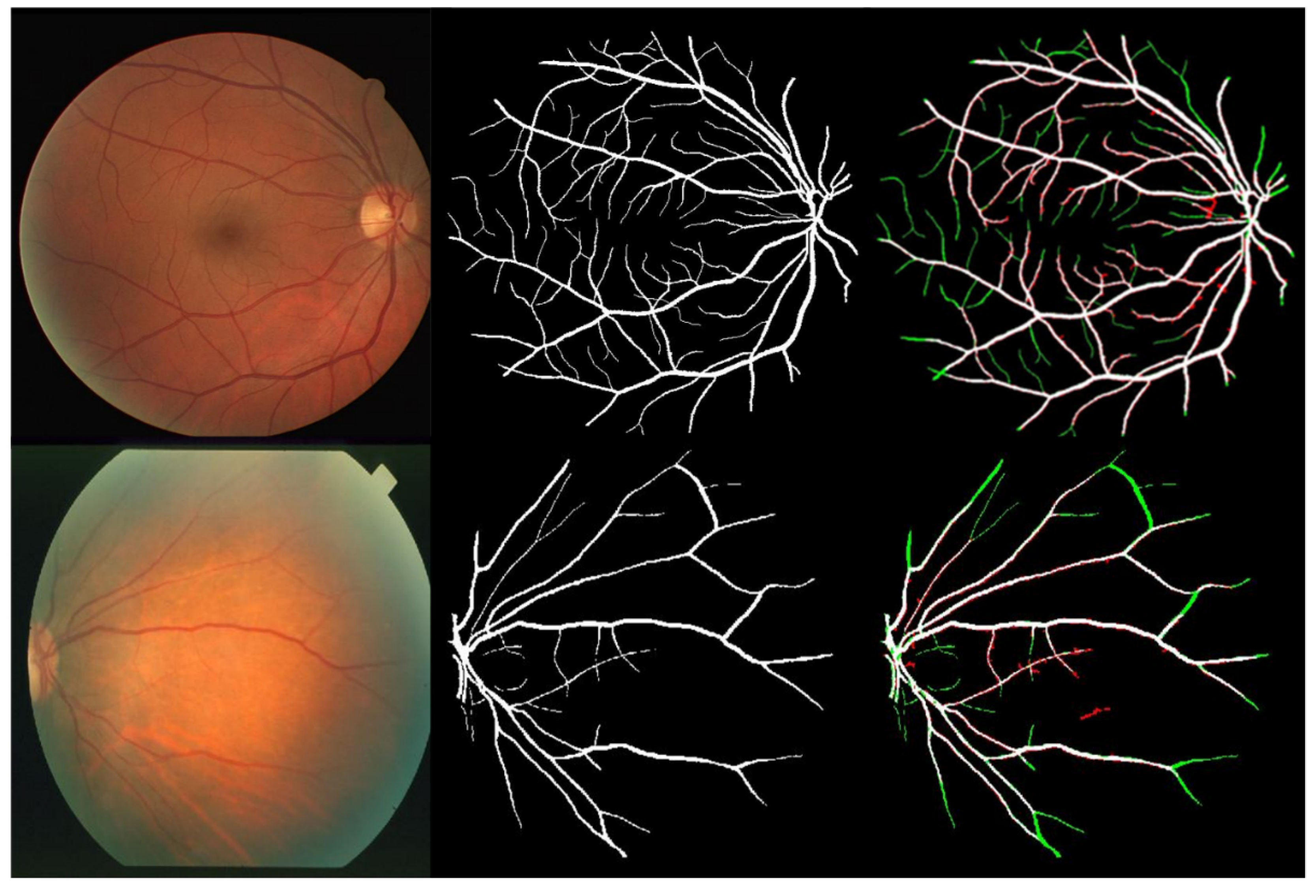
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shah, S.A.A.; Laude, A.; Faye, I.; Tang, T.B. Automated microaneurysm detection in diabetic retinopathy using curvelet transform. J. Biomed. Opt. 2016, 21, 101404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schwartz, R.; Dodge, J.; Smith, N.A.; Etzioni, O. Green ai. Commun. ACM 2020, 63, 54–63. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Chatterjee, S.; Katz, N.; Nelson, M.; Goldbaum, M. Detection of blood vessels in retinal images using two-dimensional matched filters. IEEE Trans. Med. Imaging 1989, 8, 263–269. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soares, J.V.; Leandro, J.J.; Cesar, R.M.; Jelinek, H.F.; Cree, M.J. Retinal vessel segmentation using the 2-D Gabor wavelet and supervised classification. IEEE Trans. Med. Imaging 2006, 25, 1214–1222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vonikakis, V.; Andreadis, I.; Papamarkos, N. Robust document binarization with OFF center-surround cells. Pattern Anal. Appl. 2011, 14, 219–234. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Tang, T.B.; Faye, I.; Laude, A. Blood vessel segmentation in color fundus images based on regional and Hessian features. Graefe’s Arch. Clin. Exp. Ophthalmol. 2017, 255, 1525–1533. [Google Scholar] [CrossRef]
- Al-Rawi, M.; Karajeh, H. Genetic algorithm matched filter optimization for automated detection of blood vessels from digital retinal images. Comput. Methods Programs Biomed. 2007, 87, 248–253. [Google Scholar] [CrossRef]
- Cinsdikici, M.G.; Aydın, D. Detection of blood vessels in ophthalmoscope images using MF/ant (matched filter/ant colony) algorithm. Comput. Methods Programs Biomed. 2009, 96, 85–95. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, L.; Zhang, L.; Karray, F. Retinal vessel extraction by matched filter with first-order derivative of Gaussian. Comput. Biol. Med. 2010, 40, 438–445. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; You, J.; Zhang, D. Vessel segmentation and width estimation in retinal images using multiscale production of matched filter responses. Expert Syst. Appl. 2012, 39, 7600–7610. [Google Scholar] [CrossRef]
- Oliveira, W.S.; Teixeira, J.V.; Ren, T.I.; Cavalcanti, G.D.; Sijbers, J. Unsupervised retinal vessel segmentation using combined filters. PLoS ONE 2016, 11, e0149943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saroj, S.K.; Kumar, R.; Singh, N.P. Fréchet PDF based Matched Filter Approach for Retinal Blood Vessels Segmentation. Comput. Methods Programs Biomed. 2020, 194, 105490. [Google Scholar] [CrossRef] [PubMed]
- Staal, J.; Abràmoff, M.D.; Niemeijer, M.; Viergever, M.A.; Van Ginneken, B. Ridge-based vessel segmentation in color images of the retina. IEEE Trans. Med. Imaging 2004, 23, 501–509. [Google Scholar] [CrossRef] [PubMed]
- Hoover, A.; Kouznetsova, V.; Goldbaum, M. Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response. IEEE Trans. Med. Imaging 2000, 19, 203–210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raju, G.; Nair, M.S. A fast and efficient color image enhancement method based on fuzzy-logic and histogram. AEU-Int. J. Electron. Commun. 2014, 68, 237–243. [Google Scholar] [CrossRef]
- Zuiderveld, K. Contrast limited adaptive histogram equalization. Graph. Gems 1994, 474–485. [Google Scholar]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image analysis using mathematical morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 4, 532–550. [Google Scholar] [CrossRef]
- Gabor, D. Theory of communication. Part 1: The analysis of information. J. Inst. Electr. Eng.-Part III Radio Commun. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef] [Green Version]
- Nelson, R.; Kolb, H. ON and OFF pathways in the vertebrate retina and visual system. Vis. Neurosci. 2004, 1, 260–278. [Google Scholar]
- Werner, J.S.; Chalupa, L.M. The Visual Neurosciences; Mit Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Shah, S.A.A.; Shahzad, A.; Khan, M.A.; Lu, C.K.; Tang, T.B. Unsupervised method for retinal vessel segmentation based on gabor wavelet and multiscale line detector. IEEE Access 2019, 7, 167221–167228. [Google Scholar] [CrossRef]
- Thangaraj, S.; Periyasamy, V.; Balaji, R. Retinal vessel segmentation using neural network. IET Image Processing 2018, 12, 669–678. [Google Scholar] [CrossRef]
- Sai, Z.; Yanping, L. Retinal Vascular Image Segmentation Based on Improved HED Network. Acta Optica Sinica 2020, 40, 0610002. [Google Scholar]
- Tang, S.; Yu, F. Construction and verification of retinal vessel segmentation algorithm for color fundus image under BP neural network model. J. Supercomput. 2021, 77, 3870–3884. [Google Scholar] [CrossRef]
- Adapa, D.; Joseph Raj, A.N.; Alisetti, S.N.; Zhuang, Z.; Naik, G. A supervised blood vessel segmentation technique for digital Fundus images using Zernike Moment based features. PLoS ONE 2020, 15, e0229831. [Google Scholar] [CrossRef]
- Sayed, M.A.; Saha, S.; Rahaman, G.A.; Ghosh, T.K.; Kanagasingam, Y. An innovate approach for retinal blood vessel segmentation using mixture of supervised and unsupervised methods. IET Image Processing 2021, 15, 180–190. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, X.; Cheng, K.-T. Joint segment-level and pixel-wise losses for deep learning based retinal vessel segmentation. IEEE Trans. Biomed. Eng. 2018, 65, 1912–1923. [Google Scholar] [CrossRef]
- Soomro, T.A.; Afifi, A.J.; Gao, J.; Hellwich, O.; Paul, M.; Zheng, L. Strided U-Net model: Retinal vessels segmentation using dice loss. In Proceedings of the 2018 Digital Image Computing: Techniques and Applications (DICTA), Canberra, Australia, 10–13 December 2018. [Google Scholar]
- Jiang, Z.; Zhang, H.; Wang, Y.; Ko, S.B. Retinal blood vessel segmentation using fully convolutional network with transfer learning. Comput. Med. Imaging Graph. 2018, 68, 1–15. [Google Scholar] [CrossRef]
- Alom, M.Z.; Hasan, M.; Yakopcic, C.; Taha, T.M.; Asari, V.K. Recurrent residual convolutional neural network based on u-net (r2u-net) for medical image segmentation. arXiv 2018, arXiv:1802.06955. [Google Scholar]
- Khan, T.M.; Alhussein, M.; Aurangzeb, K.; Arsalan, M.; Naqvi, S.S.; Nawaz, S.J. Residual connection-based encoder decoder network (RCED-Net) for retinal vessel segmentation. IEEE Access 2020, 8, 131257–131272. [Google Scholar] [CrossRef]
- Wu, Y.; Xia, Y.; Song, Y.; Zhang, Y.; Cai, W. NFN+: A novel network followed network for retinal vessel segmentation. Neural Netw. 2020, 126, 153–162. [Google Scholar] [CrossRef]
- Sathananthavathi, V.; Indumathi, G. Encoder enhanced atrous (EEA) unet architecture for retinal blood vessel segmentation. Cogn. Syst. Res. 2021, 67, 84–95. [Google Scholar]
- Biswal, B.; Pooja, T.; Subrahmanyam, N.B. Robust retinal blood vessel segmentation using line detectors with multiple masks. IET Image Processing 2018, 12, 389–399. [Google Scholar] [CrossRef]
- Wu, Y.; Xia, Y.; Song, Y.; Zhang, Y.; Cai, W. Morphological operations with iterative rotation of structuring elements for segmentation of retinal vessel structures. Multidimens. Syst. Signal Processing 2019, 30, 373–389. [Google Scholar]
- Sundaram, R.; Ks, R.; Jayaraman, P. Extraction of blood vessels in fundus images of retina through hybrid segmentation approach. Mathematics 2019, 7, 169. [Google Scholar] [CrossRef] [Green Version]
- Khawaja, A.; Khan, T.M.; Khan, M.A.; Nawaz, S.J. A multi-scale directional line detector for retinal vessel segmentation. Sensors 2019, 19, 4949. [Google Scholar] [CrossRef] [Green Version]
- Upadhyay, K.; Agrawal, M.; Vashist, P. Unsupervised multiscale retinal blood vessel segmentation using fundus images. IET Image Processing 2020, 14, 2616–2625. [Google Scholar] [CrossRef]
- Palanivel, D.A.; Natarajan, S.; Gopalakrishnan, S. Retinal vessel segmentation using multifractal characterization. Appl. Soft Comput. 2020, 94, 106439. [Google Scholar] [CrossRef]
- Pachade, S.; Porwal, P.; Kokare, M.; Giancardo, L.; Meriaudeau, F. Retinal vasculature segmentation and measurement framework for color fundus and SLO images. Biocybern. Biomed. Eng. 2020, 40, 865–900. [Google Scholar] [CrossRef]
- Tian, F.; Li, Y.; Wang, J.; Chen, W. Blood Vessel Segmentation of Fundus Retinal Images Based on Improved Frangi and Mathematical Morphology. Comput. Math. Methods Med. 2021. [Google Scholar] [CrossRef]
- Mardani, K.; Maghooli, K. Enhancing retinal blood vessel segmentation in medical images using combined segmentation modes extracted by DBSCAN and morphological reconstruction. Biomed. Signal Processing Control 2021, 69, 102837. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Wang, J.J.; Wong, T.Y. Retinal vascular changes in pre-diabetes and prehypertension: New findings and their research and clinical implications. Diabetes Care 2007, 30, 2708–2715. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| TP | a pixel decided by the proposed system as vessel pixel, and it represents also vessel pixel according to ground truth |
| TN | a pixel decided by the proposed system as nonvessel pixel, and it is also non vessel pixel according to ground truth |
| FP | a pixel decided by the proposed system as vessel pixel, but it is non vessel pixel according to ground truth |
| FN | a pixel decided by the proposed system as non vessel pixel, but it represents vessel pixel according to ground truth |
| Scale | Surround Size, | Center Size, | ||
|---|---|---|---|---|
| = S, short | 7 | 0 | 33 | 25 |
| = L, large | 9 | 3 | 90 | 75 |
| DRIVE | STARE | |||||
|---|---|---|---|---|---|---|
| Image No. | Sen | Spe | Acc | Sen | Spe | Acc |
| 1. | 0.7797 | 0.9755 | 0.9579 | 0.5861 | 0.9715 | 0.9405 |
| 2. | 0.7564 | 0.9825 | 0.9592 | 0.5115 | 0.9737 | 0.9427 |
| 3. | 0.6944 | 0.9825 | 0.9536 | 0.7331 | 0.9617 | 0.9479 |
| 4. | 0.6894 | 0.9874 | 0.9598 | 0.6490 | 0.9814 | 0.9566 |
| 5. | 0.6795 | 0.9872 | 0.9581 | 0.6882 | 0.9826 | 0.9558 |
| 6. | 0.6594 | 0.9865 | 0.9545 | 0.8365 | 0.9714 | 0.9620 |
| 7. | 0.6976 | 0.9857 | 0.9592 | 0.8078 | 0.9681 | 0.9552 |
| 8. | 0.7068 | 0.9759 | 0.9525 | 0.7920 | 0.9716 | 0.9582 |
| 9. | 0.6949 | 0.9834 | 0.9599 | 0.8085 | 0.9707 | 0.9579 |
| 10. | 0.7308 | 0.9816 | 0.9608 | 0.7373 | 0.9774 | 0.9579 |
| 11. | 0.6877 | 0.9825 | 0.9559 | 0.7728 | 0.9767 | 0.9621 |
| 12. | 0.7718 | 0.9737 | 0.9561 | 0.8483 | 0.9749 | 0.9650 |
| 13. | 0.7028 | 0.9789 | 0.9517 | 0.7370 | 0.9752 | 0.9539 |
| 14. | 0.7958 | 0.9728 | 0.9584 | 0.6646 | 0.9798 | 0.9511 |
| 15. | 0.7506 | 0.9775 | 0.9612 | 0.6784 | 0.9803 | 0.9541 |
| 16. | 0.7358 | 0.9781 | 0.9560 | 0.6051 | 0.9831 | 0.9442 |
| 17. | 0.6797 | 0.9798 | 0.9542 | 0.7540 | 0.9828 | 0.9622 |
| 18. | 0.7443 | 0.9756 | 0.9571 | 0.7206 | 0.9888 | 0.9751 |
| 19. | 0.8303 | 0.9745 | 0.9624 | 0.7663 | 0.9775 | 0.9684 |
| 20. | 0.7543 | 0.9735 | 0.9573 | 0.6305 | 0.9716 | 0.9486 |
| Mean | 0.7271 | 0.9798 | 0.9573 | 0.7164 | 0.9760 | 0.9560 |
| Dataset | DRIVE | STARE | |||||
|---|---|---|---|---|---|---|---|
| Method/First Author | Year | Acc | Sen | Spe | Acc | Sen | Spe |
| Supervised | |||||||
| Thangaraj [22] | 2018 | 0.9606 | 0.8014 | 0.9753 | 0.9435 | 0.8339 | 0.9536 |
| Zhang [23] | 2019 | 0.9544 | 0.8175 | 0.9767 | 0.9656 | 0.8068 | 0.9838 |
| Tang [24] | 2020 | 0.9477 | 0.7338 | 0.9730 | 0.9498 | 0.7518 | 0.9734 |
| Adapa [25] | 2020 | 0.9450 | 0.6994 | 0.9811 | 0.9486 | 0.6298 | 0.9839 |
| Sayed [26] | 2021 | 0.958 | 0.786 | 0.973 | 0.953 | 0.831 | 0.9630 |
| Deep Learning | |||||||
| Yan [27] | 2018 | 0.9542 | 0.7653 | 0.9818 | 0.9612 | 0.7581 | 0.9846 |
| Soomro [28] | 2018 | 0.9480 | 0.739 | 0.956 | 0.947 | 0.748 | 0.9620 |
| Jiang [29] | 2018 | 0.9624 | 0.7540 | 0.9825 | 0.9734 | 0.8352 | 0.9846 |
| Alom [30] | 2018 | 0.9556 | 0.7792 | 0.9813 | 0.9712 | 0.8298 | 0.9862 |
| Khan [31] | 2020 | 0.9649 | 0.8252 | 0.9787 | - | - | - |
| Wu [32] | 2020 | 0.9582 | 0.7996 | 0.9813 | 0.9672 | 0.7963 | 0.9863 |
| Sathananthavathi [33] | 2021 | 0.9577 | 0.7918 | 0.9708 | 0.9445 | 0.8021 | 0.9561 |
| Unsupervised | |||||||
| Biswal [34] | 2018 | 0.9500 | 0.7100 | 0.9700 | 0.9500 | 0.7000 | 0.9700 |
| Pal [35] | 2019 | 0.9431 | 0.6129 | 0.9744 | - | - | - |
| Sundaram [36] | 2019 | 0.9300 | 0.6900 | 0.9400 | - | - | - |
| Khawaja [37] | 2019 | 0.9553 | 0.8043 | 0.9730 | 0.9545 | 0.8011 | 0.9694 |
| Upadhyay [38] | 2020 | 0.9560 | 0.7890 | 0.9720 | 0.9610 | 0.7360 | 0.9810 |
| Palanivel [39] | 2020 | 0.9480 | 0.7375 | 0.9788 | 0.9542 | 0.7484 | 0.9780 |
| Pachade [40] | 2020 | 0.9552 | 0.7738 | 0.9721 | 0.9543 | 0.7769 | 0.9688 |
| Tian [41] | 2021 | 0.9554 | 0.6942 | 0.9802 | 0.9492 | 0.7019 | 0.9771 |
| Mardani [42] | 2021 | 0.9519 | 0.7667 | 0.9692 | 0.9524 | 0.7969 | 0.9664 |
| Proposed Method | 2022 | 0.9573 | 0.7271 | 0.9798 | 0.9560 | 0.7164 | 0.9760 |
| DRIV | STARE | ||||
|---|---|---|---|---|---|
| Method | System Specs | Acc | T in sec | Acc | T in sec |
| Thangaraj [22] | 360 GHz Intel Core i7 20 GB RAM | 0.9606 | 156 | 0.9435 | 203 |
| Adapa [25] | 2 * Intel Xeon E2620 v4, 64 GB RAM, Nvidia Tesla K40 GPU | 0.9450 | 9 | 0.9486 | 9 |
| Alom [30] | GPU machine besides 56 G of RAM and an NIVIDIA GEFORCE GTX-980 Ti. | 0.9556 | 2.84 | 0.9712 | 6.42 |
| Sathananthavathi [33] | Intel Core i5, 32 GB RAM | 0.9577 | 10 | 0.9445 | 10 |
| Biswal [34] | Intel core i3, 1.7 GHZ, 4 GBRAM | 0.9500 | 3.3 | 0.9500 | 3.3 |
| Khawaja [37] | Core i7, 2.21 GHz, 16 GB RAM | 0.9553 | 5 | 0.9545 | 5 |
| Palanivel [39] | 2.9 GHz, 64 GB RAM | 0.9480 | 60 | 0.9542 | 60 |
| Pachade [40] | Intel Xenon, 2.00 GHz,16 GB RAM | 0.9552 | 3.47 | 0.9543 | 6.10 |
| Proposed Method | Intel(R) Xeon(R) 3.50GHz, 32 GB RAM. | 0.9573 | 3.17 | 0.9560 | 3.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muzammil, N.; Shah, S.A.A.; Shahzad, A.; Khan, M.A.; Ghoniem, R.M. Multifilters-Based Unsupervised Method for Retinal Blood Vessel Segmentation. Appl. Sci. 2022, 12, 6393. https://doi.org/10.3390/app12136393
Muzammil N, Shah SAA, Shahzad A, Khan MA, Ghoniem RM. Multifilters-Based Unsupervised Method for Retinal Blood Vessel Segmentation. Applied Sciences. 2022; 12(13):6393. https://doi.org/10.3390/app12136393
Chicago/Turabian StyleMuzammil, Nayab, Syed Ayaz Ali Shah, Aamir Shahzad, Muhammad Amir Khan, and Rania M. Ghoniem. 2022. "Multifilters-Based Unsupervised Method for Retinal Blood Vessel Segmentation" Applied Sciences 12, no. 13: 6393. https://doi.org/10.3390/app12136393
APA StyleMuzammil, N., Shah, S. A. A., Shahzad, A., Khan, M. A., & Ghoniem, R. M. (2022). Multifilters-Based Unsupervised Method for Retinal Blood Vessel Segmentation. Applied Sciences, 12(13), 6393. https://doi.org/10.3390/app12136393






