Sliding Mode Control of Electro-Hydraulic Position Servo System Based on Adaptive Reaching Law

Abstract

For the problem of the system state variable taking a long time to reach the sliding mode surface and the chattering frequency being high in the sliding mode surface, a sliding mode control method based on the adaptive reaching law is proposed, the system state variable is introduced based on the subreaching law, and an improved variable-speed reaching law is added with reference to the characteristics of the hyperbolic tangent function. The sliding mode control method is divided into two stages, namely, the initial state to the critical value s = ±1 and the system state variable reaching the equilibrium point of the sliding mode surface, and the total time obtained is less than the sum of these two stages. Secondly, this method is adopted in the electro-hydraulic position servo system, and a sliding mode controller is established. Through an AMESim/Simulink co-simulation, it is compared with the sliding mode controller based on the traditional exponential reaching law. The results show that this method can effectively reduce the jitter of the system, reduce the time for the system to reach the sliding surface, and improve the robustness of the system.

1. Introduction

Electro-hydraulic servo systems have been widely used in excavators [1], hydraulic load simulators [2,3], and industrial robots [4] due to their advantages of a high output power, high control precision, and fast response speed. However, the electro-hydraulic servo system itself has the characteristics of nonlinearity and parameter uncertainty and is affected by friction leakage and external disturbance during the movement of the hydraulic actuator, which is not conducive to the accurate control of the position of the servo system. Sliding mode control (SMC) has a strong antidisturbance ability and is widely used in electro-hydraulic servo systems. The basic idea of SMC is to drive the system states to an internally stable reduced-order system within finite time [5,6,7,8], which means that the motion of the controlled system is divided into two stages: one is “reaching” and the other is “sliding” [9]. However, there are still some problems in SMC, especially the chattering problem [10].

Many scholars have conducted extensive research on the problem of sliding mode chattering. The methods to solve this problem include quasi-sliding mode method [11,12,13], high-order sliding mode method [14], adaptive fuzzy integral sliding mode velocity control [15], boundary layer method [16], and dynamic sliding mode method [17]. Xue et al. [18] designed a new sliding mode controller, which could make the position error converge to zero in a certain period of time without external disturbances, but the controller output parameters still had chattering. Pandey et al. [19] proposed an adaptive reaching-law controller that reached the sliding surface at the fastest speed, thereby ignoring chattering. Most of the methods mentioned above combine the exponential reaching law and the constant velocity reaching law to weaken the chattering. Although the exponential reaching law can improve the dynamic characteristics of the system and reduce the chattering by adjusting the parameters of the reaching law, it cannot completely eliminate the chattering of the system. Ma et al. [20] proposed a variable structure control with a neural network and an optimized fractional-order selection policy, which could suppress the combined error in the boundedness of approximating double Euler difference errors. Liu et al. [21] proposed a new exponential reaching law method, which could speed up the convergence while adding power function terms. Yu et al. [22] proposed a method combining the exponential reaching law and power reaching law, which could effectively solve the problem of the arrival time of the power reaching law being too long. Zong et al. [23] proposed an exponential reaching law method, which combined with the mismatched uncertain system to weaken the buffeting of the system, and the stability of the system was ensured. Pan et al. [24] combined the isokinetic reaching law with the bipower reaching law to accelerate the global convergence of the sliding mode variable structure. Dong et al. [25] proposed a class of globally nonsingular SMC laws, called logarithmic sliding mode control, which led to a higher tracking precision and a faster local convergence rate than those of some classical SMCs. To attenuate the effect of parameter uncertainties and uncertain nonlinearities in the hydraulic system, other nonlinear control schemes have been proposed, such as the disturbance observer [26,27,28,29,30], state observer [31,32,33], and adaptive control [34,35,36,37].

According to the characteristics of SMC, this paper proposes an improved adaptive reaching law SMC algorithm to control the position of the valve-controlled asymmetric cylinder system, so that it can quickly track the desired trajectory, reduce the system response time, and improve the robustness of the system. An AMESim/Simulink co-simulation was carried out to compare between the SMC controller based on the exponential reaching law and the SMC controller based on the adaptive reaching law to verify the rationality of the proposed algorithm.

The rest of the paper is organized as follows. The second section describes the problem formulation and dynamic models. The third section presents the proposed SMC controller based on the adaptive reaching law. The fourth section presents the simulation analyses. The final section draws conclusions.

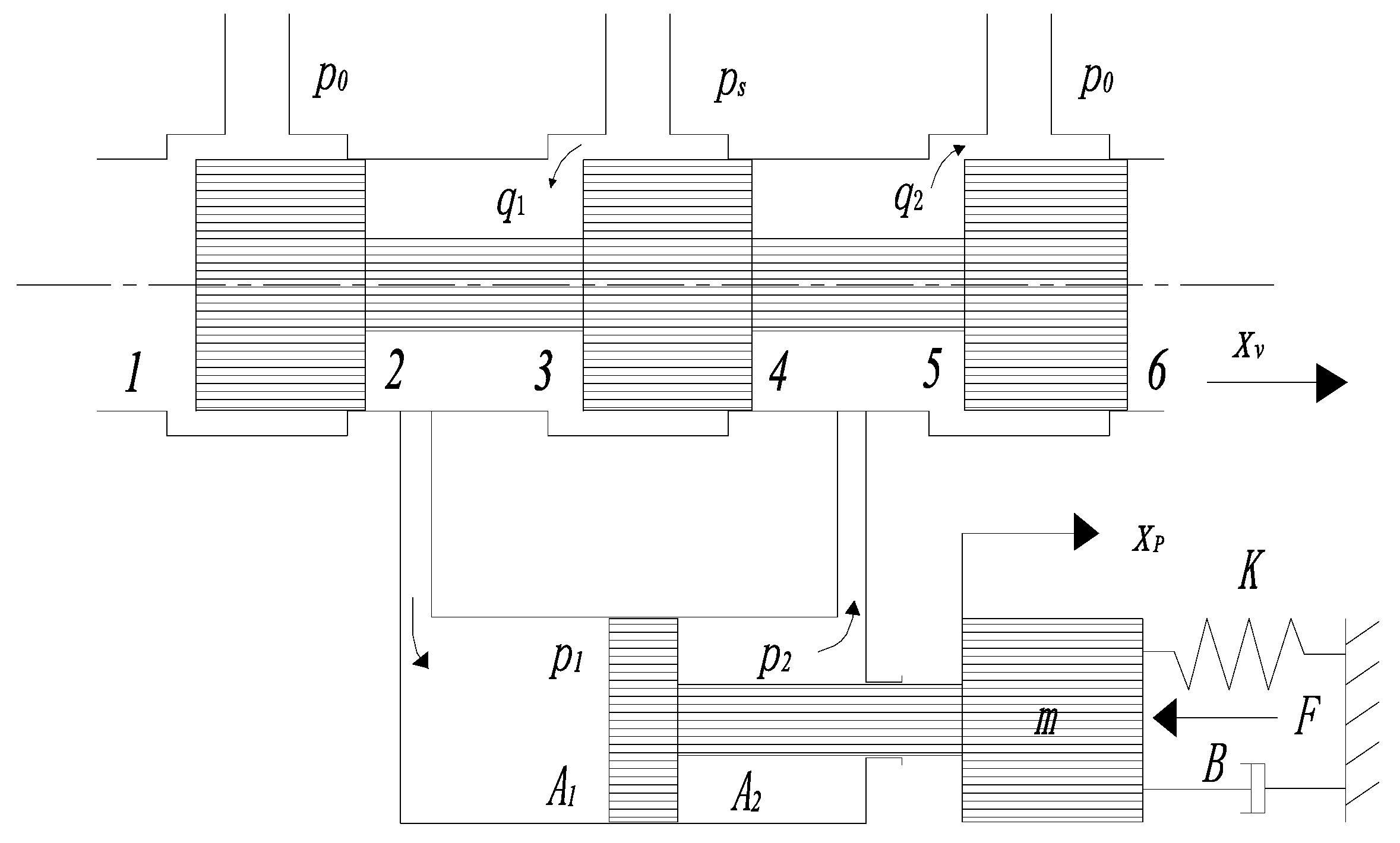
2. Problem Formulation and Dynamic Models

In the electro-hydraulic servo system, compared with the symmetrical hydraulic cylinder, the asymmetrical cylinder has the advantages of occupying a small space, being a simple structure and having a low cost, so it is widely used. In this paper, a four-way three-position (4/3) valve-controlled asymmetric hydraulic cylinder was used as the power mechanism of the electro-hydraulic servo system; the structure diagram of the valve-controlled asymmetric hydraulic cylinder is shown in Figure 1.

Let the positive direction of the displacement of the spool of the servo valve be the direction shown by the $x_v$ arrow in Figure 1, at time $x_v>0$. Let the ratio of the effective area of the bore area to the rod area of the asymmetric cylinder be $n=A_2/A_1$, where $A_1$ is the effective area of the bore, $A_2$ is the effective area of the rod.

When $x_v>0$, the spool moves to the right, the piston rod extends, and the load pressure is

$$p_L=p_1-n{p}_2$$

(1)

and the load flow is:

$$q_L=q_1$$

(2)

When, $x_v<0$, the spool moves to the left, the piston rod retracts, the load pressure is

$$p_L=p_2-n{p}_1$$

(3)

and the load flow is:

$$q_L=q_2$$

(4)

The flow continuity equation of the piston chamber of the valve-controlled asymmetric hydraulic cylinder is:

$$q_1=A_1\frac{d{x}_p}{dt}+C_{ip}(p_1-p_2)+C_{ep}{p}_1+\frac{V_1}{{\beta }_e}\frac{d{p}_1}{dt}$$

(5)

The flow continuity equation of the rod chamber of the valve-controlled asymmetric hydraulic cylinder is:

$$q_2=A_2\frac{d{x}_p}{dt}+C_{ip}(p_1-p_2)-C_{ep}{p}_2-\frac{V_2}{{\beta }_e}\frac{d{p}_2}{dt}$$

(6)

where $V_1$ is the effective volume of the piston-side chamber; $V_2$ is the effective volume of the rod-side chamber; ${\beta }_e$ is the effective bulk modulus of the hydraulic oil; $C_{ip}$ is the internal leakage coefficient of the cylinder; $C_{ep}$ is the external leakage coefficient of the cylinder; $x_p$ is the displacement of the piston; $p_1$ is the pressure of the piston-side chamber; and $p_2$ is the pressure of the rod-side chamber.

The positive direction of piston displacement is defined as the direction shown by the $x_p$ arrow in Figure 1, when the piston extends. Taking $x_p$ > 0 as an example, the flow equation of the four-way three-position (4/3) valve is established as

$$\left\{\begin{array}{l}{q}_1=C_d\omega x_v\sqrt{\frac{2(p_s-p_1)}{\rho }}\\ q_2={\mathrm{C}}_d\omega x_v\sqrt{\frac{2p_2}{\rho }}\end{array}\right.$$

(7)

where $C_d$ is the flow coefficient of the valve; $\omega$ is the area gradient of the valve; and $\rho$ is the oil density. The flow rate of the piston-side chamber can be expressed by the product of the velocity of the piston and the effective area of the bore area. Similarly, the flow rate of the rod-side chamber can be expressed by the product of the velocity of the piston and the effective area of the rod area. Therefore, the relationship between the flow rate of the piston-side chamber and the flow rate of the rod-side chamber is

$$\frac{q_2}{q_1}=\frac{v{A}_2}{v{A}_1}=\frac{A_2}{A_1}=n$$

(8)

where $v$ is the velocity of the piston.

The pressure of the piston-side chamber can be expressed as

$$p_1=\frac{n^3{p}_s+p_L}{n^3+1}$$

(9)

The pressure of the rod-side chamber can be expressed as

$$p_2=\frac{n^2(p_s-p_L)}{n^3+1}$$

(10)

where $p_s$ is the system pressure.

Equations (1), (2) and (7)–(10) can be combined into the load flow equation:

$$q_L=\eta x_v\sqrt{p_s-p_L}$$

(11)

where $\eta =C_d\omega \sqrt{\frac{2}{p(1+n^3)}}$ is a constant.

Linearizing Equation (7), we obtain

$$q_L=\frac{\partial q_L}{\partial x_v}{x}_v+\frac{\partial q_L}{\partial p_L}{p}_L=K_v{x}_v-K_c{p}_L$$

(12)

where $K_v$ is the flow gain of the valve and $K_c$ is the flow-pressure coefficient of the valve.

From Equations (1), (2), (5) and (6), the load flow is obtained as

$$\begin{array}{l}{q}_L=q_1=A_1\frac{d{x}_p}{dt}+C_{ip}(p_1-p_2)+C_{ep}{p}_1+\frac{V_1}{{\beta }_e}\frac{d{p}_1}{dt}\\ =A_1{\dot{V}}_1+C_{ic}{p}_L+C_{tc}{P}_s+\frac{{\dot{p}}_L{V}_e}{4{\beta }_e}\end{array}$$

(13)

where $C_{ic}=\frac{(1+n^2)C_{ip}+C_{ep}}{1+n^3}$ is the equivalent leakage coefficient of the cylinder;$C_{tc}=\frac{n^2[n(C_{ip}+C_{ep})-C_{ip}]}{1+n^3}$ is the incidental leakage coefficient of the cylinder; and $V_e=\frac{4V_1}{1+n^3}$ is the equivalent volume of the cylinder.

The resulting force equation between the hydraulic cylinder and the load is

$$A_1{p}_1-A_2{p}_2=A_1{P}_L=m{\ddot{x}}_p+B{\dot{x}}_p+K{x}_p+F$$

(14)

where m is the equivalent load mass; B is the equivalent load damping; K is the equivalent load stiffness; and F is the equivalent load force.

Equations (5), (12) and (14) are the three basic equations and the displacement equation of the valve-controlled asymmetric hydraulic cylinder, Laplace transformed, can be obtained as

$$X_p=\frac{Q_{L0}(s)-\frac{K_{ce}}{A_1{}^2}(1+\frac{V_e}{4{\beta }_e{K}_{cc}}s)F-\frac{C_{tc}{P}_s}{A_1}}{\frac{m{V}_e}{4{\beta }_e{A}_1{}^2}{s}^3+(\frac{m{K}_{ce}}{A_1{}^2}+\frac{B{V}_e}{4{\beta }_e{A}_1{}^2})s^2+(1+\frac{B{K}_{ce}}{A_1{}^2}+\frac{K{V}_e}{4{\beta }_e{A}_1{}^2})s+\frac{K{K}_{ce}}{A_1{}^2}}$$

(15)

where $K_{ce}=K_c+C_{ic}$ is the total flow-pressure coefficient; $Q_{L0}(s)$ is obtained by the Laplace transform of $q_{L0}$; $q_{L0}=K_v{x}_v$ is the change in load flow caused only by the displacement of the spool; and $P_s$ is the Laplace transform of the supply pressure $p_s$.

Supposing the spring stiffness is $K=0$, the damping coefficient $\frac{A_1{}^2}{K_{ce}}$ is usually much larger than $B$, so that $\frac{B{K}_{ce}}{A_1{}^2}<<1$. Under Equation (15), it reduces to

$$\begin{array}{l}{X}_p=\frac{\frac{Q_{L0}(s)}{A_1}-(K_{ce}+\frac{V_e}{4{\beta }_e}s)\frac{F}{A_1{}^2}-\frac{C_{tc}{P}_s}{A_1}}{\frac{m{V}_e}{4{\beta }_e{A}_1{}^2}{s}^3+\frac{m{K}_{ce}}{A_1{}^2}{s}^2+s}\\ =\frac{\frac{Q_{L0}(s)}{A_1}-(K_{ce}+\frac{V_e}{4{\beta }_e}s)\frac{F}{A_1{}^2}-\frac{C_{tc}{P}_s}{A_1}}{s(\frac{s^2}{{\omega }_h{}^2}+\frac{2{\xi }_{h}s}{{\omega }_h}+1)}\end{array}$$

(16)

where ${\omega }_h=\sqrt{\frac{4{\beta }_e{A}_1{}^2}{m{V}_e}}$ is the hydraulic natural frequency and ${\xi }_h=\frac{K_{ce}}{A_1}\sqrt{\frac{{\beta }_{e}m}{V_e}}$ is the damping ratio.

When $x_v<0$, the same formula as Formula (16) can be deduced in the same way.

3. Design of Sliding Mode Controller Based on Adaptive Reaching Law

3.1. Design of Sliding Surface

The nonlinear effect of the servo valve is not considered in the electro-hydraulic servo system, and it is simplified as a proportional link, through the mathematical model of the electro-hydraulic servo system, the transfer function of the control voltage of the servo valve to the piston displacement of the hydraulic cylinder is obtained as

$$G(s)=\frac{K_{sys}}{s(\frac{s^2}{{\omega }_h{}^2}+\frac{2{\xi }_{h}s}{{\omega }_h}+1)}$$

(17)

where $K_{sys}$ is the system’s open-loop gain obtained by simplifying it into a proportional link without considering the nonlinear influence of the servo valve. Then, the state equation of the electro-hydraulic position servo system is as follows

$$\left\{\begin{array}{l}\dot{X}=Ax+Bu\\ y=Cx\end{array}\right.$$

(18)

$$A=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& -{\omega }_h{}^2& -2{\xi }_h{\omega }_h \end{array}\right]$$

(19)

$$B=\left[0 0 K_{sys}{\omega }_h{}^2\right]$$

(20)

$$C=\left[1 0 0\right]$$

(21)

In Equations (19)–(21), the controlled object is the third-order system, and $X={\left[x_1 x_2 x_3\right]}^T$ is the system’s state variable. $x_1$ is the piston displacement of the cylinder; $x_2$ is the piston velocity of the cylinder; $x_3$ is the piston acceleration of the cylinder; $u$ is the system’s control input; and $y$ is the system’s output.

The state equation of the system model can be expressed as

$$\left\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ {\dot{x}}_3=-{\omega }_h{}^2{x}_2-2{\xi }_h{\omega }_h{x}_3+K_{sys}{\omega }_h{}^{2}u\end{array}\right.$$

(22)

$$y=x_1$$

(23)

The displacement tracking error of the system is

$$e=r-y$$

(24)

where $r$ is the desired motion trajectory.

The error vector of the system is defined as

$$E={[e_1 e_2 e_3]}^T={\left[r-y \dot{r}-\dot{y} \ddot{r}-\ddot{y}\right]}^T$$

(25)

The error state equation can be written according to Equations (22) and (23):

$$\left\{\begin{array}{l}{\dot{e}}_1=e_2\\ {\dot{e}}_2=e_3\\ {\dot{e}}_3=-{\omega }_h{}^2{e}_2-2{\xi }_h{\omega }_h{e}_3-K_{sys}{\omega }_h{}^{2}u+{\omega }_h{}^2\dot{r}+2{\xi }_h{\omega }_h\ddot{r}+\stackrel{⃛}{r}\end{array}\right.$$

(26)

The designed sliding mode switching function is

$$s=c_1{e}_1+c_2{e}_2+e_3$$

(27)

The state equation of the sliding mode motion is

$$\left\{\begin{array}{l}{\dot{e}}_1=e_2\\ {\dot{e}}_2=e_3\\ {\dot{e}}_3=-{\omega }_h{}^2{e}_2-2{\xi }_h{\omega }_h{e}_3-K_{sys}{\omega }_h{}^{2}u+{\omega }_h{}^2\dot{r}+2{\xi }_h{\omega }_h\ddot{r}+\stackrel{⃛}{r}\\ c_1{e}_1+c_2{e}_2+e_3=0\end{array}\right.$$

(28)

For satisfying $s=c_1{e}_1+c_2{e}_2+e_3=0$, simplifying the state Equation (28) of the sliding mode motion yields

$$\left\{\begin{array}{l}{\dot{e}}_1=e_2\\ {\dot{e}}_2=e_3=-c_1{e}_1-c_2{e}_2\end{array}\right.$$

(29)

Equation (29) determines the dynamic quality of the sliding mode, and $c_1$ and $c_2$ are obtained by the pole configuration method.

3.2. Controller Design

Step 1: Designing a suitable controller can make the sliding points outside the sliding mode switching surface reach the sliding mode switching surface within a certain period of time, that is to say, the following conditional expression is satisfied

$$\dot{s}=0$$

(30)

The equivalent control part can be derived from Equation (27) to obtain

$$\begin{array}{ll}\dot{s}& =c_1{\dot{e}}_1+c_2{\dot{e}}_2+{\dot{e}}_3\\ & =c_1{\dot{e}}_1+c_2{\dot{e}}_2-{\omega }_h{}^2{e}_2-2{\xi }_h{\omega }_h{e}_3-K_{sys}{\omega }_h{}^{2}u+{\omega }_h{}^2\dot{r}+2{\xi }_h{\omega }_h\ddot{r}+\stackrel{⃛}{r}\\ & =c_1{e}_2+c_2{e}_3-{\omega }_h{}^2{e}_2-2{\xi }_h{\omega }_h{e}_3-K_{sys}{\omega }_h{}^{2}u+{\omega }_h{}^2\dot{r}+2{\xi }_h{\omega }_h\ddot{r}+\stackrel{⃛}{r}\end{array}$$

(31)

From conditional Equation (30), the equivalent control $u_{eq}$ can be obtained as

$$u_{eq}=\frac{1}{K_{sys}{\omega }_h{}^2}\left[\begin{array}{l}(c_1-{\omega }_h{}^2)e_2+(c_2-2{\xi }_h{\omega }_h)e_3\\ -K_{sys}{\omega }_h{}^{2}u+{\omega }_h{}^2\dot{r}+2{\xi }_h{\omega }_h\ddot{r}+\stackrel{⃛}{r}\end{array}\right]$$

(32)

Step 2: Design of the reaching law. For the traditional exponential reaching law which is commonly used,

$$\dot{s}=-\xi \mathrm{sgn}(s)-\zeta s,\xi >0,\zeta >0$$

(33)

where

$$\mathrm{sgn}(s)=\left\{\begin{array}{l}1 s>0\\ -1 s<0\end{array}\right.$$

(34)

Combining (31) and (33) we get

$$\dot{s}=c_1{e}_2+c_2{e}_3+{\dot{e}}_3=-\xi \mathrm{sgn}(s)-\zeta s$$

(35)

Substituting into (31) we get

$$\begin{array}{l}\dot{s}=c_1{e}_2+c_2{e}_3-{\omega }_h{}^2{e}_2-2{\xi }_h{\omega }_h{e}_3-K_{sys}{\omega }_h{}^{2}u+{\omega }_h{}^2\dot{r}+2{\xi }_h{\omega }_h\ddot{r}+\stackrel{⃜}{r}\\ =-\xi \mathrm{sgn}(s)-\zeta s\end{array}$$

(36)

The exponential reaching law SMC control law $u$ is designed as:

$$u=\frac{1}{K_{sys}{\omega }_h{}^2}\left[\begin{array}{l}(c_1-{\omega }_h{}^2)e_2+(c_2-2{\xi }_h{\omega }_h)e_3+{\omega }_h{}^2\dot{r}+2{\xi }_h{\omega }_h\ddot{r}\\ +\stackrel{⃛}{r}+\xi \mathrm{sgn}(s)+\zeta s\end{array}\right]$$

(37)

If $\xi$ is too small, the approach velocity will be very slow, and the adjustment process will be too slow; on the contrary, if $\xi$ is too large, the system velocity will be large, and the jitter will be large when the system reaches the switching surface.

A better adaptive reaching law for reducing system jitter is adopted below. The constructed adaptive reaching law is

$$\dot{s}=-\xi {\left|s\right|}^2\mathrm{sgn}(s)-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)$$

(38)

Combining Equations (31) and (38), we obtain

$$\dot{s}=c_1{e}_2+c_2{e}_3+{\dot{e}}_3=-\xi {\left|s\right|}^2\mathrm{sgn}(s)-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)$$

(39)

Substituting into Equation (31) yields:

$$\begin{array}{l}\dot{s}=c_1{e}_2+c_2{e}_3-{\omega }_h{}^2{e}_2-2{\xi }_h{\omega }_h{e}_3-K_{sys}{\omega }_h{}^{2}u\\ +{\omega }_h{}^2\dot{r}+2{\xi }_h{\omega }_h\ddot{r}+\stackrel{⃛}{r}\\ =-\xi {\left|s\right|}^2\mathrm{sgn}(s)-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)\end{array}$$

(40)

The SMC actual control law $u$ is designed as

$$u=\frac{1}{K_{sys}{\omega }_h{}^2}\left[\begin{array}{l}(c_1-{\omega }_h{}^2)e_2+(c_2-2{\xi }_h{\omega }_h)e_3+{\omega }_h{}^2\dot{r}+2{\xi }_h{\omega }_h\ddot{r}\\ +\stackrel{⃛}{r}+\xi {\left|s\right|}^2\mathrm{sgn}(s)+\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)\end{array}\right]$$

(41)

where $\xi$ and $\zeta$ are the adaptive reaching law parameters, and $\xi >0,\zeta >0$.

3.3. Characteristic Analysis of SMC Controller Based on Adaptive Reaching Law

When the system state variable $x$ is far away from the sliding mode surface, ${\left|s\right|}^2$ is the largest, $\underset{x\to \infty }{\lim }\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)=\zeta$, $-\xi {\left|s\right|}^2\mathrm{sgn}(s)$ plays a major role in the controller output, and

$-\xi {\left|s\right|}^2\mathrm{sgn}(s)$ ensuring that the rate of approaching the sliding mode surface is large enough.

When the system state variable $x$ moves in the direction close to the sliding mode surface, $s$ decreases, $-\xi {\left|s\right|}^2\mathrm{sgn}(s)$ approaches zero, and $-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)$ plays a major role in the output of the controller:

$$\underset{x\to 0^{+}}{\lim }\zeta \frac{1-e^{-\left|x\right|}}{(1+e^{-\left|x\right|})x}=\frac{\zeta }{2}$$

(42)

where $-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}$ converges to near the origin $\frac{\zeta x}{2}$ and the approach velocity decreases with the decrease of $\left|x\right|$.

Next, the characteristics of the SMC controller using the adaptive reaching law are analyzed and proved. Only when the reaching law meets the arrival condition can the existence of the sliding mode state be guaranteed, that is, it satisfies $s\dot{s}<0$.

Theorem 1.

The adaptive reaching law has reachability.

Proof of Theorem 1.

Suppose a Lyapunov function $V=s^2/2$, and derivate this function to obtain $\dot{V}=s\dot{s}=-\xi {\left|s\right|}^3-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\left|s\right|$. From the adaptive approach rate parameter $\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}>0$, we obtain $\dot{V}<0$, it can be seen that the system satisfies the arrival condition, that is, the adaptive reaching law $\dot{s}=-\xi {\left|s\right|}^2\mathrm{sgn}(s)-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)$ satisfies the arrival condition. □

Theorem 2.

For the adaptive reaching law, the reaching law can make the system reach the sliding mode surface in a certain time, that is, the system converges to$s=\dot{s}=0$in a certain time.

Proof of Theorem 2.

Assuming the initial position $s(0)>1$, the proof of the arrival time of the system is divided into two stages. □

• Approach $s=1$ from the initial postion $s(0)$. At this stage $-\xi {\left|s\right|}^2\mathrm{sgn}(s)>>-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)$, ignoring the $-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)$ term influence, that is $\frac{ds}{dt}=-\xi s^2$, by integrating it, we obtain

  $${\displaystyle {\int }_{s\left(0\right)}^1{s}^{-2}ds={\displaystyle {\int }_0^{t_1}-\xi dt}}$$

  (43)

  and $t_1$ as

  $$t_1=\frac{1-s{(0)}^{-1}}{\xi }$$

  (44)
• From $s=1$, approach $s=0$. At this stage $-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}\mathrm{sgn}(s)>>-\xi {\left|s\right|}^2\mathrm{sgn}(s)$, ignoring the shadowing of $-\xi {\left|s\right|}^2\mathrm{sgn}(s)$, that is, $\frac{ds}{dt}=-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}$, by integrating it, we obtain

  $${\displaystyle {\int }_0^{t_1}ds={\displaystyle {\int }_0^{t_2}-\zeta \frac{1-e^{-\left|x\right|}}{1+e^{-\left|x\right|}}dt}}$$

  (45)

  and $t_2$ as

  $$t_2=\frac{1+e^{-\left|x\right|}}{\zeta (1-e^{-\left|x\right|})}$$

  (46)

It can be obtained that the total time $t^{\prime }$ for the system state trajectory to reach the sliding surface is

$$t^{\prime }=t_1+t_2=\frac{1-s{(0)}^{-1}}{\xi }+\frac{1+e^{-\left|x\right|}}{\zeta (1-e^{-\left|x\right|})}$$

(47)

Assuming that the second-stage system state $\left|x\right|$ lies between ${\left|x\right|}_{\min }$ and ${\left|x\right|}_{\max }$, and the above derivation ignores secondary factors, then $t<\frac{1-s{(0)}^{-1}}{\xi }+\frac{1+e^{-\left|x_{\min }\right|}}{\zeta (1-e^{-\left|x_{\min }\right|})}$.

It can be seen that the electro-hydraulic position servo system designed in this paper can reach the sliding surface in a limited time. The schematic diagram of the SMC system based on the adaptive reaching law is shown in Figure 2. The AMESim/Simulink co-simulation block diagram is shown in Figure 3.

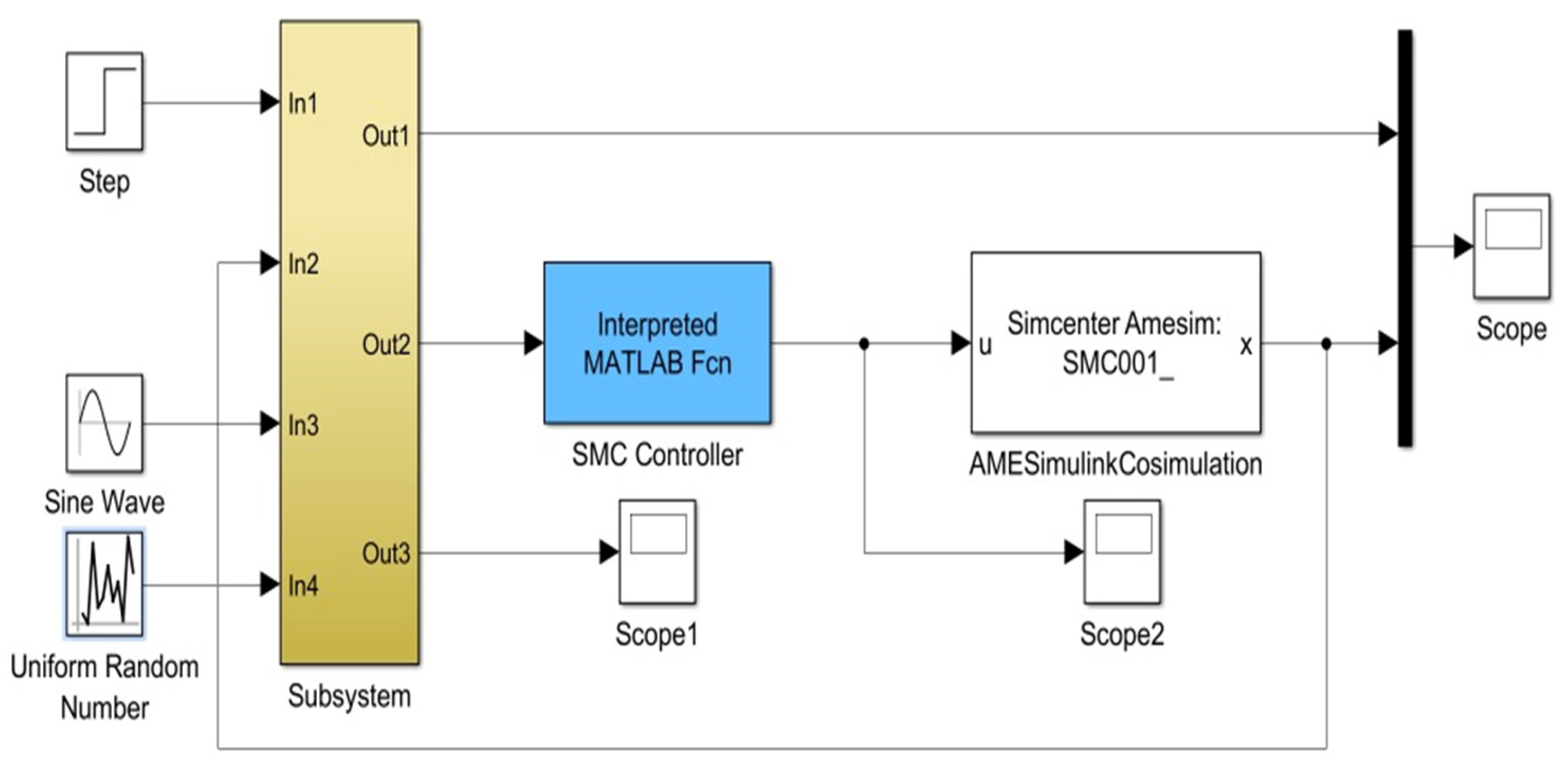
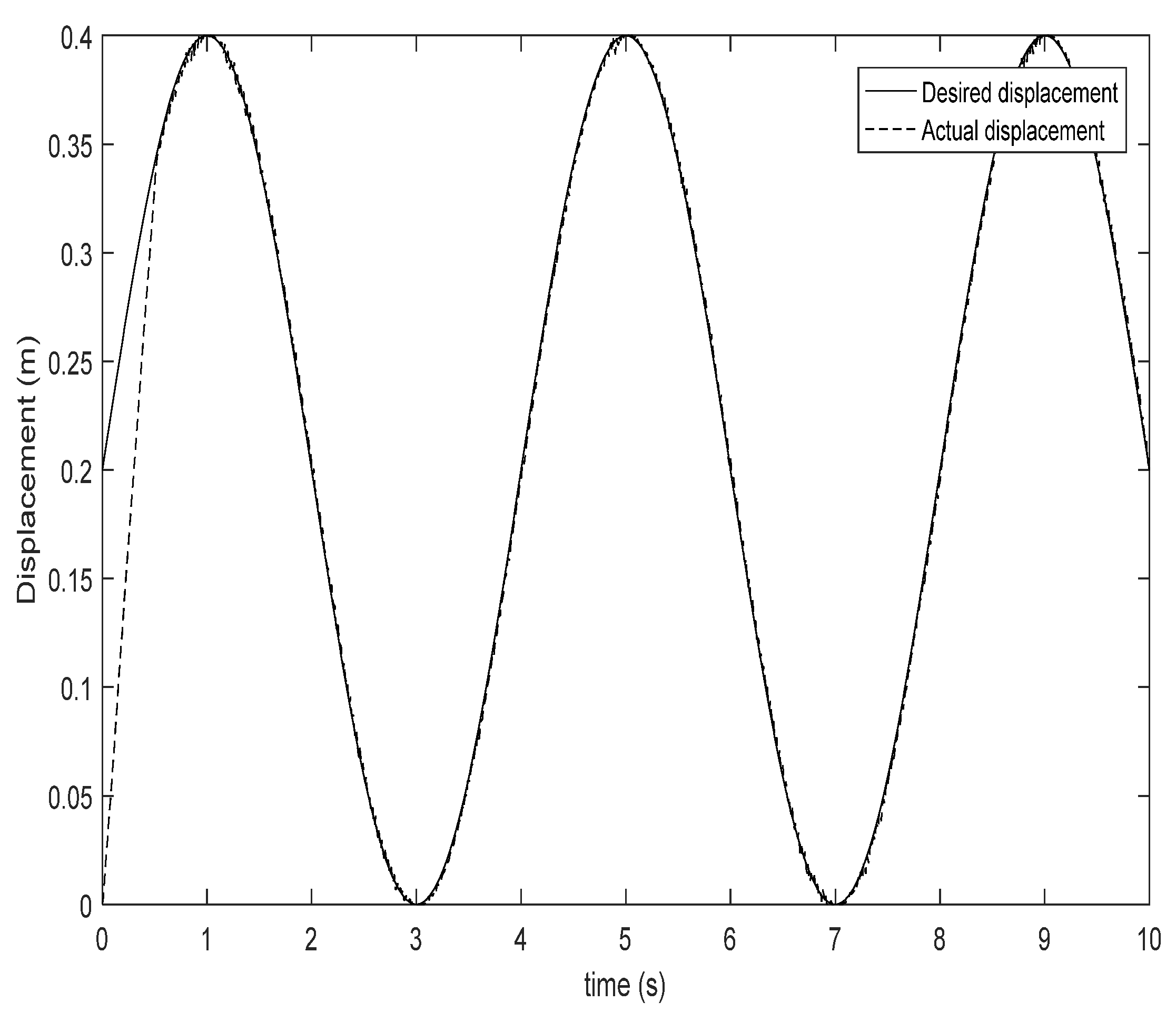
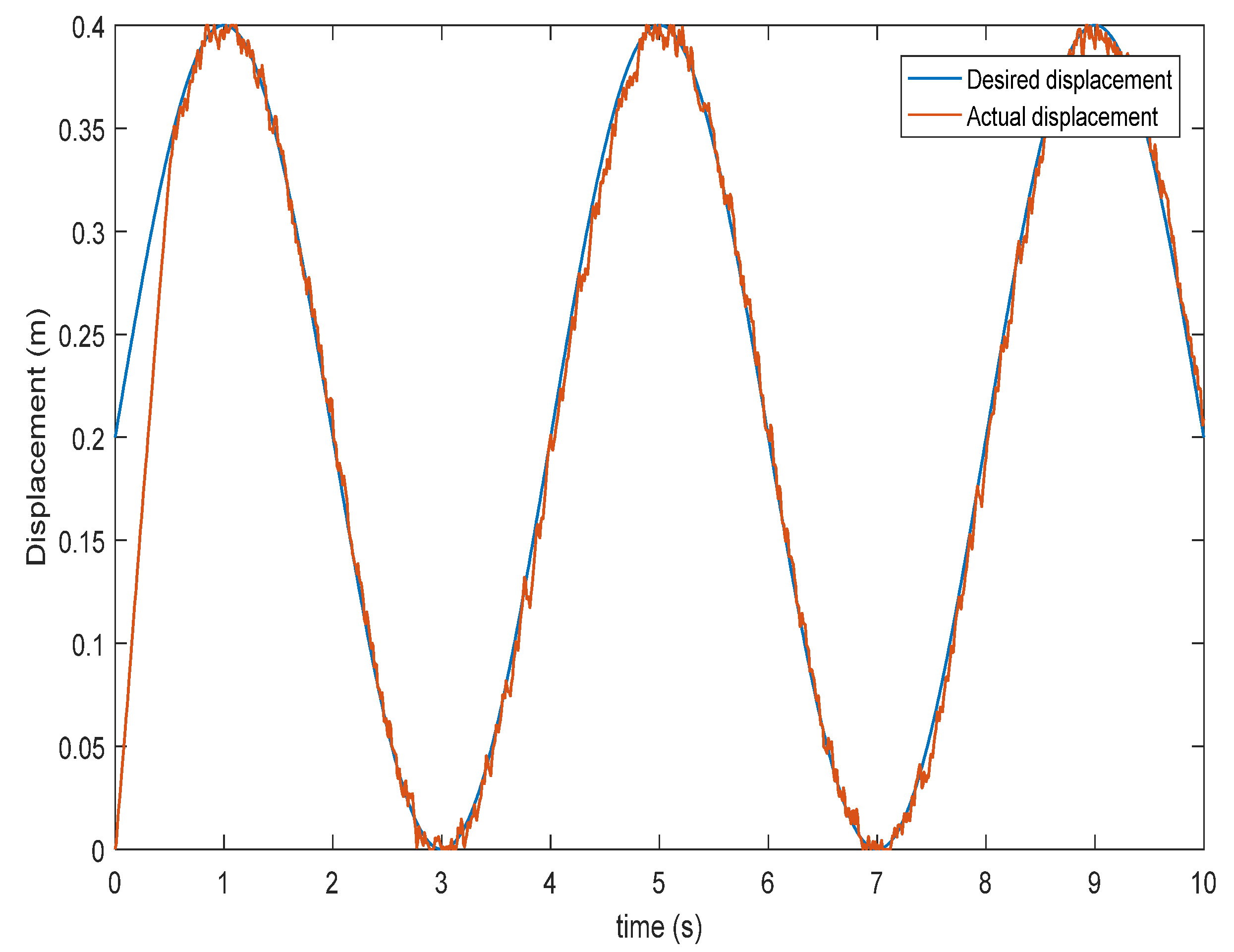
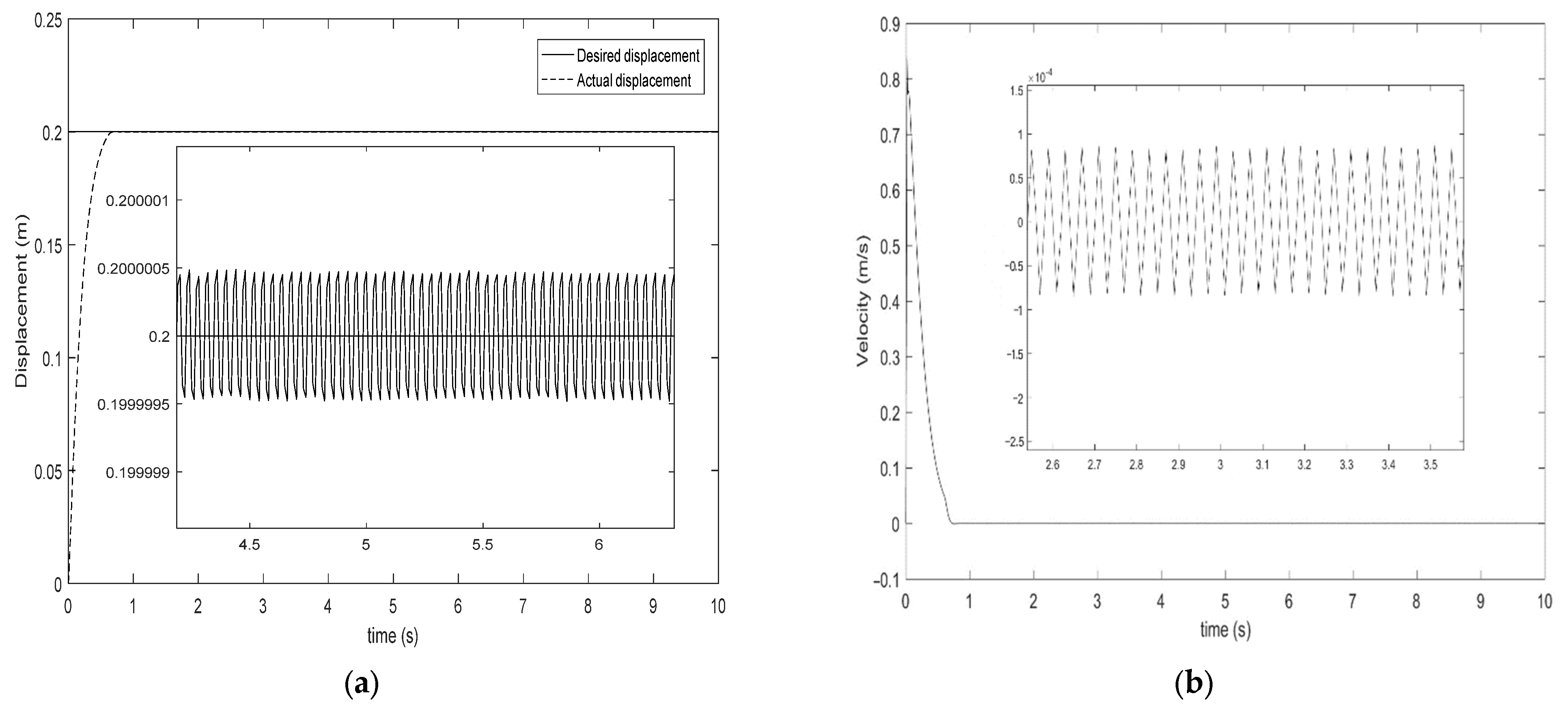
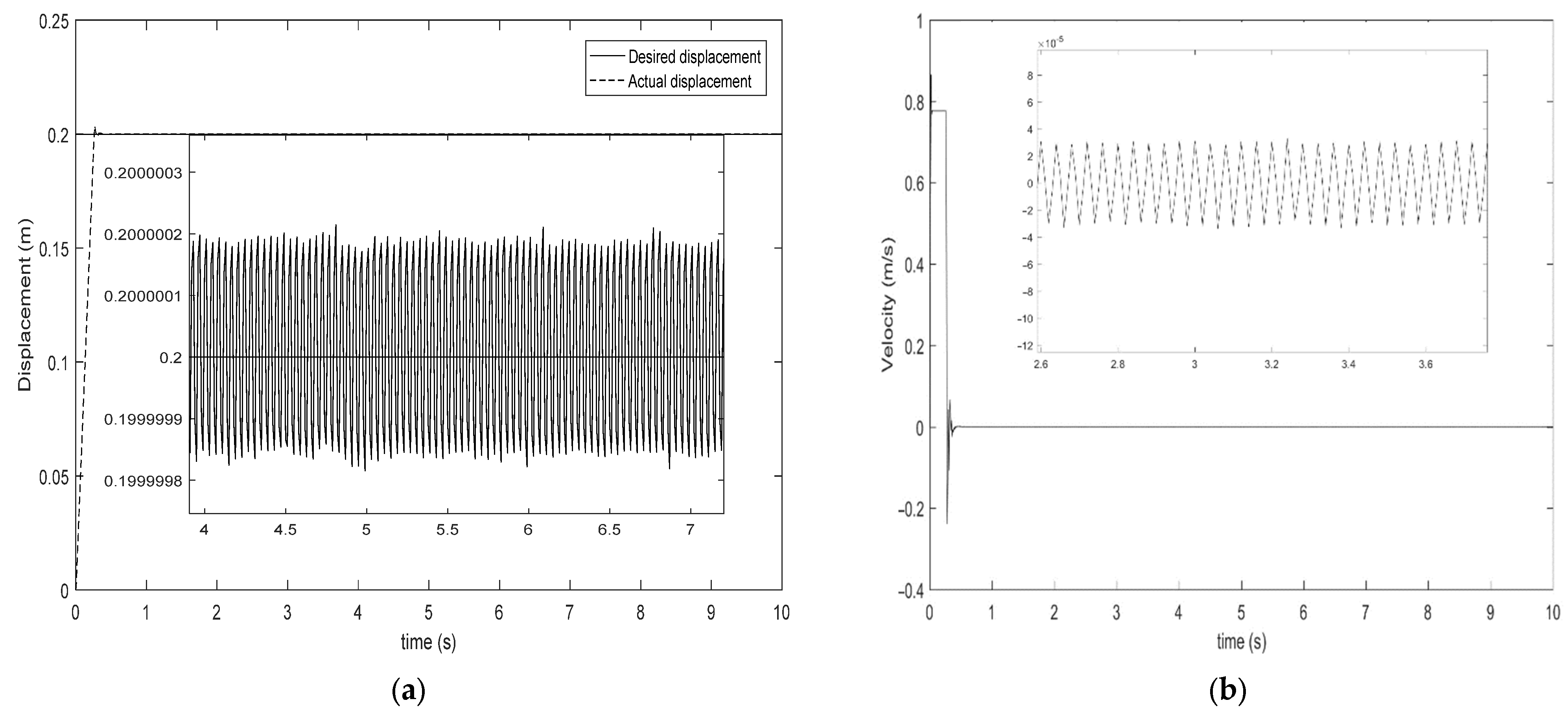
4. Simulation Analyses

Some parameters of the electro-hydraulic position servo system studied in this paper are shown in

Table 1. Parameters of electro-hydraulic position servo system.

Name	Parameter
Maximum stroke of hydraulic cylinder L	0.4 m
Hydraulic cylinder inner diameter D	63 mm
Piston rod diameter d	45 mm
Servo valve rated voltage u	10 V
Servo valve flow q	60 L/min
System working pressure ps	15 MPa
Oil return pressure p0	0 MPa

, the parameters of the adaptive reaching law SMC algorithm are shown in

Table 2. Parameters of adaptive reaching law SMC algorithm.

Name	Parameter
$\mathrm{System} \mathrm{open} \mathrm{loop} \mathrm{gain} K_{sys}$	1.86
$\mathrm{Parameter} c_1$	29,258
$\mathrm{Parameter} c_2$	68.8
Parameter $\xi$	5
Parameter $\zeta$	20
Valve-controlled cylinder natural Frequency	296 rad/s
Valve-controlled cylinder damping ratio	0.2

, and the parameters of the exponential reaching law SMC algorithm are shown in

Table 3. Parameters of exponential reaching law SMC algorithm.

Name	Parameter
$\mathrm{System} \mathrm{open} \mathrm{loop} \mathrm{gain} K_{sys}$	1.86
$\mathrm{Parameter} c_1$	29,258
$\mathrm{Parameter} c_2$	68.8
Parameter $\xi$	5
Parameter $\zeta$	20
Valve-controlled cylinder natural Frequency	296 rad/s
Valve-controlled cylinder damping ratio	0.2

. The nonlinear electro-hydraulic position servo system model was used with AMESim in the AMESim/Simulink co-simulation. The sampling time in the simulation was 0.001 s.

The paper uses the co-simulation function of AMESim and Simulink to simulate the system. Giving a sinusoidal signal, the SMC algorithm based on the exponential reaching law and the SMC algorithm based on the adaptive reaching law were used for the simulation and the obtained curves were compared and analyzed. Figure 4 is the tracking characteristic curve of the SMC system based on the exponential reaching law, and Figure 5 is the tracking characteristic curve of the SMC system based on the adaptive reaching law. Compared with the SMC algorithm based on the traditional exponential reaching law, the SMC algorithm of the adaptive reaching law has a great improvement in the control accuracy, and the following effect is obviously better than that of the SMC system using the traditional exponential reaching law algorithm. As shown in Figure 6, compared with the exponential reaching law SMC algorithm, the adaptive reaching law SMC algorithm can adaptively adjust the system control variables, so that the final displacement tracking effect is better.

A bounded white noise interference signal was added to the given sinusoidal signal, and the exponential reaching law and the adaptive reaching law SMC controllers were used for the simulation, respectively. It can be seen from Figure 7 and Figure 8 that the displacement tracking effect of the adaptive reaching law SMC algorithm is obviously better than that of the exponential reaching law SMC algorithm, after being disturbed. The proposed adaptive reaching law SMC controller improves the robustness of the system.

Giving a step signal, we used the SMC algorithm based on the exponential reaching law and the SMC algorithm based on the adaptive reaching law to simulate the piston displacement trajectory and piston velocity trajectory. It can be seen from Figure 9 that the SMC algorithm based on the exponential reaching law can make the piston reach a given position, but there is buffeting, the piston displacement buffeting range is ±0.0005 mm, and the piston velocity buffeting is ±0.0001 m/s. It can be seen from Figure 10 that the chattering range generated by the SMC algorithm based on the adaptive reaching law makes the piston reach the given position at ±0.0002 mm, compared with the SMC algorithm based on the exponential reaching law, where the chattering is only two-fifths of that when using the exponential reaching law, and the piston velocity buffeting is ±0.00003 m/s, only three-tenths of the velocity buffeting in Figure 9. The convergence velocity of the adaptive reaching law is faster than that of the traditional exponential reaching law. In addition, when the piston reaches the sliding mode surface, the buffeting of the system can be adaptively adjusted according to the system state variables, and finally converges to the equilibrium point of the electro-hydraulic position servo system. It can be seen that the SMC algorithm using the adaptive reaching law can obviously weaken the chattering problem caused by the SMC algorithm using the traditional exponential reaching law, the chattering of the piston displacement and velocity is obviously reduced, and the system still has a good tracking.

5. Conclusions

In this paper, the dynamic models of the valve-controlled asymmetrical hydraulic cylinder were studied, and a simplified mathematical model of the electro-hydraulic position servo system was given by ignoring the nonlinear factors of the servo valve. The SMC method was studied in this paper. The SMC method based on the exponential reaching law is frequently used to control the displacement and velocity of the piston. However, this method leads to a large sliding mode chattering. Therefore, a novel SMC method based on the adaptive reaching law was designed in the paper. At the same time, a comparative analysis was conducted on the SMC controller using the traditional exponential reaching law and the adaptive reaching law. The simulation results showed that the method could effectively suppress the sliding mode chattering of the electro-hydraulic position servo system.