Predicting Tensile Strength for Prestressed Reinforced Concrete-Driven Piles
Abstract
:1. Introduction
2. Tensile Strength of Reinforced-Concrete-Driven Piles
3. A Case Study: Verification of the Proposed Approach
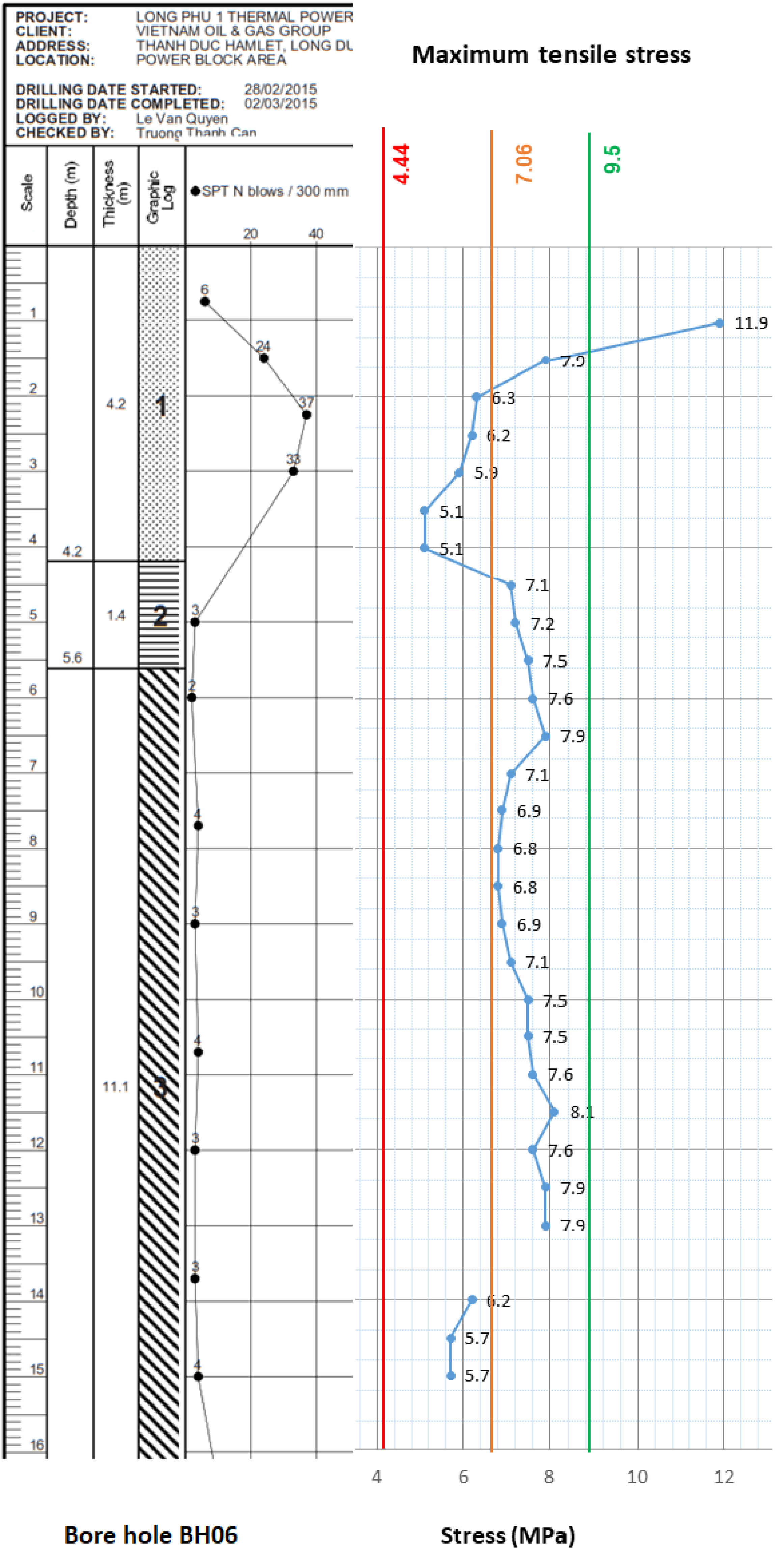
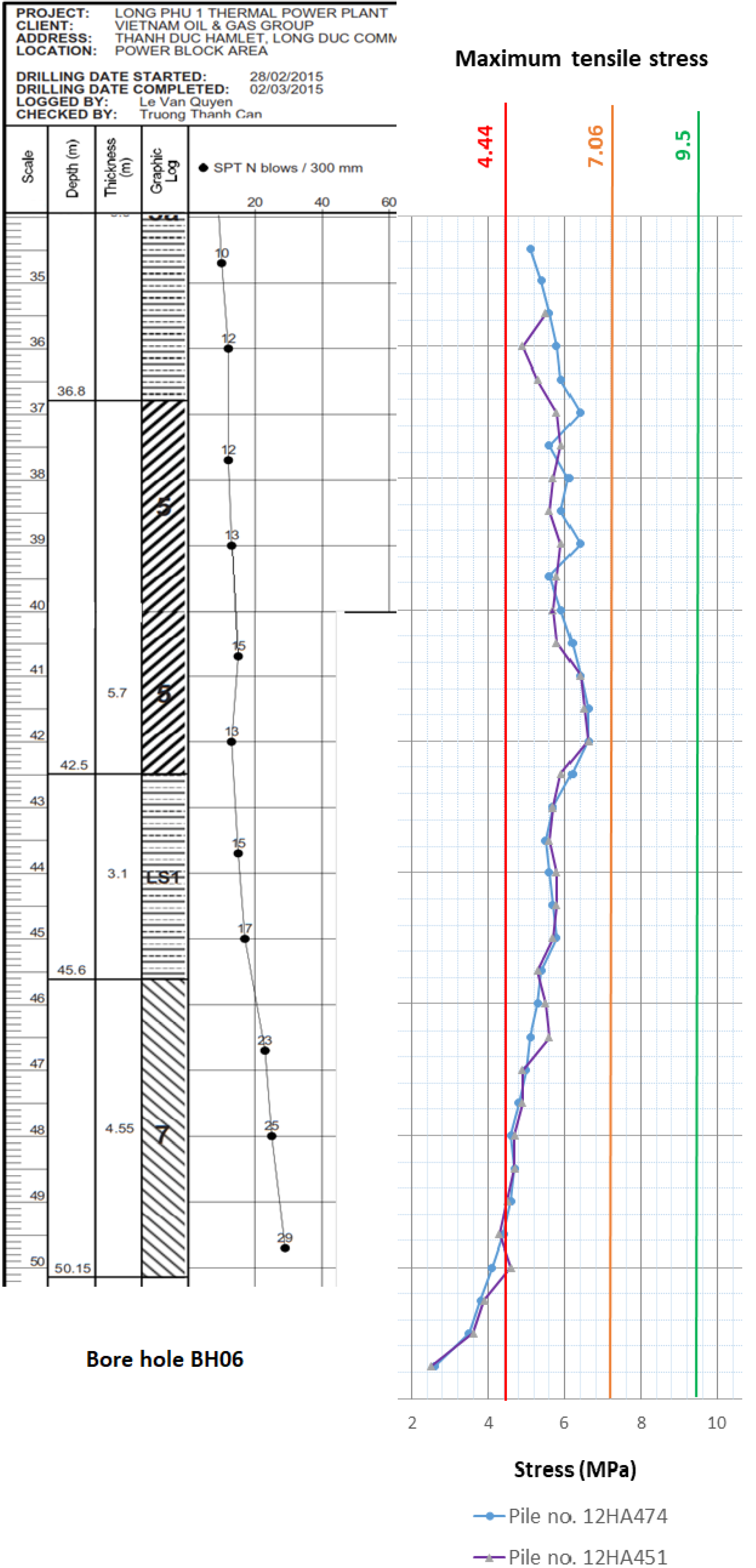
4. Pile Tensile-Stress Measurement
5. Analysis of Pile-Induced Tensile Stress and Strength
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Likins, G.; Rausche, F. Pile Damage Prevention and Assessment Using Dynamic Monitoring and the Beta Method. In Soil Behavior Fundamentals to Innovations in Geotechnical Engineering, Proceeding of the Geo-Congress; American Society of Civil Engineers: Reston, VA, USA, 2014. [Google Scholar]
- Lowery, L.L.; Hirsch, T.J.; Edwards, T.C.; Coyle, H.M.; Samson, C.H., Jr. Chapter VIII—Prediction of driving stress. In Pile-Driving Analysis by One-Dimensional Wave Theory: State of the Art; Texas Transportation Institute: College Station, TX, USA, 1970; pp. 25–32. [Google Scholar]
- Hirsch, T.J.; Samson, C.H., Jr. Driving practices for pre-stressed concrete piles. In Research Report Number 33-3-Piling Behavior; Texas Transportation Institute: College Station, TX, USA, 1966. [Google Scholar]
- Davisson, M.T.; Manuel, F.S.; Amstrong, R.M. Chapter 5: Piles containing concrete. In Allowable Stresses in Piles; Federal Highway Administration Bulletin: Georgetown, VA, USA, 1983; pp. 41–55. [Google Scholar]
- American Association of State Highway and Transportation Officials. Section 10: Foundation. In AASHTO LRFD Bridge Design Specifications, 7th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2014; pp. 1208–1251. [Google Scholar]
- Hannigan, P.J.; Rausche, F.; Likins, G.E.; Robinson, B.R.; Becker, M.L. Section 8.6 Concrete piles. In Geotechnical Engineering Circular No. 12: Design and Construction of Driven Pile Foundations; U.S. Department of Transportation: Washington, DC, USA, 2016; Volume I, pp. 459–464. [Google Scholar]
- ACI Committee 318. Chapter 22—Sectional strength. In Building Code Requirements for Reinforced Concrete (ACI 318-2002); American Concrete Institute: Farmington Hills, MI, USA, 2008; pp. 397–434. [Google Scholar]
- BS 8007; Design of Concrete Structures for Retaining Aqueous Liquids. British Standards Institution, BSI: London, UK, 2003.
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004; pp. 27–36.
- JCI. Chapter 4—Verification of Cracking due to Heat or Hydration of Cement. In Guidelines for Control of Cracking of Mass Concrete 2016; Japan Concrete Institute: Tokyo, Japan, 2017; pp. 36–71. [Google Scholar]
- Japan Society of Civil Engineers. Section 4—Material Properties. In JSCE Guidelines for Concrete No.15 “Standard Specifications for Concrete Structures–Design”; JSCE: Tokyo, Japan, 2010; pp. 404–409. [Google Scholar]
- AIJ. Recommendations for Practice of Thermal Cracking Control of Massive Concrete in Building; Architectural Institute of Japan: Tokyo, Japan, 2008; p. 69. [Google Scholar]
- Canadian Standards Association. Design of Concrete Structures CAN/CSA-A23.3-04; Standards Council of Canada: Ottawa, ON, Canada, 2007; p. 214. [Google Scholar]
- Standards New Zealand. The Design of Concrete Structures and Commentary—NZS 3101 Parts 1 and 2*; Standards New Zealand: Wellington, New Zealand, 2006; p. 753.
- IS 456:2000; Plain and Reinforced Concrete Code of Practice—4th Revision. Bureau of Indian Standards—BIS: Manak Bhavan, New Delhi, India, 2007; p. 114.
- FIB Special Activity Group 5. Chapter 5—Materials. In Model Code 2010; The International Federation for Structural Concrete (FIB): Lausanne, Switzerland, 2010; Volume 1, pp. 107–232. [Google Scholar]
- Научнo-исследoвательским, прoектнo-кoнструктoрским и технoлoгическим институтoм бетoна и железoбетoна “НИИЖБ”. Section 7—Прoведение испытаний. In ГОСТ 10180—Бетoны. Метoды Определения Прoчнoсти пo Кoнтрoльным Образцам; Kodeks JSC: Saint-Petersburg, Russia, 2018; pp. 15–19. [Google Scholar]
- TCVN 3119; Hardened Concrete–Test Method for Flexural Tensile Strength. Directorate for Standards, Metrology and Quality, Vietnamese Mynistry of Construction: Hanoi, Vietnam, 1993; pp. 1–3.
- TCVN 3120; Heavyweight Concrete—Method for Determination of Direct Tensile Strength. Directorate for Standards, Metrology and Quality, Vietnamese Mynistry of Construction: Hanoi, Vietnam, 1993; pp. 1–5.
- Vietnamese Mynistry of Construction. Section 5: Materials for plain concrete and reinforcement concrete. In TCVN 5574—Concrete and Reinforced Concrete Structure—Design Standard; Directorate for Standards, Metrology and Quality: Hanoi, Vietnam, 2012; pp. 1–3. [Google Scholar]
- ACI 543R-12; Guide to Design, Manufacture, and Installation of Concrete Piles. American Concrete Institute: Farmington Hills, MI, USA, 2012.
- Rozalija, K.; David, D. Chapter 3 Results. In Effects of Aggregate Type, Size, and Content on Concrete Strength and Fracture Energy; University of Kansas Center for Research, Inc.: Lawrence, KS, USA, 1997; p. 73. [Google Scholar]
- Robin, G. Tuchscherer; Oguzhan Bayrak. Allowable Tensile Stress Limit at Prestressed Transfer. ACI Struct. J. 2009, 106, 279–287. [Google Scholar]
- Raphael, J.M. Tensile Strength of Concrete. In ACI Journal, Proceedings; American Concrete Institute: Farmington Hills, MI, USA, 1984; Volume 81, pp. 158–165. [Google Scholar]
- Shah, S.P.; Ahmad, S.H. Structural Properties of High-Strength Concrete and Its Implications for Precast Pre-Stressed Concrete. J. Pre-Stressed Concr. Inst. 1985, 30, 92–119. [Google Scholar]
- Goble, G.G.; Fricke, K.; Likins, G.E. Driving stresses in concrete piles. PCI J. 1976, 21, 70–88. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, J.; Lao, W. Construction Control and Pile Body Tensile Stresses Distribution Pattern during Driving. J. Geotech. Geoenviron. Eng. 2007, 133, 9. [Google Scholar] [CrossRef]


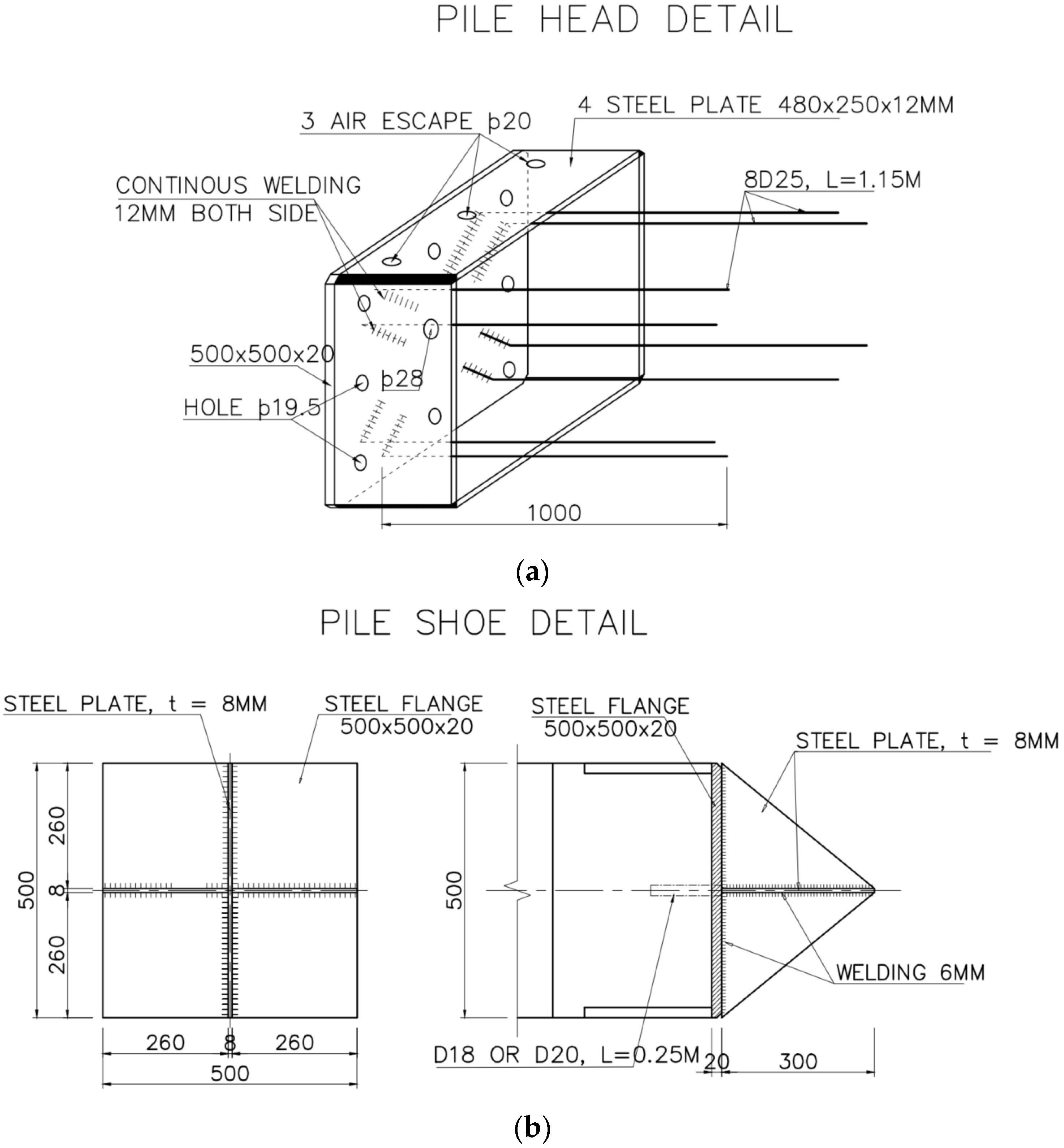

| Standards (or Codes) | Correlations in MPa | Tensile Strength Testing Methods | Type of Compressive Samples |
|---|---|---|---|
| ACI 318-2002 [7] | Modulus of Rupture | Cylinder | |
| BS 8007 [8] | Split Cylinder | Cube | |
| CEN (2002) [9] | Modulus of Rupture | Cylinder | |
| JCI 2016 [10] | Split Cylinder | Cylinder | |
| JSCE 2002 [11] | Split Cylinder | Cylinder | |
| AIJ 2008 [12] | Split Cylinder | Cylinder | |
| CAN/CSA A23.3-04 (2007) [13] | Modulus of Rupture | Cylinder | |
| NZS-3101 [14] | Modulus of Rupture | Cylinder | |
| IS 456-2000 [15] | Modulus of Rupture | Cylinder | |
| CEB-FIB 2010 [16] | (For concrete grades ≤ C50) | Axial tension | Cylinder |
| Descriptions | Units | Values |
|---|---|---|
| Power stroke | Nm | 244 − 122 |
| Number of stroke | 1/min | 35 − 50 |
| Max. blow of impact | mm | 4518 |
| Impact weight | Ton | 7.2 |
| Dimensions (L × W × H) | mm | 5990 × 1130 × 980 |
| Design | No. of Cables | Pile Tensile Strength (MPa) | |||
|---|---|---|---|---|---|
| Not Accounting for Concrete Tensile Strength (Most Standards) | Accounting for Concrete Tensile Strength AASHTO [5] | Accounting for Concrete Tensile Strength (Equation (4)) | Difference between Equation (4) and AASHTO [5] | ||
| Initial | 4 | 2.68 | 4.44 | 7.06 | +59% |
| Revised | 8 | 5.12 | 6.89 | 9.5 | +38% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.N.; Pham, T.Q.; Vu, T.T.; Malik, A.A.; Dinh, D.N. Predicting Tensile Strength for Prestressed Reinforced Concrete-Driven Piles. Appl. Sci. 2022, 12, 7112. https://doi.org/10.3390/app12147112
Nguyen TN, Pham TQ, Vu TT, Malik AA, Dinh DN. Predicting Tensile Strength for Prestressed Reinforced Concrete-Driven Piles. Applied Sciences. 2022; 12(14):7112. https://doi.org/10.3390/app12147112
Chicago/Turabian StyleNguyen, Thuyet N., Thang Q. Pham, Thuy T. Vu, Adnan A. Malik, and Duc N. Dinh. 2022. "Predicting Tensile Strength for Prestressed Reinforced Concrete-Driven Piles" Applied Sciences 12, no. 14: 7112. https://doi.org/10.3390/app12147112






