Mosar: Efficiently Characterizing Both Frequent and Rare Motifs in Large Graphs

Abstract

Due to high computational costs, exploring motif statistics (such as motif frequencies) of a large graph can be challenging. This is useful for understanding complex networks such as social and biological networks. To address this challenge, many methods explore approximate algorithms using edge/path sampling techniques. However, state-of-the-art methods usually over-sample frequent motifs and under-sample rare motifs, and thus they fail in many real applications such as anomaly detection (i.e., finding rare patterns). Furthermore, it is not feasible to apply existing weighted sampling methods such as stratified sampling to solve this problem, because it is difficult to sample subgraphs from a large graph in a direct manner. In this paper, we observe that rare motifs of most real-world networks have “more edges” than frequent motifs, and motifs with more edges are sampled by random edge sampling with higher probabilities. Based on these two observations, we propose a novel motif sampling method, Mosar, to estimate motif frequencies. In particular, our Mosar method samples frequent and rare motifs with different probabilities, and tends to sample motifs with low frequencies. As a result, the new method greatly reduces the estimation errors of these rare motifs. Finally, we conducted extensive experiments on a variety of real-world datasets with different sizes, and our experimental results show that the Mosar method is two orders of magnitude more accurate than state-of-the-art methods.

1. Introduction

Recently, exploring small connected subgraph patterns (i.e., motifs) in networks has attracted more and more attention in both academia and industry. These patterns have been widely used in various applications such as evolutionary pattern characterization in online social networks [1,2,3,4], pattern recognition in gene expression profiling [5], interaction prediction in protein–protein networks [6], and coarse-grained topology generation [7]. For example, Kunegis et al. [2] studied the significance of subgraph patterns such as “the enemy of my enemy is my friend” and “the friend of my friend is my friend” to evaluate the stability of “friend or foe” social networks such as Slashdot Zoo (www.slashdot.org, accessed on 6 March 2022). Refs. [8,9] explored network traffic activity graphs (TAGs) and observed that TAGs of different applications (e.g., FTP, Web, and P2P) exhibited different motif patterns.

Motif frequency and concentration are two popular statistics studied in many applications. Suppose that there exist Nk-node connected and induced subgraphs (CISes) in G and there exist n CIS which are isomorphic to a motif M. Then, the motif frequency and concentration of M is defined as n and $n/N$, respectively. The huge number of these subgraphs poses a great challenge for computing these two statistics. For instance, in two medium-sized networks, Slashdot [10] and Epinions [11], with only $1.0\times {10}^5$ nodes and $1.0\times {10}^6$ edges [12], there exist more than $2.0\times {10}^{10}$ four-node CIS. Furthermore, because the number of k-node CIS generally increases exponentially with k, the number of five-node CIS is higher in both of these graphs. To solve this problem, many existing works [12,13,14,15,16] have explored approximate algorithms to estimate these statistics, making a trade-off between accuracy and computational time. These methods perform node sampling, edge sampling, or path sampling on the original graph and use the sampled graph to inference the statistics of all subgraphs in the original graph. The above sampling schemes usually prefer frequent motifs and under-sample rare ones (i.e., motifs with low frequencies). Among them, both [16] and our method can estimate motif frequencies, although our method is mainly biased towards rare motifs, and the algorithms of the two are different. As a result, these methods exhibit large errors for estimating rare motifs’ statistics, and fail in many real applications such as anomaly detection (i.e., finding rare or unusual patterns) [17,18] and community search (i.e., finding the densest subgraphs and cliques) [19,20].

A potential way to solve the above problem is stratified sampling with the proportionate allocation strategy [21], the basic idea of which can be simply described as follows. For a motif M with frequency n (i.e., G has n CIS isomorphic to M), we suppose that each of its CISe (i.e., CIS in G isomorphic to M) is independently sampled with the same probability $\gamma$. Then, we estimate the motif frequency n as $\widehat{n}=\frac{m}{\gamma }$, where m is the number of sampled CIS for which the original CIS are isomorphic to M. We can easily find that the variance of $\widehat{n}$ is $n(\frac{1}{\gamma }-1)$, which implies that we can reduce the estimation error by increasing $\gamma$. With a fixed sampling budget, we can reduce the total estimation errors of characterizing all motifs by assigning larger probabilities to motifs with lower frequencies. However, it is not feasible to directly sample CIS in a graph with pre-defined probability $\gamma$, which hinders us from performing stratified sampling.

To address the above challenge, in this paper we propose a novel method called Mosar, (Motif Sampling and Retrieving), to estimate all motif frequencies. Mosar first obtains a sampled graph $G^{*}$ from the graph G under study using random edge sampling, i.e., each and every edge in G is sampled with the same probability p. In our experiments, we observe that motifs with more edges usually have lower frequencies for many real-world graphs. Moreover, the probability of a k-node CIS s in G also appearing as a k-node CIS in $G^{*}$ increases with the number of edges in s, where k is the size of motifs under study. For example, an unclosed wedge and a triangle in G are observed in $G^{*}$ with probabilities $p^2$ and $3p^2-2p^3$, respectively (note that $3p^2-2p^3\approx 3p^2$ when $p<0.1$). Thus, Mosar can be simply viewed as a novel weighted motif sampling method, and it tends to sample rare motifs. Clearly, $G^{*}$ may exhibit different motif statistics from G due to two kinds of uncertainties: (1) CIS in $G^{*}$ and their original CIS in G may be different; and (2) CIS are not sampled uniformly. For example, Figure 1 shows that a sample graph $G^{*}$ has three-node directed motif concentrations which differ greatly from G; the Flickr graph [22] is used as G and $G^{*}$ is obtained by randomly sampling each edge of G with the same probability 0.05. To remove the error introduced by these two uncertainties, Mosar retrieves the original CIS of all k-node CIS in $G^{*}$ and then builds a probabilistic model to “re-weight" sampled CIS to compute motif statistics. Our experiments on a variety of public datasets show that our method is two orders of magnitude more accurate state-of-the-art methods.

The rest of this paper is organized as follows. The problem formulation is presented in Section 3. Section 4 presents our motif sampling method, Mosar, and the corresponding methods of estimating motif frequencies and concentrations. The performance evaluation and testing results are presented in Section 5. Section 2 summarizes related work, and concluding remarks follow.

2. Related Work

There is an immense body of literature on the characterization of three-, four-, and five-node CIS in a single large graph. However, many of these works focus on the triangle counting problem [23,24,25,26,27,28,29] and cannot be easily extended to count other CIS.

In this section, we briefly review practical algorithms that approximately count all three-, four-, and five-node CIS in a large static graph. While Alon et al. [30] proposed a color-coding method to reduce the computational cost of counting subgraphs, it is not scalable to large graphs [31]. OmidiGenes et al. [32] proposed a subgraph enumeration and counting method using edge sampling. However, this method suffers from unknown sampling bias. To estimate subgraph class concentrations, Kashtan et al. [13] proposed a connected subgraph sampling method, however, their method is computationally expensive when calculating the weight of each sampled subgraph used for correcting bias introduced by sampling. To address this drawback, FANMOD [14] samples subgraphs based on building a subgraph enumeration tree, which requires that the graph is fitted into memory. Recently, Paredes and Ribeiro [33] have proposed RAND-FaSE to estimate the frequency of all CIS with an efficient tree data structure, where the leaves are the subgraph occurrences. Wang et al. [16] built a transition probability matrix between the motif statistics in the original and sampled graph. With the motif statistics in sampled graph, they provide an unbiased estimator for all three-, four-, and five-node CIS. Marco et al. [34] presented a general algorithm using colour coding to approximately count motifs beyond five nodes. Ryan et al. [35] developed an unbiased graphlet estimation framework by sampling edges and their local neighbourhood. The new Motivo algorithm proposed in [36] scales well to larger graphs while providing more accurate counts of motifs than ever before, both for most frequent motifs and for extremely rare motifs. The general framework proposed in [37], called HONE, is used to learn such structural node embeddings from networks through subgraph patterns in node neighborhoods. The Random Walks in [38] have been used as the basis for many proximity-based community detection methods. These methods are similar to theh random edge sampling in the first step of our Mosar method, although with many differences in its implementation. In addition, Refs. [12,15,39,40,41,42] proposed sampling methods to estimate online social networks’ motif concentrations when the graph’s topology is not available in advance and it is costly to crawl the entire topology. However, the above methods under-sample rare motifs, and thus exhibit large errors for characterizing such motifs.

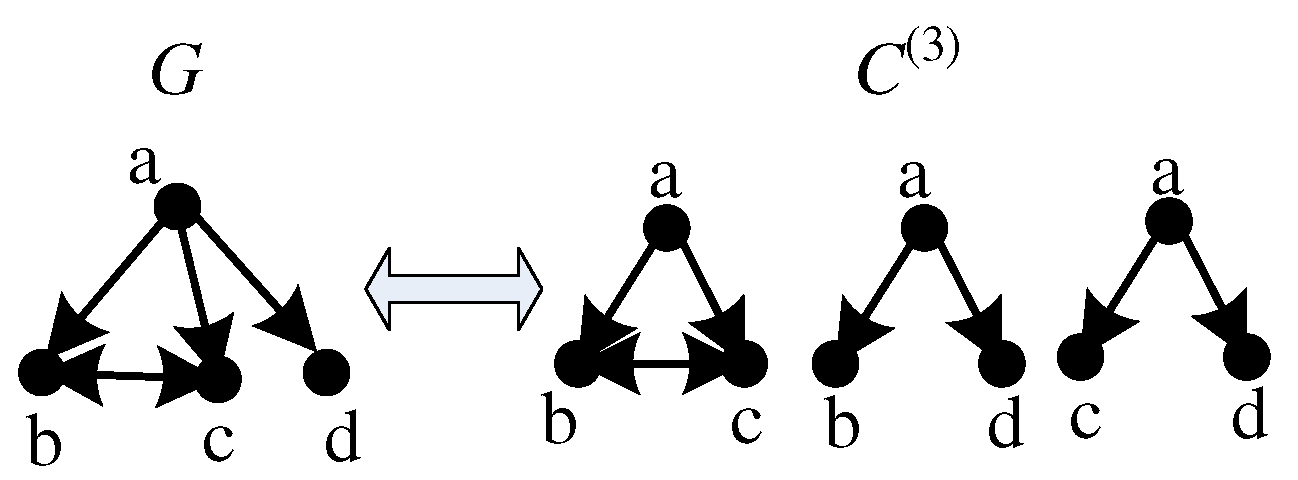
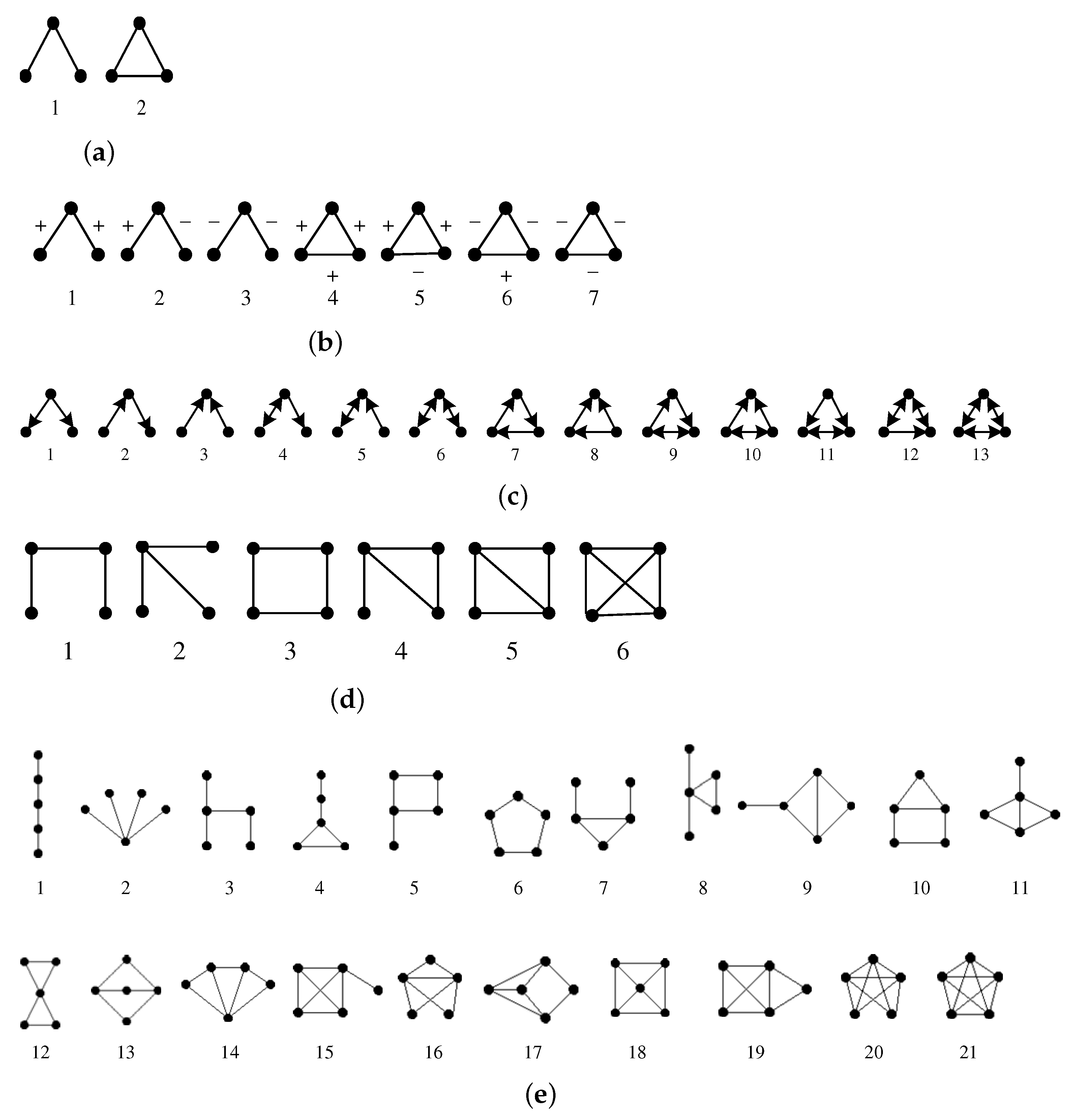
3. Problem Formulation

In this section, we introduce motif statistics. For readability, the notations used throughout the paper are listed in

Table 1. Table of notations.

G	$\mathit{G}=(\mathit{V},\mathit{E},\mathit{L})$ is the graph of interest
$G^{*}$	$G^{*}=(V^{*},E^{*},L^{*})$ is a sampled graph
$V\left(s\right),s\in C^{\left(k\right)}$	set of nodes in k-node CIS s
$E\left(s\right),s\in C^{\left(k\right)}$	set of edges in k-node CIS s
$M\left(s\right)$	motif class ID of CIS s
$T_k$	number of k-node subgraph classes
$M_i^{\left(k\right)}$	i-th k-node motif
$C^{\left(k\right)}$	set of k-node CIS in G
$C^{(k,*)}$	set of k-node CIS in $G^{*}$
$C_i^{\left(k\right)}$	set of CIS in G isomorphic to $M_i^{\left(k\right)}$
$n^{\left(k\right)}=\left|C^{\left(k\right)}\right|$	number of k-node CIS in G
$n_i^{\left(k\right)}=\left|C_i^{\left(k\right)}\right|$	number of CIS in G isomorphic to $M_i^{\left(k\right)}$
${\omega }_i^{\left(k\right)}=\frac{n_i^{\left(k\right)}}{n^{\left(k\right)}}$	concentration of motif $M_i^{\left(k\right)}$ in G
P	matrix $P={\left[P_{ij}\right]}_{1\le i,j\le T_k}$
$P_{i,j}$	probability that $s^{*}$ isomorphic to $M_i^{\left(k\right)}$ given s isomorphic to $M_j^{\left(k\right)}$
$Z_j$	$Z_j=\{i:i=1,\dots ,T_k,\mathrm{and}{P}_{i,j}>0\}$
${\varphi }_{i,j}$	number of subgraphs of $M_j^{\left(k\right)}$ isomorphic to $M_i^{\left(k\right)}$
$S_{G^{*},G}^{\left(k\right)}$	$S_{G^{*},G}^{\left(k\right)}=\{(s^{*},s):s^{*}\in C^{(k,*)},s\in C^{\left(k\right)},$                                   $V\left(s^{*}\right)=V\left(s\right)\}$
${\pi }_{i,j}(s_1,s_2)$	$s_1$ and $s_2$ are two k-node CIS in G isomorphic to motif $M_j^{\left(k\right)}$. Let $s_1^{*}$ and $s_2^{*}$ be the induced subgraphs of node sets $V\left(s_1\right)$ and $V\left(s_2\right)$ in $G^{*}$, respectively. ${\pi }_{i,j}(s_1,s_2)$ is defined as the probability that $s_1^{*}$ and $s_2^{*}$ are both isomorphic to motif $M_i^{\left(k\right)}$.
$m_{i,j}^{\left(k\right)}$	number of elements $(s^{*},s)\in S_{G^{*},G}^{\left(k\right)}$, where $s^{*}$ is isomorphic to motif $M_i^{\left(k\right)}$ and s is isomorphic to motif $M_j^{\left(k\right)}$
p	probability of sampling an edge
q	$q=1-p$

. We denote the graph of interest as a labeled undirected graph $G=(V,E,L)$, where V is the set of nodes, E is a set of undirected edges, and L is a set of labels $l_{u,v}$ associated with undirected edges $(u,v)\in E$. For example: (1) directed networks use labels $l_{u,v}\in \{\to ,\leftarrow ,\leftrightarrow \}$ to indicate the direction of the edges $(u,v)\in E$; (2) $l_{u,v}\in \{+,-\}$ for edges in signed networks having positive or negative labels; (3) a regular undirected graph can be represented by setting L to null.

To formally define the motif frequency of G, first, we introduce a few notations. An induced subgraph of G, $G^{\prime }=(V^{\prime },E^{\prime },L^{\prime })$, is a subgraph with its edges and associated labels all in G, i.e., $V^{\prime }\subset V$, $E^{\prime }=\{(u,v):u,v\in V^{\prime },(u,v)\in E\}$, $L^{\prime }=\{l_{u,v}:(u,v)\in E^{\prime }\}$. Denote $C^{\left(k\right)}$ as the set of all CIS with k nodes in G, and $n^{\left(k\right)}=\left|C^{\left(k\right)}\right|$. We provide a simple example in Figure 2, where $n^{\left(3\right)}=3$. We partition $C^{\left(k\right)}$ into $T_k$ equivalence classes $C_1^{\left(k\right)},\dots ,C_{T_k}^{\left(k\right)}$ without overlapping where CIS within each $C_i^{\left(k\right)}$ are isomorphic. Next, we present several examples to illustrate our notations. Figure 3a reveals all three-node motifs of unlabeled undirected networks. When G is an unlabeled and undirected network, then the number of three-node motifs is $T_3=2$, and $C_1^{\left(3\right)}$ and $C_2^{\left(3\right)}$ are the sets of CIS in G isomorphic to the first and second motifs in Figure 3a, respectively. Figure 3b reveals all three-node motifs when G is any signed network; in this case, $T_3=7$. Figure 3c reveals all motifs with three nodes for any directed network; in such a case, $T_3=13$. Figure 3d reveals all four-node motifs of any unlabeled and undirected network; in this case, $T_4=6$. Figure 3e shows all five-node motifs of any unlabeled and undirected network; in this case, $T_5=21$. Throughout the paper, $C_i^{\left(k\right)}$ is defined as the set of CIS in G that are isomorphic to the i-th k-node motif $M_i^{\left(k\right)}$. Define the frequency of motif $M_i^{\left(k\right)}$ as $n_i^{\left(k\right)}=\left|C_i^{\left(k\right)}\right|$, i.e., the number of CIS in $C_i^{\left(k\right)}$. For example, $C_1^{\left(3\right)}$ includes two CIS for the directed graph G in Figure 2: (1) the CIS made up of a, b, and d, and (2) the CIS made up of a, c, and d. Thus, $n_1^{\left(3\right)}=2$. In this paper, we focus on designing fast and accurate sampling methods to reduce the time needed to count motif frequencies.

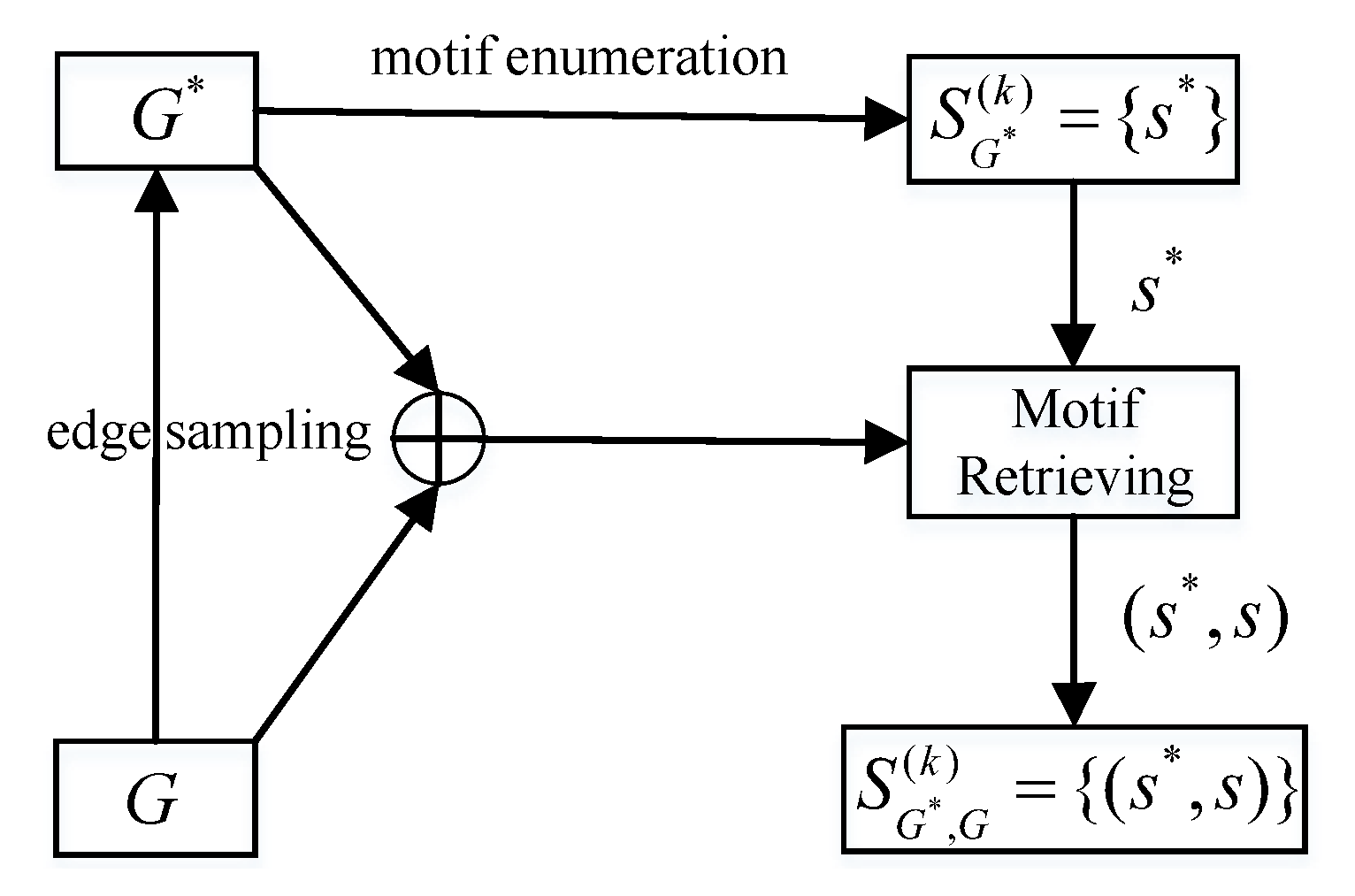
4. Motif Sampling and Retrieving

In this section, we start by introducing our Mosar method for motif sampling. After that, we present a probabilistic model to analyze its sampling bias. On the basis of this model, we put forward a method to correct the sampling error for estimating motif frequencies. Finally, we provide lower error bounds for our estimates.

4.1. Sampling Motifs over G

Figure 4 shows an overview of Mosar. Mosar first generates a subgraph $G^{*}=(V^{*},E^{*},L^{*})$ of $G=(V,E,L)$ by iterating each edge and sampling it with the same probability p. We assume that $G^{*}$ can be fitted into memory, which can be easily achieved using a small p. Then, Mosar uses existing CIS enumeration methods such as [16] to enumerate all k-node CIS of $G^{*}$. For a graph s, let $V\left(s\right)$ and $E\left(s\right)$ denote the set of nodes and edges contained in s. For a k-node CIS $s^{*}$ of $G^{*}$, let s be its original k-node CIS, which is defined as the k-node CIS of G with the same nodes in $s^{*}$, i.e., $V\left(s\right)=V\left(s^{*}\right)$. We can easily find that $s^{*}$ can be quite different from s. To eliminate the estimation error introduced by this uncertainty, when traversing $s^{*}$, we combine the edge information of the original graph G to retrieve the s of the original graph. Formally, we let $C^{(k,*)}$ denote all k-node CIS of $G^{*}$. Finally, we obtain all pairs of CIS $s^{*}\in C^{(k,*)}$ and their original CIS, $s\in C^{\left(k\right)}$, i.e.,

$$\begin{array}{c}\hfill S_{G^{*},G}^{\left(k\right)}=\{(s^{*},s):s^{*}\in C^{(k,*)},s\in C^{\left(k\right)},V\left(s^{*}\right)=V\left(s\right)\}.\end{array}$$

(1)

The pseudocode of Mosar is shown in Algorithm 1.

Algorithm 1: The pseudocode of Mosar.

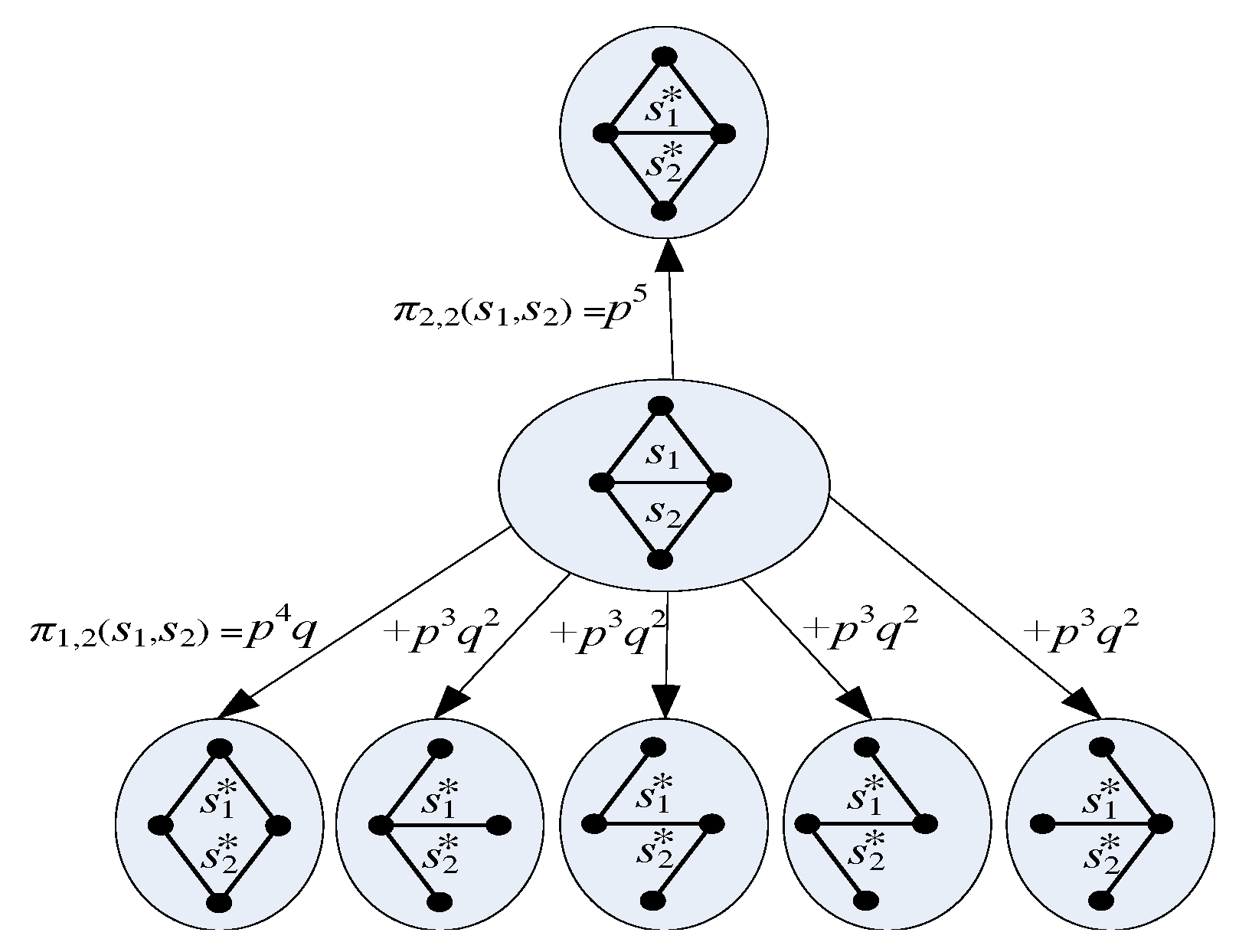
4.2. Probabilistic Model of Mosar

We build a probabilistic model of pairs $(s^{*},s)\in S_{G^{*},G}^{\left(k\right)}$, which is similar to the model in [16]. Define $P_{i,j}$ as the probability that $s^{*}$ is isomorphic to motif $M_i^{\left(k\right)}$ given that s is isomorphic to motif $M_j^{\left(k\right)}$, i.e.,

$$\begin{array}{c}\hfill P_{i,j}=P(M\left(s^{*}\right)=M_i^{\left(k\right)}|M\left(s\right)=M_j^{\left(k\right)}).\end{array}$$

(2)

To obtain $P_{i,j}$, first of all, we compute ${\varphi }_{i,j}$, which is defined as the quantity of subgraphs of $M_j^{\left(k\right)}$ isomorphic to $M_i^{\left(k\right)}$. For instance, $M_2^{\left(3\right)}$, i.e., the triangle, includes three subgraphs isomorphic to $M_1^{\left(3\right)}$, i.e., the unclosed wedge for the undirected graph in Figure 3a. Thus, we have ${\varphi }_{1,2}=3$ for three-node undirected motifs. When $i=j$, we let ${\varphi }_{i,j}=1$. For four- and five-node motifs, it is no easy thing to acquire ${\varphi }_{i,j}$ manually; we use the method in [16] to compute ${\varphi }_{i,j}$. Let $q=1-p$; then, we have

$$\begin{array}{c}\hfill P_{i,j}={\varphi }_{i,j}{p}^{|E(M_i^{\left(k\right)})|}{q}^{|E\left(M_j^{\left(k\right)}\right)|-|E\left(M_i^{\left(k\right)}\right)|}.\end{array}$$

(3)

For example, we have $P_{1,2}=3p^{2}q$ and $P_{2,2}=p^3$ for the undirected three-node motifs in Figure 3a.

4.3. Motif Frequency Estimation

Using the probabilistic model above, we put forward a method a method to estimate motif frequencies. The pseudocode for motif frequency estimation is shown in Algorithm 2.  

Algorithm 2: The pseudocode for Motif Frequency Estimation.

Define $m_{i,j}^{\left(k\right)}$, $1\le i\le T_k$, as the number of pairs $(s^{*},s)\in S_{G^{*},G}^{\left(k\right)}$, where $s^{*}$ is isomorphic to motif $M_i^{\left(k\right)}$ and s is isomorphic to motif $M_j^{\left(k\right)}$. Then, the expectation of $m_{i,j}^{\left(k\right)}$ is computed as

$$\begin{array}{c}\hfill \mathbb{E}\left[m_{i,j}^{\left(k\right)}\right]=P_{i,j}{n}_j^{\left(k\right)}.\end{array}$$

(4)

When $P_{i,j}>0$, we have the following estimator of $n_j^{\left(k\right)}$:

$$\begin{array}{c}\hfill {\widehat{n}}_j^{(k,i)}=\frac{m_{i,j}^{\left(k\right)}}{P_{i,j}}.\end{array}$$

(5)

Denote $Z_j=\{i:i=1,\dots ,T_k,\mathrm{and}{P}_{i,j}>0\}$. Thus, we have $|Z_j|$ estimators of $n_j^{\left(k\right)}$, i.e., ${\widehat{n}}_j^{(k,i)}$, $i\in Z_j$. Let $s_1$ and $s_2$ be two k-node CIS in G isomorphic to the j-th k-node motif. Denote $s_1^{*}$ and $s_2^{*}$ as the induced subgraphs of node sets $V\left(s_1\right)$ and $V\left(s_2\right)$ in $G^{*}$, respectively. Define ${\pi }_{i,j}(s_1,s_2)$ as the probability that $s_1^{*}$ and $s_2^{*}$ are both isomorphic to the i-th k-node motif. We can easily find that ${\pi }_{i,j}(s_1,s_2)=P_{i,j}^2$ when $s_1$ and $s_2$ have no common edges (i.e., $E\left(s_2\right)\cap E\left(s_1\right)\ne \varnothing$), and ${\pi }_{i,j}(s_1,s_2)>P_{i,j}^2$ otherwise. For example, as shown in Figure 5, we have ${\pi }_{1,2}(s_1,s_2)=p^{4}q+4p^3{q}^2$ and ${\pi }_{2,2}(s_1,s_2)=p^5$ for the undirected three-node motifs in Figure 3a. Then, we have the following theorem.

Theorem 1.

For each $i\in Z_j$, ${\widehat{n}}_j^{(k,i)}$ is an unbiased estimator of $n_j^{\left(k\right)}$, i.e.,

$$\begin{array}{c}\hfill \mathbb{E}\left({\widehat{n}}_j^{(k,i)}\right)=n_j^{\left(k\right)},\end{array}$$

(6)

and the variance of ${\widehat{n}}_j^{(k,i)}$ is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \mathrm{Var}\left({\widehat{n}}_j^{(k,i)}\right)=\frac{1}{P_{i,j}}{n}_j^{\left(k\right)}(1-P_{i,j})\hfill \\ \hfill & +\frac{1}{P_{i,j}^2}\sum _{s_1,s_2\in C_j^{\left(k\right)},s_1\ne s_2,E\left(s_1\right)\cap E\left(s_2\right)\ne \varnothing }({\pi }_{i,j}(s_1,s_2)-P_{i,j}^2).\hfill \end{array}\end{array}$$

(7)

Proof. 

From (4), we have

$$\begin{array}{c}\hfill \mathbb{E}\left({\widehat{n}}_j^{(k,i)}\right)=\frac{\mathbb{E}\left(m_{i,j}^{\left(k\right)}\right)}{P_{i,j}}=n_j^{(k,i)}.\end{array}$$

(8)

Place $\mathbf{1}\left(\mathbb{X}\right)$ to indicate a signal function that the predicate $\mathbb{X}$ is true and equal to one, and zero otherwise. Define function

$$\begin{array}{c}\hfill \delta \left(s\right)=\mathbf{1}(\exists s^{*},(s^{*},s)\in S_{G^{*},G}^{\left(k\right)}).\end{array}$$

(9)

Then we can write ${\widehat{n}}_j^{(k,i)}$ as

$$\begin{array}{c}\hfill {\widehat{n}}_j^{(k,i)}=\frac{1}{P_{i,j}}\sum _{s\in C_j^{\left(k\right)}}\delta \left(s\right)\end{array}$$

(10)

Thus, $\mathrm{Var}\left({\widehat{n}}_j^{(k,i)}\right)$ is computed as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{Var}\left({\widehat{n}}_j^{(k,i)}\right)& =\frac{1}{P_{i,j}^2}\mathrm{Var}(\sum _{s\in C_j^{\left(k\right)}}\delta \left(s\right))\hfill \\ \hfill & =\frac{1}{P_{i,j}^2}\sum _{s_1\in C_j^{\left(k\right)}}\sum _{s_2\in C_j^{\left(k\right)}}\mathrm{Cov}(\delta \left(s_1\right),\delta \left(s_2\right))\hfill \\ \hfill & =\frac{1}{P_{i,j}^2}\sum _{s_1\in C_j^{\left(k\right)}}\sum _{s_2\in C_j^{\left(k\right)}}{\pi }_{i,j}(s_1,s_2)-P_{i,j}^2.\hfill \end{array}\end{array}$$

(11)

Finally, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \mathrm{Var}\left({\widehat{n}}_j^{(k,i)}\right)=\frac{1}{P_{i,j}}{n}_j^{\left(k\right)}(1-P_{i,j})\hfill \\ \hfill & +\frac{1}{P_{i,j}^2}\sum _{s_1,s_2\in C_j^{\left(k\right)},s_1\ne s_2,E\left(s_1\right)\cap E\left(s_2\right)\ne \varnothing }({\pi }_{i,j}(s_1,s_2)-P_{i,j}^2).\hfill \end{array}\end{array}$$

(12)

In the derivation above, we use ${\pi }_{i,j}(s_1,s_2)=P_{i,j}$ when $s_1=s_2$, and ${\pi }_{i,j}(s_1,s_2)=P_{i,j}^2$ when $s_1$ and $s_2$ have no common edges. □

Example: For the undirected three-node motifs in Figure 3a, ${\widehat{n}}_2^{(3,1)}$ and ${\widehat{n}}_2^{(3,2)}$ are two estimators of $n_2^{\left(3\right)}$, i.e., the number of triangles in G. Note that ${\widehat{n}}_2^{(3,2)}$ is the same estimator of $n_2^{\left(3\right)}$ in [23]. Let $\mathsf{\Gamma }$ be the number of pairs of triangles that are not edge disjoint. Then, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \mathrm{Var}\left({\widehat{n}}_2^{(3,1)}\right)\hfill \\ \hfill & =\frac{n_2^{\left(3\right)}(3p^{2}q-9p^4{q}^2)+2\mathsf{\Gamma }(p^{4}q+4p^3{q}^2-9p^4{q}^2)}{9p^4{q}^2}.\hfill \end{array}\end{array}$$

(13)

and

$$\begin{array}{c}\hfill \mathrm{Var}\left({\widehat{n}}_2^{(3,2)}\right)=\frac{n_2^{\left(3\right)}(p^3-p^6)+2\mathsf{\Gamma }(p^5-p^6)}{p^6}.\end{array}$$

(14)

We can easily find that $\mathrm{Var}\left({\widehat{n}}_2^{(3,1)}\right)$ is smaller than $\mathrm{Var}\left({\widehat{n}}_2^{(3,2)}\right)$ when $p<\frac{5}{6}$. When $p\ll 1$ and $n_2^{\left(3\right)}\gg p\mathsf{\Gamma }$, we have $\mathrm{Var}\left({\widehat{n}}_2^{(3,1)}\right)\approx \frac{n_2^{\left(3\right)}}{3p^2}$ and $\mathrm{Var}\left({\widehat{n}}_2^{(3,2)}\right)\approx \frac{n_2^{\left(3\right)}}{p^3}$; therefore, ${\widehat{n}}_2^{(3,1)}$ is $\sqrt{\frac{3}{p}}$ times more accurate than ${\widehat{n}}_2^{(3,2)}$.

Finally, we estimate $n_j^{\left(k\right)}$ using the following mix estimator:

$$\begin{array}{c}\hfill {\widehat{n}}_j^{\left(k\right)}=\sum _{i\in Z_j}{\alpha }_{i,j}{\widehat{n}}_j^{(k,i)},\end{array}$$

(15)

where parameters $0\le {\alpha }_{i,j}\le 1$, and ${\sum }_{i\in Z_j}{\alpha }_{i,j}=1$. ${\alpha }_{i,j}$ is used to determine the relative importance of ${\widehat{n}}_j^{(k,i)}$. Suppose that all ${\widehat{n}}_j^{(k,i)}$ are independent. Then, the variance of ${\widehat{n}}_j^{\left(k\right)}$ is

$$\begin{array}{c}\hfill \mathrm{Var}\left({\widehat{n}}_j^{\left(k\right)}\right)=\sum _{i\in Z_j}{\alpha }_{i,j}^2\mathrm{Var}\left({\widehat{n}}_j^{(k,i)}\right).\end{array}$$

(16)

Next, we compute optimal ${\alpha }_{i,j}$ to minimize $\mathrm{Var}\left({\widehat{n}}_j^{\left(k\right)}\right)$. Define Lagrange function $\psi$ as

$$\begin{array}{c}\hfill \psi =\sum _{i\in Z_j}{\alpha }_{i,j}^2\mathrm{Var}\left({\widehat{n}}_j^{(k,i)}\right)+\lambda (\sum _{i\in Z_j}{\alpha }_{i,j}-1).\end{array}$$

(17)

The derivatives of $\psi$ with respect to ${\alpha }_{i,j}$ and $\lambda$ are

$$\begin{array}{c}\hfill \frac{\partial \psi }{\partial {\alpha }_{i,j}}=2{\alpha }_{i,j}\mathrm{Var}\left({\widehat{n}}_j^{(k,i)}\right)+\lambda ,i\in Z_j,\end{array}$$

(18)

and

$$\begin{array}{c}\hfill \frac{\partial \psi }{\partial \lambda }=\sum _{i\in Z_j}{\alpha }_{i,j}-1.\end{array}$$

(19)

To obtain a ${\widehat{n}}_j^{\left(k\right)}$ with the smallest error, we solve the equations $\frac{\partial \psi }{\partial \lambda }=0$, and $\frac{\partial \psi }{\partial \lambda }=0$, $i\in Z_j$, and have

$$\begin{array}{c}\hfill {\alpha }_{i,j}=\frac{{\mathrm{Var}}^{-1}\left({\widehat{n}}_j^{(k,i)}\right)}{{\sum }_{l\in Z_j}{\mathrm{Var}}^{-1}\left({\widehat{n}}_j^{(k,l)}\right)},i\in Z_j.\end{array}$$

(20)

When it is difficult to compute $\mathrm{Var}\left({\widehat{n}}_j^{(k,i)}\right)$ exactly, we approximate $\mathrm{Var}\left({\widehat{n}}_j^{(k,i)}\right)\approx n_j^{\left(k\right)}(1-P_{i,j})P_{i,j}^{-1}$ and then set parameters ${\alpha }_{i,j}$ as

$$\begin{array}{c}\hfill {\alpha }_{i,j}=\frac{P_{i,j}{(1-P_{i,j})}^{-1}}{{\sum }_{l\in Z_j}{P}_{l,j}{(1-P_{l,j})}^{-1}},i\in Z_j.\end{array}$$

(21)

4.4. Discussion

Compared to the online methods of analyzing streaming graphs in [16,43] (i.e., the graph of interest is given as a stream of edges and each edge can be accessed and processed only once), Mosar needs to pass over the graph file of interest twice, with the additional pass performed to remove uncertainty introduced by sampling. However, we observe that passing over the graph requires much less time than enumerating and classifying subgraphs even for a small sampling probability p. For example, in our experiments we observed that the computational time needed for passing over the graph file of interest on disk was no more than 7% of the time needed to enumerate and classify CIS in the sampled graph when $p=0.01$. Thus, to sample the same number of CIS, Mosar requires effectively the same computational time as the methods in [16,43].

5. Data Evaluation

In this section, in the first place, we introduce our experimental datasets. In the second place we present experimental results to evaluate the performance of our Mosar method compared to the most advanced methods. Our experiments were conducted on a server with a Quad-Core AMD Opeteron (tm) 8379 HE CPU 2.39 GHz processor and 128 GB DRAM memory.

5.1. Datasets

We performed our experiments on the following available datasets in public summarized in

Table 2. Graph datasets used in our experiments. “edges” refers to the quantity of edges in the undirected graph generated by discarding edge labels. “max-degree” denotes the maximum quantity of edges for a node in an undirected graph.

Graph	Nodes	Edges	Max-Degree
Flickr [22]	1,715,255	15,555,041	27,236
Pokec [44]	1,632,803	22,301,964	14,854
LiveJournal [22]	5,189,809	48,688,097	15,017
YouTube [22]	1,138,499	2,990,443	28,754
Wiki-Talk [45]	2,394,385	4,659,565	100,029
Web-Google [46]	875,713	4,322,051	6332
soc-Epinions1 [11]	75,897	405,740	3044
soc-Slashdot08 [10]	77,360	469,180	2539
soc-Slashdot09 [10]	82,168	504,230	2552
sign-Epinions [47]	119,130	704,267	3558
sign-Slashdot08 [47]	77,350	416,695	2537
sign-Slashdot09 [47]	82,144	504,230	2552
com-DBLP [48]	317,080	1,049,866	343
com-Amazon [48]	334,863	925,872	549
p2p-Gnutella08 [49]	6301	20,777	97
ca-GrQc [50]	5241	14,484	81
ca-CondMat [50]	23,133	93,439	279
ca-HepTh [50]	9875	25,937	65

.

• Online social networks: Flickr [22], Pokec [44], LiveJournal [44], YouTube [22], soc-Epinions1 [11], and soc-Slash-dot08 [10]. Flickr, LiveJournal, and YouTube are popular photo, blog, and video sharing websites, respectively, where a user can subscribe to other user updates such as photos, blogs, and videos. Pokec is the most popular online social network in Slovakia, and has been in existence for more than ten years. These networks can be represented by directed graphs, where nodes represent users and a directed edge from node u to node v indicates that user u subscribes to user v or user u tags user v as a friend. Soc-Epinions1 [11] is a directed graph of the Epinions website in 2003, where a directed edge from node u to node v indicates that user u trusts user v. Soc-Slashdot08 and Soc-Slashdot09 [10] are graphs of the technology-related news website Slashdot released in 2008 and 2009, respectively, where the edge between node u and node v means that user u has marked user v as a friend.
• Web graph: Web-Google [46]. The Web-Google dataset was released in 2002 by Google as a part of a Google Programming Contest; nodes represent web pages and directed edges represent hyperlinks between them.
• Signed networks: sign-Epinions, sign-Slashdot08, and sign-Slashdot09 [47]. Epinions and Slashdot networks can be represented by a signed graph, where a positive edge from user u to user v means that u trusts v in the Epinions website or u marks v as a friend on the Slashdot website. A negative edge from u to v means a distrust relationship on the Slashdot website or that u tags user v as a foe on the Epinions website.
• Collaboration networks: ca-HepTh [50], ca-GrQc [50], and ca-CondMat [50]. arXiv is an online repository of electronic preprints of scientific papers in many fields, such as mathematics, physics, and computer science. The datasets ca-GR-QC, ca-HEP-TH, and ca-CondMat consist of arXiv e-prints and cover scientific collaborations between authors of papers submitted to the General Relativity and Quantum Cosmology category, the High-Energy Physics—Theory category, and the Condensed Matter category, respectively [50]. These networks can all be represented by undirected graphs. If author u co-authored a paper with author v, the graph contains an undirected edge from u to v.
• Peer-to-peer network: p2p-Gnutella08 [49]. Gnutella is a peer-to-peer file sharing network. Nodes in the p2p-Gnutella08 dataset represent users in the Gnutella network and edges represent connections between Gnutella users.
• Communication network: Wiki-Talk [45]. Wikipedia is a free encyclopedia written collaboratively by volunteers around the world. Each registered user has a talk page that she/he and other users can edit in order to communicate and discuss updates to various articles on Wikipedia. Nodes in the Wiki-Talk dataset represent registered users on Wikipedia and a directed edge from node u to node v indicates that user u at least once edited a talk page of user v.
• Product network: com-Amazon [48]. The dataset was collected by crawling the Amazon website based on the Amazon website’s “Customers Who Bought This Item Also Bought” feature. If a product u is frequently co-purchased with product v, the graph contains an undirected edge from u to v.

5.2. Error Metric

Similar to [16], in our experiments we studied the normalized root mean square error (NRMSE) to measure the relative error of the motif frequency estimate ${\widehat{n}}_i$ with respect to its true value $n_i$, $i=1,2,\dots$. $\mathrm{NRMSE}\left({\widehat{n}}_i\right)$ is defined as:

$$\begin{array}{c}\hfill \mathrm{NRMSE}\left({\widehat{n}}_i\right)=\frac{\sqrt{\mathrm{MSE}\left({\widehat{n}}_i\right)}}{n_i},i=1,2,\dots ,\end{array}$$

(22)

where $\mathrm{MSE}\left({\widehat{n}}_i\right)$ is defined as

$$\begin{array}{c}\hfill \mathrm{MSE}\left({\widehat{n}}_i\right)=\mathbb{E}\left[{({\widehat{n}}_i-n_i)}^2\right]=\mathrm{var}\left({\widehat{n}}_i\right)+{\left(\mathbb{E}\left[{\widehat{n}}_i\right]-n_i\right)}^2.\end{array}$$

(23)

We can find out that the $\mathrm{MSE}\left({\widehat{n}}_i\right)$ decomposes into the sum of the variance and bias of the estimator ${\widehat{n}}_i$, both of which are important and must be as small as possible to achieve better estimation performance. When ${\widehat{n}}_i$ is an unbiased estimator of $n_i$, then $\mathrm{MSE}\left(\widehat{n}\right)=\mathrm{var}\left(\widehat{n}\right)$, as a consequence, $\mathrm{NRMSE}\left({\widehat{n}}_i\right)$ is the equivalent of the normalized standard error of ${\widehat{n}}_i$, which is $\mathrm{NRMSE}\left({\widehat{n}}_i\right)=\sqrt{\mathrm{var}\left({\widehat{n}}_i\right)}/n_i$. Please note that our metrics use relative error, and thus we reckon values as large as $\mathrm{NRMSE}\left({\widehat{n}}_i\right)=1$ to be acceptable when $n_i$ is small. In our experiments, we average the estimates and calculate their NRMSEs over 100 runs.

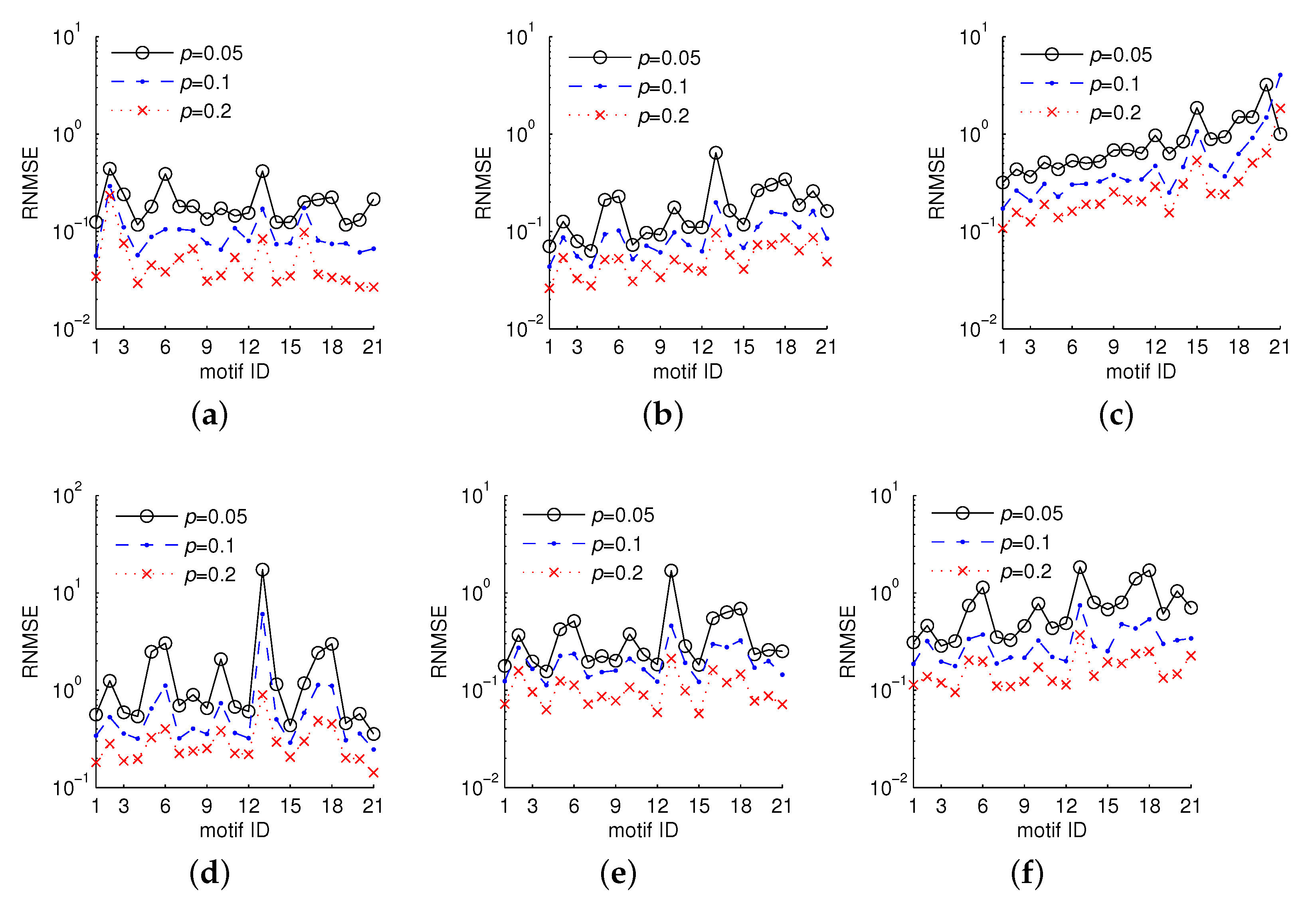
5.3. Accuracy Results

Above all, we evaluated the performance of our method in estimating the motif frequencies of three-node on graphs with millions of nodes (Flickr, Pokec, LiveJournal, YouTube, Web-Google, and Wiki-talk) while comparing our results with the basic truth calculated via brute force methods. Calculating the ground truth of four-node and five-node motif frequencies for large graphs is computationally intensive. Even for a relatively small graph such as soc-Slashdot08, enumerating and counting all of its three-node CIS takes almost 20 h. To overcome this difficulty, experiments with four-node CISes were performed on four medium-size graphs (soc-Epinions1, soc-Slashdot08, soc-Slashdot09, com-DBLP and com-Amazon), and experiments with five-node CIS were performed on four relatively small graphs (ca-GR-QC, ca-HEP-TH, ca-CondMat and p2p-Gnutella08) where the ground-truth could be calculated. We specifically evaluated the performance of our method in estimating the motif frequencies of signed graphs such as sign-Epinions, sign-Slashdot08 and sign-Slashdot09.

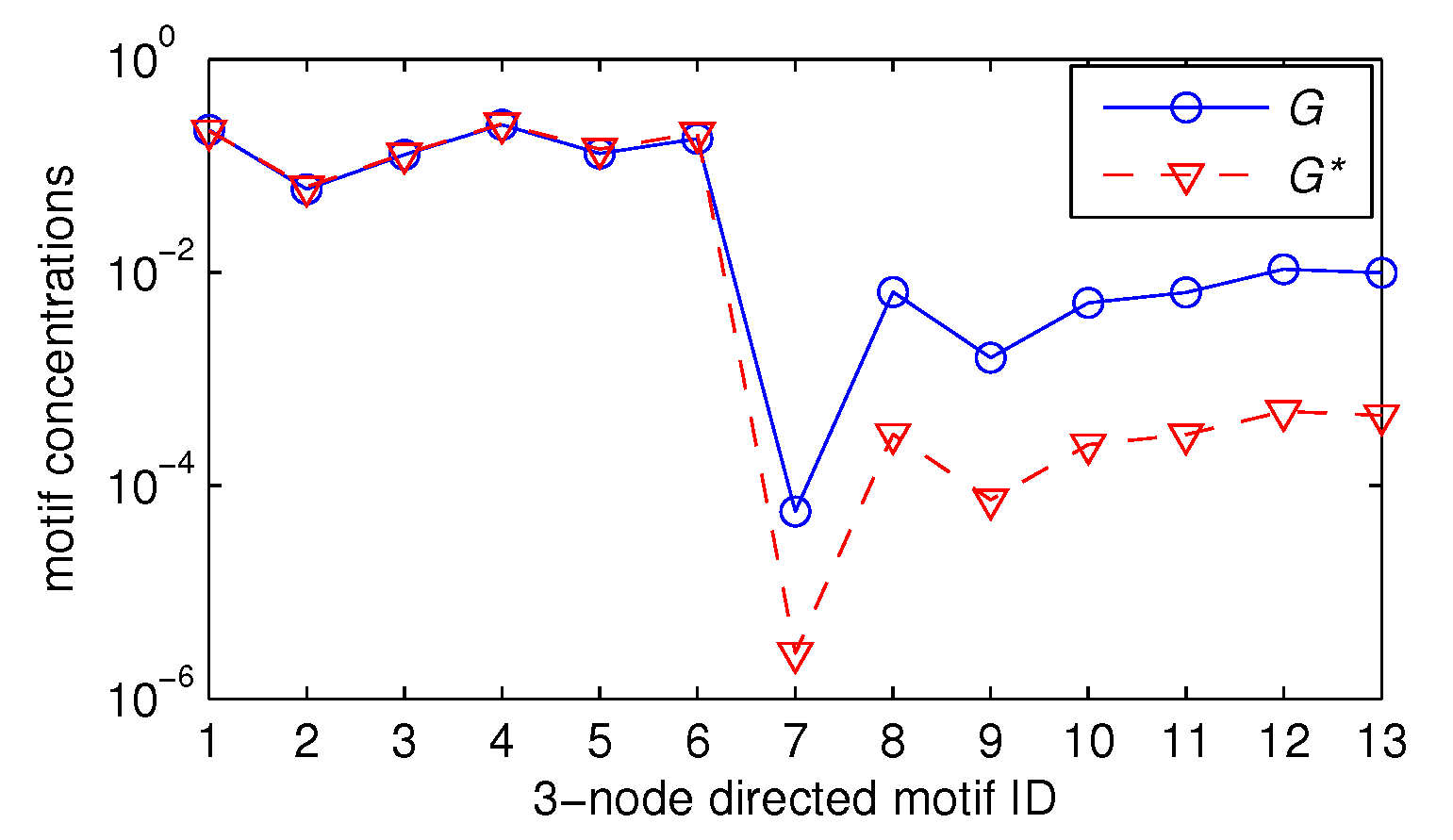
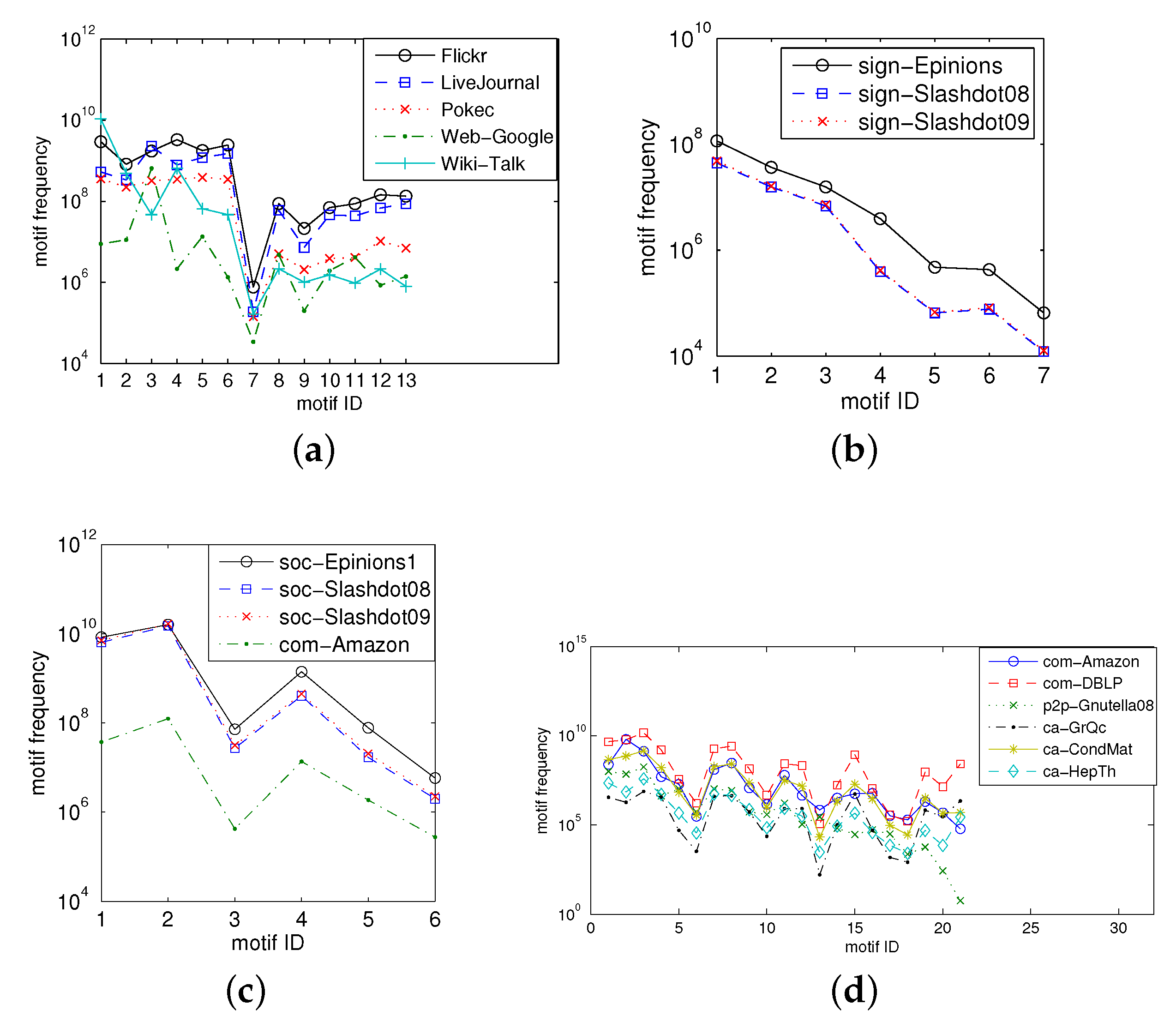
5.3.1. Values of Three-, Four-, and Five-Node Motif Frequencies

Figure 6 and

Table 3. Real values of three-node undirected motif frequencies (i is the motif ID).

i	Flickr	Pokec	Live- Journal	Wiki- Talk	Web- Google
undirected three-node motifs
1	1.30 × 10${}^{10}$	1.99 × 10${}^9$	6.59 × 10${}^9$	1.26 × 10${}^{10}$	6.87 × 10${}^8$
2	5.49 × 10${}^8$	3.26 × 10${}^7$	3.11 × 10${}^8$	9.20 × 10${}^6$	1.34 × 10${}^7$

show the real values of the three-, four-, and five-node motif frequencies of the graphs studied in this paper. Table 3 and Figure 6a show the real values of three-node directed motif frequencies for the undirected and directed graphs of Flickr, Pokec, LiveJournal, Wiki-Talk, and Web-Google, respectively. Here, undirected graphs are obtained by discarding the edge directions of directed graphs. Among all three-node directed motifs, the seventh motif exhibits the smallest frequency for all these directed graphs. Flickr, Pokec, LiveJournal, Wiki-Talk, and Web-Google have $1.35\times {10}^{10}$, $2.02\times {10}^9$, $6.90\times {10}^9$, $1.2\times {10}^{10}$, and $7.00\times {10}^8$ three-node CIS, respectively. Figure 6b reveals the actual values of the three-node signed motif frequencies for the graphs Sign-Epinions, sign-Slashdot08, and sign-Slashdot09. Sign-Epinions, sign-Slashdot08, and sign-Slashdot09 have $1.72\times {10}^8$, $6.72\times {10}^7$, and $7.25\times {10}^7$ three-node CIS, respectively. Figure 6c reveals the actual values of four-node undirected motif frequencies for the graphs soc-Epinions1, soc-Slashdot08, soc-Slashdot09, and com-Amazon. Graphs soc-Epinions1, soc-Slashdot08, soc-Slashdot09, and com-Amazon have $2.58\times {10}^{10}$, $2.17\times {10}^{10}$, $2.42\times {10}^{10}$, and $1.78\times {10}^8$ four-node CIS, respectively. Figure 6d reveals the actual values of five-node undirected motif frequencies for com-Amazon, com-DBLP, p2p-Gnutella08, ca-GrQc, ca-CondMat, and ca-HepTh. Com-Amazon, com-DBLP, p2p-Gnutella08, ca-GrQc, ca-CondMat, and ca-HepTh have $8.50\times {10}^9$, $3.34\times {10}^{10}$, $3.92\times {10}^8$, $3.64\times {10}^7$, $3.32\times {10}^9$, and $8.73\times {10}^7$ five-node CIS, respectively.

5.3.2. Estimating Three-Node Motif Frequencies

Table 4. NRMSEs of $n_i^{\left(3\right)}$, the concentration estimates of three-node undirected motifs for $p=0.01$ and $p=0.05$, respectively (i is the motif ID).

i	Flickr	Pokec	Live- Journal	Wiki- Talk	Web- Google
$p=0.01$
1	8.3 × 10${}^{-3}$	1.3 × 10${}^{-2}$	2.8 × 10${}^{-2}$	2.5 × 10${}^{-2}$	2.6 × 10${}^{-2}$
2	1.3 × 10${}^{-2}$	1.3 × 10${}^{-2}$	1.7 × 10${}^{-2}$	4.4 × 10${}^{-2}$	2.4 × 10${}^{-2}$
$p=0.05$
1	4.2 × 10${}^{-3}$	5.0 × 10${}^{-3}$	3.4 × 10${}^{-3}$	1.3 × 10${}^{-2}$	1.2 × 10${}^{-2}$
2	4.7 × 10${}^{-3}$	4.1 × 10${}^{-3}$	4.3 × 10${}^{-3}$	1.6 × 10${}^{-2}$	8.1 × 10${}^{-3}$

reveals our estimated NRMSEs of three-node undirected motif frequencies at $p=0.01$ and $p=0.05$, respectively, using graphs fpr Flickr, Pokec, LiveJournal, Wiki-Talk and Web-Google. The triangular motif structure with $id=2$ in the undirected motif in Table 4 is more rare, thus, the result with $id=2$ is better compared with [16]. We can see that the NRMSE for $p=0.05$ is about ten times less than the NRMSE for $p=0.01$. When $p=0.01$ for all these five graphs, the NRMSEs are less than $0.05$. Figure 7 reveals our estimated NRMSEs for three-node directed motif frequencies at $p=0.01$ and $p=0.05$. Likewise, we observe that NRMSE at $p=0.05$ is almost ten times less than NRMSE at $p=0.01$. The NRMSE of our estimates of $n_7^{\left(3\right)}$ (i.e., the seventh three-node directed motif frequency) exhibits the largest error. Except $n_7^{\left(3\right)}$, the NRMSEs of the other motif frequency estimates are smaller than 0.01 when $p=0.05$. Figure 8 reveals our estimated NRMSEs for three-node signed and undirected motif frequencies for $p=0.01$, $p=0.05$, and $p=0.1$ using the graphs Sign-Epinions, sign-Slashdot08, and sign-Slashdot09. For all three signed graphs, the NRMSEs are less than 0.5, 0.1, and 0.06 for $p=0.01$, $p=0.05$, and $p=0.1$.

5.3.3. Estimating Four-Node Motif Frequencies

Figure 9 reveals the NRMSEs of ${\widehat{n}}_i^{\left(4\right)}$, frequency estimates of four-node undirected motifs for $p=0.05$, $p=0.1$, and $p=0.2$, respectively, using the graphs soc-Epinions1, soc-Slashdot08, soc-Slashdot09, and com-Amazon. We can see that the NRMSEs of the other motif frequency estimates are smaller than 0.2, 0.1, and 0.07 for $p=0.05$, $p=0.1$, and $p=0.2$, respectively.

5.3.4. Estimating Five-Node Motif Frequencies

Figure 10 shows the NRMSEs of ${\widehat{n}}_i^{\left(5\right)}$, the estimates of five-node undirected motif frequencies for $p=0.1$, $p=0.2$, and $p=0.3$, respectively. The experiment was conducted on the graphs com-Amazon, com-DBLP, p2p-Gnutella08, ca-GrQc, ca-CondMat, and ca-HepTh. We can see that most five-node undirected motifs of all graphs except ca-GrQc have NRMSEs smaller than 1 and 0.1 for $p=0.05$ and $p=0.1$, respectively. For instance, the largest three graphs, com-Amazon, com-DBLP, and ca-CondMat, exhibit smaller errors than the other graphs, while the smallest graph, ca-GrQc, has a larger NRMSE.

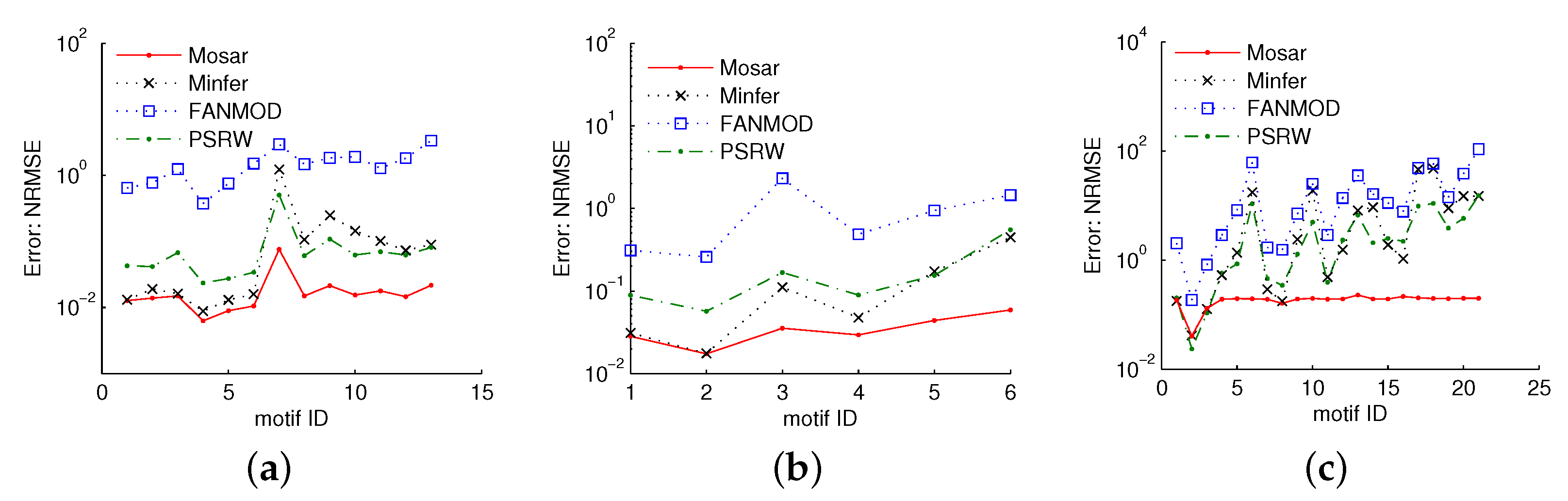
5.4. Comparison to Previous Work

5.4.1. Motif Concentration Estimation

Figure 11a–c show the results of our methods for estimating three-, four-, and five-node motif concentrations in comparison with the state-of-the-art methods FANMOD [14], PSRW [12], and Minfer [16] with the same computational time. We set the same edge sampling probability for Mosar and Minfer. We observed that these two methods have almost the same runtime. This is because Mosar and Minfer spend much less time reading the graph files than enumerating and classifying the subgraphs. For example, the computational time needed to pass over the graph file of interest on disk was 3.8%, 6%, 7%, 5%, and 1.9% of the time required to enumerate and classify subgraphs in the sampled graph for Flickr, livejournal, Pokec, Web-Google, and Wiki-Talk, respectively, when using Mosar and Minfer to estimate three-node directed motif frequencies and set $p=0.01$. Figure 11 shows that Mosar exhibits almost one order fewer errors than the other methods for estimating concentrations of three- and four-node rare motifs, and two orders fewer errors than Minfer for estimating concentrations of five-node rare motifs.

5.4.2. Triangle Counting

We compared the performance of our method for estimating the number of triangles with the state-of-the-art method ${\mathrm{gSH}}_T$ [43]. To compare Mosar and ${\mathrm{gSH}}_T$ under the same computational cost, we set the parameters of ${\mathrm{gSH}}_T$ as ${\mathrm{gSH}}_T(p,p)$. As alluded to, the runtime of Mosar is then almost same as ${\mathrm{gSH}}_T(p,p)$, and the probabilities of observing a triangle (sampled as a closed or unclosed wedge) are $p_T\approx 3p^{2}q$ and $p_T\approx p^2$ for Mosar and ${\mathrm{gSH}}_T$, respectively. Let $n_T$ be the number of triangles and ${\widehat{n}}_T$ be an estimate of $n_T$; then, the variance of ${\widehat{n}}_T$ is nearly $\frac{n_T}{p_T}$. Thus, the variance of Mosar is up to three times larger than ${\mathrm{gSH}}_T$. This is consistent with the results shown in Figure 12, where $p=0.01$. We can see that the NRMSE of Mosar is nearly 1.7 times smaller than ${\mathrm{gSH}}_T$.

6. Conclusions

In this paper, we develop a weighted motif sampling method, Mosar, to accurately estimate the frequency of both frequent and rare motifs. Mosar first obtains a sampled graph $G^{*}$ and then enumerates all CIS in $G^{*}$. To reduce the estimate errors, Mosar samples those rare motifs with higher probabilities. We build a probabilistic model of the CIS in both $G^{*}$ and G, then use this to drive a motif frequency estimation method with a theoretical guarantee. Finally, we performed experiments on various publicly availably datasets to evaluate the performance of our Mosar method. Our experimental results show that Mosar is over two orders of magnitude more accurate than the current state-of-the-art algorithms. In the future, we plan to extend our method to dynamic graphs with edge insertions and deletions.