1. Introduction
The interaction of a tunnel’s surrounding rock supports has been a focus of research globally [
1,
2,
3]. The tunnel support structure is complex and difficult to predict, especially for initial support, for which loads originate directly from the surrounding rock that is closely attached to it [
4,
5]. The actual load distribution law of surrounding rocks is extremely complicated due to the uncertainty of construction, the complexity of surrounding rock, and the variability of environment [
6]. The measurement results suggest that the stress concentration bias, and uneven distribution of the surrounding rock load are common in the initial support [
7,
8,
9]. The tunnel support system can be considered as a curved beam structure in its cross section, and its stability is correlated with the load’s size. The load distribution mode also significantly affects the stability of the system and may even play a leading role [
10]. Accordingly, optimizing and adjusting the load distribution mode of tunnel support structure takes on a great theoretical and practical significance in the structural safety of the tunnel construction period, disease control of the tunnel operation period, and subsequent lining optimization design. The initial support of the tunnel should bear all the surrounding rock loads at the early stage, and its stress characteristics are correlated with the safety of the tunnel construction period and the load distribution of the subsequent secondary lining. The initial support of the tunnel is the key stress structure in the tunnel support system [
11,
12]. The existing research has achieved fruitful results in the interaction relationship of support surrounding rock, as well as in the analysis and evaluation of support stress.
In 1912, the Swedish geologist Haim put forward the hypothesis of isotropic isobaric pressure, holding that the surrounding rock pressure comprises approximately hydrostatic pressure and that the surrounding rock load borne by the support structure is the self weight of the overlying surrounding rock. In 1926, according to the elasticity theory, the former Soviet scholar Jinnet modified the Heim hypothesis and modified the lateral pressure coefficient [
13]. With the increase in tunnel excavation depth, Terzaghi and Protodyakonov found that the application of classical pressure theory was limited. They improved on this basis and put forward the collapse arch theory. At this stage, it was considered that the reaction force provided by the support is not all of the overlying load, and it was recognized that the surrounding rock has a certain self-bearing capacity [
14]. In the 1950s, people began to use elastic plastic mechanics to solve the problem of roadway support, among which the most famous are the Fenner and Kasterner formulae. These calculation methods provide the internal force distribution of the supporting structure in the ideal state [
15]. In the 1960s, Austrian scholar L.V. Rabcewicz put forward the New Austrian Tunneling Method Theory (NATM). The idea of this theory is to make full use of the self-bearing capacity of the surrounding rock, and the surrounding rock itself becomes an important part of the supporting structure; the result is a jointly formed bearing circle comprising the surrounding rock and the supporting structure [
16,
17]. In the 1970s, Salamon and others put forward the energy support theory, and they believed that although the total energy contained in the surrounding rock was conserved, the surrounding rock released part of the energy in the process of interaction and synergistic deformation between the support structure and the surrounding rock; this part of the energy was absorbed by the support structure to achieve stability [
18]. In the 1980s, Professor Lunardi from Italy carried out theoretical and field test research on hundreds of tunnels and gradually established the geotechnical control deformation analysis method (ADECO-RS method). This new support method proposes that the load and deformation of the tunnel structure should be considered before the excavation stage [
19]. At the end of 1990s, K. Ovan proposed the concept of “yield control” type support, i.e., the support is deformed altogether with surrounding rock before failure [
20]. Subsequently, G. Anagnoston and L.Cantieni highlighted that yield support can be achieved in two forms. One is to fill the compressible layer after rigid support, and the other is to use the combination of sliding steel frame and high compressibility shotcrete [
21]. Yield support has been applied in a considerable number of tunnels.
Different forms of fine control methods of load have been proposed as more insights have been gained relative to the interaction between the surrounding rock support. Numerous studies have been conducted worldwide on the stress characteristics of the initial support and how to adjust the support stress over the past few years. “Flexible support” and “pressure-yielding structure” have been proposed based on the concept of energy absorption and energy dissipation of surrounding rock to adjust and increase the support’s force. For instance, lining supports, yielding anchor bolts, and retractable steel arches have been extensively used in the mining field [
22,
23]. Zhang et al. systematically investigated the stress characteristics, failure process and evolution characteristics, ultimate bearing capacity, and deformation of different initial supports by conducting model experiments [
24]. In accordance with different yield criteria, Hou et al. investigated the entire process of support–surrounding rock interactions based on the ideal elastic plastic model [
25]. Sun et al. introduced the spatial effect of excavation surfaces into the interaction relationship between the support and surrounding rock and studied the entire process of dynamic interaction between support structure and surrounding rock at the early stage of deep buried tunnel [
26,
27]. Qiu et al. proposed the “limited support resistance damper”, and it is capable of effectively limiting the internal force of the support and controlling the stress release of the surrounding rock, which is used to solve the problem of tunnel support cracking caused by excessive stress [
28]. Sun et al. proposed a “flexible support” scheme (e.g., yielding support bolts) to control the continuous large deformation of surrounding rock [
29]. Existing research has been essentially based on the support characteristic curve of the surrounding rock of tunnel. The purpose of adjusting and controlling the support load is achieved by adjusting support stiffness and support timing, which facilitates the development of the theoretical tunnel system. However, there are also some shortcomings. For instance, it is difficult to design different load distributions of the surrounding rock according to different tunnel cross-section forms for increasing the bearing capacity and long-term safety of the support structure; the bias load cannot be corrected.
On the basis of previous research, this paper proposed a transfer and transmission method of tunnel surrounding rock load. To minimize the bending moment of the tunnel support structure, the load of the tunnel support system was optimized by applying active linkage adjustment loads to the initial support, which was verified in the practical engineering and provides a reference for the future tunnel support design.
2. Principle of Optimal Adjustment of Tunnel Support Load
2.1. Transfer and Transmission Mechanism of Tunnel Surrounding Rock Load
After tunnel excavation, the stiffness of support structure tends to play a certain role and provides support reaction with the continuous development of support construction and subsequent surrounding rock deformation. In general, the magnitude of the support reaction is correlated with the deformation and support stiffness. The tunnel support structure can be considered a curved beam structure in the cross section. The peak bending moment of the curved beam structure can be reduced by adjusting the load distribution of the structure. After the linkage of loads is established at different positions in the support cross section, load transfer can be achieved, and the load distribution mode of surrounding rock can be adjusted and optimized. The final phenomenon aims at increasing the overall safety and stability of the tunnel support system. The specific principles are presented as follows (
Figure 1).
As depicted in the figure, a load transfer adjustment device was set up at a certain distance between the support structure and surrounding rock, and then the adjustment devices at different positions were connected in series through the oil pipe, thus rendering correlations between the loads at different points. The adjustment of load size at different positions was controlled by the cylinder diameter in the adjustment device. To produce a ratio of PA, PB, and PC in the figure in the form of x:y:z, the ratio of diameters of the adjusting oil cylinder A, B, and C was set to . Subsequently, the load at the adjusting point will always be adjusted in accordance with the original ratio regardless of the change of the surrounding rock load.
In theory, if the adjustment points are dense enough, any form of load distribution mode can be obtained using the above method, which is equivalent to establishing a load transition adjusting layer between the surrounding rock and the support structure of the tunnel. The adjusting layer correlates the different loads in the support cross section at a specific proportion using the convergence constraint theory of the surrounding rock and the load transfer mechanism of hydraulic adjustment devices. Next, the appropriate proportion of load adjustment distribution was calculated according to the shape of tunnel section; thus, the active optimization adjustments of tunnel-surrounding rock loads can be achieved.
2.2. Load Adjustment Distribution Ratio
Under actual conditions, setting adjustment points that are too dense is unlikely. According to the form and quantity of steel arch frames comprising a tunnel’s cross section combined with the convenience of field implementation and other factors, 15 adjusting units were finally determined and arranged in a cross section for a standard three-lane highway tunnel, and the specific distribution positions are presented in
Figure 2.
The above 15 adjusting units correspond to three different load adjustment ratios. The internal force of tunnel support structure can be obtained based on symmetric hingeless arches. This is calculated using the elastic center method, and the analysis and calculation diagram is shown in
Figure 3.
After redundant unknown forces
X1,
X2, and
X3 were calculated from the force method equation, the equilibrium conditions of the isolator or the internal force superposition formula can be used to yield the following formulas:
where
MP,
FQP, and
FNP denote the bending moment, shear force, and axial force of the section of the basic structure under load, respectively. The internal force of the structure layer was obtained.
Due to the symmetry of the structure, load, and constraint, the stress of the lining structure was also symmetrical. Thus, the left half was selected for analysis. Lastly, the distribution of tunnel bending moment caused by the adjustment of load was examined, as shown in
Figure 4, under the condition that all eight adjustment loads were of unit 1.
By adjusting the size and proportion of loads at different points, the bending moment of tunnel lining structure was the smallest when the adjusting proportion was distributed as illustrated in the
Figure 5.
Likewise, the same method can be adopted to obtain the stress of tunnel support under conventional load. The analysis model and calculation results are shown in
Figure 6 and
Figure 7 respectively.
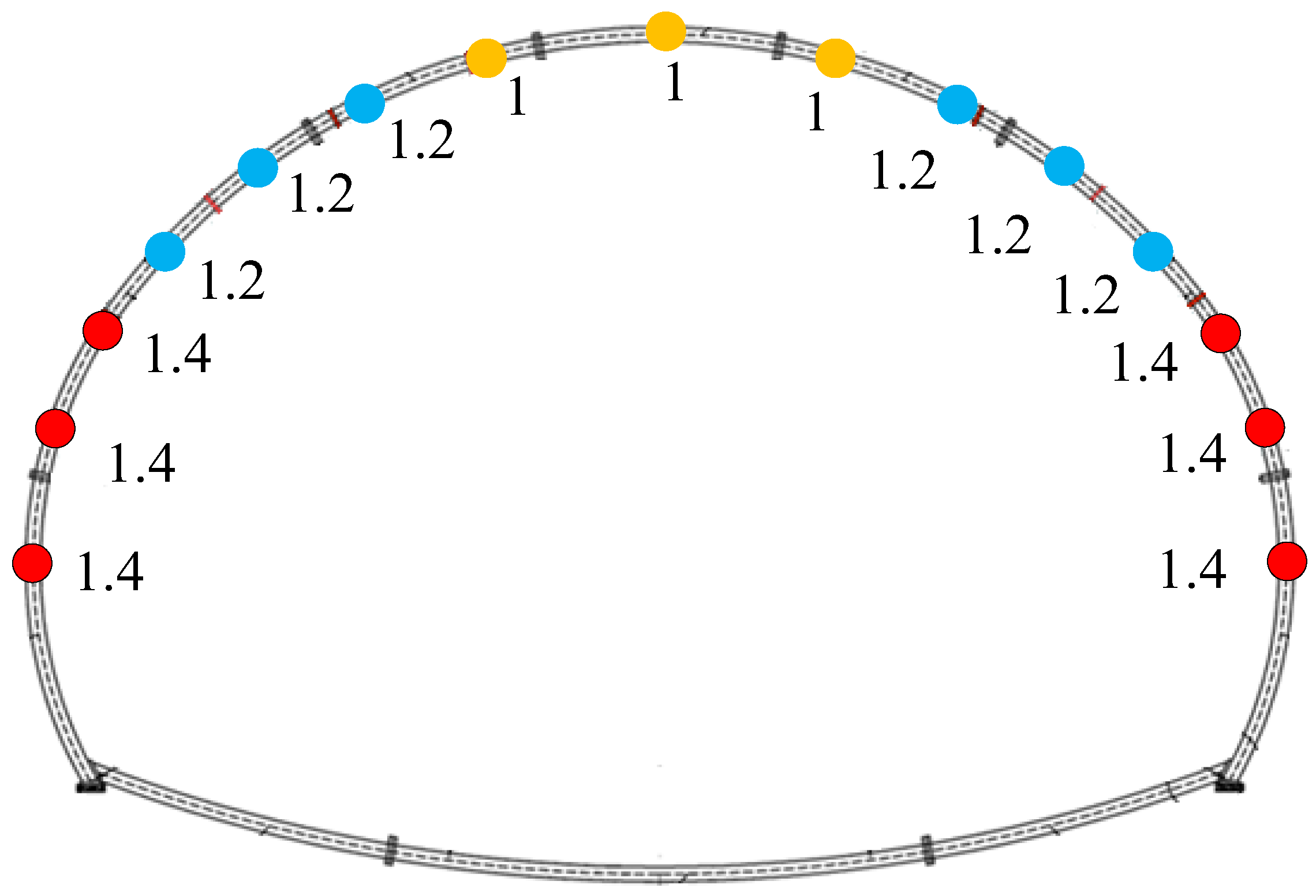
The above analysis suggests that when the load of the regulating unit of the arch is 1, the arch shoulder and the side wall correspond to 1.2 and 1.4, respectively, and a better load optimization adjustment effect can be achieved, as shown in
Figure 8.
To analyze the effect of the tunnel load adjusting unit on the support force of the tunnel, the shallow buried standard three-lane highway tunnel under grade V surrounding rock was selected as the analysis object.
Table 1 and
Table 2 list specific calculation parameters.
Lastly,
Figure 9 presents the bending moment of tunnel lining structure before and after implementation.
The above result showed that the stress state of the tunnel lining structure changed significantly before and after the implementation of load adjustments. Under the control of appropriate load adjustment ratios, the bending moment of the part above the arch foot of the tunnel structure was significantly reduced, with a maximum reduction of 78%.
The structural form of the tunnel initial support in the cross section was similar to the arch’s structure. Using the principle of the best arch axis for reference, the peak bending moment of the support structure can be effectively reduced and the load distribution of the support structure can be optimized by adjusting the pressure of the support reasonably under the surrounding rock to increase the safety and stability of the support structure. Taking the three-lane highway tunnel as an example, applying 15 active load adjustment points on the arch ring of the support structure can significantly improve the stress experienced by the tunnel support structure.
3. Design of the Load Adjustment System
The above analysis reveals that a load adjustment layer can be set between the initial support of the tunnel and the surrounding rock. The load optimization adjustment system of the tunnel surrounding rock support system comprised a load adjusting unit (
Figure 10), serial oil pipes, pressure equipment, anchor bolts, etc. (
Figure 11).
A certain number of load adjusting units were installed symmetrically on the arch frame of the tunnel, and the units were connected in series with high-pressure oil pipes to form a closed and connected loop. Different adjusting units had different load ratios (
Figure 12). The optimization and adjustment of load in tunnel cross section can be achieved by controlling the position and load ratio of the adjusting units.
The adjustment system can apply prestress at the early stage. Subsequently, the load was automatically adjusted during the convergence process of the surrounding rock of the tunnel, and a load linkage between the adjusting units was achieved; finally, the anchor bolts were used to determine and maintain the final stress after the surrounding rock was basically stable. The hydraulic load adjustment system largely comprised three parts, including load adjusting unit, oil pipeline hose, and accessories. The accessories consisted of a high-pressure ball valve, pressure gauge, etc.
The load distribution ratio of the load adjusting unit was divided into three types, which were symmetrically arranged on the left and right sides. The load proportion was achieved by the change of the area of the oil cylinder at the bottom of the adjusting unit.
Figure 11 presents the specific proportion distribution.
The adjusting units were connected by high-pressure oil pipes, the opening and closing control was managed by a ball valve, and a pressure gauge was connected to monitor the pressure.
The adjusting unit and the initial support I-beam of the tunnel were welded into one through the connecting plate. According to the overexcavation and underexcavation of the tunnel section, the screw was adopted to adjust the force-bearing tray to contact with surrounding rock. The adjusting units in the same section were connected in series through oil pipes to ensure that the same hydraulic pressure exists in the system in order to optimize the stress experienced by the tunnel’s lining using the load adjustment ratio.
A total of 15 interconnected hydraulic cylinders were used. The respective cylinder represents a load adjustment point. Each cylinder had the same hydraulic pressure inside. Different cylinder piston areas were configured in accordance with the load adjustment ratio to form a cross-sectional load adjustment unit. The load adjustment unit was constructed together with the initial support, and the initial hydraulic pressure was applied at the first time after the completion of construction. The adjustment point was closely attached to the surrounding rock to bear the surrounding rock load. Subsequently, with the development of the convergence deformation of the surrounding rock of the tunnel, the load between the load adjustment points was automatically adjusted according to the preset proportion to minimize the bending moment, i.e., the stress optimization goal of the support structure.
4. Field Implementation Effect of Load Adjustment System
Miaoshan tunnel in Ningbo city, Zhejiang Province, was selected as the support project, which is part of the Shenhai Expressway connecting line project in the Meishan Port Area of Ningbo Zhoushan Port. The tunnel section is a standard three-lane highway tunnel with compound lining. The implementation interval was IV and V grade surrounding rock, and the implementation length was 100 m. The field implementation is shown in
Figure 13.
The monitoring sections with similar surrounding rock conditions were selected to set in the implementation section and the conventional section (
Figure 14), and the load adjustment results were examined through comparative analysis.
The sensor was fixed on the steel arch together with the embedded parts in the front section. Five implementation sections were selected as test sections to develop monitoring and analysis schemes to examine the deformation and stress of the surrounding rock support structure of the tunnel. Besides conventional settlement and convergence monitoring of the tunnel, the following optional testing items were added:
- (1)
Contact pressure between surrounding rock and initial support;
- (2)
Internal force of the initial spray mixed and steel arch;
- (3)
Internal force of concrete and steel reinforcement in the second lining mold;
- (4)
Pressure monitoring of the adjustment system.
The monitoring system adopted the remote automatic acquisition method and sent back field monitoring data in real time.
The comparison diagram before and after adjustments shows that the stress on the tunnel structure was more uniform as a whole (
Figure 15), and the stress concentration phenomenon was alleviated and improved significantly. The maximum value decreased from 9.2 Mpa before adjustment to 4.1 Mpa, and the load difference at the same symmetric position also decreased significantly from 4.78 Mpa to 0.34 Mpa. As revealed by the above results, the load adjustment system can effectively reduce the effect of bias on tunnel structure.
The axial force of reinforcement meter on the internal and external sides of the steel arch before and after adjustment was compared (
Figure 16). The comparison result showed that the distribution range of axial force of reinforcement meter was larger in the section without load adjustment, and the maximum axial force appeared at the arch shoulder of comparison section 1, with the quality of 26.9 kN. After adjustment, the maximum axial force also appeared at the arch shoulder, with the size of 8.73 kN. The maximum difference between the internal and external axial forces of the compared section was 17.8 kN and that of the adjustment section was 5.4 kN.
The load adjustment system can significantly improve the stress of the structure, particularly improving the pressure difference between the inner and outer loads caused by the bending moment.
Based on the synergistic action mechanism of steel arch and shotcrete, combined with the design parameters and monitoring data of tunnel structure, the bending moment of the tunnel structure can be reversely obtained (
Figure 17).
The results showed in
Figure 18 that the maximum bending moment of the comparison section was located at the arch shoulder. The maximum value of the first comparison section was 55.7 kN·m, and the maximum value of the second comparison section was 34.9 kN·m. The maximum bending moment of the first adjustment section was 12.4 kN·m, the maximum bending moment of the second adjustment section reached 16.8 kN·m, and the maximum bending moment of the third adjustment section was 7.4 kN·m. The results of a single section indicated that the absolute value of the maximum bending moment decreased from 55.7 to 16.8, marking a decrease of nearly 70%. The average maximum value of the comparison and adjustment section decreased from 45.3 before adjustment to 12.2 after adjustment, marking a decrease of 73.1%.
Based on actual tunnel engineering, the active surrounding rock load intervention scheme was implemented in the novel tunnel to optimize and adjust the support load. The analysis and comparison of the internal force monitoring data of the support structure in the regulation section and the conventional comparison section suggest that the application of the active support load significantly changes the stress state of the initial support, the overall stress of the tunnel structure under the active support load is more uniform, the stress concentration phenomenon is significantly alleviated, and the peak bending moment and bias pressure of the support structure are effectively reduced.