Simulation Study of a New Magnetorheological Polishing Fluid Collector Based on Air Seal
Abstract
:1. Introduction
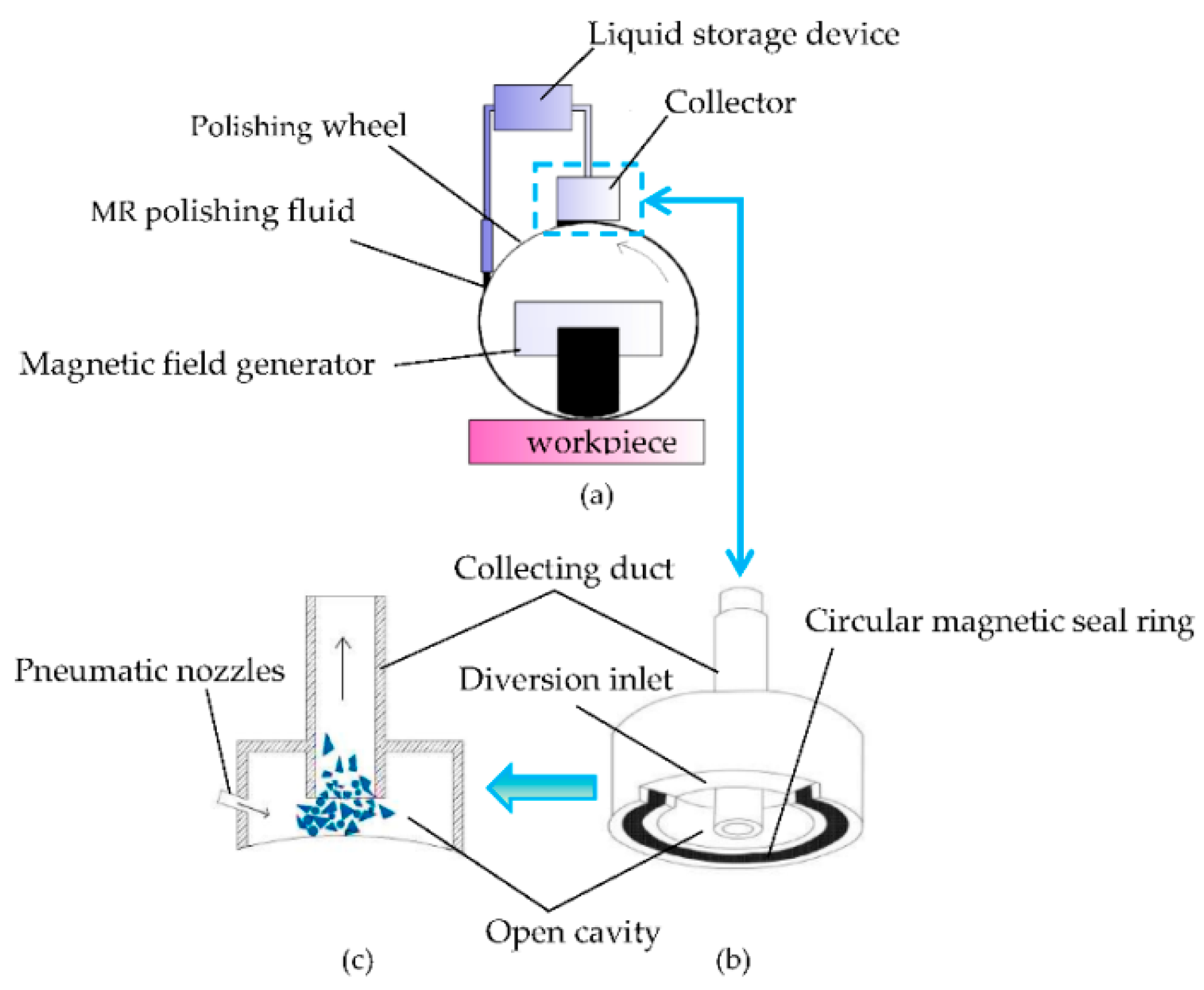
2. Geometric Structure of MR Polishing Collector
2.1. Principle of MR Polishing Liquid Collection
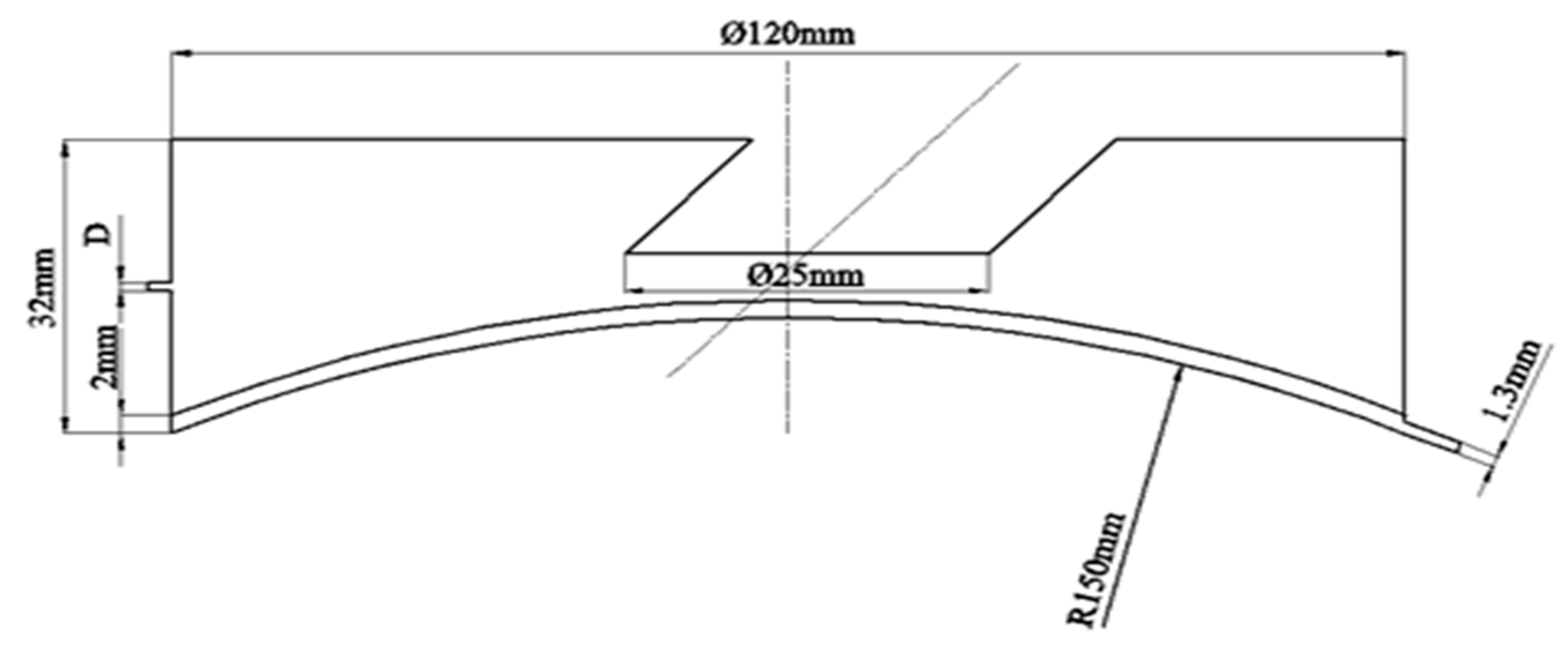
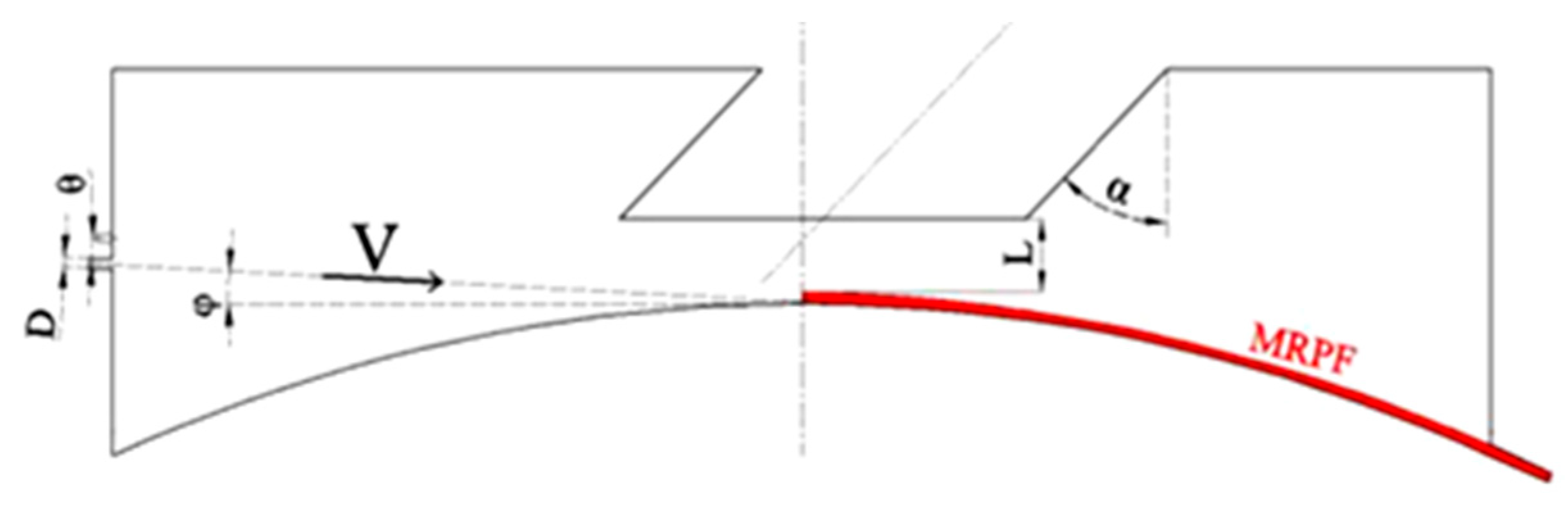
2.2. Geometric Parameters of Airflow Seal Collector
3. Simulation Parameters of MR Polishing Liquid Collector
3.1. Fluid Control Equation
3.2. Simulation Parameters
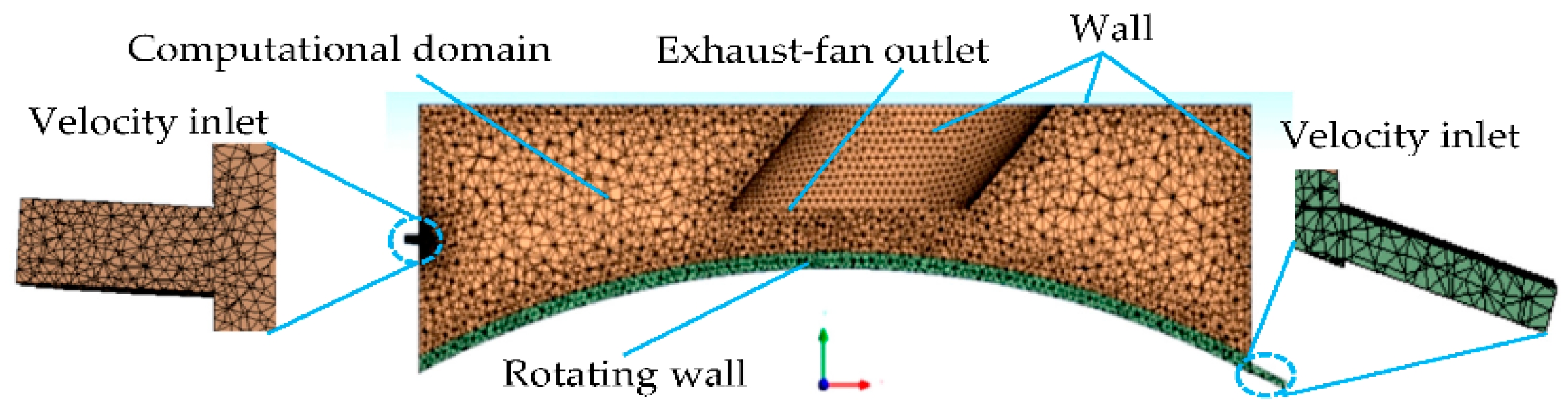
3.3. Boundary Conditions and Meshing
4. Experimental Design Using an Orthogonal Table
4.1. Evaluation Indices of Collection Effect
4.2. Design of Orthogonal Test Table
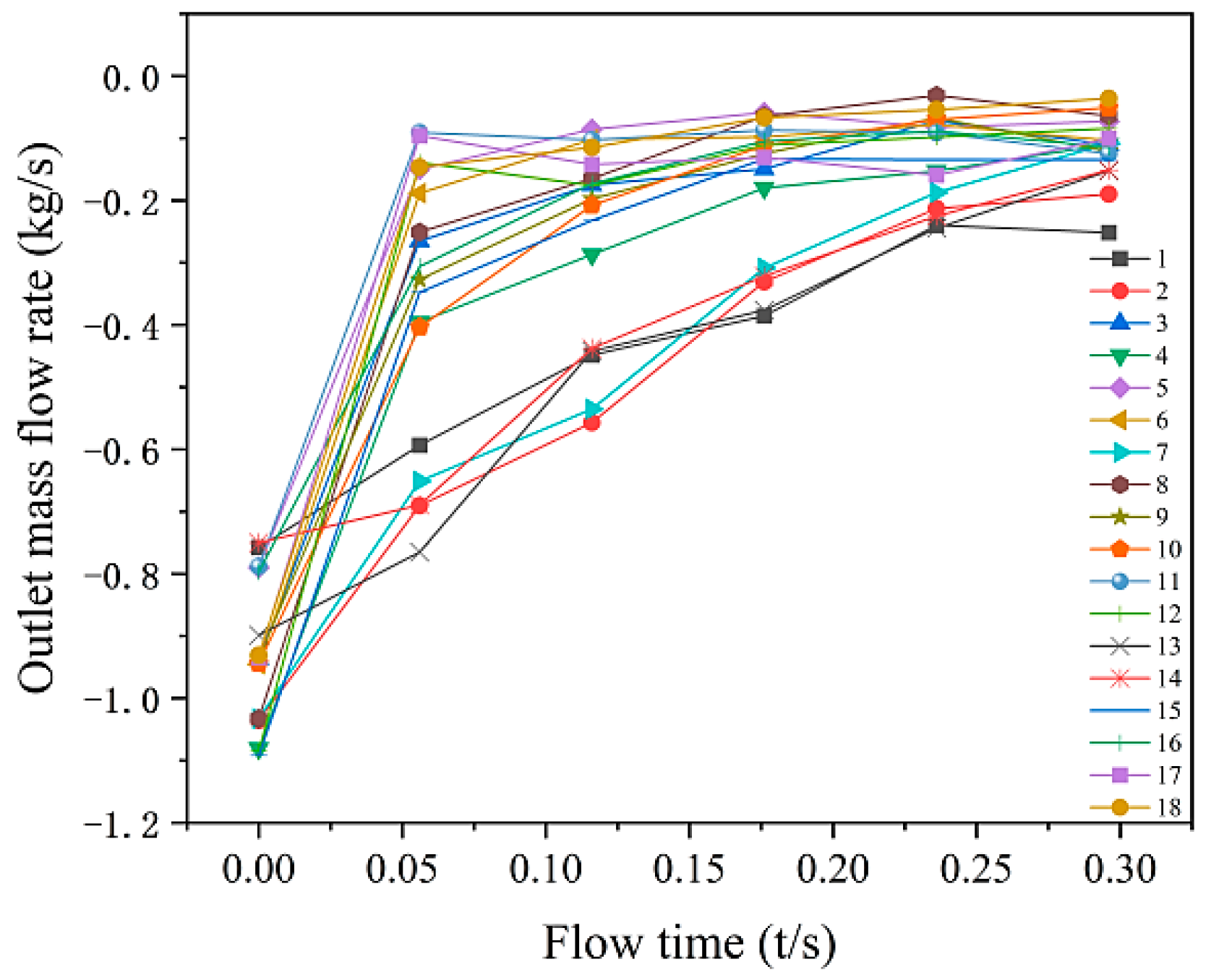
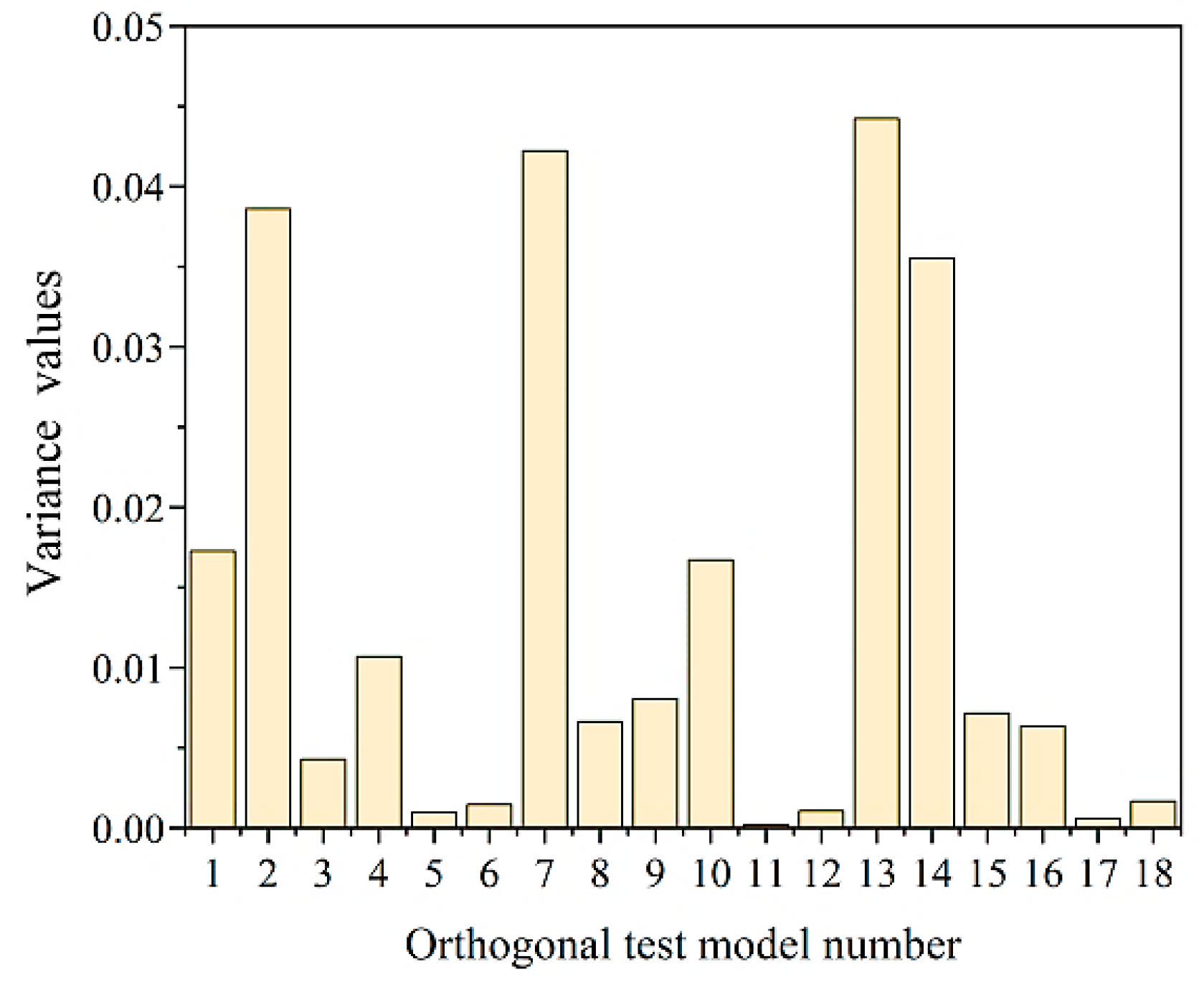
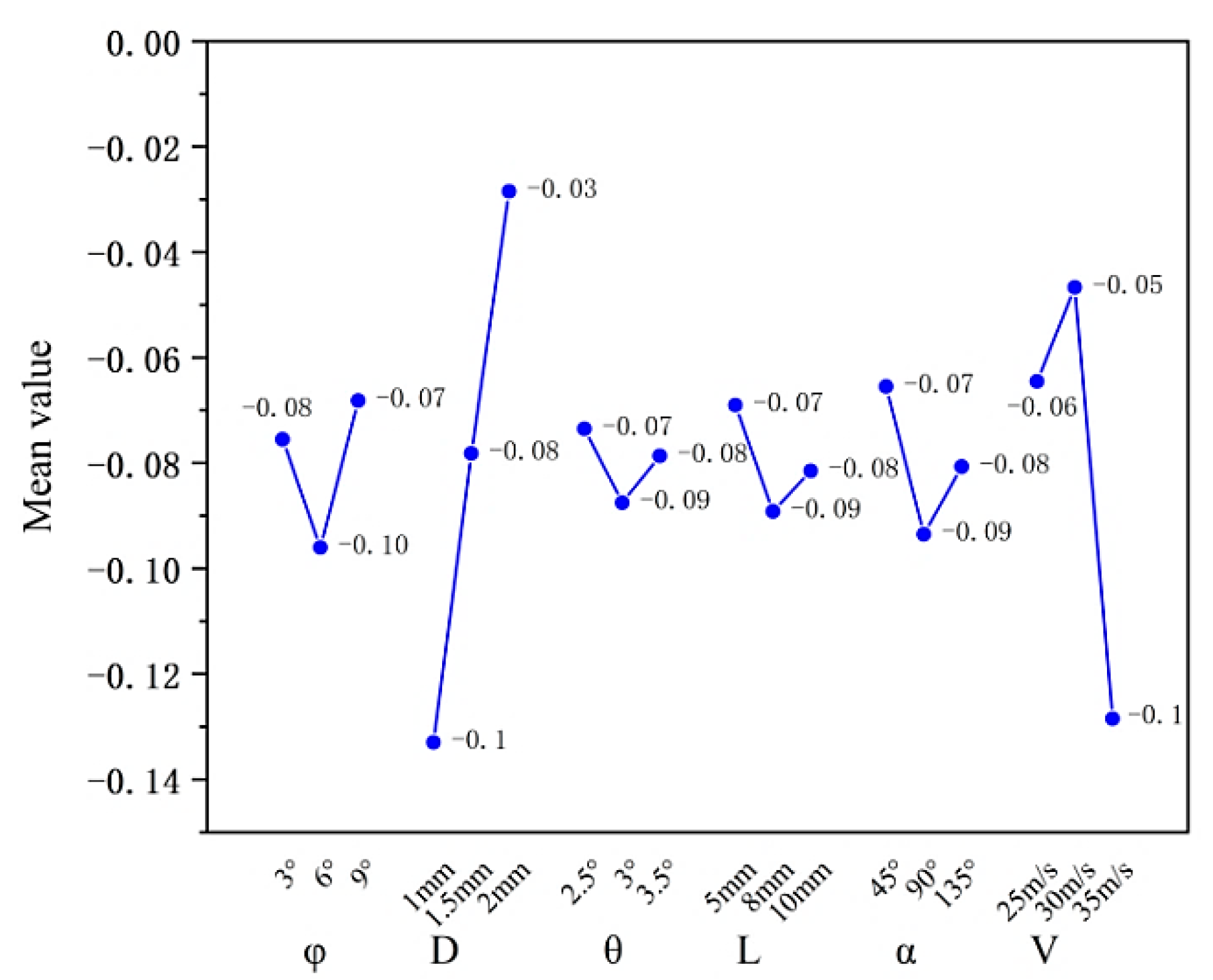
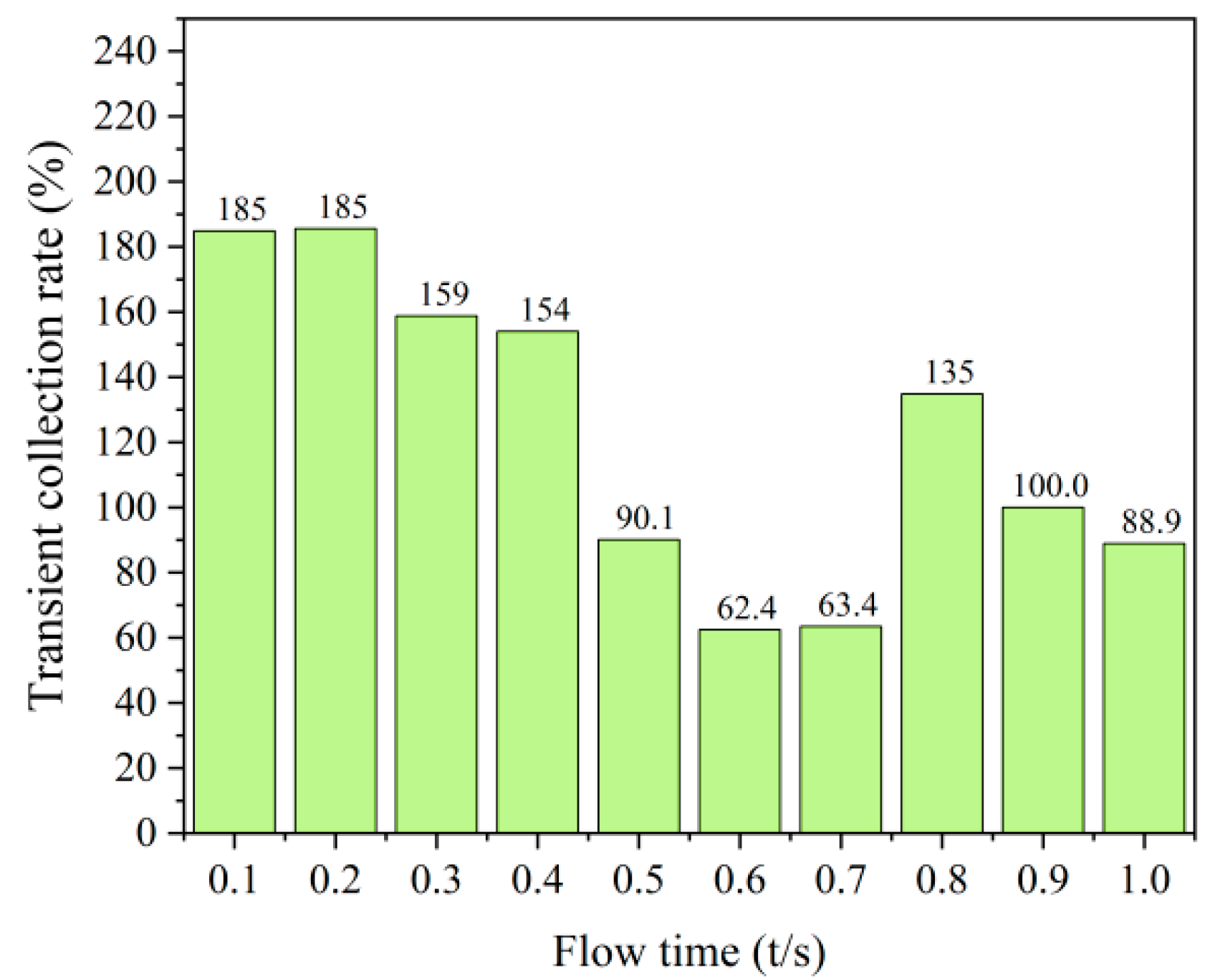
4.3. Results and Discussion of Orthogonal Test
5. Model Optimization and Analysis
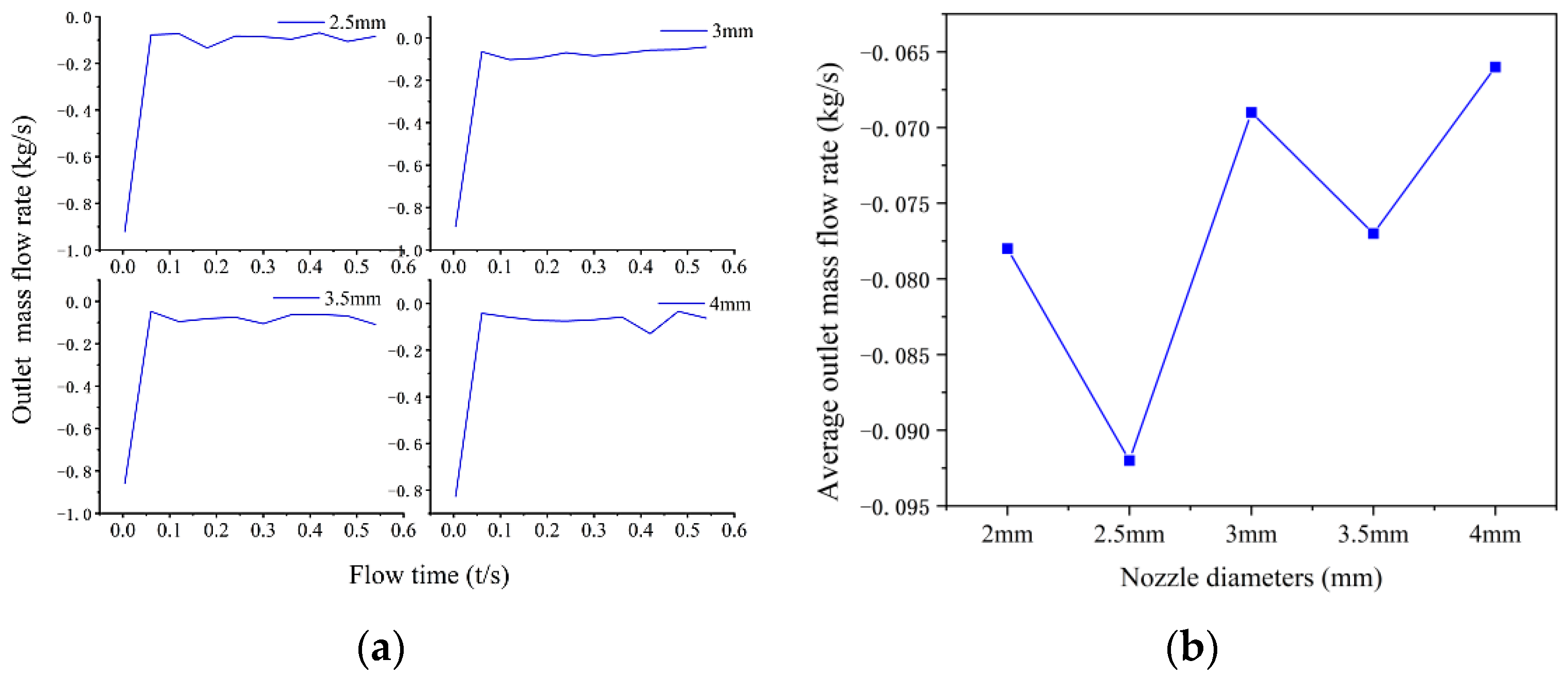
5.1. Optimization of Air Nozzle Diameter
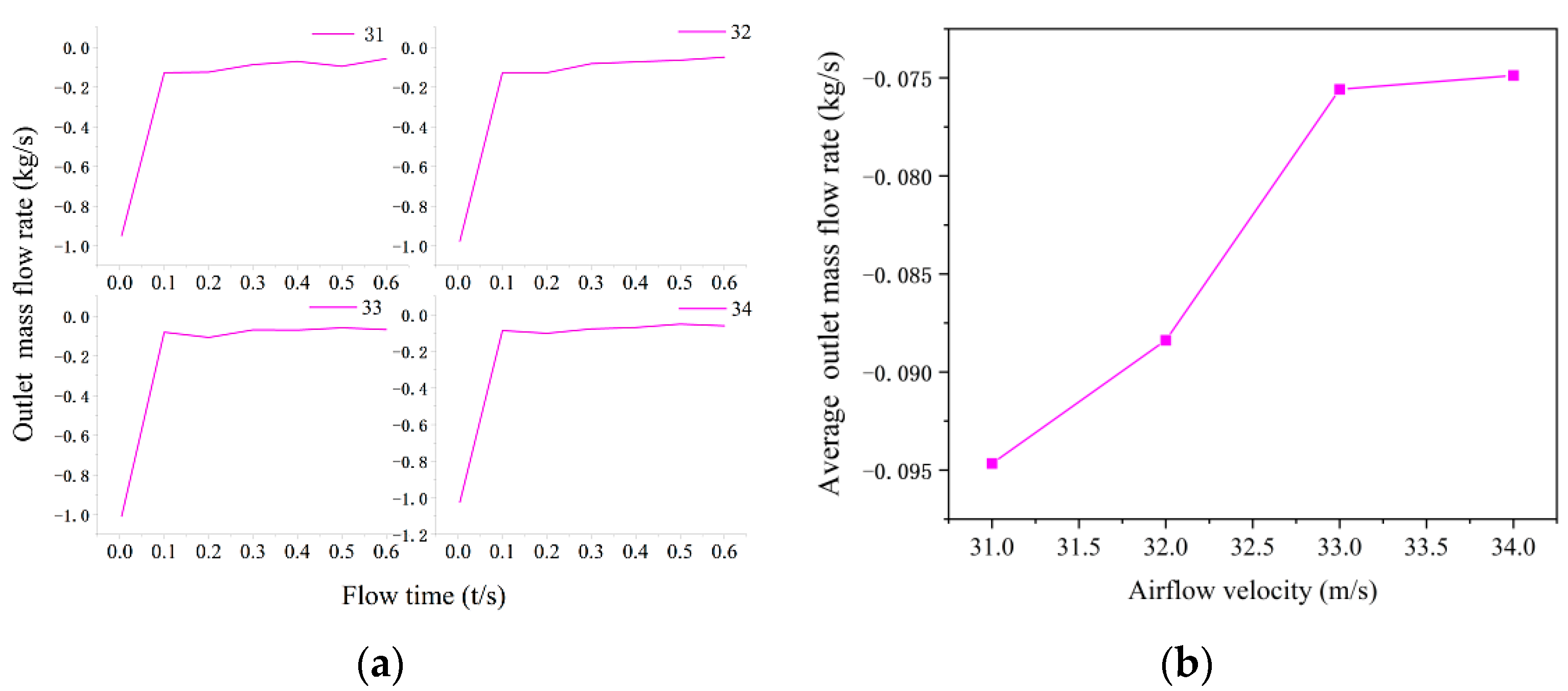
5.2. Optimization of Airflow Velocity
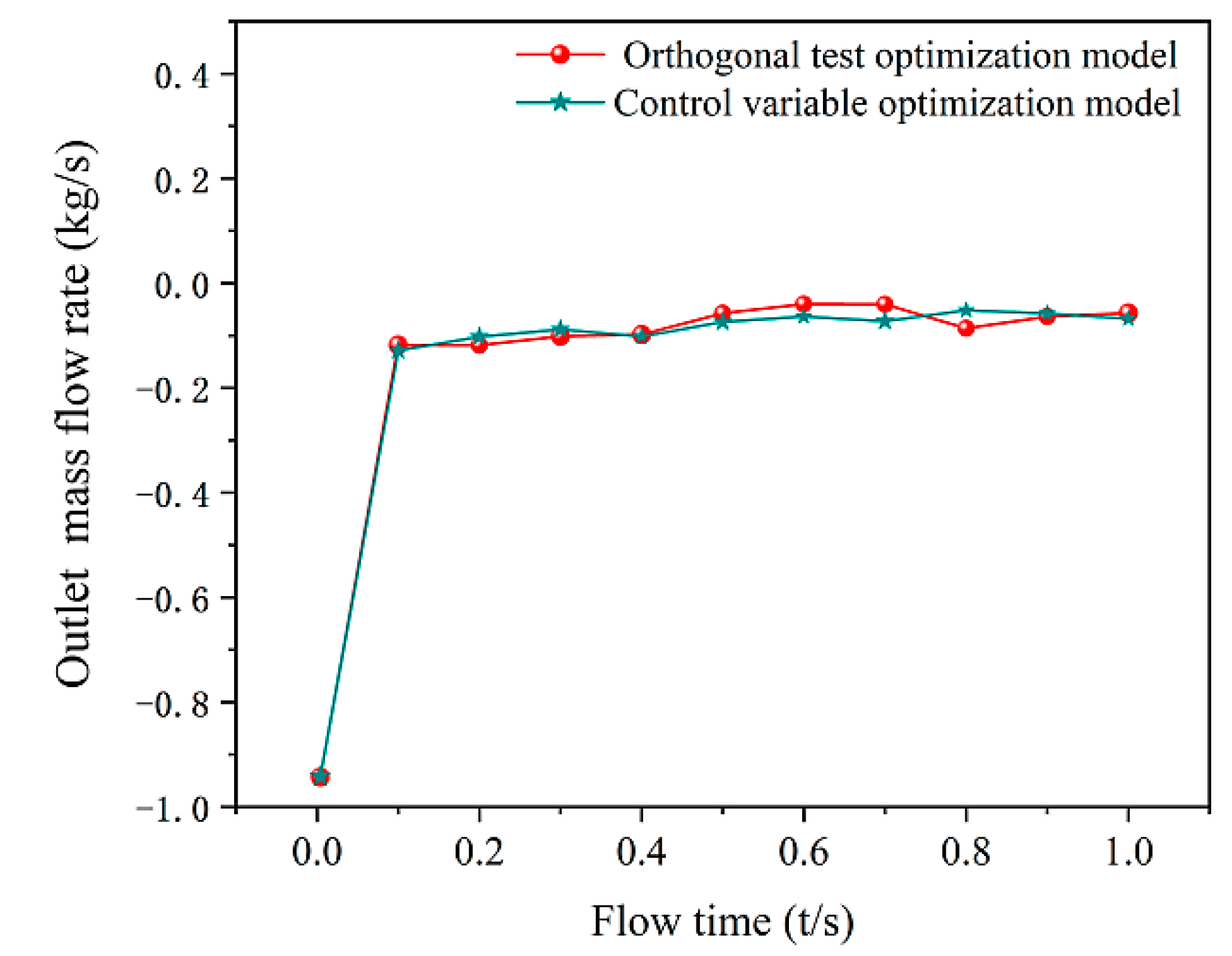
5.3. Simulation Analysis of Optimal Polishing Liquid Collection Model
6. Conclusions
- (1)
- MR polishing fluid can be rapidly collected under the combined action of the collector nozzle airflow pressure and outlet negative pressure. At 0.05 s, the outflow of polishing fluid is monitored at the collector outlet, which effectively shortens the wear time of cerium oxide abrasive particles in the MR polishing fluid on the polishing wheel.
- (2)
- In the case of 69 nozzles used in the collector simulation model, the orthogonal test results show that the main factor affecting the fluctuation of outlet flow of different MR polishing liquid collectors is the diameter of the airflow nozzle, followed by the airflow velocity of the nozzle, and the influence of nozzle spacing is the smallest.
- (3)
- Although it is feasible to collect MR polishing fluid by air seal, the optimal collector model according to orthogonal test results still fluctuates significantly within the range of 0.4–0.8 s, and the instantaneous minimum collection efficiency is 62.4% within 1 s.
- (4)
- The optimal model of orthogonal experimentation was optimized by the control variable method, and it was found that the average outlet mass flow rate was the highest when the nozzle diameter and nozzle airflow velocity were 2.5 mm and 31 m/s, respectively. Excessive nozzle diameter and airflow velocity enhance the dispersion of MR polishing fluid, resulting in a decrease in mass flow rate collected by the collector.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, H.; Guo, M.; Yin, S.; Chen, F.; Huang, S.; Lu, A.; Guo, Y. An atomic-scale and high efficiency finishing method of zirconia ceramics by using magnetorheological finishing. Appl. Surf. Sci. 2018, 444, 569–577. [Google Scholar] [CrossRef]
- Jian, Y.; Tang, T.; Swain, M.V.; Wang, X.; Zhao, K. Effect of core ceramic grinding on fracture behaviour of bilayered zirconia veneering ceramic systems under two loading schemes. Dent. Mater. 2016, 32, 1453–1463. [Google Scholar] [CrossRef] [PubMed]
- Kang, D.; Cho, H.; Yoo, Y.; Kim, J.; Park, Y.; Moon, H. Effect of polishing method on surface roughness and bacterial adhesion of zirconia-porcelain veneer. Ceram. Int. 2017, 43, 5382–5387. [Google Scholar] [CrossRef]
- Vishwas, G.; Anant, K.S. Analysis of particles in magnetorheological polishing fluid for finishing of ferromagnetic cylindrical workpiece. Part. Sci. Techol. 2018, 36, 799–807. [Google Scholar]
- Chen, S.; Zhang, B.; Huang, J.; Yang, J. Analysis of magnetorheological fluid flow considering extrusion and wall slip. Mech. Desi. Manuf. 2022, 60, 100–103. [Google Scholar]
- Hao, R.S.; Li, D.C. Development Characteristics and Application Prospects of Magnetorheological Fluids. Mech. Eng. 2005, 7, 32–33. [Google Scholar]
- Horváth, B.; Decsi, P.; Szalai, I. Measurement of the response time of magnetorheological fluids and ferrofluids based on the magnetic susceptibility response. J. Intel. Mat. Syst. Str. 2022, 33, 918–927. [Google Scholar] [CrossRef]
- Ghosh, G.; Sidpara, A.; Bandyopadhyay, P.P. Review of several precision finishing processes for optics manufacturing. J. Micromanuf. 2018, 1, 170–188. [Google Scholar] [CrossRef]
- Tang, C.X.; Wen, S.L.; Zhang, Y.; Yan, H. Magnetorheological fluid circulation system structure under the condition of small flow rate in magnetorheological polishing. Proc. Spie. Intern. Soci. Opti. Eng. 2021, 11763, 2302–2312. [Google Scholar]
- Zhang, F. Research progress of magnetorheological finishing technology at CIOMP. Laser Optoelectron. Prog. 2015, 9, 92201–92202. [Google Scholar]
- Wang, B.; Shi, F.; Tie, G.P.; Zhang, W.L. The Cause of Ribbon Fluctuation in Magnetorheological Finishing and Its Influence on Surface Mid-Spatial Frequency Erro. Micromachines 2022, 13, 697. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Kumar, V.K.A.; Yadav, H.N.S.; Das, M. CFD analysis of MR fluid applied for finishing of gear in MRAFF process. Mater. Toda. Proc. 2021, 45, 4677–4683. [Google Scholar] [CrossRef]
- Luo, B.; Yan, Q.S.; Chai, J.F.; Song, W.Q.; Pan, J.S. An ultra-smooth planarization method for controlling fluid behavior in cluster magnetorheological finishing based on computational fluid dynamics. Prec. Eng. 2022, 74, 358–368. [Google Scholar] [CrossRef]
- Manas, D.; Jain, V.K.; Ghoshdastidar, P.S. A 2D CFD simulation of MR polishing medium in magnetic field-assisted finishing process using electromagnet. Int. J. Adv. Manuf. Techol. 2015, 76, 173–187. [Google Scholar]
- Prabhat, R.; Balasubramaniam, R.; Jain, V.K. Analysis of magnetorheological fluid behavior in chemo-mechanical magnetorheological finishing (CMMRF) process. Prec. Eng. 2017, 49, 122–135. [Google Scholar]
- Nitesh, K.D.; Dubey, N.K.; Sidpara, A. Numerical and experimental study of influence function in magnetorheological finishing of oxygen-free high conductivity (OFHC) copper. Smart Mater. Struct. 2021, 30, 015034. [Google Scholar]
- Yang, H.; Gu, J.H.; Huang, W.; He, J.G. Cross-experimental study on the influence mechanism of the secondary section of the polished ribbon on the pressure field creation. Manuf. Techol. Mach. Tool. 2022, 6, 18–24. [Google Scholar]
- Yang, H.; Ren, F.J.; Zhang, Y.F.; Huang, W.; He, J.G.; Jia, Y. Numerical analysis of formation mechanism of shear force field in the entrance zone of magnetorheological polishing. Opti. Techol. 2022, 48, 153–158. [Google Scholar]
- Zhang, J.J. Research on Distribution of Ultra-Precision Magnetorheological Finishing Force at Semiconductor Wafer; Beijing Jiaotong University: Beijing, China, 2020; p. 86. [Google Scholar]
- Gao, S. Research on Consistency of Two-Phase Flow Effect of Magnetorheological Polishing Liquid; Beijing Jiaotong University: Beijing, China, 2020; p. 92. [Google Scholar]
- Zhang, Z.J.; Yin, X.M.; Liu, J.G. Preparation and performance of composite coating with wear resistance on buff wheel. Corr. Prot. 2008, 7, 407–409. [Google Scholar]
- He, J.H. Tribological Performance of the Surface of Magnetic Rheological Polishing Wheel Treated by Microarc Oxidation; University of Electronic Science and Techolnology of China: Chengdu, China, 2016; p. 76. [Google Scholar]
- William, K. Multiple application of magnetorheological effect in high precision finishing. J. Intel. Mat. Syst. Struct. 2002, 13, 401–404. [Google Scholar]
- Dong, G.Z. Design of Small-Aperture Magnetorheological Finishing and the Device Key Technology Research; Changsha University of Science and Technology: Changsha, China, 2015; p. 76. [Google Scholar]
- Lu, J.Y. Research on Inverted Device for Magnetorheological Finishing; Harbin Institute of Technology: Harbin, China, 2008; p. 54. [Google Scholar]
- Wang, A.W. Study and Application on the Key Techniques of Magnetorheological Finishing Processing and Device; Donghua University: Shanghai, China, 2008; p. 107. [Google Scholar]
- Wang, D.W. A Recovery Device for Sealing Structure and Magnetorheological Polishing Liquid. CN Patent CN216151878U, 18 September 2021. [Google Scholar]
- Li, Y.; He, J.G.; Huang, W.; Zhang, Y.F.; Qian, L.H. Analysis of influence factors on magnetorheological polishing wheel wear. Lubr. Seal. 2019, 44, 126–131. [Google Scholar]
- Li, Y. Study on Wear Mechanism and Suppression Method of Magnetorheological Polishing Wheel; China Academy of Engineering Physics: Mianyang, China, 2019; p. 66. [Google Scholar]
- Tan, C.; Zhang, K.P. Research Advance in Granular Flow Mathematical Model; Hebei University of Science and Technology: Shijiazhuang, China, 2013; pp. 34, 293–296, 380. [Google Scholar]
- Zhao, B.J.; Yuan, S.Q.; Liu, H.L.; Huang, Z.F.; Ming, G. Simulation of solid-liquid two-phase turbulent flow in double-channel pump based on Mixture model. J. Agricult. Eng. 2008, 1, 7–12. [Google Scholar]
- Hu, H.; Da, Y.F.; Peng, X.Q. Design and research of the inverted device for magnetorheological finishing. Avia. Prec. Manufact. Techol. 2006, 6, 5–8. [Google Scholar]
- Dong, G.Z.; Hu, H.; Li, S.Y.; Yang, C. Design and optimization of small bore magnetorheological finishing device for permanent magnet. Nanotechol. Prec. Eng. 2015, 13, 251–257. [Google Scholar]
- Ma, Z.Q. Study on Preparation and Properties of Magnetorheological Polishing Fluid for Ultra Precision Polishing of Miconductor Wafer; Beijing Jiaotong University: Beijing, China, 2021; p. 85. [Google Scholar]




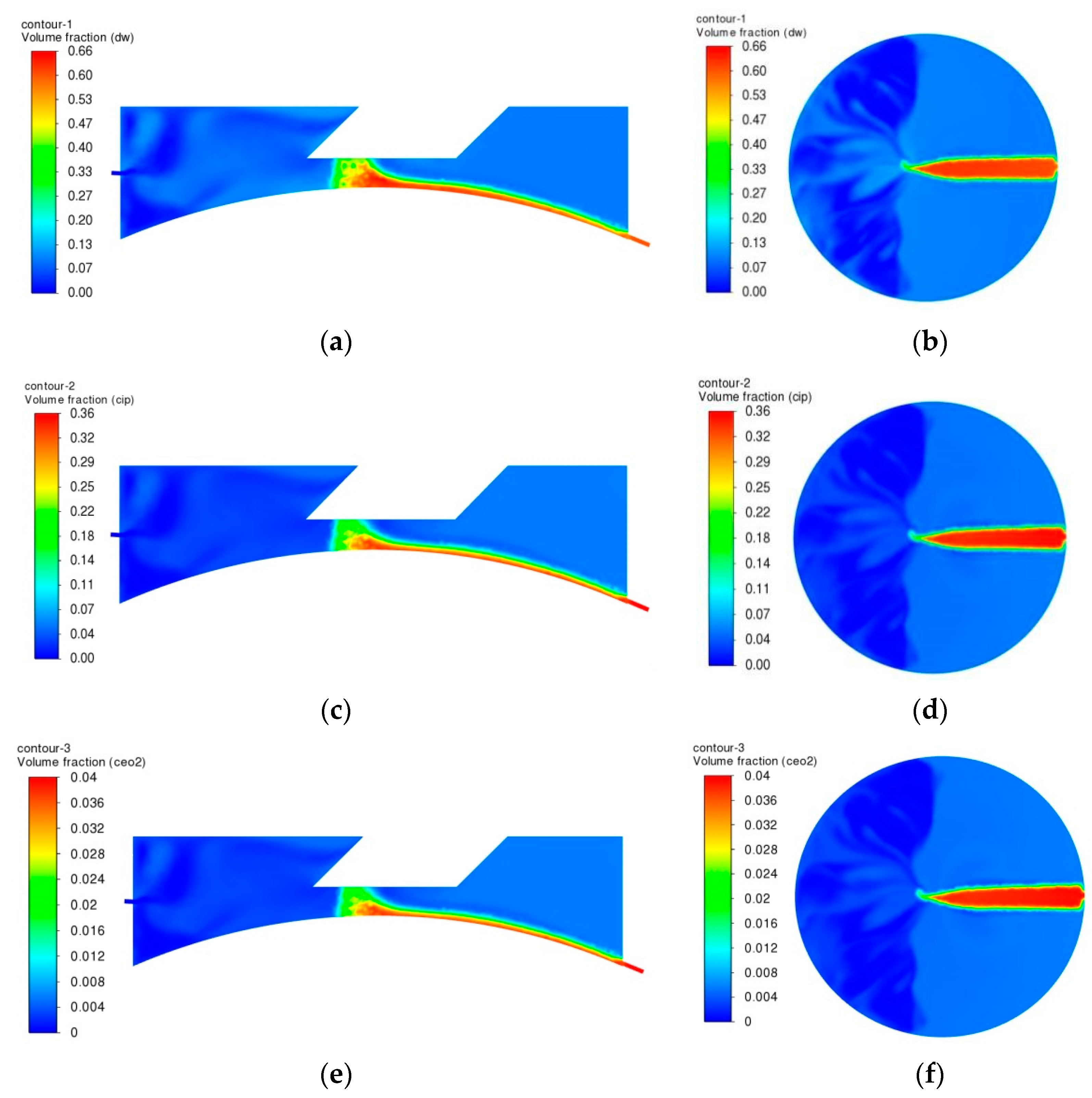

| Component | DW | CIP | CeO2 |
| Density (g/cm3) | 1.0 | 7.8 | 7.13 |
| Viscosity (Pa·s) | 0.001 | 1.72 × 10−5 | 1.72 × 10−5 |
| Volume fraction (%) | 60 | 36 | 4 |
| Particle size (um) | 3 | 3 | |
| Permeability (H/m) | 1 | 1000 | 1 |
| Conductivity (S/m) | 5.89 × 10−8 |
| Factor 1 φ | Factor 2 D | Factor 3 θ | Factor 4 L | Factor 5 α | Factor 6 V | |
|---|---|---|---|---|---|---|
| Level 1 | 3° | 1 mm | 2.5° | 5 mm | 45° | 25 m/s |
| Level 2 | 6° | 1.5 mm | 3° | 8 mm | 90° | 30 m/s |
| Level 3 | 9° | 2 mm | 3.5° | 10 mm | 135° | 35 m/s |
| Item | Level | Factor 1 φ | Factor 2 D | Factor 3 θ | Factor 4 L | Factor 5 α | Factor 6 V |
|---|---|---|---|---|---|---|---|
| K-value | 1 | −0.45 | −0.80 | −0.44 | −0.41 | −0.39 | −0.39 |
| 2 | −0.58 | −0.47 | −0.53 | −0.54 | −0.56 | −0.28 | |
| 3 | −0.41 | −0.17 | −0.47 | −0.49 | −0.48 | −0.77 | |
| Kavg value | 1 | −0.08 | −0.13 | −0.07 | −0.07 | −0.07 | −0.06 |
| 2 | −0.10 | −0.08 | −0.09 | −0.09 | −0.09 | −0.05 | |
| 3 | −0.07 | −0.03 | −0.08 | −0.08 | −0.08 | −0.13 | |
| Best level | 3 | 3 | 1 | 1 | 1 | 2 | |
| R | 0.03 | 0.10 | 0.01 | 0.02 | 0.03 | 0.08 |
| Source of Variance | SS | DF | Mean Square Deviation | F | Contribution Rate (%) |
|---|---|---|---|---|---|
| Factor 1 | 0.003 | 2 | 0.0013 | 0.982 | 0.067 |
| Factor 2 | 0.033 | 2 | 0.0164 | 12.812 | 44.345 |
| Factor 3 | 0.001 | 2 | 0.0003 | 0.235 | 2.871 |
| Factor 4 | 0.001 | 2 | 0.0006 | 0.471 | 1.984 |
| Factor 5 | 0.002 | 2 | 0.0012 | 0.918 | 0.309 |
| Factor 6 | 0.022 | 2 | 0.0112 | 8.718 | 28.976 |
| Error | 0.006 | 5 | 0.0013 | / | / |
| Summation | 0.068 | 17 | / | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Chen, G.; Zhang, W.; Peng, Y.; Cao, S.; He, J. Simulation Study of a New Magnetorheological Polishing Fluid Collector Based on Air Seal. Appl. Sci. 2022, 12, 7433. https://doi.org/10.3390/app12157433
Li M, Chen G, Zhang W, Peng Y, Cao S, He J. Simulation Study of a New Magnetorheological Polishing Fluid Collector Based on Air Seal. Applied Sciences. 2022; 12(15):7433. https://doi.org/10.3390/app12157433
Chicago/Turabian StyleLi, Mingchun, Guanci Chen, Wenbin Zhang, Yunfeng Peng, Shuntao Cao, and Jiakuan He. 2022. "Simulation Study of a New Magnetorheological Polishing Fluid Collector Based on Air Seal" Applied Sciences 12, no. 15: 7433. https://doi.org/10.3390/app12157433
APA StyleLi, M., Chen, G., Zhang, W., Peng, Y., Cao, S., & He, J. (2022). Simulation Study of a New Magnetorheological Polishing Fluid Collector Based on Air Seal. Applied Sciences, 12(15), 7433. https://doi.org/10.3390/app12157433





