Analysis of Train Car-Body Comfort Zonal Distribution by Random Vibration Method
Abstract
:1. Introduction
2. Establishment and Solution of the Motion Equation
2.1. Motion Equation of Train System Based on MCM
- (1)
- The interaction is nonexistent among vehicle elements.
- (2)
- Each vehicle element is composed of a rigid car-body, bogies, and wheel sets.
- (3)
- The springs of a train are linearly elastic, while the dampers are linearly viscous.
- (4)
- Each vehicle element is a linear stationary system; namely, the mass, damping, and stiffness matrices of train are constant.
- (5)
- The train moves at a constant speed.
- (6)
- The wheels and rails fit snugly. The relative displacement between the track and the bridge deck, as well as the elastic effect of the track–bridge system, are neglected.
- (7)
- The track irregularity is a zero-mean stationary Gaussian random process.
2.2. Motion Equation of Train System Based on the PEM
3. Sperling Index Based on Vibratory Acceleration History and PSD
3.1. Zonal Distribution Deduction of Sperling Index Based on Vibratory Acceleration History
3.2. Zonal Distribution Deduction of Sperling Index Based on Vibratory Acceleration PSD
4. Case Study
4.1. Parameters of Track Irregularity and Train
4.2. Demonstration of the Methodological Correctness
- In Figure 4a,c, the expected value μ and the limits of the 3σ normal distribution of the vibration response of the Car-Body center using MCM–NβM and PEM-FRF, respectively, are in substantial agreement. The response patterns are also well within the bounds of the 3σ principle for normal distributions. Compared to MCM, which required multiple solutions, the PEM was much more accurate and efficient.
- In Figure 4b,d, the preliminary probability density curve calculated using MCM-NβM agrees with the theoretical normal distribution calculated using PEM-FRF.
- In general, the train vibration acceleration under track irregularities obeyed the stationary zero-mean normal distribution, the statistical properties of which can be described by the 3σ-principle, and which is consistent with the original assumption regarding the track irregularities as a stationary zero-mean Gaussian random process. Therefore, it was demonstrated that the methodology was correct and suitable for the analysis outlined in the following sections.
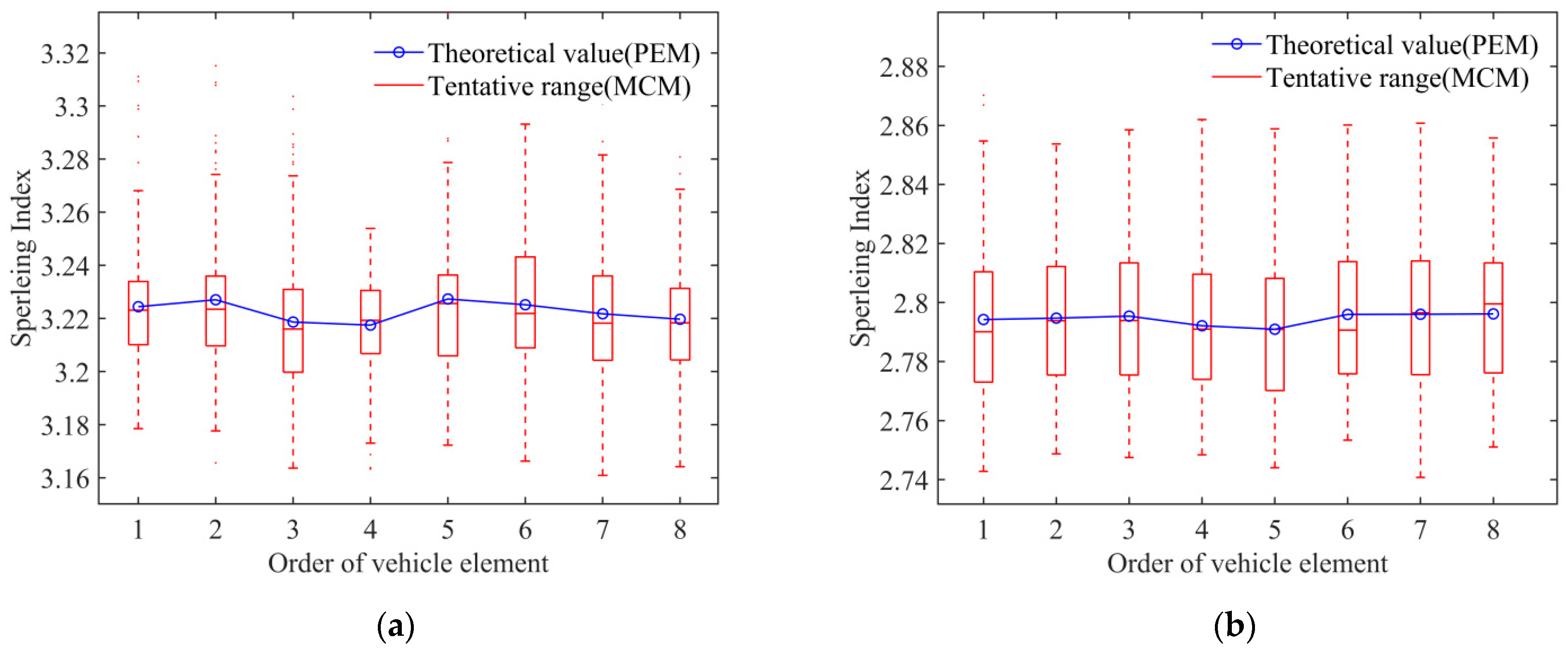
4.3. Analysis of the Car-Body Center Comfort in Different Vehicle Elements
- The variations in the theoretical Sperling index of the car-body center according to the PEM between the different vehicle elements were insignificant for both the horizontal and vertical components. The theoretical Sperling index for the horizontal component was obviously higher than that for the vertical component;
- In all sequences of vehicle elements, the difference between the upper and lower provisional range limits of the Sperling index sampling distribution according to MCM did not exceed 0.12 for both the horizontal and vertical components;
- In general, the discomfort was strongly related to the horizontal vibration acceleration of the car body. In addition, the Sperling index was a stationary indicator of comfort that was independent of the order of vehicle elements when the train was subjected to track irregularities. In this way, the comfort of the center of the car body could be characterized by simply selecting a vehicle element to analyze.
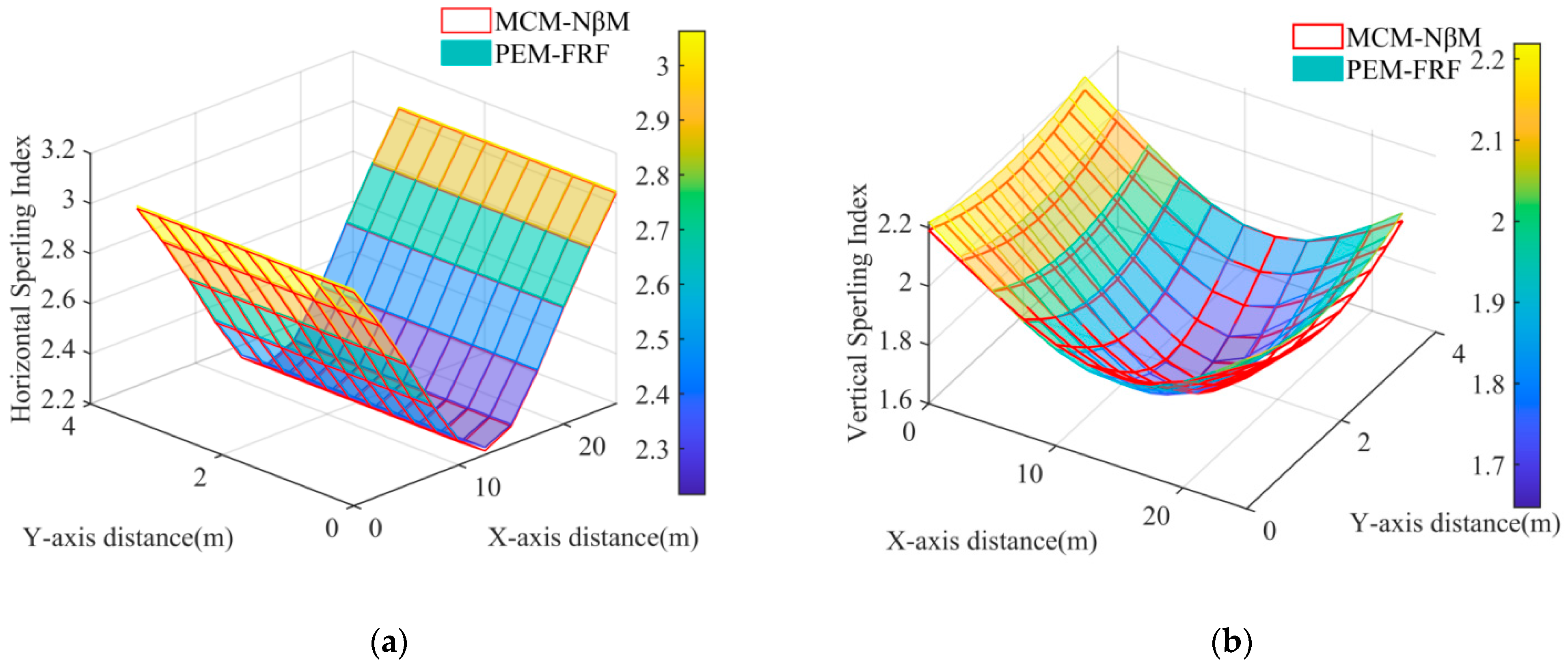
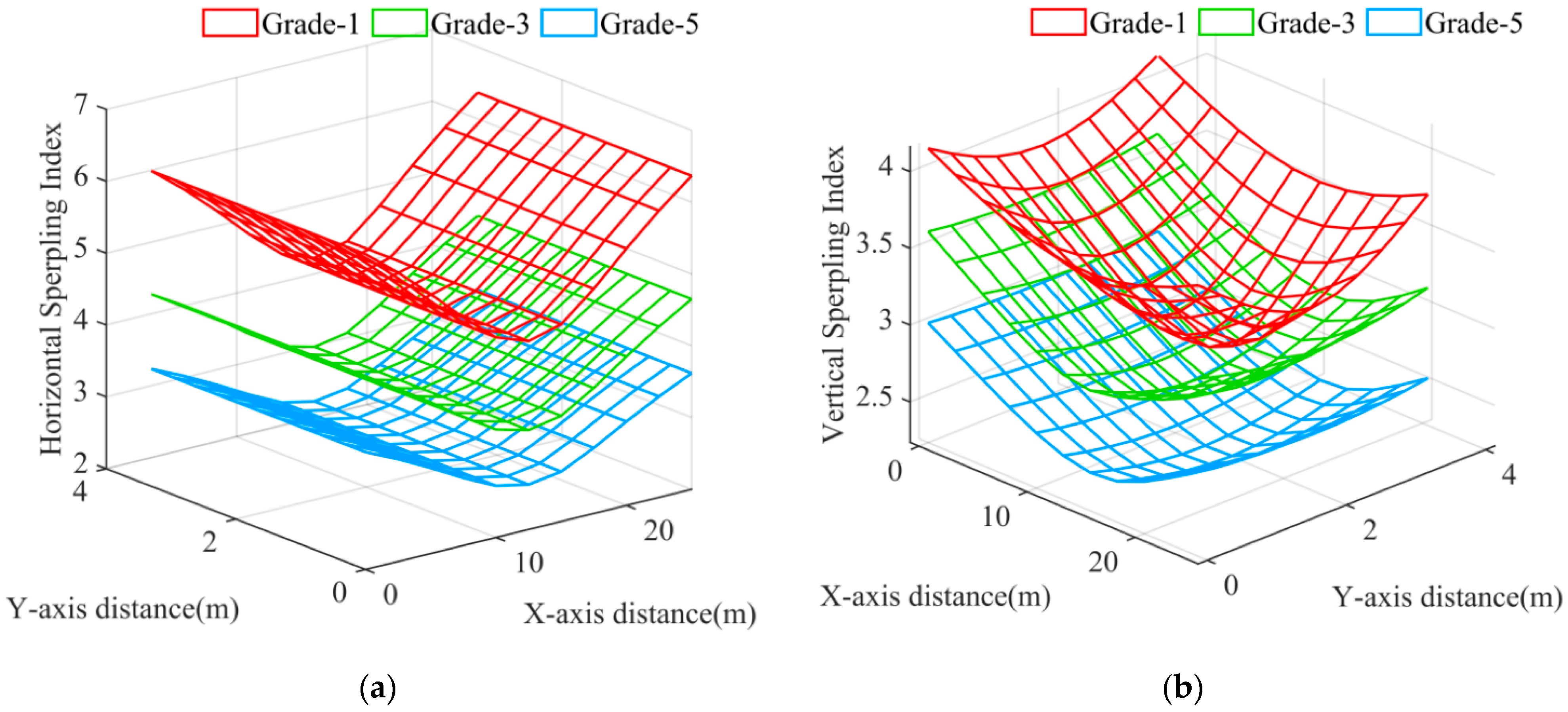
4.4. Analysis of the Zonal Distribution Characteristics of Train Comfort
- The mean network of the zonal distribution of the Sperling index calculated using MCM–NβM was almost identical to the theoretical network calculated using PEM-FRF for both the horizontal and vertical components;
- In Figure 6a, the zonal distribution of the horizontal Sperling index is symmetric with respect to the pitch and roll axis of the car-body center. It has the cylindrical shape of the letter “V” and reaches the highest line at the rear and front edges of the car-body, respectively, while it reaches the lowest line on the pitch axis of the car-body;
- In Figure 6b, the zonal distribution of the vertical Sperling index is a symmetrically curved surface with respect to the roll axis of the Car-Body center. It reaches the highest points at the four vertices of the X−Y plane, where the center of the car body is located, while the lowest point is slightly in front of the center of the car body in the direction of travel;
- Compared to Figure 5 in Section 4.3, the Sperling index of the center of the car body is smaller for both the horizontal and vertical components for Grade-6 track irregularities than for Grade-4 track irregularities;
- In general, a small track irregularity had a negative effect on train comfort, and the zonal distribution of train comfort was not strictly symmetrical with respect to the center of the car body. The most comfortable area for the vertical component was near the front of the center of the car body, while the most comfortable area for the horizontal component was on the pitching axis of the center of the car body. The realistic evaluation of train comfort could be roughly characterized by the average value of the Sperling index during train operation, while the theoretical design of train comfort could be accurately determined by the PEM.
4.5. Analysis of Influence of the Quality of Track Irregularity on the Zonal Distribution Characteristics of Train Comfort
- The symmetrical characteristic of the zonal distribution of the car-body Sperling index of the car body for the horizontal and vertical components was identical to that in Section 4.4;
- With the deterioration in the quality of the track irregularities, the values of the Sperling index for the entire network increased significantly for both the horizontal and vertical components;
- In general, train comfort deteriorated with the deterioration of the quality of track irregularities, so regular track maintenance is of great importance.
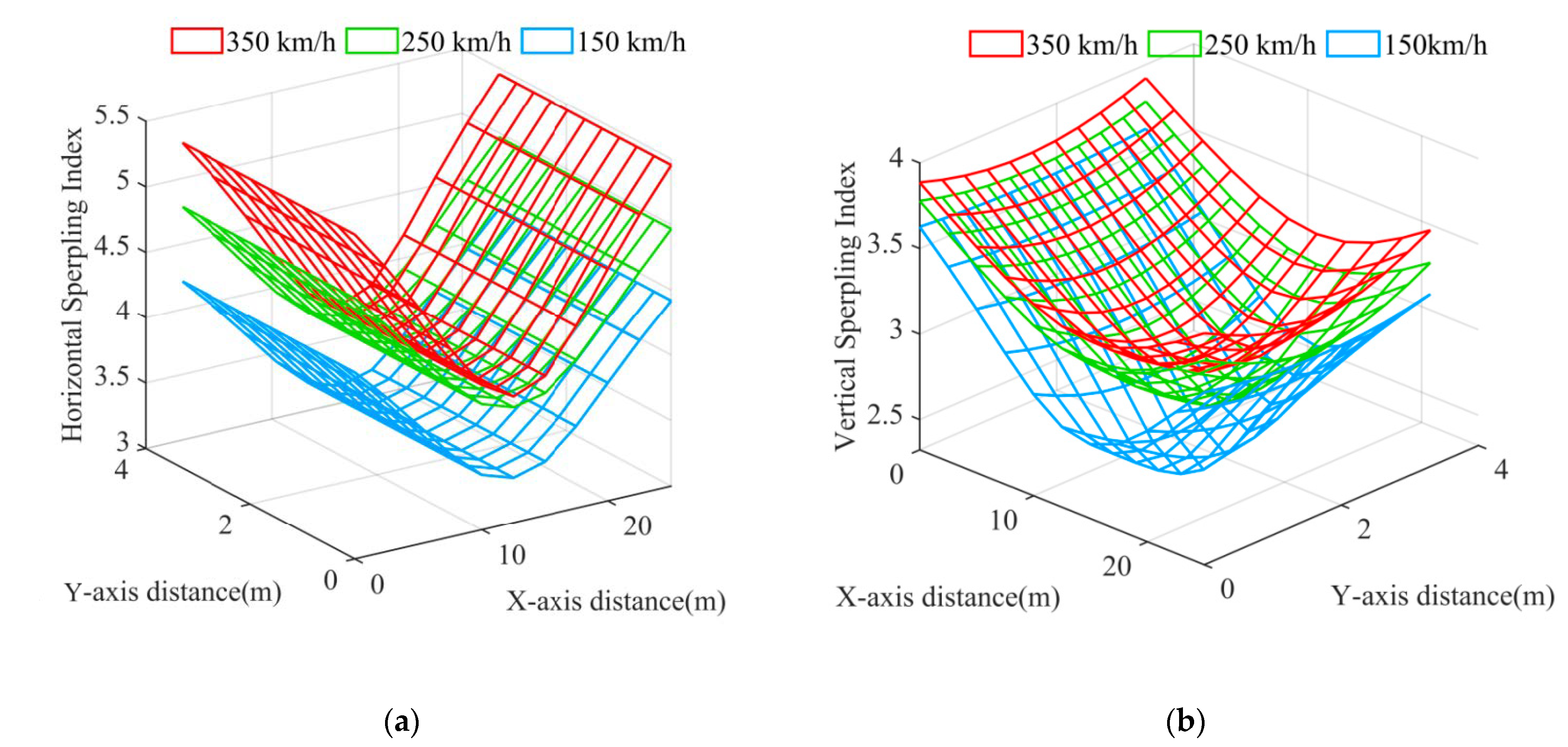
4.6. Analysis of Influence of the Train Speed on the Zonal Distribution Characteristics of Train Comfort
- The symmetrical characteristic of the zonal distribution of the car-body Sperling index of the car body was identical to that shown in Section 4.4 for both the horizontal and vertical components;
- As the train accelerated, the values of the car-body Sperling index for the entire network increased significantly for both the horizontal and vertical components;
- In general, the train comfort deteriorated when the train traveled too fast. This was because the amplitude of the vibration velocity and the acceleration of the track irregularity contained the linear and quadratic terms of the train speed V, respectively. When the train accelerated, the amplitudes increased rapidly, which increased the input excitation and led to a significant increase in the vibration response of the car body. Therefore, appropriate control of a train’s speed can help to improve passenger comfort.
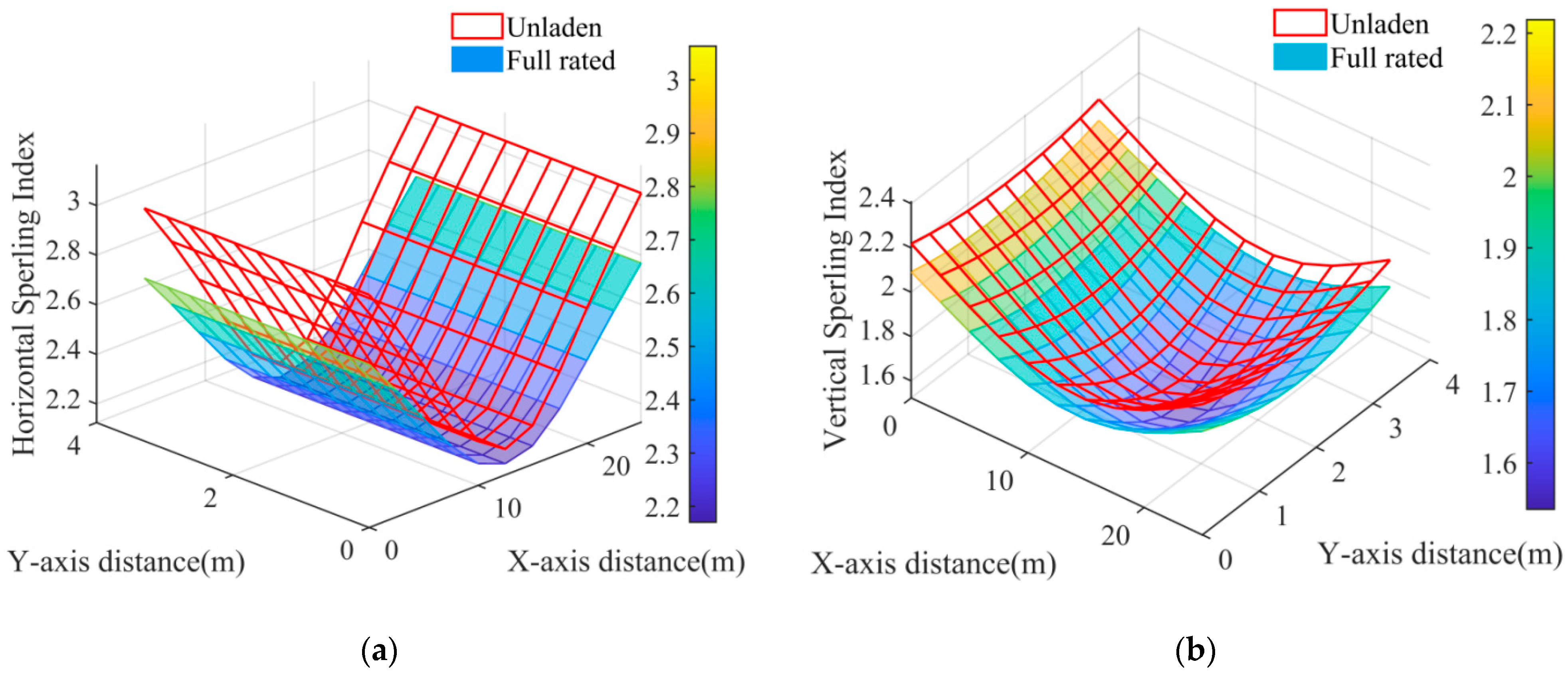
4.7. Analysis of Influence of the Car-Body Mass on the Zonal Distribution Characteristics of Train Comfort
- The symmetrical characteristics of the zonal distribution of the car body’s Sperling index for the horizontal and vertical components were identical to those shown in Section 4.4;
- With the additional mass of the car body, the values of the Sperling index for the entire mesh decreased significantly for both the horizontal and vertical components;
- In general, the comfort of the train deteriorated with the loss in the car-body mass. Therefore, it is important to reasonably distribute the number of passengers during transfer and optimize the original mass design of the car body.
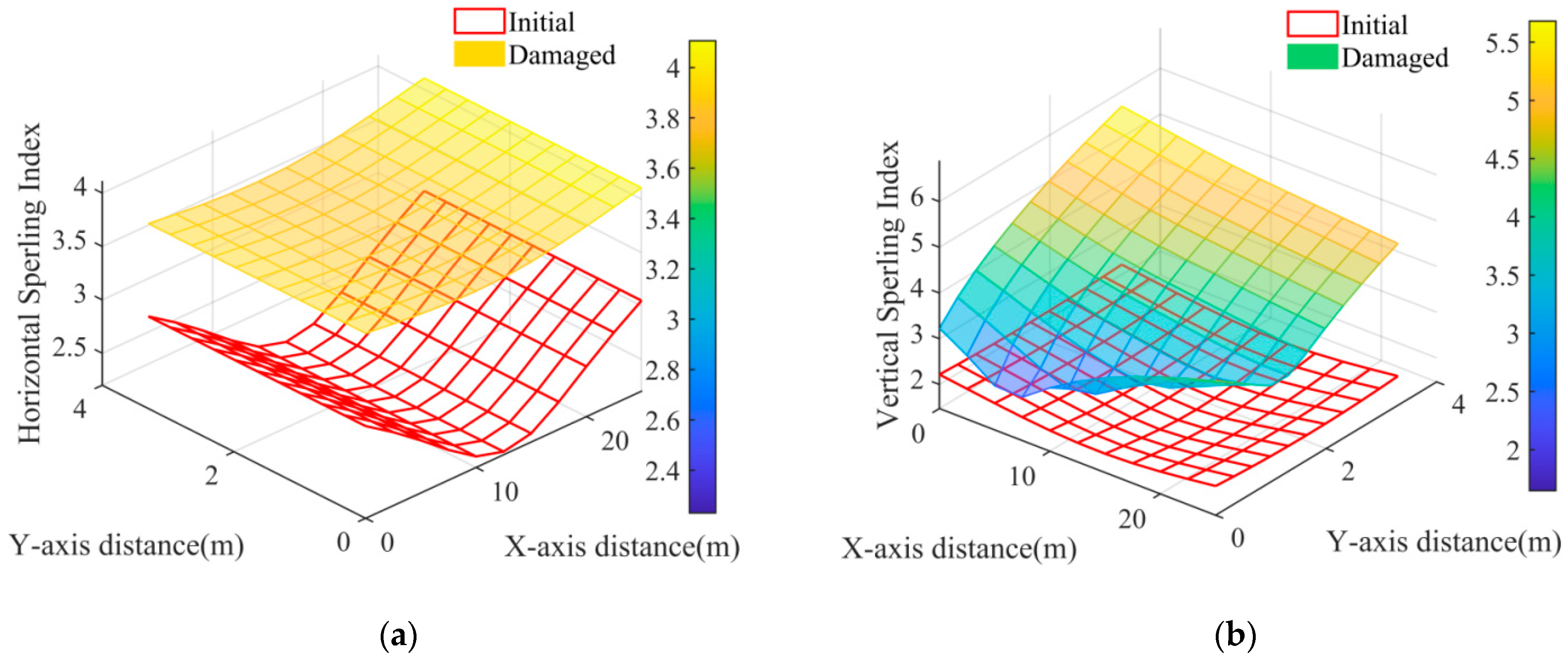
4.8. Analysis of Influence of the Damage of Secondary Suspension System on the Zonal Distribution Characteristics of Train Comfort
- In Figure 10a, the symmetrical characteristic of the network of the horizontal Sperling index after damage to a vertical spring damper in the secondary suspension system was still consistent with the initial condition, but the overall magnitude of the horizontal Sperling index was much higher than the initial condition. This was because the damaged vertical spring damper affected the lateral car-body sway by influencing the car-body roll in conjunction with the vertical car-body sway;
- It can be seen in Figure 10b that after the damage to the vertical spring damper in the secondary suspension system, the network of the vertical Sperling index could not maintain the uniformly curved surface as in the initial state, and reached the highest values when the damaged spring damper was located and gradually decreased toward the areas where the other healthy vertical spring dampers were located. The overall magnitude of the vertical Sperling index far exceeded that of the initial condition;
- In general, the damage to the secondary suspension system led to an overall deterioration in the train comfort for both the horizontal and vertical components, even if only one local vertical spring damper in the secondary suspension system was damaged. The comfort of the train suffered more on the side where the damage occurred. The train comfort for the horizontal and vertical components were not independent of each other. Therefore, it is important to consider both components comprehensively when optimizing the train comfort.
5. Conclusions
- Compared with the Monte Carlo method and depending on a large amount of samples, the pseudo-excitation Method, based on the linearity of the power spectrum density of the car-body vibratory acceleration, was more efficient to derive the accurate zonal distribution of the Sperling index.
- The realistic evaluation of train comfort can be roughly characterized by the average value of the Sperling index during train operation, while the theoretical design of train comfort can be accurately determined using the pseudo–excitation method.
- The vibration acceleration of the train during track irregularities is a stationary Gaussian random process with a zero mean value, the statistical properties of which can be described by the 3σ–principle.
- The Sperling index is a stationary indicator of comfort that is independent of the order of the vehicle elements when the train is subjected to a track irregularity. In this way, train comfort can be characterized by simply selecting a vehicle element to analyze.
- The zonal distribution of train comfort is not strictly symmetrical with respect to the center of the car body. The most comfortable area for the vertical component was located near the front of the center of the car body, while the most comfortable area for the horizontal component was located on the axis of the tilt axis of the center of the car-body center.
- The comfort of the train deteriorated with a loss in mass of the Car-Body and with irregularities in the tracks, while reasonable control of the train speed, regular maintenance of the tracks, and reasonable distribution of the number of passengers when changing trains improved the comfort of the train.
- The overall comfort of the train deteriorated even if only one local vertical spring damper in the secondary suspension system was damaged. It suffered more on the side where the damage was present. The comfort of the train was not independent of the horizontal and vertical components. To optimize the comfort of the train, it is therefore important to consider both components comprehensively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Albers, A.; Lerspalungsanti, S.; Düser, T.; Ott, S.; Wang, J. A Systematic Approach to Support Drive Train Design Using Tools for Human Comfort Evaluation and Customer Classification. In Proceedings of the ASME 2008 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Brooklyn, NY, USA, 3–6 August 2008; pp. 651–662. [Google Scholar] [CrossRef]
- Lee, Y.; Shin, K.; Song, Y.; Han, S.; Lee, M. Research of Ride Comfort for Tilting Train Simulator Using ECG. IFMBE Proc. 2009, 22, 1906–1909. [Google Scholar] [CrossRef]
- Yu, Y.L.; He, W. Comfortable Evaluation of Bridge-Station Combined Large Span High Speed Railway Station under High Speed Train Load. Appl. Mech. Mater. 2013, 477–478, 727–731. [Google Scholar] [CrossRef]
- Lu, L. The effects forthe ride comfort of high-speed trains’ operating conditions on the open and tunnel track. In Proceedings of the 2015 12th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Qingdao, China, 16–18 July 2015; Volume 3, pp. 1344–1349. [Google Scholar] [CrossRef]
- Ni, Y.; Ye, S.; Song, S. An experimental study on constructing MR secondary suspension for high-speed trains to improve lateral ride comfort. Smart Struct. Syst. 2016, 18, 53–74. [Google Scholar] [CrossRef]
- Bao, Y.; Zhai, W.; Cai, C.; Zhu, S.; Li, Y. Dynamic interaction analysis of suspended monorail vehicle and bridge subject to crosswinds. Mech. Syst. Signal Process. 2021, 156, 107707. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, X.; Shang, L.; Wu, Z.; Xu, W.; Wang, D. Influence analysis of track irregularity on running comfort of Maglev train. Transp. Syst. Technol. 2018, 4, 129–140. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, G.; Li, X.; Lu, Y.; Liu, J.; Xu, T. Comfort assessment for rehabilitation scaffold in road-railway bridge subjected to train-bridge-scaffold coupling vibration. Eng. Struct. 2020, 211, 110426. [Google Scholar] [CrossRef]
- Alehashem, S.M.S.; Ni, Y.Q.; Liu, X.Z. A Full-Scale Experimental Investigation on Ride Comfort and Rolling Motion of High-Speed Train Equipped With MR Dampers. IEEE Access 2021, 9, 118113–118123. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, Z.; Fan, C.; Zhou, J.; Yi, S.; Peng, Y.; Gao, K. Assessment of passenger long-term vibration discomfort: A field study in high-speed train environments. Ergonomics 2022, 65, 659–671. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Xiang, P.; Dong, P.; Zhang, X.; Zeng, J. Analysis of the effects of vibration modes on fatigue damage in high-speed train bogie frames. Eng. Fail. Anal. 2018, 89, 222–241. [Google Scholar] [CrossRef]
- Li, Y.-C.; Feng, S.-J.; Chen, H.-X.; Chen, Z.-L.; Zhang, D.-M. Random vibration of train-track-ground system with a poroelastic interlayer in the subsoil. Soil Dyn. Earthq. Eng. 2019, 120, 1–11. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; He, G.; Chen, J.; Peng, X. Multipoint Random Vibration Analysis of Train Converter Equipment. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Tan, S.; Yu, Z.; Shan, Z.; Mao, J. Influences of train speed and concrete Young’s modulus on random responses of a 3D train-track-girder-pier coupled system investigated by using PEM-ScienceDirect. Eur. J. Mech. A/Solids 2018, 74, 297–316. [Google Scholar] [CrossRef]
- Jin, T.; Liu, Z.; Sun, S.; Ren, Z.; Deng, L.; Yang, B.; Christie, M.D.; Li, W. Development and evaluation of a versatile semi-active suspension system for high-speed railway vehicles. Mech. Syst. Signal Process. 2019, 135, 106338. [Google Scholar] [CrossRef]
- Arnaud, W. Hamiltonian Monte Carlo with application to train-track-bridge coupled interactions subjected to seismic excitation with uncertainties. 2021; preprint. [Google Scholar] [CrossRef]
- Yao, J.; Fang, L. Building Vibration Prediction Induced by Moving Train with Random Forest. J. Adv. Transp. 2021, 2021, 6642071. [Google Scholar] [CrossRef]
- Guo, G.; Cui, X.; Du, B. Random-Forest Machine Learning Approach for High-Speed Railway Track Slab Deformation Identification Using Track-Side Vibration Monitoring. Appl. Sci. 2021, 11, 4756. [Google Scholar] [CrossRef]
- Xia, H.; Zhang, N.; Guo, W. Dynamic Interaction of Train-Bridge Systems in High-Speed Railways: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, Y.; Li, Q.; Williams, F. Seismic spatial effects for long-span bridges, using the pseudo excitation method. Eng. Struct. 2004, 26, 1207–1216. [Google Scholar] [CrossRef]
- Feng, Z.; Xiao, H. Analysis of Stability and Vibration Transmission Law of Type A Metro Vehicles. J. Phys. Conf. Ser. 2021, 1846, 012029. [Google Scholar] [CrossRef]
- Gerekos, C.; Bruzzone, L.; Imai, M. A Coherent Method for Simulating Active and Passive Radar Sounding of the Jovian Icy Moons. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2250–2265. [Google Scholar] [CrossRef]
- Koyama, A.; Nicholson, D.A.; Andreev, M.; Rutledge, G.C.; Fukao, K.; Yamamoto, T. Discretized Wiener-Khinchin theorem for Fourier-Laplace transformation: Application to molecular simulations. arXiv 2020, arXiv:2004.097922020. [Google Scholar] [CrossRef]
- Wang, T. Impact in a railway truss bridge. Comput. Struct. 1993, 49, 1045–1054. [Google Scholar] [CrossRef]
- GB/T-5599-2019; Specification for Dynamic Performance Assessment and Testing Verification of Rolling Stock. Standardization Administration: Beijing, China, 2019.
- Leibovich, N.; Barkai, E. Aging Wiener-Khinchin Theorem. Phys. Rev. Lett. 2015, 115, 080602. [Google Scholar] [CrossRef] [PubMed] [Green Version]

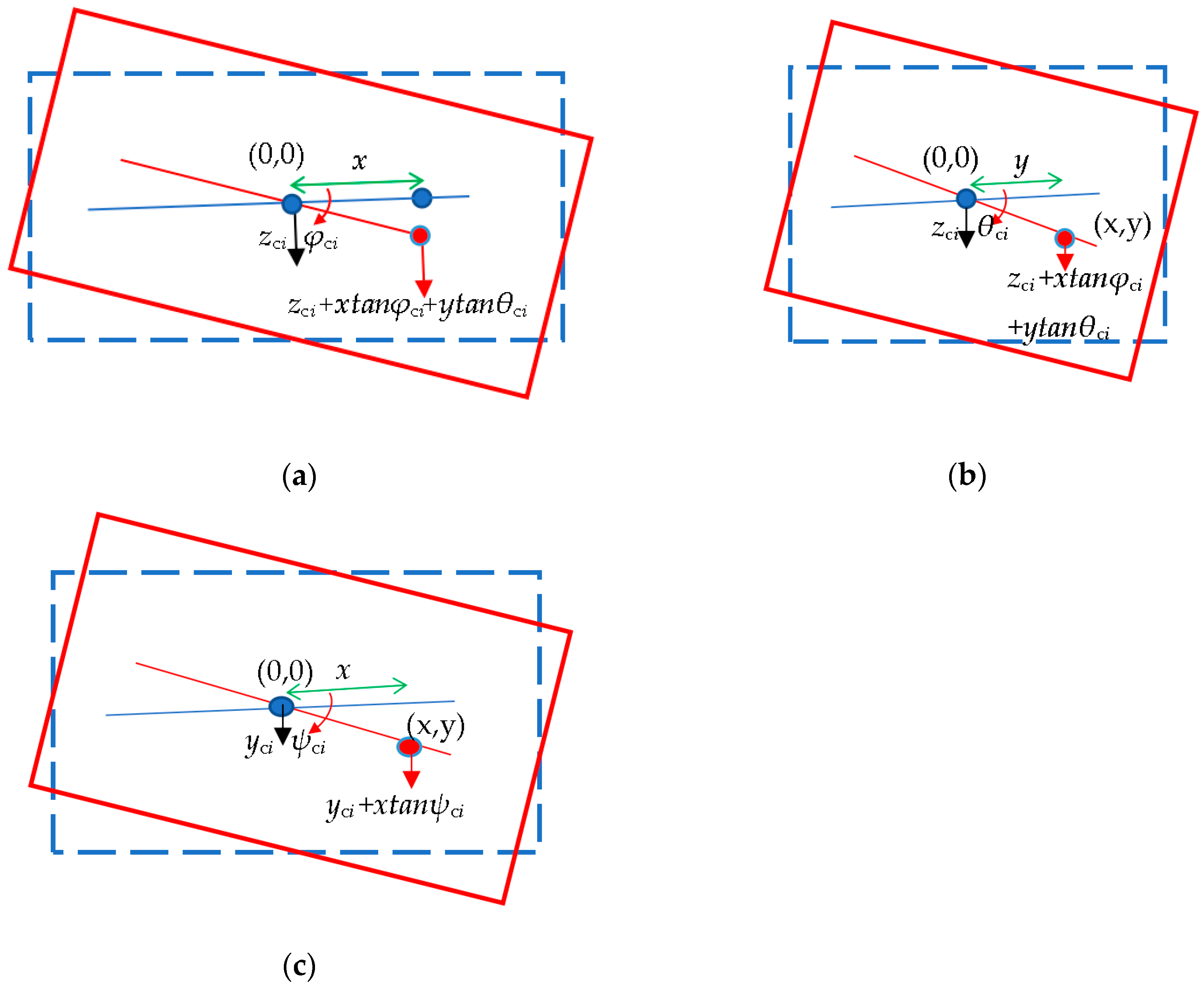
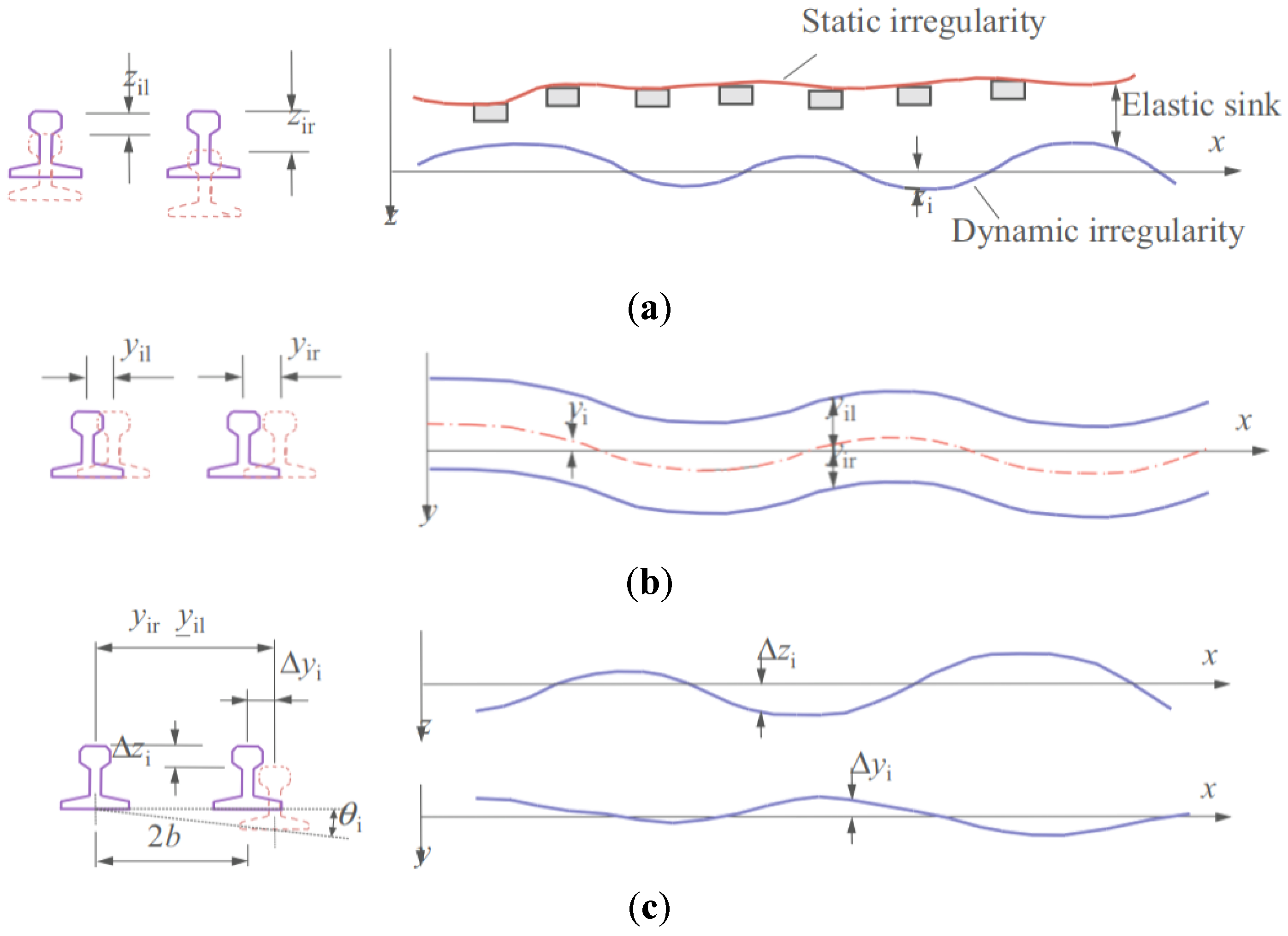

| Vehicle Element i | DOF |
|---|---|
| Car body | 5 DOFs: yci, zci, θci, φci, ψci 1 |
| Bogies | 10 DOFs: yfbi, zfbi, θfbi, φfbi, ψfbi, yrbi, zrbi, θrbi, φrbi, ψrbi |
| Wheel sets | 12 DOFs: yw1i, zw1i, θw1i, yw2i, zw2i, θw2i, yw3i, zw3i, θw3i, yw4i, zw4i, θw4i |
| Items | Grade-1 | Grade-2 | Grade-3 | Grade-4 | Grade-5 | Grade-6 |
|---|---|---|---|---|---|---|
| Alignment roughness constant Aa | 1.211 × 10−4 | 1.018 × 10−4 | 0.682 × 10−4 | 0.538 × 10−4 | 0.210 × 10−4 | 0.034 × 10−4 |
| Vertical roughness constant Av | 3.363 × 10−4 | 1.211 × 10−4 | 0.413 × 10−4 | 0.303 × 10−4 | 0.076 × 10−4 | 0.034 × 10−4 |
| Cutoff angular wave number nc | 0.6046 | 0.9308 | 0.8520 | 1.1312 | 0.8209 | 0.4380 |
| Cutoff angular wave number ns | 0.8245 | 0.8245 | 0.8245 | 0.8245 | 0.8245 | 0.8245 |
| Items | Values |
|---|---|
| Half of longitudinal distance of wheel sets d1 | 1.25 m |
| Half of longitudinal distance of bogies d2 | 8.75 m |
| Half of lateral distance of springs in 1st suspension system b1 | 1.00 m |
| Half of lateral distance of springs in 2nd suspension system b2 | 1.00 m |
| Vertical distance, car body center to 2nd suspension system h1 | 0.80 m |
| Vertical distance, 2nd suspension system to bogie center h2 | 0.20 m |
| Vertical distance, bogie center to 1st suspension system h3 | 0.10 m |
| Mass of wheel set mw | 2000 kg |
| Mass of bogie mb | 3000 kg |
| Moment of inertia of bogie in longitudinal direction Ibx | 3000 kg·m2 |
| Moment of inertia of bogie in lateral direction Iby | 3000 kg·m2 |
| Moment of inertia of bogie in vertical direction Ibz | 3000 kg·m2 |
| Mass of car body mb | 40 t·m2 |
| Moment of inertia of car body in longitudinal direction Icx | 100 t·m2 |
| Moment of inertia of car body in lateral direction Icy | 2000 t·m2 |
| Moment of inertia of car body, about vertical direction Icz | 2000 t·m2 |
| Longitudinal damping of 1st suspension system/bogie side cx1 | 1 kN·s/m |
| Lateral damping of 1st suspension system/bogie side cy1 | 1 kN·s/m |
| Vertical damping of 1st suspension system/bogie side cz1 | 20 kN·s/m |
| Longitudinal damping of 2nd suspension system/car-body side cx2 | 60 kN·s/m |
| Lateral damping of 2nd suspension system/car-body side cy2 | 60 kN·s/m |
| Vertical damping of 2nd suspension system/car-body side cz2 | 10 kN·s/m |
| Longitudinal stiffness of 1st suspension system/bogie side kx1 | 1000 kN/m |
| Lateral stiffness of 1st suspension system/bogie side ky1 | 1000 kN/m |
| Vertical stiffness of 1st suspension system/bogie side kz1 | 1000 kN/m |
| Longitudinal stiffness of 2nd suspension system/car-body side kx2 | 200 kN/m |
| Lateral stiffness of 2nd suspension system/car-body side ky2 | 200 kN/m |
| Vertical stiffness of 2nd suspension system/car-body side kz2 | 200 kN/m |
| Lower limit of angular wave number nmin | π/V rad/m |
| Upper limit of angular wave number nmax | 80π/V rad/m |
| Sampling rate of angular wave number dn | 2π/5V rad/m |
| Lower limit of time tmin | 0 s |
| Upper limit of time tmax | 10 s |
| Time sampling rate dt | 1/80 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Zhang, N.; Yao, J.; Poliakov, V. Analysis of Train Car-Body Comfort Zonal Distribution by Random Vibration Method. Appl. Sci. 2022, 12, 7442. https://doi.org/10.3390/app12157442
Wu Z, Zhang N, Yao J, Poliakov V. Analysis of Train Car-Body Comfort Zonal Distribution by Random Vibration Method. Applied Sciences. 2022; 12(15):7442. https://doi.org/10.3390/app12157442
Chicago/Turabian StyleWu, Zhaozhi, Nan Zhang, Jinbao Yao, and Vladimir Poliakov. 2022. "Analysis of Train Car-Body Comfort Zonal Distribution by Random Vibration Method" Applied Sciences 12, no. 15: 7442. https://doi.org/10.3390/app12157442






