Distribution of Magnetic Flux Density under Stress and Its Application in Nondestructive Testing
Abstract
:1. Introduction
2. Materials and Methods
3. Results, Analysis, and Discussion
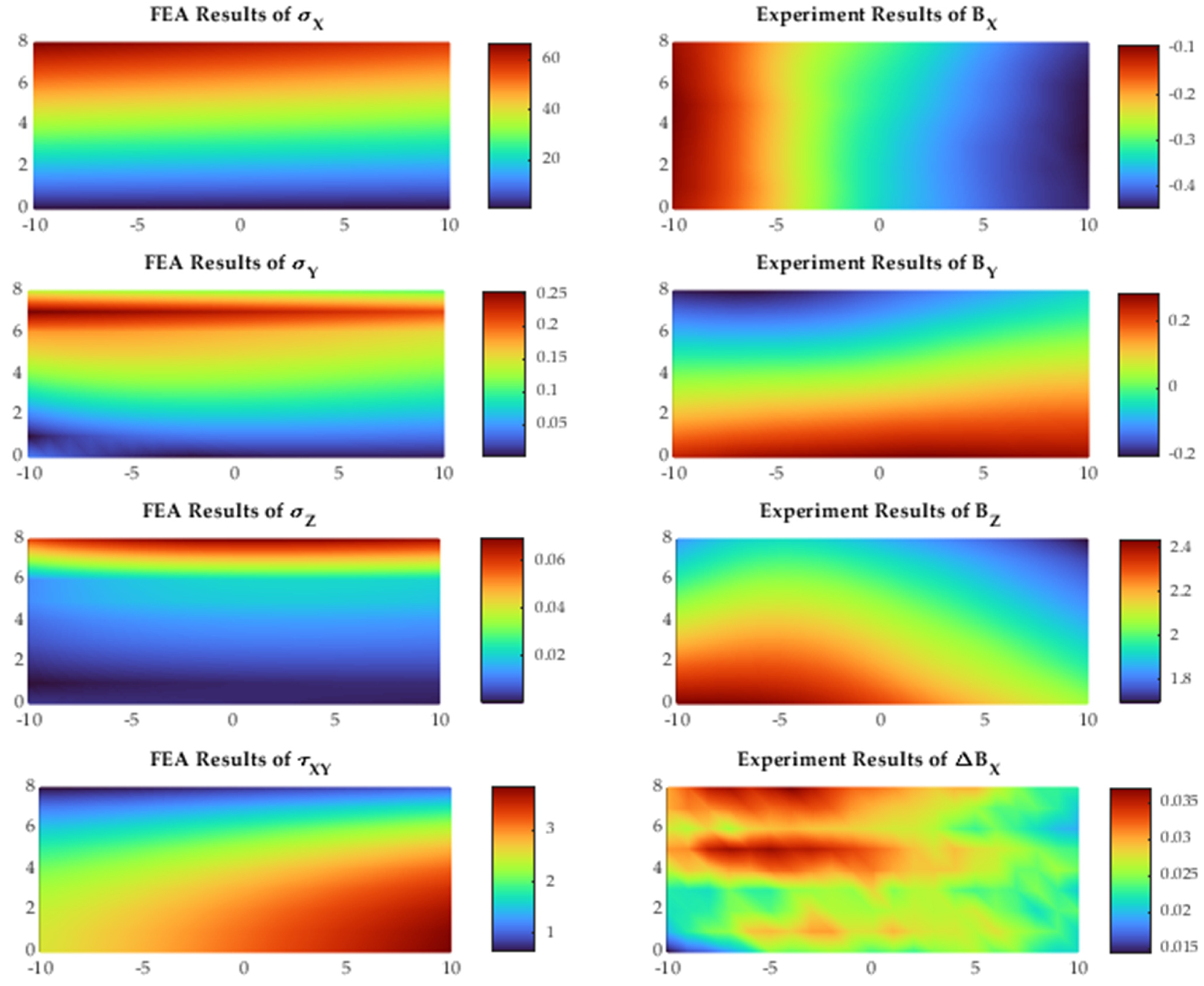
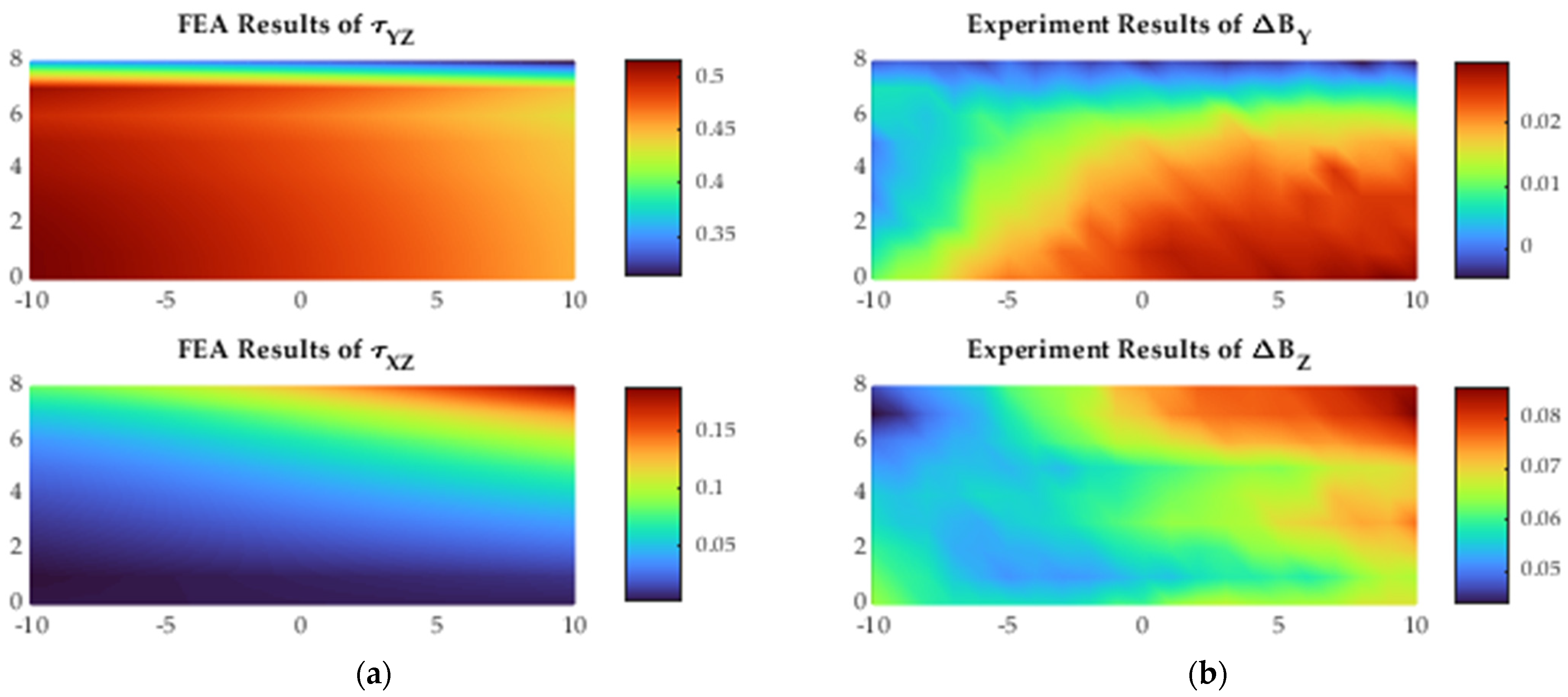
3.1. Experiments Results
3.2. Finite Element Analysis
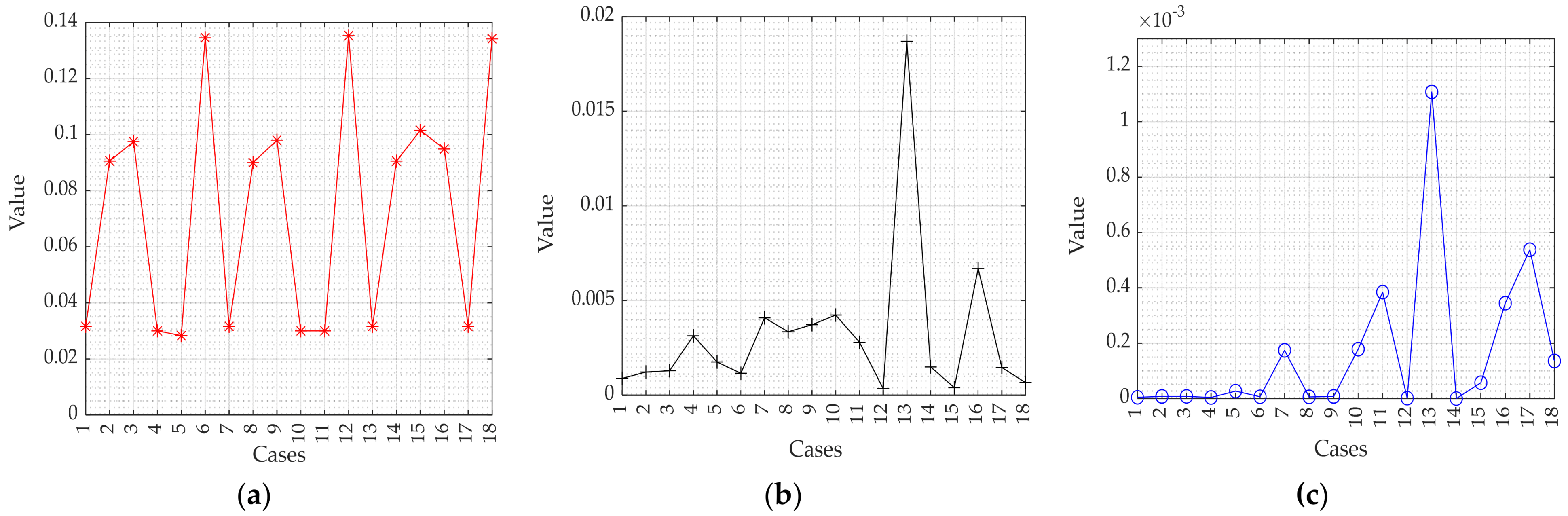
3.3. Analysis Area and Comparison
4. Conclusions
- The stresses along both X and Y directions, and the shear stress on the XY plan are affected.
- The magnetic flux density along the Y and Z direction is affected too.
- In addition, a qualitative relationship in the form of a third-order polynomial equation has been established, which is based on correlations between the stress distributions and shear stress as a function of the recovered triaxial magnetic field. The error and features resulting from the application to ascertain relationships seems to be entirely reasonable in some cases (not in all cases); indeed, these points highlight a good relationship:
- The stress along the X direction, representing the main stress;
- The vertical differential flux density, the appropriate parameter for stress characterization;
- Although MMM can be used to inspect the stress, it is cumbersome to qualitatively assess the stress because of the error.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| TMR | Tunnel magneto-resistance |
| FEM | Finite element method |
| NDT | Nondestructive testing |
| MPT | Magnetic particle testing |
| PT | Penetrant testing |
| ECT | Eddy current testing |
| MBE | Magnetic Barkhausen emission |
| MAE | Magneto-acoustic emission |
| MFL | Magnetic flux leakage |
| RMF | Residual magnetic field |
| RMS | Root mean square |
References
- Sumi, Y. Stress Concentration Problems. In Mathematical and Computational Analyses of Cracking Formation; Mathematics for Industry; Springer: Tokyo, Japan, 2014; Volume 2, pp. 17–30. [Google Scholar] [CrossRef]
- Le, M.; Kim, J.; Yang, D.; Lee, H.; Lee, J. Electromagnetic testing of a welding area using a magnetic sensor array. Int. J. Appl. Electromagn. 2017, 55, 119–124. [Google Scholar] [CrossRef]
- Wang, G.; Yan, P.; Wei, L.; Deng, Z. The Magnetic Memory Effect of Ferromagnetic Materials in the Process of Stress-Magnetism Coupling. Adv. Mater. Sci. Eng. 2017, 2017, 1284560. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Fan, J.; Ni, J.; Liu, S. Variation of Magnetic Memory Signals in Fatigue Crack Initiation and Propagation Behavior. Metals 2019, 9, 89. [Google Scholar] [CrossRef] [Green Version]
- Villegas-Saucillo, J.J.; Díaz-Carmona, J.J.; Cerón-Álvarez, C.A.; Juárez-Aguirre, R.; Domínguez-Nicolás, S.M.; López-Huerta, F.; Herrera-May, A.L. Measurement System of Metal Magnetic Memory Method Signals around Rectangular Defects of a Ferromagnetic Pipe. Appl. Sci. 2019, 9, 2695. [Google Scholar] [CrossRef] [Green Version]
- Herter, S.; Youssef, S.; Becker, M.M.; Fischer, S.C. Machine Learning Based Preprocessing to Ensure Validity of Cross-Correlated Ultrasound Signals for Time-of-Flight Measurements. J. Nondestruct. Eval. 2021, 40, 20. [Google Scholar] [CrossRef]
- Berkache, A.; Lee, J.; Choe, E. Evaluation of Cracks on the Welding of Austenitic Stainless Steel Using Experimental and Numerical Techniques. Appl. Sci. 2021, 11, 2182. [Google Scholar] [CrossRef]
- Lee, J.; Berkache, A.; Wang, D.; Hwang, Y.-H. Three-Dimensional Imaging of Metallic Grain by Stacking the Microscopic Images. Appl. Sci. 2021, 11, 7787. [Google Scholar] [CrossRef]
- Berkache, A.; Lee, J.; Wang, D.; Park, D.-G. Development of an Eddy Current Test Configuration for Welded Carbon Steel Pipes under the Change in Physical Properties. Appl. Sci. 2022, 12, 93. [Google Scholar] [CrossRef]
- Diguet, G.; Miyauchi, H.; Takeda, S.; Uchimoto, T.; Mary, N.; Takagi, T.; Abe, H. EMAR monitoring system applied to the thickness reduction of carbon steel in a corrosive environment. Corrosion 2022, 73, 658–668. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Liquid Penetrant and Magnetic Particle Testing at Level 2; International Atomic Energy Agency (IAEA): Vienna, Austria, 2000. [Google Scholar]
- Berkache, A.; Oudni, Z.; Mehaddene, H.; Mohellebi, H.; Lee, J. Inspection and characterization of random physical property efects by stochastic finite element method. Prz. Elektrotech. 2019, 95, 96–101. [Google Scholar] [CrossRef]
- Huang, L.; Liao, C.; Song, X.; Chen, T.; Zhang, X.; Deng, Z. Research on Detection Mechanism of Weld Defects of Carbon Steel Plate Based on Orthogonal Axial Eddy Current Probe. Sensors 2020, 20, 5515. [Google Scholar] [CrossRef]
- Krkoška, L. Investigation of Barkhausen Noise Emission in Steel Wires Subjected to Different Surface Treatments. Coatings 2020, 10, 912. [Google Scholar] [CrossRef]
- O’Sullivan, D.; Cotterell, M.; Cassidy, S.; Tanner, D.A.; Mészárosc, I. Magneto-acoustic emission for the characterisation of ferritic stainless steel microstructural state. J. Magn. Magn. Mater. 2004, 271, 381–389. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Wang, R.; Qiu, G.; Hu, Y.; Kang, Y. Mechanism of Magnetic Flux Leakage Detection Method Based on the Slotted Ferromagnetic Lift-Off Layer. Sensors 2022, 22, 3587. [Google Scholar] [CrossRef]
- Leng, J.; Xu, M.; Zhou, G.; Wu, Z. Effect of initial remanent states on the variation of magnetic memory signals. NDT E Int. 2012, 52, 23–27. [Google Scholar] [CrossRef]
- Pengpeng, S.; Ke, J.; Xiaojing, Z. A magnetomechanical model for the magnetic memory method. Int. J. Mech. Sci. 2017, 124–125, 229–241. [Google Scholar] [CrossRef]
- Bao, S.; Jin, P.; Zhao, Z.; Fu, M. A Review of the Metal Magnetic Memory Method. J. Nondestruct. Eval. 2020, 39, 11. [Google Scholar] [CrossRef]
- Zhang, Z. Wavelet Energy Entropy Based Multi-Sensor Data Fusion for Residual Stress Measurement Using Innovative IntenseMagnetic Memory Method. In Proceedings of the 2009 9th International Conference on Electronic Measurement Instruments, Beijing, China, 16–19 August 2009; pp. 1044–1047. [Google Scholar] [CrossRef]
- Chady, T.; Łukaszuk, R. Examining Ferromagnetic Materials Subjected to a Static Stress Load Using the Magnetic Method. Materials 2021, 14, 3455. [Google Scholar] [CrossRef]
- Dubov, A.A. A study of metal properties using the method of magnetic memory. Metal. Sci. Heat Treat. 1997, 39, 401–405. [Google Scholar] [CrossRef]
- Dubov, A.; Dubov, A. Application of the metal magnetic memory method for detection of defects at the initial stage of their development for prevention of failures of power engineering welded steel structures and steam turbine parts. Weld. World 2014, 58, 225–236. [Google Scholar] [CrossRef]
- Shi, P.; Jin, K.; Zhang, P.; Xie, S.; Chen, Z.; Zheng, X. Quantitative Inversion of Stress and Crack in Ferromagnetic Materials Based on Metal Magnetic Memory Method. IEEE Trans. Magn. 2018, 54, 1–11. [Google Scholar] [CrossRef]
- Ren, S.; Ren, X.; Duan, Z.; Fu, Y. Studies on influences of initial magnetization state on metal magnetic memory signal. NDT E Int. 2019, 103, 77–83. [Google Scholar] [CrossRef]
- Chady, T.; Łukaszuk, R.D.; Gorący, K.; Żwir, M.J. Magnetic Recording Method (MRM) for Nondestructive Evaluation of Ferromagnetic Materials. Materials 2022, 15, 630. [Google Scholar] [CrossRef]
- Roskosz, M. Metal magnetic memory testing of welded joints of ferritic and austenitic steels. NDT E Int. 2011, 44, 305–310. [Google Scholar] [CrossRef]
- Dubov, A.; Kolokolnikov, S. Assessment of the material state of oil and gas pipeline based on the metal magnetic memory method. Weld. World 2012, 56, 11–19. [Google Scholar] [CrossRef]
- Witoś, M. The MMM expert system: From a reference signal to the method validation. Fatigue Aircr. Struct. 2012, 1, 123–140. [Google Scholar] [CrossRef]
- Huang, H.; Jiang, S.; Liu, R.; Liu, Z. Investigation of magnetic memory signals induced by dynamic bending load in fatigue crack propagation process of structural steel. J. Nondestruct. Eval. 2014, 33, 407–412. [Google Scholar] [CrossRef]
- Xu, K.; Qiu, X.; Tian, X. Theoretical investigation of metal magnetic memory testing technique for detection of magnetic flux leakage signals from buried defect. Nondestruct. Test. Eval. 2018, 33, 45–55. [Google Scholar] [CrossRef]
- Liu, B.; Ma, Z.Y. Quantitative study on the propagation characteristics of MMM signal for stress internal detection of long-distance oil and gas pipeline. NDT E Int. 2018, 100, 40–47. [Google Scholar] [CrossRef]
- Leng, J.C.; Xu, M.Q. Magnetic field variation induced by cyclic bending stress. NDT E Int. 2009, 42, 410–414. [Google Scholar] [CrossRef]
- Shi, C.L.; Dong, S.Y. Stress concentration degree affects spontaneous magnetic signals of ferromagnetic steel under dynamic tension load. NDT E Int. 2010, 43, 8–12. [Google Scholar] [CrossRef]
- Roskosz, M.; Bieniek, M. Evaluation of residual stress in ferromagnetic steels based on residual magnetic field. NDT E Int. 2012, 45, 55–62. [Google Scholar] [CrossRef]
- Li, J.W.; Zhong, S. The variation of surface magnetic field induced by fatigue stress. J. Nondestruct. Eval. 2013, 32, 238–241. [Google Scholar] [CrossRef]
- Hu, Z.; Fan, J.; Wu, S.; Dai, H.; Liu, S. Characteristics of Metal Magnetic Memory Testing of 35CrMo Steel during Fatigue Loading. Metals 2018, 8, 119. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Yao, K.; Wu, L.; Li, X.; Wang, Y.-S. Application of Metal Magnetic Memory Testing Technology to the Detection of Stress Corrosion Defect. Appl. Sci. 2020, 10, 7083. [Google Scholar] [CrossRef]
- Cheng, D.K. Fundamentals of Engineering Electromagnetics; Saffron House: London, UK, 2014. [Google Scholar]
- Kim, J.; Le, M.; Park, J.; Seo, H.; Jung, G.; Lee, J. Measurement of residual stress using linearly integrated GMR sensor arrays. J. Mech. Sci. Technol. 2018, 32, 623–630. [Google Scholar] [CrossRef]
- Zhao, W.; Tao, X.; Ye, C.; Tao, Y. Tunnel Magnetoresistance Sensor with AC Modulation and Impedance Compensation for Ultra-Weak Magnetic Field Measurement. Sensors 2022, 22, 1021. [Google Scholar] [CrossRef]
- Struik, D.J. A Source Book in Mathematics, 1200–1800; Princeton Legacy Library; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Ngo, D.; Kang, B. Taylor-Series-Based Reconfigurability of Gamma Correction in Hardware Designs. Electronics 2021, 10, 1959. [Google Scholar] [CrossRef]
- Fleishman, A.L. A method for simulating non-normal distributions. Psychometrika 1978, 43, 521–532. [Google Scholar] [CrossRef]

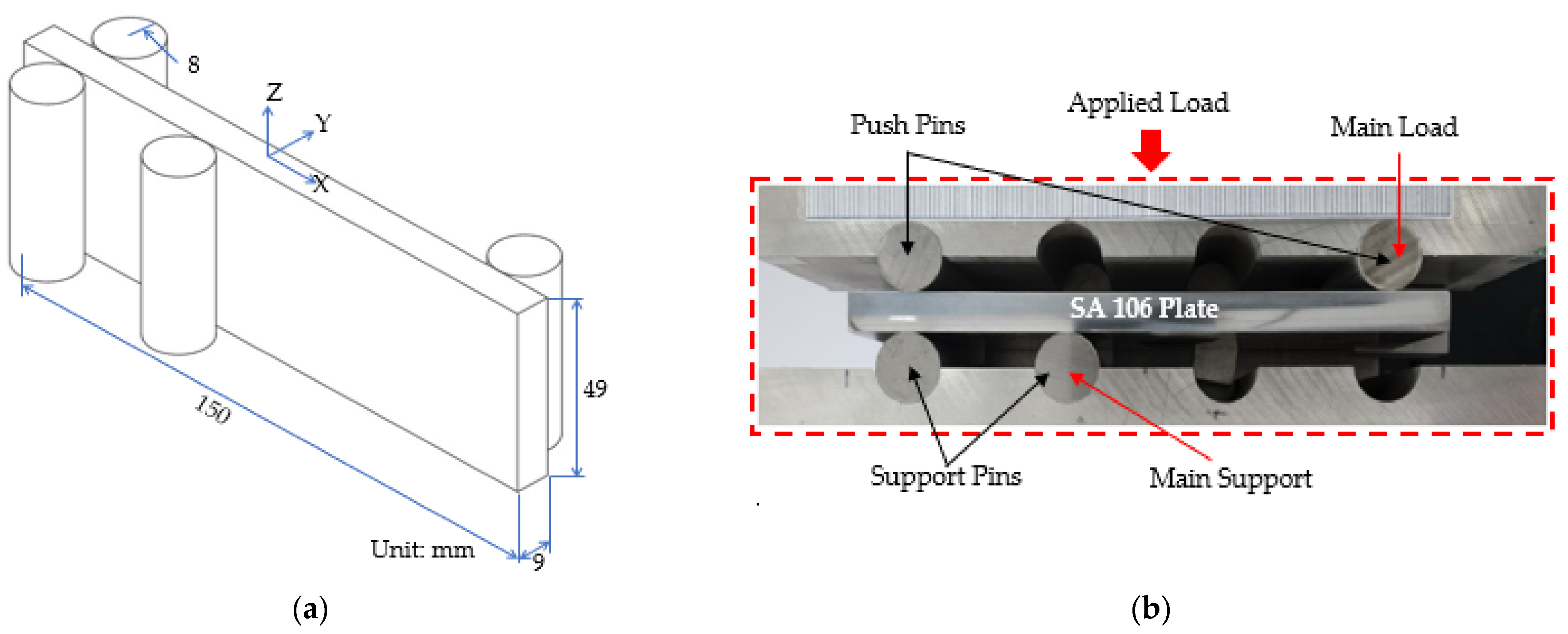


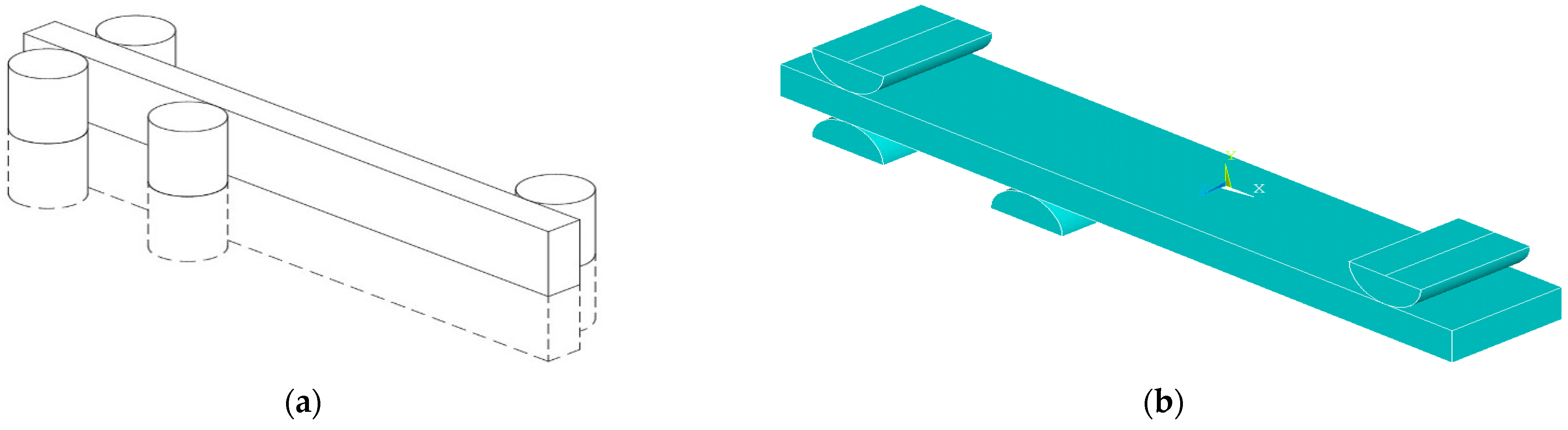


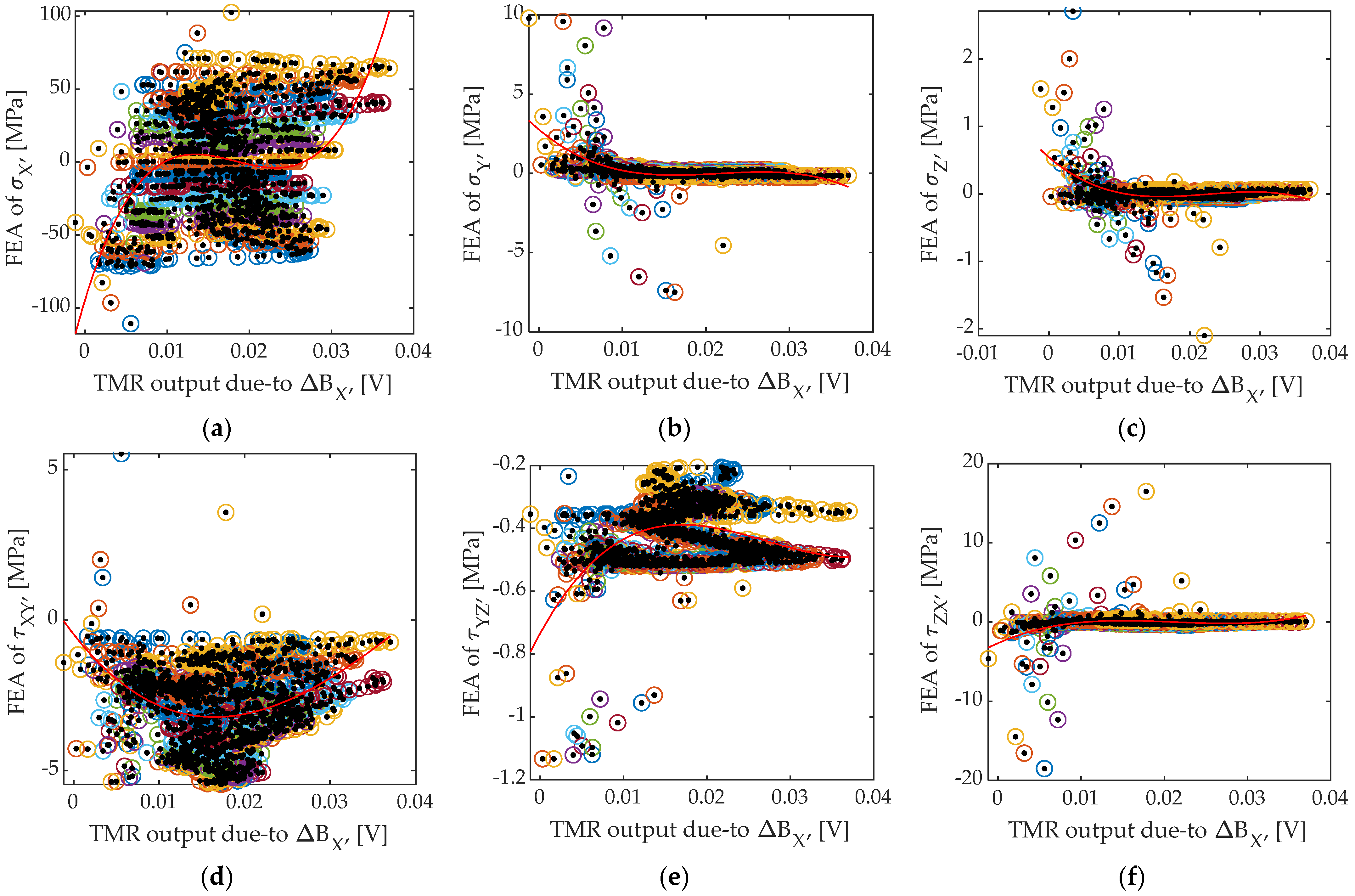
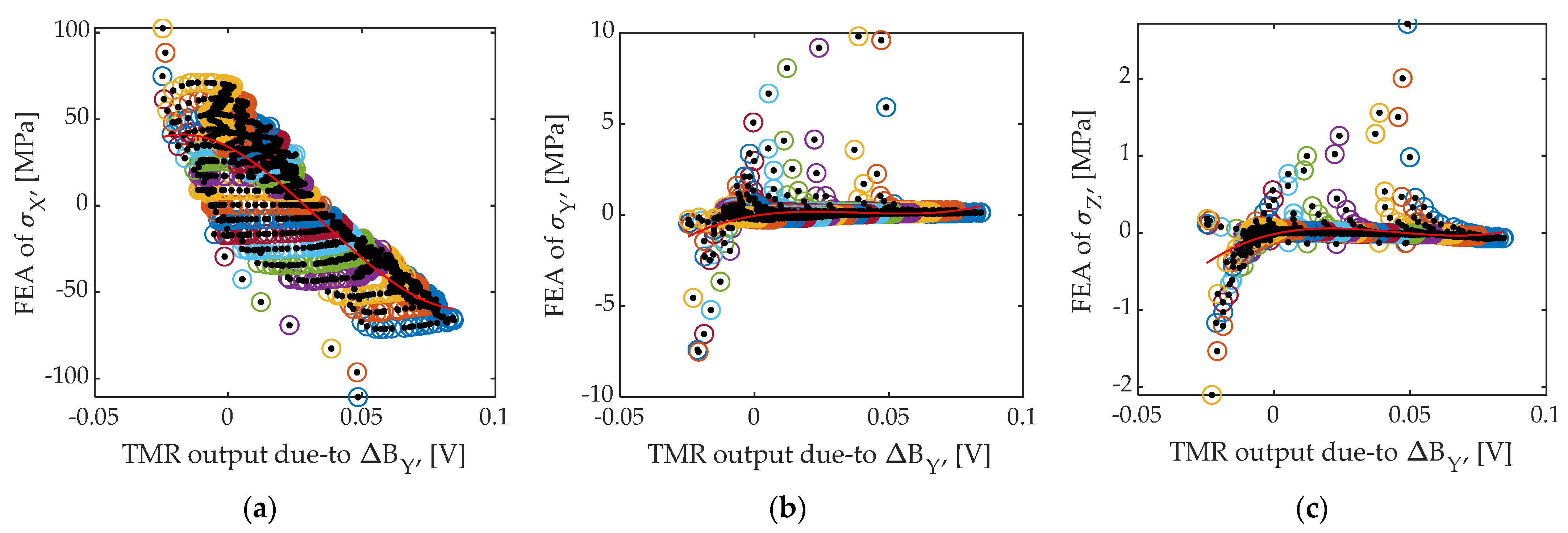
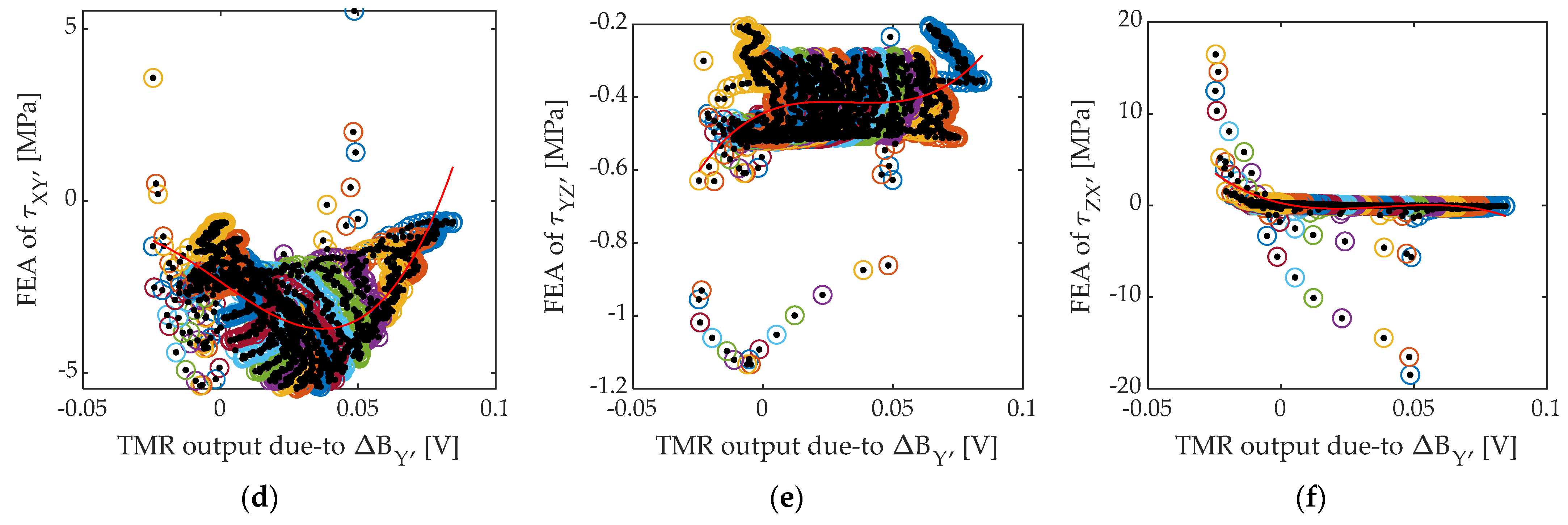
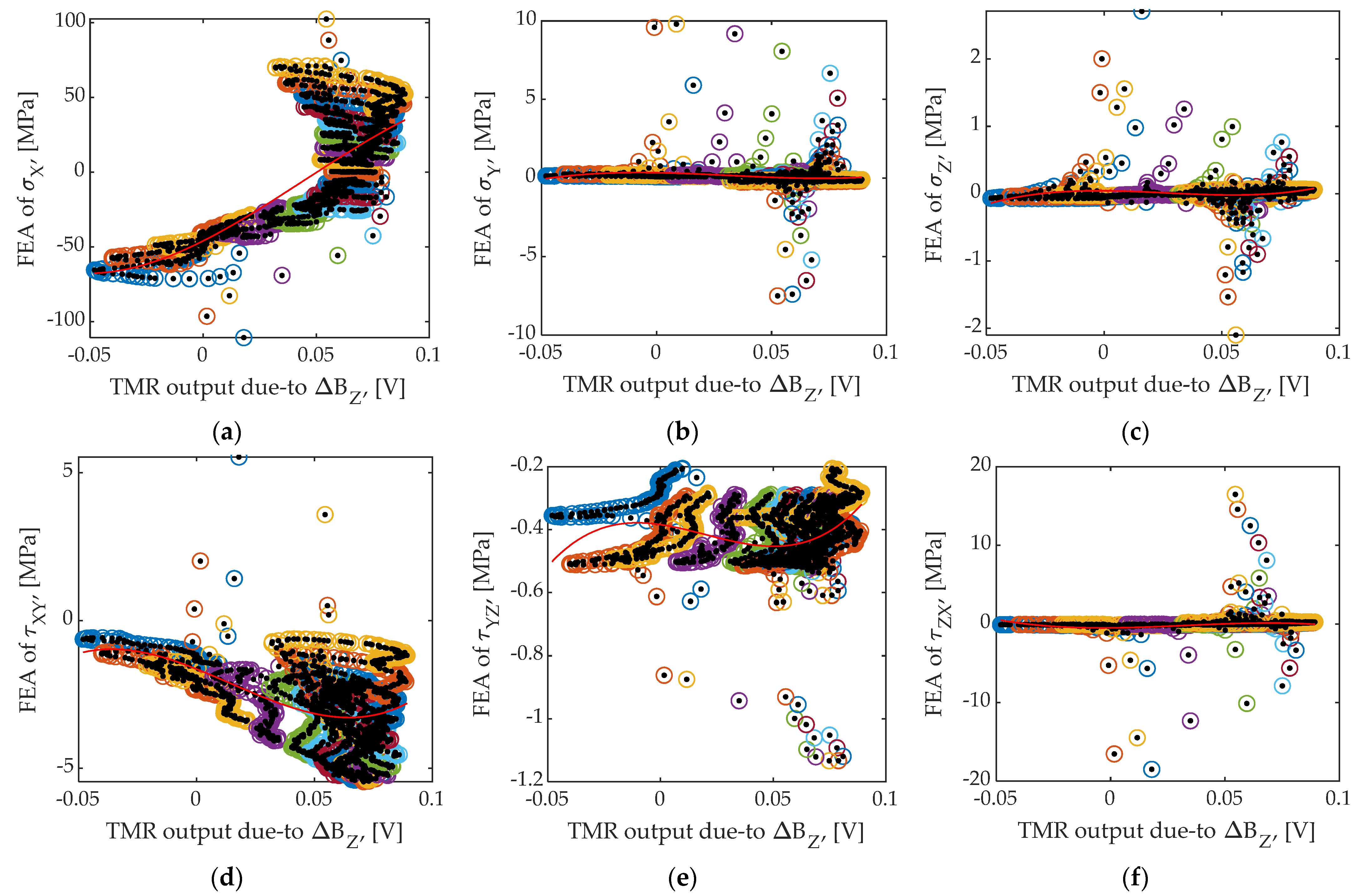
| Parameter | Value |
|---|---|
| Young’s modulus | 210 GPa |
| Poisson ratio | 0.3 |
| Relative permeability | 260 |
| Case | Transformation Coefficient Values, Error, and Features | ||||||
|---|---|---|---|---|---|---|---|
| 1st Coefficient | 2nd Coefficient | 3rd Coefficient | Constancy (C) | ||||
| 1 | −94.5 | 0.0316 | |||||
| 2 | 2.78 | −445.5 | 0.0906 | 0.0012 | |||
| 3 | 0.543 | −89.72 | 4366 | 0.0975 | 0.0013 | ||
| 4 | −0.4634 | −362.1 | 104 | 0.0300 | 0.0031 | ||
| 5 | −0.7341 | 47.89 | −2050 | 0.0283 | 0.0018 | ||
| 6 | −2.642 | 461.2 | 0.1345 | 0.0012 | |||
| 7 | 33.92 | −792.9 | 0.0316 | 0.0041 | |||
| 8 | −0.04409 | 23.83 | −743.2 | 6368 | 0.0900 | 0.0034 | |
| 9 | −0.01645 | 7.931 | −248.5 | 1880 | 0.0980 | 0.0037 | |
| 10 | −2.355 | −55.7 | 22.79 | 0.0300 | 0.0042 | ||
| 11 | −0.4443 | 3.218 | −104.3 | 1048 | 0.0300 | 0.0028 | |
| 12 | 0.2511 | −66.29 | 2156 | 0.1353 | |||
| 13 | −46.01 | 763.3 | 4817 | 0.0316 | 0.0011 | 0.0187 | |
| 14 | 0 | −2.472 | −143.8 | 1512 | 0.0906 | 0 | 0.0015 |
| 15 | 0.04189 | −0.2911 | −52.87 | 678.8 | 0.1015 | ||
| 16 | −1.643 | −31.71 | −196 | 4541 | 0.0949 | 0.0067 | |
| 17 | −0.384 | −1.047 | −40.25 | 672.9 | 0.0316 | 0.0015 | |
| 18 | −0.4819 | 2.362 | 319.4 | −3229 | 0.1342 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berkache, A.; Lee, J.; Wang, D.; Sim, S. Distribution of Magnetic Flux Density under Stress and Its Application in Nondestructive Testing. Appl. Sci. 2022, 12, 7612. https://doi.org/10.3390/app12157612
Berkache A, Lee J, Wang D, Sim S. Distribution of Magnetic Flux Density under Stress and Its Application in Nondestructive Testing. Applied Sciences. 2022; 12(15):7612. https://doi.org/10.3390/app12157612
Chicago/Turabian StyleBerkache, Azouaou, Jinyi Lee, Dabin Wang, and Sunbo Sim. 2022. "Distribution of Magnetic Flux Density under Stress and Its Application in Nondestructive Testing" Applied Sciences 12, no. 15: 7612. https://doi.org/10.3390/app12157612
APA StyleBerkache, A., Lee, J., Wang, D., & Sim, S. (2022). Distribution of Magnetic Flux Density under Stress and Its Application in Nondestructive Testing. Applied Sciences, 12(15), 7612. https://doi.org/10.3390/app12157612








