Synthesized Transmitting Coil for Magnetic Focusing of Pulsed Eddy Current for Downhole Casing Inspection
Abstract
:1. Introduction
2. Working Principle and Model of the PEC System
3. Synthesized Transmitting Coil
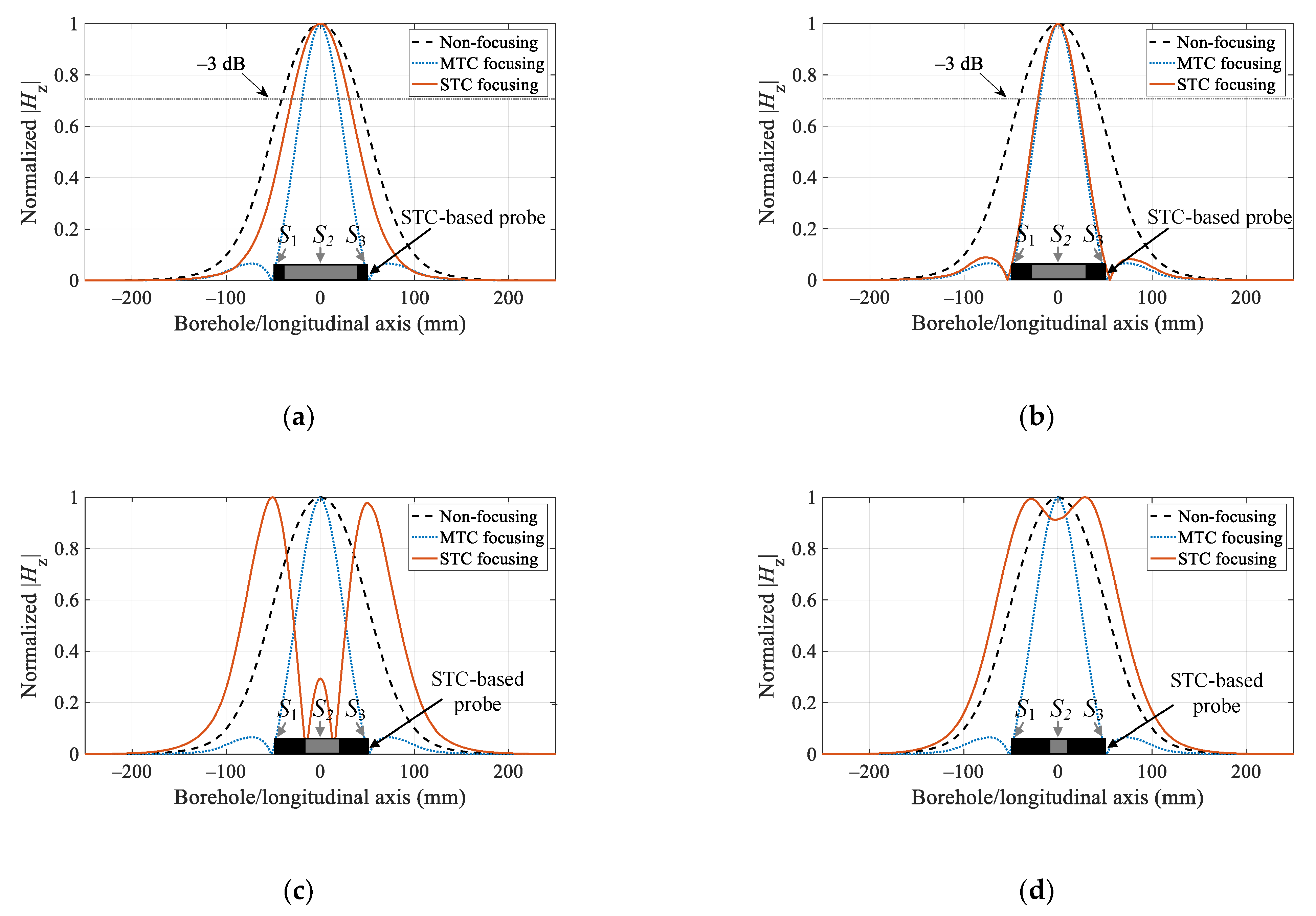
3.1. Magnetic Focusing
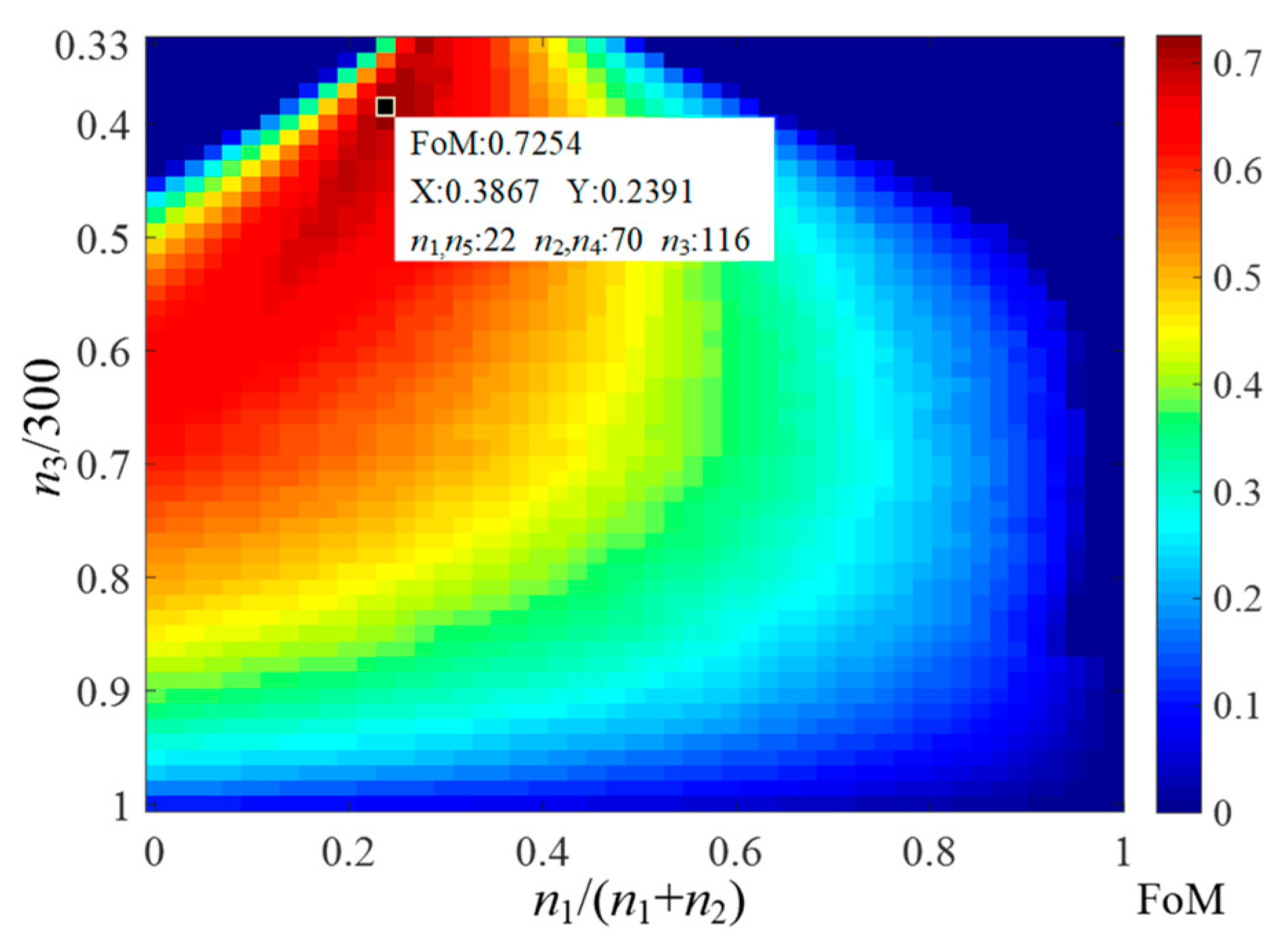
3.2. Optimization of the STC Parameters Using FoM
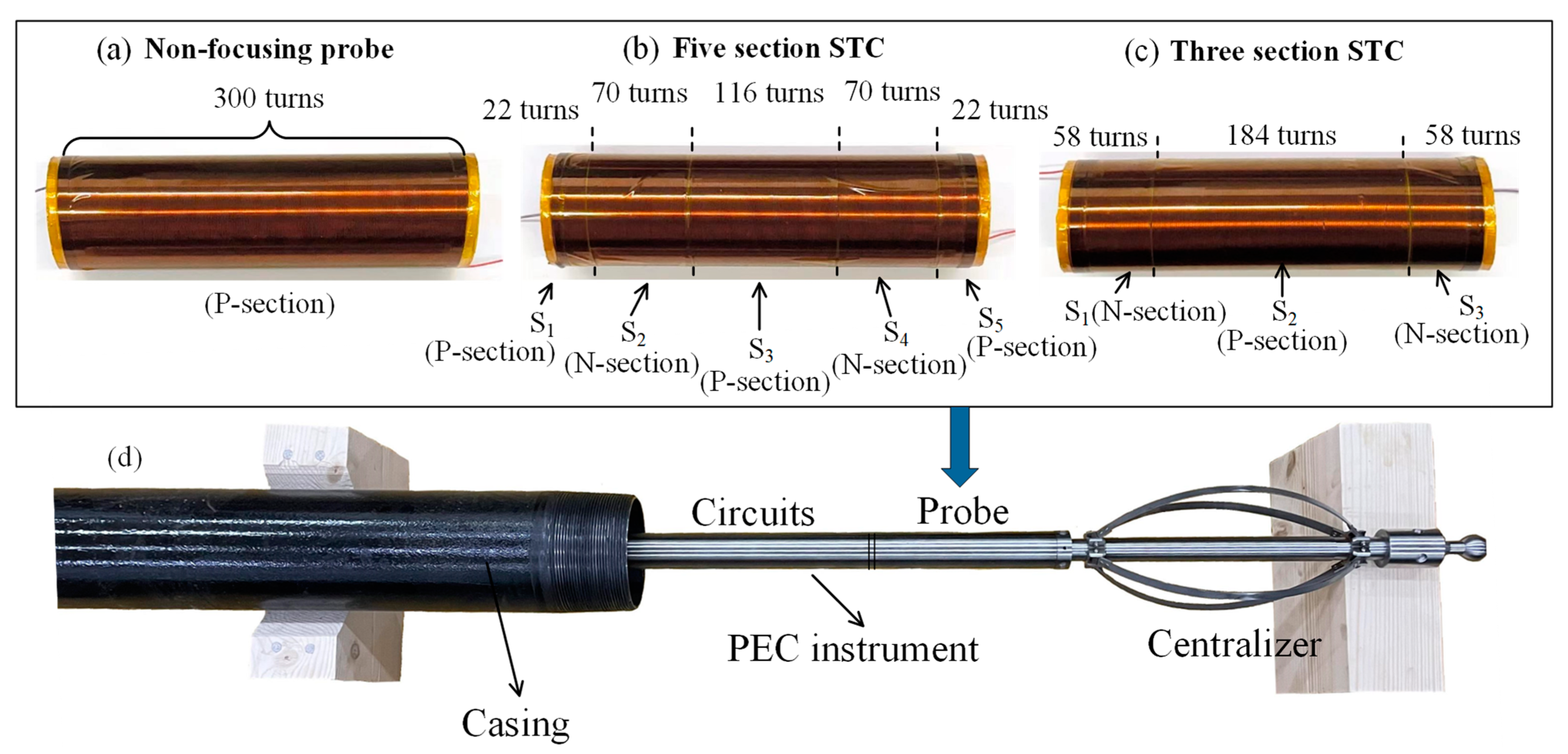
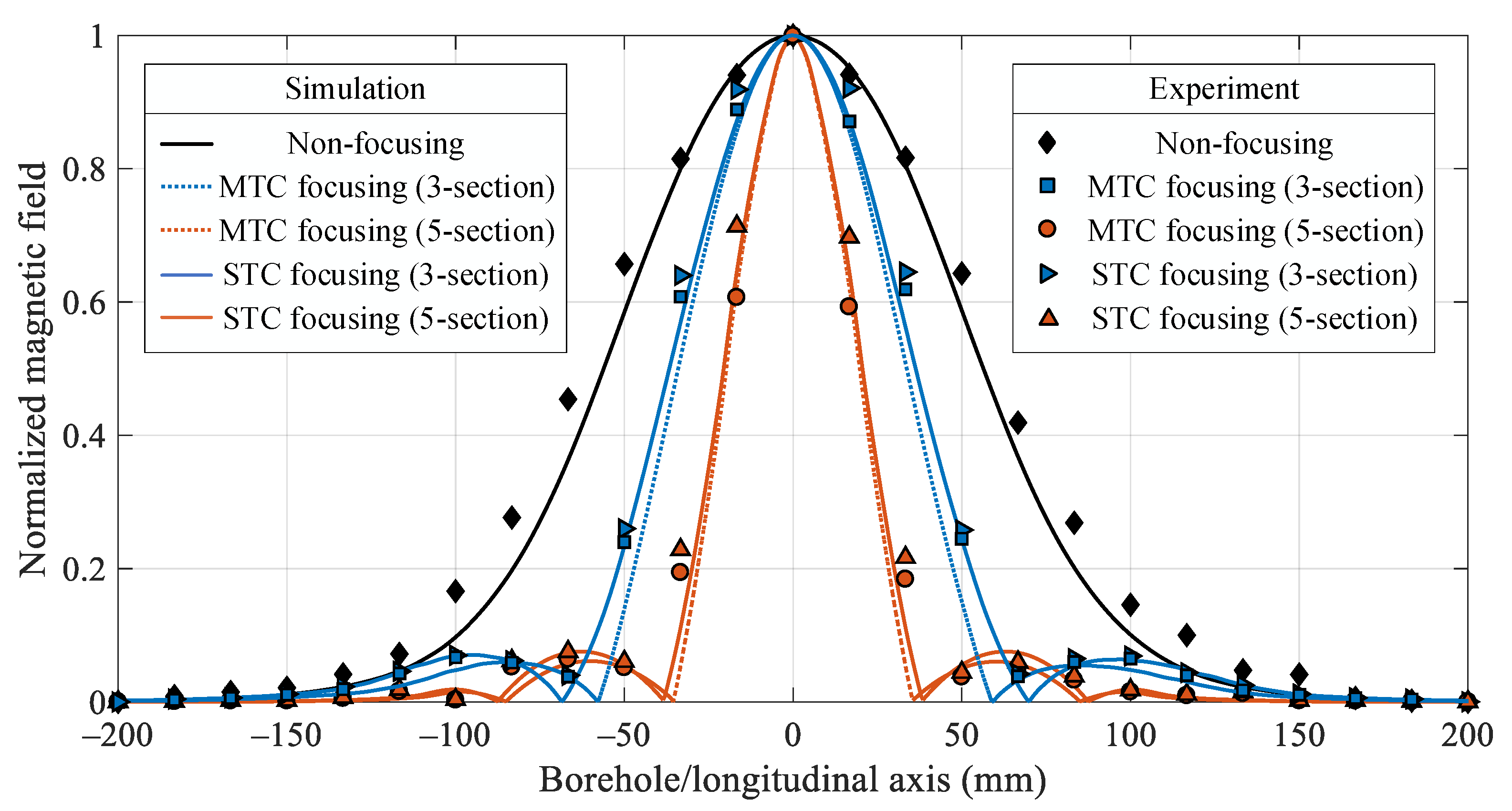
4. Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malekmohammadi, H.; Migali, A.; Laureti, S.; Ricci, M. A Pulsed Eddy Current Testing Sensor Made of Low-Cost Off-the-Shelf Components: Overview and Application to Pseudo-Noise Excitation. IEEE Sens. J. 2021, 21, 23578–23587. [Google Scholar] [CrossRef]
- Meng, T.; Tao, Y.; Chen, Z.; Avila, J.R.S.; Ran, Q.; Shao, Y.; Huang, R.; Xie, Y.; Zhao, Q.; Zhang, Z.; et al. Depth Evaluation for Metal Surface Defects by Eddy Current Testing Using Deep Residual Convolutional Neural Networks. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Yan, B.; Li, Y.; Liu, Z.; Ren, S.; Chen, Z.; Lu, X.; Abidin, I.M.Z. Pulse-Modulation Eddy Current Imaging for 3D Profile Reconstruction of Subsurface Corrosion in Metallic Structures of Aviation. IEEE Sens. J. 2021, 21, 28087–28096. [Google Scholar] [CrossRef]
- Niu, C.; Wang, L.; Wang, Y.; Zhai, Y.; Qu, H.; Liu, Y.; Wang, Q. Numerical Analysis of Eddy Current Induced by z-Gradient Coil in a Superconducting MRI Magnet. IEEE Trans. Appl. Supercond. 2020, 30, 1–6. [Google Scholar] [CrossRef]
- Xiao, Q.; Feng, J.; Xu, Z.; Zhang, H. Receiver Signal Analysis on Geometry and Excitation Parameters of Remote Field Eddy Current Probe. IEEE Trans. Ind. Electron. 2021, 69, 3088–3098. [Google Scholar] [CrossRef]
- Suresh, V.; Abudhahir, A.; Daniel, J. Characterization of Defects on Ferromagnetic Tubes Using Magnetic Flux Leakage. IEEE Trans. Magn. 2019, 55, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Nie, Y.; Qi, P.; Zhang, N.; Ye, C. Inspection of Defect Under Thick Insulation Based on Magnetic Imaging with TMR Array Sensors. IEEE Trans. Magn. 2021, 58, 1–10. [Google Scholar] [CrossRef]
- Liu, C.; Dang, B.; Wang, H.; Shen, X.; Yang, L.; Ren, Z.; Dang, R.; Kang, Y.; Sun, B. Multiple-Transmit Focusing for the Nondestructive Testing of Downhole Casings Based on Borehole Transient Electromagnetic Systems. IEEE Access 2020, 8, 210978–210987. [Google Scholar] [CrossRef]
- Fu, Y.; Yu, R.; Peng, X.; Ren, S. Investigation of casing inspection through tubing with pulsed eddy current. Nondestruct. Test. Eval. 2012, 27, 353–374. [Google Scholar] [CrossRef]
- Wu, T.; Bowler, J.; Theodoulidis, T.P.; Th, T. Eddy Current Induction by a Coil Whose Axis is Perpendicular to that of a Tube. IEEE Trans. Magn. 2017, 53, 6201709. [Google Scholar] [CrossRef]
- Zhou, H.; Hou, K.; Pan, H.; Chen, J.; Wang, Q. Study on the Optimization of Eddy Current Testing Coil and the Defect Detection Sensitivity. Press. Vessel. Technol. Prep. Future 2015, 130, 1649–1657. [Google Scholar] [CrossRef] [Green Version]
- Dang, B.; Yang, L.; Du, N.; Liu, C.; Dang, R.; Wang, B.; Xie, Y. Auxiliary Sensor-Based Borehole Transient Electromagnetic System for the Nondestructive Inspection of Multipipe Strings. Sensors 2017, 17, 1836. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Gao, B.; Ma, Q.; Xie, L.; Tian, G.Y.; Yin, Y. Multi-Layer Magnetic Focusing Sensor Structure for Pulsed Remote Field Eddy Current. IEEE Sens. J. 2018, 19, 2490–2499. [Google Scholar] [CrossRef] [Green Version]
- Tsukada, K.; Hirata, T.; Goda, Y.; Sakai, K.; Kiwa, T. Hybrid Magnetic Sensor Combined With a Tunnel Magnetoresistive Sensor and High-Temperature Superconducting Magnetic-Field-Focusing Plates. IEEE Trans. Appl. Supercond. 2018, 29, 8800405. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, B.; Kim, H.R.; Rim, C.-T.; Kim, Y.-S. Single-Variable-Input Active Sidelobe Suppression Method for Synthesized Magnetic Field Focusing Technology and Its Optimization. IEEE Trans. Ind. Electron. 2019, 67, 9813–9823. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, B.H.; Kim, H.R.; Rim, C.T. 2-D synthesized magnetic field focusing technology With loop coils distributed in a rectangular formation. IEEE Trans. Ind. Electron. 2019, 66, 5558–5566. [Google Scholar] [CrossRef]
- Liu, C.; Dang, B.; Wang, H.Y.; Yang, L.; Dang, J.; Shen, X.; Dang, R. Synthesised magnetic field focusing for the non-destructive testing of oil and gas well casing pipes using pulsed eddy-current array. IEEE Trans. Magn. 2022. [Google Scholar] [CrossRef]
- Cubero, D.; Marmugi, L.; Renzoni, F. Exploring the limits of magnetic field focusing: Simple planar geometries. Results Phys. 2020, 19, 103562. [Google Scholar] [CrossRef]
- Tanaka, H.; Iizuka, H. Kilohertz Magnetic Field Focusing Behavior of a Single-Defect Loop Array Characterized by Curl of the Current Distribution With Delta Function. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1088–1091. [Google Scholar] [CrossRef]
- Mohammed, A.I.; Oyeneyin, B.; Atchison, B.; Njuguna, J. Casing structural integrity and failure modes in a range of well types—A review. J. Nat. Gas Sci. Eng. 2019, 68, 102898. [Google Scholar] [CrossRef]
- Wu, S.N.; Zhang, L.B.; Fan, J.C.; Zhang, X.M.; Zhou, Y.F.; Wang, D.G. Prediction analysis of downhole tubing leakage location for offshore gas production wells (in English). Measurement 2018, 127, 546–553. [Google Scholar] [CrossRef]
- Ulapane, N.; Thiyagarajan, K.; Miro, J.V.; Kodagoda, S. Surface Representation of Pulsed Eddy Current Sensor Signals for Improved Ferromagnetic Material Thickness Quantification. IEEE Sens. J. 2020, 21, 5413–5422. [Google Scholar] [CrossRef]
- Kaufman, A.A.; Yu, A. Dashevsky. In Principles of Induction Logging; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Li, J.H.; Farquharson, C.G.; Hu, X.Y. Three effective inverse Laplace transform algorithms for computing time domain electromagnetic responses (in English). Geophysics 2016, 81, E113–E128. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Liu, C.; Dang, J.; Zhao, Y.; Dang, B.; Dang, R. Synthesized Transmitting Coil for Magnetic Focusing of Pulsed Eddy Current for Downhole Casing Inspection. Appl. Sci. 2022, 12, 7695. https://doi.org/10.3390/app12157695
Yang L, Liu C, Dang J, Zhao Y, Dang B, Dang R. Synthesized Transmitting Coil for Magnetic Focusing of Pulsed Eddy Current for Downhole Casing Inspection. Applied Sciences. 2022; 12(15):7695. https://doi.org/10.3390/app12157695
Chicago/Turabian StyleYang, Ling, Changzan Liu, Jingxin Dang, Yang Zhao, Bo Dang, and Ruirong Dang. 2022. "Synthesized Transmitting Coil for Magnetic Focusing of Pulsed Eddy Current for Downhole Casing Inspection" Applied Sciences 12, no. 15: 7695. https://doi.org/10.3390/app12157695





