Theoretical and Numerical Study on Buongiorno’s Model with a Couette Flow of a Nanofluid in a Channel with an Embedded Cavity
Abstract
:1. Introduction
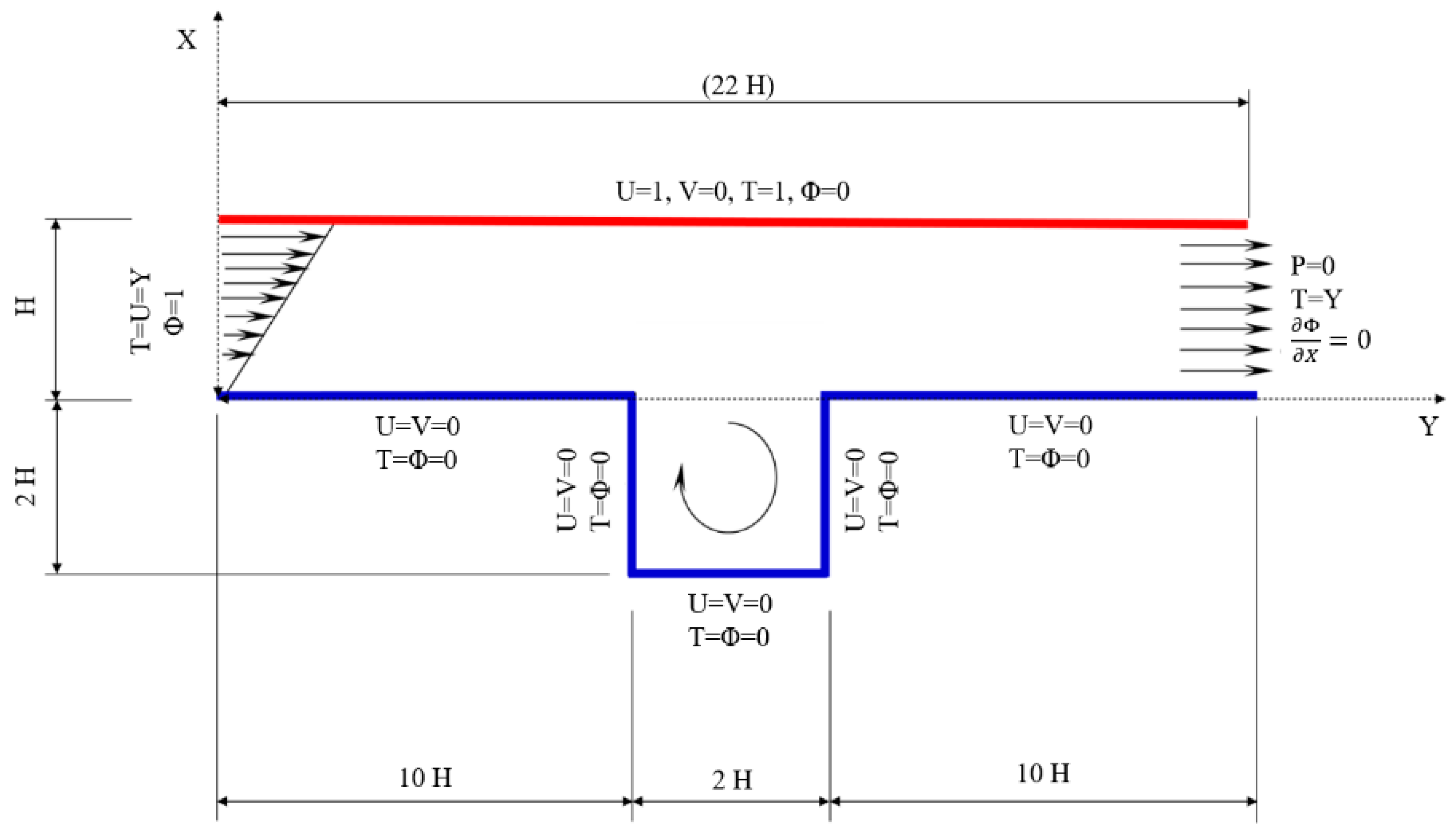
2. Mathematical Model
- Continuity equation
- Momentum equations in X and Y direction
- Energy equation
- Nanoparticles equation
- Inlet
- Outlet
- Hot wall
- Horizontal cold walls
- Vertical cold walls
3. Mesh and Validation
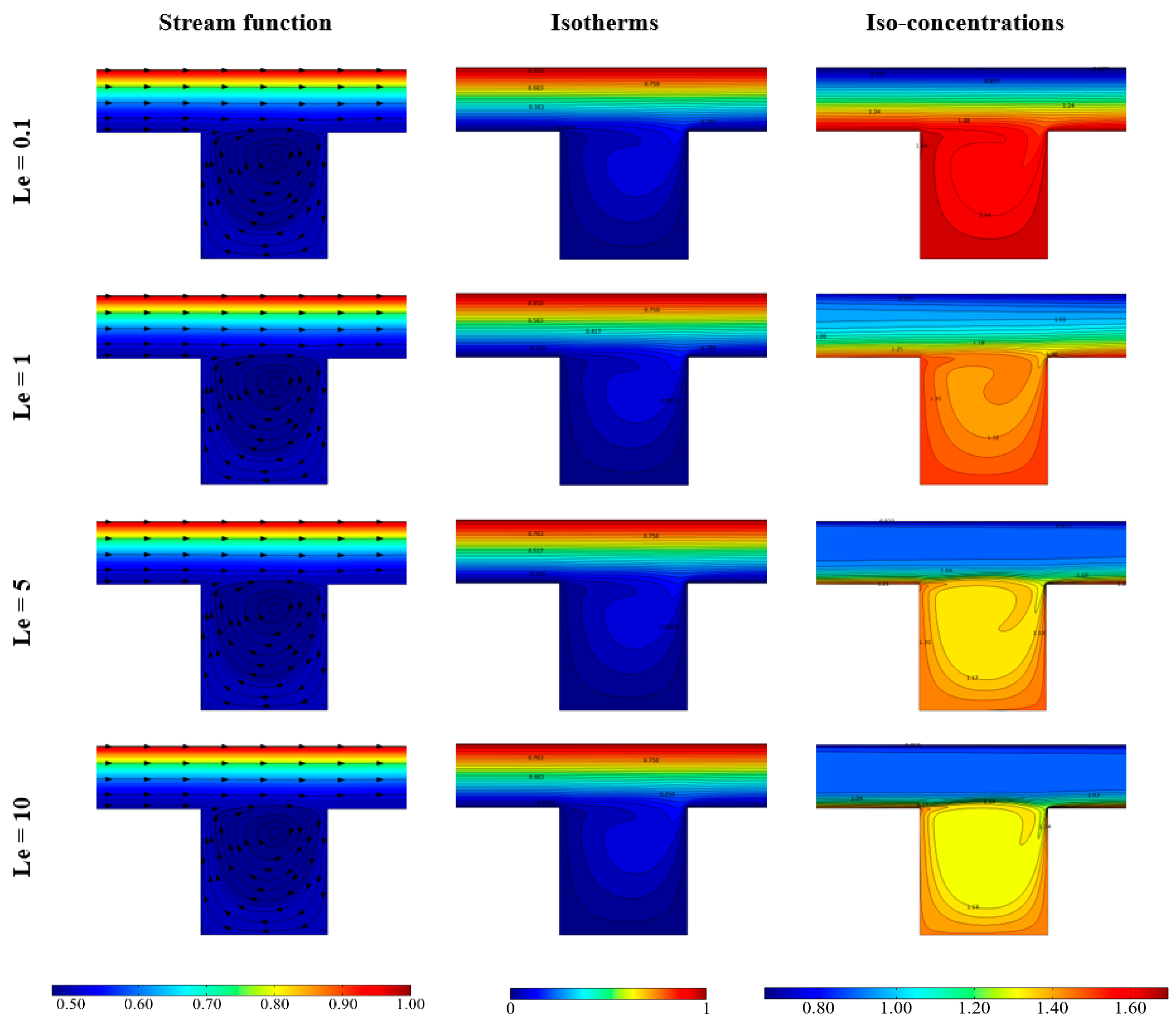
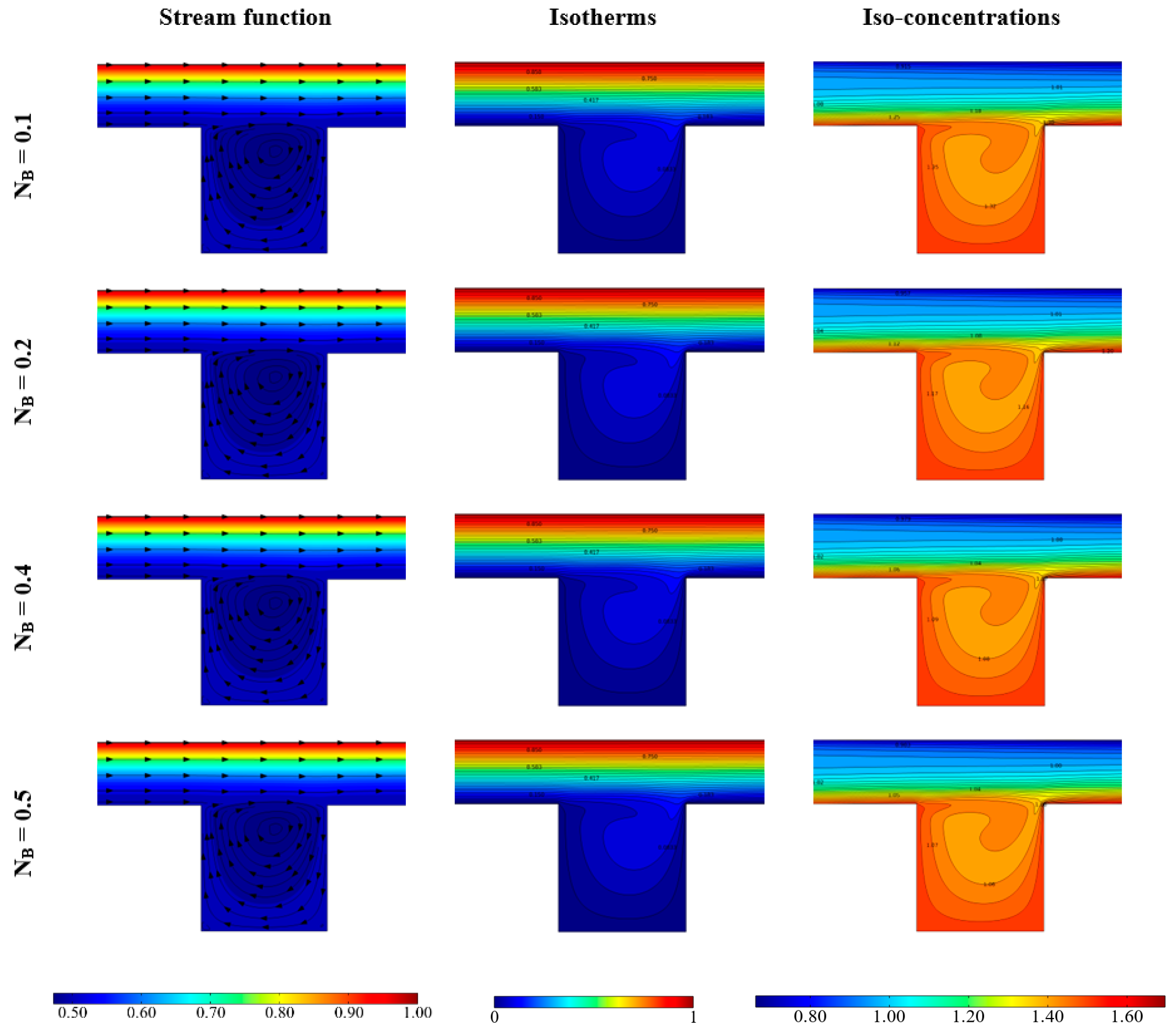
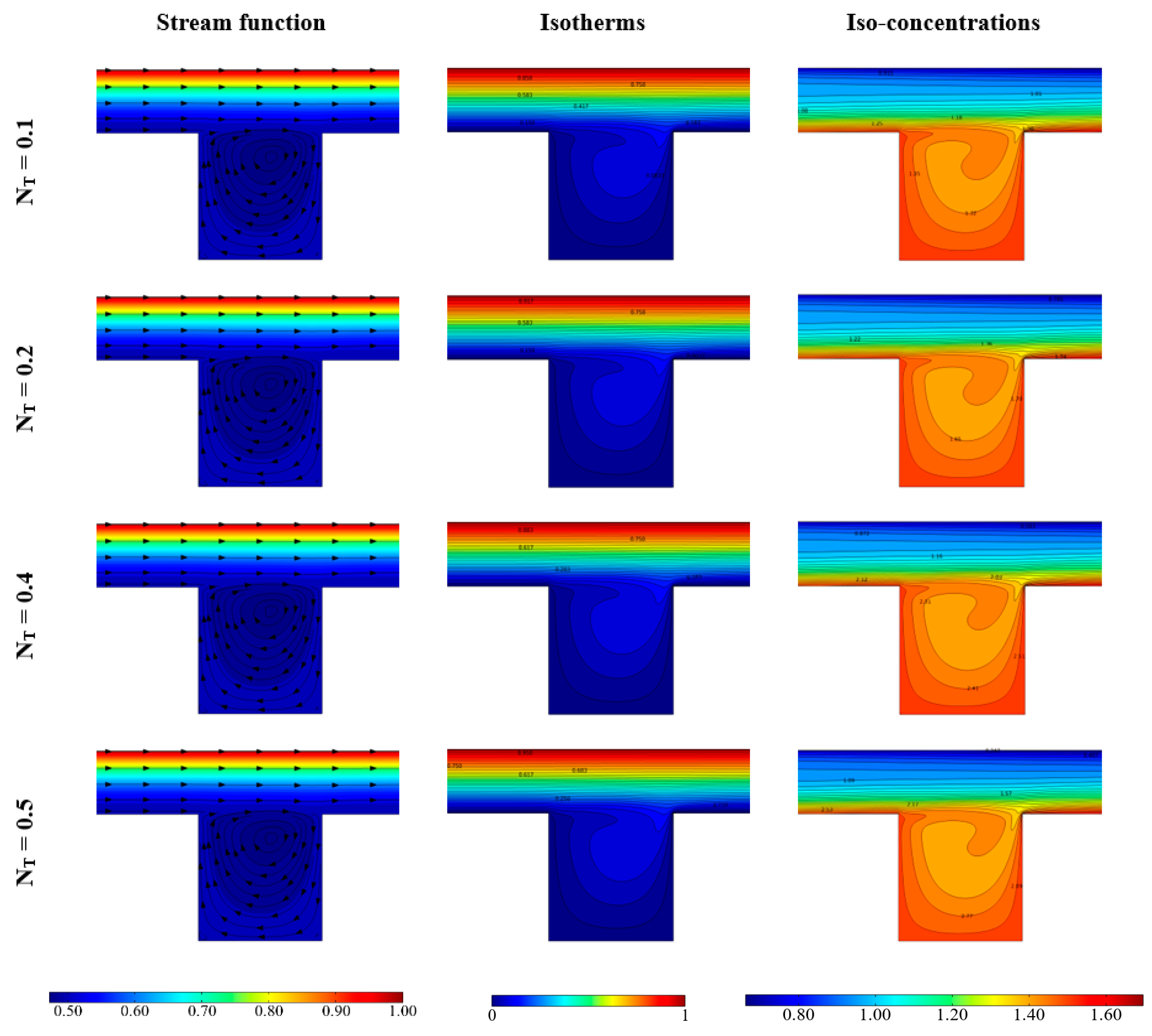
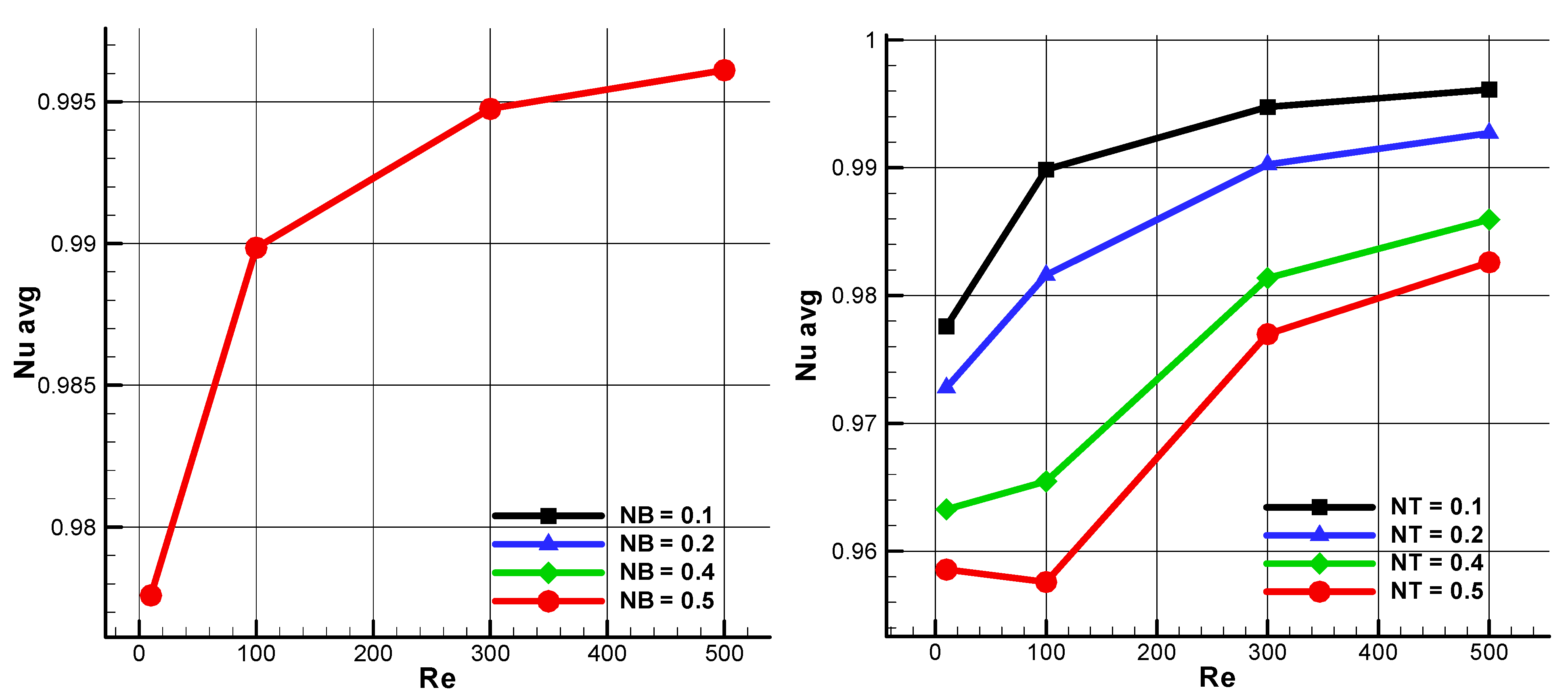
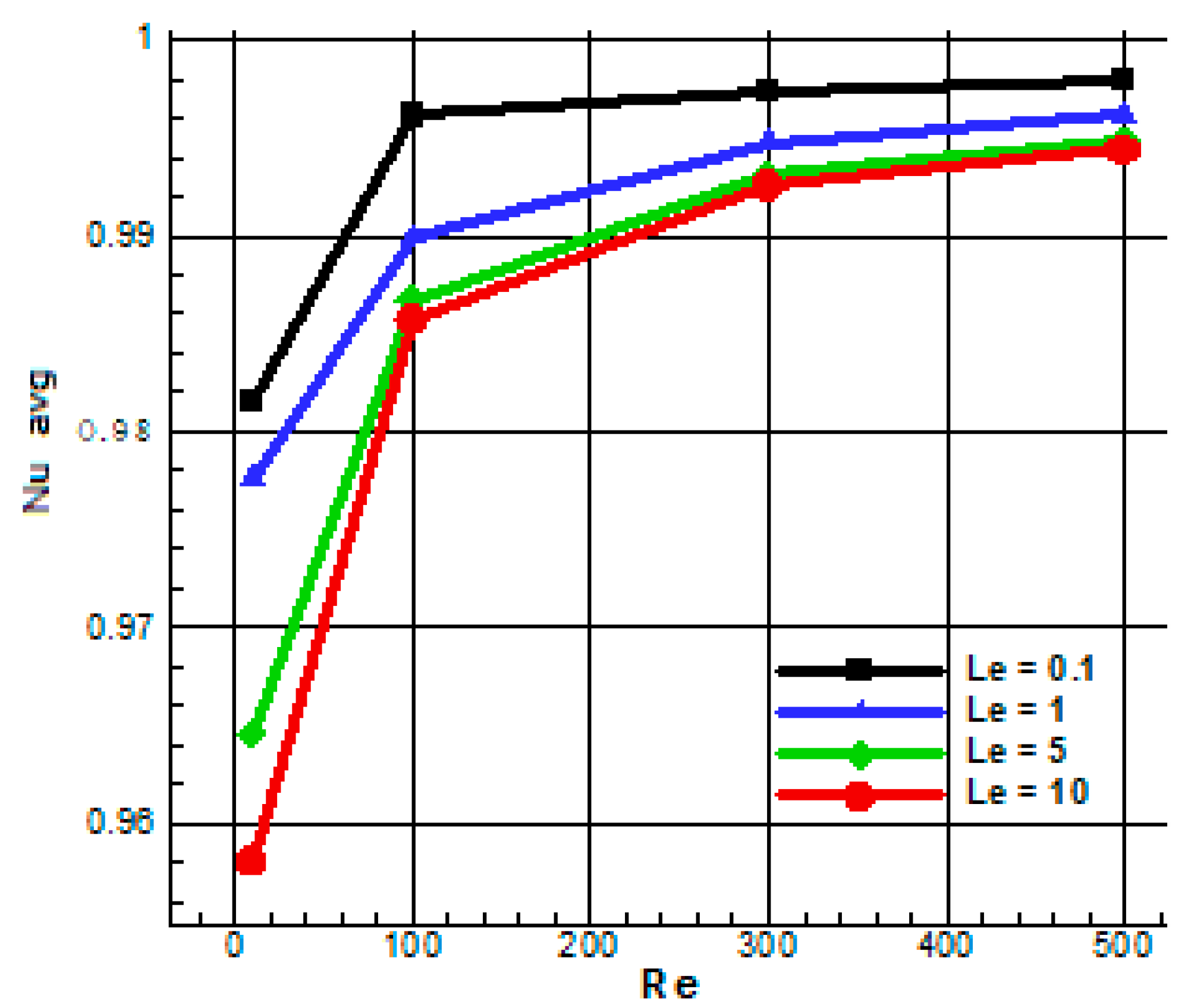
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cp | Fluid specific heat constant [J/kg K] |
| DB | Brownian motion coefficient |
| DT | Thermophoresis coefficient |
| dP | Nanoparticles diameter |
| H | Cavity dimension |
| k | Thermal conductivity [W/m K] |
| kP | Nanoparticles thermal conductivity [W/m K] |
| Le | Lewis number |
| NB | Brownian diffusivity number |
| NT | Thermophoresis number |
| Nu | Nusselt number |
| P | Nanofluid pressure [Pa] |
| p | Dimensionless pressure |
| Pr | Prandtl number |
| Re | Reynolds number |
| T | Local nanofluid temperature [K] |
| Th | Hot wall temperature [K] |
| U | x-component velocity [m/s] |
| U0 | Slip velocity [m/s] |
| V | y-component velocity [m/s] |
| (u,v) | Dimensionless velocity components |
| X | x-coordinate [m] |
| Y | y-coordinate [m] |
| (x,y) | Dimensionless coordinates |
| α | Thermal diffusivity [m2/s] |
| Θ | Dimensionless temperature |
| µ | Nanofluid dynamic viscosity [Pa s] |
| ρ | Nanofluid density [kg/m3] |
| φ | Nanoparticles concentration [#/L] |
| Φ | Dimensionless concentration |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles: Technical Report ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Choi, S. Enhancing thermal conductivit of fluids with nanoparticles. In Developments and Applications of Non-Newtonian Flows; Siginer, D.A., Wang, H.P., Eds.; FED-V.231/MD-V; ASME: New York, NY, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Panduro, E.A.C.; Finotti, F.; Largiller, G.; Lervåg, K.Y. A review of the use of nanofluids as heat-transfer fluids in parabolic-trough collectors. Appl. Therm. Eng. 2022, 211, 118346. [Google Scholar] [CrossRef]
- Yan, S.R.; Aghakhani, S.; Karimipour, A. Influence of a membrane on nanofluid heat transfer and irreversibilities inside a cavity with two constant-temperature semicircular sources on the lower wall: Applicable to solar collectors. Phys. Scr. 2020, 95, 085702. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Mahian, O. Natural convection in an inclined cavity with time-periodic temperature boundary conditions using nanofluids: Application in solar collectors. Int. J. Heat Mass Transf. 2018, 116, 751–761. [Google Scholar] [CrossRef]
- Hady, F.M.; Ibrahim, F.S.; Abdel-Gaied, S.M.; Eid, M.R. Effect of heat generation/absorption on natural convective boundary-layer flow from a vertical cone embedded in a porous medium filled with a non-Newtonian nanofluid. Int. Commun. Heat Mass Transf. 2011, 38, 1414–1420. [Google Scholar] [CrossRef]
- Alsaedi, A.; Awais, M.; Hayat, T. Effects of heat generation/absorption on stagnation point flow of nanofluid over a surface with convective boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4210–4223. [Google Scholar] [CrossRef]
- Jalilpour, B.; Jafarmadar, S.; Ganji, D.D.; Shotorban, A.B.; Taghavifar, H. Heat generation/absorption on MHD stagnation flow of nanofluid towards a porous stretching sheet with prescribed surface heat flux. J. Mol. Liq. 2014, 195, 194–204. [Google Scholar] [CrossRef]
- Rawat, S.K.; Mishra, A.; Kumar, M. Numerical study of thermal radiation and suction effects on copper and silver water nanofluids past a vertical Riga plate. Multidiscip. Model. Mater. Struct. 2019, 15, 714–736. [Google Scholar] [CrossRef]
- Patil, P.M.; Shashikant, A.; Hiremath, P.S. Diffusion of liquid hydrogen and oxygen in nonlinear mixed convection nanofluid flow over vertical cone. Int. J. Hydrog. Energy 2019, 44, 17061–17071. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Azimikivi, H.; Purmahmud, N.; Mirzaee, I. Rib shape and nanoparticle diameter effects on natural convection heat transfer at low turbulence two-phase flow of AL2O3-water nanofluid inside a square cavity: Based on Buongiorno’s two-phase model. Therm. Sci. Eng. Prog. 2020, 20, 100587. [Google Scholar] [CrossRef]
- Rawat, S.K.; Upreti, H.; Kumar, M. Comparative Study of Mixed Convective MHD Cu-Water Nanofluid Flow over a Cone and Wedge using Modified Buongiorno’s Model in Presence of Thermal Radiation and Chemical Reaction via Cattaneo-Christov Double Diffusion Model. J. Appl. Comput. Mech. 2021, 7, 1383–1402. [Google Scholar]
- Ma, Y.; Mohebbi, R.; Rashid, M.M.; Yang, Z. Study of nanofluid forced convection heat transfer in a bent channel by means of lattice Boltzmann method. Phys. Fluids 2018, 30, 032001. [Google Scholar] [CrossRef]
- Rossi di Schio, E.; Celli, M.; Barletta, A. Effects of Brownian Diffusion and Thermophoresis on the Laminar Forced Convection of a Nanofluid in a Channel. J. Heat Transf. 2014, 136, 022401. [Google Scholar] [CrossRef]
- Mehrez, Z.; Bouterra, M.; El Cafsi, A.; Belghith, A. Heat transfer and entropy generation analysis of nanofluids flow in an open cavity. Comput. Fluids 2013, 88, 363–373. [Google Scholar] [CrossRef]
- Makinde, O.D.; Omar, A.; Tshehla, M.S. Computational Modelling of Couette Flow of Nanofluids with Viscous Heating and Convective Cooling. J. Comput. Math. 2014, 2014, 631749. [Google Scholar] [CrossRef] [Green Version]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Mobin, N. Numerical Simulation and Mathematical Modeling of Electro-Osmotic Couette–Poiseuille Flow of MHD Power-Law Nanofluid with Entropy Generation. Symmetry 2019, 11, 1038. [Google Scholar] [CrossRef] [Green Version]
- Hussain, S.; Sameh, E.A.; Akbar, T. Entropy generation analysis in MHD mixed convection of hybrid nanofluid in an open cavity with a horizontal channel containing an adiabatic obstacle. Int. J. Heat Mass Transf. 2017, 114, 1054–1066. [Google Scholar] [CrossRef]
- Seyyedi, S.M.; Dogonchi, A.S.; Hashemi-Tilehnoee, M.; Waqas, M.; Ganji, D.D. Entropy generation and economic analyses in a nanofluid filled L-shaped enclosure subjected to an oriented magnetic field. Appl. Therm. Eng. 2020, 168, 114789. [Google Scholar] [CrossRef]
- Biserni, C.; Impiombato, A.N.; Aminhossein, J.; Rossi di Schio, E.; Semprini, G. Formation and Topology of vortices in Couette Flow over open cavities. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2020; Volume 197, p. 10005. [Google Scholar]


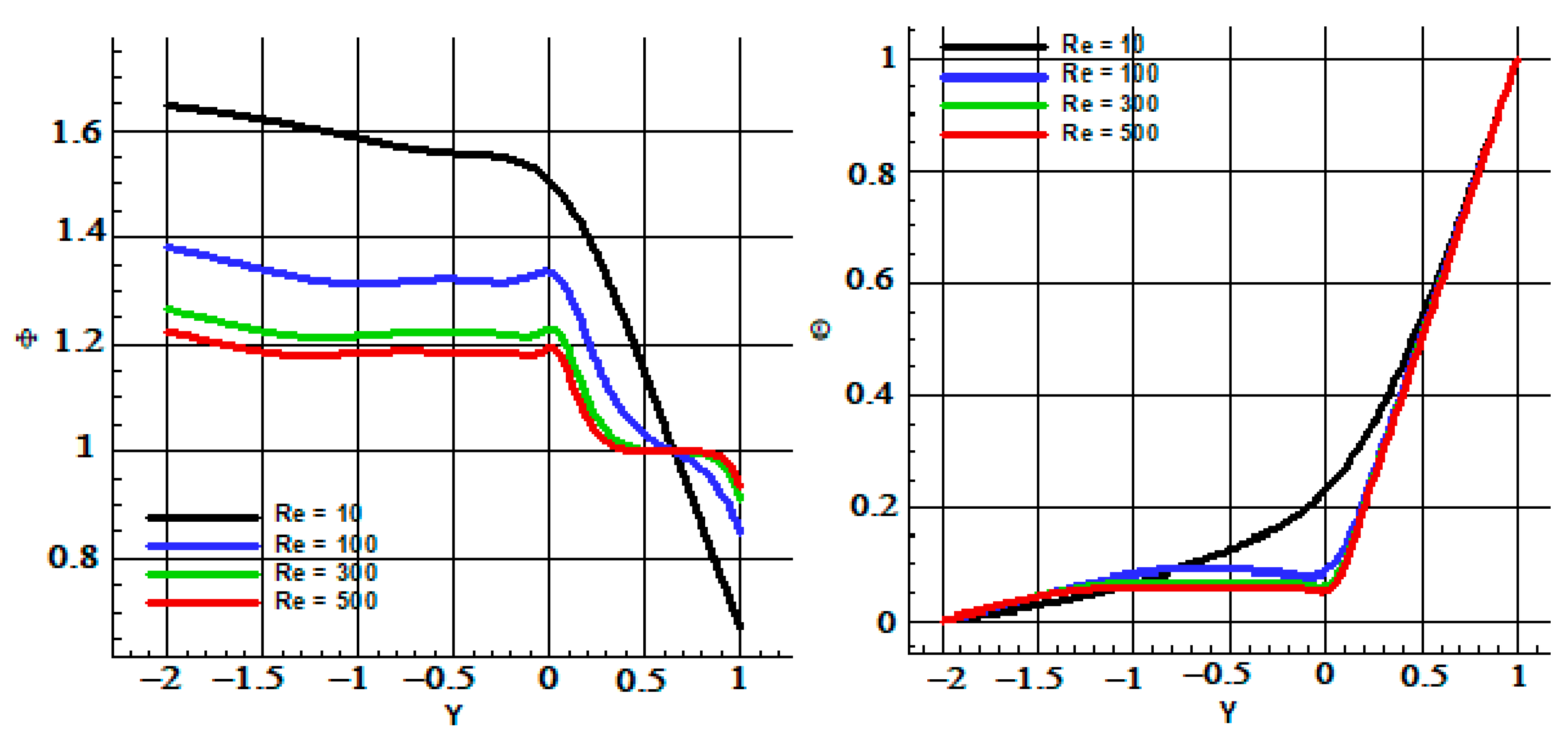
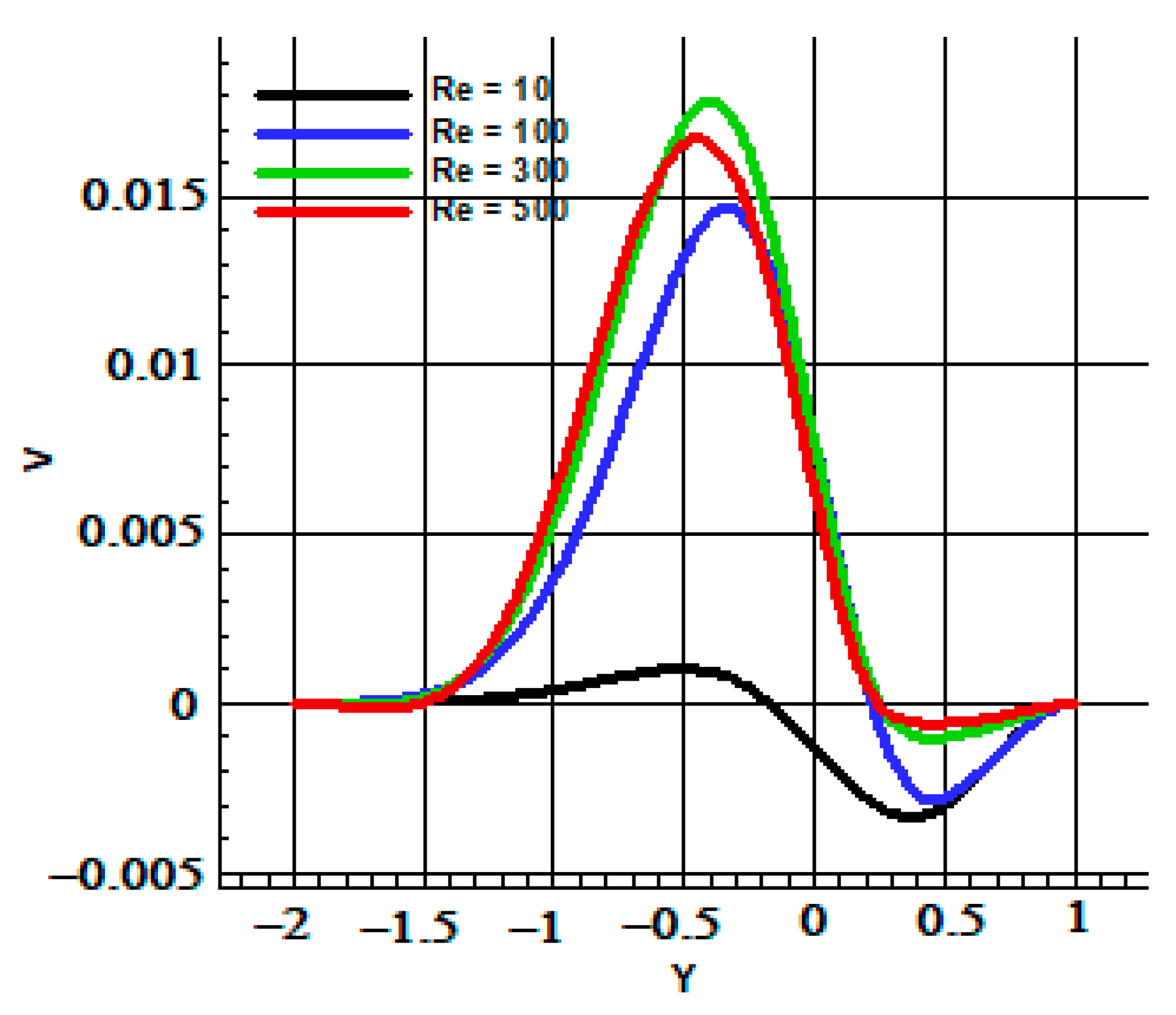
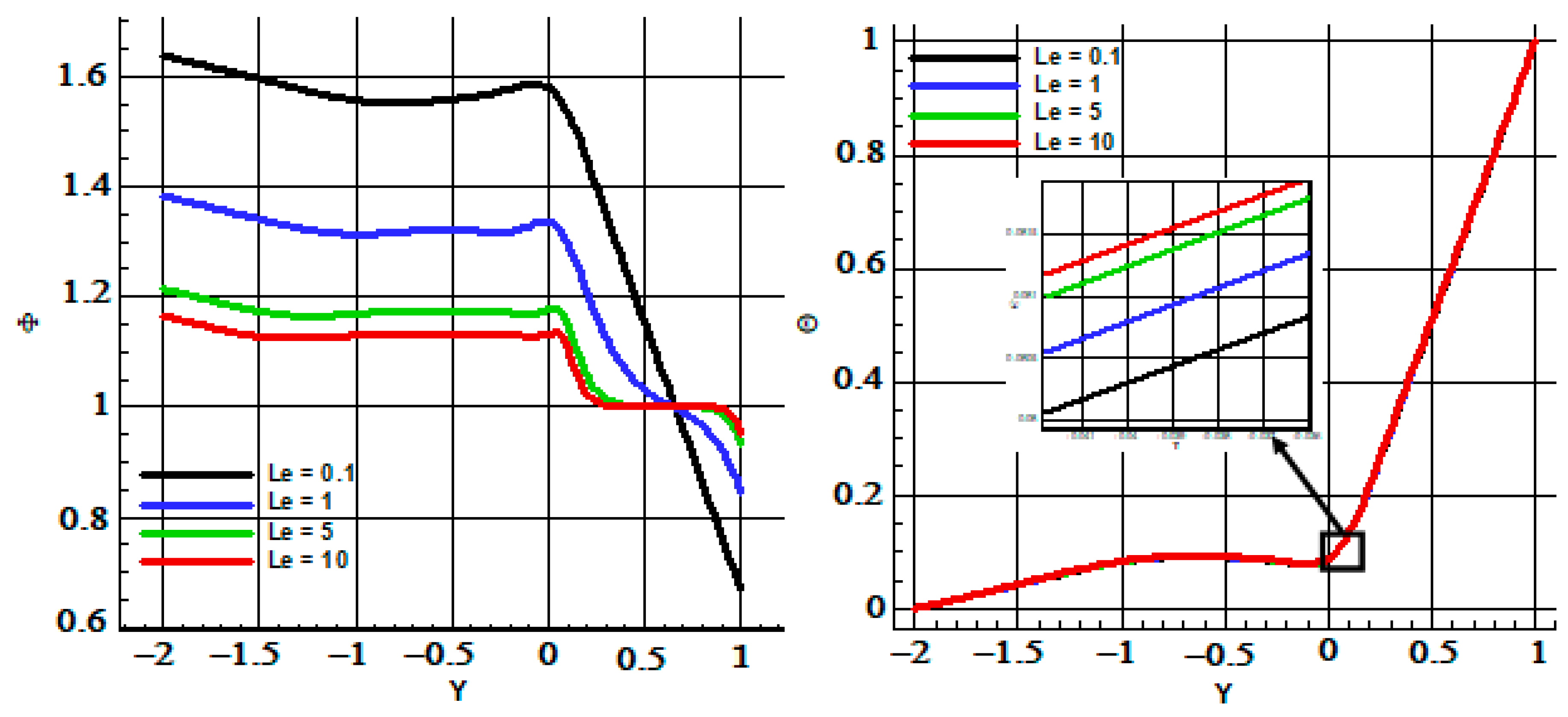
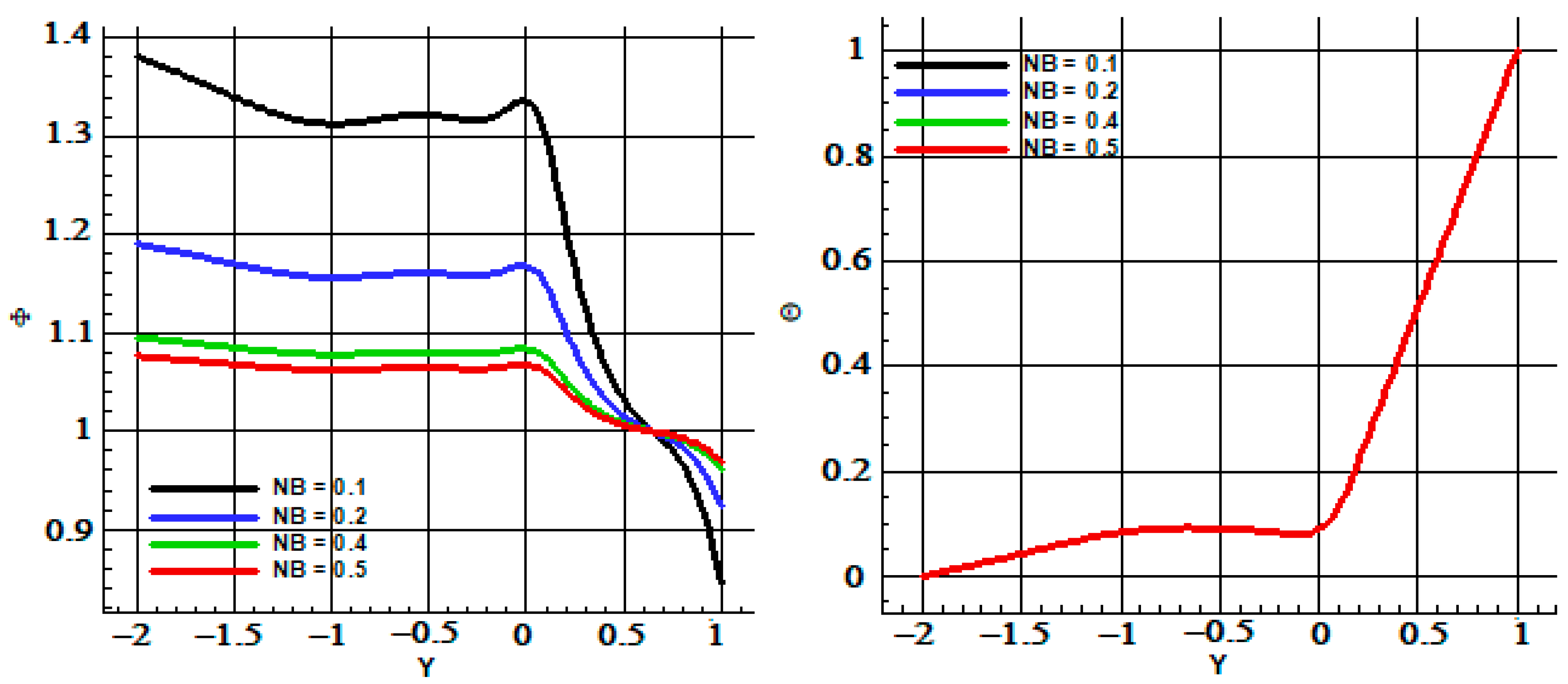

| # | N | ||||
|---|---|---|---|---|---|
| 1 | 1246 | 0.60210 | 0.43391 | 1.04165 | 0.98558 |
| 2 | 30,449 | 0.60199 | 0.43461 | 1.03690 | 0.98569 |
| 3 | 59,520 | 0.60198 | 0.43463 | 1.03601 | 0.98571 |
| 4 | 77,826 | 0.60198 | 0.43463 | 1.03600 | 0.98572 |
| 5 | 120,360 | 0.60198 | 0.43464 | 1.03599 | 0.98573 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossi di Schio, E.; Impiombato, A.N.; Mokhefi, A.; Biserni, C. Theoretical and Numerical Study on Buongiorno’s Model with a Couette Flow of a Nanofluid in a Channel with an Embedded Cavity. Appl. Sci. 2022, 12, 7751. https://doi.org/10.3390/app12157751
Rossi di Schio E, Impiombato AN, Mokhefi A, Biserni C. Theoretical and Numerical Study on Buongiorno’s Model with a Couette Flow of a Nanofluid in a Channel with an Embedded Cavity. Applied Sciences. 2022; 12(15):7751. https://doi.org/10.3390/app12157751
Chicago/Turabian StyleRossi di Schio, Eugenia, Andrea Natale Impiombato, Abderrahim Mokhefi, and Cesare Biserni. 2022. "Theoretical and Numerical Study on Buongiorno’s Model with a Couette Flow of a Nanofluid in a Channel with an Embedded Cavity" Applied Sciences 12, no. 15: 7751. https://doi.org/10.3390/app12157751







