Design Optimization and Electromagnetic Performance Analysis of an Axial-Flux Permanent Magnet Brushless DC Motor with Unequal-Thickness Magnets
Abstract
:1. Introduction
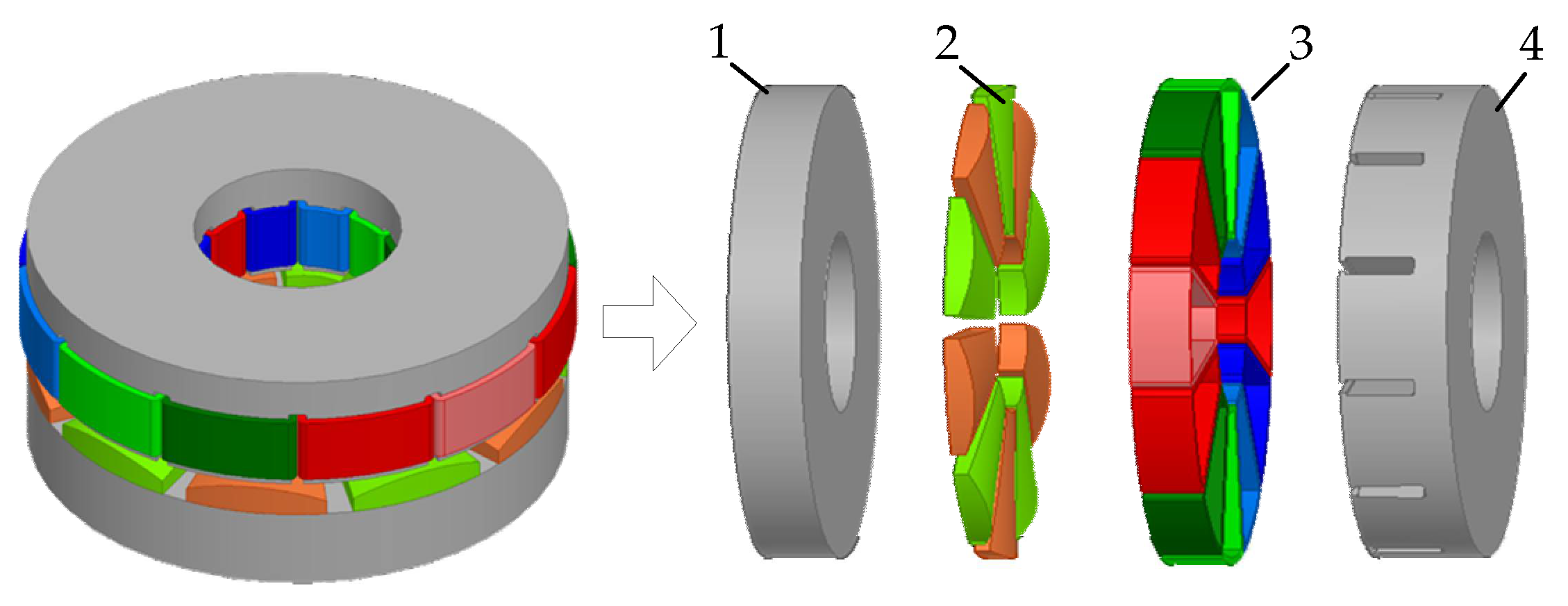
2. Structure of AFPMBLDCM
2.1. Topology of AFPMBLDCM
2.2. Unequal-Thickness Arc-Shaped Permanent Magnets
3. Main Parameter of AFPMBLDCM
3.1. Number of Poles/Slots
3.2. Power and Torque
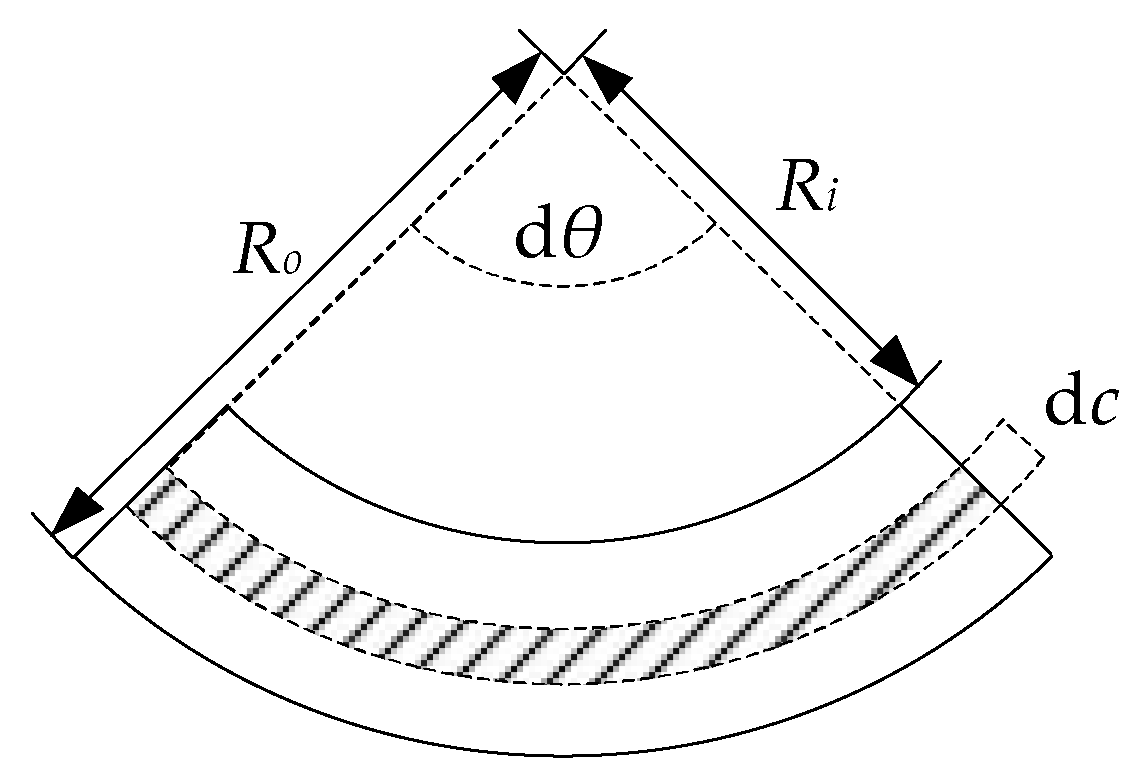
3.3. Size of AFPMBLDCM Structure
3.4. No-Load Back EMF
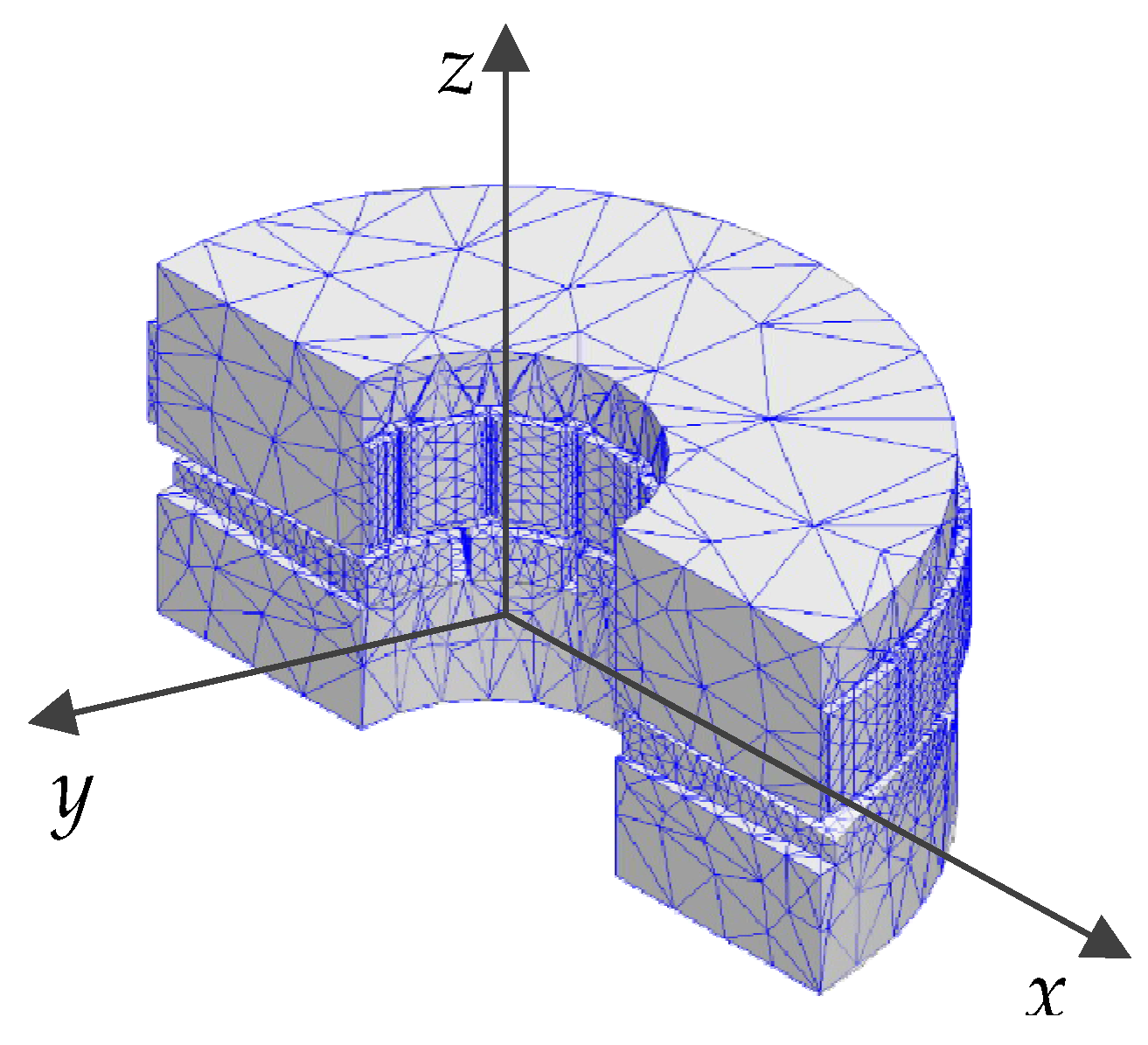
4. Electromagnetic Performance Analysis
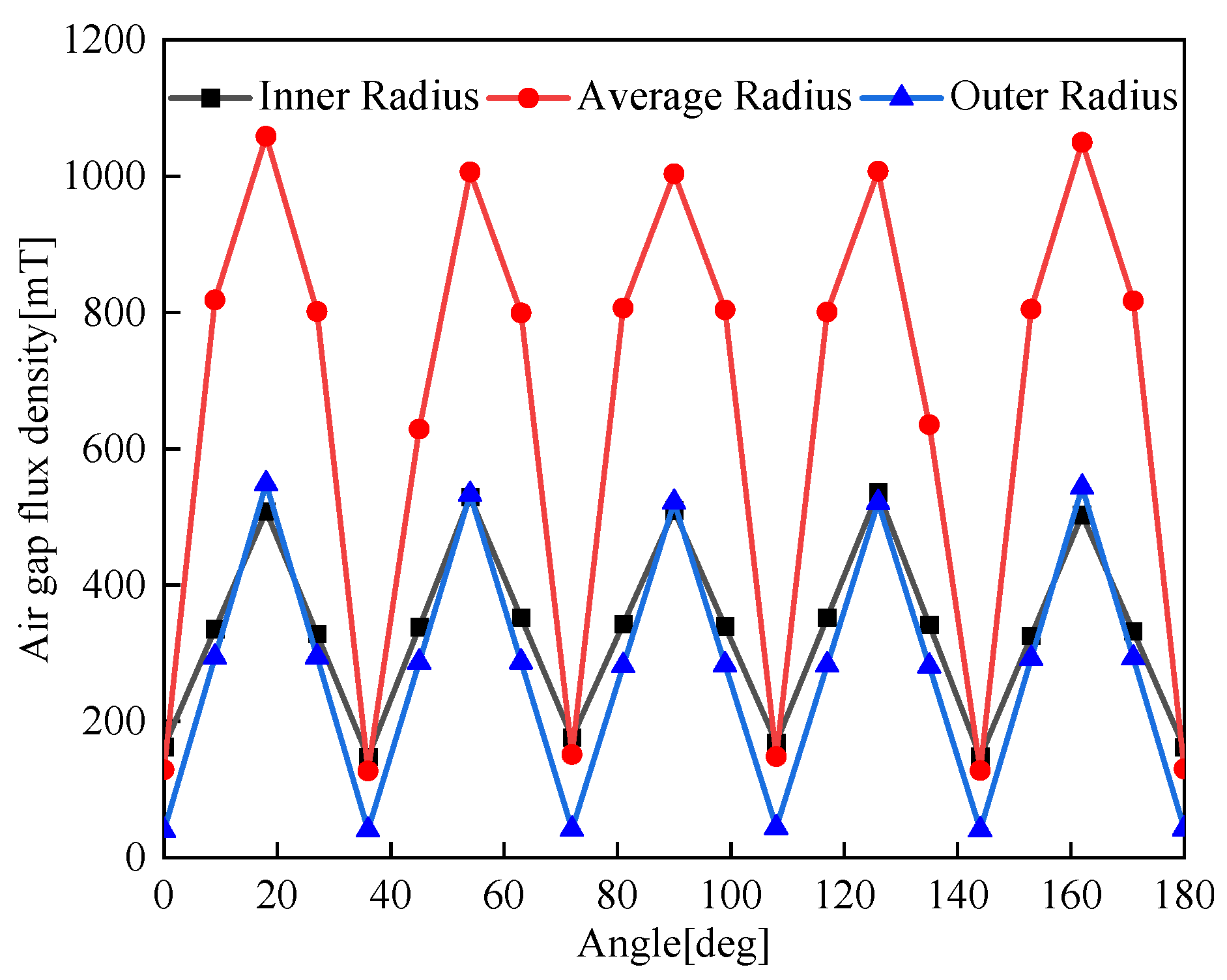
4.1. Air-Gap Magnetic Density
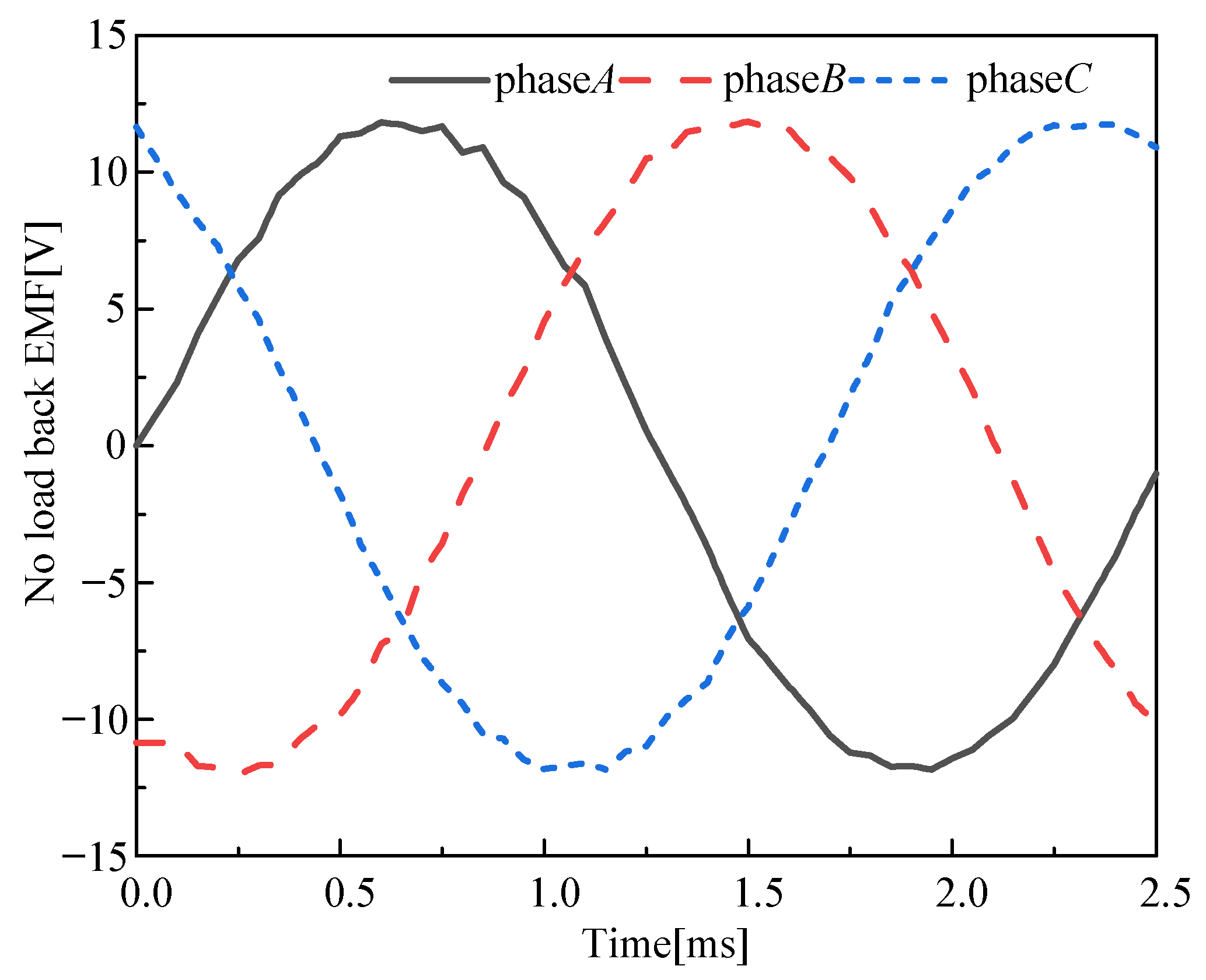
4.2. No-Load Back EMF
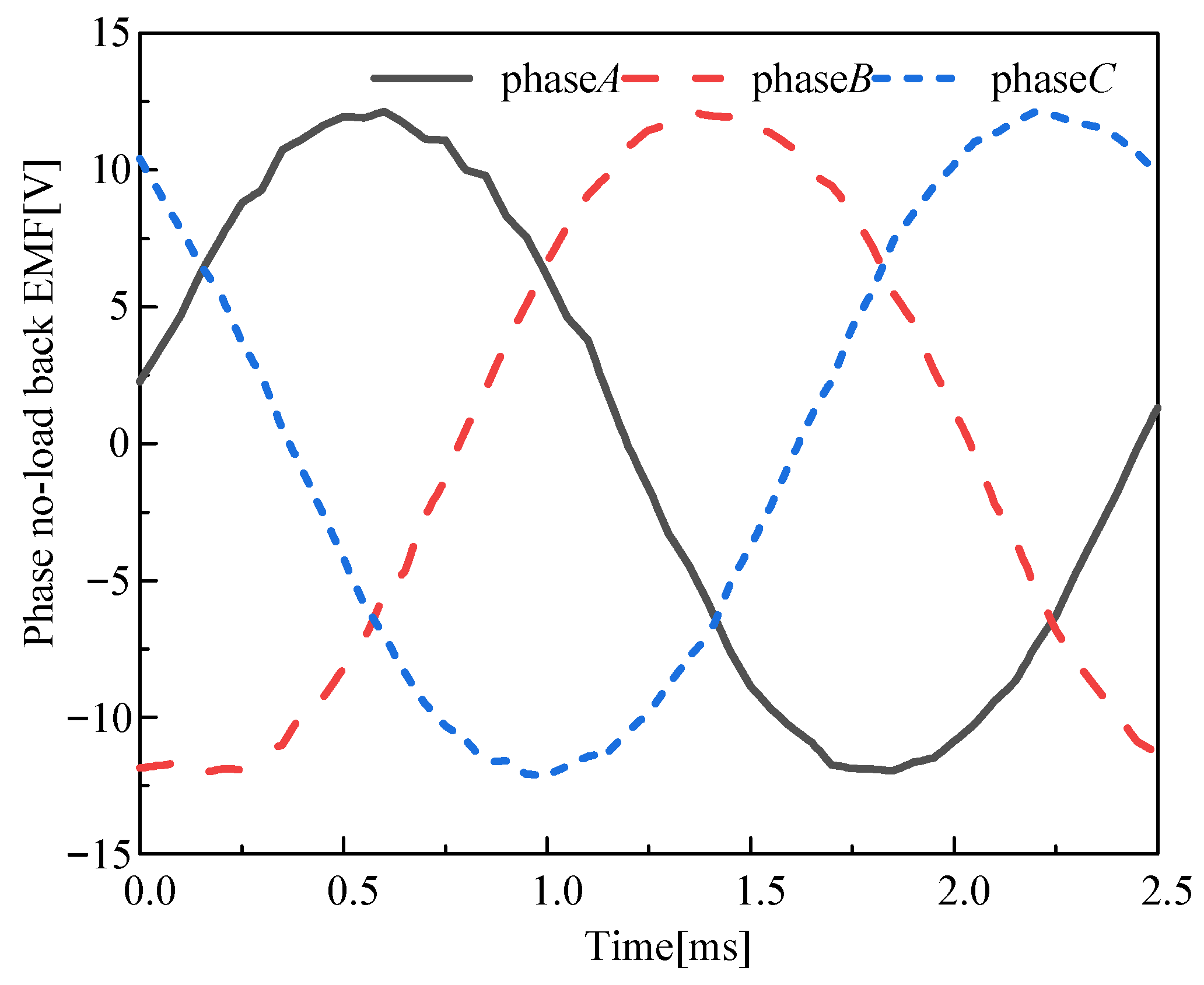
4.3. Load Back EMF
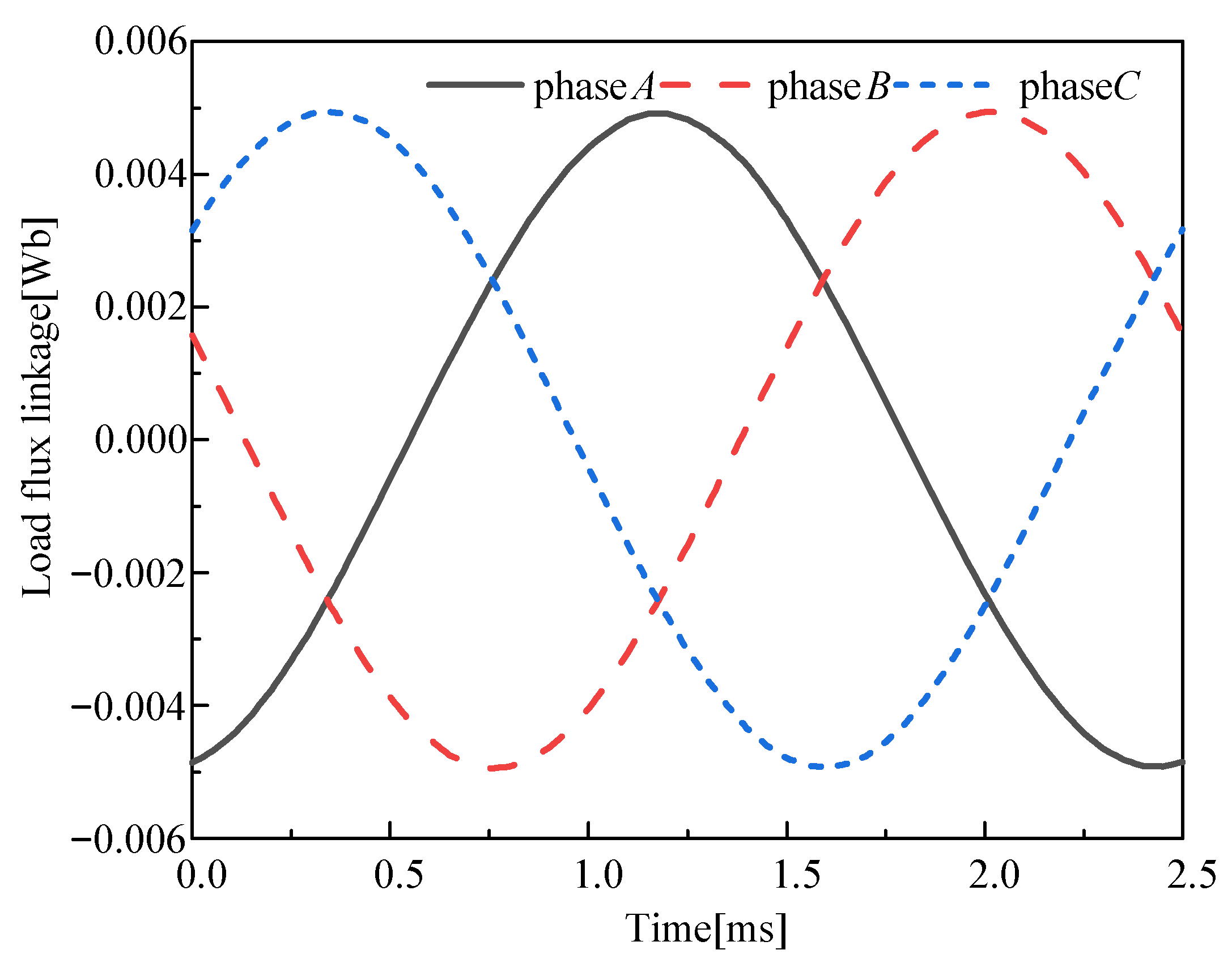
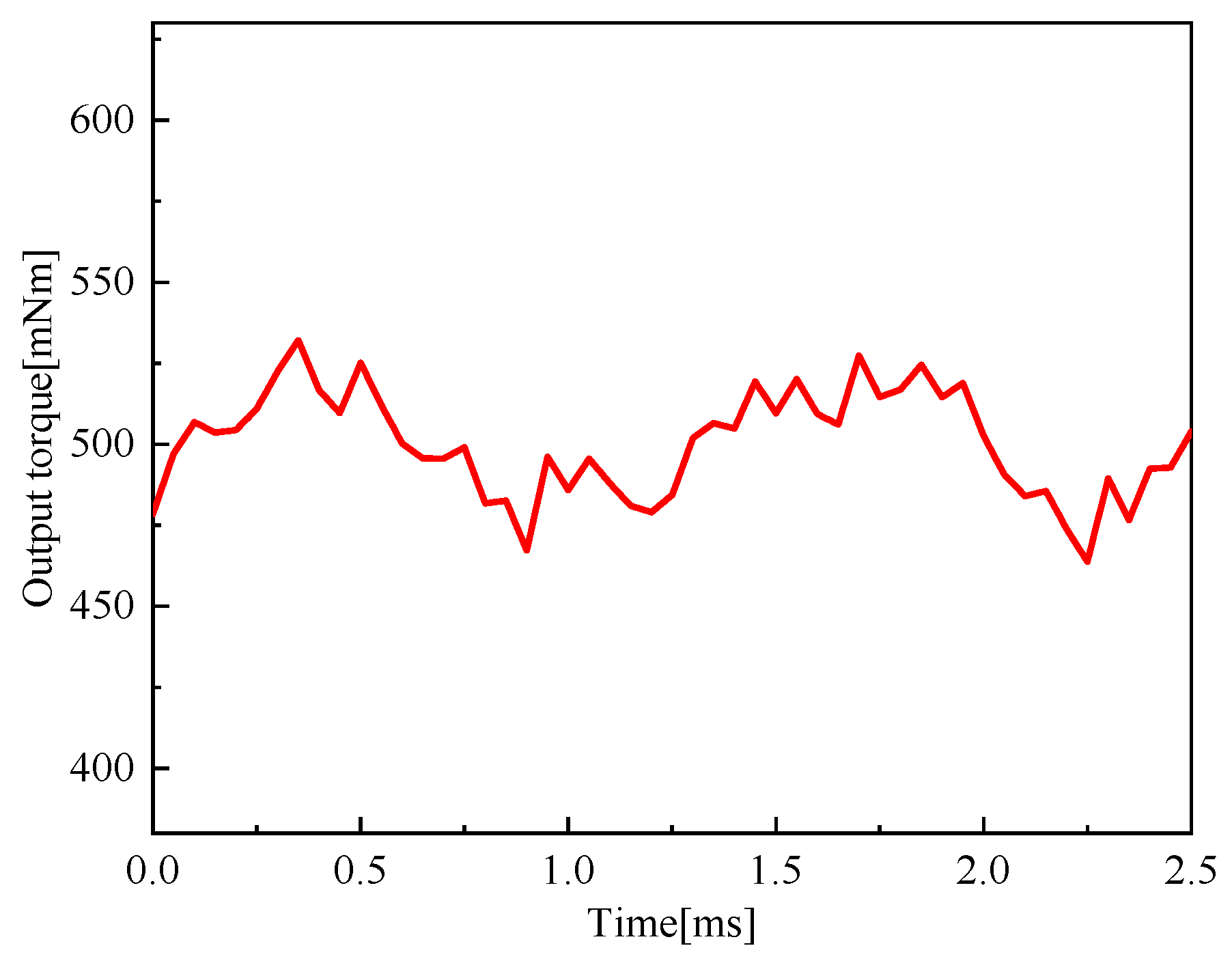
4.4. Flux Linkage and Torque
5. Optimization of Cogging Torque
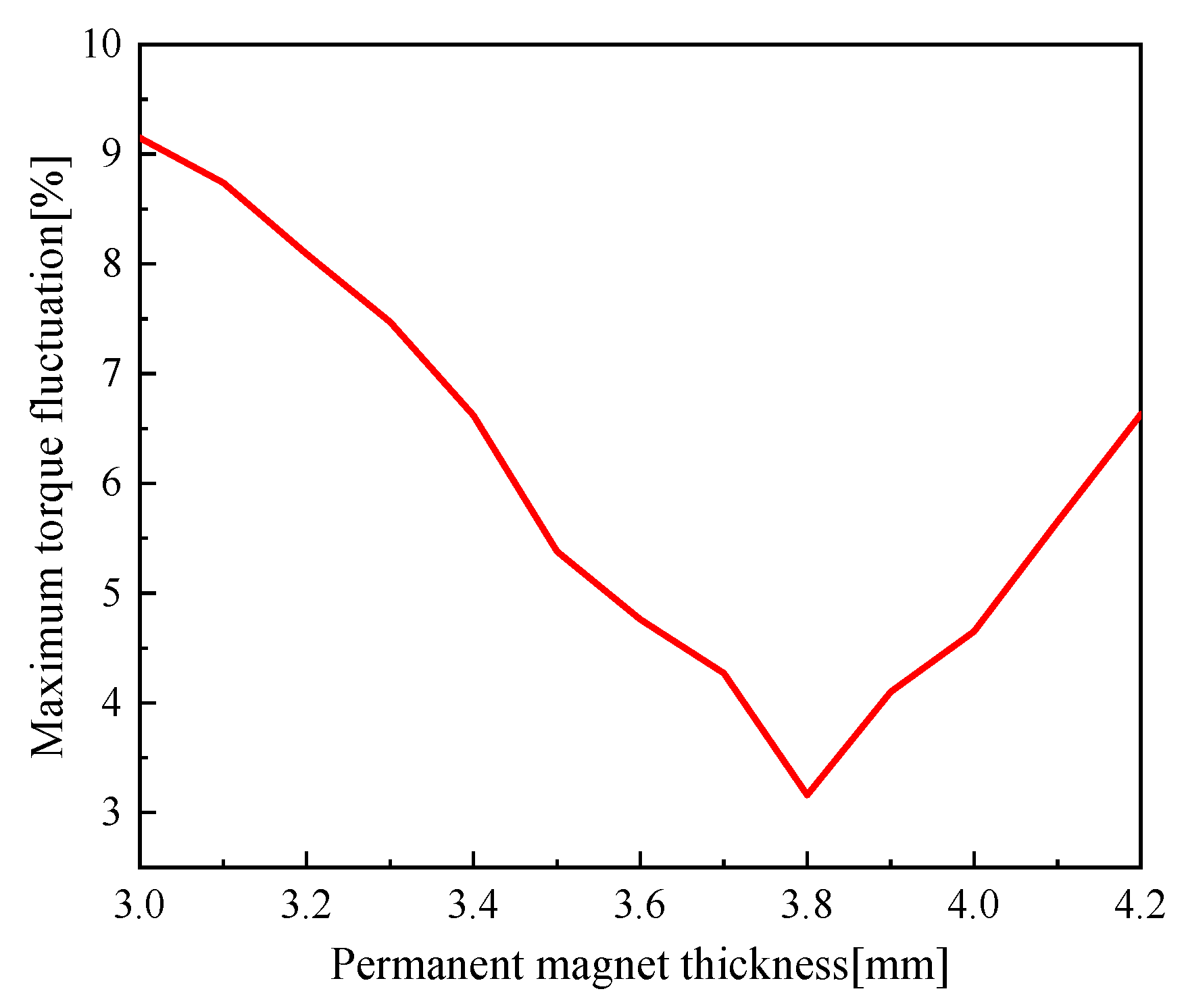
5.1. Influence of Permanent Magnet Thickness on Cogging Torque
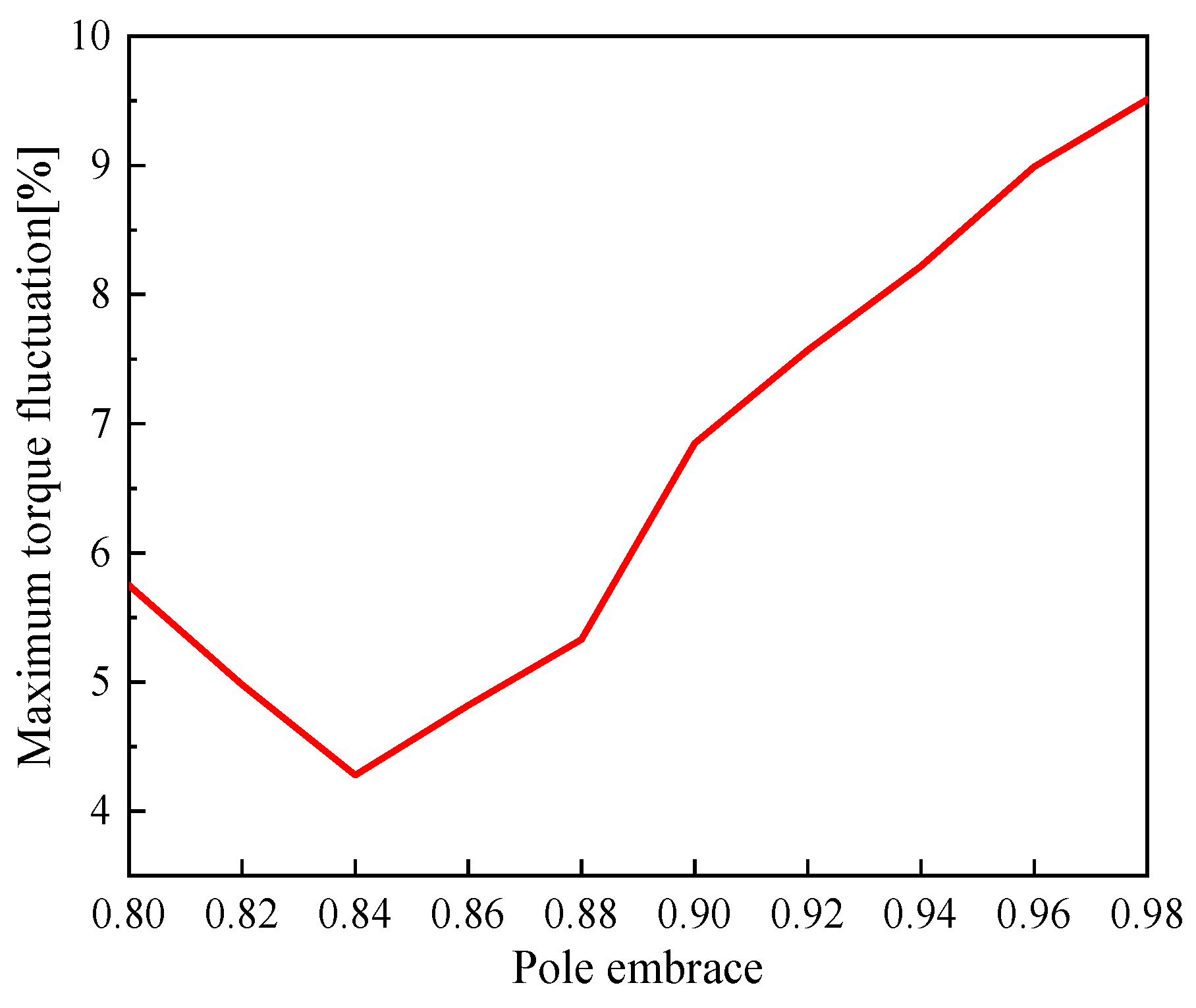
5.2. Influence of Polar Arc Coefficient on Cogging Torque
5.3. Influence of Arc Radius of Permanent Magnet on Cogging Torque
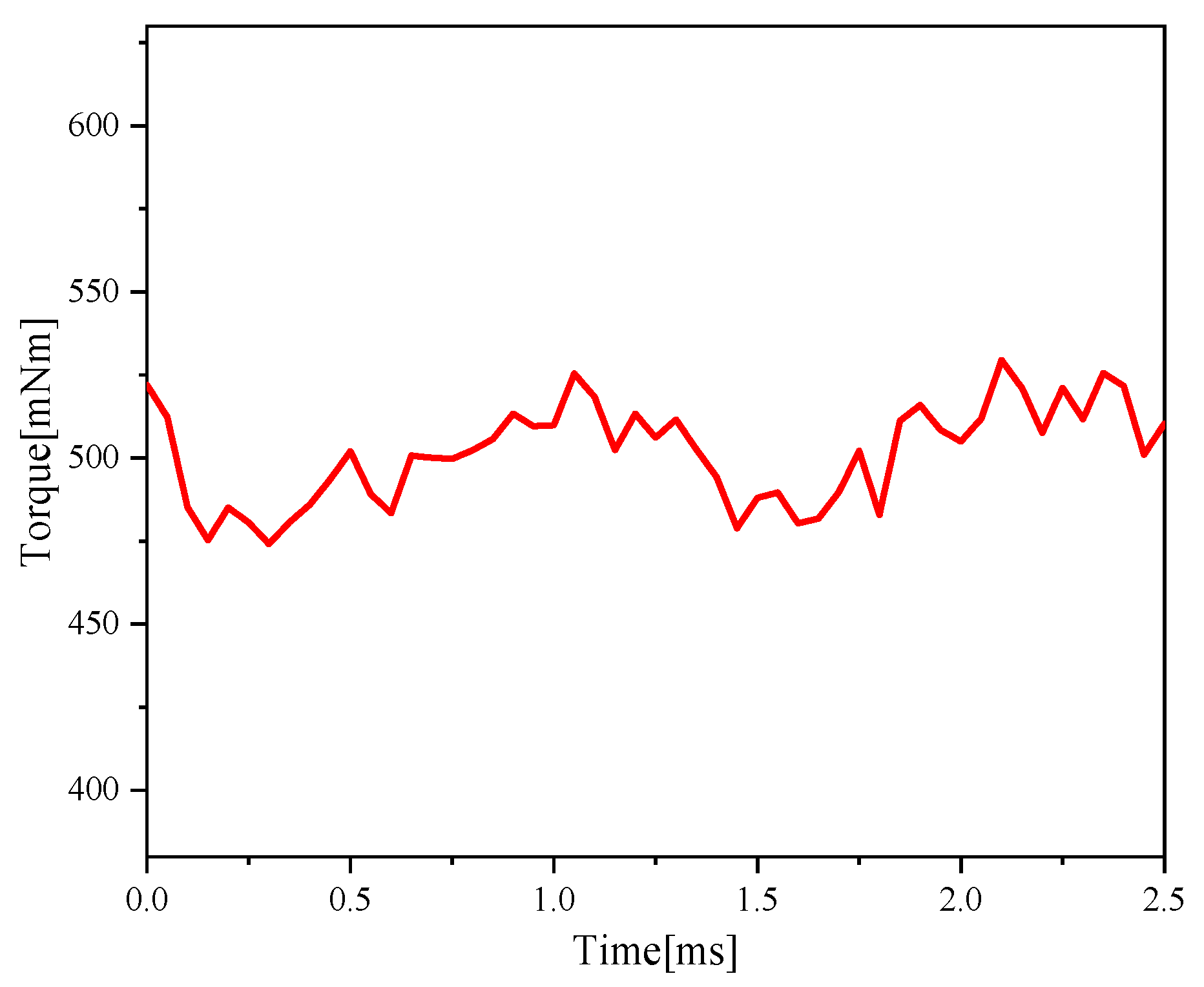
5.4. Optimization Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Capponi, F.G.; Donato, D.G.; Caricchi, F. Recent advances in axial-flux permanent-magnet machine technology. IEEE Trans. Ind. Appl. 2012, 48, 2190–2205. [Google Scholar] [CrossRef]
- Zhu, G.; Li, L.; Liu, X.; Chen, H.; Jiang, W.; Xue, M.; Li, M. Design optimization of a HTS-modulated PM wind generator. IEEE Trans. Appl. Supercond. 2021, 31, 5204004. [Google Scholar] [CrossRef]
- Kappatou, J.; Zalokostas, G.; Spyratos, D. 3-D FEM analysis, prototyping and tests of an axial flux permanent-magnet wind generator. Energies 2017, 10, 1269. [Google Scholar] [CrossRef] [Green Version]
- Balachandran, T.; Yoon, A.; Lee, D.; Xiao, J.; Haran, K.S. Ultra-High-Field, High-efficiency superconducting machines for offshore wind Turbines. IEEE Trans. Magn. 2021, 58, 8700805. [Google Scholar]
- Rata, M.; Rata, G.; Filote, C.; Raboaca, M.S.; Graur, A.; Afanasov, C.; Felseghi, A.-R. The electrical vehicle simulator for charging station in mode 3 of IEC 61851-1 Standard. Energies 2020, 13, 176. [Google Scholar] [CrossRef] [Green Version]
- Kelouaz, M.; Ouazir, Y.; Hadjout, L.; Mezani, S.; Lubin, T.; Berger, K.; Lévêque, J. 3D magnetic field modeling of a new superconducting synchronous machine using reluctance network method. Phys. C Supercond. 2018, 548, 5–13. [Google Scholar] [CrossRef] [Green Version]
- Meyyappan, C.; Ravichandran, C.S. Generation of free energy using a compact flywheel. In Proceedings of the International Conference on Electronics and Renewable Systems (ICEARS 2022), Tuticorin, India, 16–18 March 2022; pp. 174–180. [Google Scholar]
- Gao, P.; Gu, Y.; Wang, X. The design of a permanent magnet in-wheel motor with dual-stator and dual-field-excitation used in electric vehicles. Energies 2018, 11, 424. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi Darmani, M.; Hooshyar, H. Optimal design of axial flux permanent magnet synchronous motor for electric vehicle applications using GA and FEM. J. Electr. Comput. Eng. Innov. 2015, 3, 89–97. [Google Scholar]
- Bandarkar, A.W.; Yilmaz, S.; De Abreu-Garcia, J.A. CFD based design of an impeller for a novel integrated motor-compressor system. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 3820–3824. [Google Scholar]
- Mohamed, A.H.; Vansompel, H.; Sergeant, P. An integrated modular motor drive with shared cooling for axial flux motor drives. IEEE Trans. Ind. Electron. 2021, 68, 10467–10476. [Google Scholar] [CrossRef]
- Lee, C.; Liu, C.; Chau, K. A magnetless axial-flux machine for range-extended electric vehicles. Energies 2014, 7, 1483–1499. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Han, Q.; Dai, Y.; Hua, M. Study on the Electromagnetic design and analysis of axial flux permanent magnet synchronous motors for electric vehicles. Energies 2019, 12, 3451. [Google Scholar] [CrossRef] [Green Version]
- Marcolini, F.; de Donato, G.; Capponi, F.G.; Caricchi, F. Direct Oil Cooling of end-windings in torus-type axial-flux permanent-magnet machines. IEEE Trans. Ind. Appl. 2021, 57, 2378–2386. [Google Scholar] [CrossRef]
- Gonzalez-Lopez, D.A.; Tapia, J.A.; Wallace, R.; Valenzuela, A. Design and test of an axial flux permanent-magnet machine with field control capability. IEEE Trans. Magn. 2008, 44, 2168–2173. [Google Scholar] [CrossRef]
- Liu, X.P.; Chen, D.; Wang, M.; Huang, Y.F.; Xie, Q.H. Analysis of mechanical dynamics and flux weakening ability for a variable flux axial field permanent magnet electrical machine. Trans. Chin. Eletrotechnol. Soc. 2016, 31, 54–62. [Google Scholar]
- Luo, X.; Niu, S. Maximum power point tracking sensorless control of an axial-flux permanent magnet verneer wind power generator. Energies 2016, 9, 581. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.; Sun, X.; Liu, Y.; Zhou, W. Fault-tolerant model predictive current control of five-phase permanent magnet synchronous hub motor considering current constraints. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 18 November–16 December 2020; pp. 1–5. [Google Scholar]
- Yazdani-Asrami, M.; Song, W.; Zhang, M.; Yuan, W.; Pei, X. Magnetization loss in HTS coated conductor exposed to harmonic external magnetic fields for superconducting rotating machine applications. IEEE Access 2021, 9, 77930–77937. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, X.; Cai, Y.; Yang, Z.; Lei, G.; Guo, Y.; Zhu, J. Torque analysis and dynamic performance improvement of a PMSM for EVs by skew angle optimization. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Ji, J.H.; Sun, Y.K.; Zhu, J.H.; Zhao, W.X. Design, analysis and experimental validation of a modular permanent-magnet machine. Trans. Chin. Eletrotechnol. Soc. 2015, 30, 243–252. [Google Scholar]
- Deng, W.; Zuo, S. Analytical modeling of the electromagnetic vibration and noise for an external-rotor axial-flux in-wheel motor. IEEE Trans. Ind. Electron. 2018, 65, 1991–2000. [Google Scholar] [CrossRef]
- Kumar, P.; Srivastava, R.K. Influence of rotor magnet shapes on performance of axial flux permanent magnet machines. Prog. Electromagn. Res. 2018, 85, 155–165. [Google Scholar] [CrossRef] [Green Version]
- Neethu, S.; Nikam, S.P.; Sikam, S. High-speed coreless axial-flux permanent-magnet motor with printed circuit board winding. IEEE Trans. Ind. Appl. 2019, 55, 1954–1962. [Google Scholar]
- Lu, Y.; Li, J.; Lu, H.X. Six-phase double-stator inner-rotor axial flux PM machines with novel detached winding. IEEE Trans. Ind. Appl. 2017, 53, 1931–1941. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, M.; Zhou, Y.; Xu, W.; Wan, Z. Design and analysis for multi-disc coreless axial-flux permanent-magnet synchronous machine. IEEE Trans. Appl. Supercond. 2021, 31, 5203804. [Google Scholar] [CrossRef]
- Zhao, J.; Quan, X.; Sun, X. Design of a novel axial flux rotor consequent-pole permanent magnet machine. IEEE Trans. Appl. Supercond. 2020, 30, 5205506. [Google Scholar] [CrossRef]
- Bilal, M.; Ikram, J.; Fida, A.; Bukhari, S.S.H.; Haider, N.; Ro, J.S. Performance improvement of dual stator axial flux spoke type permanent magnet vernier machine. IEEE Access 2021, 9, 64179–64188. [Google Scholar] [CrossRef]
- Lei, G.; Bramerdorfer, G.; Ma, B.; Guo, Y.; Zhu, J. Robust design optimization of electrical machines: Multi-objective approach. IEEE Trans. Energy Convers. 2021, 36, 390–401. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Multi-objective design optimization of an IPMSM based on multilevel strategy. IEEE Trans. Ind. Electron. 2021, 68, 139–148. [Google Scholar] [CrossRef]
- Dhulipati, H.; Ghosh, E.; Mukundan, S.; Korta, P.; Tjong, J.; Kar, N.C. Advanced design optimization technique for torque profile improvement in six-phase PMSM using supervised machine learning for direct-drive EV. IEEE Trans. Energy Convers. 2019, 34, 2041–2051. [Google Scholar] [CrossRef]
- Ikram, J.; Khan, N.; Khaliq, S.; Kwon, B.I. Reduction of torque ripple in an axial flux generator using arc shaped trapezoidal magnets in an asymmetric overhang configuration. J. Magn. 2016, 21, 577–585. [Google Scholar] [CrossRef] [Green Version]
- Nakata, T.; Sanada, M.; Morimoto, S.; Inoue, Y. Automatic design of IPMSMs using a genetic algorithm combined with the coarse-mesh FEM for enlarging the high-efficiency operation area. IEEE Trans. Ind. Electron. 2017, 64, 9721–9728. [Google Scholar] [CrossRef]
- Baig, M.A.; Ikram, J.; Iftikhar, A.; Bukhari, S.S.H.; Khan, N.; Ro, J.S. Minimization of cogging torque in axial field flux switching machine using arc shaped triangular magnets. IEEE Access 2020, 8, 227193–227201. [Google Scholar] [CrossRef]
- Yousuf, M.; Khan, F.; Ikram, J.; Badar, R.; Bukhari, S.S.H.; Ro, J.S. Reduction of torque ripples in multi-stack slotless axial flux machine by using right angled trapezoidal permanent magnet. IEEE Access 2021, 9, 22760–22773. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Rated power/P | 240 W |
| Rated speed/n | 4800 rpm |
| Outer diameter/Do | 65 mm |
| Inner diameter/Di | 25 mm |
| Number of slots/q | 12 |
| Number of poles/p | 10 |
| Number of turns of winding/N | 14 turns |
| Length of air gap/δ | 0.8 mm |
| Polar arc coefficient/αi | 0.8 (initial value) |
| Arc radius of permanent magnet/rh | 19 (initial value) |
| Permanent magnet thickness/hm | 3.4 (initial value) |
| Parameter | Value |
|---|---|
| Average value/Tav | 500.191 mNm |
| Instantaneous maximum/Tmax | 532.112 mNm |
| Instantaneous minimum/Tmin | 454.818 mNm |
| Maximum torque volatility | 9.07% |
| Parameter | Initial Value | Minimum Value | Maximum Value | Step Size |
|---|---|---|---|---|
| Polar arc coefficient/αi | 0.8 | 0.8 | 0.98 | 0.02 |
| Permanent magnet thinkness rh/mm | 3.4 | 3 | 4.2 | 0.1 |
| Arc radius of permanent magnet hm/mm | 19 | 18 | 24 | 1 |
| Parameter | Value |
|---|---|
| Average value/Tav | 499.993 mNm |
| Instantaneous minimum/Tmin | 486.947 mNm |
| Instantaneous maximum/Tmax | 514.596 mNm |
| Maximum torque volatility | 2.92% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Wang, B.; Zhang, T.; Gu, Q. Design Optimization and Electromagnetic Performance Analysis of an Axial-Flux Permanent Magnet Brushless DC Motor with Unequal-Thickness Magnets. Appl. Sci. 2022, 12, 7863. https://doi.org/10.3390/app12157863
Wu S, Wang B, Zhang T, Gu Q. Design Optimization and Electromagnetic Performance Analysis of an Axial-Flux Permanent Magnet Brushless DC Motor with Unequal-Thickness Magnets. Applied Sciences. 2022; 12(15):7863. https://doi.org/10.3390/app12157863
Chicago/Turabian StyleWu, Shasha, Baojian Wang, Tao Zhang, and Quanhao Gu. 2022. "Design Optimization and Electromagnetic Performance Analysis of an Axial-Flux Permanent Magnet Brushless DC Motor with Unequal-Thickness Magnets" Applied Sciences 12, no. 15: 7863. https://doi.org/10.3390/app12157863
APA StyleWu, S., Wang, B., Zhang, T., & Gu, Q. (2022). Design Optimization and Electromagnetic Performance Analysis of an Axial-Flux Permanent Magnet Brushless DC Motor with Unequal-Thickness Magnets. Applied Sciences, 12(15), 7863. https://doi.org/10.3390/app12157863





