A Graph-Based k-Nearest Neighbor (KNN) Approach for Predicting Phases in High-Entropy Alloys
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Notation Definitions
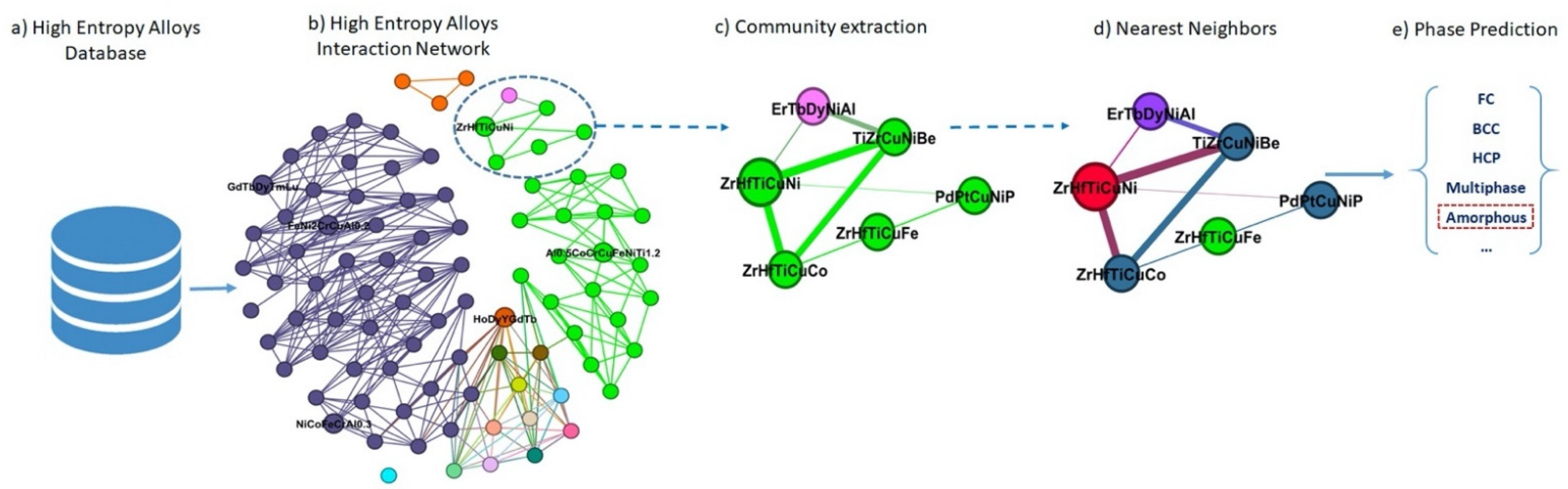
- Social network graph. A social network can be mapped to the graph , where is the node set and is the edge set.
- Neighbors. A node is a neighbor of node in graph if there is an edge .
- HEA interaction network. The HEA compounds are nodes, and the interaction between two compounds are edges that are mapped into a social network [19].
- Target compound. The node considered for phase prediction in the HEA interaction network is called the target compound.
- Voting. The HEA compound is classified by a plurality vote of its neighbors in the KNN algorithm, with the HEA compound being assigned to the phase most common among its k-nearest neighbor.
2.2. Proposed Method
2.3. Evaluation
3. Results and Discussion
4. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ye, Y.; Wang, Q.; Lu, J.; Liu, C.; Yang, Y. High-entropy alloy: Challenges and prospects. Mater. Today 2016, 19, 349–362. [Google Scholar] [CrossRef]
- Risal, S.; Zhu, W.; Guillen, P.; Sun, L. Improving phase prediction accuracy for high entropy alloys with machine learning. Comput. Mater. Sci. 2021, 192, 110389. [Google Scholar] [CrossRef]
- Sheng, G.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. Mater. Int. 2011, 21, 433–446. [Google Scholar]
- Chang, Y.-J.; Jui, C.-Y.; Lee, W.-J.; Yeh, A.-C. Prediction of the composition and hardness of high-entropy alloys by machine learning. JOM 2019, 71, 3433–3442. [Google Scholar] [CrossRef]
- Chanda, B.; Jana, P.P.; Das, J. A tool to predict the evolution of phase and Young’s modulus in high entropy alloys using artificial neural network. Comput. Mater. Sci. 2021, 197, 110619. [Google Scholar] [CrossRef]
- Dixit, S.; Singhal, V.; Agarwal, A.; Rao, A.P. Multi-label phase-prediction in high-entropy-alloys using Artificial-Neural-Network. Mater. Lett. 2020, 268, 127606. [Google Scholar] [CrossRef]
- Machaka, R. Machine learning-based prediction of phases in high-entropy alloys. Comput. Mater. Sci. 2021, 188, 110244. [Google Scholar] [CrossRef]
- Wu, L.; Liu, L.; Wang, Y.; Zhai, Z.; Zhuang, H.; Krishnaraju, D.; Wang, Q.; Jiang, H. A machine learning-based method to design modular metamaterials. Extrem. Mech. Lett. 2020, 36, 100657. [Google Scholar] [CrossRef]
- Agarwal, A.; Prasada Rao, A. Artificial intelligence predicts body-centered-cubic and face-centered-cubic phases in high-entropy alloys. JOM 2019, 71, 3424–3432. [Google Scholar] [CrossRef]
- Krishna, Y.V.; Jaiswal, U.K.; Rahul, M. Machine learning approach to predict new multiphase high entropy alloys. Scr. Mater. 2021, 197, 113804. [Google Scholar] [CrossRef]
- Jalali, M.; Tsotsalas, M.; Wöll, C. MOFSocialNet: Exploiting Metal-Organic Framework Relationships via Social Network Analysis. Nanomaterials 2022, 12, 704. [Google Scholar] [CrossRef] [PubMed]
- Rickman, J.; Balasubramanian, G.; Marvel, C.; Chan, H.; Burton, M.-T. Machine learning strategies for high-entropy alloys. J. Appl. Phys. 2020, 128, 221101. [Google Scholar] [CrossRef]
- Bhandari, U.; Rafi, M.R.; Zhang, C.; Yang, S. Yield strength prediction of high-entropy alloys using machine learning. Mater. Today Commun. 2021, 26, 101871. [Google Scholar] [CrossRef]
- Wen, C.; Wang, C.; Zhang, Y.; Antonov, S.; Xue, D.; Lookman, T.; Su, Y. Modeling solid solution strengthening in high entropy alloys using machine learning. Acta Mater. 2021, 212, 116917. [Google Scholar] [CrossRef]
- Qiao, L.; Liu, Y.; Zhu, J. A focused review on machine learning aided high-throughput methods in high entropy alloy. J. Alloys Compd. 2021, 877, 160295. [Google Scholar] [CrossRef]
- Lee, S.Y.; Byeon, S.; Kim, H.S.; Jin, H.; Lee, S. Deep learning-based phase prediction of high-entropy alloys: Optimization, generation, and explanation. Mater. Des. 2021, 197, 109260. [Google Scholar] [CrossRef]
- Yan, Y.; Lu, D.; Wang, K. Accelerated discovery of single-phase refractory high entropy alloys assisted by machine learning. Comput. Mater. Sci. 2021, 199, 110723. [Google Scholar] [CrossRef]
- Jaiswal, U.K.; Krishna, Y.V.; Rahul, M.; Phanikumar, G. Machine learning-enabled identification of new medium to high entropy alloys with solid solution phases. Comput. Mater. Sci. 2021, 197, 110623. [Google Scholar] [CrossRef]
- Ghouchan Nezhad Noor Nia, R.; Jalali, M.; Mail, M.; Ivanisenko, Y.; Kübel, C. Machine Learning Approach to Community Detection in a High-Entropy Alloy Interaction Network. ACS Omega 2022, 7, 12978–12992. [Google Scholar] [CrossRef]
- Visa, S.; Ramsay, B.; Ralescu, A.L.; Van Der Knaap, E. Confusion matrix-based feature selection. MAICS 2011, 710, 120–127. [Google Scholar]
- Armah, G.K.; Luo, G.; Qin, K. A deep analysis of the precision formula for imbalanced class distribution. Int. J. Mach. Learn. Comput. 2014, 4, 417–422. [Google Scholar] [CrossRef] [Green Version]
- Berrar, D. Cross-Validation. In Reference Module in Life Sciences; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghouchan Nezhad Noor Nia, R.; Jalali, M.; Houshmand, M. A Graph-Based k-Nearest Neighbor (KNN) Approach for Predicting Phases in High-Entropy Alloys. Appl. Sci. 2022, 12, 8021. https://doi.org/10.3390/app12168021
Ghouchan Nezhad Noor Nia R, Jalali M, Houshmand M. A Graph-Based k-Nearest Neighbor (KNN) Approach for Predicting Phases in High-Entropy Alloys. Applied Sciences. 2022; 12(16):8021. https://doi.org/10.3390/app12168021
Chicago/Turabian StyleGhouchan Nezhad Noor Nia, Raheleh, Mehrdad Jalali, and Mahboobeh Houshmand. 2022. "A Graph-Based k-Nearest Neighbor (KNN) Approach for Predicting Phases in High-Entropy Alloys" Applied Sciences 12, no. 16: 8021. https://doi.org/10.3390/app12168021
APA StyleGhouchan Nezhad Noor Nia, R., Jalali, M., & Houshmand, M. (2022). A Graph-Based k-Nearest Neighbor (KNN) Approach for Predicting Phases in High-Entropy Alloys. Applied Sciences, 12(16), 8021. https://doi.org/10.3390/app12168021







