The Effect of Viscous Dampers on the Seismic Performance of Curved Viaducts with the Combined Use of Steel Stoppers
Abstract
:1. Introduction
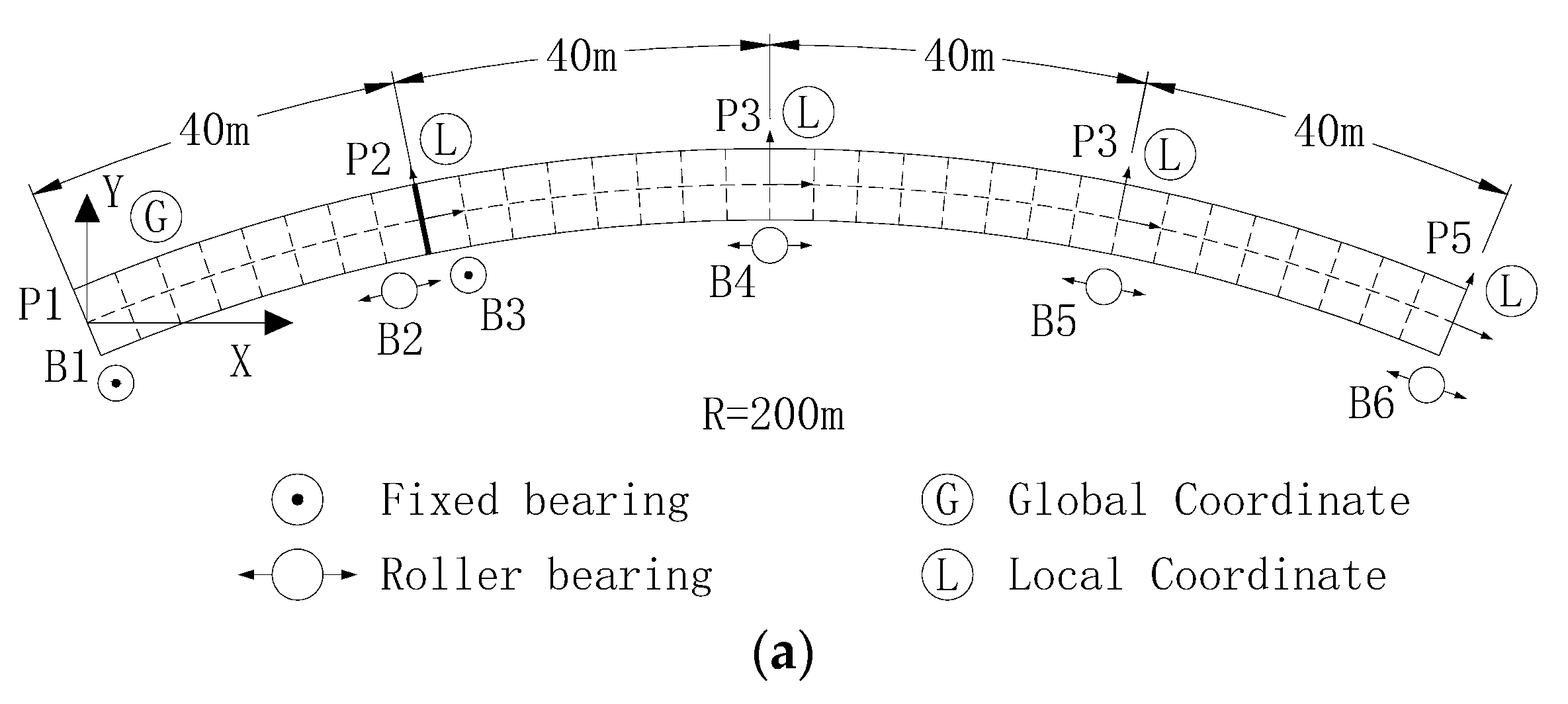
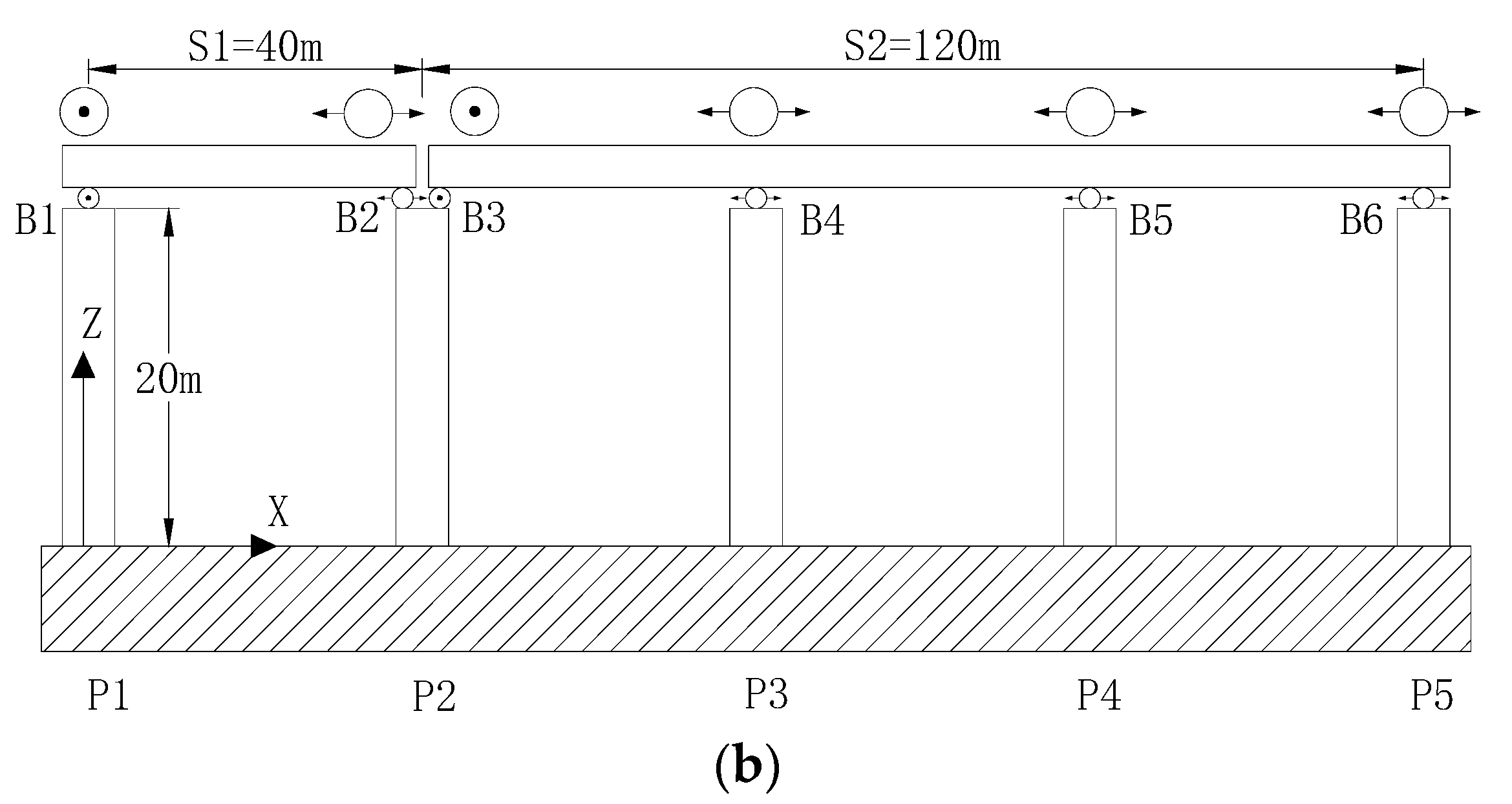
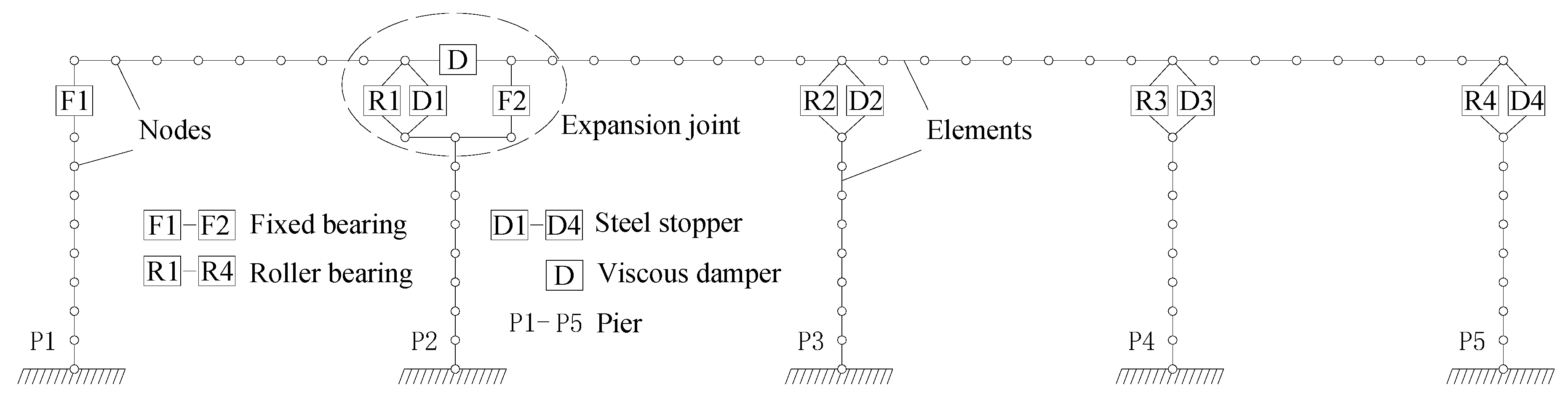
2. Numerical Finite Element Model
2.1. Superstructures and Piers
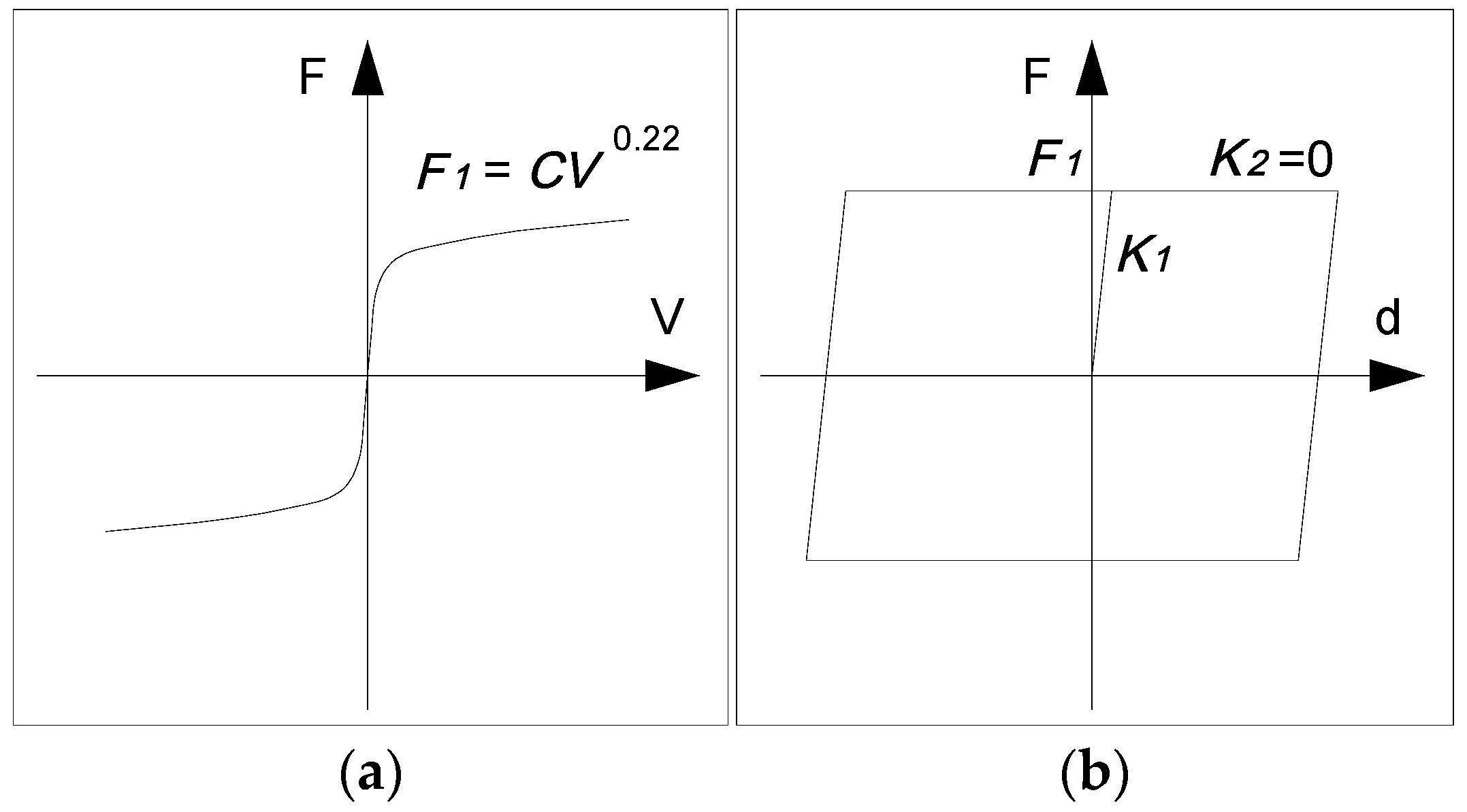
2.2. Viscous Damper
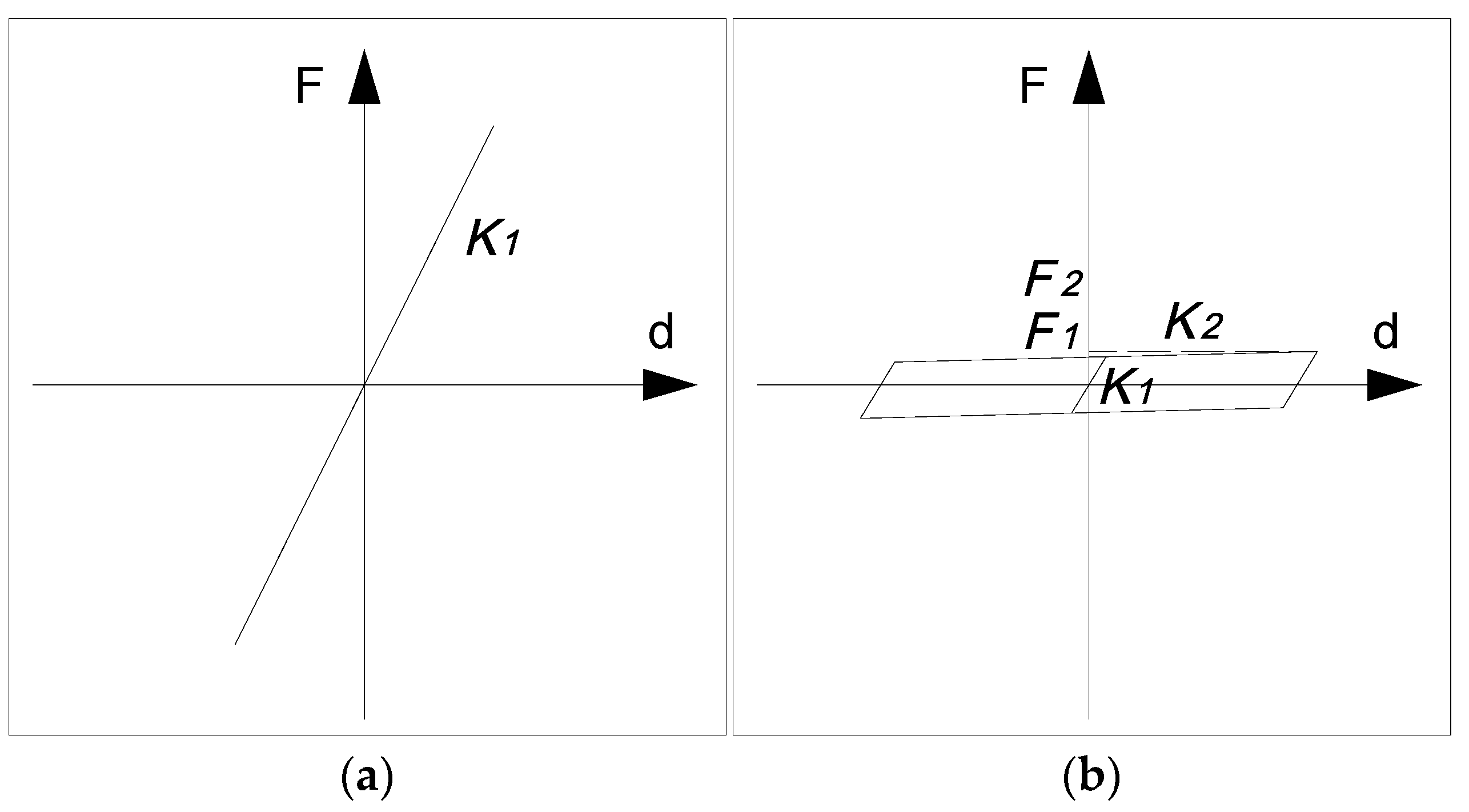
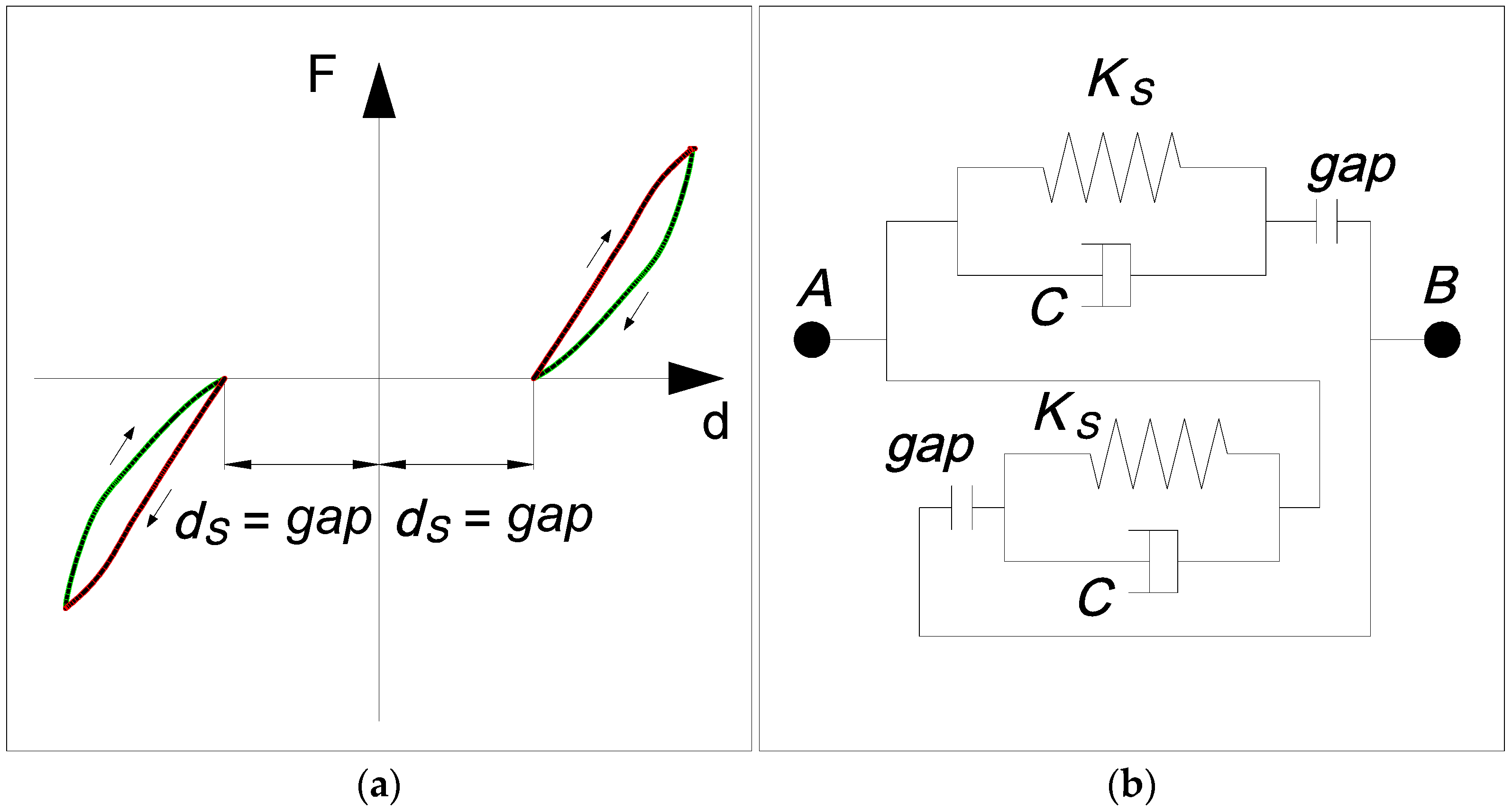
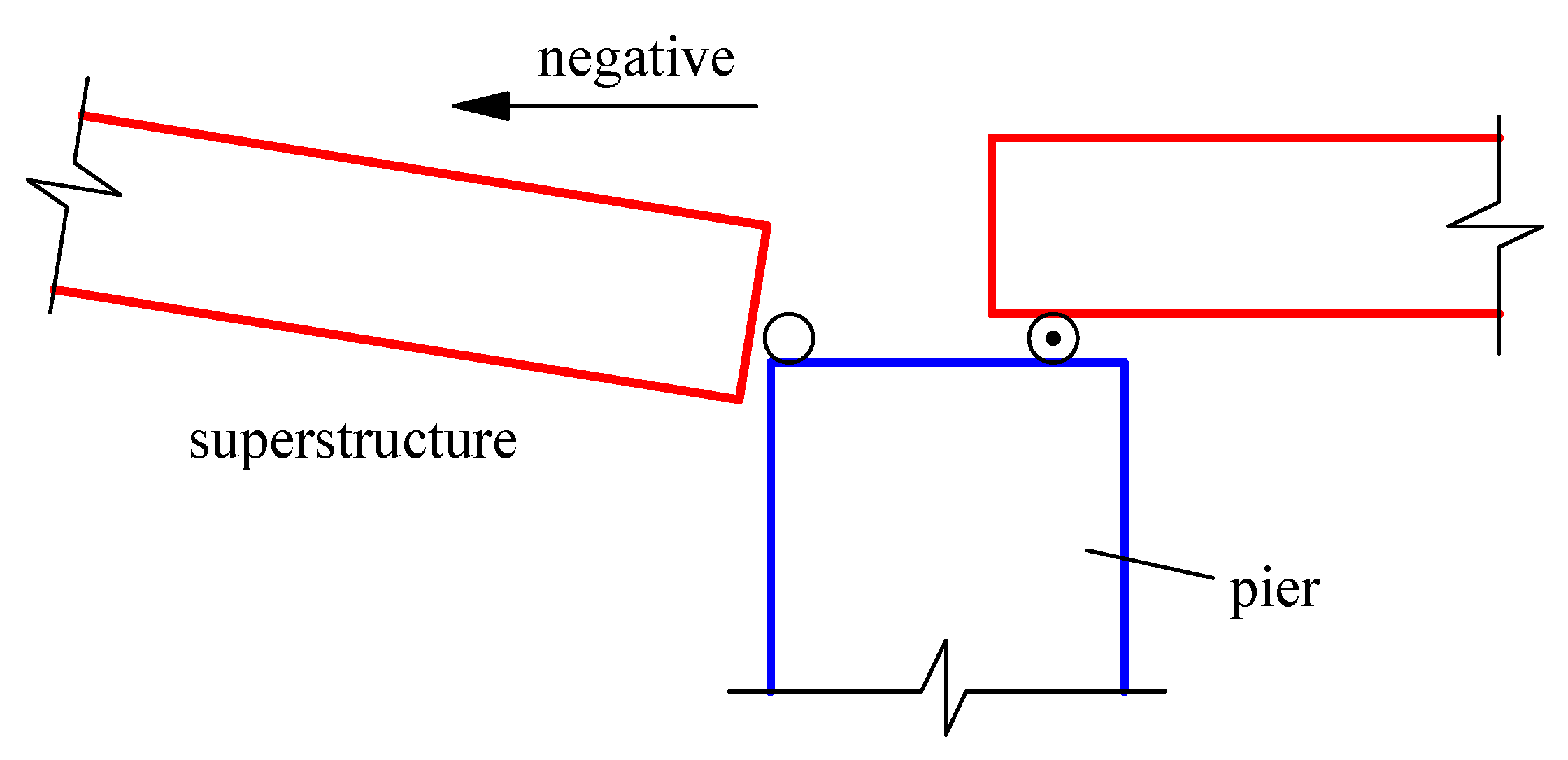
2.3. Bearing Supports and Stoppers
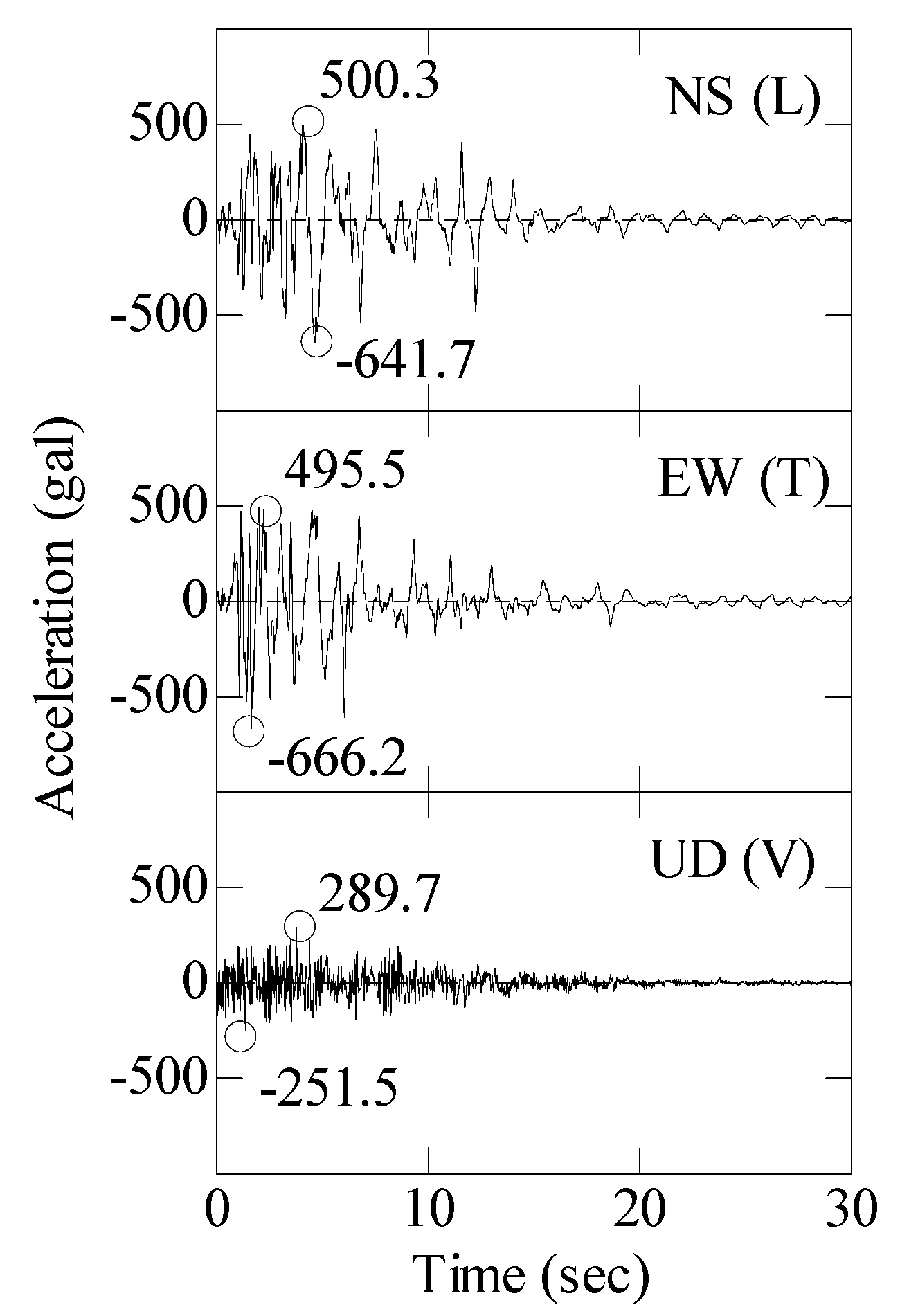
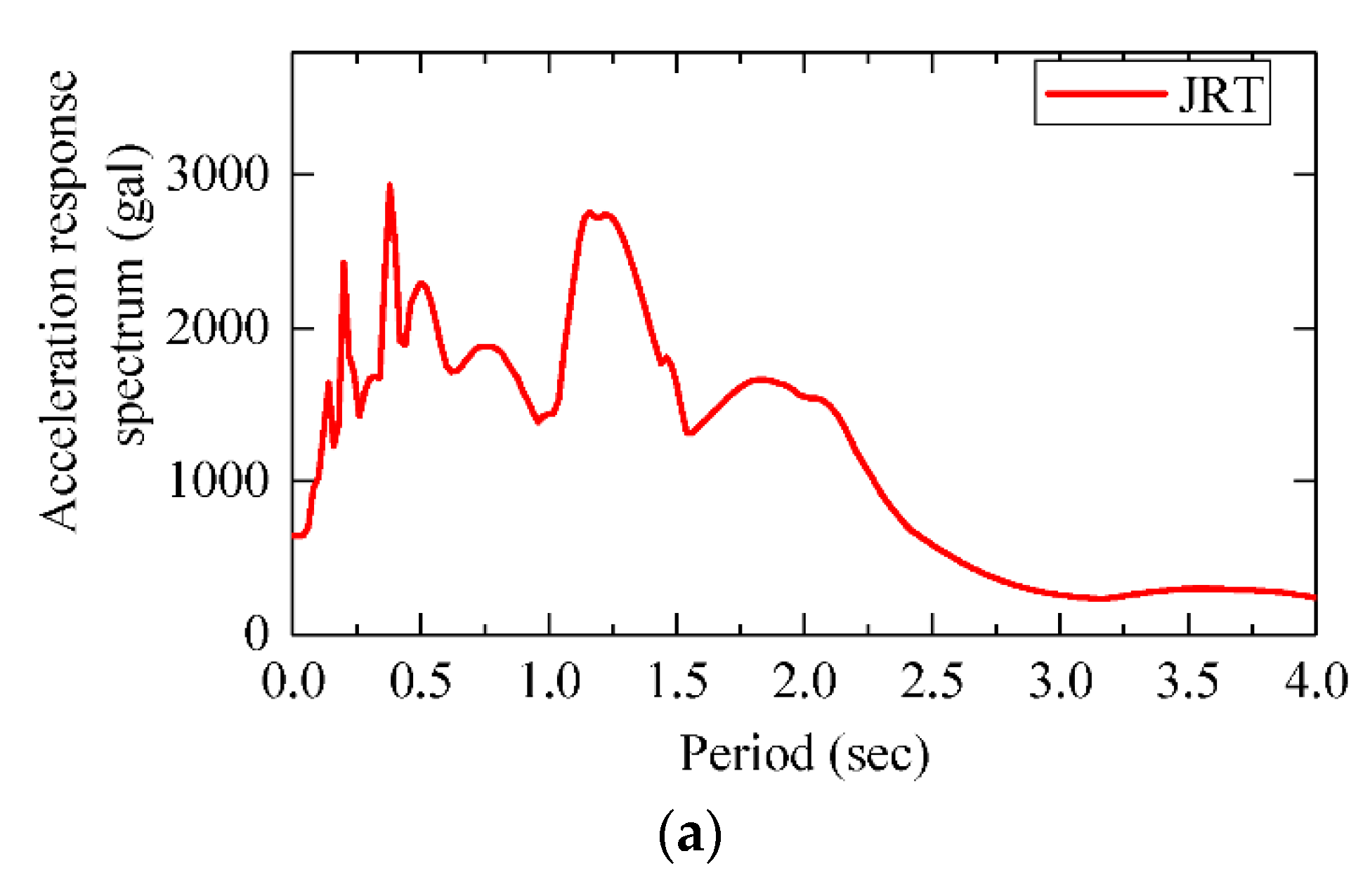
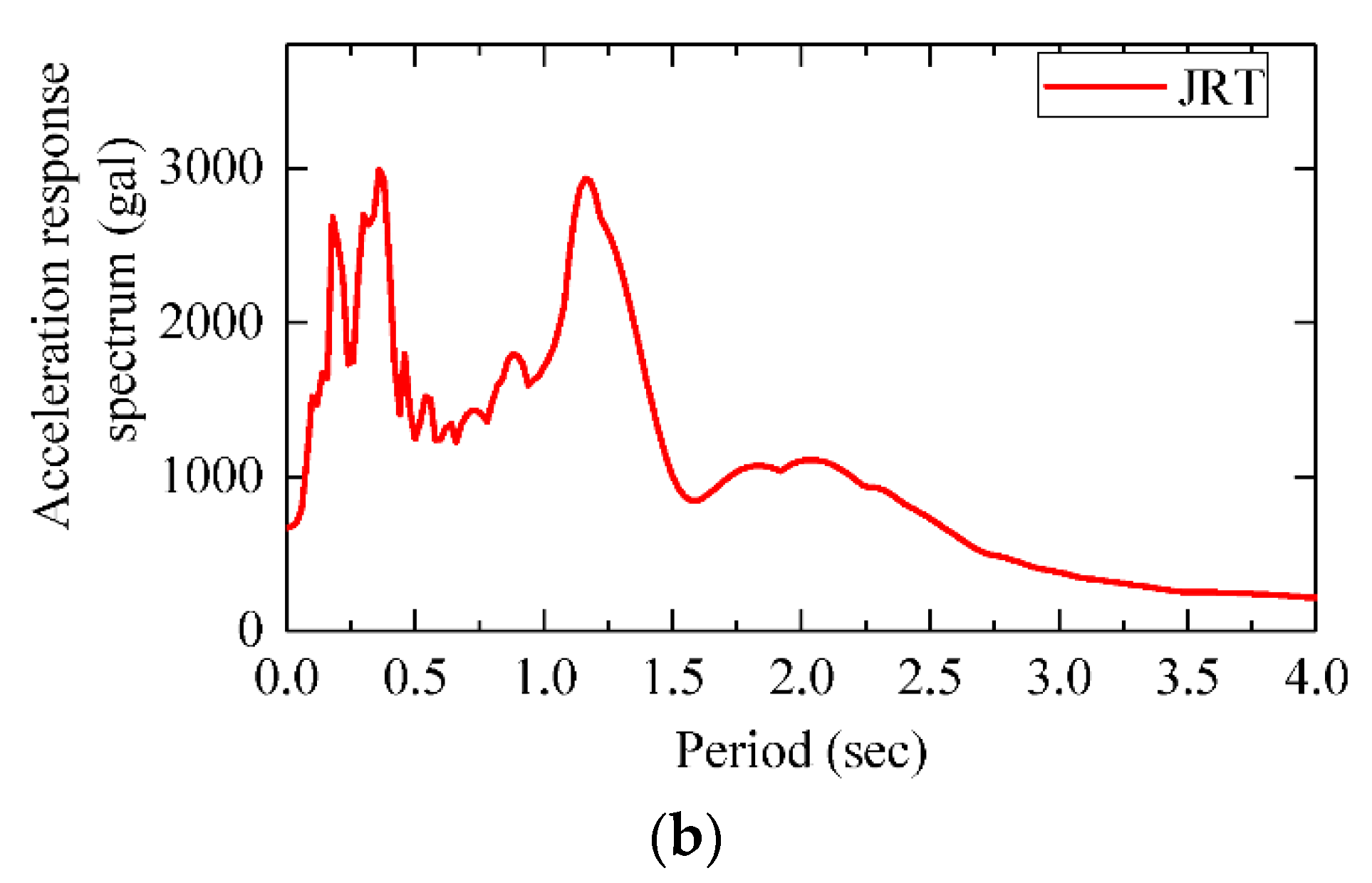
3. Analysis Method
4. Numerical Results
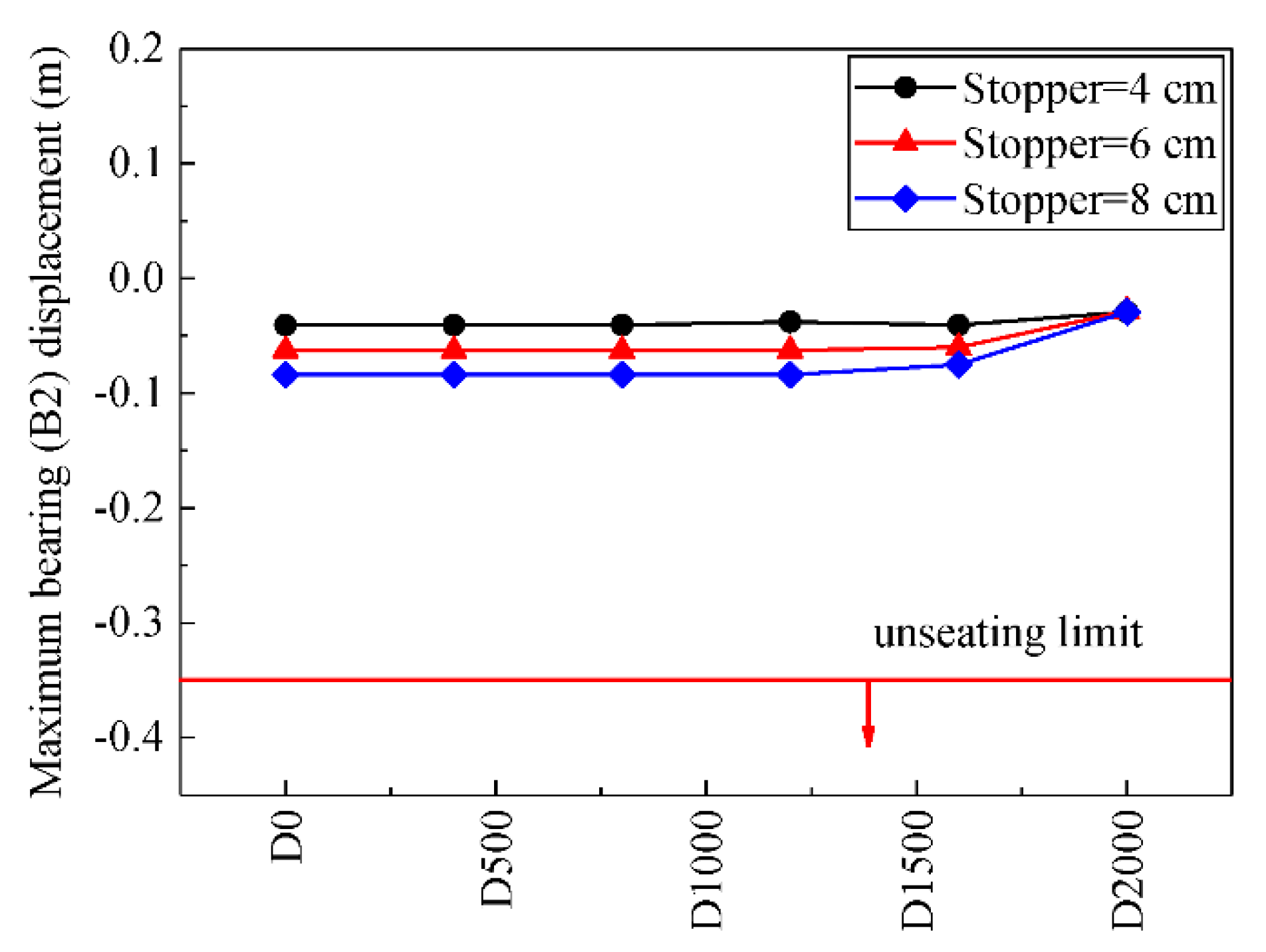
4.1. Deck Unseating Damage
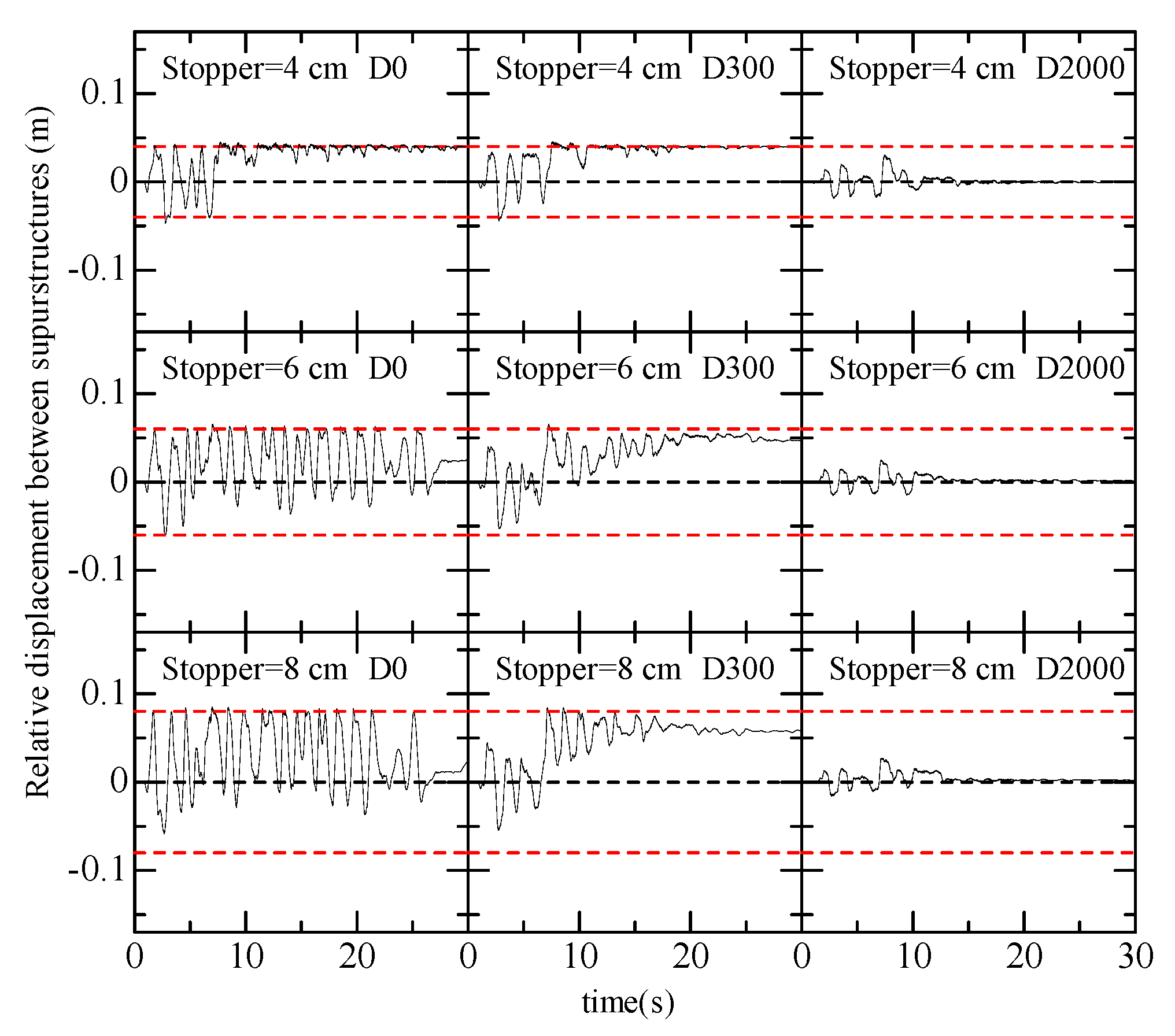
4.2. Relative Displacement between Superstructures
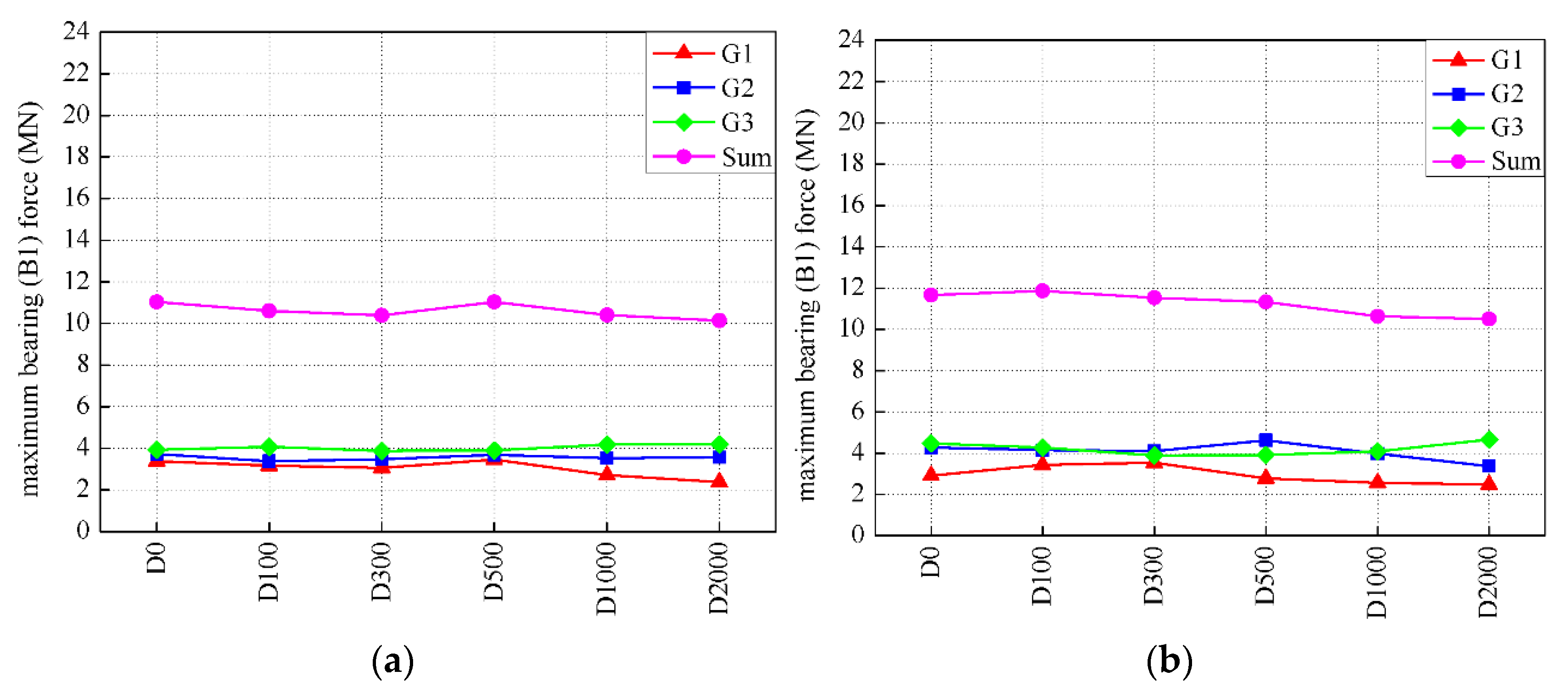
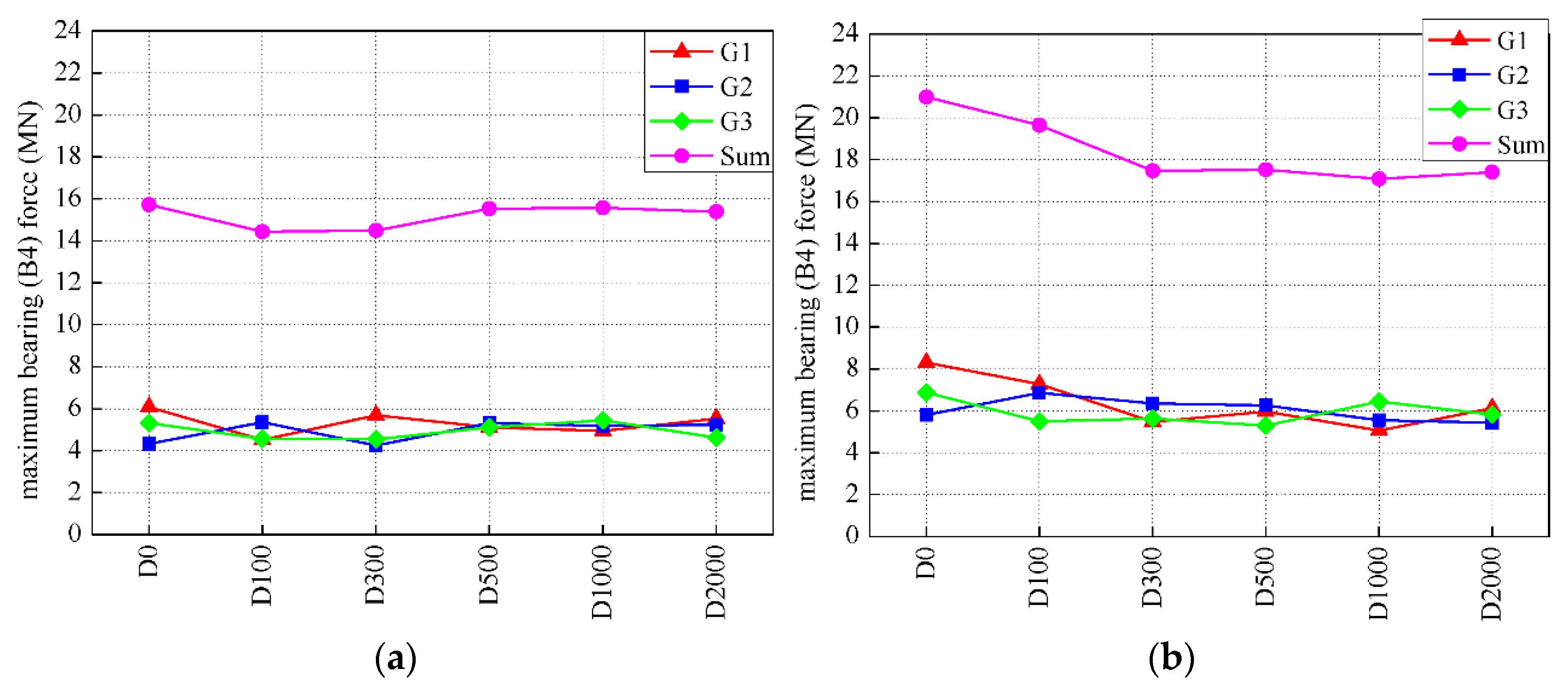
4.3. Bearing Forces and Pounding Forces
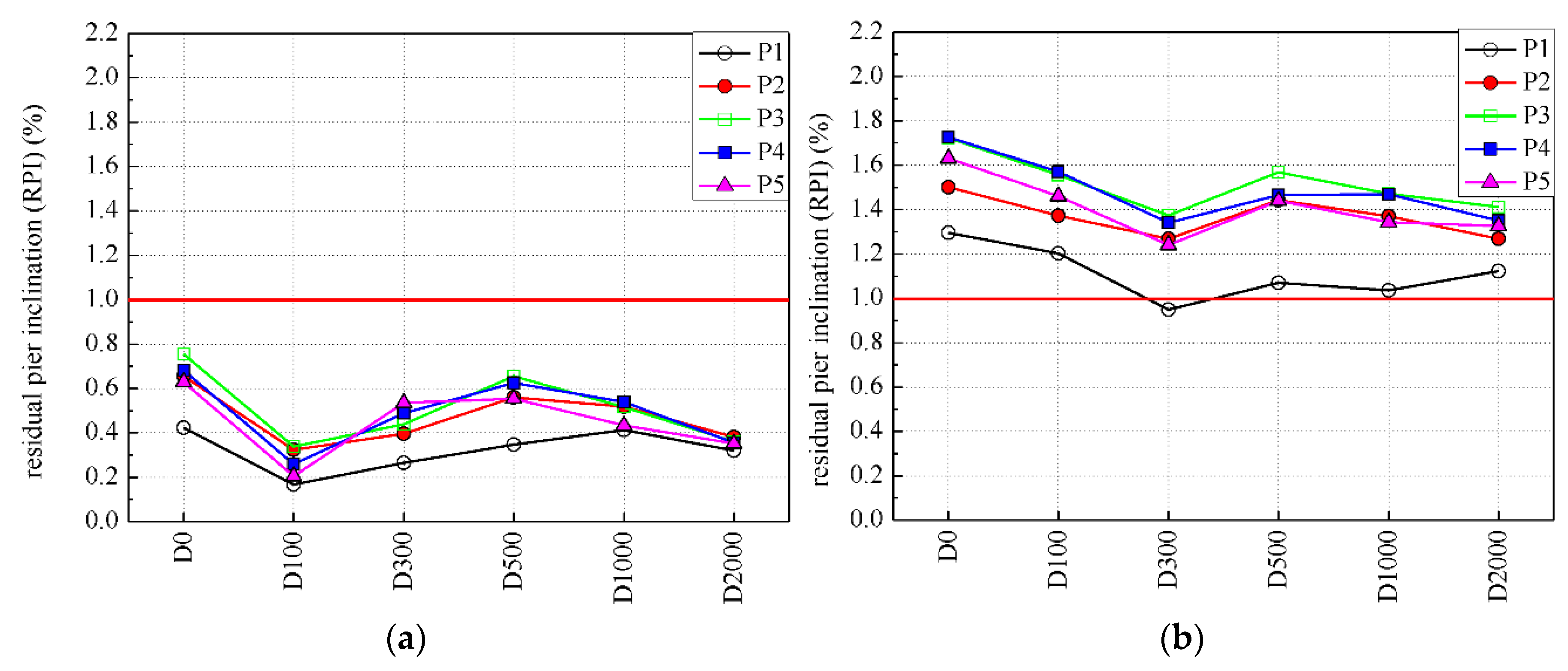
4.4. Pier Damage
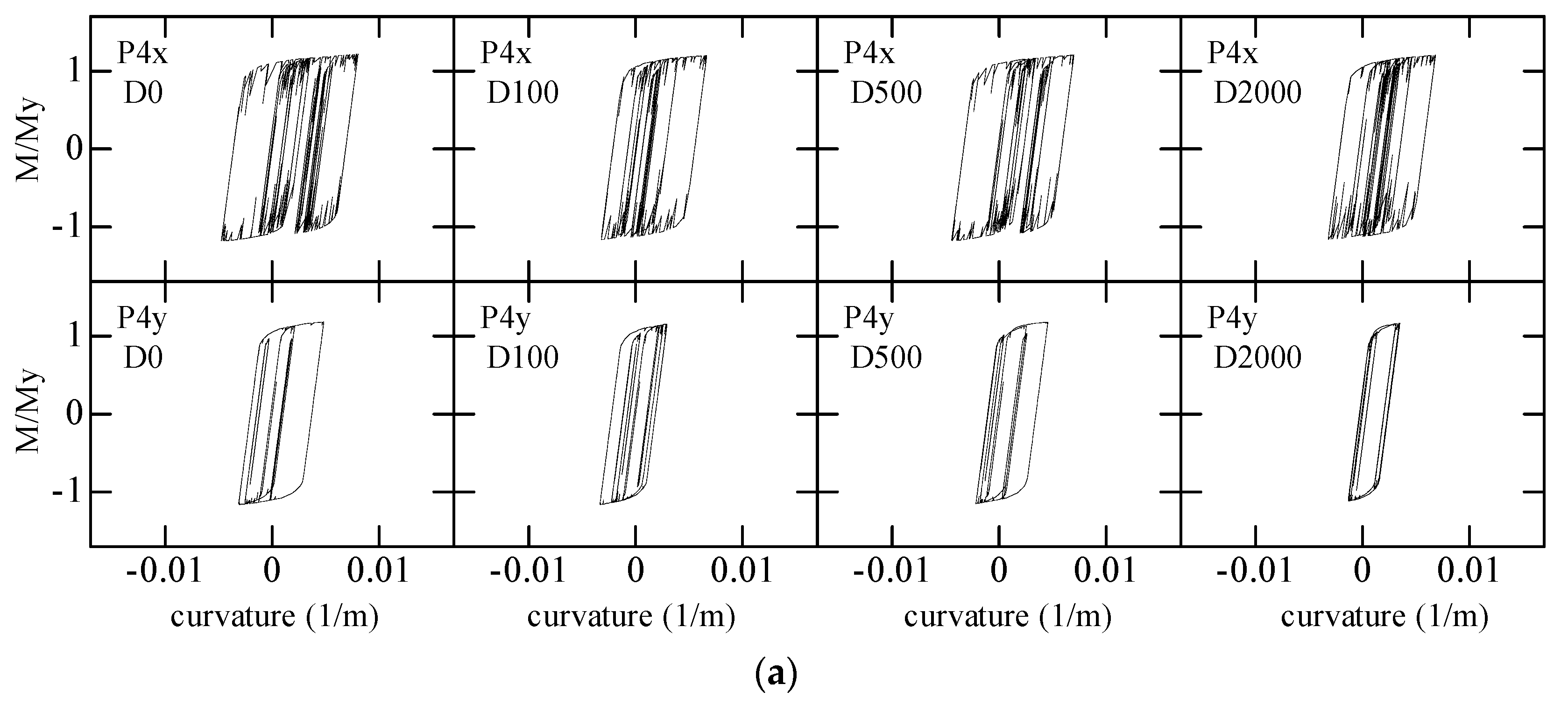
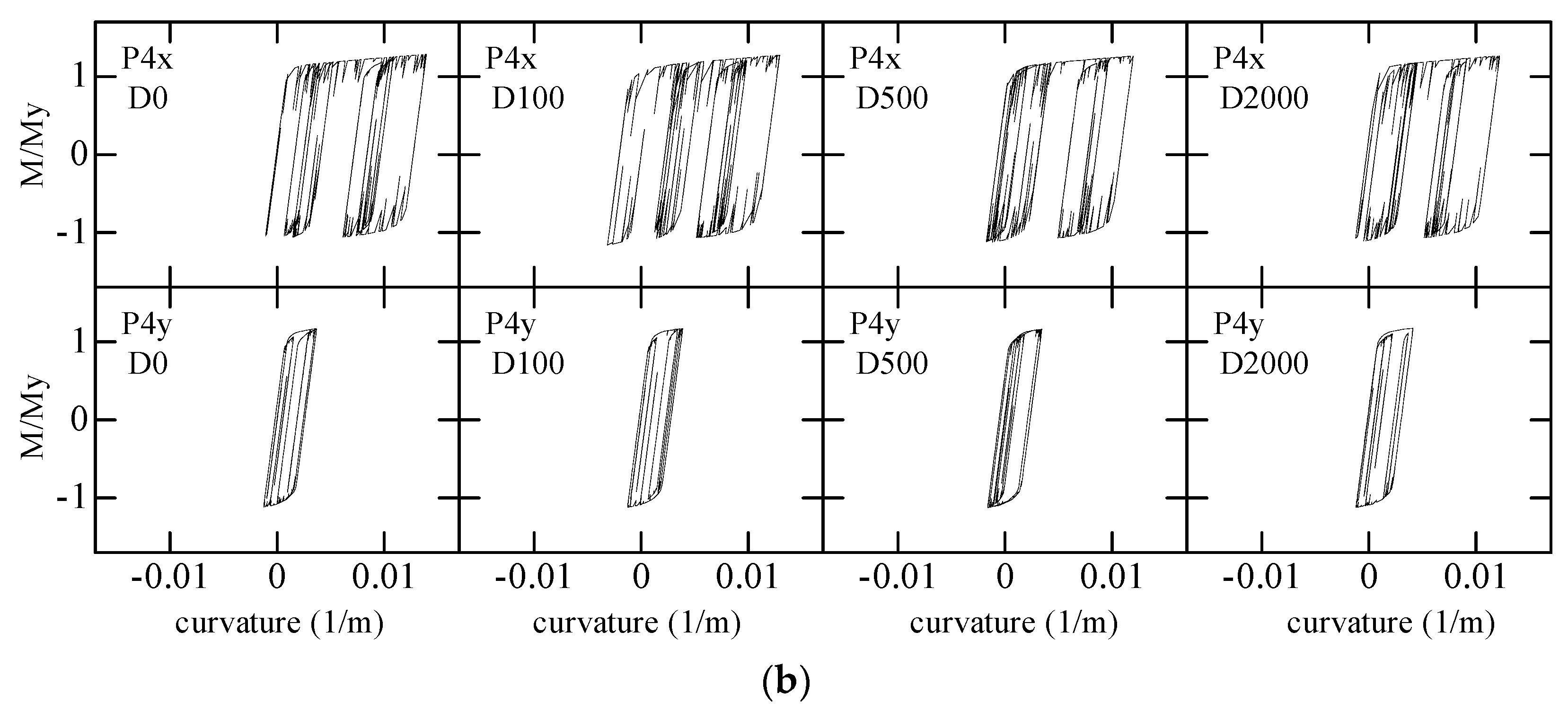
4.5. Relationship of Bending Moment and Curvature
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Japan Road Association. Specifications for Highway Bridges—Part V Seismic Design; Japan Road Association: Tokyo, Japan, 2012. (In Japanese) [Google Scholar]
- Itani, A.M.; Bruneau, M.; Carden, L.; Buckle, I.G. Seismic behavior of steel girder bridge superstructures. J. Bridge Eng. 2004, 9, 243–249. [Google Scholar] [CrossRef]
- Taflanidis, A.A. Optimal probabilistic design of seismic dampers for the protection of isolated bridges against near-fault seismic excitations. Eng. Struct. 2011, 33, 3496–3508. [Google Scholar] [CrossRef]
- Li, B.; Bi, K.M.; Chouw, N.; Butterworth, J.W.; Hao, H. Experimental investigation of spatially varying effect of ground motions on bridge pounding. Earthq. Eng. Struct. Dyn. 2012, 41, 1959–1976. [Google Scholar] [CrossRef]
- Hao, H.; Bi, K.M.; Chouw, N.; Ren, W.X. State-of-the-art review on seismic induced pounding response of bridge structures. J. Earthq. Tsunami 2013, 7, 1350019. [Google Scholar] [CrossRef]
- Zanardo, G.; Hao, H.; Modena, C. Seismic response of multi-span simply supported bridges to a spatially varying earthquake ground motion. Earthq. Eng. Struct. D 2002, 31, 1325–1345. [Google Scholar] [CrossRef]
- Mendez Galindo, C.; Gil Belda, J.; Hayashikawa, T. Non-linear seismic dynamic response of curved steel bridges equipped with LRB supports. Steel Constr. 2010, 3, 34–41. [Google Scholar] [CrossRef]
- Tian, Q.; Hayashikawa, T.; Song, G.Q.; Zhang, C. Study on the effect of cable restrainers stiffness on the seismic performance of curved viaducts combined use of steel stoppers. J. Earthq. Tsunami 2019, 13, 1950006. [Google Scholar] [CrossRef]
- Tian, Q.; Hayashikawa, T.; Ren, W.X. Effectiveness of shock absorber device for damage mitigation of curved viaduct with steel bearing supports. Eng. Struct. 2016, 109, 61–74. [Google Scholar] [CrossRef]
- Tian, Q.; Hayashikawa, T.; Xiong, J.G.; Lei, B. Seismic performance of curved viaducts with shock absorber devices of different stiffness in great earthquakes. J. Earthq. Tsunami 2018, 12, 1850013. [Google Scholar] [CrossRef]
- Maghsoudi-Barmi, A.; Khansefid, A.; Khaloo, A.; Moeini, M.E. Probabilistic seismic performance assessment of optimally designed highway bridge isolated by ordinary unbonded elastomeric bearings. Eng. Struct. 2021, 247, 113058. [Google Scholar] [CrossRef]
- Maghsoudi-Barmi, A.; Khansefid, A.; Khaloo, A.; Ehteshami Moeini, M. Seismic risk assessment of optimally designed highway bridge isolated by ordinary unbounded elastomeric bearings. Numer. Methods Civ. Eng. 2021, 6, 10–21. [Google Scholar] [CrossRef]
- Khaloo, A.; Maghsoudi-Barmi, A.; Moeini, M.E. August. Numerical parametric investigation of hysteretic behavior of steel-reinforced elastomeric bearings under large shear deformation. Structures 2020, 26, 456–470. [Google Scholar] [CrossRef]
- Kawashima, K.; Unjoh, S. Seismic response control of bridges by variable dampers. J. Struct. Eng. ASCE 1994, 120, 2583–2601. [Google Scholar] [CrossRef]
- Wu, Y.X.; Huang, J.; Lin, S.Z.; Qi, A. Design and application status of seismic isolation constitution of building. China Civ. Eng. J. 2018, 51, 62–73, 94. [Google Scholar]
- Khedmatgozar Dolati, S.S.; Mehrabi, A.; Khedmatgozar Dolati, S.S. Application of viscous damper and laminated rubber bearing pads for bridges in seismic regions. Metals 2021, 11, 1666. [Google Scholar] [CrossRef]
- Ruangrassamee, A.; Kawashima, K. Control of nonlinear bridge response with pounding effect by variable dampers. Eng. Struct. 2003, 25, 593–606. [Google Scholar] [CrossRef]
- Hwang, J.-S.; Tseng, Y.-S. Design formulations for supplemental viscous dampers to highway bridges. Earthq. Eng. Struct. D 2005, 34, 1627–1642. [Google Scholar] [CrossRef]
- Domaneschi, M. Feasible control solutions of the ASCE benchmark cable-stayed bridge. Struct. Control. Health Monit. 2010, 17, 675–693. [Google Scholar] [CrossRef]
- Talyan, N.; Elias, S.; Matsagar, V. Earthquake response control of isolated bridges using supplementary passive dampers. Pract. Period. Struct. 2021, 26, 04021002. [Google Scholar] [CrossRef]
- Chen, X.; Xiong, J. Seismic resilient design with base isolation device using friction pendulum bearing and viscous damper. Soil Dyn. Earthq. Eng. 2022, 153, 107073. [Google Scholar] [CrossRef]
- Mendez Galindo, C.; Ruiz Julian, F.D.; Hayashikawa, T. Seismic performance of isolated curved steel viaducts under level II earthquakes. J. Struct. Eng. 2009, 55, 699–708. [Google Scholar]
- Maleki, S. Effect of deck and support stiffness on seismic response of slab-girder bridges. Eng. Struct. 2002, 24, 219–226. [Google Scholar] [CrossRef]
- Abdel Raheem, S.E. Pounding mitigation and unseating prevention at expansion joints of isolated multi-span bridges. Eng. Struct. 2009, 31, 2345–2356. [Google Scholar] [CrossRef]
- Somerville, P.G. Magnitude scaling of the near fault rupture directivity pulse. Phys. Earth Planet. Inter. 2003, 137, 201–212. [Google Scholar] [CrossRef]



| Pier or Girder | A (m2) | Ix (m4) | a Iy (m4) |
|---|---|---|---|
| P1 | 0.4500 | 0.3798 | 0.3798 |
| P2 | 0.4700 | 0.4329 | 0.4329 |
| P3 | 0.4700 | 0.4329 | 0.4329 |
| P4 | 0.4700 | 0.4329 | 0.4329 |
| P5 | 0.4500 | 0.3798 | 0.3798 |
| G1 | 0.2100 | 0.1005 | 0.0994 |
| G2 | 0.4200 | 0.1609 | 0.2182 |
| G3 | 0.2100 | 0.1005 | 0.0994 |
| Type of Damper | Attenuation Coefficient C | Power Exponent α | Stiffness K1 (MN/m) | Stopper = 4 cm | Stopper = 6 cm | Stopper = 8 cm |
|---|---|---|---|---|---|---|
| Resistance Force F1 (MN) | Resistance Force F1 (MN) | Resistance Force F1 (MN) | ||||
| D0 | — | — | — | — | — | — |
| D100 | 117 | 0.22 | 90 | 0.105 | 0.108 | 0.111 |
| D300 | 350 | 0.22 | 130 | 0.313 | 0.324 | 0.333 |
| D500 | 583 | 0.22 | 200 | 0.521 | 0.539 | 0.555 |
| D1000 | 1165 | 0.22 | 400 | 1.041 | 1.077 | 1.109 |
| D2000 | 2330 | 0.22 | 800 | 2.082 | 2.154 | 2.218 |
| Bearing Type | K1 (MN/m) | K2 (MN/m) | F1 (MN) | F2 (MN) |
|---|---|---|---|---|
| Fixed | 980 | - | - | - |
| Roller | 49.0 | 0.0098 | 0.0735 | 0.0754 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, C.; Tian, Q.; Zhong, L. The Effect of Viscous Dampers on the Seismic Performance of Curved Viaducts with the Combined Use of Steel Stoppers. Appl. Sci. 2022, 12, 8207. https://doi.org/10.3390/app12168207
Kang C, Tian Q, Zhong L. The Effect of Viscous Dampers on the Seismic Performance of Curved Viaducts with the Combined Use of Steel Stoppers. Applied Sciences. 2022; 12(16):8207. https://doi.org/10.3390/app12168207
Chicago/Turabian StyleKang, Caixia, Qin Tian, and Lianggen Zhong. 2022. "The Effect of Viscous Dampers on the Seismic Performance of Curved Viaducts with the Combined Use of Steel Stoppers" Applied Sciences 12, no. 16: 8207. https://doi.org/10.3390/app12168207
APA StyleKang, C., Tian, Q., & Zhong, L. (2022). The Effect of Viscous Dampers on the Seismic Performance of Curved Viaducts with the Combined Use of Steel Stoppers. Applied Sciences, 12(16), 8207. https://doi.org/10.3390/app12168207




