A Reinforcement Learning Method for Layout Design of Planar and Spatial Trusses using Kernel Regression
Abstract
:1. Introduction
2. Reinforcement Learning Task for Truss Layout Design
2.1. Problem Statement
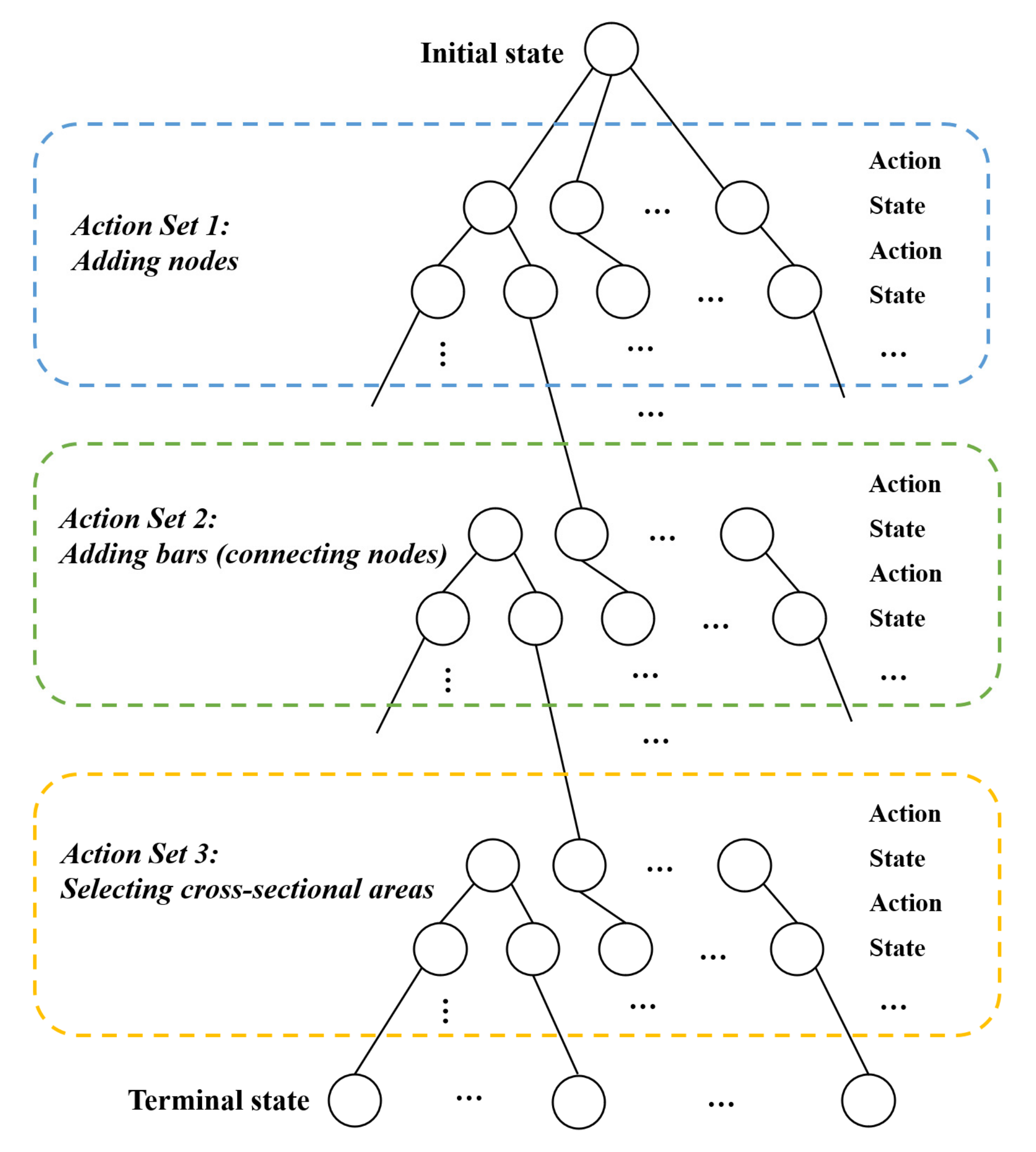
2.2. Sequential Decision Model for Truss Layout Design
| Algorithm 1 Mixed reward function for evaluation | |
| Input: Node Set , Bar Set , Current iteration Output: Reward of Structure | |
| 1: | Function //feedback signal to the agent |
| 2: | If then |
| 3: | objective of |
| 4: | If |
| 5: | Return |
| 6: | For every constraint do |
| 7: | If does not pass then |
| 8: | Return |
| 9: | End For |
| 10: | Return |
| 11: | Return |
| 12: | |
| 13: | Function //check geometry stability |
| 14: | dimension of |
| 15: | number of restricted degrees of freedom at support nodes of |
| 16: | |
| 17: | If then |
| 18: | stiffness matrix of |
| 19: | If then |
| 20: | Return True |
| 21: | Return False |
3. Methodology for Model Solving
3.1. Monte Carlo Tree Search for Truss Layout Design
3.2. Kernel Regression UCT for Truss Layout Design
| Algorithm 2 KR-UCT Algorithm for Truss Generation | |
| Input: Node Set , Bar Set , Allowed Area Interval , Number of Nodes , Design Envelope Output: Generated Node Set , Generated Bar Set | |
| 1: | //generate initial available action set |
| 2: | Whiledo |
| 3: | //the beat action in the state (P, E) |
| 4: | //allpy action to update state |
| 5: | End While |
| 6: | |
| 7: | Return //obtain the optimal truss layout |
| 8: | |
| 9: | //generate initial available action set |
| 10: | |
| 11: | If then |
| 12: | add new candidate points , is randomly sampled //node location is a multidimensional vector |
| 13: | If then |
| 14: | add a bar from all allowed bars |
| 15: | If then |
| 16: | index of the first unmodified bar |
| 17: | modify the area of to , is randomly sampled //cross-sectional area a one-dimensional vector (scalar). |
| 18: | Return |
| 19: | |
| 20: | Function //Returns the action type corresponding to the current state |
| 21: | If then |
| 22: | Return //action set 1: add nodes |
| 23: | If then |
| 24: | Return //action set 2: add bars connections |
| 25: | index of the first unmodified bar |
| 26: | If exits then |
| 27: | Return //action set 3: modify the area of the bars |
| 28: | Return |
| 29: | |
| 30: | Function//tree search algorithm |
| 31: | For to do |
| 32: | |
| 33: | While in Tree and do//selection |
| 34: | //tree policy |
| 35: | If then |
| 36: | // is defined in Equation (9) |
| 37: | If then //progressive widening |
| 38: | //see Equation (10) |
| 39: | |
| 40: | |
| 41: | If then |
| 42: | |
| 43: | If then |
| 44: | is defined in Equation (9) |
| 45: | If then //progressive widening |
| 46: | //see Equation (10) |
| 47: | modify the area of the current bar to |
| 48: | |
| 49: | |
| 50: | End While |
| 51: | If is not in the search tree then //expand |
| 52: | |
| 53: | |
| 54: | While do //default policy |
| 55: | |
| 56: | End While |
| 57: | //simulation |
| 58: | While do //backpropagation |
| 59: | use to update all related values of |
| 60: | |
| 61: | End While |
3.3. Modification for Symmetry Truss Layout Design
4. Numerical Experiments
4.1. Proof of Concept
4.2. 10-Bar Planar Truss Experiment
4.3. 39-Bar Planar Truss Experiment
4.4. Long-Span Truss Bridge Experiment
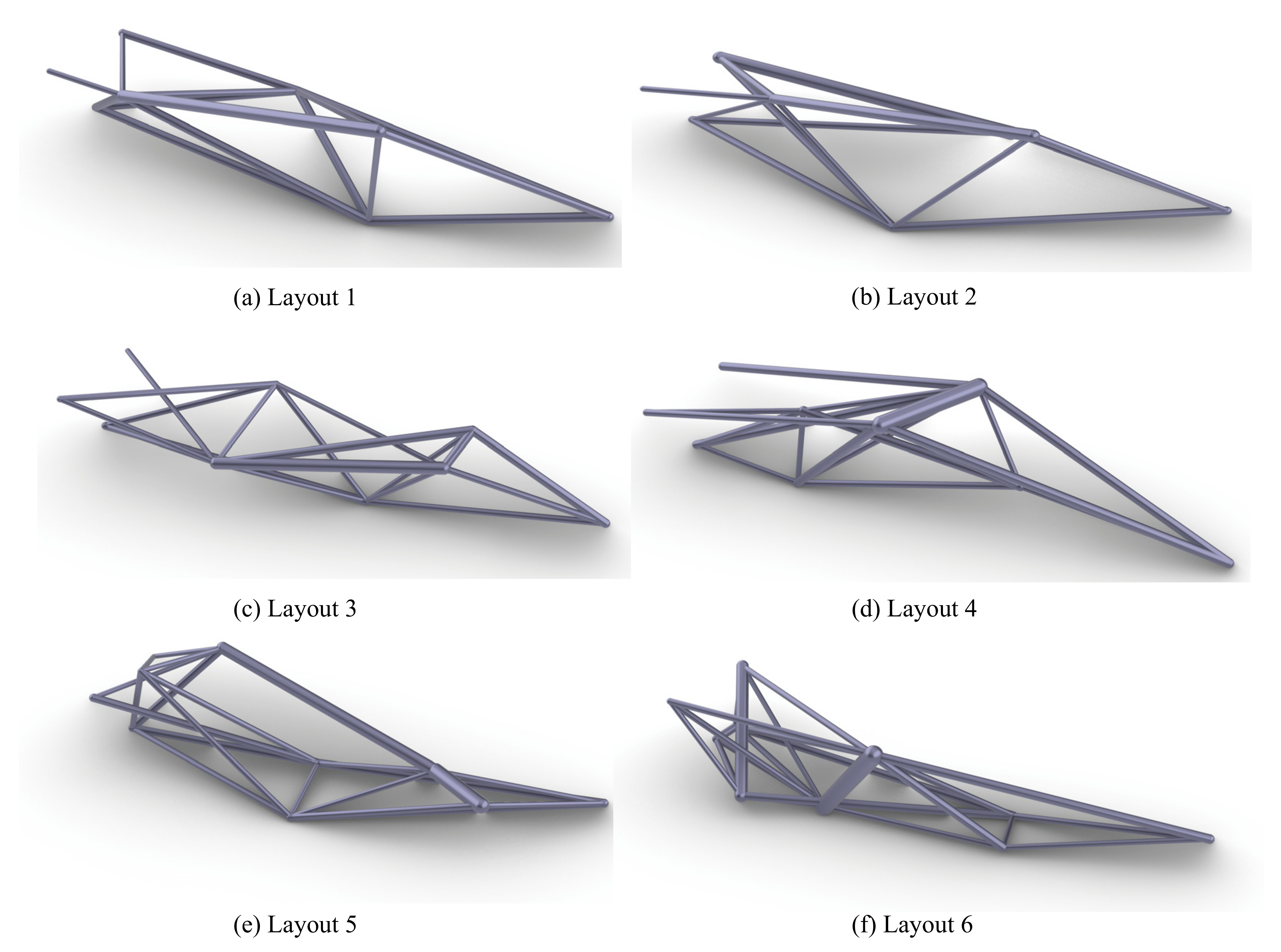
4.5. Three-Dimensional Cantilever Sundial Design
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shea, K.; Aish, R.; Gourtovai, M. Towards integrated performance-driven generative design tools. Autom. Constr. 2005, 14, 253–264. [Google Scholar] [CrossRef]
- Amir, O.; Sigmund, O. Reinforcement layout design for concrete structures based on continuum damage and truss topology optimization. Struct. Multidiscip. Optim. 2013, 47, 157–174. [Google Scholar] [CrossRef]
- Abdollahi, A.; Amini, A.; Hariri-Ardebili, M.A. An uncertainty-aware dynamic shape optimization framework: Gravity dam design. Reliab. Eng. Syst. Saf. 2022, 222, 108402. [Google Scholar] [CrossRef]
- Watson, M.; Leary, M.; Brandt, M. Generative design of truss systems by the integration of topology and shape optimisation. Int. J. Adv. Manuf. Technol. 2022, 118, 1165–1182. [Google Scholar] [CrossRef]
- Dorn, W. Automatic design of optimal structures. J. De Mec. 1964, 3, 25–52. [Google Scholar]
- Zhu, S.; Ohsaki, M.; Hayashi, K.; Guo, X. Machine-specified ground structures for topology optimization of binary trusses using graph embedding policy network. Adv. Eng. Softw. 2021, 159, 103032. [Google Scholar] [CrossRef]
- Tejani, G.G.; Savsani, V.J.; Patel, V.K.; Savsani, P.V. Size, shape, and topology optimization of planar and space trusses using mutation-based improved metaheuristics. J. Comput. Des. Eng. 2018, 5, 198–214. [Google Scholar] [CrossRef]
- Gao, G.; Liu, Z.-y.; Li, Y.-b.; Qiao, Y.-f. A new method to generate the ground structure in truss topology optimization. Eng. Optim. 2017, 49, 235–251. [Google Scholar] [CrossRef]
- Assimi, H.; Jamali, A.; Nariman-zadeh, N. Sizing and topology optimization of truss structures using genetic programming. Swarm Evol. Comput. 2017, 37, 90–103. [Google Scholar] [CrossRef]
- Hagishita, T.; Ohsaki, M. Topology optimization of trusses by growing ground structure method. Struct. Multidiscip. O 2009, 37, 377–393. [Google Scholar] [CrossRef]
- Stolpe, M. Truss optimization with discrete design variables: A critical review. Struct. Multidiscip. O 2016, 53, 349–374. [Google Scholar] [CrossRef]
- Lieu, Q.X. A novel topology framework for simultaneous topology, size and shape optimization of trusses under static, free vibration and transient behavior. Eng. Comput. 2022. [Google Scholar] [CrossRef]
- Shea, K.; Cagan, J. Languages and semantics of grammatical discrete structures. Artif. Intell. Eng. Des. Anal. Manuf. 1999, 13, 241–251. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures. Comput. Struct. 2009, 87, 267–283. [Google Scholar] [CrossRef]
- Li, L.J.; Huang, Z.B.; Liu, F.; Wu, Q.H. A heuristic particle swarm optimizer for optimization of pin connected structures. Comput. Struct. 2007, 85, 340–349. [Google Scholar] [CrossRef]
- Bellman, R. A Markovian decision process. J. Math. Mech. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Raina, A.; McComb, C.; Cagan, J. Learning to design from humans: Imitating human designers through deep learning. J. Mech. Des. 2019, 141, 111102. [Google Scholar] [CrossRef]
- Raina, A.; Cagan, J.; McComb, C. Design Strategy Network: A Deep Hierarchical Framework to Represent Generative Design Strategies in Complex Action Spaces. J. Mech. Des. 2021, 144, 4052566. [Google Scholar] [CrossRef]
- Browne, C.B.; Powley, E.; Whitehouse, D.; Lucas, S.M.; Cowling, P.I.; Rohlfshagen, P.; Tavener, S.; Perez, D.; Samothrakis, S.; Colton, S. A survey of monte carlo tree search methods. IEEE Trans. Comput. Intell. AI Games 2012, 4, 1–43. [Google Scholar] [CrossRef]
- Luo, R.; Wang, Y.; Xiao, W.; Zhao, X. AlphaTruss: Monte Carlo Tree Search for Optimal Truss Layout Design. Buildings 2022, 12, 641. [Google Scholar] [CrossRef]
- Fenton, M.; McNally, C.; Byrne, J.; Hemberg, E.; McDermott, J.; O’Neill, M. Discrete planar truss optimization by node position variation using grammatical evolution. IEEE Trans. Evol. Comput. 2015, 20, 577–589. [Google Scholar] [CrossRef]
- Miguel, L.F.F.; Lopez, R.H.; Miguel, L.F.F. Multimodal size, shape, and topology optimisation of truss structures using the Firefly algorithm. Adv. Eng. Softw. 2013, 56, 23–37. [Google Scholar] [CrossRef]
- Pyrz, M. Discrete optimization of geometrically nonlinear truss structures under stability constraints. Struct. Optim. 1990, 2, 125–131. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Maxwell, J.C.L. on the calculation of the equilibrium and stiffness of frames. Philos. Mag. J. Sci. 1864, 27, 294–299. [Google Scholar] [CrossRef]
- Kocsis, L.; Szepesvári, C. Bandit Based Monte-Carlo Planning. In Proceedings of the European Conference on Machine Learning, Berlin, Germany, 18–22 September 2006; pp. 282–293. [Google Scholar]
- Chaslot, G.M.J.; Winands, M.H.; Herik, H.J.V.D.; Uiterwijk, J.W.; Bouzy, B. Progressive strategies for Monte-Carlo tree search. New Math. Nat. Comput. 2008, 4, 343–357. [Google Scholar] [CrossRef]
- Yee, T.; Lisý, V.; Bowling, M.H.; Kambhampati, S. Monte Carlo Tree Search in Continuous Action Spaces with Execution Uncertainty. In Proceedings of the IJCAI, New York, NY, USA, 9–16 July 2016; pp. 690–697. [Google Scholar]
- Razani, R. Behavior of fully stressed design of structures and its relationshipto minimum-weight design. AIAA J. 1965, 3, 2262–2268. [Google Scholar] [CrossRef]
- Deb, K.; Gulati, S. Design of truss-structures for minimum weight using genetic algorithms. Finite Elem. Anal. Des. 2001, 37, 447–465. [Google Scholar] [CrossRef]
- Luh, G.-C.; Lin, C.-Y. Optimal design of truss structures using ant algorithm. Struct. Multidiscip. Optim. 2008, 36, 365–379. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Tseng, K.-Y. Truss structure optimization using adaptive multi-population differential evolution. Struct. Multidiscip. Optim. 2010, 42, 575–590. [Google Scholar] [CrossRef]
- Construction, A. Manual of Steel Construction: Allowable Stress Design; AISC: Chicago, IL, USA, 1989. [Google Scholar]
- Yang, Y.; Soh, C.K. Automated optimum design of structures using genetic programming. Comput. Struct. 2002, 80, 1537–1546. [Google Scholar] [CrossRef]
- Shrestha, S.M.; Ghaboussi, J. Evolution of optimum structural shapes using genetic algorithm. J. Struct. Eng. 1998, 124, 1331–1338. [Google Scholar] [CrossRef]
- Gutiérrez, N. Optimización Estructural de Armaduras Utilizando Algoritmos Genéticos. Master’s Thesis, Universidad Autónoma de Querétaro, México City, Mexico, 2007. [Google Scholar]
- Shea, K.; Zhao, X. A novel noon mark cantilever support: From design generation to realization. In Proceedings of the IASS 2004: Shell and Spatial Structures from Models to Realization, Montpellier, France, 20–24 September 2004. [Google Scholar]














| Constraints | Expression | |
|---|---|---|
| Design domain, | Check element position in | |
| Cross-sectional area | ||
| Strength | ||
| Displacement | ||
| Stability | ||
| Stiffness | ||
| Bar length | ||
| Essential Node | Node Location (mm) | Node Label |
|---|---|---|
| (0, −444,800 N) |
| Material Properties | Settings |
|---|---|
| 206,850 MPa | |
| Constraints | Parameters | Settings |
|---|---|---|
|
Xmin; Xmax Ymin; Ymax | ||
| Algorithm | UCT [20] | KR-UCT |
|---|---|---|
| Essential Node | Node Location (mm) | Node Label |
|---|---|---|
| Material Properties | Settings |
|---|---|
| Constraints | Parameters | Settings |
|---|---|---|
|
Xmin; Xmax Ymin; Ymax |
0 mm; 18,288 mm | |
| Algorithms | Assimi et al. [9] | Fenton et al. [21] | UCT [20] | KR-UCT | |
|---|---|---|---|---|---|
| Number of nodes (maxp) | 6 | 2223.5 | 2217.54 | 2223.10 | 2153.87 |
| 7 | N/A | N/A | 2255.72 | 1968.72 | |
| 8 | N/A | N/A | 2280.93 | 1852.46 | |
| 9 | N/A | N/A | 2339.62 | 2122.05 | |
| Essential Node | Node Location (mm) | Node Label |
|---|---|---|
| Material Properties | Settings |
|---|---|
| Constraints | Parameters | Settings |
|---|---|---|
|
Xmin; Xmax Ymin; Ymax | ||
| Algorithm | GA [30] | AS-API [31] | AMPDE [32] | FA [22] | IPVS [7] | KR-UCT |
|---|---|---|---|---|---|---|
| Essential Node | Node Location (mm) | Node Label |
|---|---|---|
| Material Properties | Settings |
|---|---|
| Algorithm | GA [35] | GP [34] | GA [36] | KR-UCT |
|---|---|---|---|---|
| Essential Node | Node Location (mm) | Node Label |
|---|---|---|
| Material Properties | Settings |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, R.; Wang, Y.; Liu, Z.; Xiao, W.; Zhao, X. A Reinforcement Learning Method for Layout Design of Planar and Spatial Trusses using Kernel Regression. Appl. Sci. 2022, 12, 8227. https://doi.org/10.3390/app12168227
Luo R, Wang Y, Liu Z, Xiao W, Zhao X. A Reinforcement Learning Method for Layout Design of Planar and Spatial Trusses using Kernel Regression. Applied Sciences. 2022; 12(16):8227. https://doi.org/10.3390/app12168227
Chicago/Turabian StyleLuo, Ruifeng, Yifan Wang, Zhiyuan Liu, Weifang Xiao, and Xianzhong Zhao. 2022. "A Reinforcement Learning Method for Layout Design of Planar and Spatial Trusses using Kernel Regression" Applied Sciences 12, no. 16: 8227. https://doi.org/10.3390/app12168227
APA StyleLuo, R., Wang, Y., Liu, Z., Xiao, W., & Zhao, X. (2022). A Reinforcement Learning Method for Layout Design of Planar and Spatial Trusses using Kernel Regression. Applied Sciences, 12(16), 8227. https://doi.org/10.3390/app12168227







