Theoretical and Simulation Analysis of Static and Dynamic Properties of MXene-Based Humidity Sensors
Abstract
:1. Introduction
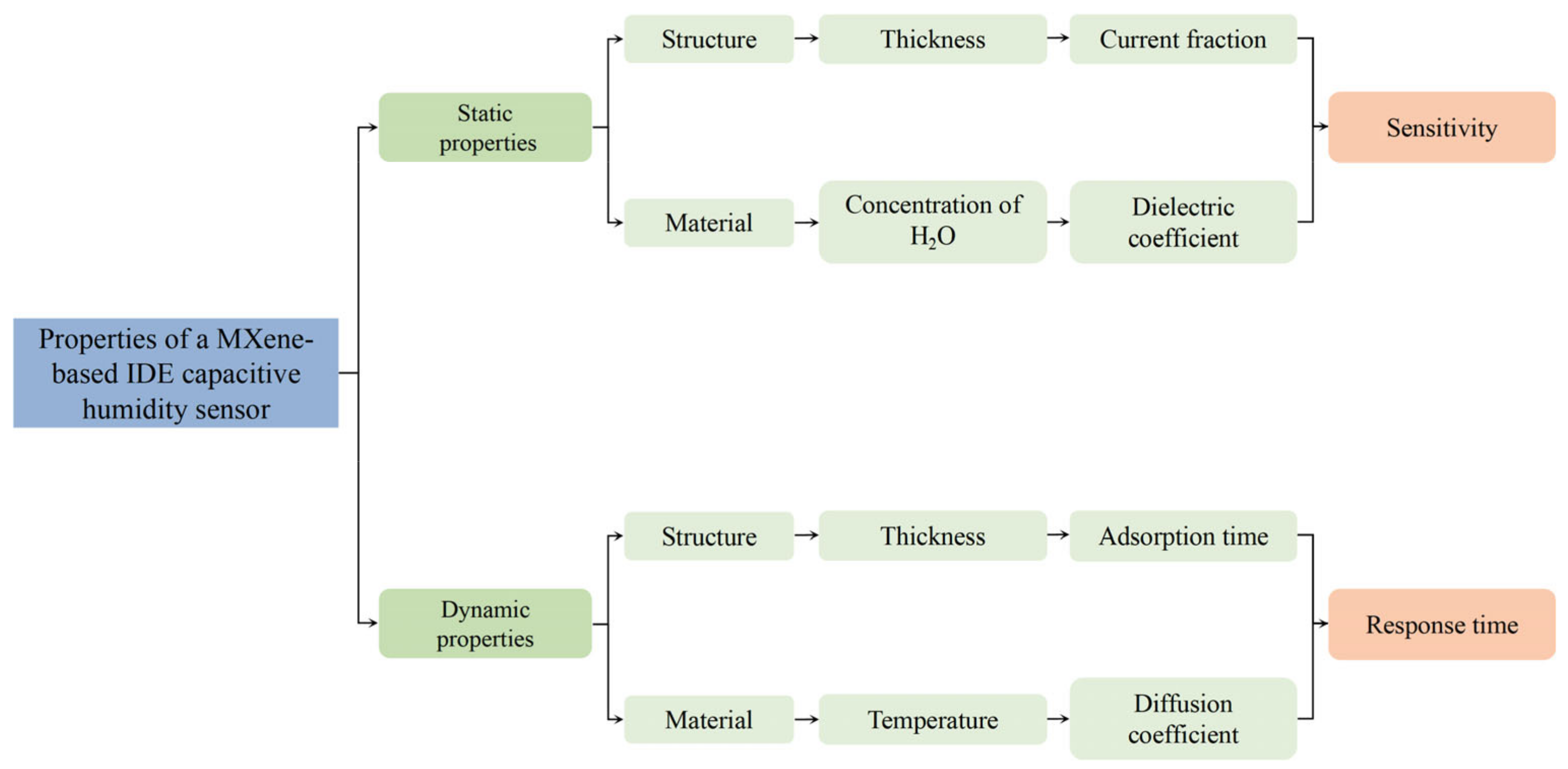
2. Static Properties Analysis
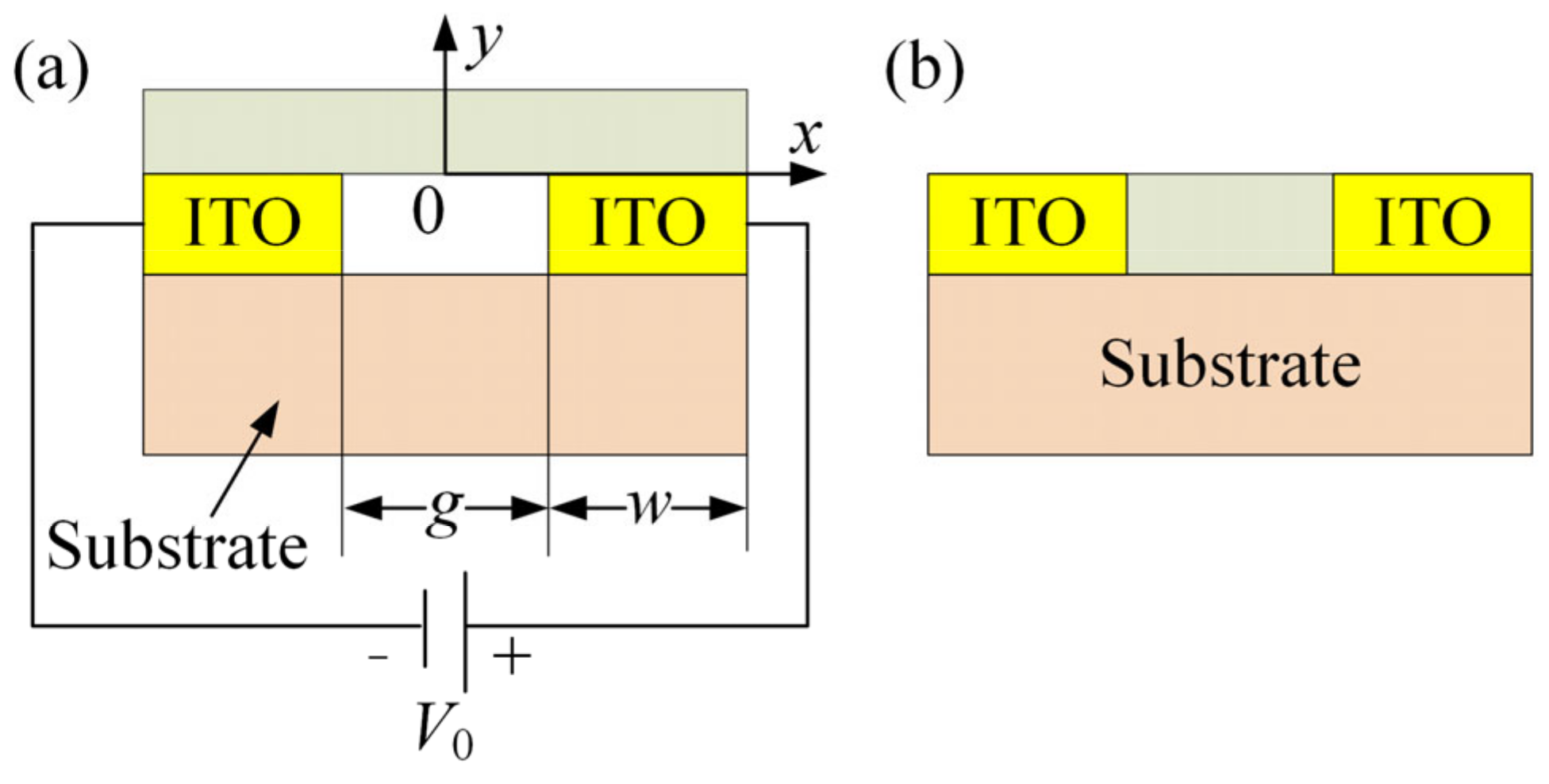
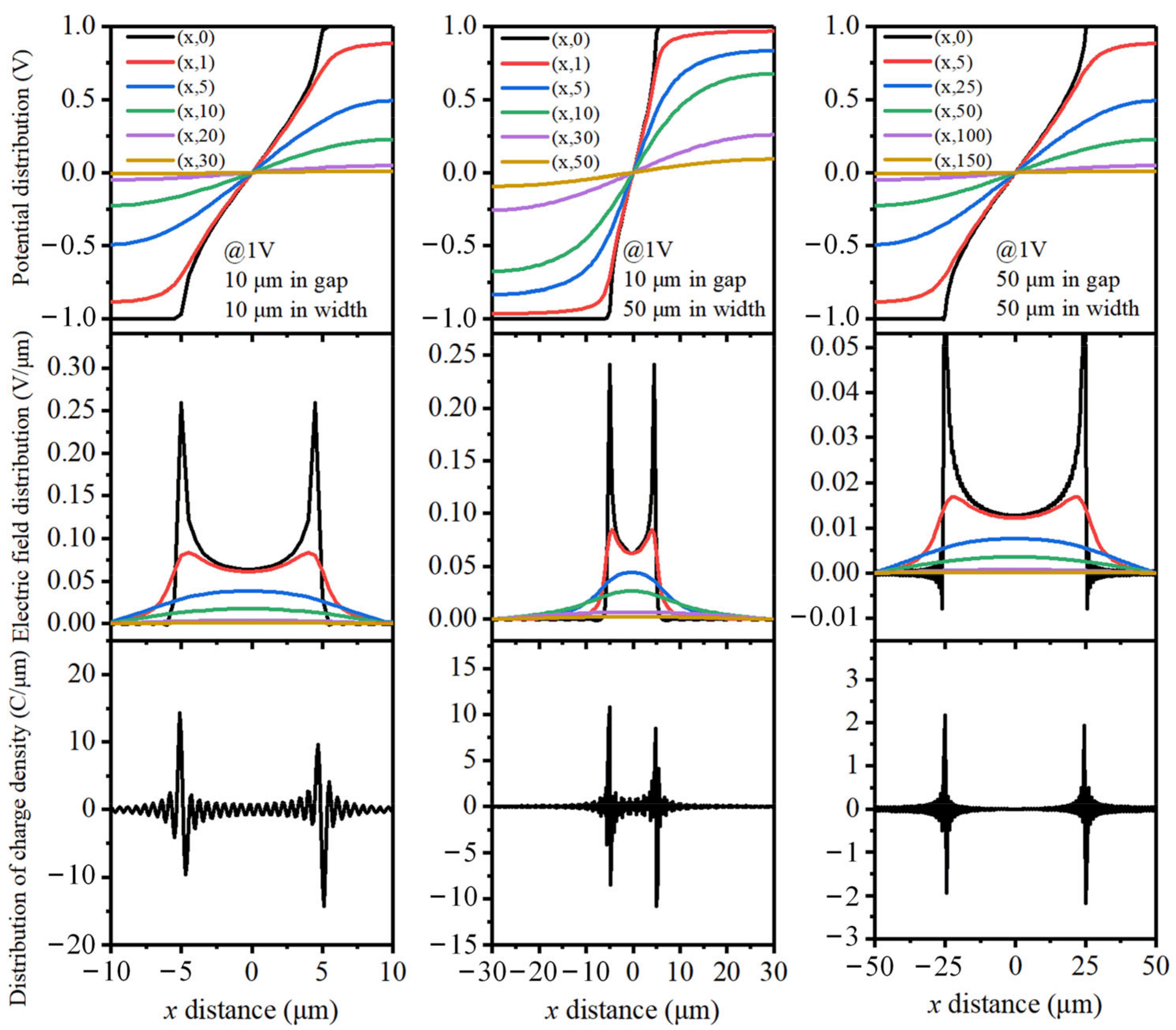
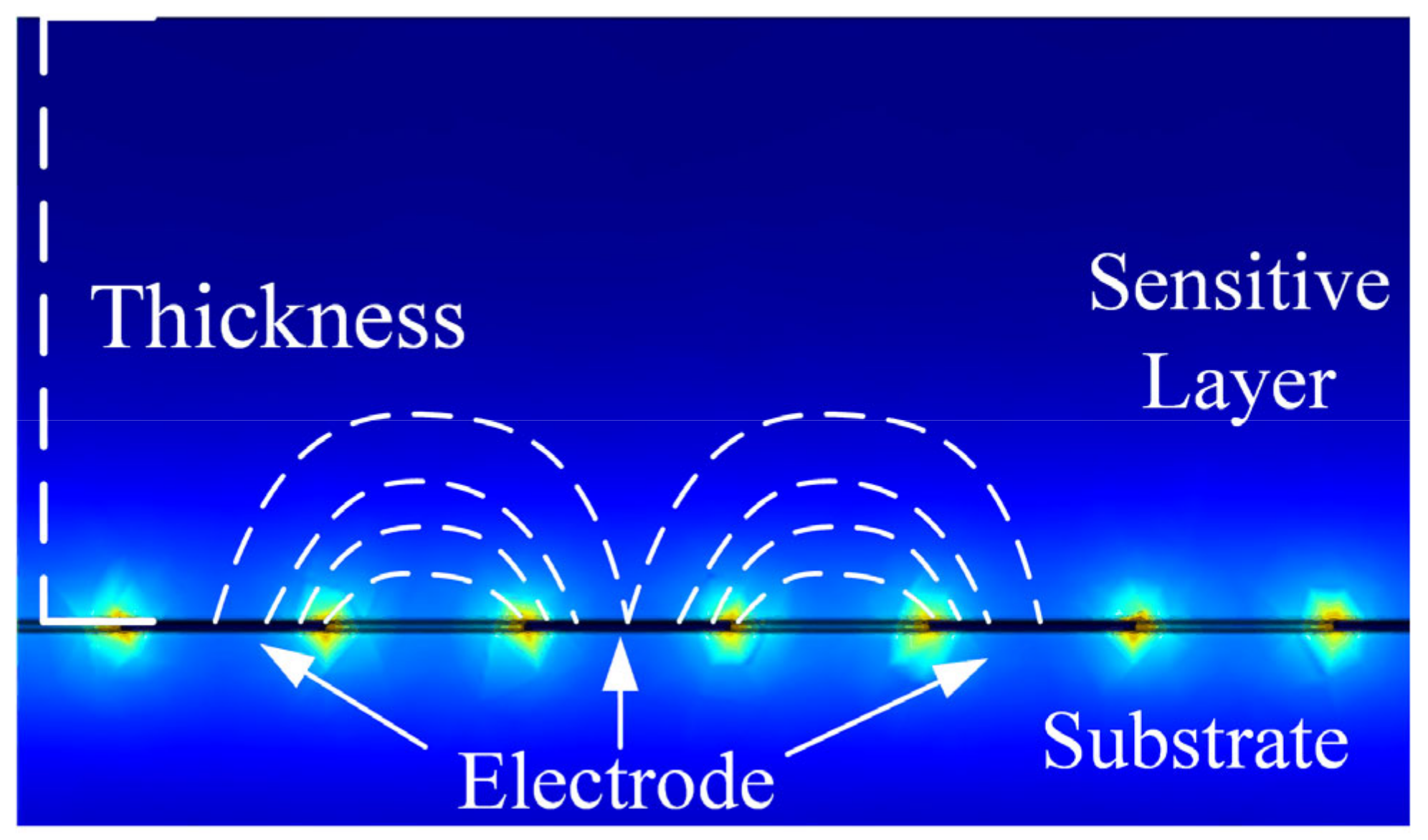
2.1. Effect of Structure on Static Properties
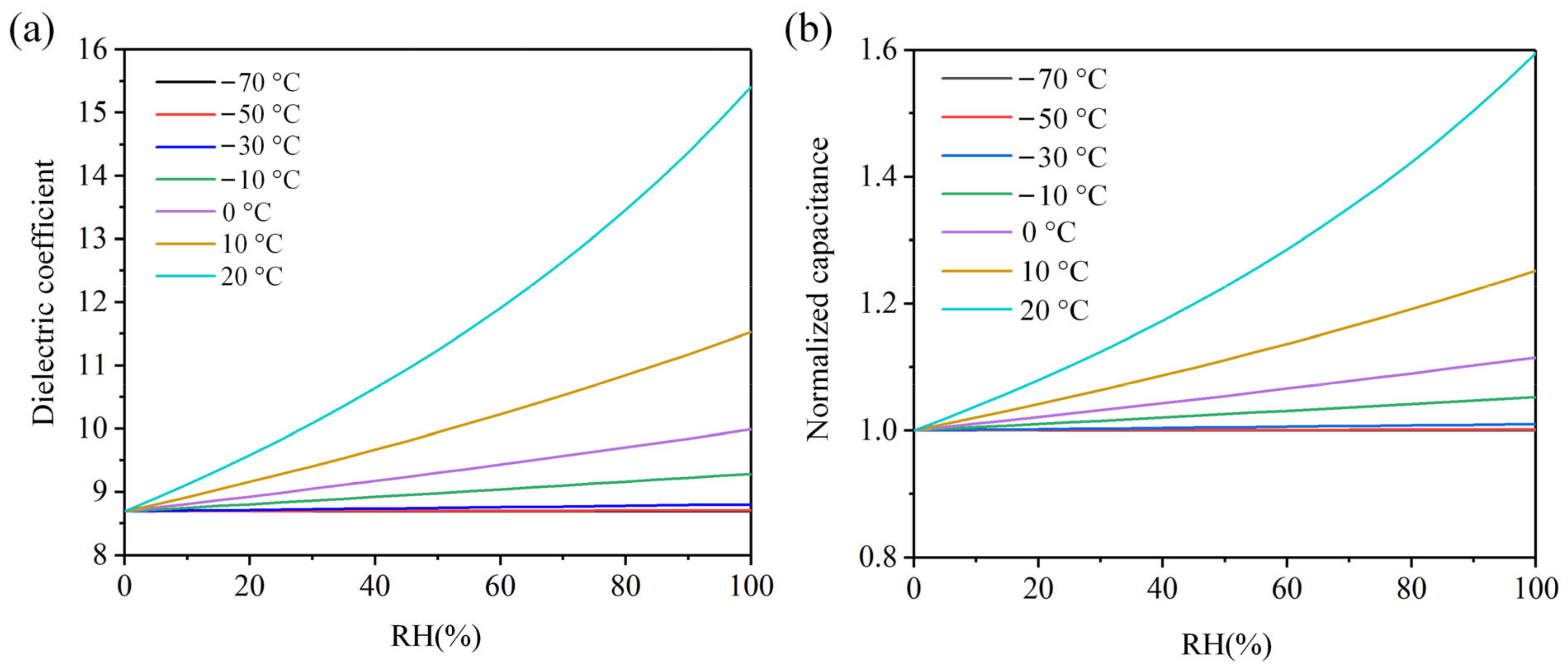
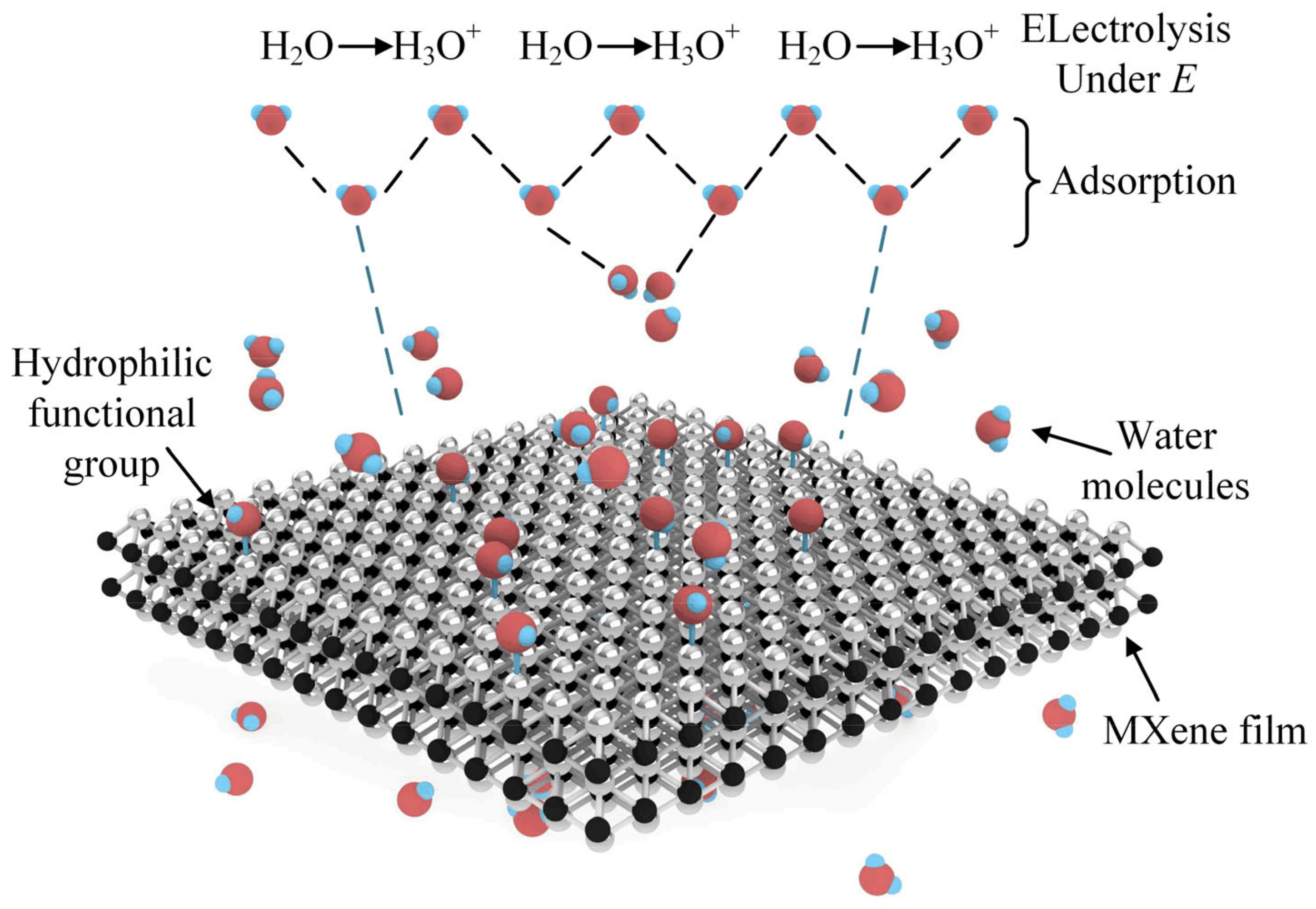
2.2. Effect of Material on Static Properties
3. Dynamic Properties Analysis
3.1. Effect of Structure on Dynamic Properties
3.2. Effect of Material on Dynamic Properties
4. Results and Discussion
5. Conclusions
- The greater the thickness, the more current flows through the sensitive layer and the greater the capacitance. However, unlike the traditional perception, when the thickness increases to a certain extent, the growing thickness does not increase the capacitance. This is because all current has passed through the sensitive layer at this point.
- When the thickness is at a tiny level, increasing the thickness does not lead to a significant increase in the response time due to the diffusion mechanism of water molecules. However, with the increase in thickness, the response time is obviously related to the change.
- In the same relative humidity conditions, the concentration of water molecules increases with temperature. The increase in water molecules results in a rise in the dielectric coefficient of the humidity-sensitive material so that the capacitance of the humidity sensor output has a positive correlation with temperature.
- When the temperature increases, the water molecules move more vigorously, resulting in a rise in the diffusion coefficient. The reaction response time is shortened by reducing the time for water molecules to fully bind to the hydrophilic groups in the sensitive layer.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pei, Y.Y.; Zhang, X.L.; Hui, Z.Y.; Zhou, J.Y.; Huang, X.; Sun, G.Z.; Huang, W. Ti3C2TX MXene for sensing applications: Recent progress, design principles, and future perspectives. ACS Nano 2021, 15, 3996–4017. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.L.; Lu, P.; Dai, J.X.; Zheng, C.T.; Zhang, T.; Yuand, W.W.; Zhang, Y. High performance humidity sensing property of Ti3C2Tx MXene-derived Ti3C2Tx/K2Ti4O9 composites. Sens. Actuators B-Chem. 2021, 326, 128969. [Google Scholar] [CrossRef]
- Cho, M.Y.; Kim, S.; Kim, I.S.; Kim, E.S.; Wang, Z.J.; Kim, N.Y.; Kim, S.W.; Oh, J.M. Perovskite-induced ultrasensitive and highly stable humidity sensor systems prepared by aerosol deposition at room temperature. Adv. Funct. Mater. 2020, 30, 1907449. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, X.D.; Yu, X.; Ding, X.; Yu, X.L.; Chen, X.P. Fast response humidity sensor based on graphene oxide films supported by TiO2 nanorods. Diam. Relat. Mater. 2020, 109, 108031. [Google Scholar] [CrossRef]
- Lv, Z.H.; Chen, D.L.; Feng, H.L.; Wei, W.; Lv, H.B. Artificial intelligence in underwater digital twins sensor networks. ACM Trans. Sens. Netw. 2022, 18, 39. [Google Scholar] [CrossRef]
- Fenner, R.; Zdankiewicz, E. Micromachined water vapor sensors: A review of sensing technologies. IEEE Sens. J. 2001, 1, s309–s317. [Google Scholar] [CrossRef]
- Blank, T.A.; Eksperiandova, L.P.; Belikov, K.N. Recent trends of ceramic humidity sensors development: A review. Sens. Actuators B-Chem. 2016, 228, 416–442. [Google Scholar] [CrossRef]
- Yang, H.; Ye, Q.Q.; Zeng, R.X.; Zhang, J.K.; Yue, L.; Xu, M.; Qiu, Z.J.; Wu, D.P. Stable and fast-response capacitive humidity sensors based on a ZnO nanopowder/PVP-RGO multilayer. Sensors 2017, 17, 2415. [Google Scholar] [CrossRef]
- Li, X.Y.; Chen, X.D.; Chen, X.P.; Ding, X.; Zhao, X. High-sensitive humidity sensor based on graphene oxide with evenly dispersed multiwalled carbon nanotubes. Mater. Chem. Phys. 2018, 207, 135–140. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Q.; Sheng, W.J.; Wang, X.B.; Zhang, K.D.; Du, L.; Zhou, J. Humidity sensors with shielding electrode under interdigitated electrode. Sensors 2019, 19, 659. [Google Scholar] [CrossRef]
- Liu, H.A.; Li, N.; Jiang, Y.; Wang, Q.; Peng, Z.C. Plasma treated MXene/Ag-based humidity sensor with ultrahigh sensitivity for gesture tracking. Mater. Sci. Eng. 2019, 563, 022046. [Google Scholar] [CrossRef]
- Huang, J.Q.; Li, B.Y.; Chen, W.H. A CMOS MEMS humidity sensor enhanced by a capacitive coupling structure. Micromachines 2016, 7, 74. [Google Scholar] [CrossRef]
- Zhou, W.H.; Wang, L.C.; Wang, L.B. A method to measure the dynamic characteristics of microhumidity sensors. IEEE Trans. Instrum. Meas. 2014, 63, 2993–3001. [Google Scholar] [CrossRef]
- Zhou, W.H.; He, X.; Wu, J.Y.; Wang, L.B.; Wang, L.C. Numerical study on response time of a parallel plate capacitive polyimide humidity sensor based on microhole upper electrode. J. Micro/Nanolithogr. MEMS MOEMS 2017, 16, 034502. [Google Scholar] [CrossRef]
- Zhao, Q.N.; Zhang, Y.J.; Duan, Z.H.; Wang, S.; Liu, C.; Jiang, Y.D.; Tai, H.L. A review on Ti3C2Tx-based nanomaterials: Synthesis and applications in gas and humidity sensors. Rare Met. 2021, 40, 1459–1476. [Google Scholar] [CrossRef]
- Naguib, M.; Mochalin, V.N.; Barsoum, M.W.; Gogotsi, Y. 25th anniversary article: MXenes: A new family of two-dimensional materials. Adv. Mater. 2014, 26, 992–1005. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.M.; Hossain, M.M.; Chowdhury, H.K. Two-dimensional MXene-based flexible nanostructures for functional nanodevices: A review. J. Mater. Chem. A 2021, 9, 3231–3269. [Google Scholar] [CrossRef]
- Alhabeb, M.; Maleski, K.; Anasori, B.; Leiyukh, P.; Clark, L.; Sin, S.; Gogotsi, Y. Guidelines for synthesis and processing of two-dimensional titanium carbide (Ti3C2TX MXene). Chem. Mater. 2017, 29, 7633–7644. [Google Scholar] [CrossRef]
- Li, T.; Yin, W.; Gao, S.W.; Sun, Y.N.; Xu, P.L.; Wu, S.H.; Kong, H.; Yang, G.Z.; Wei, G. The combination of two-dimensional nanomaterials with metal ooxide nanoparticles for gas sensors: A review. Nanomaterials 2022, 12, 982. [Google Scholar] [CrossRef]
- Li, T.; Shang, D.W.; Gao, S.W.; Wang, B.; Kong, H.; Yang, G.Z.; Shu, W.D.; Xu, P.L.; Wei, G. Two-dimensional material-based electrochemical sensors/biosensors for food safety and biomolecular detection. Biosensors 2022, 12, 314. [Google Scholar] [CrossRef]
- Liu, W.; Zheng, Y.; Wang, Z.; Wang, Z.X.; Yang, J.; Chen, M.X.; Qi, M.; Rehman, S.U.; Shum, P.P.; Zhu, L.; et al. Ultrasensitive exhaled breath sensors based on anti-resonant hollow core fiber with in situ grown ZnO-Bi2O3 nanosheets. Adv. Mater. Interfaces 2021, 8, 2001978. [Google Scholar] [CrossRef]
- Liu, L.X.; Chen, W.; Zhang, H.B.; Wang, Q.W.; Guan, F.L.; Yu, Z.Z. Flexible and multifunctional silk textiles with biomimetic leaf-like MXene/silver nanowire nanostructures for electromagnetic interference shielding, humidity monitoring, and self-derived hydrophobicity. Adv. Funct. Mater. 2019, 29, 1905197. [Google Scholar] [CrossRef]
- Li, T.K.; Zhao, T.T.; Tian, X.M.; Yuan, L.; Xue, X.Y.; Wang, Z.G.; Yin, L.Q.; Zhang, J.H. A high-performance humidity sensor based on alkalized MXenes and poly(dopamine) for touchless sensing and respiration monitoring. J. Mater. Chem. C 2022, 10, 2281–2289. [Google Scholar] [CrossRef]
- Li, R.L.; Fan, Y.; Ma, Z.H.; Zhang, D.; Liu, Y.M.; Xu, J.Q. Controllable preparation of ultrathin MXene nanosheets and their excellent QCM humidity sensing properties enhanced by fluoride doping. Microchim. Acta 2021, 188, 81. [Google Scholar] [CrossRef]
- Celerier, S.; Hurand, S.; Garnero, C.; Morisset, S.; Benchakar, M.; Habrioux, A.; Chartier, P.; Mauchamp, V.; Findling, N.; Lanson, B.; et al. Hydration of Ti3C2TX MXene: An interstratification process with major implications on physical properties. Chem. Mater. 2018, 31, 454–461. [Google Scholar] [CrossRef]
- Muckley, E.S.; Naguib, M.; Ivanov, I.N. Multi-modal, ultrasensitive, wide-range humidity sensing with Ti3C2 film. Nanoscale 2018, 10, 21689–21695. [Google Scholar] [CrossRef]
- Bhardwaj, R.; Hazra, A. MXene-based gas sensors. J. Mater. Chem. C 2021, 9, 15735–15754. [Google Scholar] [CrossRef]
- Li, N.; Jiang, Y.; Xiao, Y.; Meng, B.; Xing, C.Y.; Zhang, H.; Peng, Z.C. A fully inkjet-printed transparent humidity sensor based on a Ti3C2/Ag hybrid for touchless sensing of finger motion. Nanoscale 2019, 11, 21522–21531. [Google Scholar] [CrossRef]
- Muckley, E.S.; Naguib, M.; Wang, H.W.; Vlcek, L.; Osti, N.C.; Sacci, R.L.; Sang, X.H.; Unocic, R.R.; Xie, Y.; Tyagi, M.; et al. Multimodality of structural, electrical, and gravimetric responses of intercalated MXenes to water. ACS Nano 2017, 11, 11118–11126. [Google Scholar] [CrossRef]
- Li, X.; Lu, Y.L.; Shi, Z.H.; Liu, G.; Xu, G.; An, Z.J.; Xing, H.; Chen, Q.M.; Han, R.P.S.; Liu, Q.J. Onion-inspired MXene/chitosan-quercetin multilayers: Enhanced response to H2O molecules for wearable human physiological monitoring. Sens. Actuators B-Chem. 2021, 329, 129209. [Google Scholar] [CrossRef]
- Anasori, B.; Lukatskaya, M.R.; Gogotsi, Y. 2D metal carbides and nitrides (MXenes) for energy storage. Nat. Rev. Mater. 2017, 2, 16098. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Shi, L.Y.; Wu, F.Q.; Yuan, S.A.; Zhao, Y.; Zhang, M.H. The sol-gel template synthesis of porous TiO2 for a high performance humidity sensor. Nanotechnology 2011, 22, 275502. [Google Scholar] [CrossRef] [PubMed]
- An, H.S.; Habib, T.; Shah, S.; Gao, H.L.; Patel, A.; Echols, I.; Zhao, X.F.; Radovic, M.; Green, M.J.; Lutkenhaus, J.L. Water sorption in MXene/polyelectrolyte multilayers for ultrafast humidity sensing. ACS Appl. Nano Mater. 2019, 2, 948–955. [Google Scholar] [CrossRef]
- Li, T.F.; Yao, L.L.; Liu, Q.L.; Gu, J.J.; Luo, R.C.; Li, J.H.; Yan, X.D.; Wang, W.Q.; Liu, P.; Chen, B.; et al. Fluorine-free synthesis of high-purity Ti3C2Tx (T=OH, O) via Alkali Treatment. Angew. Chem. Int. Ed. 2018, 57, 6115–6119. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Wang, Y.; Shao, J.; Zhang, P.; Chen, Y.; Fu, Z.; Wang, S.; Zhao, W.; Zhou, Z.; Yuan, Y.; et al. Temperature and humidity sensor based on MEMS technology. AIP Adv. 2017, 11, 085126. [Google Scholar] [CrossRef]
- Otter, M.W.D. Approximate expressions for the capacitance and electrostatic potential of interdigitated electrodes. Sens. Actuators A Phys. 2001, 96, 140–144. [Google Scholar] [CrossRef]
- Talebian, E.; Talebian, M. A general review on the derivation of Clausius-Mossotti relation. Optik 2013, 124, 2324–2326. [Google Scholar] [CrossRef]
- Zhang, L.; Rahimabady, M.; Tan, S.Y.; Tan, C.Y.; Chen, S.T.; Chen, Y.F.; Yao, K.; Humbert, A.; Soccol, D.; Zang, K.Y.; et al. P(VDF-HFP) polymer as sensing material for capacitive carbon dioxide sensors. IEEE Sens. J. 2017, 17, 4349–4356. [Google Scholar] [CrossRef]
- Zhou, W.H.; Wang, L.C.; Wang, L.B. Numerical study of the structural parameter effects on the dynamic characteristics of a polyimide film micro-capacitive humidity sensor. IEEE Sens. J. 2016, 16, 5979–5986. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Hu, C.; Li, Z.; Zheng, D.; Cui, F.; Yang, X. Theoretical and Simulation Analysis of Static and Dynamic Properties of MXene-Based Humidity Sensors. Appl. Sci. 2022, 12, 8254. https://doi.org/10.3390/app12168254
Wang Y, Hu C, Li Z, Zheng D, Cui F, Yang X. Theoretical and Simulation Analysis of Static and Dynamic Properties of MXene-Based Humidity Sensors. Applied Sciences. 2022; 12(16):8254. https://doi.org/10.3390/app12168254
Chicago/Turabian StyleWang, Yikai, Chun Hu, Zhongxiang Li, Dezhi Zheng, Fei Cui, and Xiaojun Yang. 2022. "Theoretical and Simulation Analysis of Static and Dynamic Properties of MXene-Based Humidity Sensors" Applied Sciences 12, no. 16: 8254. https://doi.org/10.3390/app12168254
APA StyleWang, Y., Hu, C., Li, Z., Zheng, D., Cui, F., & Yang, X. (2022). Theoretical and Simulation Analysis of Static and Dynamic Properties of MXene-Based Humidity Sensors. Applied Sciences, 12(16), 8254. https://doi.org/10.3390/app12168254





