Hybrid VOF–Lagrangian CFD Modeling of Droplet Aerobreakup
Abstract
:1. Introduction
2. Hybrid VOF–Lagrangian Approach
2.1. VOF Method
2.2. Discrete Phase Model
3. CFD Modeling
3.1. Flow Configuration
3.2. Turbulence Modeling
3.3. CFD Solver
4. Results
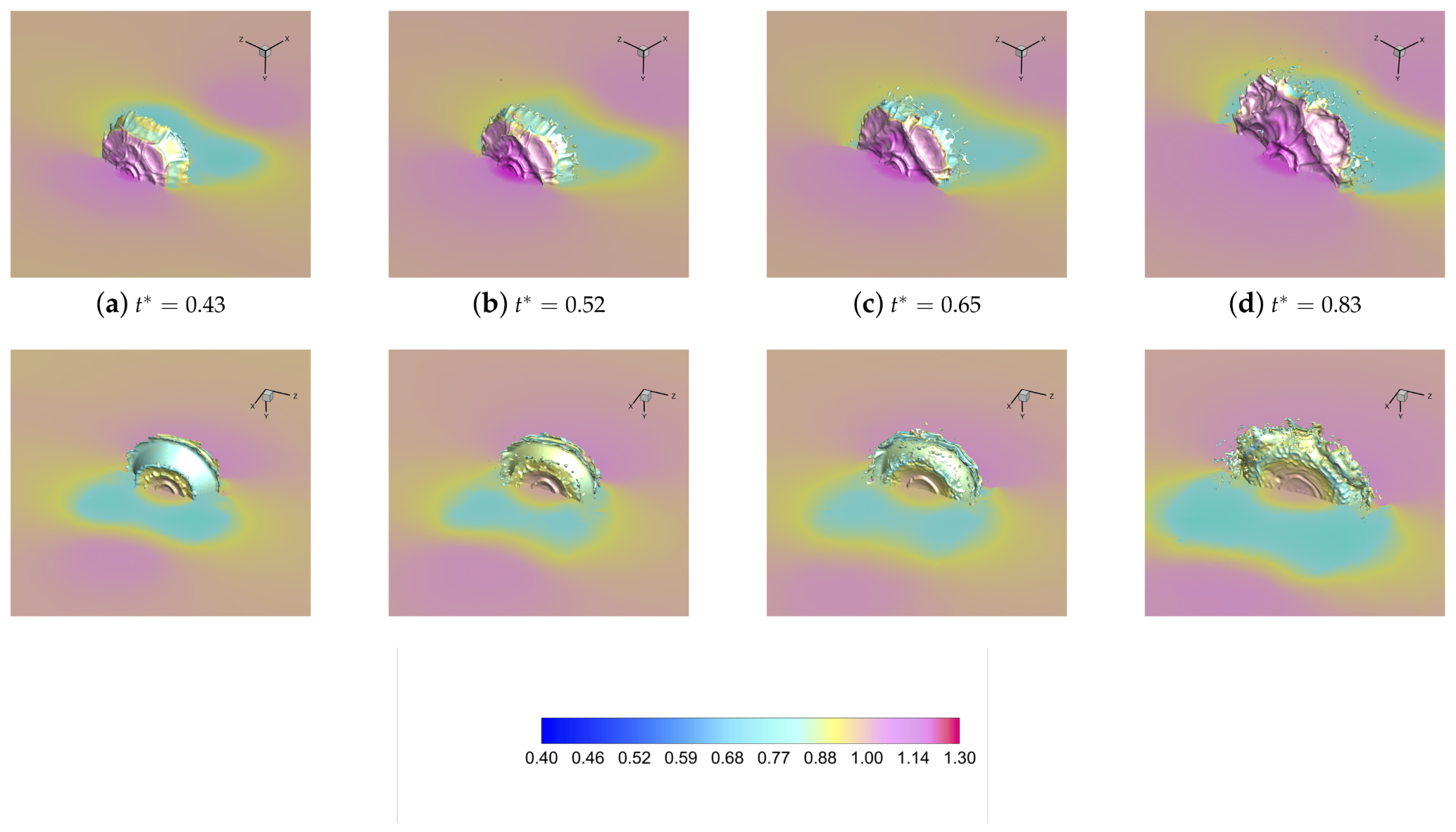
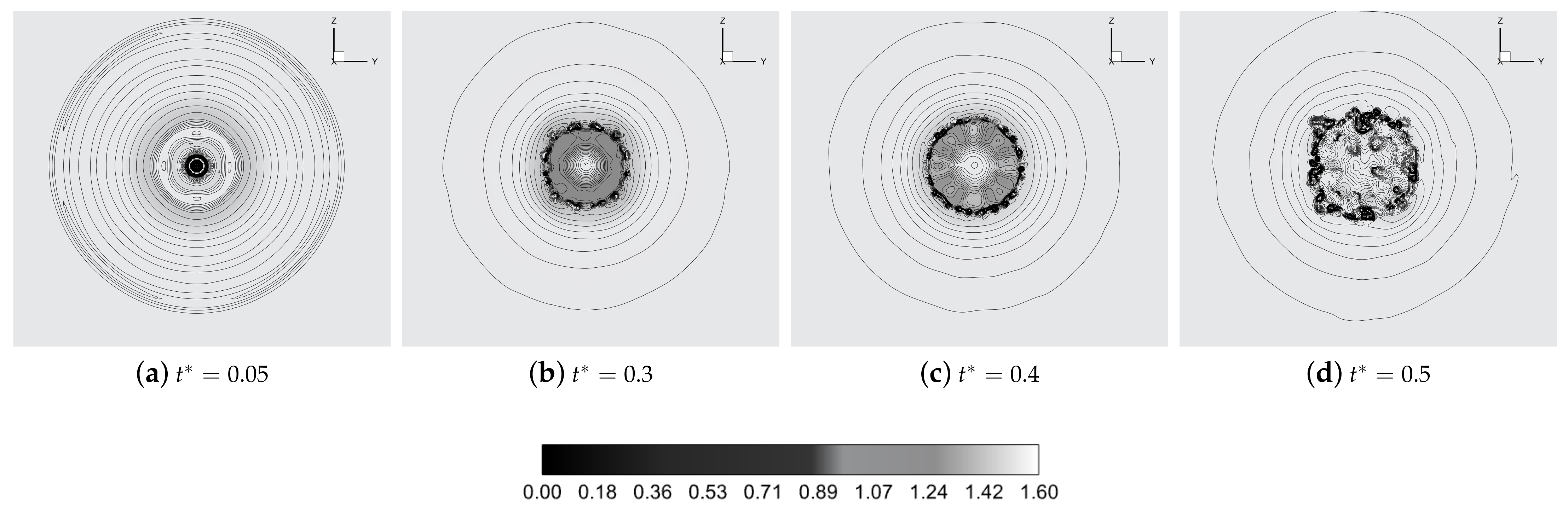
4.1. Droplet Deformation
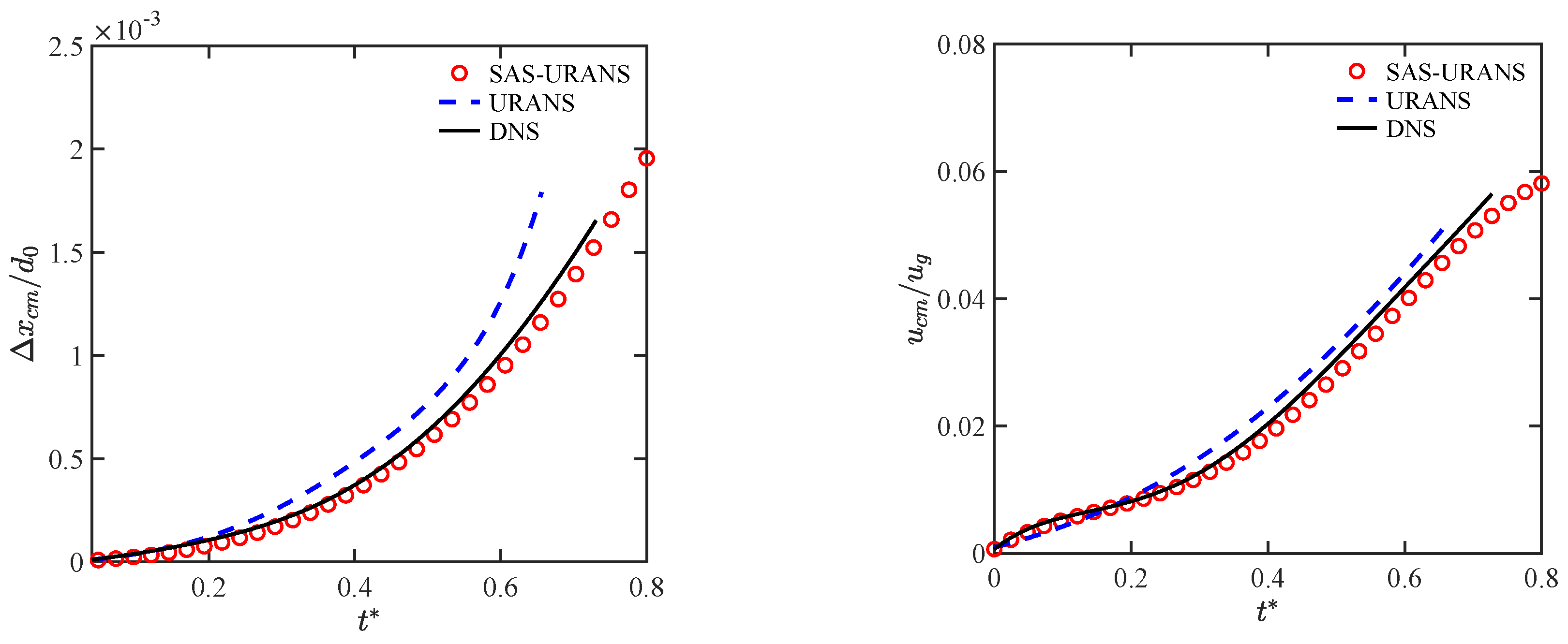
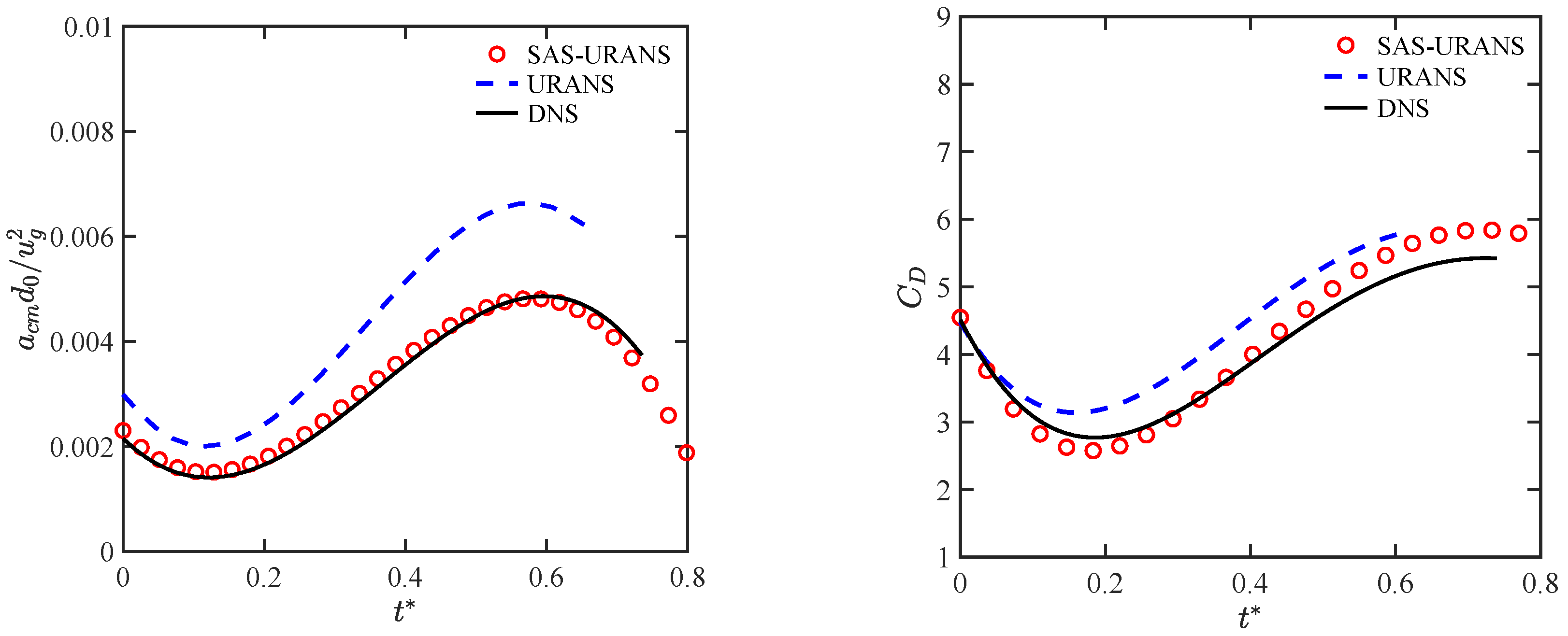
4.2. Droplet Drift
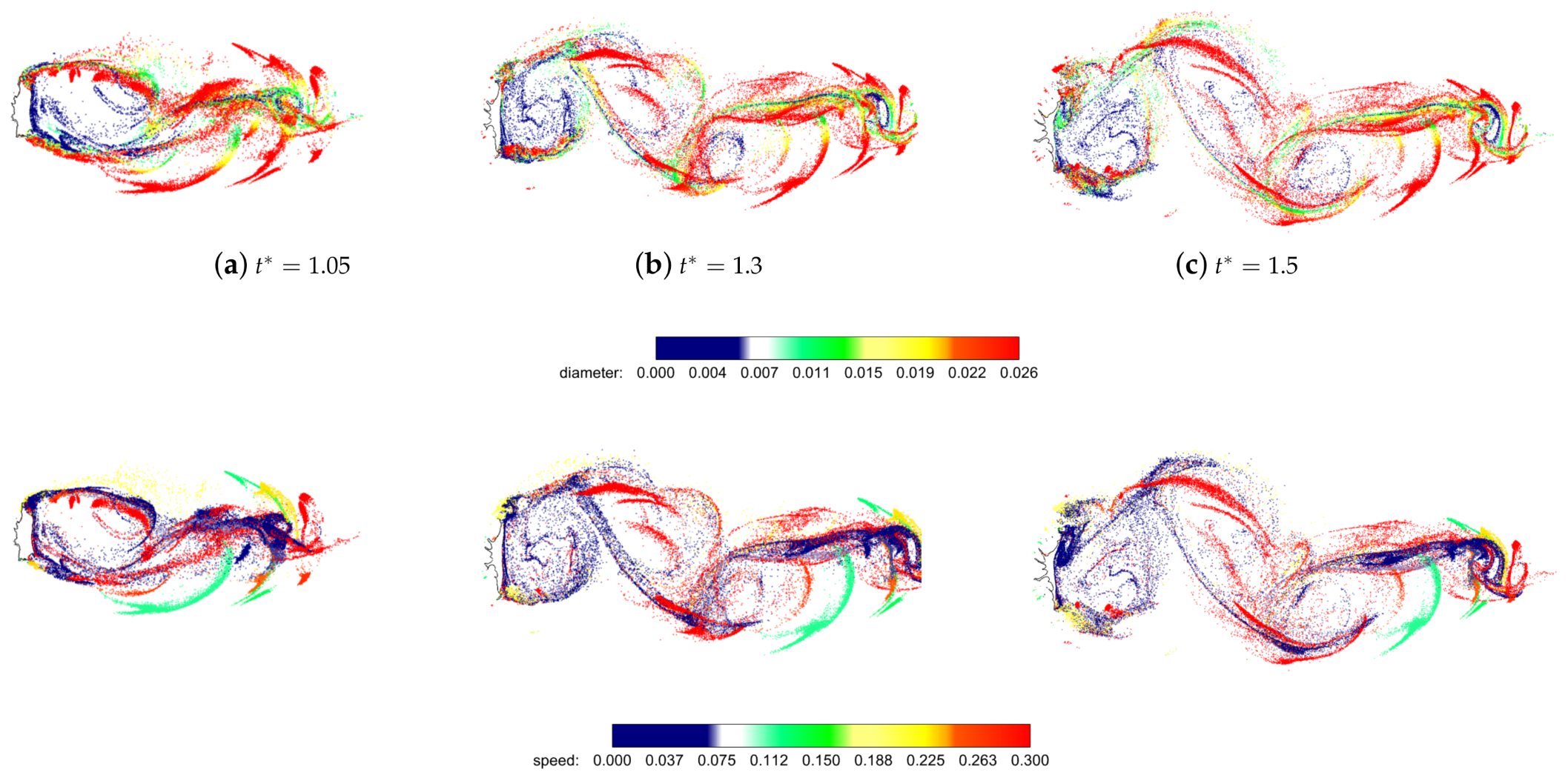
4.3. Sub-Droplets Tracking
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| CM | center-of-mass |
| DNS | direct numerical simulation |
| FV | finite volume |
| LES | large eddy simulation |
| LS | level-set |
| RT | Rayleigh–Taylor |
| SAS | scale-adaptive simulation |
| SIE | shear-induced entrainment |
| SST | shear stress transport |
| URANS | unsteady Reynolds-averaged Navier–Stokes |
| VOF | volume-of-fluid |
References
- Menter, F.; Hüppe, A.; Matyushenko, A.; Kolmogorov, D. An overview of hybrid RANS–LES models developed for industrial CFD. Appl. Sci. 2021, 11, 2459. [Google Scholar] [CrossRef]
- Theofanous, T.G. Aerobreakup of Newtonian and viscoelastic liquids. Annu. Rev. Fluid Mech. 2011, 43, 661–690. [Google Scholar] [CrossRef]
- Villermaux, E. Fragmentation. Annu. Rev. Fluid Mech. 2007, 39, 419–446. [Google Scholar] [CrossRef]
- Moylan, B.; Landrum, B.; Russell, G. Investigation of the physical phenomena associated with rain impacts on supersonic and hypersonic flight vehicles. Procedia Eng. 2013, 58, 223–231. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Li, G.J. On the physics of aerobreakup. Phys. Fluids 2008, 20, 052103. [Google Scholar] [CrossRef]
- Poplavski, S.; Minakov, A.; Shebeleva, A.; Boiko, V. On the interaction of water droplet with a shock wave: Experiment and numerical simulation. Int. J. Multiph. Flow 2020, 127, 103273. [Google Scholar] [CrossRef]
- Igra, D.; Takayama, K. Investigation of aerodynamic breakup of a cylindrical water droplet. At. Sprays 2001, 11, 167–185. [Google Scholar]
- Theofanous, T.G.; Mitkin, V.V.; Ng, C.L.; Chang, C.H.; Deng, X.; Sushchikh, S. The physics of aerobreakup. II. Viscous liquids. Phys. Fluids 2012, 24, 022104. [Google Scholar] [CrossRef]
- Wang, Z.; Hopfes, T.; Giglmaier, M.; Adams, N.A. Effect of Mach number on droplet aerobreakup in shear stripping regime. Exp. Fluids 2020, 61, 193. [Google Scholar] [CrossRef]
- Chen, H. Two-dimensional simulation of stripping breakup of a water droplet. AIAA J. 2008, 46, 1135. [Google Scholar] [CrossRef]
- Stefanitsis, D.; Koukouvinis, P.; Nikolopoulos, N.; Gavaises, M. Numerical investigation of the aerodynamic droplet breakup at Mach numbers greater than 1. J. Energy Eng. 2021, 147, 04020077. [Google Scholar] [CrossRef]
- Zhu, W.; Zheng, H.; Zhao, N. Numerical investigations on the deformation and breakup of an n-decane droplet induced by a shock wave. Phys. Fluids 2022, 34, 063306. [Google Scholar] [CrossRef]
- Sembian, S.; Liverts, M.; Tillmark, N.; Apazidis, N. Plane shock wave interaction with a cylindrical water column. Phys. Fluids 2016, 28, 056102. [Google Scholar] [CrossRef]
- Rossano, V.; De Stefano, G. Computational evaluation of shock wave interaction with a cylindrical water column. Appl. Sci. 2021, 11, 4934. [Google Scholar] [CrossRef]
- Meng, J.C.; Colonius, T. Numerical simulation of the aerobreakup of a water droplet. J. Fluid Mech. 2018, 835, 1108–1135. [Google Scholar] [CrossRef]
- Liu, N.; Wang, Z.; Sun, M.; Wang, H.; Wang, B. Numerical simulation of liquid droplet breakup in supersonic flows. Acta Astronaut. 2018, 145, 116–130. [Google Scholar] [CrossRef]
- Allaire, G.; Clerc, S.; Kokh, S. A five-equation model for the simulation of interfaces between compressible fluids. J. Comput. Phys. 2002, 181, 577–616. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Rossano, V.; Cittadini, A.; De Stefano, G. Computational evaluation of shock wave interaction with a liquid droplet. Appl. Sci. 2022, 12, 1349. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1: Theory and model description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- De Stefano, G.; Natale, N.; Reina, G.P.; Piccolo, A. Computational evaluation of aerodynamic loading on retractable landing-gears. Aerospace 2020, 7, 68. [Google Scholar] [CrossRef]
- Iannelli, P.; Denaro, F.M.; De Stefano, G. A deconvolution-based fourth-order finite volume method for incompressible flows on non-uniform grids. Int. J. Numer. Methods Fluids 2003, 43, 431–462. [Google Scholar] [CrossRef]
- Roberts, J.; Wypych, P.; Hastie, D.; Liao, R. Analysis and validation of a CFD-DPM method for simulating dust suppression sprays. Part. Sci. Technol. 2022, 40, 415–426. [Google Scholar] [CrossRef]
- Amatriain, A.; Urionabarrenetxea, E.; Avello, A.; Martín, J.M. Multiphase model to predict particle size distributions in close-coupled gas atomization. Int. J. Multiph. Flow 2022, 154, 104138. [Google Scholar] [CrossRef]
- Lin, S.; Wang, Y.; Sun, L.; Abouei Mehrizi, A.; Jin, Y.; Chen, L. Experimental and numerical investigations on the spreading dynamics of impinging liquid droplets on diverse wettable surfaces. Int. J. Multiph. Flow 2022, 153, 104135. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 1999, 31, 567–603. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Hosseinzadeh-Nik, Z.; Aslani, M.; Owkes, M.; Regele, J.D. Numerical simulation of a shock wave impacting a droplet using the adaptive wavelet-collocation method. In Proceedings of the ILASS-Americas 28th Annual Conference on Liquid Atomization and Spray Systems, Dearborn, MI, USA, 15–18 May 2016. [Google Scholar]
- Schütze, J.; Gupta, V.K.; Aguado, P.L.; Hutcheson, P.; Esch, T.; Braun, M. Increasing the predictive character of spray process simulation by multiphase model transitioning. In Proceedings of the ILASS-Europe 29th Annual Conference on Liquid Atomization and Spray Systems, Paris, France, 2–4 September 2019. [Google Scholar]
- Chang, P.; Xu, G.; Huang, J. Numerical study on DPM dispersion and distribution in an underground development face based on dynamic mesh. Int. J. Min. Sci. Technol. 2020, 30, 471–475. [Google Scholar] [CrossRef]
- Morsi, S.; Alexander, A. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Nykteri, G.; Gavaises, M. Droplet aerobreakup under the shear-induced entrainment regime using a multiscale two-fluid approach. Phys. Rev. Fluids 2021, 6, 084304. [Google Scholar] [CrossRef]
- Shyue, K.M. A fluid-mixture type algorithm for barotropic two-fluid flow problems. J. Comput. Phys. 1998, 200, 718–748. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F.R.; Lechner, R.; Cokljat, D. The scale-adaptive simulation method for unsteady flow predictions. Part 2: Application to complex flows. Flow Turbul. Combust. 2010, 85, 139–165. [Google Scholar] [CrossRef]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A correlation-based transition model using local variables - Part I: Model formulation. J. Turbomach. 2006, 128, 413–422. [Google Scholar] [CrossRef]
- De Stefano, G.; Denaro, F.M.; Riccardi, G. High-order filtering for control volume flow simulation. Int. J. Numer. Methods Fluids 2001, 37, 797–835. [Google Scholar] [CrossRef]
- Denaro, F.M.; De Stefano, G. A new development of the dynamic procedure in large-eddy simulation based on a finite volume integral approach. Application to stratified turbulence. Theoret. Comput. Fluid Dyn. 2011, 25, 315–355. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Meng, J.C.; Colonius, T. Numerical simulations of the early stages of high-speed droplet breakup. Shock Waves 2015, 25, 399–414. [Google Scholar] [CrossRef]
- Kaiser, J.W.J.; Appel, D.; Fritz, F.; Adami, S.; Adams, N.A. A multiresolution local-timestepping scheme for particle–laden multiphase flow simulations using a level-set and point-particle approach. Comput. Methods Appl. Mech. Eng. 2021, 384, 113966. [Google Scholar] [CrossRef]
- Villermaux, E.; Marmottant, P.; Duplat, J. Ligament-mediated spray formation. Phys. Rev. Lett. 2004, 92, 074501. [Google Scholar] [CrossRef] [PubMed]
- Gohardani, O. Impact of erosion testing aspects on current and future flight conditions. Prog. Aerosp. 2011, 47, 280–303. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. Hierarchical adaptive eddy-capturing approach for modeling and simulation of turbulent flows. Fluids 2021, 6, 83. [Google Scholar] [CrossRef]
- Ge, X.; De Stefano, G.; Hussaini, M.Y.; Vasilyev, O.V. Wavelet-based adaptive eddy-resolving methods for modeling and simulation of complex wall-bounded compressible turbulent flows. Fluids 2021, 6, 331. [Google Scholar] [CrossRef]
- De Stefano, G.; Brown-Dymkoski, E.; Vasilyev, O.V. Wavelet-based adaptive large-eddy simulation of supersonic channel flow. J. Fluid Mech. 2020, 901, A13. [Google Scholar] [CrossRef]
- Kasimov, N.; Dymkoski, E.; De Stefano, G.; Vasilyev, O.V. Galilean-invariant characteristic-based volume penalization method for supersonic flows with moving boundaries. Fluids 2021, 6, 293. [Google Scholar] [CrossRef]
- De Stefano, G.; Dymkoski, E.; Vasilyev, O.V. Localized dynamic kinetic-energy model for compressible wavelet-based adaptive large-eddy simulation. Phys. Rev. Fluids 2022, 7, 054604. [Google Scholar] [CrossRef]
- Ge, X.; Vasilyev, O.V.; De Stefano, G.; Hussaini, M.Y. Wavelet-based adaptive unsteady Reynolds-averaged Navier-Stokes computations of wall-bounded internal and external compressible turbulent flows. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. AIAA Paper 2018-0545. [Google Scholar]
- Ge, X.; Vasilyev, O.V.; De Stefano, G.; Hussaini, M.Y. Wavelet-based adaptive unsteady Reynolds-averaged Navier-Stokes simulations of wall-bounded compressible turbulent flows. AIAA J. 2020, 58, 1529–1549. [Google Scholar] [CrossRef]





| Parameter | Pre-Shock | Post-Shock |
|---|---|---|
| Temperature (K) | 293 | 381 |
| Pressure (kPa) | 101.3 | 239 |
| Density (kg/m) | 1.204 | 2.18 |
| Viscosity (Pa s) | ||
| Velocity (m/s) | 0 | 226 |
| Mach number | 0 | 0.577 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossano, V.; De Stefano, G. Hybrid VOF–Lagrangian CFD Modeling of Droplet Aerobreakup. Appl. Sci. 2022, 12, 8302. https://doi.org/10.3390/app12168302
Rossano V, De Stefano G. Hybrid VOF–Lagrangian CFD Modeling of Droplet Aerobreakup. Applied Sciences. 2022; 12(16):8302. https://doi.org/10.3390/app12168302
Chicago/Turabian StyleRossano, Viola, and Giuliano De Stefano. 2022. "Hybrid VOF–Lagrangian CFD Modeling of Droplet Aerobreakup" Applied Sciences 12, no. 16: 8302. https://doi.org/10.3390/app12168302
APA StyleRossano, V., & De Stefano, G. (2022). Hybrid VOF–Lagrangian CFD Modeling of Droplet Aerobreakup. Applied Sciences, 12(16), 8302. https://doi.org/10.3390/app12168302







