Study on Creep Behavior of Silty Clay Based on Fractal Derivative
Abstract
:1. Introduction
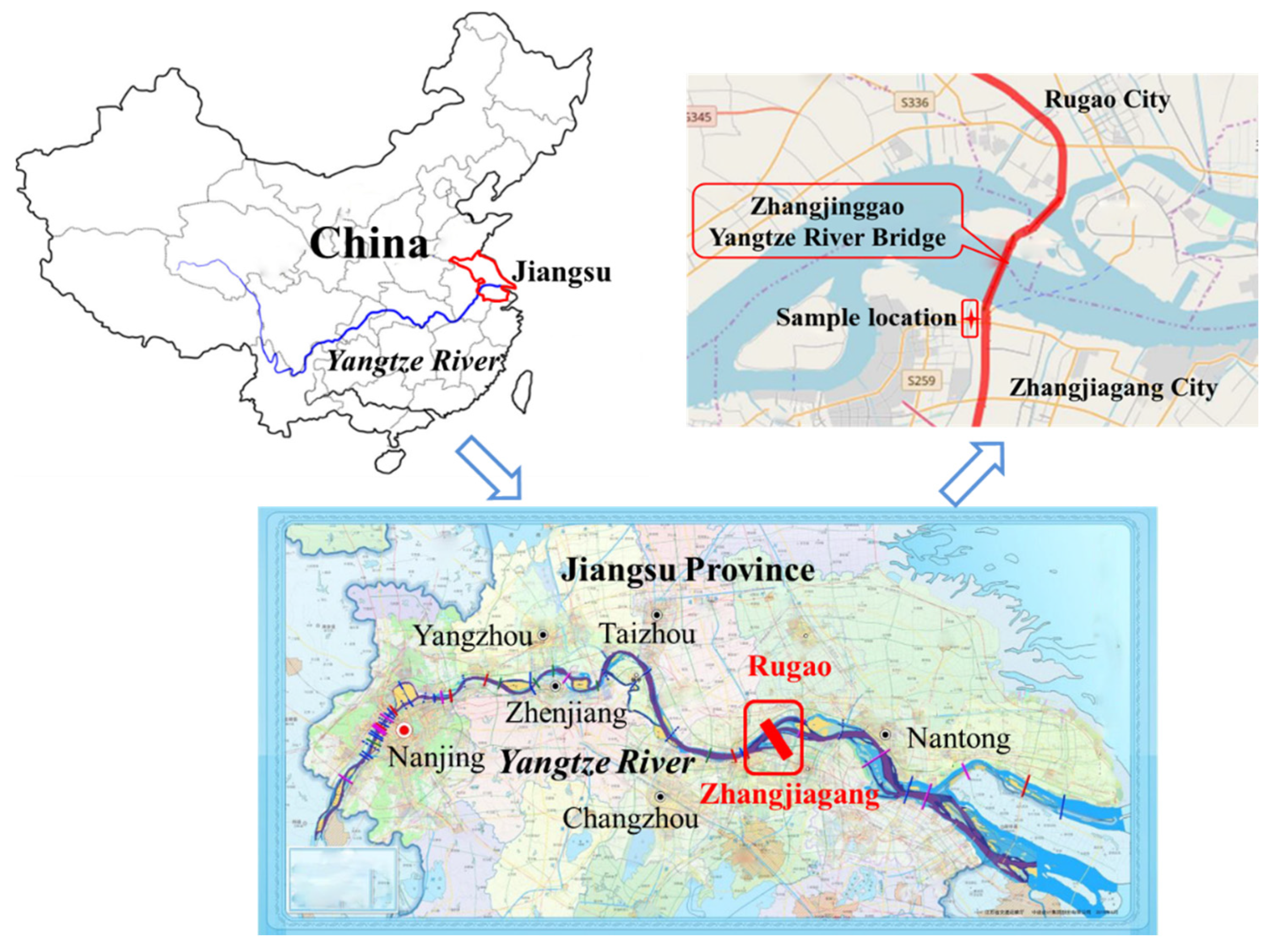
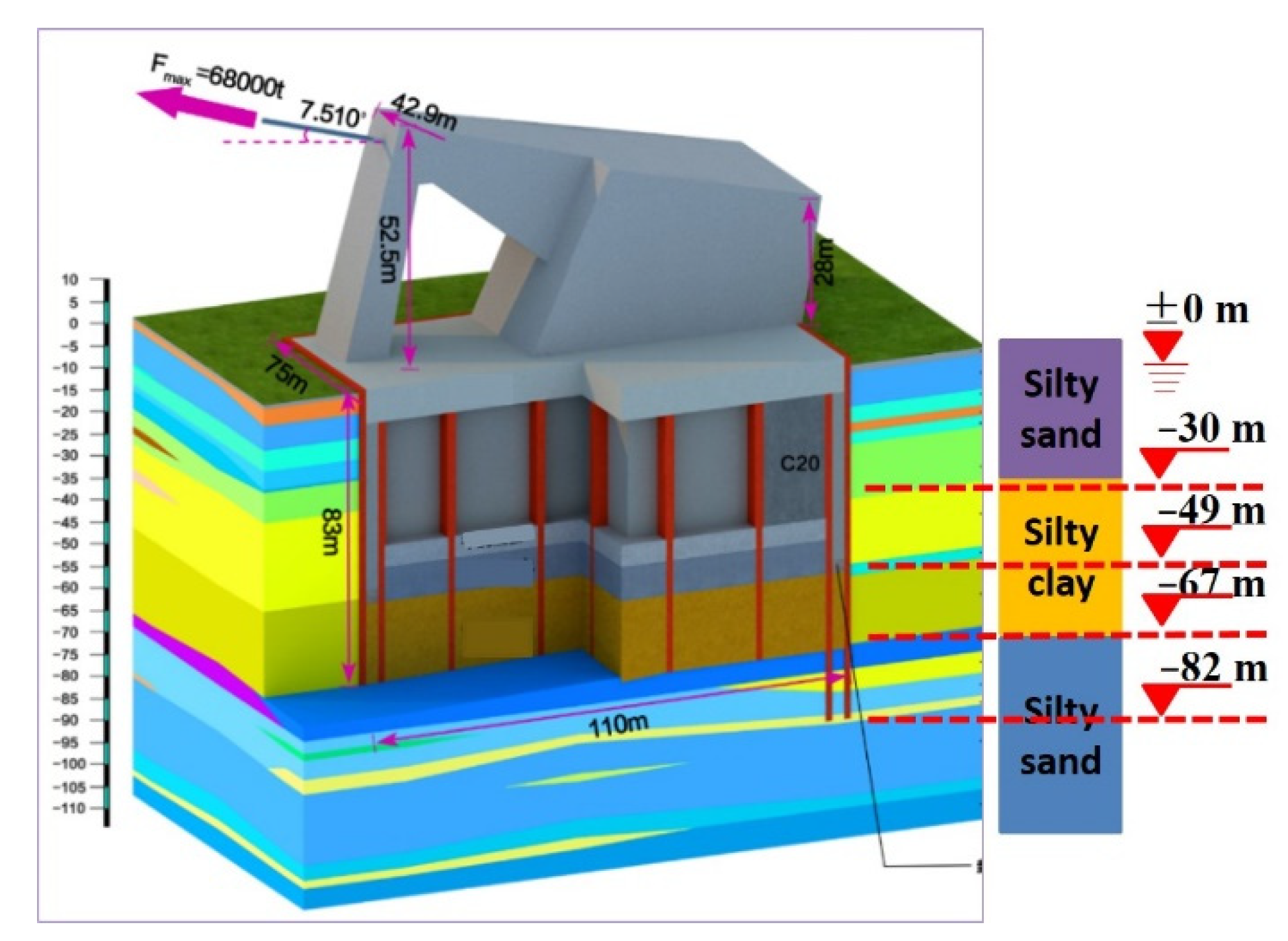
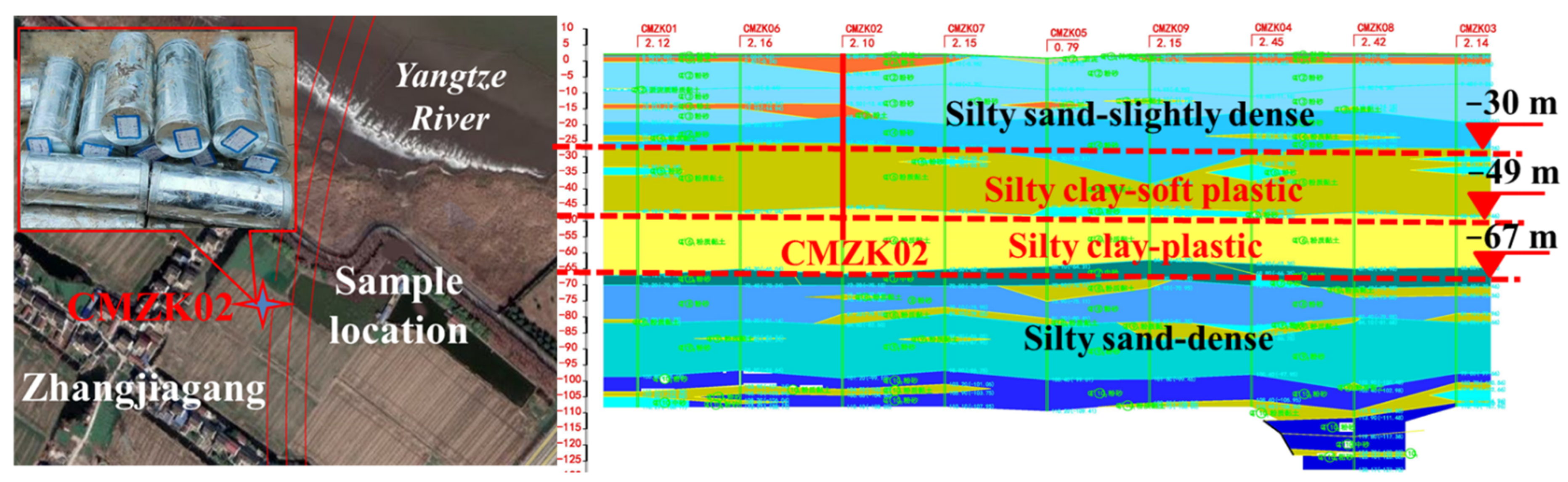
2. Test Procedure and Results
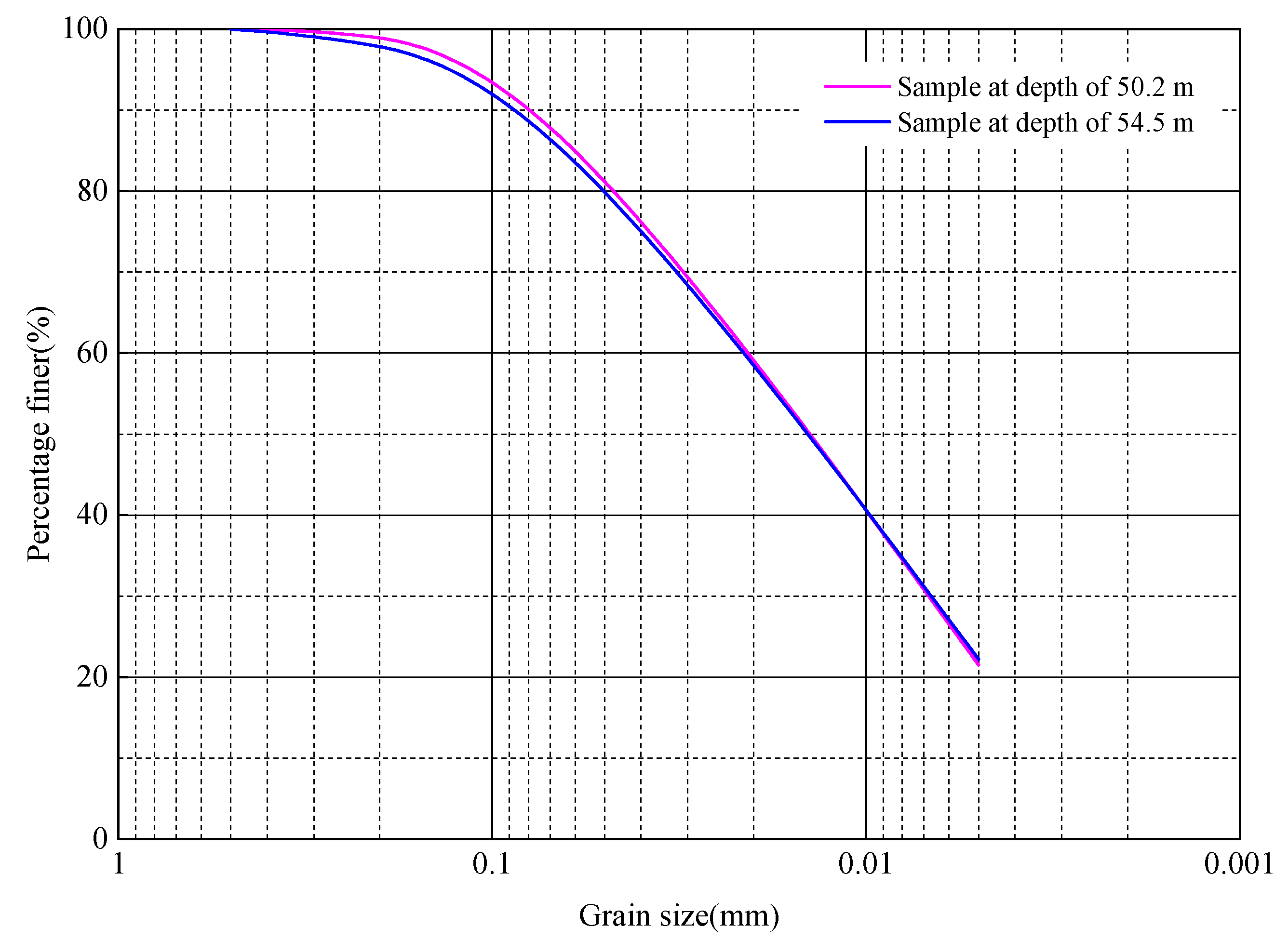
2.1. Soil Properties
2.2. Test Procedure
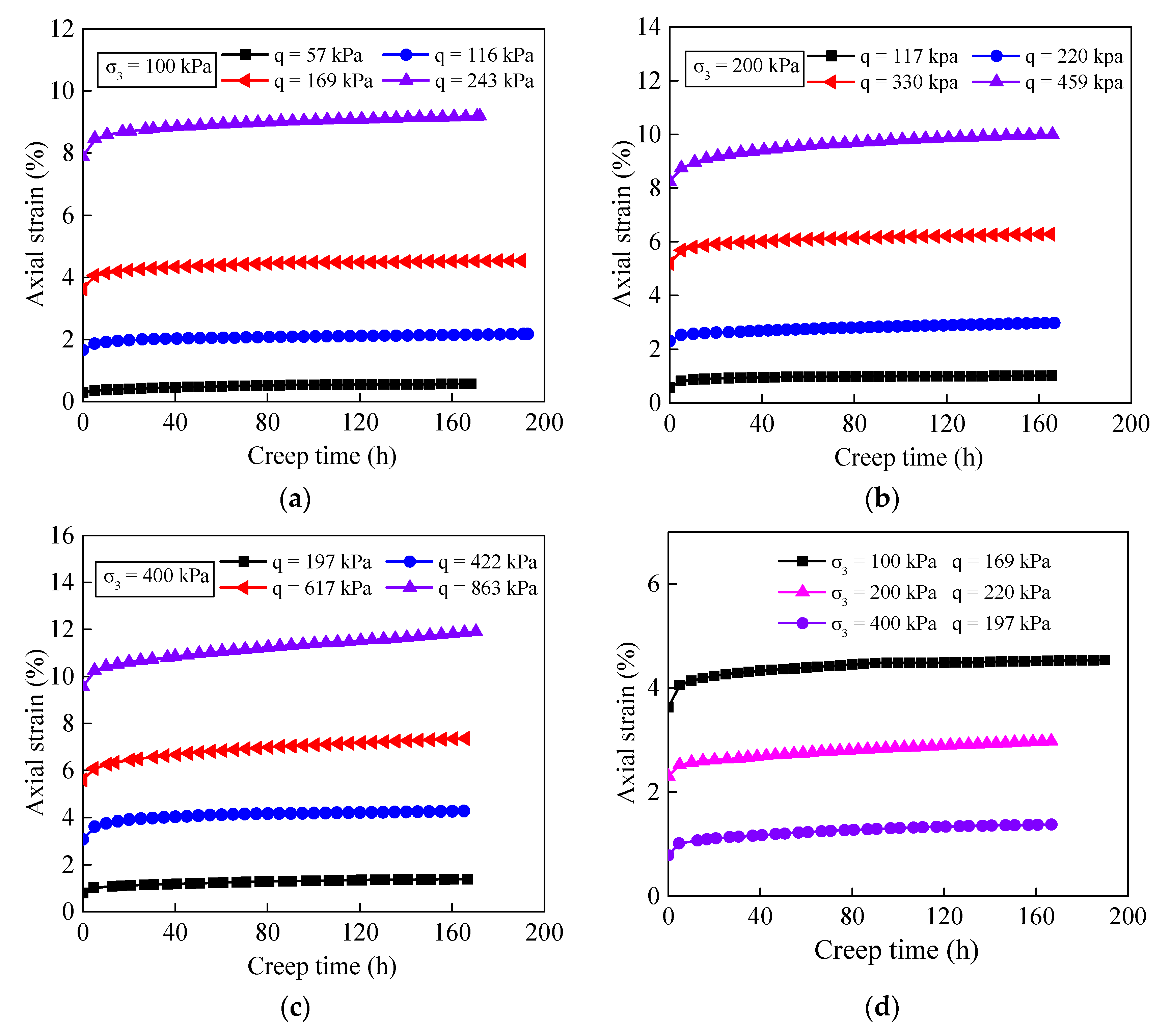
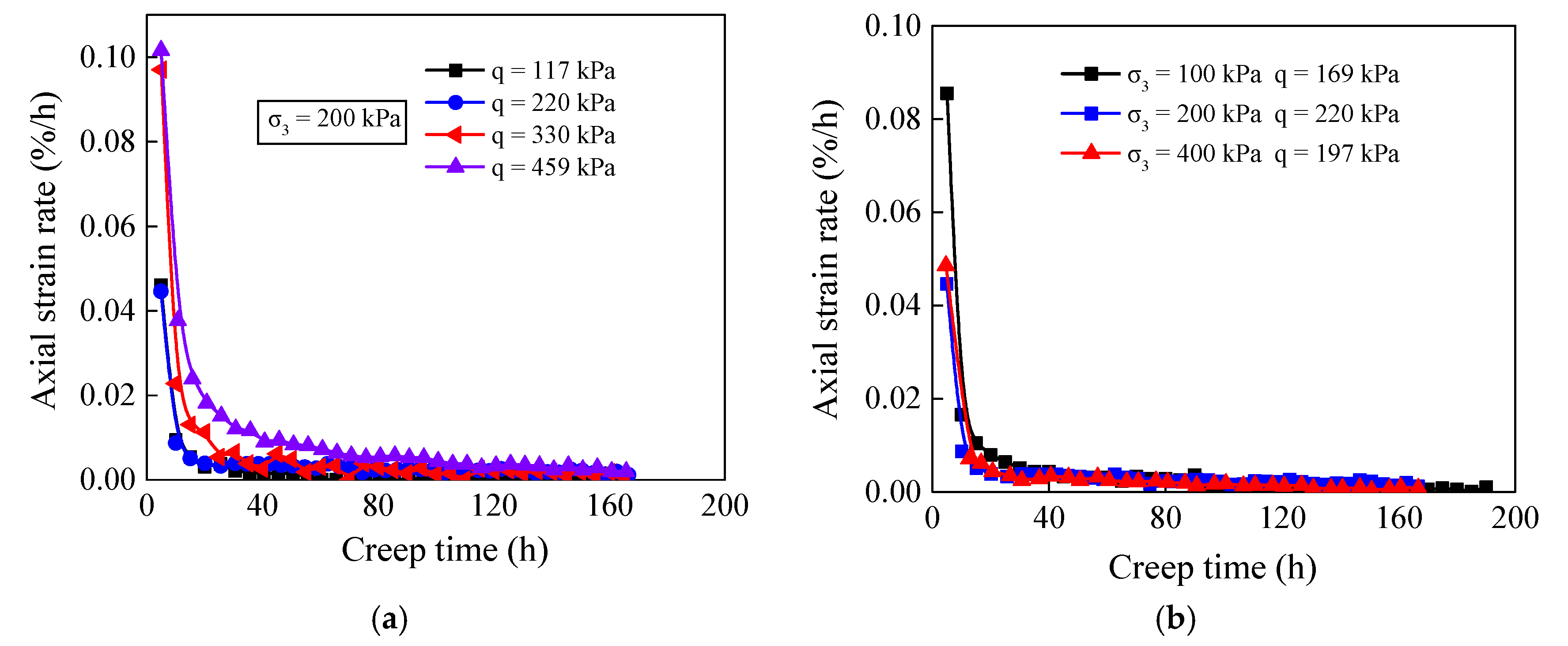
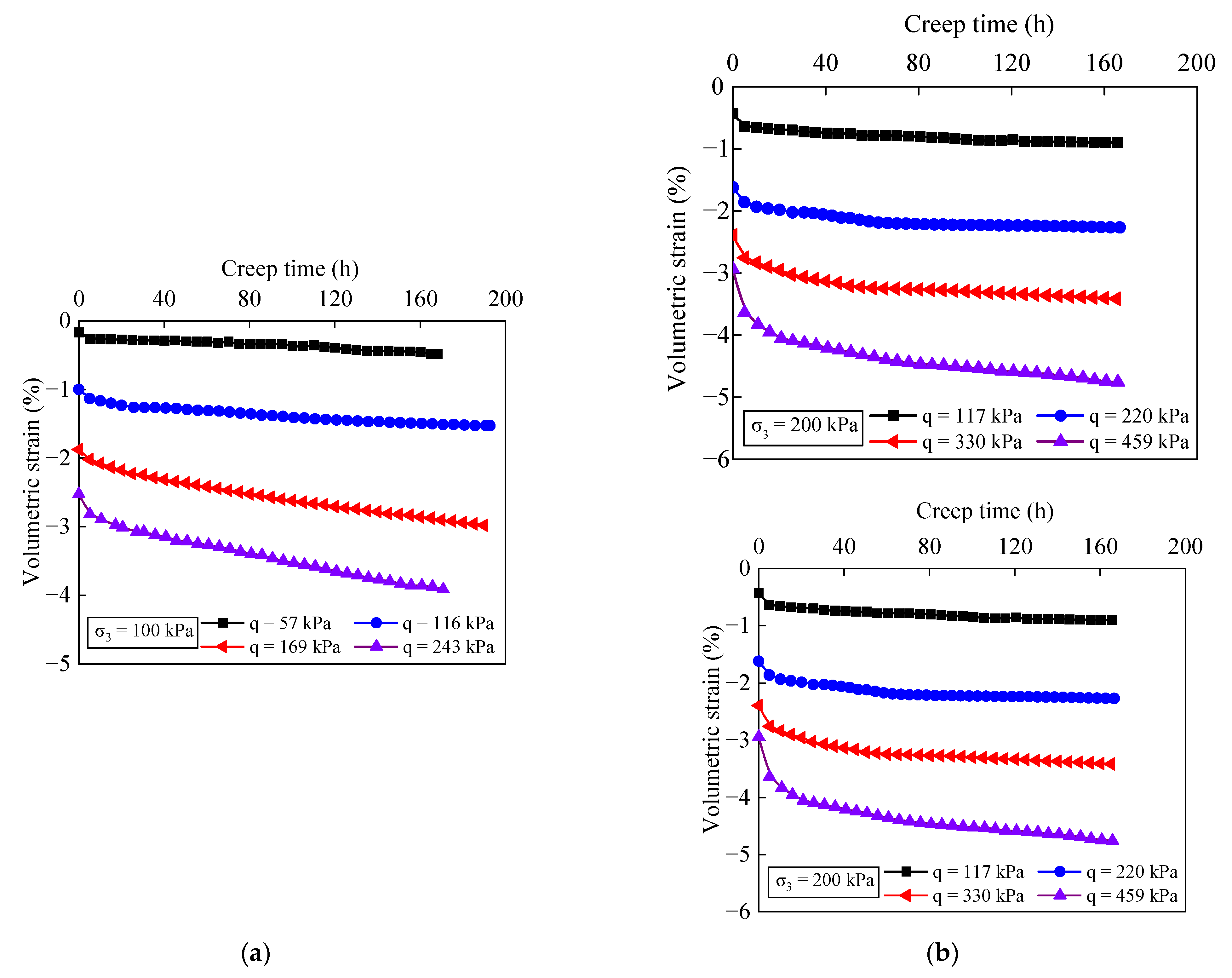
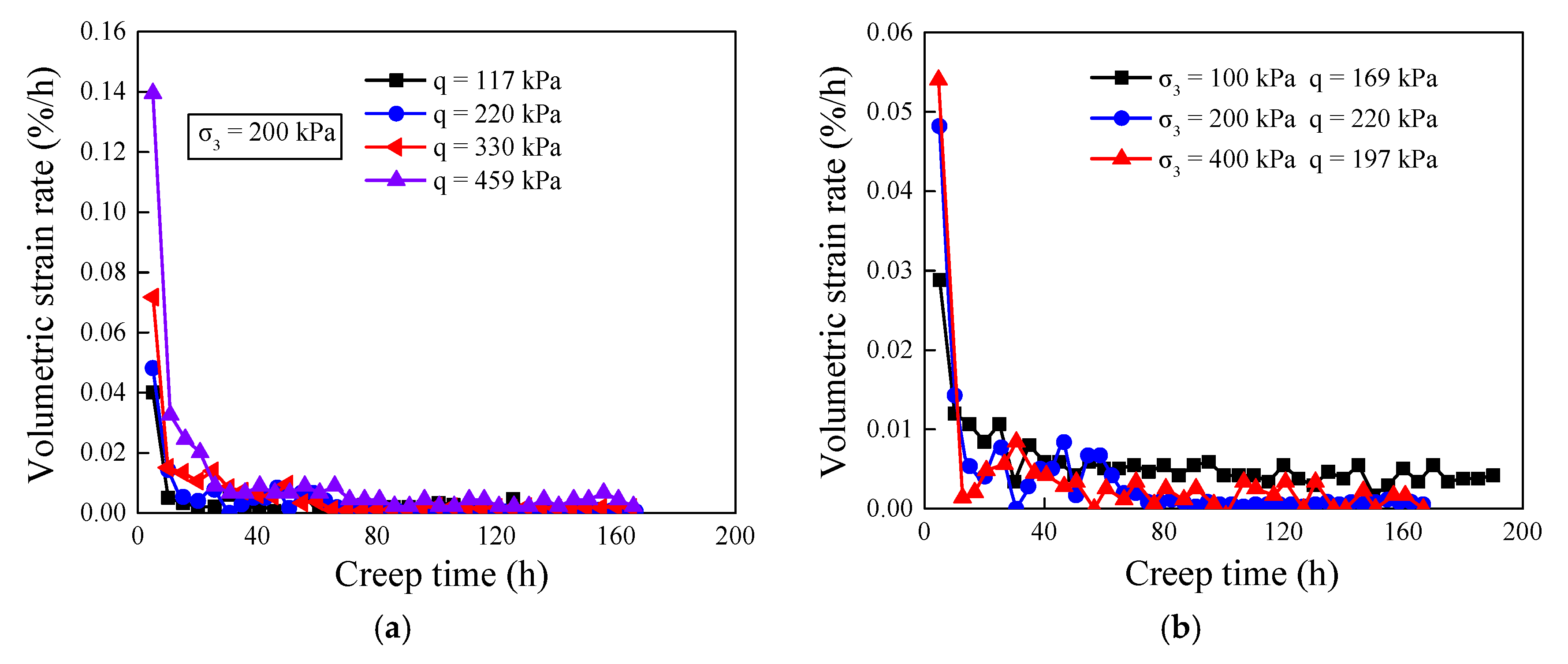
2.3. Test Results and Analysis
3. Fractal Creep Model
3.1. Basic Theory of the Fractal Derivative
3.2. Fractal Dashpot
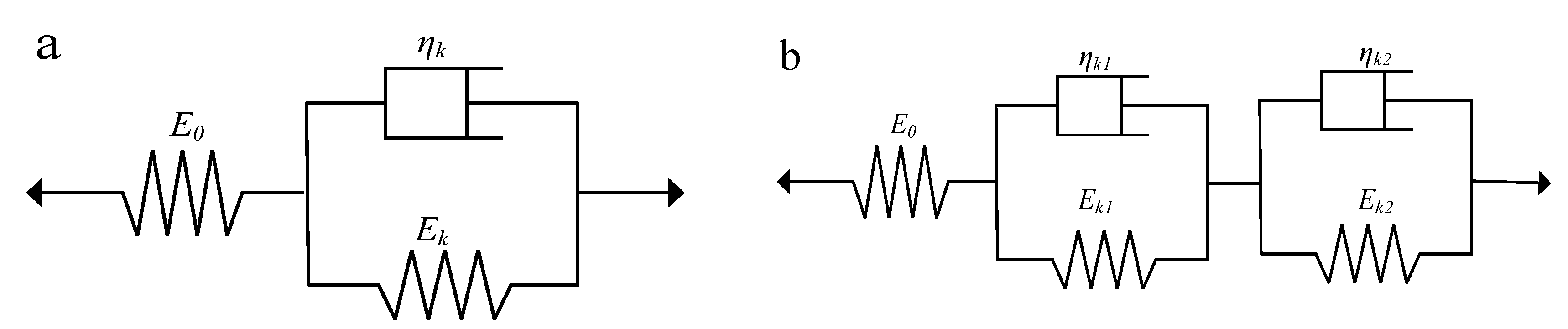
3.3. Fractal Burgers Model
4. Model Verification and Parametric Sensitivity Analysis
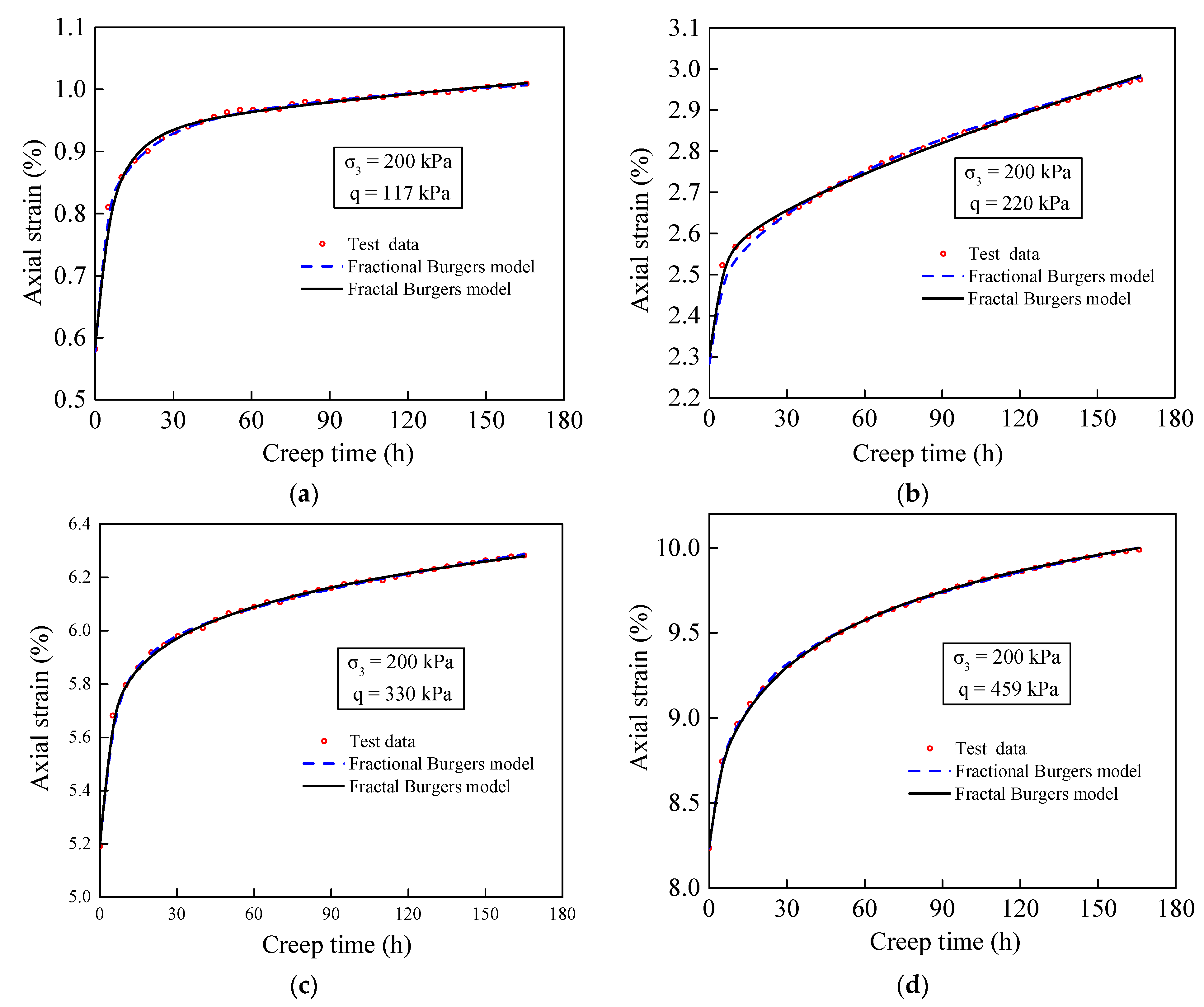
4.1. Fractal Burgers Model Verification
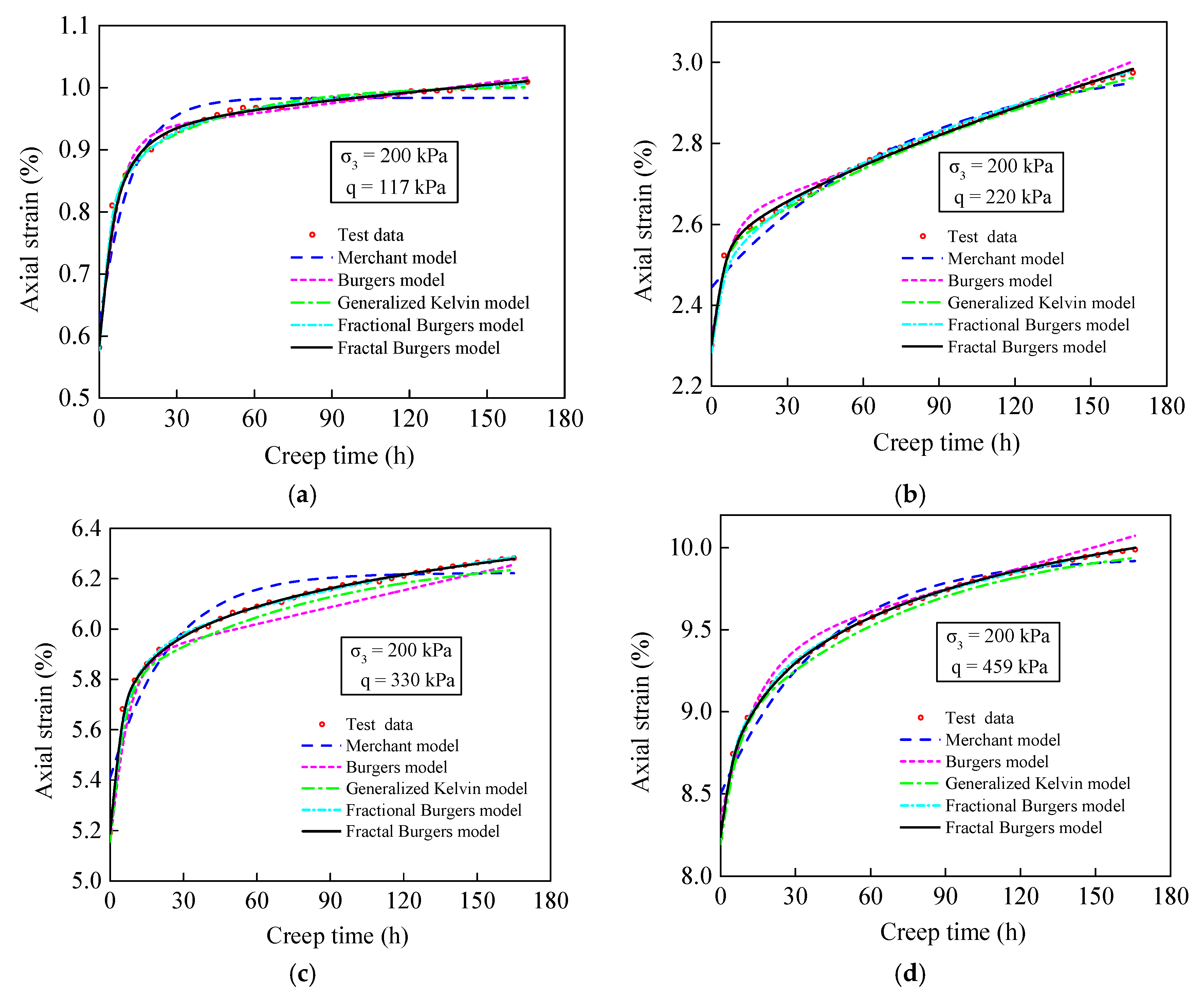
4.2. Model Comparison
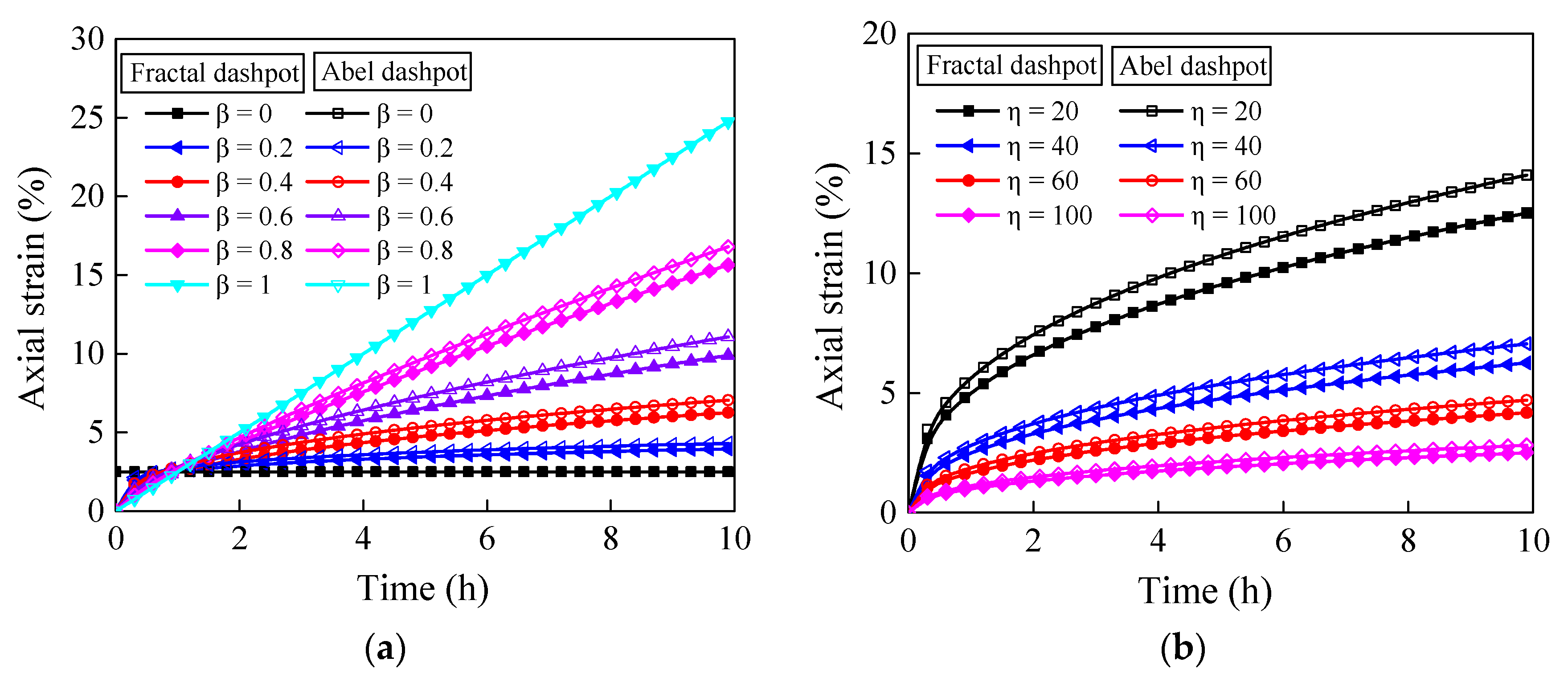
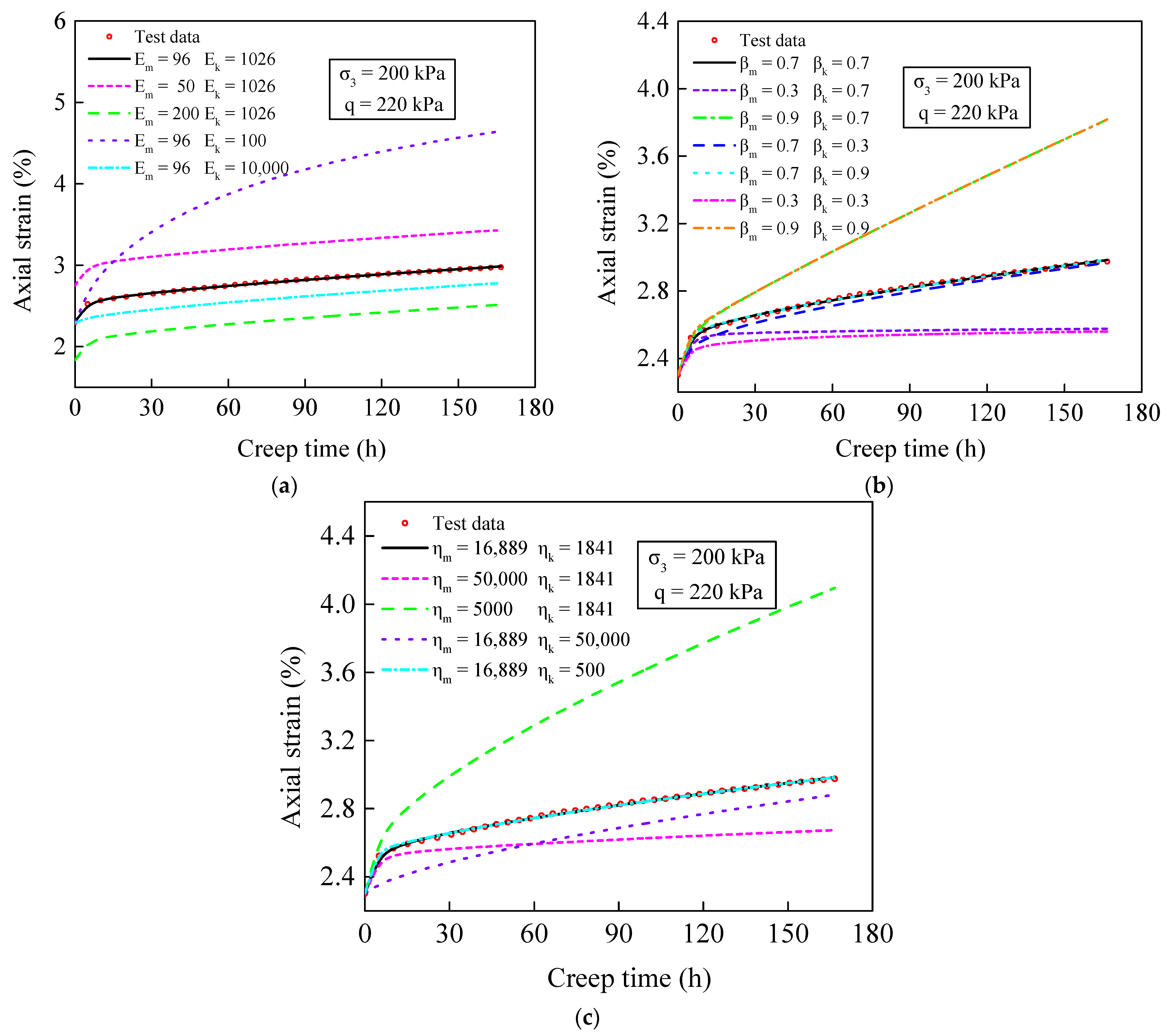
4.3. Fractal Burgers Model Parametric Sensitivity Analysis
5. Discussions
6. Conclusions
- The analysis of the triaxial consolidation drainage test indicates that the stress level and confining pressure have a significant influence on the creep characteristics of the soil. Under the state where the stress level is lower than the failure stress, the creep strain curve presents a transient creep stage and a steady-state creep stage. The soil creep curves exhibit nonlinear viscoelasticity characteristics.
- By validating the test data at different stress levels and confining pressures, the proposed fractal creep model has wide applicability for describing the transient and steady stages of soft soil based on triaxial creep tests. Compared with other creep models widely used in geotechnical materials, the proposed model can more accurately simulate the creep behavior of soil. This model has the advantages of fewer parameters and high accuracy.
- Parameter sensitivity analysis has shown that creep characteristics are the result of the combined action of multiple elements and multiple factors at the same time. Among them, the fractal derivative order is the key factor controlling the strain rate. The viscosity coefficient mainly affects the nonlinear morphology of the curve, and the creep curve of different modes can be obtained by adjusting the derivative order and viscosity coefficient in the equation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, S.; Yin, Y.; Li, B.; Wei, Y.J. Shear creep characteristics of weak carbonaceous shale in thick layered Permian limestone, southwestern China. J. Earth Syst. Sci. 2019, 128, 28. [Google Scholar] [CrossRef] [Green Version]
- Miao, H.B.; Wang, G.H. Effects of clay content on the shear behaviors of sliding zone soil originating from muddy interlayers in the Three Gorges Reservoir, China. Eng. Geol. 2021, 294, 106380. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.G.; Wu, W.; Cui, D.S.; Su, A.J.; Xiang, W. Creep properties of clastic soil in a reactivated slow-moving landslide in the Three Gorges Reservoir Region, China. Eng. Geol. 2020, 267, 105493. [Google Scholar] [CrossRef]
- Miao, F.S.; Zhao, F.C.; Wu, Y.P.; Li, L.W.; Xue, Y.; Meng, J.J. A novel seepage device and ring-shear test on slip zone soils of landslide in the Three Gorges Reservoir area. Eng. Geol. 2022, 307, 106779. [Google Scholar] [CrossRef]
- Yao, Y.P.; Huang, J.; Wang, N.D.; Luo, T.; Han, L.M. Prediction method of creep settlement considering abrupt factors. Transp. Geotech. 2020, 22, 100304. [Google Scholar] [CrossRef]
- Ding, P.; Xu, R.Q.; Zhu, Y.H.; Wen, M.J. Fractional derivative modelling for rheological consolidation of multilayered soil under time-dependent loadings and continuous permeable boundary conditions. Acta Geotech. 2022, 17, 2287–2304. [Google Scholar] [CrossRef]
- Jessen, J.; Cudmani, R. Rate- and Time-Dependent Mechanical Behavior of Foam-Grouted Coarse-Grained Soils. J. Geotech. Geoenvironmental Eng. 2022, 148, 04022022. [Google Scholar] [CrossRef]
- Oliveira, P.J.V.; Santos, S.L.; Correia, A.A.S.; Lemos, L.J.L. Numerical prediction of the creep behaviour of an embankment built on soft soils subjected to preloading. Comput. Geotech. 2019, 114, 103140. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, Y.; Shen, Y. Mathematical aspect of the state-dependent stress-dilatancy of granular soil under triaxial loading. Géotechnique 2019, 69, 158–165. [Google Scholar] [CrossRef]
- Li, D.W.; Zhang, C.C.; Ding, G.S.; Zhang, H.; Chen, J.H.; Cui, H.; Pei, W.S.; Wang, S.F.; An, L.S.; Li, P.; et al. Fractional derivative-based creep constitutive model of deep artificial frozen soil. Cold Reg. Sci. Technol. 2020, 170, 102942. [Google Scholar] [CrossRef]
- Singh, A.; Mitchell, J.K. General stress-strain-time function for soils. J. Soil Mech. Found Eng. Div. 1968, 94, 21–46. [Google Scholar] [CrossRef]
- Mesri, G.; Febres-Cordero, E.; Shields, D.R.; Castro, A. Shear stress –strain-time behaviour of clays. Géotechnique 1981, 31, 537–552. [Google Scholar] [CrossRef]
- Schiessel, H.; Metzler, R.; Blumen, A.; Nonnenmacher, T.F. Generalized viscoelastic models: Their fractional equations with solutions. J. Phys. A Math. Gen. 1995, 28, 65–67. [Google Scholar] [CrossRef]
- Sun, J. Rheology of Geotechnical Materials and Its Engineering Application; China Construction Industry Press: Beijing, China, 1999. [Google Scholar]
- Nishihara, M. Rheological properties of rocks I and II. Doshisha Eng. Rev. 1958, 8, 32–35, 85–115. [Google Scholar]
- Hou, F.; Lai, Y.M.; Liu, E.L.; Luo, H.W.; Liu, X.Y. A creep constitutive model for frozen soils with different contents of coarse grains. Cold Reg. Sci. Technol. 2018, 145, 119–126. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Wang, T. On creep behavior of mudstone in the Tianshui area, China. Bull. Eng. Geol. Environ. 2022, 81, 321. [Google Scholar] [CrossRef]
- Ye, J.H.; Haiyilati, Y.; Cao, M.; Zuo, D.J.; Chai, X.W. Creep characteristics of calcareous coral sand in the South China Sea. Acta Geotech. 2022, 148, 04022022. [Google Scholar] [CrossRef]
- Tian, X.W.; Xiao, H.B.; Li, Z.Y.; Su, H.Y.; Ouyang, Q.W.; Luo, S.P.; Yu, X.P. A Fractional Order Creep Damage Model for Microbially Improved Expansive Soils. Front. Earth Sci. 2022, 10, 942844. [Google Scholar] [CrossRef]
- Xu, B.X.; Cui, Z.D. Investigation of a fractional derivative creep model of clay and its numerical implementation. Comput. Geotech. 2020, 119, 103387. [Google Scholar] [CrossRef]
- Xiang, G.J.; Yin, D.S.; Cao, C.X.; Gao, Y.F. Creep modelling of soft soil based on the fractional flow rule: Simulation and parameter study. Appl. Math. Comput. 2021, 403, 126190. [Google Scholar] [CrossRef]
- Liang, Y.J.; Guan, P.Y. Improved Maxwell model with structural dashpot for characterization of ultraslow creep in concrete. Constr. Build. Mater. 2022, 329, 127181. [Google Scholar] [CrossRef]
- Wu, F.; Zhou, X.H.; Ying, P.; Li, C.B.; Zhu, Z.M.; Chen, J. A Study of Uniaxial Acoustic Emission Creep of Salt Rock Based on Improved Fractional-Order Derivative. Rock Mech. Rock Eng. 2022, 55, 1619–1631. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.W.; Wang, X.Y.; Wang, L.; Su, T.; Wei, Q.; Deng, T.F. A triaxial creep model for deep coal considering temperature effect based on fractional derivative. Acta Geotech. 2022, 17, 1739–1751. [Google Scholar] [CrossRef]
- Liao, M.K.; Lai, Y.M.; Liu, E.L.; Wan, X.S. A fractional order creep constitutive model of warm frozen silt. Acta Geotech. 2017, 12, 377–389. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, C.J.; Jin, H.J.; Feng, W.J.; Jin, D.D.; Zhang, G.K. A creep model for frozen soil based on the fractional Kelvin–Voigt’s model. Acta Geotech. 2022, 271, 1–17. [Google Scholar] [CrossRef]
- Cai, W.; Chen, W.; Xu, W.X. Characterizing the creep of viscoelastic materials by fractal derivative models. Int. J. Non-Linear Mech. 2016, 87, 58–63. [Google Scholar] [CrossRef]
- Liang, Y.J.; Ye, A.Q.; Chen, W.; Gatto, R.G.; Colon-Perez, L.; Mareci, T.H.; Magin, R.L. A fractal derivative model for the characterization of anomalous diffusion in magnetic resonance imaging. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 529–537. [Google Scholar] [CrossRef]
- Reyes-Marambio, J.; Moser, F.; Gana, F.; Seveion, B.; Calderom-Muno, W.R.; Palma-Behnke, R.; Estevez, P.A.; Orchard, M.; Cortes, M. A fractal time thermal model for predicting the surface temperature of air-cooled cylindrical Li-ion cells based on experimental measurements. J. Power Sources 2016, 306, 636–645. [Google Scholar] [CrossRef]
- Mashayekhi, S.; Hussaini, M.Y.; Oates, W. A physical interpretation of fractional viscoelasticity based on the fractal structure of media: Theory and experimental validation. J. Mech. Phys. Solids 2019, 128, 137–150. [Google Scholar] [CrossRef]
- Su, X.L.; Chen, W.; Xu, W. Characterizing the rheological behaviors of non-Newtonian fluid via a viscoelastic component: Fractal dashpot. Adv. Mech. Eng. 2017, 9, 968738. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, Z.; Zhou, H.W.; Liu, J.F. A fractal derivative constitutive model for three stages in granite creep. Results Phys. 2017, 7, 2632–2638. [Google Scholar] [CrossRef]
- Yao, W.M.; Hu, B.; Zhan, H.B.; Ma, C.; Zhao, N.H. A novel unsteady fractal derivative creep model for soft interlayers with varying water contents. KSCE J. Civ. Eng. 2019, 23, 5064–5075. [Google Scholar] [CrossRef]
- Kabwe, E.; Karakus, M.; Chanda, E.K. Isotropic damage constitutive model for time-dependent behaviour of tunnels in squeezing ground. Comput. Geotech. 2020, 127, 103738. [Google Scholar] [CrossRef]
- Gao, L.C.; Dai, G.L.; Wan, Z.H.; Zhu, M.X.; Zhu, W.B. Prediction of triaxial drained creep behaviors of interactive marine-terrestrial deposit soils by fractal derivative. Eur. J. Environ. Civ. Eng. 2022, 26, 3065–3078. [Google Scholar] [CrossRef]
- GB 50021-2001; Code for Investigation of Geotechnical Engineering. China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2001.
- GB/T 50123-2019; Standard for Soil Test Method. China Planning Press: Beijing, China, 2019.
- Yuan, J.Y.; Xu, C.; Zhao, C.F.; He, Z.M.; Gao, Y.B.; Su, X.; Chen, B.; Wei, D.D. Geotechnical Test and In-Situ Test; Tongji University Press: Shanghai, China, 2004. [Google Scholar]
- Deng, H.Y.; Dai, G.L.; Qiu, G.Y.; Chen, Z.S.; Lin, X. Drained creep test and component creep model of soft silty clay in Hangzhou Bay. J. Southeast Univ. Nat. Sci. Ed. 2021, 51, 318–324. [Google Scholar]
- Kong, L.W.; Zhang, X.W.; Guo, A.G.; Cai, Y. Creep behavior of Zhanjiang strong structured clay by drained triaxial test. Chin. J. Rock Mech. Eng. 2011, 30, 365–372. [Google Scholar]
- Zhao, D.; Gao, Q.F.; Hattab, M.; Hicher, P.Y.; Yin, Z.Y. Microstructural evolution of remolded clay related to creep. Transp. Geotech. 2020, 24, 100367. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA; London, UK, 1999. [Google Scholar]
- Zhou, H.W.; Wang, C.P.; Mishnaevsky, L.; Duan, Z.Q.; Ding, J.Y. A fractional derivative approach to full creep regions in salt rock. Mech. Time-Depend. Mater. 2013, 17, 413–425. [Google Scholar] [CrossRef]
- Bateman, H.; Erdelyi, A. Higher Transcendental Functions; McGraw-Hill Company: New York, NY, USA, 1953. [Google Scholar]
- Zhang, C.C.; Zhu, H.H.; Shi, B.; Liu, L.C. Theoretical investigation of interaction between a rectangular plate and fractional viscoelastic foundation. J. Rock Mech. Geotech. Eng. 2015, 45, 324–335. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Liu, R.; Qiu, C.L.; Tan, R.J. Establishment and Application of Creep Constitutive Model Related to Stress Level of Soft Soil. J. Tianjin Univ. 2018, 51, 711–719. [Google Scholar]




| Depth (m) | Water Content ω (%) | Unit Weight γ (kN/m3) | Liquid Limit ωL (%) | Plasticity Index Ip (%) |
|---|---|---|---|---|
| 50~55 | 35.4 | 18.6 | 37.5 | 14.8 |
| Test No. | σ3 (kPa) | qf (kPa) | c′ (kPa) | φ′ (°) |
|---|---|---|---|---|
| 1 | 100 | 288 | 12.4 | 33.7 |
| 2 | 200 | 568 | ||
| 3 | 300 | 836 | ||
| 4 | 400 | 1057 |
| Test No. | σ3 (kPa) | qf (kPa) | q (kPa) | Test Time (h) |
|---|---|---|---|---|
| 1 | 100 | 288 | 57 | 170 |
| 2 | 116 | 190 | ||
| 3 | 169 | 190 | ||
| 4 | 243 | 170 | ||
| 5 | 200 | 568 | 117 | 170 |
| 6 | 220 | 170 | ||
| 7 | 330 | 170 | ||
| 8 | 459 | 170 | ||
| 9 | 400 | 1057 | 197 | 170 |
| 10 | 422 | 170 | ||
| 11 | 617 | 170 | ||
| 12 | 863 | 170 |
| Hooke Spring | Newton Dashpot | Abel Dashpot | Fractal Dashpot | |
|---|---|---|---|---|
| Symbol | 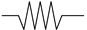 |  | 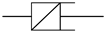 | 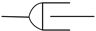 |
| Constitutive modelRelations | ||||
| Relationship of stress and strain | ||||
| The order value | ||||
| Creep model | traditional model | traditional model | fractional model | fractal model |
| σ3 (kPa) | q (kPa) | β | Em (kPa) | ηm (kPa·hβ) | Ek (kPa) | ηk (kPa·hβ) | R2 |
|---|---|---|---|---|---|---|---|
| 200 | 117 | 0.7 | 200 | 47483 | 347 | 1169 | 0.996 |
| 220 | 0.7 | 96 | 16889 | 1026 | 1841 | 0.999 | |
| 330 | 0.4 | 64 | 5546 | 511 | 1045 | 0.999 | |
| 459 | 0.5 | 56 | 18917 | 266 | 1872 | 0.999 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Q.; Dai, J.; Dai, G.; Gong, W.; Zhang, F.; Zhu, M. Study on Creep Behavior of Silty Clay Based on Fractal Derivative. Appl. Sci. 2022, 12, 8327. https://doi.org/10.3390/app12168327
Yin Q, Dai J, Dai G, Gong W, Zhang F, Zhu M. Study on Creep Behavior of Silty Clay Based on Fractal Derivative. Applied Sciences. 2022; 12(16):8327. https://doi.org/10.3390/app12168327
Chicago/Turabian StyleYin, Qian, Junping Dai, Guoliang Dai, Weiming Gong, Fan Zhang, and Mingxing Zhu. 2022. "Study on Creep Behavior of Silty Clay Based on Fractal Derivative" Applied Sciences 12, no. 16: 8327. https://doi.org/10.3390/app12168327
APA StyleYin, Q., Dai, J., Dai, G., Gong, W., Zhang, F., & Zhu, M. (2022). Study on Creep Behavior of Silty Clay Based on Fractal Derivative. Applied Sciences, 12(16), 8327. https://doi.org/10.3390/app12168327






