Data Augmentation in 2D Feature Space for Intelligent Weak Fault Diagnosis of Planetary Gearbox Bearing
Abstract
:Featured Application
Abstract
1. Introduction
2. Theoretical Background
2.1. Cyclostationary Spectrometography
2.2. Fault Classification Model
2.2.1. Convolution Layer
2.2.2. Pooling Layer
2.2.3. Fully Connected Layer
2.2.4. Output Layer
3. The Proposed Method
3.1. Construction of Two-Dimensional Feature Space
3.2. Data Augmentation Based on WSC Image Segmentation
3.3. Model Operation Process
3.4. Fault Diagnosis Based on WSC-CNNs
4. Experimental Validation
4.1. Experimental Setup and Data Description
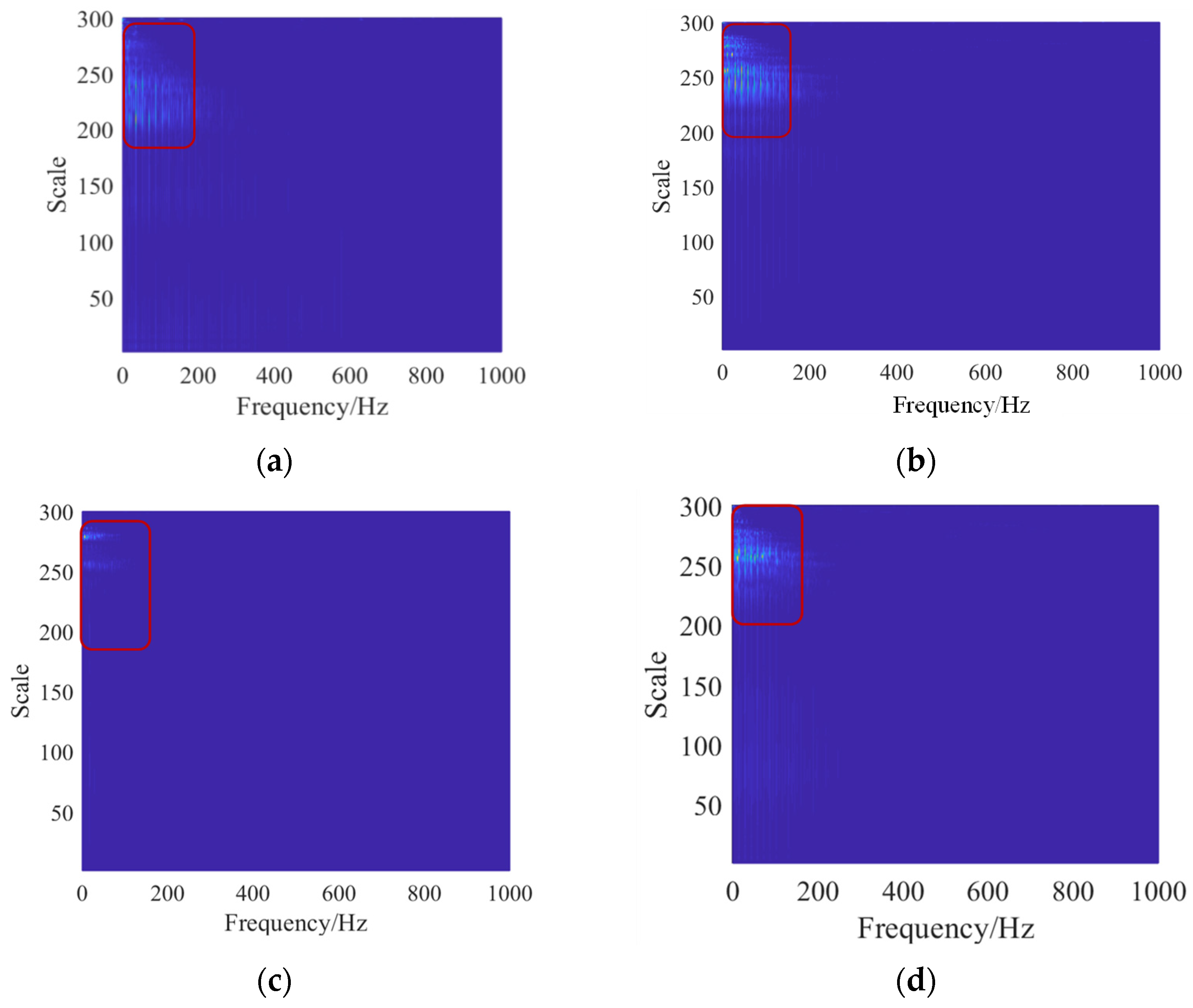
4.2. Analysis of Wavelet Cyclic Spectrum
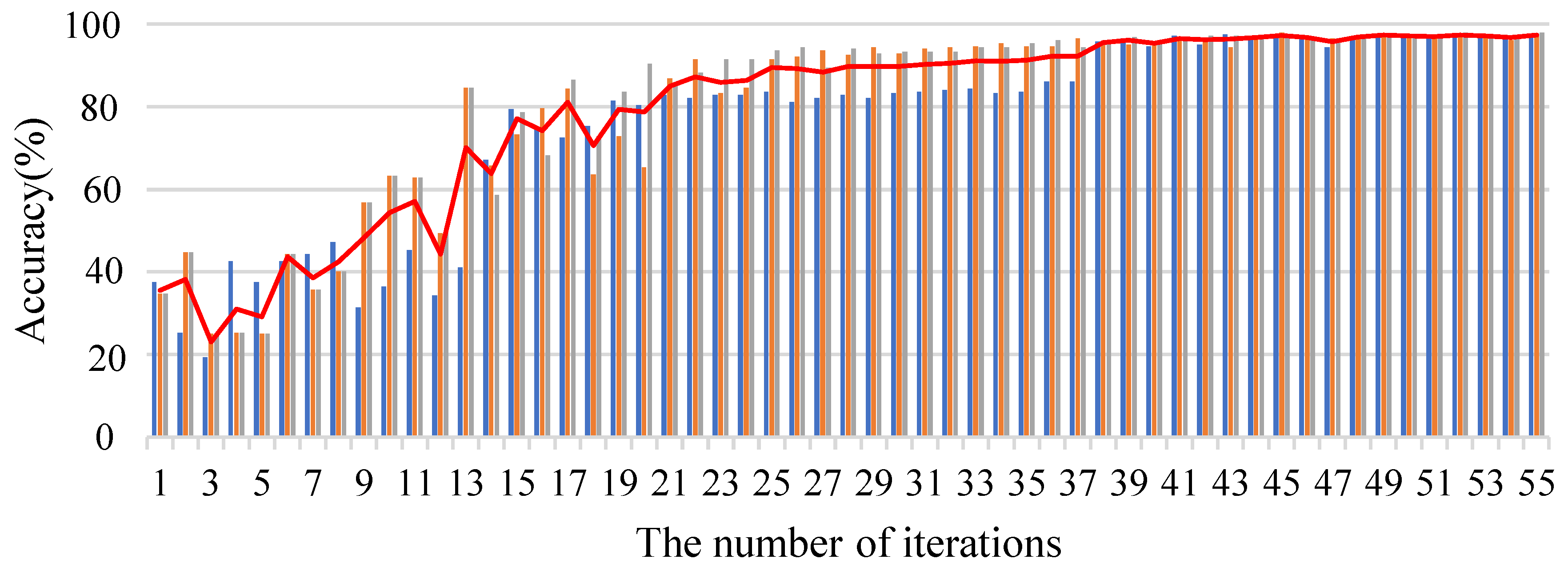
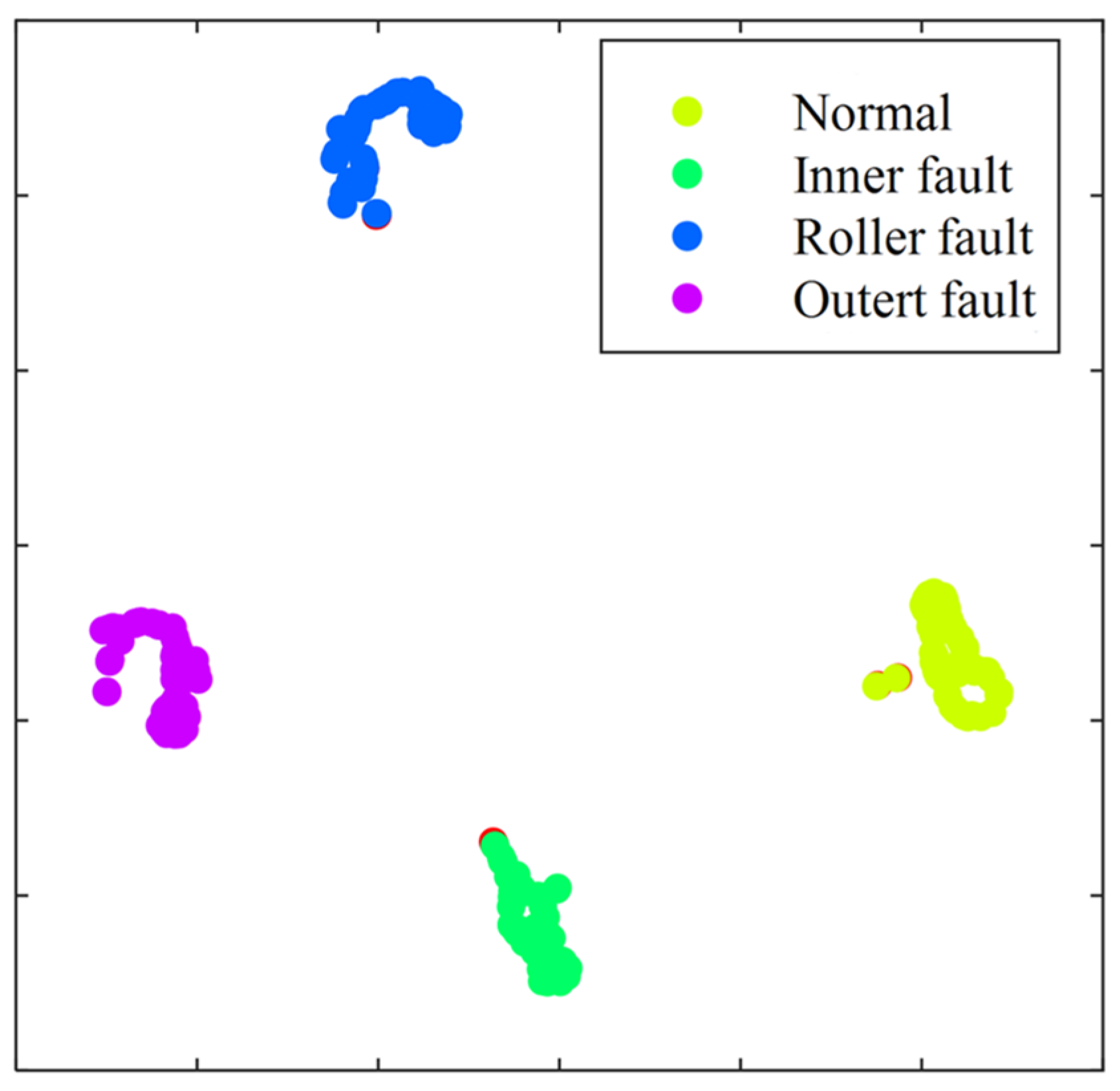
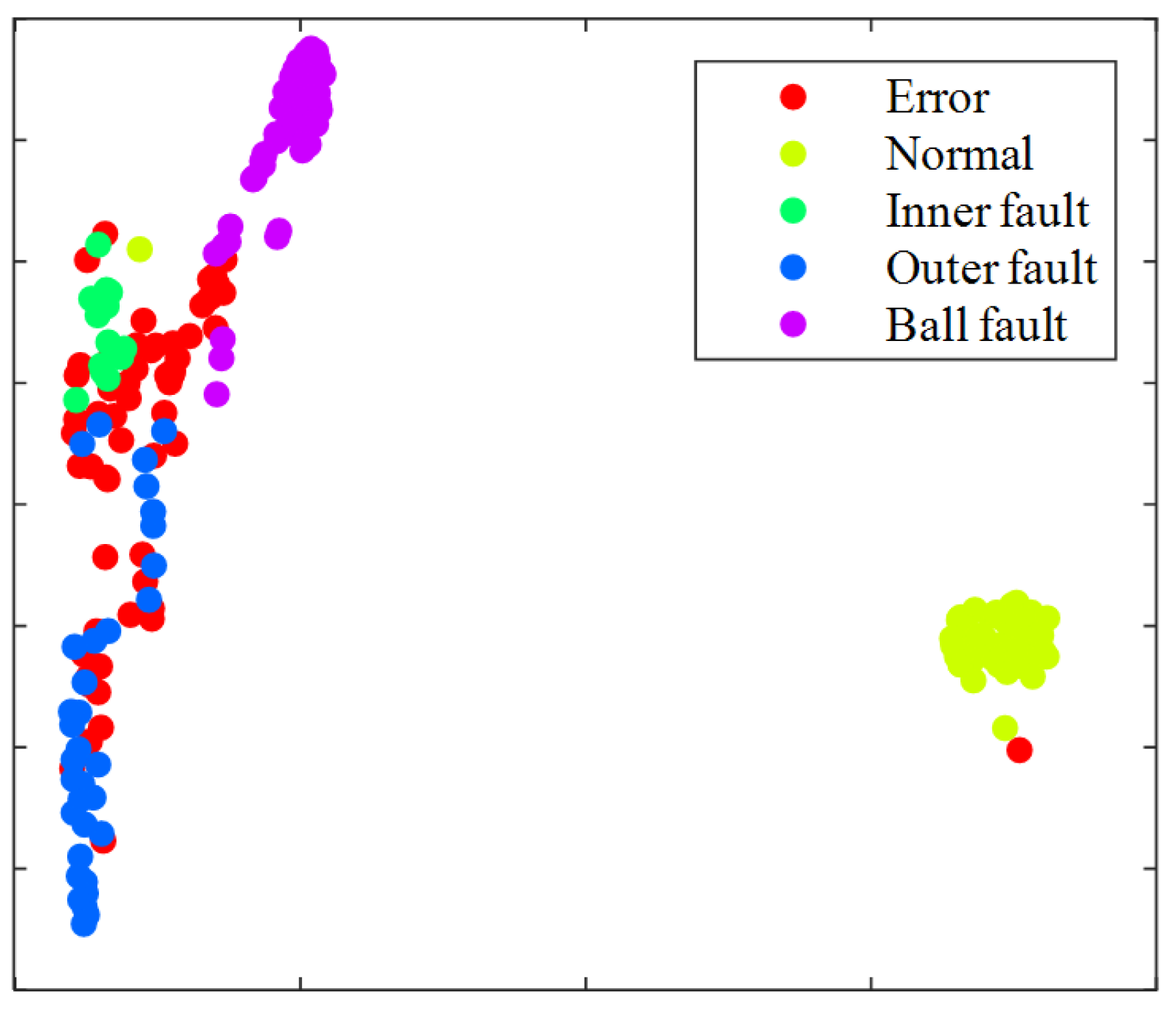
4.3. Fault Diagnosis Based on Data Feature Argumentation and CNN Model
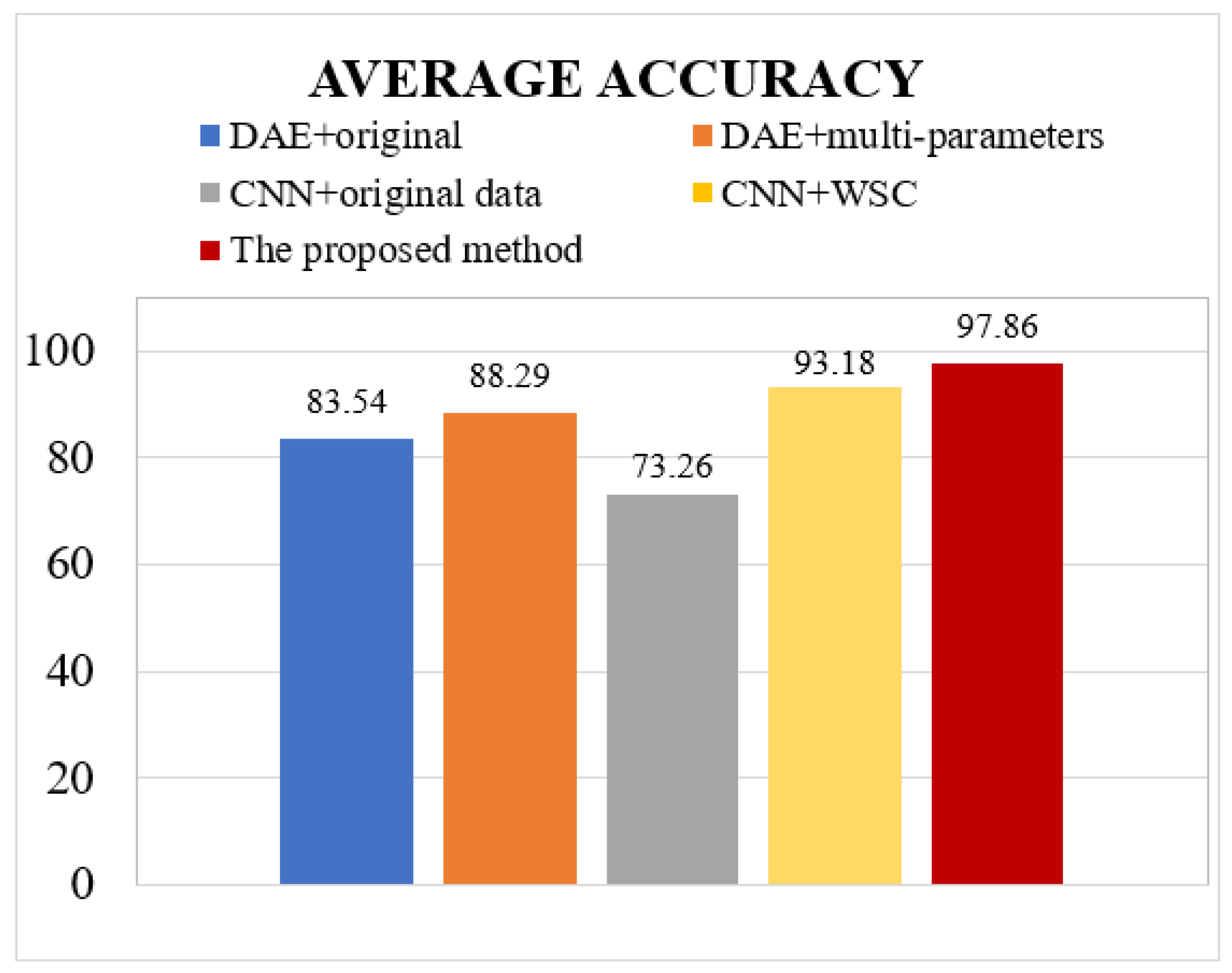
4.4. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Notation | Decipher |
| x(n) | The original signal |
| N | The size of x(n) |
| C1x | First-order cyclic statistics |
| Averaging operator | |
| t | Time |
| T | The period of cyclic statistics |
| Time offset | |
| C2x | Second-order cyclic statistic |
| x* | The conjugate of x |
| Sx(f) | Cyclic autocorrelation function spectrum |
| f | Cyclic frequency |
| Window function | |
| Sampling period | |
| L | |
| m | Spectral frequency points |
| M | The number of sub-segment window function scanned |
| c | Cyclic frequency points |
| N-P | Overlap length |
| Activation values of the i-th neuron in layer l | |
| Bias item | |
| Connection matrix | |
| S | The number of categories |
| Wavelet basis function | |
| a | Scale factor |
| b | Time factor |
| Convolution kernel | |
| B | Convolution layer output feature map |
| The size of sliding convolution window | |
| P | Pooling layer output feature |
| The size of filter and the step length of each movement | |
| fr | Planetary carrier rotation frequency |
| fs | Sun gear rotation frequency |
| fib | Planetary bearing inner race fault characteristic frequency |
| fob | Planetary bearing outer race fault characteristic frequency |
| frb | Planetary bearing rolling elements fault characteristic frequency |
References
- Jia, M.; Xu, Y.; Hong, M.; Hu, X. Multitask Convolutional Neural Network for Rolling Element Bearing Fault Identification. Shock. Vib. 2020, 2, 1–10. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J. Multi-fault diagnosis for rolling element bearings based on ensemble empirical mode decomposition and optimized support vector machines. Mech. Syst. Signal Processing 2013, 41, 127–140. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Processing 2016, 72–73, 303–315. [Google Scholar] [CrossRef]
- Cao, H.; Shao, H.; Zhong, X.; Deng, Q.; Yang, X.; Xuan, J. Unsupervised domain-share CNN for machine fault transfer diagnosis from steady speeds to time-varying speeds. J. Manuf. Syst. 2022, 62, 186–198. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Zhan, Z.; Wu, Q. A robust construction of normalized CNN for online intelligent condition monitoring of rolling bearings considering variable working conditions and sources. Measurement 2021, 174, 108973. [Google Scholar] [CrossRef]
- Han, T.; Zhang, L.; Yin, Z.; Tan, A. Rolling bearing fault diagnosis with combined convolutional neural networks and support vector machine. Measurement 2021, 177, 109022. [Google Scholar] [CrossRef]
- Chen, Z.; Li, W. Bearing Fault Feature Extraction and Fault Diagnosis Method Based on Feature Fusion Sensors. IEEE Trans. Instrum. Meas. 2017, 66, 1693–1702. [Google Scholar] [CrossRef]
- Jiang, H.; Li, X.; Shao, H.; Zhao, K. Intelligent fault diagnosis of rolling bearings using an improved deep recurrent neural network. Meas. Sci. Technol. 2018, 29, 65107. [Google Scholar] [CrossRef]
- He, Z.; Shao, H.; Jing, L.; Cheng, J.; Yang, Y. Transfer fault diagnosis of bearing installed in different machines using enhanced deep auto-encoder. Measurement 2020, 152, 107393. [Google Scholar]
- Fu, L.; Zhang, L.; Tao, J. An improved deep convolutional neural network with multiscale convolution kernels for fault diagnosis of rolling bearing. Mater. Sci. Eng. 2017, 1043, 52021. [Google Scholar] [CrossRef]
- Wang, F.; Jiang, H.; Shao, H.; Wu, S. An adaptive deep convolutional neural network for rolling bearing fault diagnosis. Meas. Sci. Technol. 2017, 28, 95005. [Google Scholar]
- Feng, J.; Lei, Y.; Lu, N.; Xing, S. Deep normalized convolutional neural network for imbalanced fault classification of machinery and its understanding via visualization. Mech. Syst. Signal Processing 2018, 110, 349–367. [Google Scholar]
- Wang, H.; Xu, J.; Yan, R.; Sun, C.; Chen, X. Intelligent Bearing Fault Diagnosis Using Multi-Head Attention-Based CNN. Procedia Manuf. 2020, 49, 112–118. [Google Scholar] [CrossRef]
- Islam, M.; Kim, J. Automated bearing fault diagnosis scheme using 2D representation of wavelet packet transform and deep convolutional neural network. Comput. Ind. 2019, 106, 142–153. [Google Scholar] [CrossRef]
- Zhu, H.; He, Z.; Wei, J.; Wang, J.; Zhou, H. Bearing Fault Feature Extraction and Fault Diagnosis Method Based on Feature Fusion. Sensors 2021, 21, 2524. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault diagnosis of rolling bearing of wind turbines based on the Variational Mode Decomposition and Deep Convolutional Neural Networks. Appl. Soft Comput. 2020, 95, 106515. [Google Scholar] [CrossRef]
- Shao, H.; Lin, J.; Zhang, L.; Galar, D.; Kumar, U. A novel approach of multisensory fusion to collaborative fault diagnosis in maintenance. Inf. Fusion 2021, 74, 65–76. [Google Scholar] [CrossRef]
- Napolitano. Cyclostationarity: New trends and applications. Signal Processing 2016, 120, 385–408. [Google Scholar] [CrossRef]
- Dalpiaz, G.; Rivola, A.; Rubini, R. Effectiveness and sensitivity of vibration processing techniques for fault detection in gears. Mech. Syst. Signal Processing 2000, 14, 387–412. [Google Scholar] [CrossRef]
- Bi, G.; Chen, J.; Zhou, F.; He, J. Application of slice spectral correlation density to gear defect detection. Arch. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 1385–1392. [Google Scholar] [CrossRef]
- Antoni, J.; Hanson, D. Detection of Surface Ships from Interception of Cyclostationary Signature with the Cyclic Modulation Coherence. IEEE J. Ocean. Eng. 2012, 37, 478–493. [Google Scholar] [CrossRef]
- Gardner. Exploitation of spectral redundancy in cyclostationary signals. IEEE Signal Processing Mag. 1991, 40, 14–36. [Google Scholar]
- Wang, D.; Shen, C. An equivalent cyclic energy indicator for bearing performance degradation assessment. J. Vib. Control. 2014, 22, 2380–2388. [Google Scholar] [CrossRef]
- Antoni, J.; Xin, G.; Hamzaoui, N. Fast computation of the spectral correlation. Mech. Syst. Signal Processing 2017, 92, 248–277. [Google Scholar] [CrossRef]
- Yang, R.; Li, H.; He, C.; Zhang, Z. Rolling element bearing weak fault diagnosis based on optimal wavelet scale cyclic frequency extraction. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2018, 232, 895–908. [Google Scholar] [CrossRef]
- Li, H.; Yang, R.; Wang, C.; He, C. Investigation on Planetary Bearing Weak Fault Diagnosis based on a Fault model and Improved Wavelet Ridge. Energies 2018, 11, 1286. [Google Scholar] [CrossRef]





| Layer | Operation | Number of Filters | Filter Size | Activation Function | Output Size |
|---|---|---|---|---|---|
| Input | / | / | / | / | (100, 100) |
| Conv | Kernels | 20 | 3 × 3 | ReLu | (98, 98, 20) |
| Pooling | Pooling size | / | 2 × 2 | Ave | (49, 49, 20) |
| Conv | Kernels | 20 | 2 × 2 | ReLu | (48, 48, 20) |
| Pooling | Pooling size | / | 2 × 2 | Ave | (24, 24, 20) |
| FC | / | 120 | / | ReLu | (120, 1) |
| FC | / | C | / | Softmax | (C, 1) |
| Fault Type Number | Fault Location | Training Sample Size | Testing Sample Size |
|---|---|---|---|
| 1 | Normal | 400 | 70 |
| 2 | Inner-race Fault | 400 | 70 |
| 3 | Outer-race Fault | 400 | 70 |
| 4 | Ball Fault | 400 | 70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; An, Z.; Huang, W.; Wang, R. Data Augmentation in 2D Feature Space for Intelligent Weak Fault Diagnosis of Planetary Gearbox Bearing. Appl. Sci. 2022, 12, 8414. https://doi.org/10.3390/app12178414
Yang R, An Z, Huang W, Wang R. Data Augmentation in 2D Feature Space for Intelligent Weak Fault Diagnosis of Planetary Gearbox Bearing. Applied Sciences. 2022; 12(17):8414. https://doi.org/10.3390/app12178414
Chicago/Turabian StyleYang, Rui, Zenghui An, Weiling Huang, and Rijun Wang. 2022. "Data Augmentation in 2D Feature Space for Intelligent Weak Fault Diagnosis of Planetary Gearbox Bearing" Applied Sciences 12, no. 17: 8414. https://doi.org/10.3390/app12178414






