Experimental Investigation and Applicability of Multi-Stage Simulations in the Case of a Thick-Walled Injection-Moulded Composite
Abstract
:1. Introduction
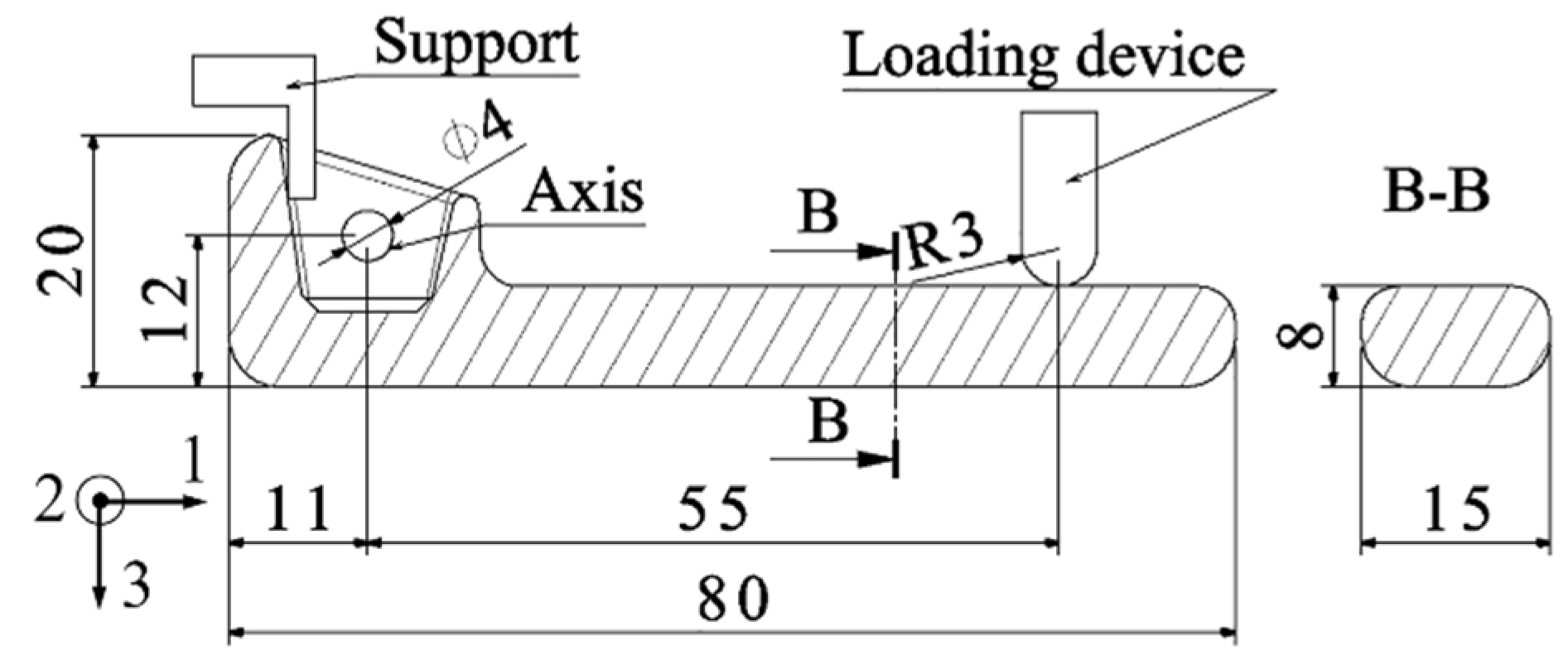
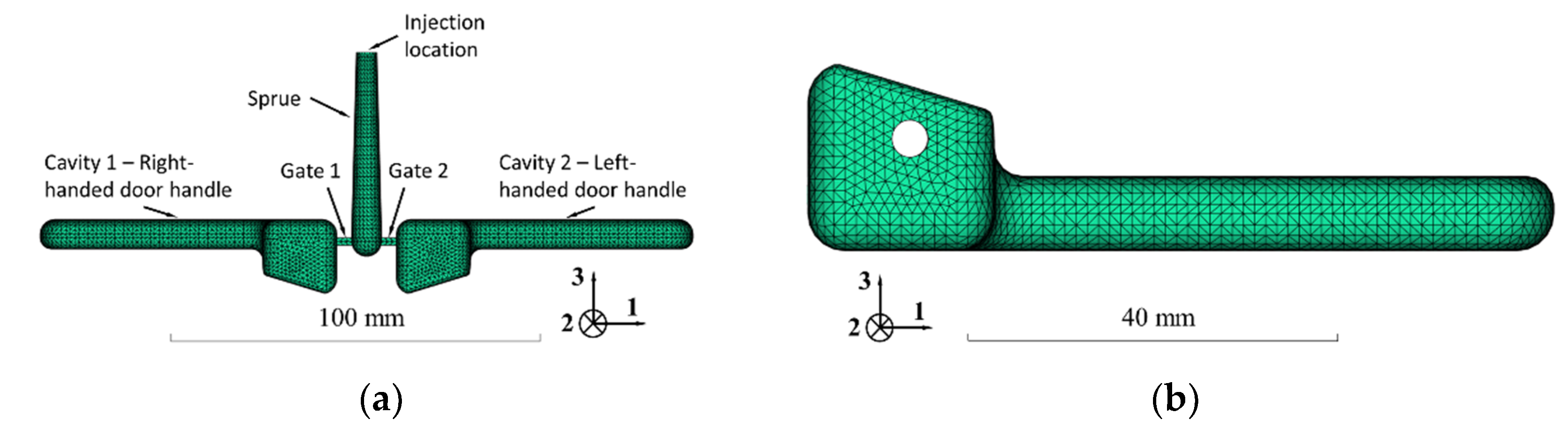
2. Materials and Methods
3. Results
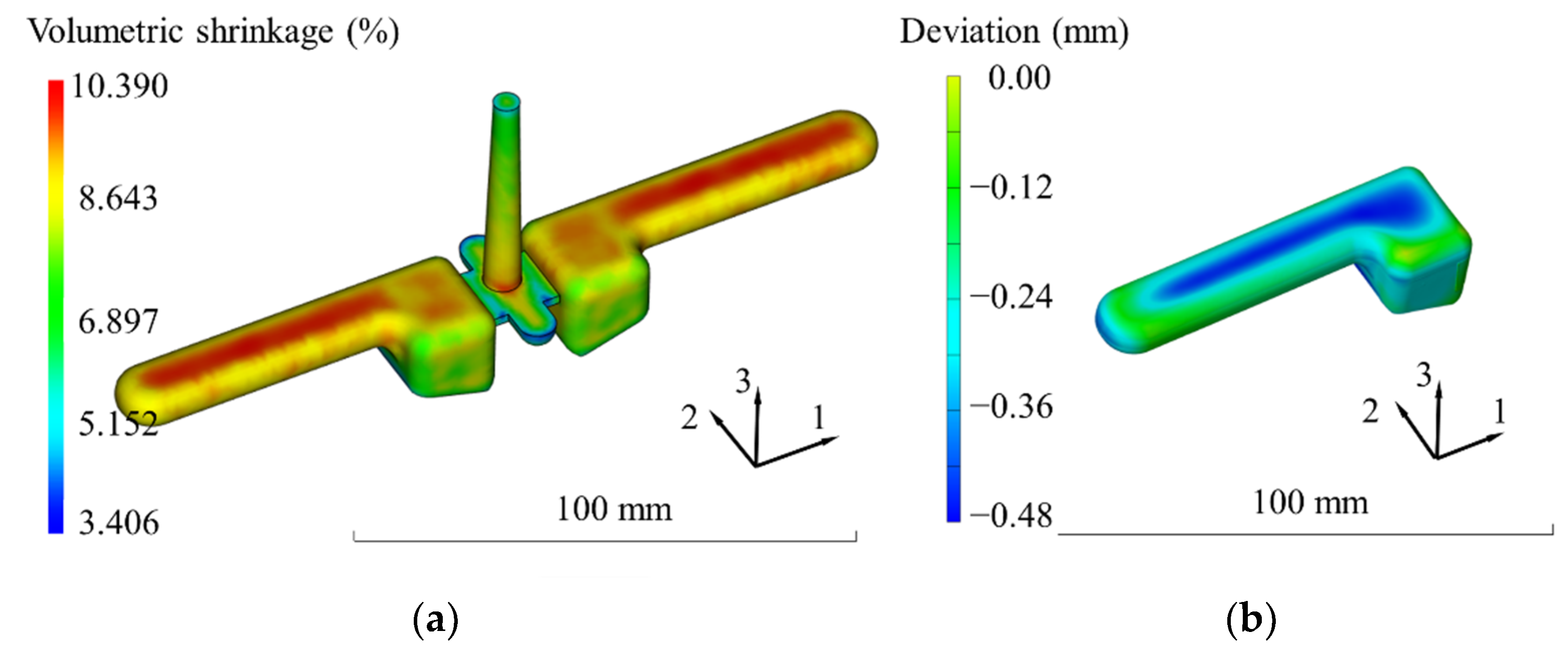
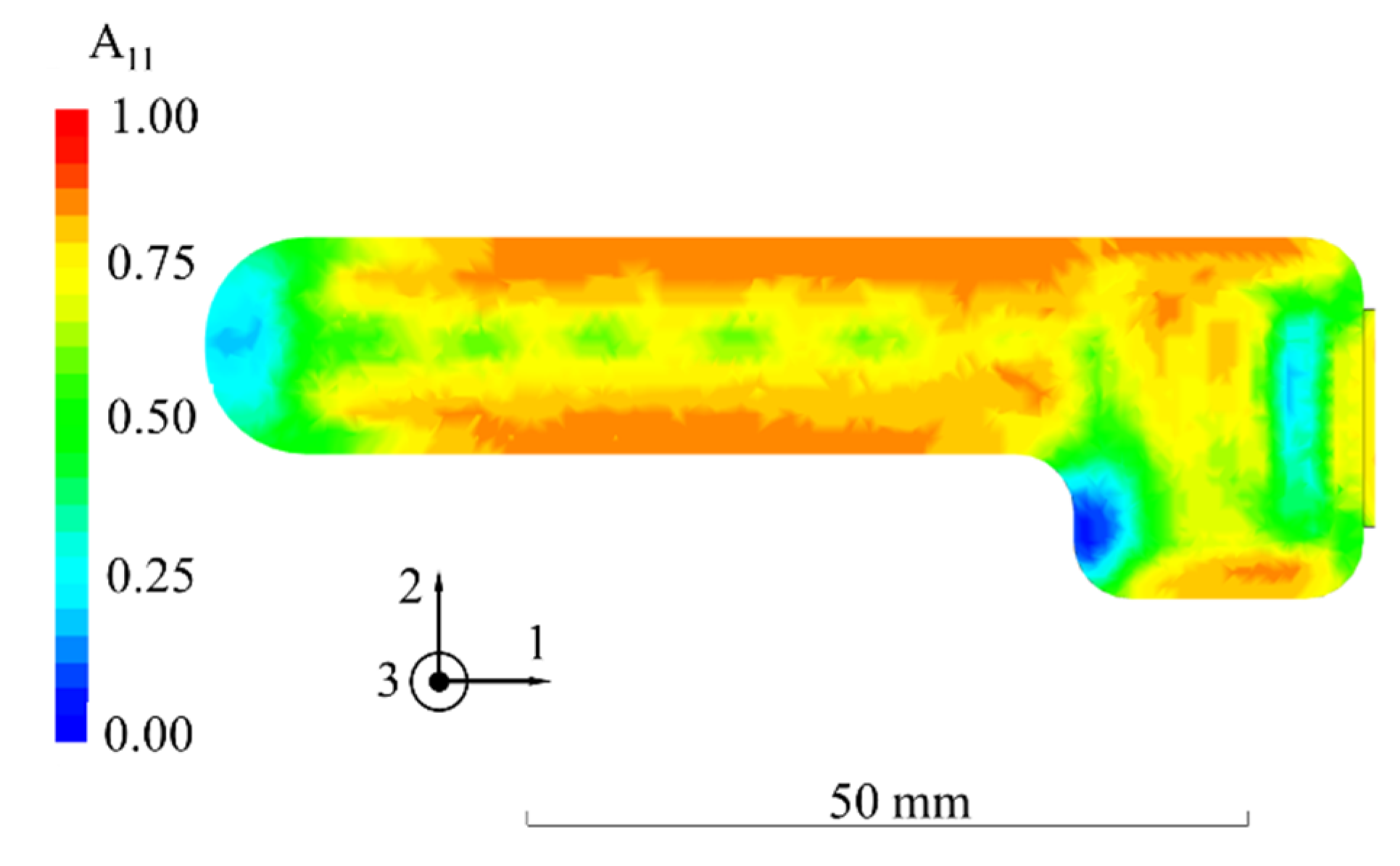
3.1. Validation of Process Simulation
3.2. Validation of FE Analysis
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nian, S.C.; Li, M.H.; Huang, M.S. Warpage control of headlight lampshades fabricated using external gas-assisted injection molding. Int. J. Heat Mass Transf. 2015, 86, 358–368. [Google Scholar] [CrossRef]
- Liu, X.; Pan, Y.; Zheng, G.; Liu, H.; Chen, Q.; Dong, M.; Liu, C.; Zhang, J.; Wang, N.; Wujcik, E.K.; et al. Overview of the Experimental Trends in Water-Assisted Injection Molding. Macromol. Mater. Eng. 2018, 303, 13. [Google Scholar] [CrossRef]
- Karger-Kocsis, J.; Kmetty, Á.; Lendvai, L.; Drakopoulos, S.X.; Bárány, T. Water-Assisted Production of Thermoplastic Nanocomposites: A Review. Materials 2015, 8, 72–95. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhao, G.; Dong, G.; Wang, J. Study on reducing sink mark depth of a microcellular injection molded part with many reinforcing ribs. J. Cell Plast. 2016, 52, 479–502. [Google Scholar] [CrossRef]
- Hopmann, C.; Robig, M. Application of a multilayer injection molding process for thick-walled optical components. J. Polym. Eng. 2016, 36, 557–562. [Google Scholar] [CrossRef]
- Sikló, B.; Cameron, K.; Kovács, J.G. Deformation analysis of short glass fiber-reinforced polypropylene injection-molded plastic parts. J. Reinf. Plast. Compos. 2011, 30, 1367–1372. [Google Scholar] [CrossRef]
- Kim, E.G.; Park, J.K.; Jo, S.H. A study on fiber orientation during the injection molding of fiber-reinforced polymeric composites: (Comparison between image processing results and numerical simulation). J. Mater. Process. Technol. 2001, 11, 225–232. [Google Scholar] [CrossRef]
- Folgar, F.; Tucker, C.L. Orientation Behavior of Fibers in Concentrated Suspensions. J. Reinf. Plast. Compos. 1984, 3, 98–119. [Google Scholar] [CrossRef]
- Wang, J.; O’Gara, J.F.; Tucker, C.L. An objective model for slow orientation kinetics in concentrated fiber suspensions: Theory and rheological evidence. J. Rheol. 2008, 52, 1179–1200. [Google Scholar] [CrossRef]
- Phelps, J.H.; Tucker, C.L. An anisotropic rotary diffusion model for fiber orientation in short- and long-fiber thermoplastics. J. Non-Newtonian Fluid Mech. 2009, 156, 165–176. [Google Scholar] [CrossRef]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H.; CoreTech System Co., Ltd.; Molecular Dynamics Tech Co., Ltd. Method and Computer Readable Media for Determining Orientation of Fibers in a Fluid. U.S. Patent No. 8,571,828, 29 October 2013. [Google Scholar]
- Advani, S.G.; Tucker, I.I.I.C.L. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Lafranche, E.; Krawczak, P.; Ciolczyk, J.P.; Maugey, J. Injection moulding of long glass fibre reinforced polyamide 6-6: Guidelines to improve flexural properties. Express Polym. Lett. 2007, 1, 456–466. [Google Scholar] [CrossRef]
- Chung, D.H.; Kwon, T.H. Fiber orientation in the processing of polymer composites. Korea-Aust. Rheol. J. 2002, 14, 175–188. [Google Scholar]
- Swain, S.S.; Samal, S.K.; Mohanty, S.; Nayak, S.K. Investigation of fibre orientation using SEM micrograph and prediction of mechanical properties through micromechanical modelling. Bull. Mater. Sci. 2016, 39, 837–846. [Google Scholar] [CrossRef]
- Neves, N.M.; Pontes, A.J.; Pouzada, A.S. Experimental Validation of Morphology Simulation in Glass Fibre Reinforced Polycarbonate Discs. J. Reinf. Plast. Compos. 2001, 20, 452–465. [Google Scholar] [CrossRef]
- Tseng, H.-C.; Chang, R.-Y.; Hsu, C.-H. The use of shear-rate-dependent parameters to improve fiber orientation predictions for injection molded fiber composites. Compos. Part A 2018, 104, 81–88. [Google Scholar] [CrossRef]
- Tseng, H.-C.; Chang, R.-Y.; Hsu, C.-H. Numerical predictions of fiber orientation and mechanical properties for injection-molded long-glass-fiber thermoplastic composites. Compos. Sci. Technol. 2017, 150, 181–186. [Google Scholar] [CrossRef]
- Tseng, H.-C.; Goto, M.; Chang, R.-Y.; Hsu, C.-H. Accurate predictions of fiber orientation and mechanical properties in long-fiber-reinforced composite with experimental validation. Polym. Compos. 2018, 39, 3434–3445. [Google Scholar] [CrossRef]
- Tseng, H.-C.; Chang, R.-Y.; Hsu, C.-H. Improved fiber orientation predictions for injection molded fiber composites. Compos. Part A 2017, 99, 65–75. [Google Scholar] [CrossRef]
- Tseng, H.-C.; Chang, R.-Y.; Hsu, C.-H. Numerical predictions of fiber orientation and mechanical properties for injection-molded long-carbon-fiber thermoplastic composites. Polym. Compos. 2018, 39, 3726–3739. [Google Scholar] [CrossRef]
- Tseng, H.-C.; Chang, R.-Y.; Hsu, C.-H. Numerical prediction of fiber orientation and mechanical performance for short/long glass and carbon fiber-reinforced composites. Compos. Sci. Technol. 2017, 144, 51–56. [Google Scholar] [CrossRef]
- Madenci, E.; Özkılıç, Y.O.; Gemi, L. Experimental and theoretical investigation on flexure performance of pultruded GFRP composite beams with damage analyses. Compos. Struct. 2020, 242, 112162. [Google Scholar] [CrossRef]
- Tarfaoui, M.; Nachtane, M.; Boudounit, H. Finite Element Analysis of Composite Offshore Wind Turbine Blades Under Operating Conditions. J. Thermal. Sci. Eng. Appl. 2019, 12, 011001. [Google Scholar] [CrossRef]
- Boudounit, H.; Tarfaoui, M.; Saifaoui, D.; Nachtane, M. Structural analysis of offshore wind turbine blades using finite element method. Wind Eng. 2020, 44, 168–180. [Google Scholar] [CrossRef]
- Mollamahmutoğlu, Ç.; Mercan, A. A novel functional and mixed finite element analysis of functionally graded micro-beams based on modified couple stress theory. Compos. Struct. 2019, 223, 110950. [Google Scholar] [CrossRef]
- Aribas, U.N.; Ermis, M.; Eratli, N.; Omurtag, M.H. The static and dynamic analyses of warping included composite exact conical helix by mixed FEM. Compos. Part B 2019, 160, 285–297. [Google Scholar] [CrossRef]
- Hirsch, P.; John, M.; Leipold, D.; Henkel, A.; Gipser, S.; Schlimper, R.; Zscheyge, M. Numerical Simulation and Experimental Validation of Hybrid Injection Molded Short and Continuous Fiber-Reinforced Thermoplastic Composites. Polymers 2021, 13, 3846. [Google Scholar] [CrossRef]
- Ronkay, F.; Bodzai, B.; Dogossy, G. Production of technical component from polymer waste. Műanyag Gumi 2010, 47, 344–347. [Google Scholar]
- Szürke, S.K.; Szalai, S.; Lakatos, I. Battery Deformation Measurement with DIC Technique. In Proceedings of the 21st International Symposium on Electrical Apparatus & Technologies (SIELA), Bourgas, Bulgaria, 3–6 June 2020. [Google Scholar] [CrossRef]
- Fiebig, I.; Schoeppner, V. Influence of fiber orientation and weld position in welding injection-molded fiber-reinforced thermoplastics. Weld World 2018, 62, 1301–1309. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Zaoutsos, S.P. 1-Viscoelastic constitutive modeling of creep and stress relaxation in polymers and polymer matrix composites. In Creep and Fatigue in Polymer Matrix Composites, 2nd ed.; Guedes, R.M., Ed.; Woodhead Publishing: Sawston, UK, 2019; pp. 3–59. [Google Scholar] [CrossRef]
- Tang, T.; Felicelli, S.D. Computational evaluation of effective stress relaxation behavior of polymer composites. Int. J. Eng. Sci. 2015, 90, 76–85. [Google Scholar] [CrossRef]
- Alagusundaramoorthy, P.; Veera Sudarsana Reddy, R. Testing and evaluation of GFRP composite deck panels. Ocean Eng. 2008, 35, 287–293. [Google Scholar] [CrossRef]

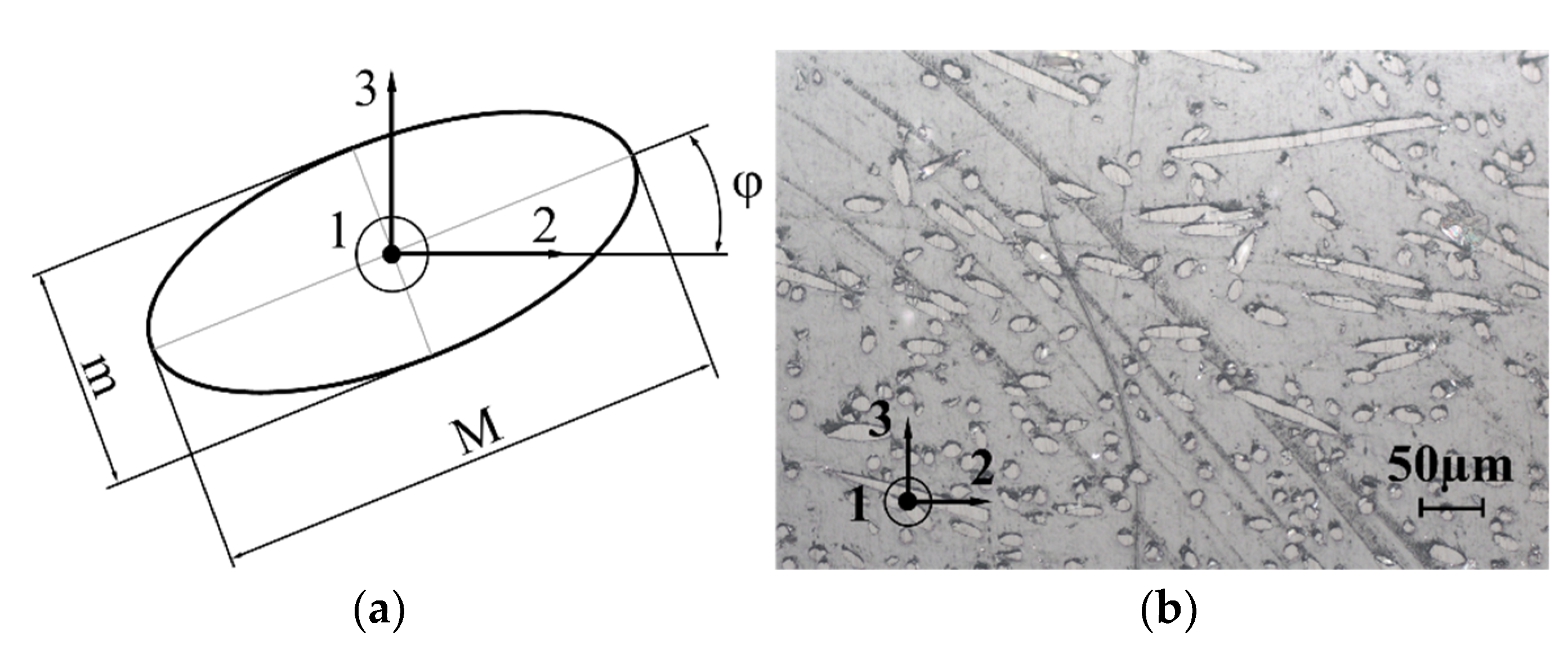


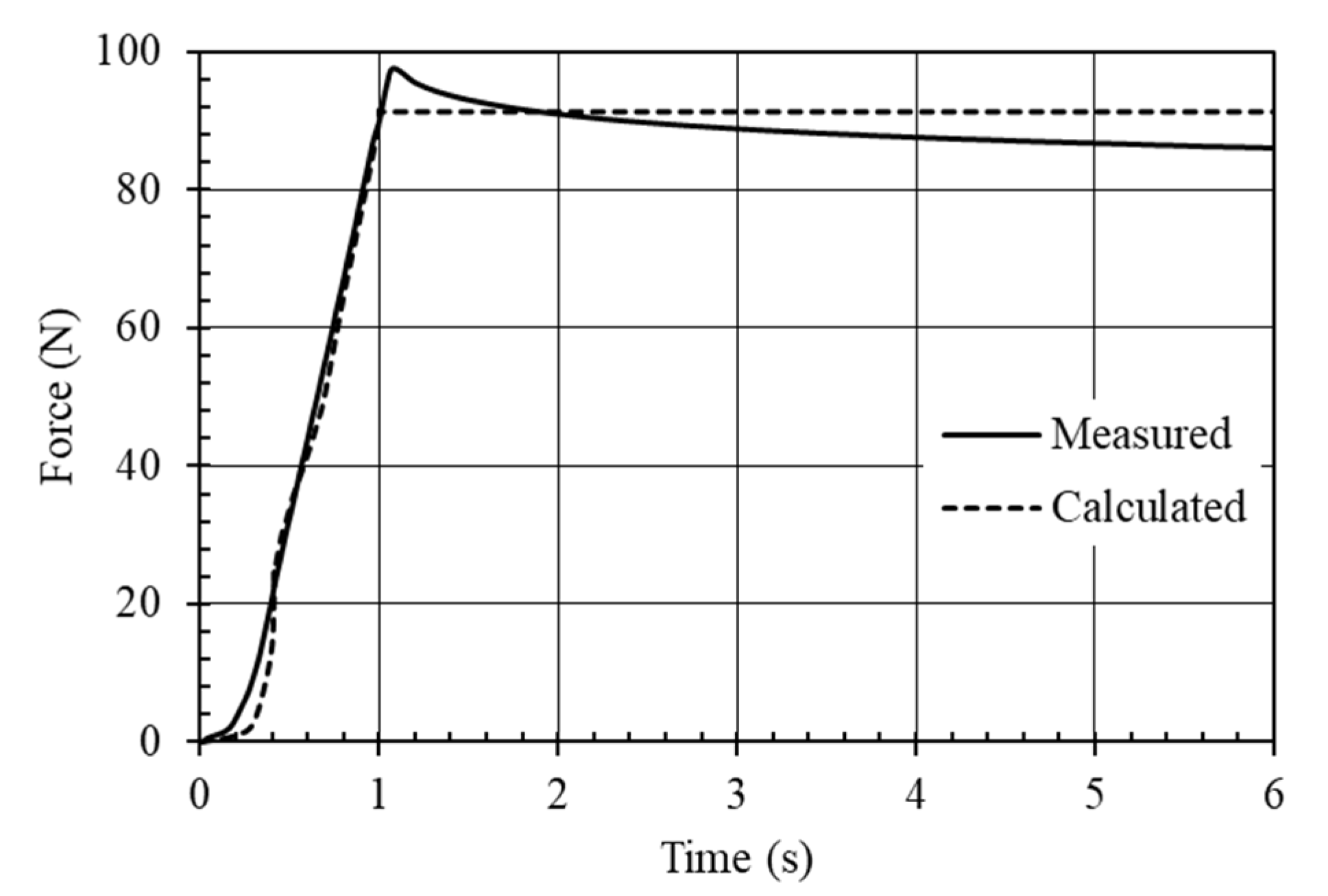
| Deflection | Reaction Force | Flexural Rigidity | Ratio | Relative Error | ||
|---|---|---|---|---|---|---|
| f | Fm | Fc | EIm | EIc | EIm/EIc | |
| (mm) | (N) | (MPa·mm4) | (−) | (%) | ||
| 2 | 45.7 | 51.9 | 1.27 | 1.44 | 0.88 | 13.39 5.93 12.24 12.26 |
| 4 | 97.4 | 91.4 | 1.35 | 1.27 | 1.07 | 5.93 |
| 6 | 159.0 | 139.5 | 1.47 | 1.29 | 1.14 | 12.24 |
| 8 | 223.8 | 195.9 | 1.55 | 1.36 | 1.14 | 12.26 |
| Mean | 10.95 | |||||
| Standard deviation | 3.39 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dogossy, G.; Morauszki, T.; Ronkay, F. Experimental Investigation and Applicability of Multi-Stage Simulations in the Case of a Thick-Walled Injection-Moulded Composite. Appl. Sci. 2022, 12, 8415. https://doi.org/10.3390/app12178415
Dogossy G, Morauszki T, Ronkay F. Experimental Investigation and Applicability of Multi-Stage Simulations in the Case of a Thick-Walled Injection-Moulded Composite. Applied Sciences. 2022; 12(17):8415. https://doi.org/10.3390/app12178415
Chicago/Turabian StyleDogossy, Gábor, Tamás Morauszki, and Ferenc Ronkay. 2022. "Experimental Investigation and Applicability of Multi-Stage Simulations in the Case of a Thick-Walled Injection-Moulded Composite" Applied Sciences 12, no. 17: 8415. https://doi.org/10.3390/app12178415







