A Machine-Learning Pipeline for Large-Scale Power-Quality Forecasting in the Mexican Distribution Grid

Abstract

Electric power distribution networks face increasing factors for power-quality (PQ) deterioration, such as distributed, renewable-energy generation units and countless high-end electronic devices loaded as controllers or in standalone mode. Consequently, government regulations are issued worldwide to set up strict PQ distribution standards; the distribution grids must comply with those regulations. This situation drives research towards PQ forecasting as a crucial part of early-warning systems. However, most of the approaches in the literature disregard the big-data nature of the problem by working on small datasets. These datasets come from short-scale off-grid configurations or selected portions of a larger power grid. This article addresses a study case from a region-sized state-owned Mexican distribution grid, where the company must preserve essential PQ standards in approximately 700 distribution circuits and 150 quality-control nodes. We implemented a machine-learning pipeline with nearly 4000 univariate forecasting models to address this challenge. The system executes a weekly forecasting pipeline and daily data ingestion and preprocessing pipeline, processing massive amounts of data ingested. The implemented system, MIRD (an acronym for Monitoreo Inteligente de Redes de Distribution—Intelligent Monitoring of Distribution Networks), is an unprecedented effort in the production, deployment, and continuous use of forecasting models for PQ indices monitoring. To the extent of the authors’ best knowledge, there is no similar work of this type in any other Latin-American distribution grid.

1. Introduction

Modern electric power systems must deal with unprecedented conditions for power-quality (PQ) deterioration, such as the growing presence of distributed, renewable-energy-based generation units, or the countless high-end electronic devices loaded as either electrical equipment controllers [1] or standalone appliances. This situation has driven increased attention of researchers towards PQ management activities, and, specifically, to PQ indices forecasting. In particular, forecasting the PQ indices for steady-state power systems, e.g., voltage deviation, voltage unbalance, frequency deviation, or flickering, is a significant problem. A substantial amount of research focuses on implementing early-warning mechanisms able to predict PQ disturbances in the future operation of different electric power configurations [1,2,3].

Most of the state-of-the-art research focuses on PQ forecasting, but it deals with small power arrangements. The data may come from real or simulated systems that provide a basis for analyzing the impact of renewable-energy ingestion on isolated power systems. Although valuable, these experiments do not face the data-scale problem of forecasting for city- or regional-size power distribution grids. On the other hand, PQ forecasting projects that use data from large distribution grids usually employ information from only a few power quality meters (PQM). As a result, the need for investigating a methodology for PQ indices forecasting in big-data environments remains.

This article presents the methodology, architecture, and results of a short-term PQ indices-forecasting project developed in Mexico for the electric-power distribution grid of CFE (the Spanish acronym for Comisión Federal de Electricidad—Federal Board of Electric Power), the state-owned enterprise responsible for the Mexican state grid and also the primary electric-power provider in the country. This article presents MIRD, a system whose main objective is the application of artificial-intelligence techniques (machine-learning-based time-series forecasting) to monitor the evolution of significant PQ indices. This monitoring process occurs at crucial coupling points of the distribution grid. Based on the Mexican Energy Law reform in the mid-2010s, CRE (the Spanish acronym for Comisión Reguladora de Energía—Energy Regulation Board), issued the general conditions and criteria for distributing electric power in Mexico. This law expresses strict regulations on the quality of delivered energy in terms of detailed PQ indices intervals and values. In particular, that law requires that CFE’s power distribution grid fulfill the following requirements (see

Table 1. PQ Indices Criteria.

PQ Index	Criterion	%	Basis
Current unbalance	<15%	80	Readings
Power factor	>0.95	80	Readings
Operation voltage	>93%, <105%	90	Quality nodes

):

• Operation voltage. The voltage a quality-control node or quality node operates at must lie within a defined interval for at least 90% of the 10-min voltage measurements in the node. This acceptance interval is 93–105% of the node’s nominal voltage. The operation voltage is calculated as the average of the three per-phase RMS voltages, as $V_{oper}=\sqrt{3}(V_{an}+V_{bn}+V_{cn})/3$.
• Electric power factor. The power factor measured at a distribution circuit must be greater than or equal to 0.95 in at least 80% of a given set of circuits. The power factor is calculated as the ratio of the real power absorbed by the load to the apparent power that flows through the circuit.
• Current unbalance. The three-phase current flowing into a distribution circuit must be within the required balance interval, which is 15% in at least 80% of a given set of circuits. The current unbalance is calculated as follows: (a) the per-phase current average is determined, (b) the largest per-phase current deviation from the average is determined, and (c) the current unbalance is the ratio of the largest deviation and the current average, expressed as a percentage.

Under these regulations, CFE requires an efficient early-warning system to meet standards and avoid penalties determined by CRE. In the past, CFE’s monitoring engineers received only a weekly report listing the performance of the distribution circuits under their command. If CFE did not meet the standards for any reason, there was nothing they could do to avoid fines issued to CFE. By providing a prediction or estimation of the PQ indices for the following week, engineers can act ahead of time, fix those circuits’ operating conditions, and improve their performances in adequate time frames. If predictions are accurate and engineers take corrective actions properly, the company saves substantial money by avoiding economic penalties. Not being fined by CRE is a desirable situation, leading to the more efficient management of the distribution networks. In the end, the total cost of energy distribution lowers, which entails lower electricity costs to the consumers.

CFE manages power distribution in Mexico on the basis of 16 divisional units and 150 distribution zones (see Figure 1). The MIRD project was planned and developed inside DCO (the Spanish Acronym for Division Centro Occidente—Central-West Division), one of the most innovative and efficient divisional units of CFE.

Table 2. Power distribution grid research context (values to 2022).

Attribute	CFE Distribution	Central-West (DCO)
Number of divisions	16	1
Number of zones	150	12
Power distribution lines (km)	933,699	43,288
Medium voltage lines (km)	522,347	31,912
Low voltage lines (km)	411,352	11,376
Number of power transformers	3269	151
Power transformers capacity (MVA)	78,895	2299
Number of distribution transformers	1,525,472	82,557
Distribution transformers capacity (MVA)	49,986	2263
Total transformers capacity (MVA)	128,881	4562
Number of substations	2164	124
Number of customer services (thousands) 1	45,705	3368
Delivered power (GWh) 1	259,112	15,736

¹ To December 2020.

shows power infrastructure and capacity figures for both CFE as a whole and DCO only. These numbers give a clear idea of the importance and magnitude of the DCO distribution grid. Moreover, a total of 5953 services connected to the DCO grid as distributed generation (as of 2021) reinforce the need for an adequate early-warning system for PQ monitoring. Across its 145 power substations, DCO is in charge of approximately 800 distribution circuits. Those distribution circuits are of considerable size, with power consumption ranging between 100 KW to 8 MW and 0 to 3 MVAR.

Every Sunday night, MIRD generates the forecast of the variables of interest of each circuit for the following week. Based on those forecasts, it computes the predicted PQ indices for that week. If there is a possibility that PQ indices will not meet the standard, MIRD sends email messages to the engineers in charge of monitoring the circuits delivering low-quality energy. Once engineers receive the message, they verify the circuits’ operating conditions and collect more information from MIRD’s web interface (or other systems that CFE has established for its day-to-day operation). Distribution engineers can then take corrective measures to prevent any incidents that would lower the circuits’ PQ indices under their responsibility. As a result, the reliability of the distribution system has increased, as well as the quality of the electric power delivered to customers.

MIRD is required to be an efficient early-warning system capable of acquiring and processing information at a big-data scale. The number of PQMs delivering data to MIRD is approximately 700 distribution circuits and nearly 150 quality-control nodes. Each circuit and node contains five and three variables of interest, respectively (although more than 30 variables are monitored, reported, and stored in the system). That required nearly 4000 univariate forecasting models capable of producing hourly forecasts for a one-week horizon. Additionally, as in most data-science endeavors, data is noisy and contains outliers and missing information. It is also worth noticing that, due to CFE’s data governance policies, developing our solution based on specialized services from public cloud providers was not an option. Therefore, MIRD was implemented entirely on-premises, based on a fast and resilient software architecture capable of dealing with the huge-scale and high-speed requirements posed by the problem. Additionally, fundamental components of that architecture had to take care of both challenging data-preprocessing operations (facing many types of data disturbance across the data-acquisition stage) and the urgent need to balance forecasting accuracy and speed.

In that context, the main contributions of this research are as follows:

• The complete implementation of a large-scale machine-learning (ML) pipeline focused on short-term PQ indices forecasting for a regional-size, state distribution grid.
• We developed our ML pipeline with the integration of modern, widely tested, open-source computing frameworks such as the big-data unified engine Apache Spark or the scientific computation library SciKit Learn.
• To our knowledge, no other regional power distribution grid in Latin America has made a parallel effort in PQ indices forecasting or early-warning operations.

The rest of the article is structured as follows: Section 2 presents an account of work found in the literature that deals with the problem of short-term PQ indices forecasting. Section 3 describes the overall architecture of MIRD as a data pipeline centered on large-scale ML operations. Section 4 and Section 5 present in detail the two most important components of the MIRD pipeline: data preprocessing and forecasting. Section 6 presents examples of the results of the MIRD operation. Finally, Section 7 presents the conclusions and lines of future work.

2. Related Work

A significant part of the early research on PQ forecasting focuses on autonomous (off-grid), renewable-energy-based, actively controlled, domestic or semi-industrial power systems loaded with multiple real devices. The importance of such isolated configurations is increasing, and the connection of local, renewable energy sources is a factor in PQ deterioration. Therefore, PQ prediction becomes key to monitoring and early-warning activities. A project developed by a team from the Technical University of Ostrava constitutes an example of this situation. The first stage of this project [3] developed a PQ forecasting model as an integrated part of active demand side management (ADSM). The model is based on a multi-layer artificial neural networks (ANN) and produces multi-step predictions for the following steady-state PQ indices: total harmonic distortion of voltage (THDV), total harmonic distortion of current (THDC), long-term flicker severity, and power frequency. In a subsequent stage of the project [4], the authors developed an ML classifier based on multiple algorithms, including ANN, support vector machine (SVM), decision tree (DT), AdaBoost, and random forest (RF), that overperformed their previous multi-layer ANN predictor. Moving the prediction output from continuous PQ-index values to a binary state classifier (PQ failure/not PQ failure) allowed the team to experiment at a higher data resolution for longer. By expanding the classification mechanism to a 32-class problem, forecasting output is now a vector of binary values for five major steady-state PQ indices (they added short-term flicker severity to the original problem). The project uses a fandom decision forest algorithm to produce the classification model. The authors use multi-objective optimization via particle swarm optimization (PSO) and Non-Dominated Sorting Genetic Algorithm II (NSGA-II) to adjust the model’s hyper-parameters. Recently, a team from the Technical University of Ostrava worked on data from an experimental off-grid platform to compare predictive performances and computation times for seven approaches to PQ indices forecasting. ANN, linear regression (LR), interaction LR, pure quadratic LR, quadratic LR, bagging DTs, and boosting DTs were used to forecast frequency, voltage, THDV, and THDC based on the history values of the system power load, and weather information (solar irradiance, wind speed, air pressure, and air temperature) [5]. The dataset used for this research comprises only two weeks of data, at 10-min resolution, for model training and only 14 values, at hourly resolution, for inference.

Weng et al. [6] use an ANN-based PQ forecasting model to predict steady-state PQ indices at the point of common coupling (PCC). They predict voltage deviation (VD), frequency deviation, three-phase voltage unbalance (VU), and harmonic distortion using environmental variables (illumination intensity and temperature) and power load values as inputs to the model. Three neural networks with different structures compose the prediction model: back propagation (BP), radial basis function (RBF), and general regression neural networks (GRNN). Hua et al. [7] predict voltage deviation (VD), frequency deviation, and harmonics using a hybrid deep ML model that includes convolutional neural network (CNN) and long short-term memory (LSTM) layers. They tested their model using an active distribution network simulated on the basis of the IEEE-13 node. Xu et al. [8] also used simulated data from the IEEE-13 node to train a model for PQ indices forecasting. The model is a neural network which applies variational mode decomposition (VMD) to the power signal. The resulting power components are used as features for an LSTM-based layer that computes a predicted power signal. The difference between real and predicted power values (residuals) are passed to a one-dimension CNN which finally outputs the target PQ indices values. This architecture is tested on a single time series of 32 K values; however, this time series is further sampled before the final layer to datasets of 4500 and 500 values for training and inference, respectively.

Several projects have investigated PQ forecasting models for city- or regional-size distribution grids. The increased data and computation requirements driven by this context calls for using diverse approaches. Bai et al. [2] developed a PQ prediction, early-warning, and control system for PCC between a 200 MW wind farm and the distribution network. This system includes a clustering analysis based on the dynamic time warping (DTW) distance performed over a set of historic, monitored environmental variables and PQ index values. A probability distribution is fitted for each data cluster and then used as the base for predicting PQ indices one day ahead via a Monte Carlo process. However, the dataset reported for this research comprises only 10 days of meter readings at a 10-min resolution. Song et al. [9] predicted steady-state PQ indices (VD, frequency deviation, three-phase VU, and THDV) using cluster analysis and SVMs. The input to the model comprises calendar information (weekday and holiday indicators), environmental-condition values (temperature, humidity, atmospheric pressure, rainfall), and power load values (active power, reactive power). The experimental study extends to one year of data; however, the dataset comprises only a single 35 kV substation of the Chinese state grid. Pan et al. [10] forecast the variables VD, THDV, and three-phase VU for a regional state grid. Their forecasting model uses phase-space reconstruction on the history of the predicted variables, least-squares SVM, and PSO. They use 2 years of readings at daily resolution for training the forecasting model; however, the dataset comprises only a single 220 kV substation.

Yong et al. [11] predict VD using principal component analysis (PCA) for dimensionality reduction, affinity propagation (AP) clustering, and a back propagation (BP) neural network. Besides the history of predicted variables, the model accepts relevant meteorological data (e.g., temperature, dew point, humidity, air pressure, wind speed, and wind direction) as exogenous information. Datasets come from the Chinese state grid and comprise 98 days in the training dataset, and two extra days for the test set, at hourly resolution. Sun et al. [12] forecast voltage deviation and the fifth harmonic content of voltage using ARIMA and a BP neural network. Datasets come from a state grid but are very small (only 29 readings at a 1-day resolution for the fifth harmonic and 310 readings at 1-min resolution for voltage deviation). Michalowska et al. [13], developed a PQ forecasting model to predict the appearance of three PQ disturbance types in the Norwegian power distribution grid: earth faults, rapid voltage changes, and voltage dips. The model takes as input target variables history and weather information; it uses random forests (RF) to produce a binary classifier. Datasets are relatively large, with five years of data at daily resolution. Zhang et al. [14] forecasted THDV using a Bayesian-optimized bidirectional LSTM neural network. Datasets also come from a city grid but comprise only one week of data, at 10-min resolution, for 5 PQM.

In close line with the research projects mentioned above, we built MIRD to produce ML-based, short-term predictions (1-h resolution, 1-week ahead) for three steady-state PQ indices: power factor (PF), three-phase current unbalance (CU), and VD. The MIRD forecasting process is indirect: to forecast these PQ indices, MIRD first builds predictions for the variables required for the computation of the PQ indices, that is, the active (kW) and reactive (kVAR) components of electric power for PF, three-phase voltage for VD, and three-phase current for CU. Forecasting of active and reactive power components lies in the domain of short-term power load forecasting, covered in a vast body of literature [15]. However, MIRD exhibits a substantial difference concerning the research projects covered in this section, which is the size of the problem it deals with: eight primary variables are required to be short-term predicted for 700+ substation metering devices based on history datasets that span from several months to years. Therefore, another significant difference is that MIRD’s design corresponds to an ML-based, PQ forecasting project, which composes the foundation for an extensive, tailor-made big-data architecture that enables CFE to perform powerful and diverse analytics on multiple levels of consumer targets. Considerations on this architecture design will be addressed in Section 3.

3. Architecture

This section describes the architecture and components of the MIRD system (see Figure 2). As previously stated, the primary objective of MIRD is to forecast selected PQ indexes for nearly 800 PQM in the CFE-DCO power distribution network. This results in a big-data environment that places the following primary requirements on MIRD’s architecture:

• MIRD relies on an efficient and resilient computing framework mounted on the available infrastructure. A set of widely tested data processing and analytics libraries integrate this computing framework.
• Although the first version of MIRD considered execution on a single server, the system architecture must provide the foundations for parallelization, scaling, and fault-tolerance in a future cluster-based operation.
• MIRD must be developed, to the maximum possible extent, using widely used, open-source software.

The preceding requirements match the foundation of most big-data architectures implemented nowadays. In this context, the architecture pattern selected for MIRD was the generic data pipeline: a succession of decoupled software components where the output of each component constitutes the input for the downstream component, with layers for artifact persistence in the middle. This architecture pattern renders simplicity and autonomy to development operations, allows the system to run processes (whenever possible, in parallel), and enables the components, if required, to scale independently. Moreover, the artifact-persistence layers in the middle not only store information but also serve a couple of essential purposes: (a) to perform faster queries on data over the different processing stages, and (b) to feed data for processing or analytics variants at different pipeline stages. MIRD components were coded in Python to ease the integration of the two programming resources that were considered essential to the architecture requirements: the Apache Spark [16] unified engine for large-scale data analytics and the SciKit Learn [17] library for scientific computing. The following subsections provide a detailed description of the components that integrate MIRD’s architecture.

3.1. Data-Ingestion Component

In our case, the primary data source for PQ monitoring is a relational database which concentrates the data reported by nearly 800 PQM across the CFE-DCO power distribution network. Data comprises multivariate time series (31 variables plus timestamp). Variables include three-phase active and reactive power, voltage and current values and unbalances, total harmonic distortion (THD), and many others. Time series in the database extend up to several years at a 10-min resolution. This massive volume of information makes any complex query on the relational database impractical, which motivated the design of a column-based replica database for MIRD. It is worth noticing that building a NoSQL database was far out of the initial scope of the project; therefore, a Parquet archive was designed to persist the different stages of data through the pipeline. Parquet is a columnar file format optimized for storage and query, compatible with many big-data computing frameworks [18].

Figure 3 shows the data-ingestion component of MIRD. The time series in the relational database represent the input for this module. A Parquet file called Incomplete Datasets keeps a record of all the PQM/date combinations that did not contain enough data in the relational database. MIRD must include those datasets in the pipeline at a later date. SparkSQL scripts extract the required time series according to the pipeline execution date. This extraction process includes all the elements included in the Incomplete Datasets archive. The database aggregates information by PQM and date and stores them separately at 10-min, 1-h, and 1-day resolutions, keeping the same schema as the original database. The next component in the pipeline receives hourly data, although 10-min and daily data are kept for other processes eventually executed outside the pipeline, e.g., visual segmentation or customized queries on the time series. Preserving redundant copies of data aggregated at different time resolutions (10-min, 1-h, and 1-day) is a common NoSQL practice that provides the system with increased query performance at the cost of disk space. The data-ingestion component of MIRD is executed daily, either automatically or via a provided manual-override operation.

3.2. Data-Preprocessing Component

Figure 4 shows the data-preprocessing component of MIRD. The primary input for this component is the Parquet archive of PQ data at a 1-h resolution, stored by the Data Ingestion module. Even though this Parquet archive contains the 31 variables delivered by PQM, this stage receives only the eight variables required to forecast PQ indexes. JSON files store the preprocessing parameters related to each PQM; those parameters are necessary to execute this component. The preprocessing component is executed daily and returns the time series containing preprocessed data for the eight required variables on the corresponding date. This data is joined with the results of the previous six daily executions to form the set of the last seven days; forecasting uses that information. A historical archive stores all previously preprocessed data sets. Scripts in this pipeline component are coded with the machine-learning library SciKit Learn.

3.3. Forecasting Component

Figure 5 shows the forecasting component of MIRD. This component takes as input the preprocessed datasets corresponding to the last seven days and a set of forecasting models serialized as Pickle files. This set includes a model for each combination of PQM–PQ variable to forecast, which yields nearly 4000 different univariate forecasting models. The forecasting component uses the machine-learning library SciKit Learn. This component outputs the predicted values for each combination PQM–PQ variable, at a 1-h resolution, for the next week. MIRD executes the forecasting component weekly; however, the system administrator can change the execution frequency to as often as 1-day.

3.4. Power-Quality-Evaluation Component

Figure 6 shows the power-quality-evaluation component of MIRD. This component takes as input the one-week-ahead predicted values of PQ variables per PQM and a set of PQ evaluation parameters stored in a relational database. SparkSQL scripts in this module calculate the values of the selected PQ indexes (power factor, voltage interval, and current unbalance) for each PQM, at a 1-h resolution, for a week ahead. The database stores the results of the detailed PQ evaluation, labeled on the PQM class as either circuit or node. A PQ aggregates evaluation uses this information at four geographical levels in the power distribution network: individual device (PQM), substation, area, and zone. MIRD executes the power-quality-evaluation component downstream of the forecasting component, i.e., weekly.

3.5. Reports and Visualization Component

Figure 7 shows the reports-and-visualization component of MIRD. This component inputs both the detailed and the aggregated PQ evaluations that result from the power-evaluation component and delivers them as tabular reports and interactive plots—reports and plots persist as HTML files. The component provides the functionality it offers, using the Django and Bokeh Python libraries. MIRD generates the PQ indexes for all PQM in the CFE-DCO power distribution network. However, it presents specific reports and visualizations to users according to their role in the management hierarchy. An external relational database provides user authentication and their corresponding access rights. A complementary functionality of this component sends a summary of reports to MIRD users via email.

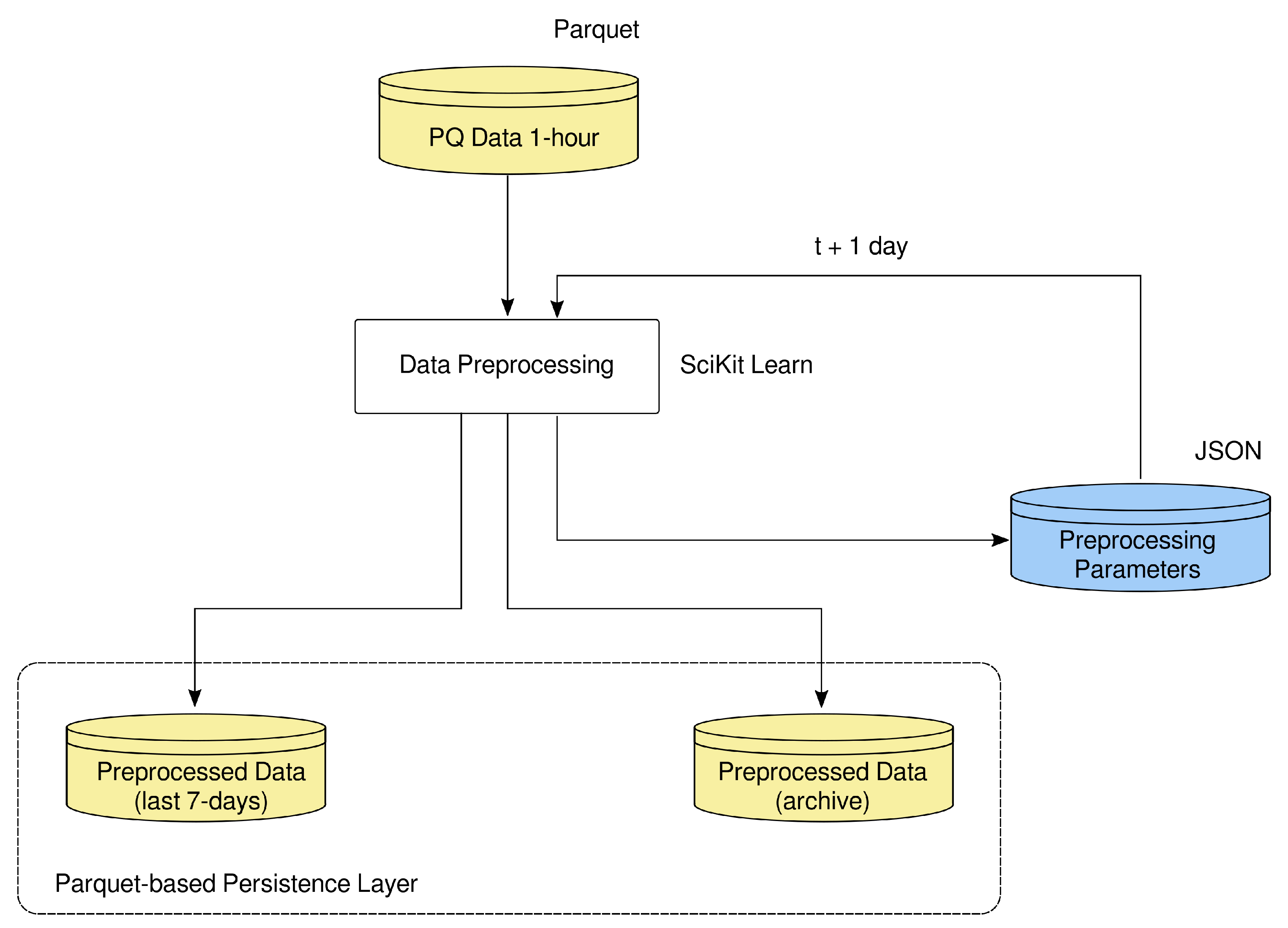
4. Data Preprocessing

Real-world databases are highly susceptible to noise, missing data, and outliers, among other disturbances. Examples of noise sources are measuring devices, rounding operations, and transmission mechanisms. Intermittent operation of measuring or transmission devices produces missing data. Periods of missing data can be as short as one reading or as long as several months. Outliers are out-of-range measurements. We can see them as a form of noise but, in some cases, they are authentic peaks (positive or negative) that result from non-characteristic behavior of the underlying system that produces the data. Noise, missing data, and outliers are responsible for data quality deterioration; these problems are more likely to happen when the system handles vast amounts of data (up to gigabytes). Data analytics pipelines such as MIRD must specifically deal with this problem as the lower the input data quality, the lower the quality of the results.

Before describing the operations of the data-preprocessing component, it is essential to understand how MIRD acquires data. CFE implemented an Internet-of-Things system across most of its assets and equipment. This system includes a PQM at the coupling point of every circuit or quality node. As previously stated, each PQM records more than 30 electrical variables at a 10-min resolution. A relational database called SIMOCE (the Spanish acronym for Sistema de Monitoreo de Calidad de la Energia—Power Quality Monitoring System) collects PQM readings, which serve CFE’s distribution engineers throughout the country. The data-ingestion component of MIRD uses SIMOCE as its data source. Afterward, the data-prepŕocessing component consists of four steps. The first step is a sub-sampling operation. PQ measurements, originally recorded at 10-min intervals, are average aggregated to a 1-h resolution, which results in 168 values per week. The second step is to locate missing data; in the absence of data, it applies an imputation process. This operation applies only when a few measurements are missing. The third step is to detect outliers. If they exist, the same missing data imputation process is applied. The preprocessed time series persists in the artifact-storage (Parquet) layer in the fourth step. The following sections explain these steps in detail.

4.1. Missing Data

Missing data result when the measuring device or the database does not record the value of the variable of interest at a given instant of the time series. Missing data can be caused by measurement, transmission, or recording problems. Douglas et al. [19] provide an example, replicated in Figure 8. The plot shows one missing data on 13 January and three successive days—16, 17, and 18—without recording information (producing missing data). In this step of data preprocessing, we count the total observations in the weekly time series. $S_{md}$ represents the missing data subset in the time series $\mathbb{S}$. If $\left|S_{md}\right|>56$ observations are missing, the system does not record the time series. It indicates that there is insufficient data to pass this combination PQM-variable to the next pipeline component. If $\left|S_{md}\right|\le 56$ observations are missing, an imputation process is executed. A recovery operation uses the Incomplete Datasets archive of the data-ingestion component.

4.2. Data Imputation

Imputation is the process of filling in missing data or replacing outliers. Imputation replaces missing or erroneous values with a “likely” value based on other available information. Imputation allows MIRD to work with statistical and machine-learning techniques designed to handle the complete datasets (see [19]). The imputation process replaces the missing data or outliers with the average of the last five observations. Let us denote the time series by $\mathbb{S}$ (see Section 5.1); each missing entry, $s_{t^{\prime }}$, in the missing data or outliers set $S_{md}$, detected at time $t^{\prime }$, can be replaced as indicated in Equation (1). The pipeline executes this process twice, once to perform imputation for missing data and again to impute outlier values.

$$s_{t^{\prime }}=\left\{\begin{array}{cc}{\mu }_{\mathbb{S}}\hfill & t^{\prime }\le 5\hfill \\ \frac{1}{5}{\displaystyle \sum _{i=1}^5}{s}_{t^{\prime }-i}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

4.3. Outliers

Time-series data can be affected by isolated events, perturbations, or errors that create inconsistencies and produce unusual data that is not consistent with the general behavior of the time series; those unusual data points are called outliers. Outliers may result from external events, measuring, or recording errors (see [20]). There are two types of outliers: global and local. Figure 9 shows global (squares) and local outliers (circles). Different methods exist to detect outliers; in this work, we use the three-sigma method for detecting the global outliers and the local outlier factor (LOF) method for detecting the local ones.

4.3.1. Global Outliers

In a time series, a global outlier is one observation that deviates significantly from the rest of the data [21]. We use the three-sigma rule to determine the percentage of values within a band around the average in a normal distribution. (2) expresses the probability of a data item lying within the three $\sigma$ band

$$Pr=(\mu -3\sigma \le s_t\le \mu +3\sigma )\approx 0.9973,$$

(2)

where $s_t$ is an observation of a normally distributed random variable, $\mu$ is the mean of the distribution $\mathbb{S}$ and $\sigma$ is the standard deviation. The three-sigma rule is a conventional heuristic—99.7% of a normally distributed population lies within three standard deviations of the mean. Therefore, values that lie outside those limits are unlikely to be produced by the underlying process. (see Figure 9) Therefore, they are considered outliers.

4.3.2. Local Outliers

Local outliers are more challenging to detect than global ones. We need to know the nature of the time series to find local outliers. For example: “The current temperature is 27 ${}^{°}$C. Is it an outlier?”. It depends, for example, on the time and location. In the city of Morelia, it is an outlier if it is the month of December at night. If it is the month of May for the day in Morelia, then the measurement is a usual case. The determination of whether the value of today’s temperature is an outlier or not depends on the context: the date, time, location, and possibly some other factors [21]. We used the local outlier factor (LOF) method in this situation [22]. The LOF method compares outliers with data in their local neighborhoods rather than the global data distribution. LOF is an outlier detection technique based on the density around an outlier; density around normal data must be higher than the density around outliers. LOF compares the relative density of a point against that of its neighbors. That ratio is an indicator of the degree to which objects are outliers. High-density points have many neighbors at a close distance, and low-density points have fewer. A typical distance measure is the Euclidean distance defined in (3).

$$d_E\left(p,o\right)=\sqrt{\sum _{i=1}^m{\left(p_i-o_i\right)}^2}$$

(3)

where m is the dimensionality of the data points. Let C be a set of objects in an m-dimensional space and p a query object. Let us denote $D^{\prime }$ as the array of objects $o\in X$, sorted by distance to p. The k-nearest neighbor ($kDistance\left(p\right)$) of p is $D_k^{\prime }$. Figure 10 shows an example where $k=3$ in two dimensions.

The k-distance neighborhood represents the set of all neighbors of p, the center of the big circle on the left of Figure 10, that are as far from p as $kDistance\left(p\right)$—see (4).

$$N_k\left(p\right)=\left\{o\right|o\in D,d\left(p,o\right)\le kDistance\left(p\right)\}$$

(4)

The reachability distance of p and o is the maximum between their distance and the $kDistance\left(p\right)$. See (5).

$$reachdis{t}_k\left(p,o\right)=max\{kDistance\left(p\right),d\left(p,o\right)\}$$

(5)

Local reachability density is the inverse of the average reachability distances. (6) shows the local reachability of point p within its k-distance neighborhood.

$$lr{d}_k\left(p\right)=\frac{|N_k\left(p\right)|}{{\displaystyle \sum _{o\in N_k\left(p\right)}}reachdis{t}_k\left(p,o\right)}$$

(6)

where $\left|N_k\left(p\right)\right|$ is not necessarily k, since there is the possibility that several neighbors are at the same distance.

The local outlier factor (LOF) of a point p is the average of the ratio of the $lr{d}_k\left(o\right)$ and $lr{d}_k\left(p\right)$ for all k-distance neighbours of p. See (7).

$$LO{F}_k\left(p\right)=\frac{{\displaystyle \sum _{o\in N_k\left(p\right)}}\frac{lr{d}_k\left(o\right)}{lr{d}_k\left(p\right)}}{\left|N_k\left(p\right)\right|}$$

(7)

We compute the LOF of every point $p\in D$ to determine outliers and discriminate outliers using (8).

$$label\left(p\right)=\left\{\begin{array}{cc}LO{F}_k\left(p\right)\approx 1,\hfill & normal\hfill \\ LO{F}_k\left(p\right)<1,\hfill & normal\hfill \\ LO{F}_k\left(p\right)>1,\hfill & outlier\hfill \end{array}\right.$$

(8)

The first two cases indicate that the density of around p is similar to or higher than that of its neighbors; therefore, the data point is labeled as normal. The last case indicates that the density around p is lower than that of its neighbors; therefore, the data point is labeled as a local outlier. The LOF method detects and labels the local outliers. This process detects outliers, as outlined above. Those points detected as outliers are corrected using data imputation.

5. Forecasting

This section describes the architecture of the forecasting models used in predicting the PQ delivered by the distribution networks of CFE-DCO. Many tests were performed using different types of models from the machine-learning area. The goal was to determine the best-suited forecasting model to solve the problem. The tested models included ARIMA, regression forests, nearest neighbors, recurrent, and feed-forward artificial neural networks. The kind of model that performed the best was MLP; i.e., it produced the smallest error with respect to the test set. To use an MLP to perform forecasting, we need to map the forecasting problem to a regression problem; phase space reconstruction achieved this mapping. After that, we used an MLP to solve the resulting regression problem.

5.1. Phase Space Reconstruction

A time series is an abstraction of the data required by the forecasting model. A time series is a sequence of scalar values of a specific variable sampled at a discrete equidistant time. Let $\mathbb{S}=[s_1,s_2,\dots ,s_t,\dots ,s_N]$ be a time series, where $s_t$ is the value of variable s at time t. The goal is to obtain the forecast of $\mathsf{\Delta }n$ consecutive values, this is $[s_{N+1},s_{N+2},\dots ,s_{N+\mathsf{\Delta }n}]$ by employing any observation available in $\mathbb{S}$. By using a time delay of $\tau$ and an embedding dimension m, it is possible to build delay vectors of the form $S_t=[s_{t-(m-1)\tau },s_{t-(m-2)\tau },\dots ,s_{t-\tau },s_t]$, where $m,\tau \in {\mathbb{Z}}^{+}$. These vectors represent a reconstruction of the m-dimensional phase space that defines the underlying system dynamics that produced the time series [23]. However, the forecasting results exhibit low accuracy using vectors composed only of samples from the variable of interest (i.e., the time series). For this reason, vector $S_t$ includes the day of the week and the hour (in minutes from the start of the day) as control variables. Thus, we append the date and time (hour) when the sample was taken to each vector $S_t$, $D_t=[\mathrm{DoW}\left(d_{t-1}\right),\mathrm{MoD}\left(d_{t-1}\right)],1\le t\le N$. (9) shows the resulting vector.

$$S_t=[\mathrm{DoW}\left(d_{t-1}\right),\mathrm{MoD}\left(d_{t-1}\right),s_{t-(m-1)\tau },s_{t-(m-2)\tau },\dots ,s_{t-\tau },s_t]$$

(9)

where $\mathrm{DoW}(·)$ returns the day of the week (as a real number from 0.0 to 0.8571 starting on Monday), and $\mathrm{MoD}(·)$ returns the minute of the day (represented as a real number from 0.0 to 0.9993). Those quantities correspond to the day and time when the delay vector ends (i.e., when the forecast is to be produced).

5.2. Forecasting Model

We model the forecasting problem based on multi-layer perceptrons (MLP). An MLP is a feed-forward artificial neural network (ANN), fully connected between layers. A learning algorithm adjusts the weights and biases of the network’s neurons using a loss function and a training algorithm. The learning algorithm achieves these adjustments by exposing the network to every sample feature vector and its target. ANN are computing systems vaguely inspired by the biological neural networks that constitute animal brains [24]. Figure 11 shows the basic structure of an artificial neuron.

A neuron n can receive multiple inputs $[x_1,x_2,\dots ,x_m]$ which are weighed individually $[w_{1n},w_{2n},\dots ,w_{mn}]$ to make an intermediate output $a_n$. That is

$$a_n=\sum _{i=1}^m{w}_i{x}_i+b_n$$

(10)

where $b_n$ represents a bias, which acts as a weight. This bias acts as an independent term in an inherently non-linear model. The output $a_n$ is passed to a $\phi (·)$ activation function which yields the output $y_n$ of the neuron. The neuron computes its output as

$$y_n=\phi \left(a_n\right)$$

(11)

By piling many neurons operating in parallel, it is possible to form a layer. ANNs usually consist of one input layer of length m, one output layer (with one or more outputs), and several hidden layers. Those hidden layers can also have a varying number of neurons [25]. Figure 12 shows a typical ANN topology.

Generally speaking, an ANN is a universal approximator. Theorem 1 states the universal approximation theorem [26].

Theorem 1.

Let $\phi (·)$ be a non-constant, bounded, and monotonically increasing continuous function. Let $I_{m_0}$ denote the $m_0$-dimensional unit hypercube ${[0,1]}^{m_0}$. The space of continuous functions on $I_{m_0}$ is denoted by $C\left(I_{m_0}\right)$. Then, given any function $f\ni C\left(I_{m_0}\right)$ and $ϵ>0$, there exists an integer $m_1$ and sets of real constants ${\alpha }_i$, $b_i$, and $w_{ij}$, where $i=1,\dots ,m_1$ and $j=1,\dots ,m_0$ such that we may define

$$F(x_1,\dots ,x_{m_0})=\sum _{i=0}^{m_1}{\alpha }_i\phi \left(\sum _{j=1}^{m_0}{w}_{ij}{x}_j+b_i\right)$$

(12)

as an approximate realization of the function $f(·)$; that is,

$$\mid F(x_1,\dots ,x_{m_0})-f(x_1,\dots ,x_{m_0})\mid <ϵ$$

for all $x_1,x_2,\dots ,x_{m_0}$ that lie in the input space.

In time-series forecasting, an ANN can identify patterns and trends in the data and adjust the weights of each neuron to match the desired output. ANNs are successful models used in time-series forecasting; research work exhibits their forecasting capabilities. Those forecasting models include applications on forecasting water demand [27], foreign exchange markets [28], market volatility [29], and more. For this work, we designed a simple MLP;

Table 3. MLP Architecture.

Component	Value
Input length	50
Hidden layers length	60, 60
Output layer length	168
Neuron activation function	$f\left(x\right)=\max (0,x)$
Weight optimizer	Adam
Maximum number of epochs	1000
Early stopping	True

describes the components of the MLP architecture.

To produce the forecasting models, we took the last 5000 values of every time series, representing a little more than six months of data. This value was set since, after preprocessing all the time series, we found that many types of equipment had regime changes around that time. To minimize the modeling time, we implemented a simple parallel computing technique. The models were trained on a cluster server with 40 computing threads. Each thread was in charge of producing, for a given PQM, the models of the individual variables. For each variable of every PQM to forecast, we produced ten independent MLP models and kept the model that obtained the lowest forecasting error. In total, the training process produced nearly 4000 univariate forecasting models spanning all individual variables in the problem context. The following section shows the results obtained in modeling those variables and PQ indices.

6. Results

The main objective of MIRD is to produce a seven-day-ahead forecast of several electrical variables for nearly 700 distribution circuits and nearly 150 quality nodes. These forecasts feed an early-warning application that enables distribution engineers to make decisions that will help them provide high-quality electric power to CFE customers. Due to the nature of the system, the forecasting models need to be highly accurate to correctly inform the state of monitored circuits and nodes. This section discusses the ability of the models to produce accurate forecasts. It is important to note that, given the number of PQM and model variables, comparing different forecasting techniques on the datasets was unfeasible. Instead, this section provides an analysis of the forecasting errors across models. This analysis will help identify the overall forecasting capability of the models. The goal is to determine if the proposed ANN topology is adequate for each combination of equipment and variable to forecast.

6.1. Forecasting Task

MIRD was designed to provide seven-day-ahead forecasts for every distribution circuit and quality node in the CFE-DCO grid. Measurement devices sample each circuit’s variables hourly, i.e., simultaneously producing 168 values for each forecasting model. (at the end of every week, each model produces the forecasts for the following week). The last seven days of each time-series data constitute the test set. The system compares the forecasted points against the test set—the ground truth—to assess the accuracy of the models.

6.2. Error Metric

Comparing and evaluating the forecasting models requires an error metric. The symmetric mean absolute percentage error (SMAPE) measures the average absolute error relative to the mean between the actual and forecast values. This measure is expressed as a percentage. SMAPE is always non-negative and bounded between 0 and 200%; values closer to zero indicate a smaller forecast error. Therefore, when comparing two models, the one that produces the smaller SMAPE is preferred. SMAPE is defined in Equation (13).

$$\mathrm{SMAPE}=\frac{100}{n}\sum _{i=0}^n\frac{\mid y_i-{\widehat{y}}_i\mid }{(\mid y_i\mid +\mid {\widehat{y}}_i\mid )/2}$$

(13)

where n is the length of the test set, $y_i$ is the i-th actual value, and ${\widehat{y}}_i$ is the i-th predicted value. We use SMAPE because it is a relative error metric that enables us to compare the error between time series in different units. SMAPE is a bounded quantity and minimizes (to a certain extent) the problem of having a 0 in the denominator of (13).

6.3. Statistical Analysis of the Forecasting Errors

Once MIRD evaluates all models, it is possible to apply descriptive statistics and determine some basic characteristics of the error distributions.

Table 4. Description of Forecasting Errors.

Statistic	Value
Mean	14.41
Standard Deviation	19.92
Minimum	0.05
25%	4.69
50%	7.49
75%	14.02
Maximum	187.48

shows the descriptive statistics of the forecasting errors.

Table 4 shows that the second and third quartiles of the errors are $7.49\%$ and $14.02\%$, respectively. The quartile values indicate that at least $75\%$ of the models are $85.98\%$ accurate, and half of the models have an accuracy of $92.51\%$. To represent this information visually, Figure 13 shows the relative frequency and cumulative frequency histograms of the SMAPE scores.

The cumulative histogram of Figure 13 shows that inside the first bin (models with SMAPE error from 0 to $8.33\%$) lie around $63\%$ of the models; a total of $82\%$ of the models lie between the first and second bins (SMAPE ≤ 16.66%). This information reflects that the great majority of the models were performing their respective forecasts with reasonable accuracy. In many cases, the bad performance of models (e.g., those producing an error larger than $25\%$) was due to the low quality of the source data; that is, missing data, outliers, and noise. A question that arises by examining the histogram is: what forecasting models predict their respective variables the best? To answer this question, the models were divided in three categories: models with an SMAPE ≤ 10% (Figure 14), models with an SMAPE in the range >10% and ≤20% (Figure 15), and models with an SMAPE > 20% (Figure 16).

These figures show that the voltage variables are the easiest to predict, given their low variation range; their SMAPE was $<10\%$. On the other extreme, the kVAR variable represents $66\%$ of the total models in the category of SMAPE $\ge 20\%$. These percentages indicate that kVAR is the most challenging variable to predict. The rest of the variables are almost uniformly present in each set. Except for kVAR, there is no evidence of bias towards any variable; i.e., the accuracy of any given model depends on the quality of the data provided. To further prove that the model design was adequate, one model from each category was randomly selected to conduct a brief analysis of its forecasting errors. Figure 17 shows the forecasts made by a model with SMAPE $<10\%$. The forecast correctly follows the actual data with small differences during parts of the day, except for the first day when the model could not predict a sudden change. Note that the model accurately reaches the lows and highs of the day for most days.

Figure 18 shows the forecasts made by a model with 10% ≤ SMAPE < 20%. The model follows the general behavior of the curve, although the actual values contain abrupt changes. In addition, the actual values show a large unexpected increment during the first readings. These readings showcase an important disadvantage of the system; it cannot forecast sudden changes.

Figure 19 shows the forecasts of a model with SMAPE ≥ 20%. This case is similar to the previous model, where the forecasts followed the curve’s general shape. However, since the forecasts are made seven days in advance, it is impossible to anticipate such behavioral changes in the time series.

The trained models were capable of following the overall shape of the respective curves with varying degrees of success. The reasonable-error indices indicate that the models could generalize the time-series’ behavior during training without overfitting. Quantile plots of the errors produced by the models allow us to visually identify if data distribution follows a normal one (or any other distribution used as reference). When developing and training forecasting models, the errors (represented as the blue dots in the plots) should follow a normal distribution (represented by the continuous red line). The corresponding figures show that the approximation of the errors to a normal distribution becomes worse as their SMAPE score increases, as expected. Figure 20 shows that the errors contain a slightly positive bias in the mean, and, at the extremes, the outliers deviate moderately from the theoretical distribution. Figure 21 exhibits a higher number of outliers with a considerable outlier on the right side of the plot. Figure 22 shows many outliers occupying almost an entire quantile in both extremes of the plot. These plots indicate that the model with SMAPE $<10\%$ is the one that best approximates a normal distribution, while the errors of the other two models do follow a normal distribution.

7. Conclusions

This section discusses the general framework of applicability of the presented solution to forecasting PQ indices, emphasizing MIRD’s salient features. In a second part, this section proposes the directions for future work.

7.1. Discussion and General Conclusions

PQ indices forecasting has gained attention due to increasing PQ deterioration factors in electric power systems, such as distributed, renewable-energy-based generation units or non-linear electronic devices. Most of the recent research on PQ forecasting uses relatively small datasets. The data may come from domestic or semi-industrial, off-grid electric-power configurations or from gathering information from only a few PQM in power distribution grids; some of them even come from simulation data. The state-of-the-art disregards the big-data nature of PQ forecasting for city- or regional-size grids, focusing mainly on harmonic distortion (voltage total harmonic distortion—THDv) at a fine-grained level of detail.

This paper presents MIRD, a large-scale ML system for short-term PQ indices forecasting implemented at a Mexican, region-sized power distribution grid. MIRD is an early-warning system that produces one-week-ahead predictions at hourly resolution for the three-phase current unbalance and the power factor of nearly 700 distribution circuits. It also forecasts the operation voltage of nearly 150 quality-control nodes. This problem accounts for more than 4000 uni-variate forecast models executed weekly over massive amounts of data.

MIRD operates on massive amounts of real data (sensed by IoT devices in the network), produces a large number of trained ANN-based forecasting models, and monitors the distribution network autonomously. Such a system has no precedent in the Latin-American electrical industry.

In developing the system we present in this article, we tested several forecasting models and selected the type of model that best served the forecasting goals and could be implemented on premises with the available resources. Given those conditions, we could not afford more sophisticated models such as LSTM ANN, which take much longer to train and do not improve accuracy by much. Those facts lead to the decision to use feed forward multi-layer perceptron networks as a general model with acceptable forecasting accuracy and which are not as computationally expensive as other models.

Experimental results show that, although non-linearity in the underlying system that produces the data makes predicting reactive power (kVAR) a difficult task, MIRD’s overall predictive performance is encouraging. A total of 63% of the forecasting models produce SMAPE values under 8.33%, while 82% of the forecasting models produce SMAPE values under 16.66%. Given the uniqueness of the system we present here, we cannot compare its results against other systems; the authors did not find any such systems reported in the literature.

Most governments have issued strict PQ standards that power distribution grids must follow. PQ forecasting becomes crucial to ubiquitous early-warning PQ deterioration systems. However, to properly approach this task, it is essential to bear in mind the large-scale nature of the data when it comes to power grids that serve millions of customers. The practical value of MIRD lies in that, by reporting the likely behavior of each circuit and node one week in advance, MIRD allows the distribution engineers to produce corrective measures before delivering low-quality energy to the users. The delivery of high-quality energy by CFE allows the company to reach world-level standards. In addition, by maintaining the energy quality within the required intervals, CFE avoids expensive fines by the Mexican regulatory organization (CRE).

7.2. Future Work

Future work on MIRD includes for the following research lines:

• NoSQL database implementation. The growing volume of the Parquet-based persistence layer of MIRD could eventually decrease the complete pipeline’s performance. We must perform the required research to design a new persistence layer; proven strategies in this field point to replacing our Parquet-based layer with a faster and more efficient NoSQL database [30]. For this task, we must evaluate different NoSQL databases (columnar, key-value, document-based).
• Parallel implementation. The data-preprocessing and the forecasting components of MIRD use SciKit Learn, designed to run on single-device hardware configurations. Given the massive amount of data managed by MIRD, it is advisable to distribute the SciKit Learn code or migrate those components to a computing framework that runs in distributed mode. Although many programming resources can distribute SciKit Learn jobs, Apache Spark, which already is the basis for the data-ingestion and the power-quality-evaluation components, is a convenient option upon which to base this upgrade.
• Forecast-model enhancement. MIRD’s forecasting models rely on MLP neural networks. Recently, we started experimenting with deep-learning models for MIRD based on long short-term memory (LSTM) networks, encoder–decoder networks, and transformers that have constantly reported better predictive performance than MLPs [31,32,33]. Our results suggest adding forecasting models based on such neural-network architectures to MIRD. However, having more powerful neural networks also means requiring more computing capacity. Therefore, this research line reinforces the need for achieving parallel implementation.
• Migration to an ML-pipeline development framework. We started the MIRD project in mid-2017 with early and preliminary prototypes and forecasting models. At that time, the availability of a fully integrated, end-to-end, production-ready framework for ML-pipeline development was still an idea. Today, many widely tested, open-source frameworks for ML-pipeline authoring are available [34,35,36]. Given the solid technical support and implementation expertise associated with these frameworks, it is worth analyzing a migration of the complete functionality of MIRD to one of them.