Creep Behavior of Rocks and Its Application to the Long-Term Stability of Deep Rock Tunnels
Abstract
:1. Introduction
2. General Creep Background
3. Mechanism of Rock Creep
4. Introduction to Creep Test Methods, Monitoring Methods, and Data Processing
5. Potential Factors Influencing Rock Creep
5.1. Hydraulic Pressure, Stress Level, Water Content, and Temperature
5.2. Damage and Time-to-Failure
5.3. Consideration on Tunnel Lining Structures
6. Mechanical Models and Creep Constitutive Models
6.1. Mechanical Models
6.2. Constitutive Creep Models of Rocks
6.3. Creep Constitutive Models in Deep Mines and Caverns
7. On the Applicability of Constitutive Models of Rock Creep to Deep Tunnels
7.1. Homogeneity and Isotropy of Rocks
7.2. Isothermal Conditions
7.3. Static or Quasi-Static Conditions
7.4. Specific Stress Conditions
8. Simple Example for a Specific Case
- -
- Potential factors such as water content and temperature that strongly influence the creep behavior of salt rocks seem not to be taken into account in the model.
- -
- Tertiary creep is not introduced in the model. In fact, the modeling of the tertiary creep requires to take into account damage variables or nonlinear elements [98].
9. Convergence and Post-Creep Behavior of Rocks Surrounding the Tunnels
10. Discussions
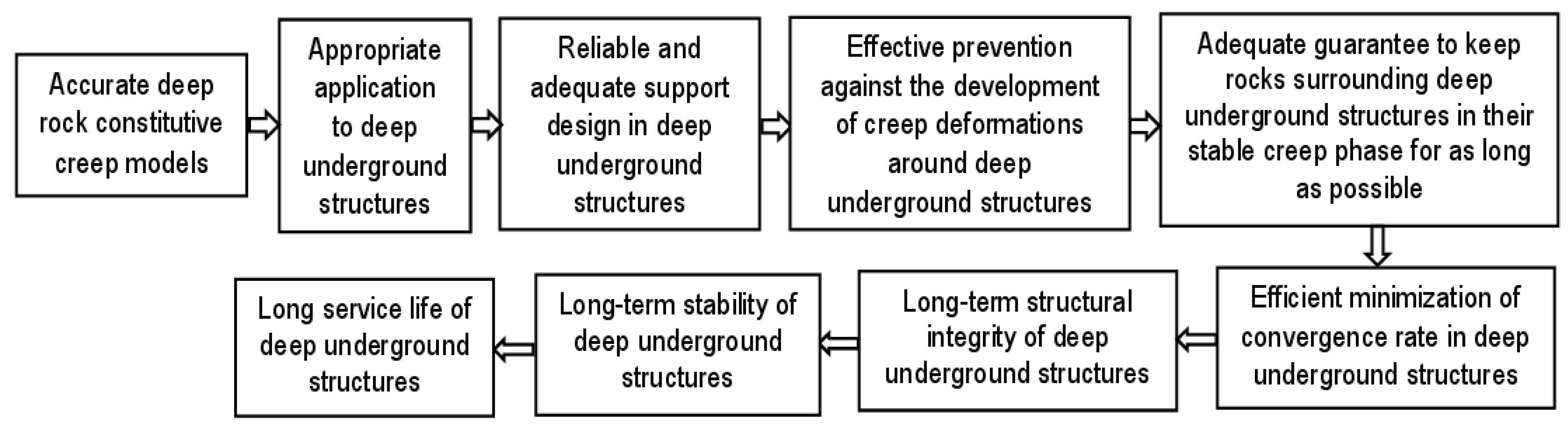
11. Conclusions and Perspectives for Future Research
11.1. Conclusions
- Regardless of the rock type, creep character is very common and is influenced by several potential factors which are mainly stress level, hydraulic pressure, water content, temperature, damage, and time-to-failure. The creep deformation mechanisms of rocks are mainly brittle, ductile, and semi-brittle. Under the long-term action of stresses, brittle failure is mostly common in hard rocks, while soft rocks mostly fail in a ductile manner. Semi-brittle failure is predominant in many hard rock types in deep rocky environments when there are combined influences of high stresses, high pressures, and high temperatures.
- Rock creep properties are usually determined through different laboratory experiments accompanied by monitoring methods. The collected data are adequately processed and used as the basis for decision-making in the early stages of deep rock engineering projects as well as for studying the long-term stability of different types of deep underground structures such as tunnels, mines and caverns. However, one of the key concerns with evaluating the creep properties of rocks is the duration considered in laboratory experiments which does not truly reflect the full exposure duration of rocks in realistic situations. To this end, compared to the exposure times in the field, the observation times in laboratory are too short to detect with great precision the characteristics and conditions of rock creep. To explore more broadly and more concretely the creep properties of rocks, it is suggested to combine their microscopic and macroscopic characteristics. Furthermore, as each monitoring method has its limitations, to achieve more accurate results, it is suggested that these methods be combined appropriately. Importantly, long-term monitoring is necessary to effectively ensure long-term performance of host rocks and therefore long-term stability of the underground structures.
- Many constitutive models of rock creep have been devised. They are habitually used to design support systems that must keep stable the surrounding rocks of the underground structures over a long period of time. However, much effort is still needed for the rigorous applicability of such models to deep tunnels. In fact, most of such models are established on the basis of simplifying assumptions that do not fully express the characteristics and conditions of actual deep rocks. For instance, since the coupling of many internal factors is unclear, most scholars extend the one-dimensional models to three-dimensional creep models, despite the fact that rocks are naturally three-dimensional stress media. Then, for the external factors, despite their significant individual influences on rock creep, additional investigations on their coupling effects are necessary. Nonetheless, precise and appropriate correction factors can be applied to these models to enhance their suitability to deep tunnels. Therefore, tunnel support systems generally designed to cope with total creep deformation can be more responsive and more efficient. Note that only accurate creep constitutive models can properly represent the overall contribution of rock creep to the time-dependent behavior of rocks.
- It is also noticed that, until now, numerous constitutive models of rock creep have been designed on the basis of parameters estimated from loading process of rock mechanical properties. However, the long-term safety and stability of deep excavations cannot be minutely described by the loading process alone, but rather by the combined loading-unloading process of rock mechanical properties. Indeed, if only one process is considered, the unloading can be more suitable to reflect the long-term states of underground structures. Nevertheless, little research takes into account the unloading process of rock masses to design constitutive models of rock creep. The need to thoroughly study the creep properties of rock during the unloading process is essential to properly ensure the long-term safety and stability of tunnels.
- To avoid large convergence deformations and premature failures of deep tunnels, effective measures must be adopted to maintain stable rock creep for as long as possible. Tunnel support systems must have sufficient resistance, but above all they must be put in place quickly according to the excavation sequences, in order to decrease and stabilize adequately rock pressure. Stabilization of rock pressure is extremely important to prevent any rapid evolution of rock creep. The secondary lining of the deep tunnels must be installed within a quick and reasonable time after excavation, without exceeding 40 days.
- When the entire existence time of the secondary creep phase is over, tertiary creep begins, and long-term stability is no longer guaranteed. Tertiary creep control remains difficult because the degree of rock damage therein is very high. However, it is crucial to accurately estimate the remaining lifetime of deep tunnels after the onset of the tertiary creep conditions. In case of lack of precise data, the tunnels should be automatically decommissioned. This can prevent casualties resulting from partial or total failure of tunnels. Indeed, the extent of damage and the creep deformations being generally uncontrollable during the accelerated creep phase, the recovery of the tunnels is very rarely possible. The best solution to ensure the long-term stability of tunnels is therefore to adopt effective measures that maintain rock creep at its stable stage as durable as possible.
11.2. Perspectives for Future Research
- -
- The effects of potential influencing factors on rock creep need further investigation. In fact, it is noteworthy to study the simultaneous effects of the hydraulic pressure, water content, stress level, temperature, and damage factor on long-term stability of deep tunnels built in heterogeneous rocky environments and subject to high stress.
- -
- Based on different specific case studies, it is extremely important to compare the accuracy of different existing creep constitutive models for stronger conclusions. The influence of individual factors on different creep constitutive models can also be further investigated.
- -
- Based on the heterogeneity and anisotropy of the rocky media, quantify the creep life of deep rock tunnels considering the effects of the potential influencing factors. It is also of high interest to accurately estimate the level of damage that can trigger accelerated creep for various rock types.
- -
- As the tertiary creep needs to be modeled more reliably, it is extremely significant to accurately assess the remaining lifetime of deep tunnel after the onset of tertiary creep conditions in the secondary linings and in the surrounding rocks in realistic conditions.
- -
- Since natural rocks are three-dimensional stress media, it is of utmost importance to establish accurate creep constitutive models based on efficient 3D derivation methods. In addition, by taking into account the characteristics and realistic conditions of rocks, these models will be much more suitable for deep rock tunnels. To accurately predict the long-term life of deep tunnels, it is also of huge importance to establish constitutive creep models of the complex formed with the surrounding rocks and the support systems.
- -
- So far, there are numerous research outcomes regarding the design of creep constitutive models based on loading process of rock mechanical properties, but few on the unloading process. Developing creep models based on the rock unloading process has enormous advantages for the safety and long-term stability of deep underground structures.
- -
- It is significant to monitor the creep behavior of rocks based on the combinations of many traditional methods such as computed tomography, ultra-pulse wave velocity, scanning electron microscope, acoustic emission, etc. Appropriate and robust remote sensing techniques and geographic information systems should be considered for in-depth in situ monitoring.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VOFCM | Variable-order fractional creep model |
| IEFV | Improved elastic element Fractional variable |
| BDT | Brazilian disk test |
| FENLCM | Five-element non-linear creep damage model |
| HFD | Hadamard fractional derivative |
| CTVDE | Coupled thermo-visco-plastic damage element |
| NLVEPDM | Non-linear visco-elastic–plastic damage model |
| VEPCM | Visco-elasto-plastic creep model |
| GKM | Generalized Kelvin model |
| NLVPCM | Non-linear viscoelastic-plastic creep model |
| EVPD | Visco-elastic visco-plastic with isotropic damage |
| UCC | Ubiquitous corrosion Coulomb |
| FDCD | Fractional derivative creep damage |
| List of symbols | |
| Pore water pressure | |
| Initial stress; constant stress; deviatoric stress | |
| ; | Applied stress |
| Respectively 1st, 2nd, and 3rd principal stress | |
| ; | Respectively second and first partial derivatives of the stress |
| Stress increment | |
| ; | Shear stress; initial shear stress at time |
| Critical shear stress at critical time | |
| Increase rate of the shear stress | |
| ; | Yield stress; creep strength |
| ; | Deviatoric stress tensor |
| Constant value of the deviatoric stress tensor | |
| Three-dimensional creep threshold | |
| ; | Long-term strength |
| Second invariant of the deviatoric visco-plastic strain tensor | |
| Onset of tertiary creep expressed by the second invariant of the deviatoric visco-plastic strain tensor | |
| Main stress tensor; spherical stress tensor | |
| Kronecker function | |
| Yield function | |
| Strain before accelerating creep | |
| Creep strain | |
| 3D creep strain | |
| Respectively second and first partial derivatives of the creep strain | |
| Creep time | |
| Creep time; unloading time | |
| n-th level charge start time | |
| Viscosity coefficient of rocks | |
| Viscosity coefficient at temperature | |
| Bulk modulus | |
| Elastic shear modulus, viscoelastic shear modulus | |
| Viscoelastic shear modulus | |
| Shear modulus | |
| Elastic modulus, viscoelasticity modulus; shear modulus | |
| Elastic modulus of rocks | |
| Elastic, or viscoelasticity modulus of rocks | |
| Elastic modulus at temperature | |
| Accelerating creep exponent with no water pressure | |
| fitting parameters | |
| Fitting parameter that represents the duration of stress; internal frictional angle | |
| Transition time between the 2nd and 3rd creep phases | |
| Gamma function | |
| Parameter controlling the damage evolution with time, nonlinearity constant in the NLVPCM | |
| Fractional order derivative | |
| Constants related to the materials | |
| Tertiary creep factor ) | |
| Additional criterion for tertiary creep | |
| Viscous parameters | |
| Initial damage variable | |
| Initial strain value of the tertiary creep | |
| Creep parameters | |
| Constants | |
| Relaxation time of materials | |
| Damage factor | |
| Crack initiation stress under compression conditions | |
| Function to control of the shape of time−creep strain curve in the tertiary (accelerating) creep | |
| Damage variable | |
| Positive non-dimensional constant | |
References
- Scheidegger, A.E. On the Rheology of Rock Creep. Rock Mech. 1970, 2, 138–145. [Google Scholar] [CrossRef]
- Qiu, S.L.; Feng, X.T.; Xiao, J.Q.; Zhang, C.Q. An Experimental Study on the Pre-Peak Unloading Damage Evolution of Marble. Rock Mech. Rock Eng. 2014, 47, 401–419. [Google Scholar] [CrossRef]
- Niu, L.; Zhu, W.; Cheng, Z.; Guan, K.; Qin, T. Numerical simulation on excavation-induced damage of rock under quasi static unloading and dynamic disturbance. Environ. Earth Sci. 2017, 76, 614. [Google Scholar] [CrossRef]
- Fu, T.F.; Xu, T.; Wasantha, P.L.P.; Yang, T.H.; Nara, Y.; Heng, Z. Time-dependent deformation and fracture evolution around underground excavations. Geomat. Nat. Haz. Risk 2020, 11, 2615–2633. [Google Scholar] [CrossRef]
- Cui, G.; Qi, J.; Wang, D. Research on large deformation control technology of tunnels in squeezing rock and its application. Sci. Progress 2020, 103, 36850420923167. [Google Scholar] [CrossRef]
- Zhu, W.; Li, S.; Li, S.; Niu, L. Influence of Dynamic Disturbance on the Creep of Sandstone: An Experimental Study. Rock Mech. Rock Eng. 2019, 52, 1023–1039. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, X.; Xu, C.; Zhou, C.; He, C.; Ying, C. Time-dependent behavior of saturated silty mudstone under different confining pressures. Bull. Eng. Geol. Environ. 2020, 79, 2621–2634. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, X.; Cao, R.; Wen, Z. Improved nonlinear Burgers shear creep model based on the time-dependent shear strength for rock. Environ. Earth Sci. 2020, 79, 149. [Google Scholar] [CrossRef]
- Li, G.; Wang, Y.; Wang, D.; Yang, X.; Wang, L.; Li, Y.; Zhang, S. Creep damage model of rock with varying-parameter under the step loading and unloading conditions. Sci. Rep. 2021, 11, 24057. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Q.; Liu, Y. Long-term stability analysis of the left bank abutment slope at Jinping I hydropower station. J. Rock Mech. Geotech. Eng. 2016, 8, 398–404. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Chen, Q.; Basack, S.; Xu, R.; Shi, Z. Biaxial Creep Test Study on the Influence of Structural Anisotropy on Rheological Behavior of Hard Rock. J. Mater. Civ. Eng. 2016, 28, 04016104. [Google Scholar] [CrossRef]
- Lv, S.; Wang, W.; Liu, H. A Creep Damage Constitutive Model for a Rock Mass with Nonpersistent Joints under Uniaxial Compression. Math. Prob. Eng. 2019, 2019, 4361458. [Google Scholar] [CrossRef]
- Hashiba, K.; Fukui, K. Time-Dependent Behaviors of Granite: Loading-Rate Dependence, Creep, and Relaxation. Rock Mech. Rock Eng. 2016, 49, 2569–2580. [Google Scholar] [CrossRef]
- Cao, P.; Youdao, W.; Yixian, W.; Haiping, Y.; Bingxiang, Y. Study on nonlinear damage creep constitutive model for high-stress soft rock. Environ. Earth Sci. 2016, 75, 900. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.; Han, C. Nonlinear damage creep model based on fractional theory for rock materials. Mech. Time-Depend. Mater. 2021, 25, 341–352. [Google Scholar] [CrossRef]
- Challamel, N.; Lanos, C.; Casandjian, C. Stability analysis of quasi-brittle materials—Creep under multiaxial loading. Mech. Time-Depend. Mater. 2006, 10, 35–50. [Google Scholar] [CrossRef]
- Cao, P.; Wan, L.H.; Wang, Y.X.; Huang, Y.H.; Zhang, X.Y. Viscoelasto-plastic properties of deep hard rocks under water environment. Trans. Nonferrous Metal Soc. China 2011, 21, 2711–2718. [Google Scholar] [CrossRef]
- Chen, B.R.; Zhao, X.J.; Feng, X.T.; Zhao, H.B.; Wang, S.Y. Time-dependent damage constitutive model for the marble in the Jinping II hydropower station in China. Bull. Eng. Geol. Environ. 2014, 73, 499–515. [Google Scholar] [CrossRef]
- Mei, Y.; Xianbiao, M.; Xinyu, H. Shear creep characteristics and constitutive model of limestone. Int. J. Min. Sci. Technol. 2016, 26, 423–428. [Google Scholar] [CrossRef]
- Liu, H.Z.; Xie, H.Q.; He, J.D.; Xiao, M.L.; Zhuo, L. Nonlinear creep damage constitutive model for soft rocks. Mech. Time-Depend. Mater. 2017, 21, 73–96. [Google Scholar] [CrossRef]
- Tang, H.; Wang, D.; Huang, R.; Pei, X.; Chen, W. A new rock creep model based on variable-order fractional derivatives and continuum damage mechanics. Bull. Eng. Geol. Environ. 2018, 77, 375–383. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, H.; Zou, Q.; Li, C.; Chen, J.; Gao, R. Viscoelastic-plastic damage creep model for salt rock based on fractional derivative theory. Mech. Mater. 2020, 150, 103600. [Google Scholar] [CrossRef]
- Gao, Y.; Yin, D. A full-stage creep model for rocks based on the variable-order fractional calculus. Appl. Math. Model. 2021, 95, 435–446. [Google Scholar] [CrossRef]
- Li, X.; Yin, Z. Analysis of Shear Characteristics of Deep, Anchored Rock Mass under Creep Fatigue Loading. Adv. Civ. Eng. 2021, 2021, 2326237. [Google Scholar] [CrossRef]
- Qian, L.; Zhang, J.; Wang, X.; Li, Y.; Zhang, R.; Xu, N.; Li, Z. Creep strain analysis and an improved creep model of granite based on the ratio of deviatoric stress-peak strength under different confining pressures. Environ. Earth Sci. 2022, 81, 109. [Google Scholar] [CrossRef]
- Kumar, K.R.; Hajibeygi, H. Multiscale simulation of inelastic creep deformation for geological rocks. J. Comput. Phys. 2021, 440, 110439. [Google Scholar] [CrossRef]
- Sterpi, D.; Gioda, G. Visco-Plastic Behaviour around Advancing Tunnels in Squeezing Rock. Rock Mech. Rock Eng. 2009, 42, 319–339. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, Y. Triaxial mechanical creep behavior of sandstone. Min. Sci. Technol. 2010, 20, 339–349. [Google Scholar] [CrossRef]
- Paraskevopoulou, C.; Diederichs, M. Analysis of time-dependent deformation in tunnels using the Convergence-Confinement Method. Tunn. Undergr. Space Technol. 2018, 71, 62–80. [Google Scholar] [CrossRef]
- Andargoli, M.B.E.; Shahriar, K.; Ramezanzadeh, A.; Goshtasbi, K. The analysis of dates obtained from long-term creep tests to determine creep coefficients of rock salt. Bull. Eng. Geol. Environ. 2019, 78, 1617–1629. [Google Scholar] [CrossRef]
- Wang, R.; Li, L.; Simon, R. A model for describing and predicting the creep strain of rocks from the primary to the tertiary stage. Int. J. Rock Mech. Min. Sci. 2019, 123, 104087. [Google Scholar] [CrossRef]
- Kabwe, E.; Karakus, M.; Chanda, E.K. Isotropic damage constitutive model for time-dependent behaviour of tunnels in squeezing ground. Comput. Geotech. 2020, 127, 103738. [Google Scholar] [CrossRef]
- Song, F.; Rodriguez-Dono, A.; Olivella, S.; Gens, A. Coupled solid-fluid response of deep tunnels excavated in saturated rock masses with a time-dependent plastic behaviour. Appl. Math. Model. 2021, 100, 508–535. [Google Scholar] [CrossRef]
- Chen, C.; Xu, T.; Heap, M.J.; Baud, P. Influence of unloading and loading stress cycles on the creep behavior of Darley Dale Sandstone. Int. J. Rock Mech. Min. Sci. 2018, 112, 55–63. [Google Scholar] [CrossRef]
- Malan, D.F. Time-dependent Behaviour of Deep Level Tabular Excavations in Hard Rock. Rock Mech. Rock Eng. 1999, 32, 123–155. [Google Scholar] [CrossRef]
- Malan, D.F. Simulating the Time-dependent Behaviour of Excavations in Hard Rock. Rock Mech. Rock Eng. 2002, 35, 225–254. [Google Scholar] [CrossRef]
- Herrmann, J.; Rybacki, E.; Sone, H.; Dresen, G. Deformation Experiments on Bowland and Posidonia Shale—Part II: Creep Behavior at In Situ pc-T Conditions. Rock Mech. Rock Eng. 2020, 53, 755–779. [Google Scholar] [CrossRef]
- Aydan, O.; Akagi, T.; Kawamoto, T. The Squeezing Potential of Rock Around Tunnels: Theory and Prediction with Examples Taken from Japan. Rock Mech. Rock Eng. 1996, 29, 125–143. [Google Scholar] [CrossRef]
- Damjanac, B.; Fairhurst, C. Evidence for a Long-Term Strength Threshold in Crystalline Rock. Rock Mech. Rock Eng. 2010, 43, 513–531. [Google Scholar] [CrossRef]
- Jian-feng, L.; Lu, W.; Jian-liang, P.; Lu, Z.; Yu, B. Experimental study on creep deformation and long-term strength of unloading-fractured marble. Eur. J. Environ. Civ. Eng. 2015, 19, s97–s107. [Google Scholar] [CrossRef]
- Fahimifar, A.; Karami, M.; Fahimifar, A. Modifications to an elasto-viscoplastic constitutive model for prediction of creep deformation of rock samples. Soils Found. 2015, 55, 1364–1371. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Wang, W.; Wan, W.; Li, S.; Ma, W.; Wang, Y. Creep Behavior of Intact and Cracked Limestone Under Multi-Level Loading and Unloading Cycles. Rock Mech. Rock Eng. 2017, 50, 1409–1424. [Google Scholar] [CrossRef]
- Fei, W.; Jie, L.; Quanle, Z.; Cunbao, L.; Jie, C.; Renbo, G. A triaxial creep model for salt rocks based on variable-order fractional derivative. Mech. Time-Depend. Mater. 2021, 25, 101–118. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, J.; Ren, Y.; Liang, C.; Zhang, Q. Study on long-term uniaxial compression creep mechanical behavior of rocksalt-mudstone combined body. Int. J. Damage Mech. 2021, 31, 275–293. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, W.Y.; Shao, J.F.; Zhao, H.B.; Wang, W. Experimental investigation of creep behavior of clastic rock in Xiangjiaba Hydropower Project. Water Sci. Eng. 2015, 8, 55–62. [Google Scholar] [CrossRef]
- Fabre, G.; Pellet, F. Creep and time-dependent damage in argillaceous rocks. Int. J. Rock Mech. Min. Sci. 2006, 43, 950–960. [Google Scholar] [CrossRef]
- Trzeciak, M.; Sone, H.; Dabrowski, M. Long-term creep tests and viscoelastic constitutive modeling of lower Paleozoic shales from the Baltic Basin, N Poland. Int. J. Rock Mech. Min. Sci. 2018, 112, 139–157. [Google Scholar] [CrossRef]
- Bikong, C.; Hoxha, D.; Shao, J.F. A micro-macro model for time-dependent behavior of clayey rocks due to anisotropic propagation of microcracks. Int. J. Plast. 2015, 69, 73–88. [Google Scholar] [CrossRef]
- Li, X.; Shao, Z. Investigation of Macroscopic Brittle Creep Failure Caused by Microcrack Growth Under Step Loading and Unloading in Rocks. Rock Mech. Rock Eng. 2016, 49, 2581–2593. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, X.T.; Zhang, X.; Yang, C. Brittle and ductile creep behavior of Jinping marble under true triaxial stress. Eng. Geol. 2019, 258, 105157. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B.; Read, R.S. Identifying crack initiation and propagation thresholds in brittle rock. Can. Geotech. J. 1998, 35, 222–233. [Google Scholar] [CrossRef]
- Ma, C.C.; Li, T.B.; Xing, H.L.; Zhang, H.; Wang, M.J.; Liu, T.Y.; Chen, G.Q.; Chen, Z.Q. Brittle Rock Modeling Approach and its Validation Using Excavation-Induced Micro-Seismicity. Rock Mech. Rock Eng. 2016, 49, 3175–3188. [Google Scholar] [CrossRef]
- Cook, N.G.W. An experiment proving that dilatancy is a pervasive volumetric property of brittle rock loaded to failure. Rock Mech. 1970, 2, 181–188. [Google Scholar] [CrossRef]
- Nicolas, A.; Fortin, J.; Regnet, J.B.; Verberne, B.A.; Plümper, O.; Dimanov, A.; Spiers, C.J.; Guéguen, Y. Brittle and semibrittle creep of Tavel limestone deformed at room temperature. J. Geophys. Res. Solid Earth 2017, 122, 4436–4459. [Google Scholar] [CrossRef]
- Kaiser, P.K.; Morgenstern, N.R. Phenomenological model for rock with time-dependent strength. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 153–165. [Google Scholar] [CrossRef]
- Miura, K.; Okui, Y.; Horii, H. Micromechanics-based prediction of creep failure of hard rock for long-term safety of high-level radioactive waste disposal system. Mech. Mater. 2003, 35, 587–601. [Google Scholar] [CrossRef]
- Diederichs, M.S. The 2003 Canadian Geotechnical Colloquium: Mechanistic interpretation and practical application of damage and spalling prediction criteria for deep tunnelling. Can. Geotech. J. 2007, 44, 1082–1116. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Strength, Creep and Frictional Properties of Gas Shale Reservoir Rocks. In Proceedings of the 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. ARMA 10-463. [Google Scholar]
- Wang, S.; Zhao, W.; Fu, X.; Zhang, Z.; Wang, T.; Ge, J. A universal method for quantitatively evaluating rock brittle-ductile transition behaviors. J. Petro. Sci. Eng. 2020, 195, 107774. [Google Scholar] [CrossRef]
- Ulloa, J.; Wambacq, J.; Alessi, R.; Samaniego, E.; Degrande, G.; François, S. A micromechanics-based variational phase-field model for fracture in geomaterials with brittle-tensile and compressive-ductile behavior. J. Mech. Phys. Solids 2022, 159, 104684. [Google Scholar] [CrossRef]
- Paraskevopoulou, C.; Perras, M.; Diederichs, M.; Amann, F.; Löw, S.; Lam, T.; Jensen, M. The three stages of stress relaxation—Observations for the time-dependent behaviour of brittle rocks based on laboratory testing. Eng. Geol. 2017, 216, 56–75. [Google Scholar] [CrossRef]
- Firme, P.A.L.P.; Brandao, N.B.; Roehl, D.; Romanel, C. Enhanced double-mechanism creep laws for salt rocks. Acta Geotech. 2018, 13, 1329–1340. [Google Scholar] [CrossRef]
- Reber, J.E.; Pec, M. Comparison of brittle- and viscous creep in quartzites: Implications for semibrittle flow of rocks. J. Struct. Geol. 2018, 113, 90–99. [Google Scholar] [CrossRef]
- Rybacki, E.; Herrmann, J.; Wirth, R.; Dresen, G. Creep of Posidonia Shale at Elevated Pressure and Temperature. Rock Mech. Rock Eng. 2017, 50, 3121–3140. [Google Scholar] [CrossRef]
- Nardini, L.; Rybacki, E.; Krause, M.; Morales, L.F.G.; Dresen, G. Control of the geometric arrangement of material heterogeneities on strain localization at the brittle-to-ductile transition in experimentally deformed carbonate rocks. J. Struct. Geol. 2020, 135, 104038. [Google Scholar] [CrossRef]
- Hu, K.; Zhu, Q.Z.; Chen, L.; Shao, J.F.; Liu, J. A Micromechanics-Based Elastoplastic Damage Model for Rocks with a Brittle–Ductile Transition in Mechanical Response. Rock Mech. Rock Eng. 2018, 51, 1729–1737. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks—Part 2: Ductile creep, brittle strength, and their relation to the elastic modulus. Geophysics 2013, 78, D393–D402. [Google Scholar] [CrossRef]
- Zhang, G.; Lei, Z.; Cheng, H. Shear Creep Simulation of Structural Plane of Rock Mass Based on Discontinuous Deformation Analysis. Mat. Prob. Eng. 2017, 2017, 1582825. [Google Scholar] [CrossRef]
- Wang, J.; Xu, J.; Nie, Z.; Liu, L.; Qin, M.; Ou, R. Creep Fracture Characteristics of Fractured Rock Mass Strengthened with Toughened Epoxy Resin. Adv. Civ. Eng. 2021, 2021, 1582745. [Google Scholar] [CrossRef]
- Khormani, M.; Jaari, V.R.K.; Aghayan, I.; Ghaderi, S.H.; Ahmadyfard, A. Compressive strength determination of concrete specimens using X-ray computed tomography and finite element method. Constr. Build. Mater. 2020, 256, 119427. [Google Scholar] [CrossRef]
- Wulff, A.M.; Hashida, T.; Watanabe, K.; Takahashi, H. Attenuation behaviour of tuffaceous sandstone and granite during microfracturing. Geophys. J. Int. 1999, 139, 395–409. [Google Scholar] [CrossRef] [Green Version]
- Jia, S.; Wen, C.; Wu, B. A nonlinear elasto-viscoplastic model for clayed rock and its application to stability analysis of nuclear waste repository. Energy Sci. Eng. 2020, 8, 150–165. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.B.; Xu, W.Y.; Shao, J.F. Change in the permeability of clastic rock during multi-loading triaxial compressive creep tests. Géotech. Lett. 2015, 5, 167–172. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.H.; Hu, Y.Z. Experimental investigation on the fracture behaviour of black shale by acoustic emission monitoring and CT image analysis during uniaxial compression. Geophys. J. Int. 2018, 213, 660–675. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, C.; Kannan, L.G.; Rao, K.S.; Ayothiraman, R. Estimation of creep parameters of rock salt from uniaxial compression tests. Int. J. Rock Mech. Min. Sci. 2018, 107, 243–248. [Google Scholar] [CrossRef]
- Rassouli, F.S.; Zoback, M.D. Long-term creep experiments on Haynesville shale rocks. In Proceedings of the 49th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015. ARMA-2015-532. [Google Scholar]
- Rassouli, F.S.; Zoback, M.D. Comparison of Short-Term and Long-Term Creep Experiments in Shales and Carbonates from Unconventional Gas Reservoirs. Rock Mech. Rock Eng. 2018, 51, 1995–2014. [Google Scholar] [CrossRef]
- Liu, K.; Rassouli, F.S.; Liu, B.; Ostadhassan, M. Creep Behavior of Shale: Nanoindentation vs. Triaxial Creep Tests. Rock Mech. Rock Eng. 2021, 54, 321–335. [Google Scholar] [CrossRef]
- Wang, X.; Song, L.; Xia, C.; Han, G.; Zhu, Z. Nonlinear Elasto-Visco-Plastic Creep Behavior and New Creep Damage Model of Dolomitic Limestone Subjected to Cyclic Incremental Loading and Unloading. Sustainability 2021, 13, 12376. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X. Study on Nonlinear Damage Creep Model for Rocks under Cyclic Loading and Unloading. Adv. Mater. Sci. Eng. 2021, 2021, 5512972. [Google Scholar] [CrossRef]
- Matei, A.; Cristescu, N.D. The effect of volumetric strain on elastic parameters for rock salt. Mech. Cohes.-Frict. Mater. 2000, 5, 113–124. [Google Scholar] [CrossRef]
- Zhao, N.; Jiang, H. Mathematical methods to unloading creep constitutive model of rock mass under high stress and hydraulic pressure. Alexandria Eng. J. 2021, 60, 25–38. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Kang, Y.; Wang, D.; Ye, D. Experimental research on creep properties of limestone under fluid–solid coupling. Environ. Earth Sci. 2015, 73, 7011–7018. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, J.; Sepehrnoori, K.; Li, Y.; Li, Z. The influences of stress level, temperature, and water content on the fitted fractional orders of geomaterials. Mech. Time-Depend. Mater. 2020, 24, 221–232. [Google Scholar] [CrossRef]
- Li, S.; Chen, C.; Zhang, F.; Yao, X. Creep behavior of sandstone containing impact-induced microcracks. Mech. Time-Depend. Mater. 2021. [Google Scholar] [CrossRef]
- Montero-Cubillo, N.S.; Galindo, R.A.; Olalla, C.; Muñiz-Ménendez, M. Pull-out creep laboratory test for soft rocks. Int. J. Rock Mech. Min. Sci. 2021, 144, 104811. [Google Scholar] [CrossRef]
- Jia, C.J.; Xua, W.Y.; Wang, R.B.; Wang, S.S.; Lin, Z.N. Experimental investigation on shear creep properties of undisturbed rock discontinuity in Baihetan Hydropower Station. Int. J. Rock Mech. Min. Sci. 2018, 104, 27–33. [Google Scholar] [CrossRef]
- Wang, X.; Huang, L.; Yan, C.; Lian, B. HKCV Rheological Constitutive Model of Mudstone under Dry and Saturated Conditions. Adv. Civ. Eng. 2018, 2018, 2621658. [Google Scholar] [CrossRef]
- Frenelus, W.; Peng, H.; Zhang, J. Long-Term Degradation, Damage and Fracture in Deep Rock Tunnels: A review on the effects of Excavation Methods. Frattura Integ. Strut. 2021, 15, 128–150. [Google Scholar] [CrossRef]
- Okubo, S.; Fukui, K.; Hashiba, K. Long-term creep of water-saturated tuff under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2010, 47, 839–844. [Google Scholar] [CrossRef]
- Xiong, L.; Li, T.; Yang, L. Biaxial Compression Creep Test on Green-schist Considering the Effects of Water Content and Anisotropy. KSCE J. Civ. Eng. 2014, 18, 103–112. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L. Effect of water and temperature on short-term and creep mechanical behaviors of coal measures mudstone. Environ. Earth Sci. 2017, 76, 597. [Google Scholar] [CrossRef]
- Hashiba, K.; Fukui, K.; Kataoka, M.; Chu, S.Y. Effect of water on the strength and creep lifetime of andesite. Int. J. Rock Mech. Min. Sci. 2018, 108, 37–42. [Google Scholar] [CrossRef]
- Li, Z.; Liu, S.; Ren, W.; Fang, J.; Zhu, Q.; Dun, Z. Multiscale Laboratory Study and Numerical Analysis of Water-Weakening Effect on Shale. Adv. Mater. Sci. Eng. 2020, 2020, 5263431. [Google Scholar] [CrossRef]
- Cai, X.; Zhou, Z.; Liu, K.; Du, X.; Zang, H. Water-Weakening Effects on the Mechanical Behavior of Different Rock Types: Phenomena and Mechanisms. Appl. Sci. 2019, 9, 4450. [Google Scholar] [CrossRef]
- Zhu, C.; Arson, C. A thermo-mechanical damage model for rock stiffness during anisotropic crack opening and closure. Acta Geotech. 2014, 9, 847–867. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.P.; Liu, J.F.; Liu, Y.M.; Su, R.; Wang, J. A damage-mechanism-based creep model considering temperature effect in granite. Mech. Res. Commun. 2014, 56, 76–82. [Google Scholar] [CrossRef]
- Fan, L.; Wang, W.; Yuan, C.; Peng, W. Research on large deformation mechanism of deep roadway with dynamic pressure. Energy Sci. Eng. 2020, 8, 3348–3364. [Google Scholar] [CrossRef]
- Kinoshita, N.; Yasuhara, H. Thermally Induced Behavior of the Openings in Rock Mass Affected by High Temperatures. Int. J. Geomech. 2011, 11, 124–130. [Google Scholar] [CrossRef]
- Ye, G.L.; Nishimura, T.; Zhang, F. Experimental study on shear and creep behaviour of green tuff at high temperatures. Int. J. Rock Mech. Min. Sci. 2015, 79, 19–28. [Google Scholar] [CrossRef]
- Xu, T.; Zhou, G.L.; Heap, M.J.; Zhu, W.C.; Chen, C.F.; Baud, P. The Influence of Temperature on Time-Dependent Deformation and Failure in Granite: A Mesoscale Modeling Approach. Rock Mech. Rock Eng. 2017, 50, 2345–2364. [Google Scholar] [CrossRef]
- Yang, S.Q.; Hu, B. Creep and Long-Term Permeability of a Red Sandstone Subjected to Cyclic Loading After Thermal Treatments. Rock Mech. Rock Eng. 2018, 51, 2981–3004. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, M.; Han, L.; Pu, H.; Chen, Y. Experimental research on the influence of loading rate on the mechanical properties of limestone in a high-temperature state. Bull. Eng. Geol. Environ. 2019, 78, 3479–3492. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, Y.; Liu, Q.; Ma, H. Investigation of the excavation damaged zone around deep TBM tunnel using a Voronoi-element based explicit numerical manifold method. Int. J. Rock Mech. Min. Sci. 2018, 112, 158–170. [Google Scholar] [CrossRef]
- Tian, M.; Han, L.; Meng, Q.; Jin, Y.; Meng, L. In situ investigation of the excavation-loose zone in surrounding rocks from mining complex coal seams. J. App. Geoph. 2019, 168, 90–100. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, W.; Lv, H. Creep energy damage model of rock graded loading. Resul. Phys. 2019, 12, 1119–1125. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Y.; Gao, F.; Zhang, X. Researches on Damage Evolution and Acoustic Emission Characteristics of Rocks. Adv. Civ. Eng. 2018, 2018, 3108065. [Google Scholar] [CrossRef]
- Shojaei, A.; Taleghani, D.A.; Li, G. A continuum damage failure model for hydraulic fracturing of porous rocks. Int. J. Plasticity 2014, 59, 199–212. [Google Scholar] [CrossRef]
- Eslami, J.; Hoxha, D.; Grgi, D. Estimation of the damage of a porous limestone using continuous wave velocity measurements during uniaxial creep tests. Mech. Mater. 2012, 49, 51–65. [Google Scholar] [CrossRef]
- Wang, M.; Cai, M. A grain-based time-to-failure creep model for brittle rocks. Comput. Geotech. 2020, 119, 103344. [Google Scholar] [CrossRef]
- Amitrano, D. Rupture by damage accumulation in rocks. Int. J. Fract. 2006, 139, 369–381. [Google Scholar] [CrossRef]
- Brantut, N.; Heap, M.J.; Meredith, P.G.; Baud, P. Time-dependent cracking and brittle creep in crustal rocks: A review. J. Struct. Geol. 2013, 52, 17–43. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, X.; Wang, Y.; Yong, R.; Fan, X.; Du, S.; Zhao, Y. Improved Nonlinear Nishihara Shear Creep Model with Variable Parameters for Rock-Like Materials. Adv. Civ. Eng. 2020, 2020, 7302141. [Google Scholar] [CrossRef]
- Tsai, L.S.; Hsieh, Y.M.; Weng, M.C.; Huang, T.H.; Jeng, F.S. Time-dependent deformation behaviors of weak sandstones. Int. J. Rock Mech. Min. Sci. 2008, 45, 144–154. [Google Scholar] [CrossRef]
- Chen, Z.; He, C.; Yang, W.; Guo, W.; Li, Z.; Xu, G. Impacts of geological conditions on instability causes and mechanical behavior of large-scale tunnels: A case study from the Sichuan–Tibet highway, China. Bull. Eng. Geol. Environ. 2020, 79, 3667–3688. [Google Scholar] [CrossRef]
- Li, X.; Konietzky, H. Time to Failure Prediction Scheme for Rocks. Rock Mech. Rock Eng. 2014, 47, 1493–1503. [Google Scholar] [CrossRef]
- Nedjar, B.; Le Roy, R. An approach to the modeling of viscoelastic damage. Application to the long-term creep of gypsum rock materials. Int. J. Num. Anal. Meth. Geomech. 2013, 37, 1066–1078. [Google Scholar] [CrossRef]
- Cao, W.; Chen, K.; Tan, X.; Chen, X. A novel damage-based creep model considering the complete creep process and multiple stress levels. Comput. Geotech. 2020, 124, 103599. [Google Scholar] [CrossRef]
- Cui, G.; Ma, J. Shaking table test on the seismic response of the portal section in soft and hard rock junction. Sci. Progress 2021, 104, 1–16. [Google Scholar] [CrossRef]
- Amitrano, D.; Helmstetter, A. Brittle creep, damage, and time to failure in rocks. J. Geophys. Res. Solid Earth 2006, 111, B11201. [Google Scholar] [CrossRef]
- Sisodiya, M.; Zhang, Y. A Time-Dependent Directional Damage Theory for Brittle Rocks Considering the Kinetics of Microcrack Growth. Rock Mech. Rock Eng. 2022, 55, 2693–2710. [Google Scholar] [CrossRef]
- Xu, G.; Gutierrez, M. Study on the damage evolution in secondary tunnel lining under the combined actions of corrosion degradation of preliminary support and creep deformation of surrounding rock. Transport. Geotech. 2021, 27, 100501. [Google Scholar] [CrossRef]
- Hao, X.J.; Feng, X.T.; Yang, C.X.; Jiang, Q.; Li, S.J. Analysis of EDZ Development of Columnar Jointed Rock Mass in the Baihetan Diversion Tunnel. Rock Mech. Rock Eng. 2016, 49, 1289–1312. [Google Scholar] [CrossRef]
- Nie, X.; Zhang, Q. A System of Monitoring and Dimensioning Tunnel Support. Rock Mech. Rock Eng. 1994, 27, 23–36. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, C.; Zhang, H. Analysis of Surrounding Rock Creep Effect on the Long-Term Stability of Tunnel Secondary Lining. Shock Vibr. 2021, 2021, 4614265. [Google Scholar] [CrossRef]
- Wu, G.; Chen, W.; Tian, H.; Jia, Z.; Yang, J.; Tan, X. Numerical evaluation of a yielding tunnel lining support system used in limiting large deformation in squeezing rock. Environ. Earth Sci. 2018, 77, 439. [Google Scholar] [CrossRef]
- Sandrone, F.; Labiouse, V. Analysis of the evolution of road tunnels equilibrium conditions with a convergence–confinement approach. Rock Mech. Rock Eng. 2010, 43, 201–218. [Google Scholar] [CrossRef]
- Arnau, O.; Molins, C.; Blom, C.B.M.; Walraven, J.C. Longitudinal time-dependent response of segmental tunnel linings. Tunn. Undergr. Space Technol. 2012, 28, 98–108. [Google Scholar] [CrossRef]
- Huang, M.; Zhan, J.W.; Xu, C.S.; Jiang, S. New Creep Constitutive Model for Soft Rocks and Its Application in the Prediction of Time-Dependent Deformation in Tunnels. Int. J. Geomech. 2020, 20, 04020096. [Google Scholar] [CrossRef]
- Do, D.P.; Tran, N.T.; Mai, V.T.; Hoxha, D.; Vu, M.N. Time-Dependent Reliability Analysis of Deep Tunnel in the Viscoelastic Burger Rock with Sequential Installation of Liners. Rock Mech. Rock Eng. 2020, 53, 1259–1285. [Google Scholar] [CrossRef]
- Wang, H.N.; Li, Y.; Ni, Q.; Utili, S.; Jiang, M.J.; Liu, F. Analytical Solutions for the Construction of Deeply Buried Circular Tunnels with Two Liners in Rheological Rock. Rock Mech. Rock Eng. 2013, 46, 1481–1498. [Google Scholar] [CrossRef]
- Song, F.; Rodriguez-Dono, A.; Olivella, S. Hydro-mechanical modelling and analysis of multi-stage tunnel excavations using a smoothed excavation method. Comput. Geotech. 2021, 135, 104150. [Google Scholar] [CrossRef]
- Chu, Z.; Wu, Z.; Liu, Q.; Liu, B. Analytical Solutions for Deep-Buried Lined Tunnels Considering Longitudinal Discontinuous Excavation in Rheological Rock Mass. J. Eng. Mech. 2020, 146, 04020047. [Google Scholar] [CrossRef]
- Chen, J.; Luo, Y.; Li, Y.; Zhao, P.; Xu, D.; Wang, Q. The change of rock mass pressure of Lianchengshan tunnel. Environ. Earth Sci. 2020, 79, 192. [Google Scholar] [CrossRef]
- Kovári, K.; Staus, J. Basic Considerations on Tunnelling in Squeezing Ground. Rock Mech. Rock Eng. 1996, 29, 203–210. [Google Scholar] [CrossRef]
- Gioda, G.; Cividini, A. Numerical Methods for the Analysis of Tunnel Performance in Squeezing Rocks. Rock Mech. Rock Eng. 1996, 29, 171–193. [Google Scholar] [CrossRef]
- Barla, G.; Debernardi, D.; Sterpi, D. Time-Dependent Modeling of Tunnels in Squeezing Conditions. Int. J. Geomech. 2012, 12, 697–710. [Google Scholar] [CrossRef]
- Dwivedi, R.D.; Goel, R.K.; Singh, M.; Viladkar, M.N.; Singh, P.K. Prediction of Ground Behaviour for Rock Tunnelling. Rock Mech. Rock Eng. 2019, 52, 1165–1177. [Google Scholar] [CrossRef]
- Yadav, P.; Sharan, S. Numerical Investigation of Squeezing in Underground Hard Rock Mines. Rock Mech. Rock Eng. 2019, 52, 1211–1229. [Google Scholar] [CrossRef]
- Xu, G.; He, C.; Yang, Q.; Wang, B. Progressive failure process of secondary lining of a tunnel under creep effect of surrounding rock. Tunn. Undergr. Space Technol. 2019, 90, 76–98. [Google Scholar] [CrossRef]
- Birchall, T.J.; Osman, A.S. Response of a tunnel deeply embedded in a viscoelastic medium. Int. J. Numer. Anal. Meth. Geomech. 2012, 36, 1717–1740. [Google Scholar] [CrossRef]
- Yang, W.; Gamage, R.P.; Huang, C.; Luo, G.; Guo, J.; Wang, S. Loading History Effect on Creep Deformation of Rock. Energies 2018, 11, 1462. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.N.; Chen, X.P.; Jiang, M.J.; Song, F.; Wu, L. The analytical predictions on displacement and stress around shallow tunnels subjected to surcharge loadings. Tunn. Undergr. Space Technol. 2018, 71, 403–427. [Google Scholar] [CrossRef]
- Zheng, H.; Cai, Q.; Zhou, W.; Lu, X.; Li, M.; Qi, C.; Jiskani, I.M.; Zhang, Y. Creep Behaviours of Argillaceous Sandstone: An Experimental and Modelling Study. Appl. Sci. 2020, 10, 7602. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.C.; Gao, J.X.; An, Z.X.; Yang, X.H.; Nie, B.S. Creep characteristics and constitutive model of coal under triaxial stress and gas pressure. Energy Sci. Eng. 2020, 8, 501–514. [Google Scholar] [CrossRef]
- Song, Y.; Wang, H.; Chang, Y.; Li, Y. Nonlinear creep model and parameter identification of mudstone based on a modified fractional viscous body. Environ. Earth Sci. 2019, 78, 607. [Google Scholar] [CrossRef]
- Hou, R.; Zhang, K.; Tao, J.; Xue, X.; Chen, Y. A Nonlinear Creep Damage Coupled Model for Rock Considering the Effect of Initial Damage. Rock Mech. Rock Eng. 2019, 52, 1275–1285. [Google Scholar] [CrossRef]
- Yang, S.Q.; Xu, P.; Ranjith, P.G.; Chen, G.F.; Jing, H.W. Evaluation of creep mechanical behavior of deep-buried marble under triaxial cyclic loading. Arab. J. Geosci. 2015, 8, 6567–6582. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, Q.; Li, S.; Wang, S. Time-Dependent Behavior of Diabase and a Nonlinear Creep Model. Rock Mech. Rock Eng. 2014, 47, 1211–1224. [Google Scholar] [CrossRef]
- Yang, S.Q.; Cheng, L. Non-stationary and non-linear visco-elastic shear creep model for shale. Int. J. Rock Mech. Min. Sci. 2011, 48, 1011–1020. [Google Scholar] [CrossRef]
- Xu, G.; He, C.; Chen, Z.; Yang, Q. Transversely isotropic creep behavior of phyllite and its influence on the long-term safety of the secondary lining of tunnels. Eng. Geol. 2020, 278, 105834. [Google Scholar] [CrossRef]
- Mansouri, H.; Ajalloeian, R. Mechanical behavior of salt rock under uniaxial compression and creep tests. Int. J. Rock Mech. Min. Sci. 2018, 110, 19–27. [Google Scholar] [CrossRef]
- Garra, R.; Mainardi, F.; Spada, G. A generalization of the Lomnitz logarithmic creep law via Hadamard fractional calculus. Chaos Sol. Fract. 2017, 102, 333–338. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, N.; Feng, X.; Kan, J. Experimental Investigation of the Creep Behaviour of Coal by Monitoring Changes of Acoustic Properties. Appl. Sci. 2018, 8, 633. [Google Scholar] [CrossRef]
- Zhao, K.; Liu, Y.; Li, Y.; Ma, H.; Hou, W.; Yu, C.; Liu, H.; Feng, C.; Yang, C. Feasibility analysis of salt cavern gas storage in extremely deep formation: A case study in China. J. Energy Storage 2022, 47, 103649. [Google Scholar] [CrossRef]
- Wagner, H. Deep Mining: A Rock Engineering Challenge. Rock Mech. Rock Eng. 2019, 52, 1417–1446. [Google Scholar] [CrossRef]
- Deng, H.; Zhou, H.; Li, L. Fractional creep model of temperature-stress-time coupled damage for deep coal based on temperature-equivalent stress. Results Phys. 2022, 39, 105765. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, C.; Gamage, R.P.; Zhang, G. Uncovering the creep deformation mechanism of rock-forming minerals using nanoindentation. Int. J. Min. Sci. Technol. 2022, 32, 283–294. [Google Scholar] [CrossRef]
- Moghadam, S.N.; Mirzabozorg, H.; Noorzad, A. Modeling time-dependent behavior of gas caverns in rock salt considering creep, dilatancy and failure. Tunn. Undergr. Space Technol. 2013, 33, 171–185. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Zheng, Y.; Duan, P.; Ding, S. Study on tri-axial creep experiment and constitutive relation of different rock salt. Safety Sci. 2012, 50, 801–805. [Google Scholar] [CrossRef]
- Urai, J.; Spiers, C.; Zwart, H.; Lister, G.S. Weakening of rock salt by water during long-term creep. Nature 1986, 324, 554–557. [Google Scholar] [CrossRef]
- Li, S.Y.; Urai, J.L. Rheology of rock salt for salt tectonics modelling. Pet. Sci. 2016, 13, 712–724. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zhang, B.; Yu, X.; Xu, N.; Ye, J. Long-Term Stability and Deformation Behaviour of Anhydrite Mine-Out for Crude Oil Storage. Rock Mech. Rock Eng. 2020, 53, 1719–1735. [Google Scholar] [CrossRef]
- Tang, S.B.; Yu, C.Y.; Heap, M.J.; Chen, P.Z.; Ren, Y.G. The Influence of Water Saturation on the Short- and Long-Term Mechanical Behavior of Red Sandstone. Rock Mech. Rock Eng. 2018, 51, 2669–2687. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, J.; Zhao, C.; Ren, Y.; Liang, C. Creep-damage constitutive model based on fractional derivatives and its application in salt cavern gas storage. J. Energy Storage 2021, 44, 103403. [Google Scholar] [CrossRef]
- Nadimi, S.; Shahriar, K.; Sharifzadeh, M.; Moarefvand, P. Triaxial creep tests and back analysis of time-dependent behavior of Siah Bisheh cavern by 3-Dimensional Distinct Element Method. Tunn. Undergr. Space Technol. 2011, 26, 155–162. [Google Scholar] [CrossRef]
- Xuyang, C.; Xufeng, W.; Dongsheng, Z.; Dongdong, Q.; Ya, W.; Jiyao, W.; Zechao, C. Creep and Control of the Deep Soft Rock Roadway (DSRR): Insights from Laboratory Testing and Practice in Pingdingshan Mining Area. Rock Mech. Rock Eng. 2022, 55, 363–378. [Google Scholar] [CrossRef]
- Yang, Y.; Lai, X.; Luo, T.; Yuan, K.; Li, G. Study on creep constitutive model of stratified siltstone and its application to instability analysis in mining. Environ. Earth Sci. 2022, 81, 270. [Google Scholar] [CrossRef]
- Song, Y.; Li, Y. Study on the constitutive model of the whole process of macroscale and mesoscale shear damage of prestressed anchored jointed rock. Bull. Eng. Geol. Environ. 2021, 80, 6093–6106. [Google Scholar] [CrossRef]
- Zhou, H.; Jia, W.; Xie, S.; Su, T.; Zhang, L.; Ma, B.; Hou, W. A statistical damage-based fractional creep model for Beishan granite. Mech. Time-Depend. Mater. 2022. [Google Scholar] [CrossRef]
- Barton, N.; Quadros, E. Anisotropy is Everywhere, to See, to Measure, and to Model. Rock Mech. Rock Eng. 2015, 48, 1323–1339. [Google Scholar] [CrossRef]
- Sakha, M.; Nejati, M.; Aminzadeh, A.; Ghouli, S.; Saar, M.O.; Driesner, T. On the validation of mixed-mode I/II crack growth theories for anisotropic rocks. Int. J. Solids Struct. 2022, 241, 111484. [Google Scholar] [CrossRef]
- Zhu, H.; Yan, J.; Liang, W. Challenges and Development Prospects of Ultra-Long and Ultra-Deep Mountain Tunnels. Engineering 2019, 5, 384–392. [Google Scholar] [CrossRef]
- Qin, D.; Wang, X.; Zhang, D.; Chen, X. Study on Surrounding Rock-Bearing Structure and Associated Control Mechanism of Deep Soft Rock Roadway Under Dynamic Pressure. Sustainability 2019, 11, 1892. [Google Scholar] [CrossRef]
- Mu, W.; Li, L.; Chen, D.; Wang, S.; Xiao, F. Long-term deformation and control structure of rheological tunnels based on numerical simulation and on-site monitoring. Eng. Failure Anal. 2020, 118, 104928. [Google Scholar] [CrossRef]
- Sulem, J.; Panet, M.; Guenot, A. Closure analysis in deep tunnels. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, 145–154. [Google Scholar] [CrossRef]
- Kontogianni, V.; Psimoulis, P.; Stiros, S. What is the contribution of time-dependent deformation in tunnel convergence? Eng. Geol. 2006, 82, 264–267. [Google Scholar] [CrossRef]
- Panet, M.; Sulem, J. Convergence-Confinement Method for Tunnel Design, 1st ed.; Springer: Gewerbestrasse, Switzerland, 2022; pp. 1–151. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Han, Y.; Kou, Y.Y.; Li, L.; Du, J.H. Three-Dimensional, Real-Time, and Intelligent Data Acquisition of Large Deformation in Deep Tunnels. Adv. Civ. Eng. 2021, 2021, 6671118. [Google Scholar] [CrossRef]
- Iasiello, C.; Torralbo, J.C.G.; Fernandez, C.T. Large deformations in deep tunnels excavated in weak rocks: Study on Y-Basque high-speed railway tunnels in northern Spain. Undergr. Space 2021, 6, 636–649. [Google Scholar] [CrossRef]
- Luo, T.; Wang, S.; Zhang, C.; Liu, X. Parameters deterioration rules of surrounding rock for deep tunnel excavation based on unloading effect. Dyna 2017, 92, 648–654. [Google Scholar] [CrossRef]
- Chen, C.; Li, T.; Ma, C.; Zhang, H.; Tang, J.; Zhang, Y. Hoek-Brown Failure Criterion-Based Creep Constitutive Model and BP Neural Network Parameter Inversion for Soft Surrounding Rock Mass of Tunnels. Appl. Sci. 2021, 11, 10033. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Q.; Liu, B.; Liu, X.; Pan, Y.; Liu, J. Experimental Study on the Dilatancy and Fracturing Behavior of Soft Rock Under Unloading Conditions. Int. J. Civ. Eng. 2017, 15, 921–948. [Google Scholar] [CrossRef]
- Deleruyelle, F.; Bui, T.A.; Wong, H.; Dufour, N.; Tran, D.K.; Zhang, X.S. Analytical study of the post-closure behavior of a deep tunnel in a porous creeping rock mass. C. R. Mécanique 2016, 344, 649–660. [Google Scholar] [CrossRef]
- Chin, P.H.; Rogers, J.D. Creep Parameters of Rocks on an Engineering Scale. Rock Mech. Rock Eng. 1987, 20, 137–146. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Ren, T. A Theoretical and Experimental Study of Stress–Strain, Creep and Failure Mechanisms of Intact Coal. Rock Mech. Rock Eng. 2020, 53, 5641–5658. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, J.; Wang, J.; Li, F.; Zhou, Y. Research on nonlinear damage hardening creep model of soft surrounding rock under the stress of deep coal resources mining. Energy Rep. 2022, 8, 1493–1507. [Google Scholar] [CrossRef]
- Hamza, O.; Stace, R. Creep properties of intact and fractured muddy siltstone. Int. J. Rock Mech. Min. Sci. 2018, 106, 109–116. [Google Scholar] [CrossRef]
- Sainoki, A.; Tabata, S.; Mitri, H.S.; Fukuda, D.; Kodama, J.I. Time-dependent tunnel deformations in homogeneous and heterogeneous weak rock formations. Comput. Geotech. 2017, 92, 186–200. [Google Scholar] [CrossRef]
- Zha, E.; Zhang, Z.; Zhang, R.; Wu, S.; Li, C.; Ren, L.; Gao, M.; Zhou, J. Long-term mechanical and acoustic emission characteristics of creep in deeply buried jinping marble considering excavation disturbance. Int. J. Rock Mech. Min. Sci. 2021, 139, 104603. [Google Scholar] [CrossRef]
- Mohammadi, M.; Hossaini, M.F.; Bagloo, H. Rock bolt supporting factor: Rock bolting capability of rock mass. Bull. Eng. Geol. Environ. 2017, 76, 231–239. [Google Scholar] [CrossRef]
- Mishra, B.; Verma, P. Uniaxial and triaxial single and multistage creep tests on coal-measure shale rocks. Int. J. Coal Geol. 2015, 137, 55–65. [Google Scholar] [CrossRef]
- Zhang, G.H.; Jiao, Y.Y.; Wang, H. Outstanding issues in excavation of deep and long rock tunnels: A case study. Can. Geotech. J. 2014, 51, 984–994. [Google Scholar] [CrossRef]
- Jain, A.; Rao, K.S. Empirical correlations for prediction of tunnel deformation in squeezing ground condition. Tunn. Undergr. Space Technol. 2022, 125, 104501. [Google Scholar] [CrossRef]
- Hu, X.; Gutierrez, M. Analytical model for deep tunnel with an adaptive support system in a viscoelastic-burger’s rock. Transport. Geotech. 2022, 35, 100775. [Google Scholar] [CrossRef]
- Deng, H.S.; Fu, H.L.; Shi, Y.; Zhao, Y.Y.; Hou, W.Z. Countermeasures against large deformation of deep-buried soft rock tunnels in areas with high geostress: A case study. Tunn. Undergr. Space Technol. 2022, 119, 104238. [Google Scholar] [CrossRef]
- Oggeri, C.; Oreste, P.; Spagnoli, G. Creep behaviour of two-component grout and interaction with segmental lining in tunnelling. Tunn. Undergr. Space Technol. 2022, 119, 104216. [Google Scholar] [CrossRef]
- Wu, H.; Fan, F.; Yang, X.; Wang, Z.; Lai, J.; Xie, Y. Large deformation characteristics and treatment effect for deep bias tunnel in broken phyllite: A case study. Eng. Fail. Anal. 2022, 135, 106045. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, P.; Wang, P. Multi-factors influence of anchorage force on surrounding rock under coupling effect of creep rock mass and bolt/cable. Geomat. Nat. Haz. Risk 2021, 12, 328–346. [Google Scholar] [CrossRef]
- Maqsood, Z.; Koseki, J.; Miyashita, Y.; Xie, J.; Kyokawa, H. Experimental study on the mechanical behaviour of bounded geomaterials under creep and cyclic loading considering effects of instantaneous strain rates. Eng. Geol. 2020, 276, 105774. [Google Scholar] [CrossRef]

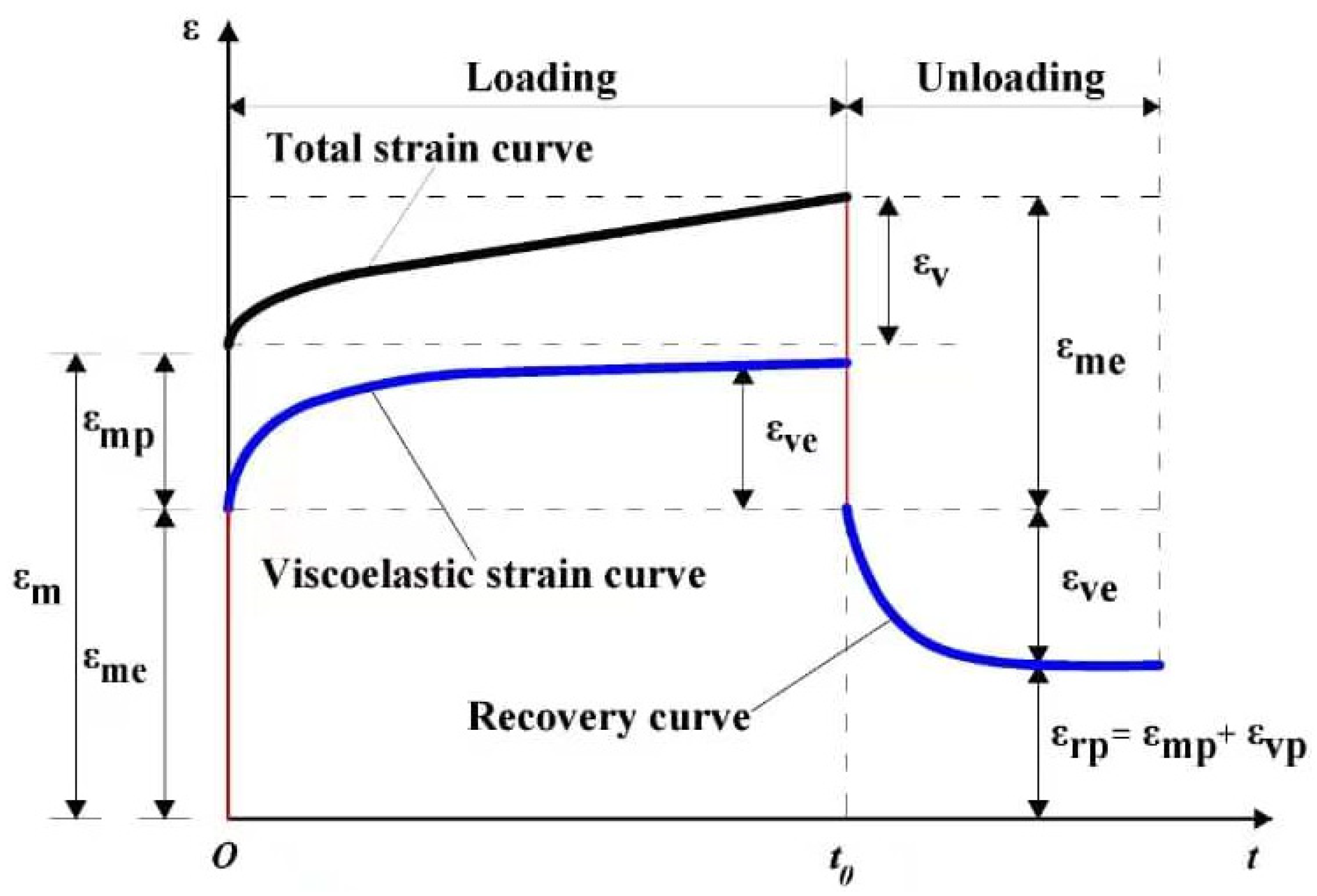

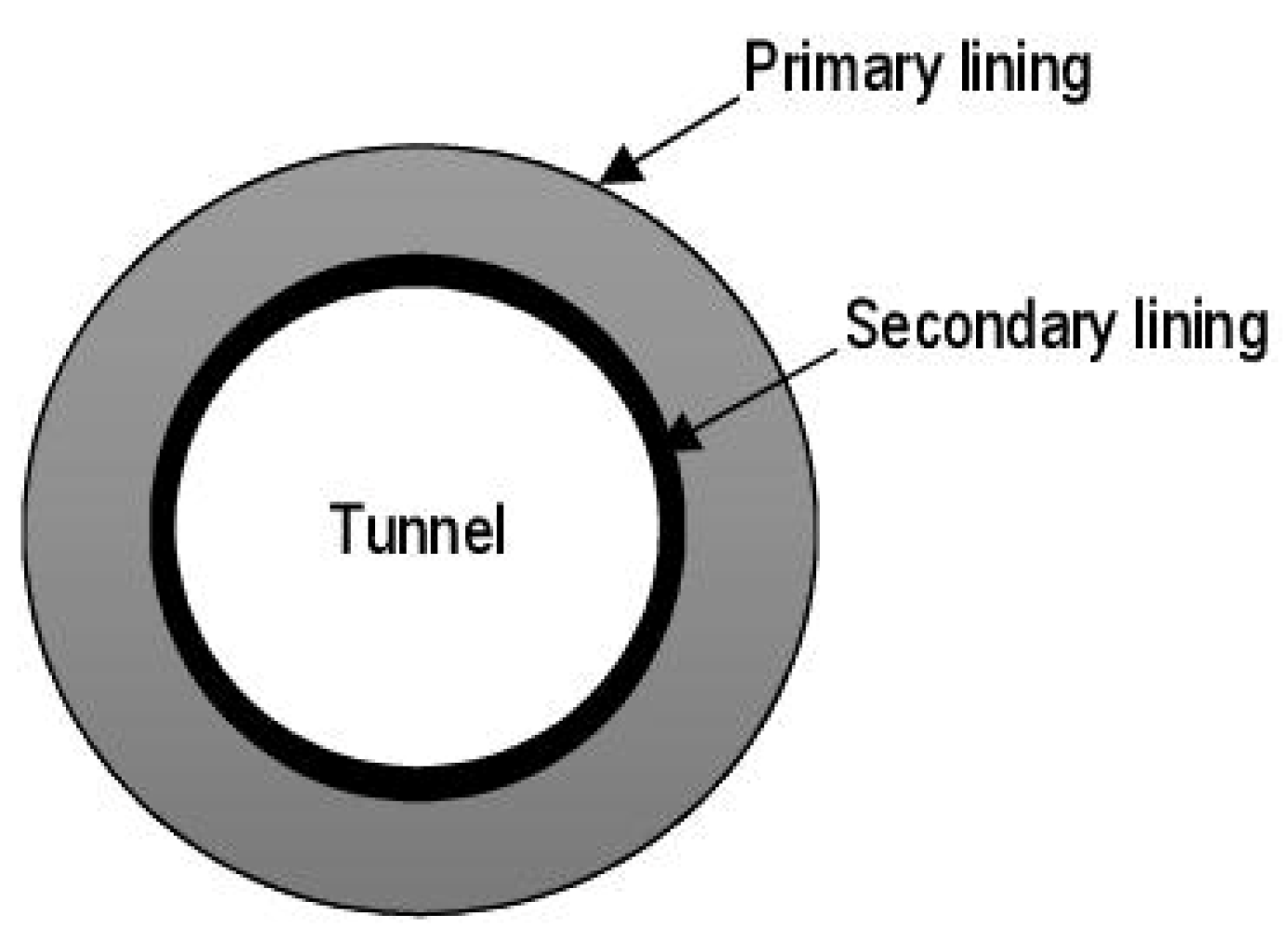

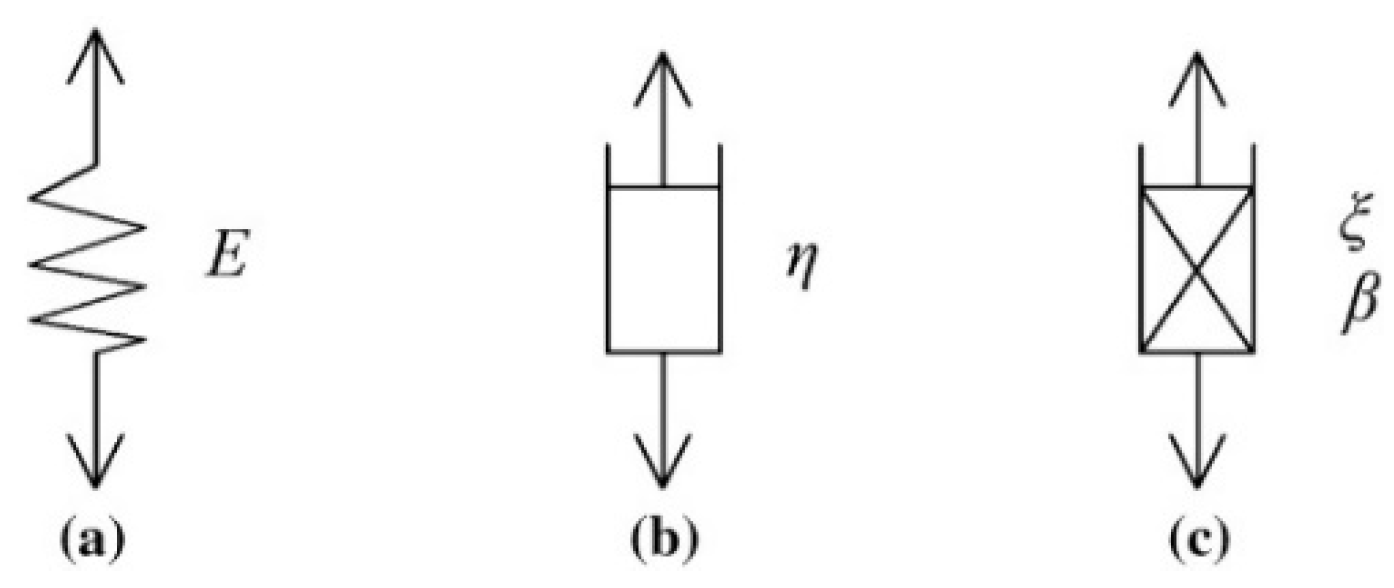
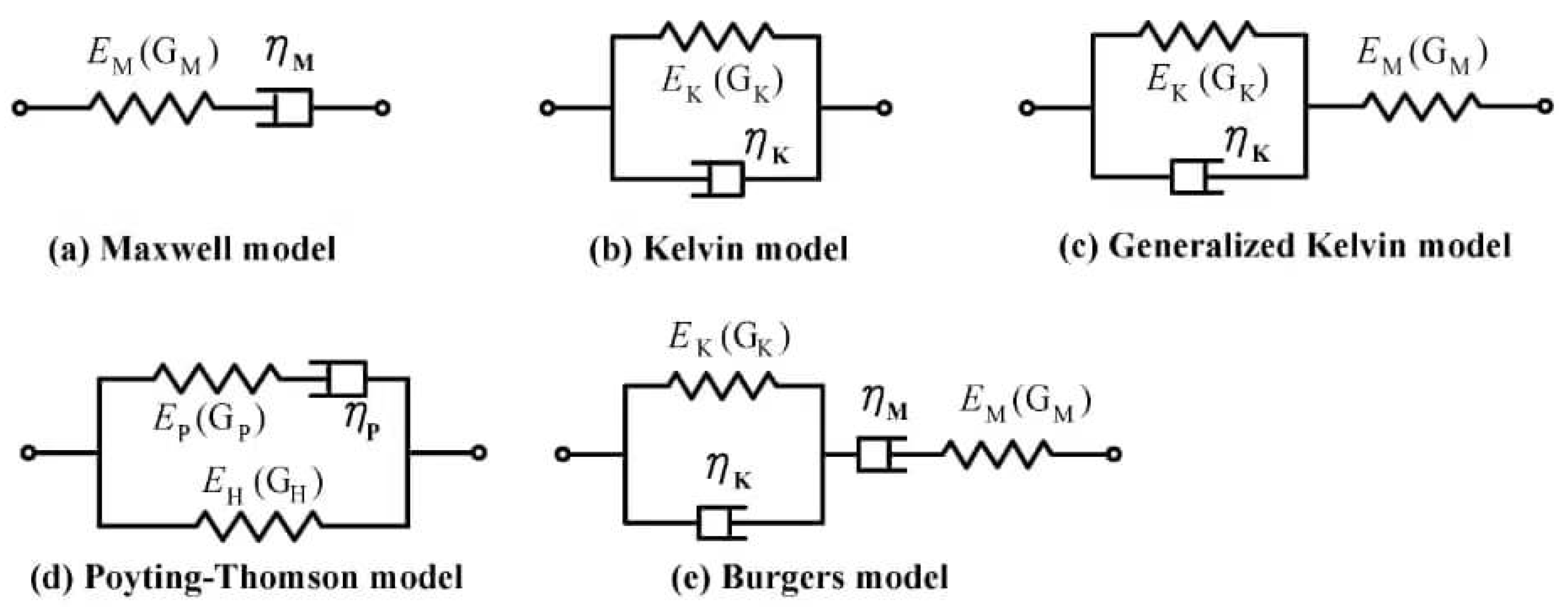

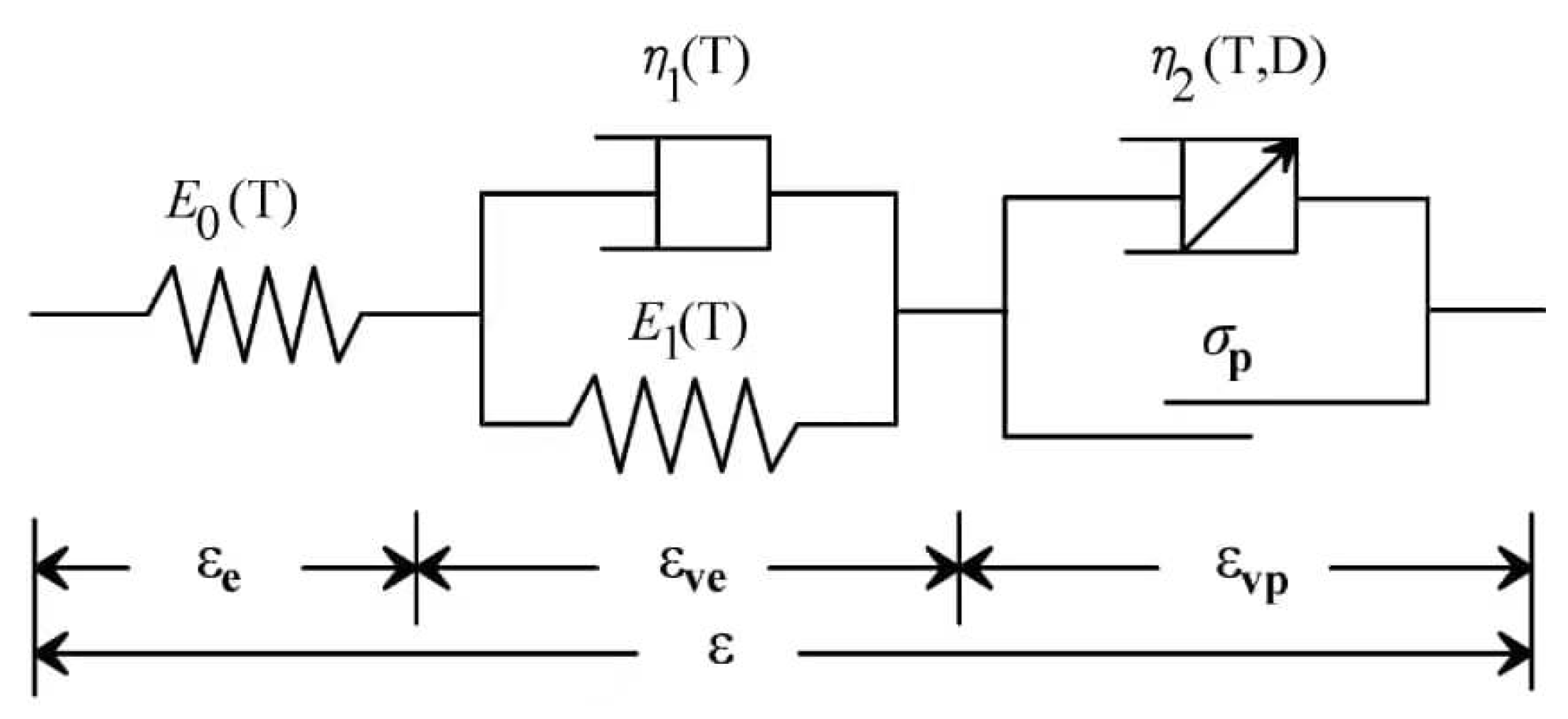

| Study (Year) | Rock Type | Specimen Conditions | Testing Type | Duration of Tests (Days) | Effect of Water on Rock Creep |
|---|---|---|---|---|---|
| Okubo et al., (2010) [90] | Tage tuff | Waterlogged | Uniaxial compression creep tests | 912.5–4380 | Creep behavior of water-saturated Tage tuff is shortened. |
| Xiong et al., (2014) [91] | Green-schist | Immersed in clean water | Biaxial compression creep tests | 32.5–46.6 | The increase in instantaneous axial and lateral strains is caused by the increase of water content. |
| Liu et al., (2015) [83] | Limestone | Saturated and immersed in water | Triaxial compression creep tests | 8–40 | The increase in water and hydraulic pressure results in an increase in creep strain and creep strain rate. |
| Lu and Wang (2017) [92] | Mudstone | Saturated in purified water | Uniaxial compression tests and multistage creep tests | 1.90–2.30 | The reduction in short-term mechanical properties and the increase in both creep strain and creep strain rate are provoked by the presence of water. |
| Hashiba et al., (2018) [93] | Andesite | Saturated in deionized water | Uniaxial compression tests | 30–60 | The creep lifetime is drastically reduced by the presence of water. It is about 180 times shorter in wet conditions than in dry conditions, under the same stress conditions. |
| Li et al., (2020) [94] | Shale | Waterlogged | Uniaxial, triaxial, and BDT tests | 2–90 | With the presence of water, the mechanical behavior of shale is remarkably affected in the triaxial test. Under the uniaxial tests, there is reduction from 58% to 62% for the compressive modulus and strength. The latter also decrease in 36% under BDT. |
| Cai et al., (2019) [95] | Granite, marble, and sandstone. | Saturated in water | Uniaxial compression tests and acoustic emission | 2–10 | Water considerably affects the mechanical characteristics of rocks, and mainly decreases elastic modulus, critical strain, and uniaxial compressive strength. |
| Study (Year) | Rock Type | Specimen Conditions | Testing Type | Duration of Tests (Days) | Effect of Temperature on Rock Creep |
|---|---|---|---|---|---|
| Kinoshita and Yasuhara (2011) [99] | Sandstone | Immersed and enclosed in hot purified water at and . | Uniaxial compression creep test | 180 | At high temperature, the mechanical properties of uniaxial compressive strength, modulus of elasticity and creep behavior of sandstones are drastically reduced. |
| Ye et al., (2015) [100] | Green Tuff | Saturated with water put into heating system at different temperatures (, , ). | Triaxial compression tests and triaxial creep tests | 69 | The rise in temperature induces an increase in the creep rupture time and a variation in the maximum shear strength. |
| Lu and Wang (2017) [92] | Mudstone | Saturated in purified water and enclosed in a heat-controlled environment at 20 °C, 50 °C and 80 °C. | Multistage creep tests | 1.90–2.30 | Creep strain and creep strain rate can be accelerated by the rise of temperature. The effects of temperature are aggravated when there is water in the rocks. |
| Rybacki et al., (2017) [64] | Shale | Contained a water content of 1–2% by weight, stored in oven at 50 °C, tested at a temperature of up to 200 °C, under a pressure of 50–200 MPa. | Creep tests | 2–7 | The increase in temperature leads to the increase of the primary creep strain as well as the decrease of the creep resistance. |
| Xu et al., (2017) [101] | Granite | Heated at different temperatures: 23, 40, 50, 75, and . | Creep tests | 0.13–0.48 | There is an increase in creep strain rate and a decrease in rupture time with increasing temperature. |
| Yang and Hu (2018) [102] | Red sandstone | Dried and heated at 300, 700, and . | Triaxial creep test | 3.5–33.3 | Under increasing temperature, the axial total strain increases. |
| Meng et al., (2019) [103] | Limestone | Heated at constant rate under different temperatures 200, 400, 500, 600, and . | Uniaxial compression test | 0.22 | Increasing temperature leads to an increase in peak strain and ductility, as well as a reduction in peak stress and modulus of elasticity. |
| Creep Mechanical Model | Creep Phase Described | Relevant Behavior |
|---|---|---|
| Kelvin model | Primary (transient) creep | Visco-elastic |
| Maxwell model | Secondary (steady) creep | Between hardening and softening |
| Visco-plastic model | Tertiary (accelerated) creep | Non-linear strain increment and rupture |
| Burgers model | Primary and secondary creep | Merging first and second phase creep behaviors |
| Merchant (HK) model | Stable creep (hard rock, low load) | Between hardening and softening |
| Poyting–Thomson (HM) model | Primary creep | Visco-elastic |
| Bingham model | Primary and secondary creep | Behavior of the primary and secondary creep |
| Nishihara model | Secondary and tertiary creep | Behavior of the secondary and tertiary creep |
| Study (Year) | Specific Rock Type | Testing Type and Conditions | Duration of Tests (Days) | Creep Constitutive Model | Creep Equations or Creep Constitutive Equations | Equation Number | Comments |
|---|---|---|---|---|---|---|---|
| Zhao and Jiang (2021) [82] | Fine sandstone | Triaxial unloading creep test under high stress and high water pressure. Homogeneous and isotropic rocks | 11.25 | NLVPCM | (13) | No dynamic disturbance. No temperature variation. | |
| Wang et al., (2020) [7] | Silty mudstone | Triaxial compression tests and triaxial creep tests under different confining pressures | 20.8 | IEFV | (14) | Quasi-static stresses. No variation in temperature and humidity. | |
| Zhang et al., (2020) [145] | Coal | Triaxial creep tests under different gas pressures. Room temperature | 1.5 | Non-linear Nishihara model | (15) | 3D model obtained by extending the 1D model. No dynamic perturbation. | |
| Song et al., (2019) [146] | Mudstone | Uniaxial compression tests and uniaxial creep tests. Different stress levels. Average humidity at 25.5%. | 4.86 | FENLCM | (16) | No dynamic disturbance. Ambient temperature considered. | |
| Hou et al., (2019) [147] | Sandstone | Uniaxial creep tests under multi-loads. Different initial damage states taken into account. | 7.5 | NLVEPDM | (17) | Quasi-static stresses. No temperature and water content data. | |
| Yang et al., (2015) [148] | Marble | Triaxial compression test under Cyclic loadings. Constant hydrostatic stress | 4.16 | VEPCM | (18) | Quasi-static stresses. Ambient temperature considered. | |
| Chen et al., (2014) [97] | Granite | Unconfined compressive loading tests at different temperatures. Triaxial creep tests at ambient temperature. | 0.18–0.46 | CTVDE | (19) | Static stresses considered. Damage evolution accounted. No water content data | |
| Yang et al., (2014) [149] | Diabase | Triaxial creep tests under different stress levels. Ambient temperature. | 41.6 | NLVEPCM | (20) | 3D model based on the extension of the related 1D model. No dynamic perturbation. No water content data. | |
| Yang and Cheng (2011) [150] | Shale | Shear creep test under constant temperature and moisture | 11.25 | HK | (Non-stationary shear creep) (Non-linear shear creep model) | (21) | Quasi-static stresses. |
| Study (Year) | General Rock Type | Testing Type and Conditions | Duration of Tests (Days) | Creep Constitutive Model | Creep Equations or Creep Constitutive Equations | Equation Number | Comments |
|---|---|---|---|---|---|---|---|
| Gao and Yin (2021) [23] | All types | Uniaxial compression creep tests under two stress levels. | 2–10 | VOFCM | (22) | Quasi-static stresses. Water effect accounted. No temperature data. | |
| Kabwe et al., (2020) [32] | Squeezing rocks | Creep tests under specific confining pressure. Damage accounted. Numerical simulation. | 1250 | EVDP | (23) | 3D creep model based on extension of the 1D model. No data on water content and temperature. | |
| Xu et al., (2020) [151] | Layered stratum | Uniaxial compression creep tests and numerical simulation. Rocks are transversely isotropic. | 10–33 | Burgers model | (24) | Quasi-static conditions. Water effects accounted. No data on temperature. | |
| Wang et al., (2019) [31] | All types | Triaxial compression tests under different stress levels. Homogeneous and isotropic media. | 33 | UCC creep model | (25) | No dynamic disturbance. No data on water content and temperature. | |
| Mansouri and Ajalloeian (2018) [152] | Salt rock | Uniaxial compression and creep tests under three axial stresses. | 14–30 | Burgers model | (26) | Quasi-static stresses. Ambient temperature. No water content data. | |
| Liu et al., (2017) [20] | Soft rocks | Uniaxial and triaxial compression creep tests. Constant confining pressures. Ambient temperature, constant humidity. | 8 | Improved Nishihara model | (27) | Axial creep model based on the 3D model. No dynamic disturbance. Damage variable accounted. | |
| Garra et al., (2017) [153] | Igneous rocks | Integro-differential methods with logarithmic kernel | No data | HFD | (28) | No data on water content and temperature. | |
| Cao et al., (2011) [17] | Hard rocks | Creep tests under water environment | 6.25–9 | GKM | (loading conditions) (unloading conditions) | (29) | Quasi-static stresses. No temperature data. |
| Study (Year) | Rock Type | Testing Type and Conditions | Duration of Tests (Days) | Creep Constitutive Model | Creep Equations or Creep Constitutive Equations | Equation Number | Comments |
|---|---|---|---|---|---|---|---|
| Lyu et al., (2021) [165] | Salt rocks (deep caverns) | Long-term uniaxial creep tests. Numerical simulation. | 700–875 | FDCD | (30) | Creep model based on the 3D model. No dynamic disturbance. Damage variable accounted. | |
| Fan et al., (2020) [98] | Coal (deep mines) | Creep tests under high stress and high pressure. | No data | Improved Burgers Creep model | (31) | Damage accounted. Dynamic pressure considered. | |
| Wang et al., (2020) [163] | Anhydrite rock (deep mines) | Uniaxial compressive creep test under staged incremental loading. | 24–42 | Burgers model | (32) | Quasi static stress. Ambient temperature |
| (MPa) | ||||
|---|---|---|---|---|
| 10 | 1.71 | 1250 | 67.67 | 53.46 |
| 12 | 1.36 | 400 | 7.54 | 9.05 |
| 15 | 1.26 | 98.04 | 5.82 | 4.66 |
| Time (Year) | |||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 10 | |||
| 50 | |||
| 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frenelus, W.; Peng, H.; Zhang, J. Creep Behavior of Rocks and Its Application to the Long-Term Stability of Deep Rock Tunnels. Appl. Sci. 2022, 12, 8451. https://doi.org/10.3390/app12178451
Frenelus W, Peng H, Zhang J. Creep Behavior of Rocks and Its Application to the Long-Term Stability of Deep Rock Tunnels. Applied Sciences. 2022; 12(17):8451. https://doi.org/10.3390/app12178451
Chicago/Turabian StyleFrenelus, Wadslin, Hui Peng, and Jingyu Zhang. 2022. "Creep Behavior of Rocks and Its Application to the Long-Term Stability of Deep Rock Tunnels" Applied Sciences 12, no. 17: 8451. https://doi.org/10.3390/app12178451
APA StyleFrenelus, W., Peng, H., & Zhang, J. (2022). Creep Behavior of Rocks and Its Application to the Long-Term Stability of Deep Rock Tunnels. Applied Sciences, 12(17), 8451. https://doi.org/10.3390/app12178451






