Experimental and Numerical Studies on Fatigue Characteristics of CFRP Shaft Tube
Abstract
:1. Introduction
2. Numerical Investigations
2.1. Constitutive Models for Composite Materials
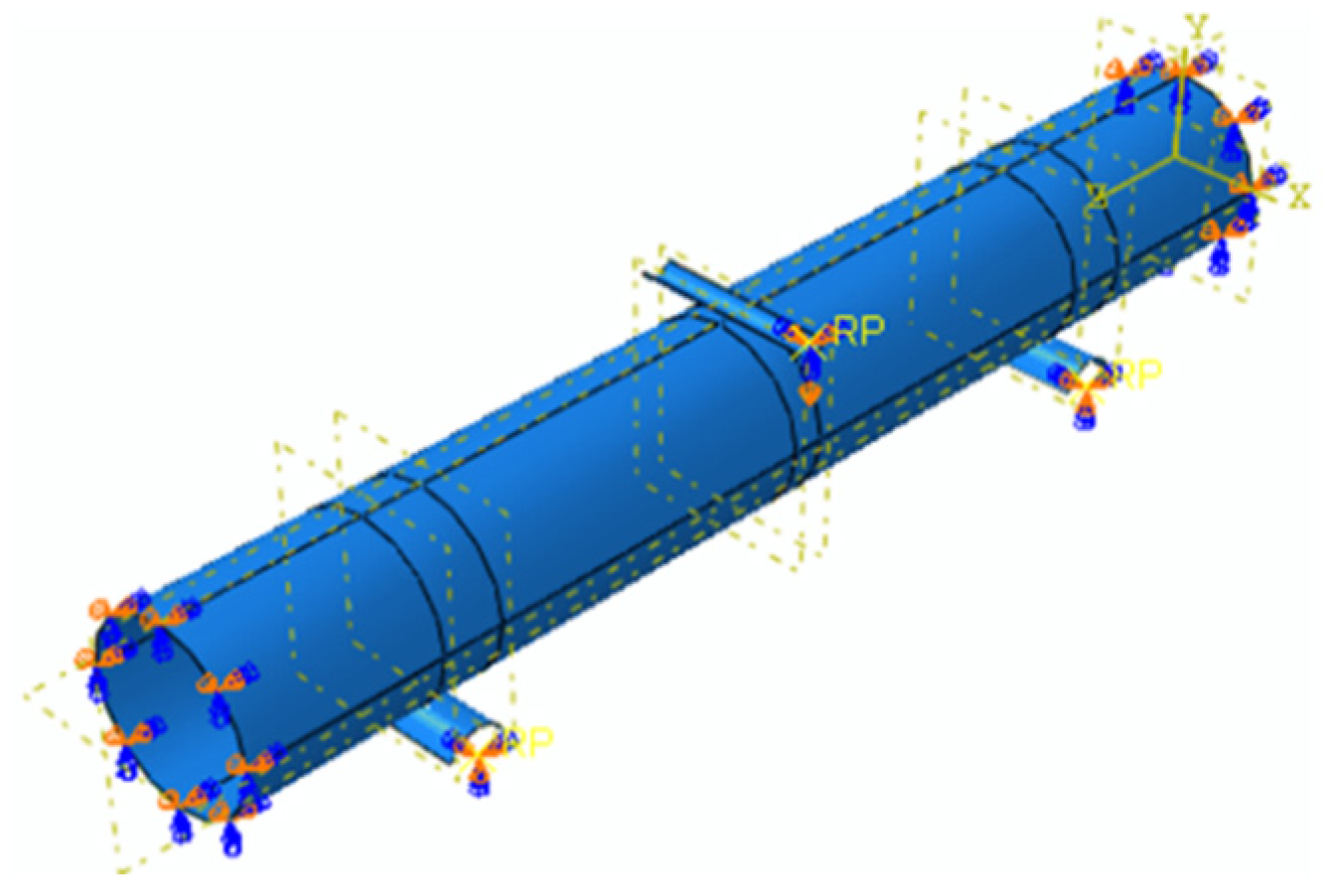
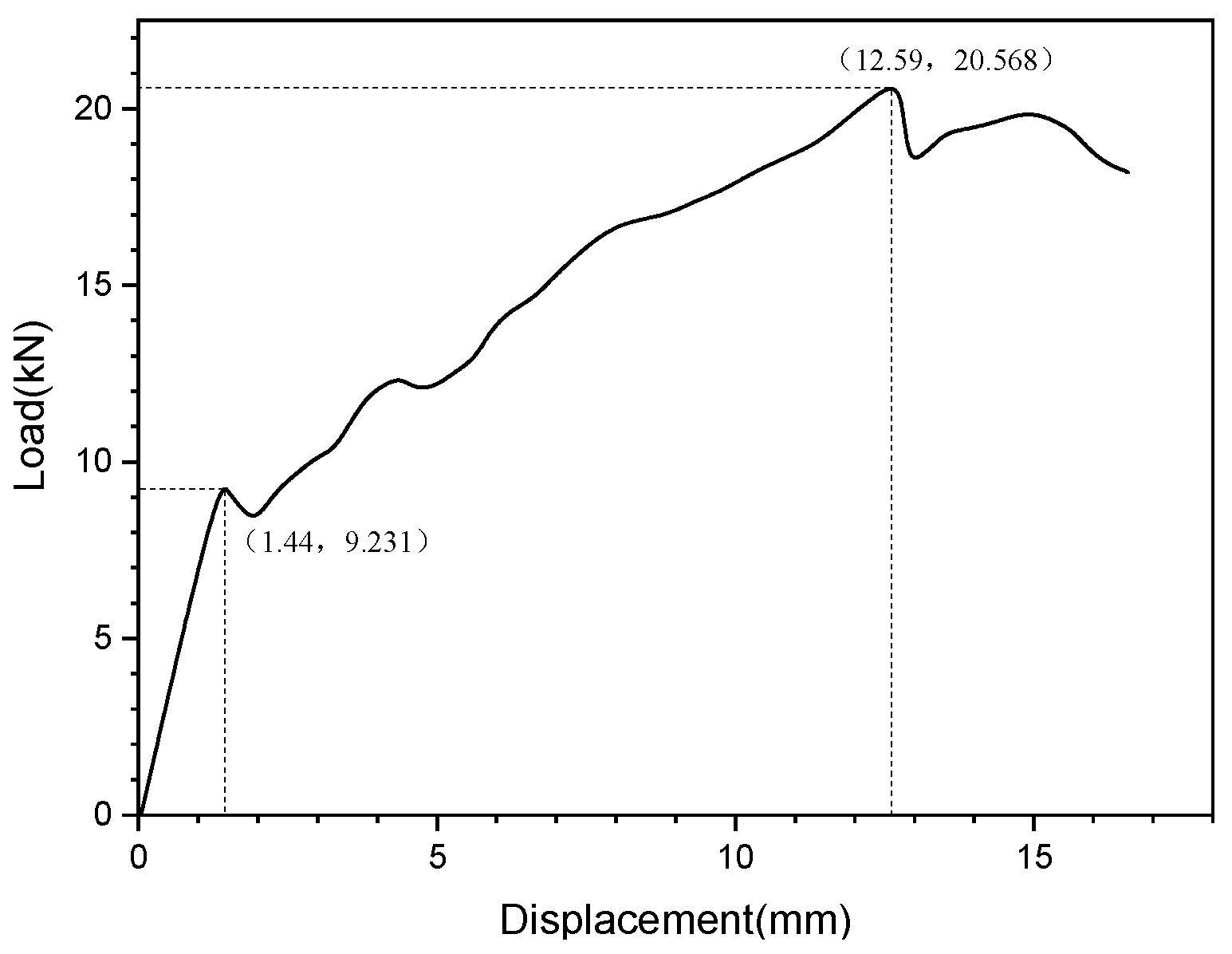
2.2. Quasi-Static Bending Fatigue Simulation Analysis
2.3. Fatigue Simulation Analysis
2.3.1. Fatigue Life of CFRP Shaft Tube under Different Load Coefficient
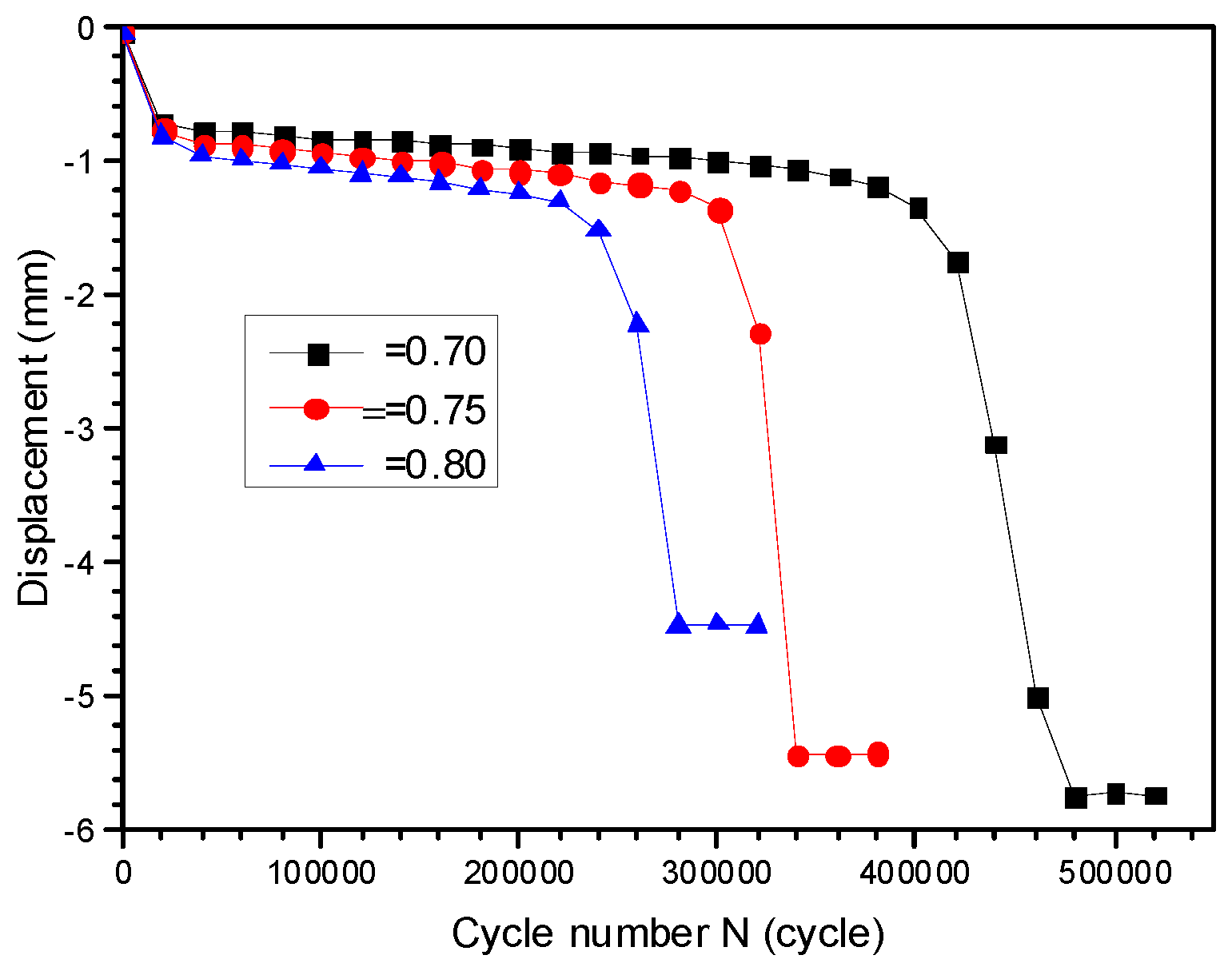
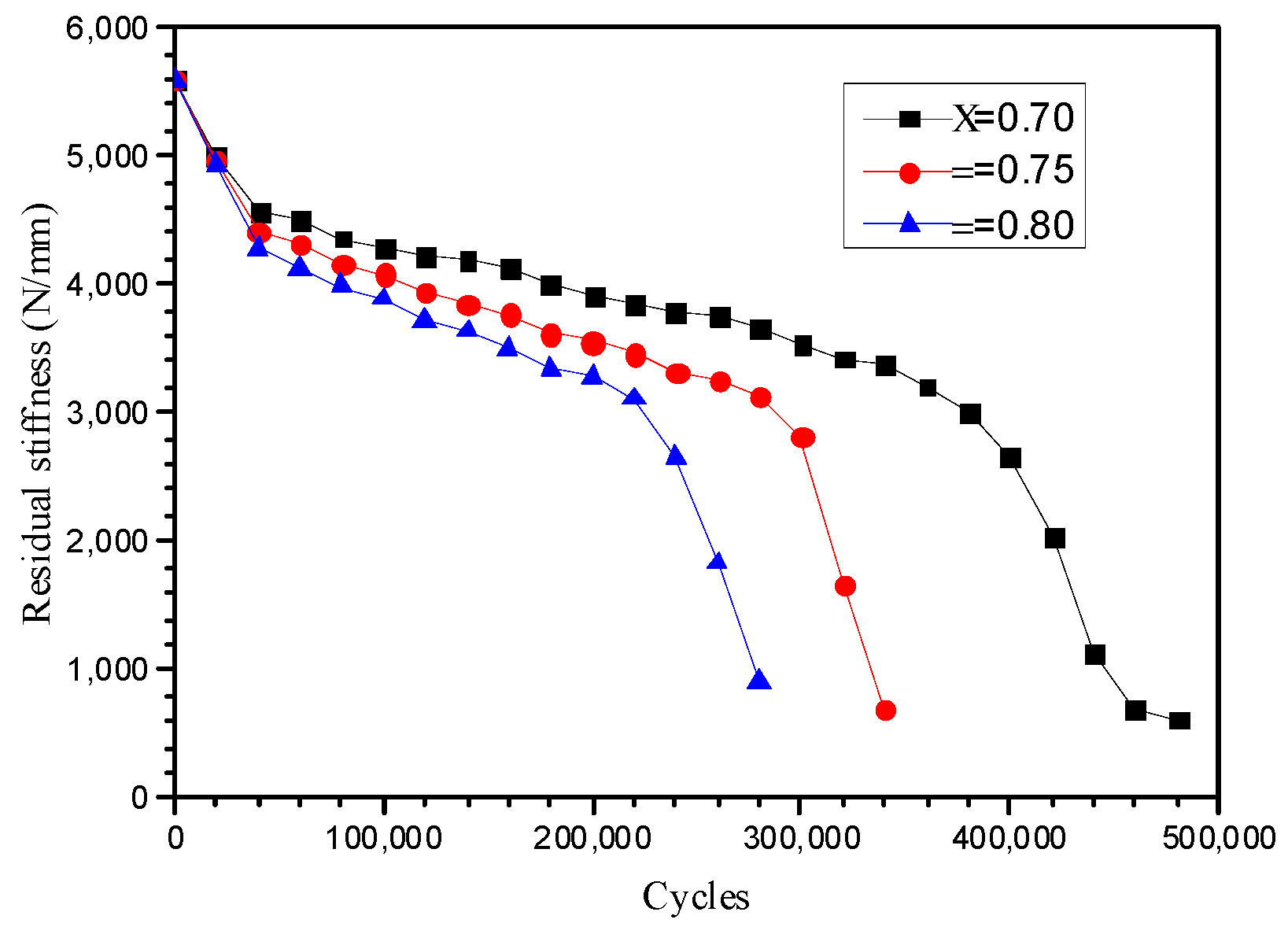
2.3.2. Residual Stiffness of CFRP Shaft Tube under Different Load Coefficients
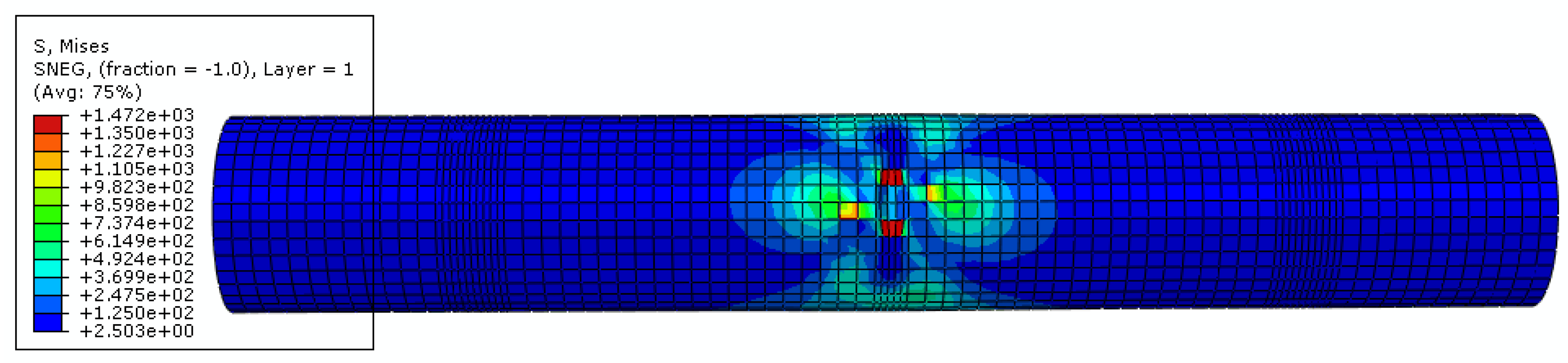
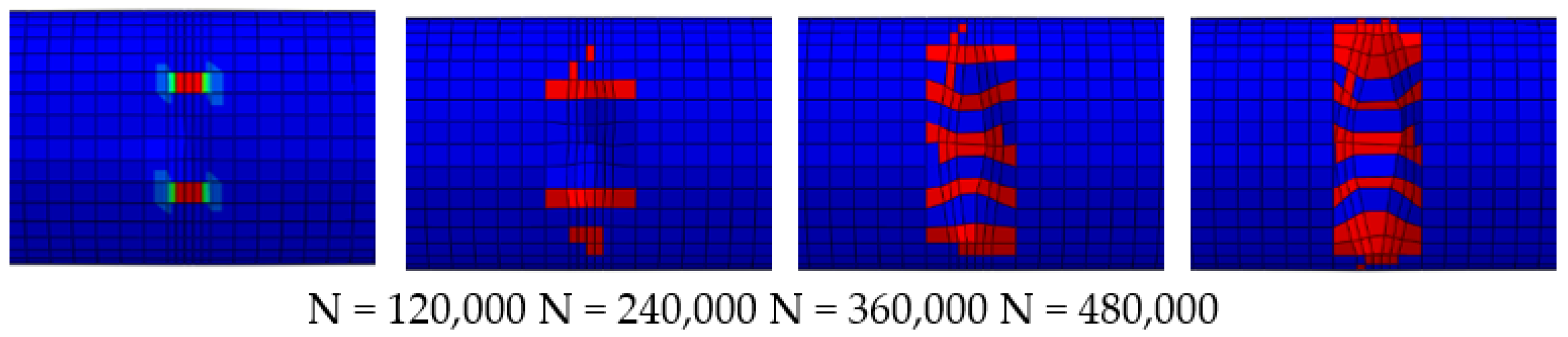
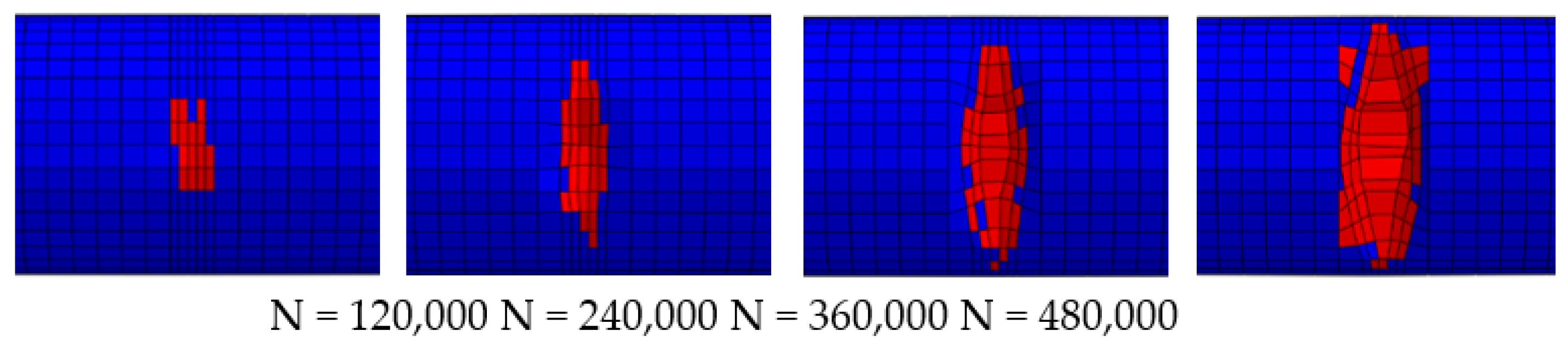
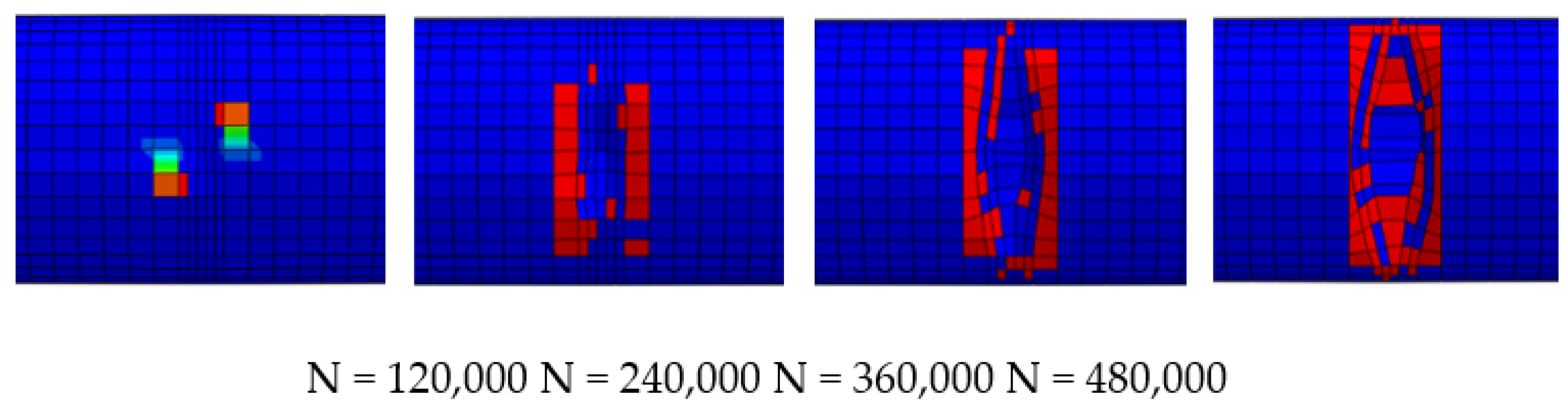
2.4. Simulation Results of Fatigue Damage Evolution
3. Experimental Procedure
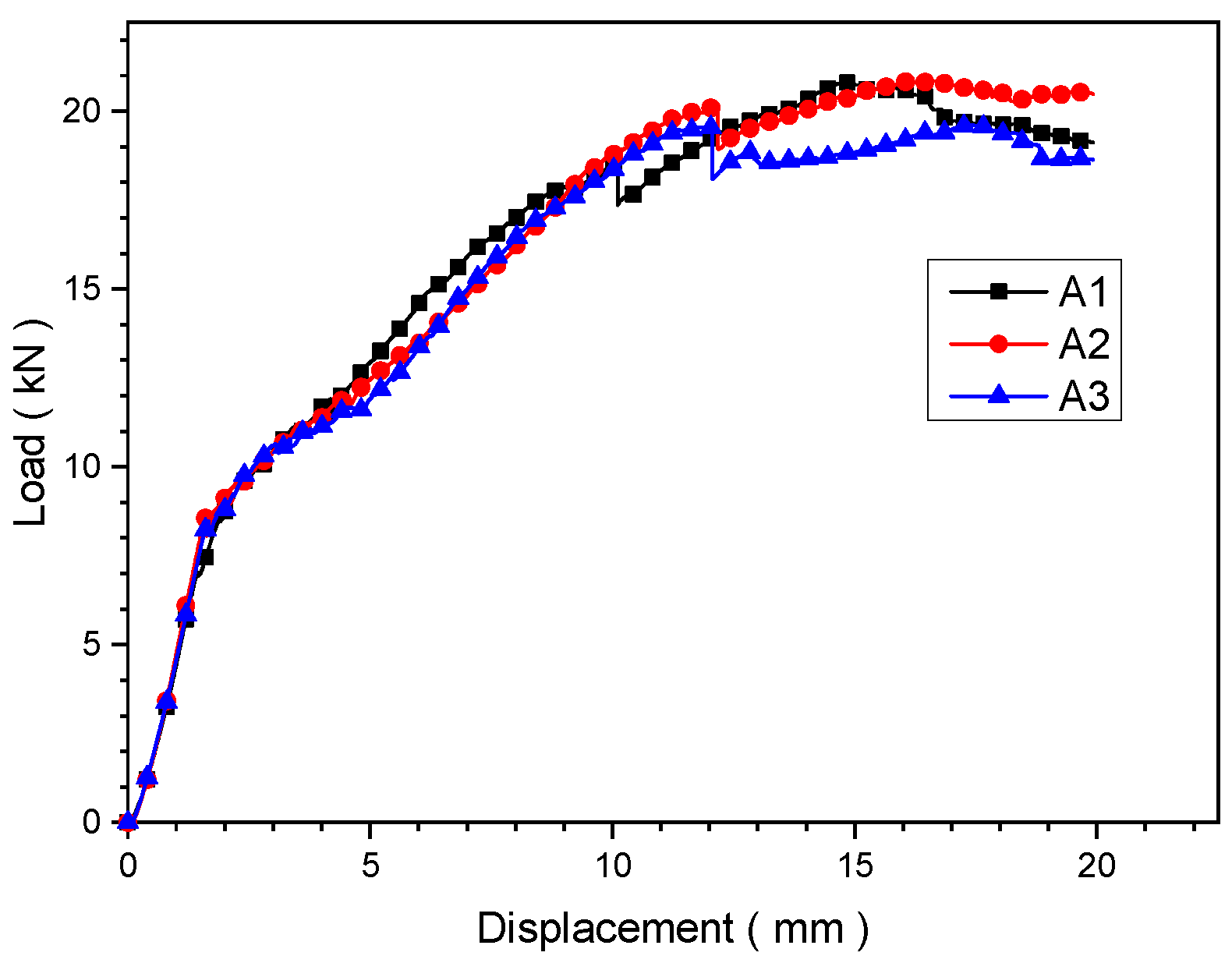
3.1. Static Tests
3.2. Fatigue Tests
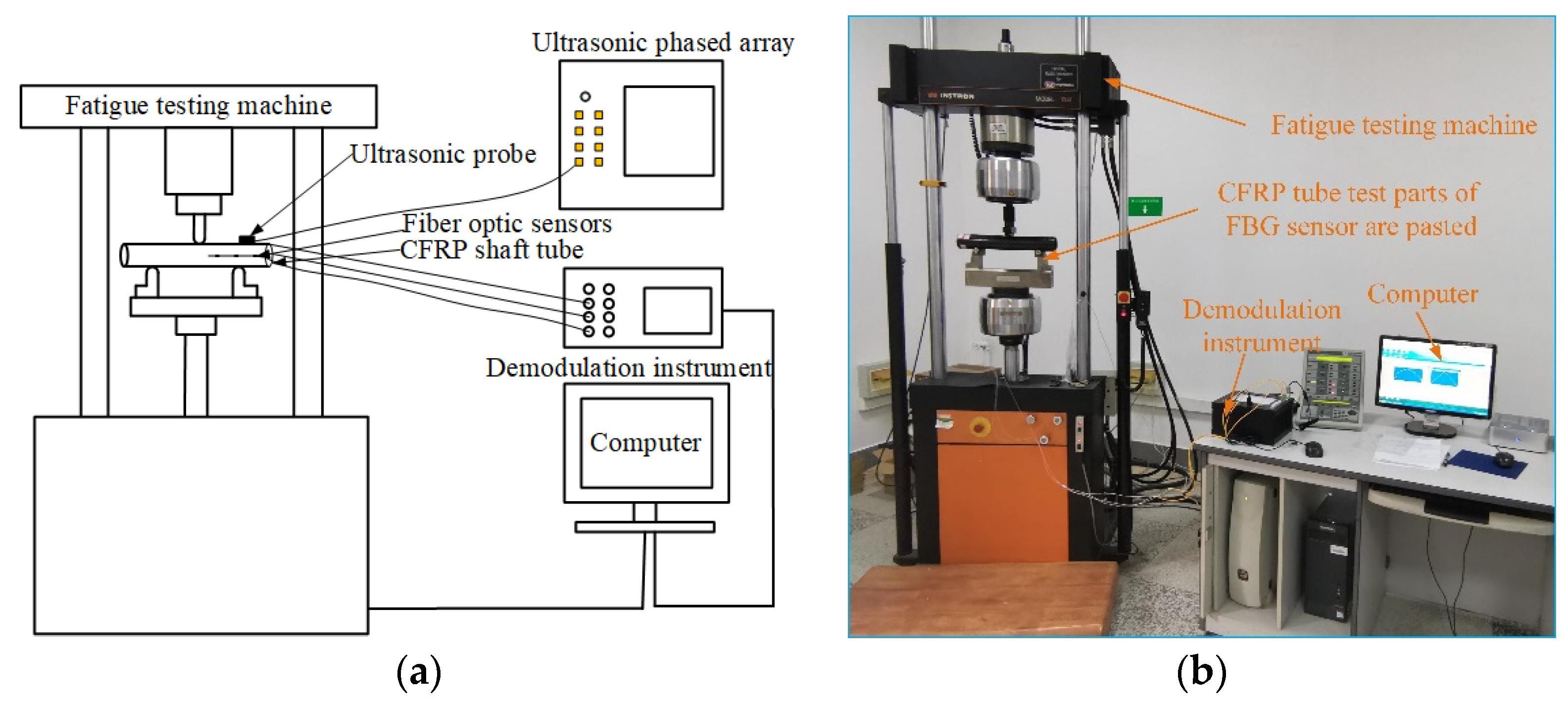
3.2.1. Experimental Process
3.2.2. Experimental Conditions
- 1.
- Determination of fatigue loading load
- 2.
- Fatigue damage evolution experiment of CFRP shaft tube based on ultrasonic scanning
- Sound speed measurement
- TCG calibration
- Sensitivity calibration
- Scanning detection
- 3.
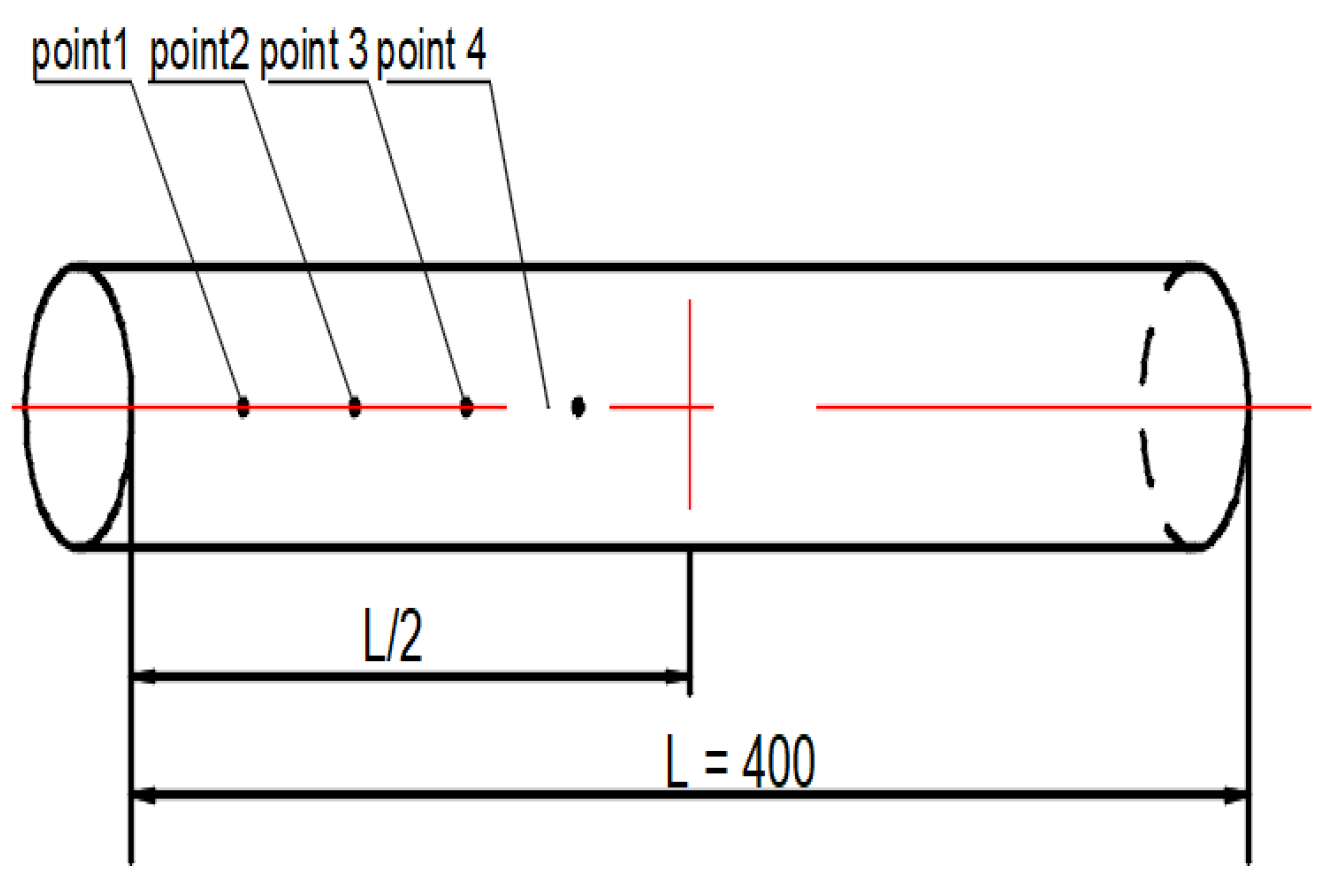
- CFRP shaft tube FBG sensor network layout.
3.3. Results and Analysis
3.3.1. Fatigue Life of Test Pieces under Different Load Factors
3.3.2. Residual Stiffness of Test Pieces under Different Load Factors
3.3.3. Fatigue Damage Evolution Experiment of Test Pieces Based on Ultrasonic Scanning
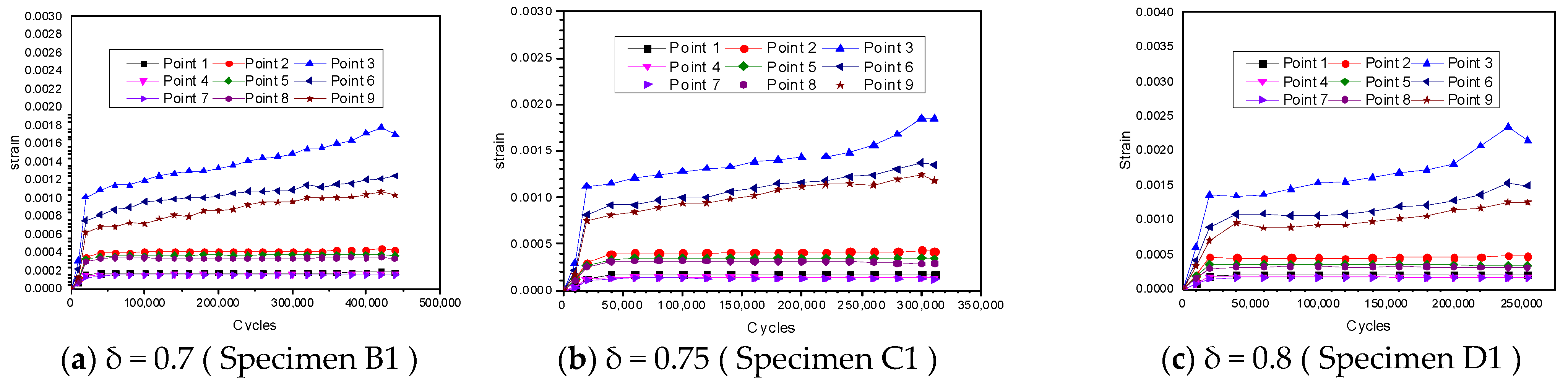
3.3.4. Strain of Each Measuring Point of Test Pieces under Different Load Factors
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- O’Dwyer, D.; O’Dowd, N.; McCarthy, C. Numerical micromechanical investigation of interfacial strength parameters in a carbon fibre composite material. J. Compos. Mater. 2013, 48, 749–760. [Google Scholar] [CrossRef]
- Wicaksono, S.; Chai, G.B. Life prediction of woven CFRP structure subject to static and fatigue loading. Compos. Struct. 2015, 119, 185–194. [Google Scholar] [CrossRef]
- Yu, Q.; Wu, Y. Fatigue retrofitting of cracked steel beams with CFRP laminates. Compos. Struct. 2018, 192, 232–244. [Google Scholar] [CrossRef]
- Gong, M.; Sun, S.; Sun, L.; Tian, A.; Li, Q. Simulation and experimentation of wide frequency electromagnetic shielding coating used for carbon fiber composite materials of track vehicles. Int. J. Mod. Phys. B 2019, 33, 1940020. [Google Scholar] [CrossRef]
- Yang, T.; He, M.; Niu, X.; Du, Y. Experimental investigation of the three-point bending fatigue prop-series of carbon fiber composite laminates. Adv. Mater. Sci. 2017, 1, 7–13. [Google Scholar]
- Koch, I.; Zscheyge, M.; Tittmann, K.; Gude, M. Numerical fatigue analysis of CFRP components. Compos. Struct. 2017, 168, 392–401. [Google Scholar] [CrossRef]
- Neidigk, S.; Le, J.; Roach, D.; Duvall, R.; Rice, T. Use of nondestructive inspection and fiber optic sensing for damage characterization in carbon fiber fuselage structure. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 9–13 March 2014; Volume 9063, pp. 1–8. [Google Scholar] [CrossRef]
- Fernandes, H.; Zhang, H.; Figueiredo, A.; Ibarra-Castanedo, C.; Guimarares, G.; Maldague, X. Carbon fiber composites inspection and defect characterization using active infra-red thermography: Numerical simulations and experimental results. Appl. Opt. 2016, 55, 46–53. [Google Scholar] [CrossRef] [PubMed]
- Shan, N. Applications Research in Ultrasonic testing of Carbon Fiber Composite Based on an Optical Fiber F-p Sensor. In Proceedings of the Eighth International Symposium on Advanced Optical Manufacturing and Testing Technology, Suzhou, China, 7 November 2016; Volume 9685, pp. 1–6. [Google Scholar] [CrossRef]
- Amaro, A.M.; Reis, P.N.B.; Moura MFSF de Santos, J.B. Damage detection on laminated composite materials using several NDT techniques. Insight Non-Destr. Test. Cond. Monit. 2012, 54, 14–20. [Google Scholar] [CrossRef]
- Stawiarski, A.; Muc, A.; Kędziora, P. Damage Detection, Localization and Assessment in Multilayered Composite Structure with Delaminations. Key Eng. Mater. 2013, 542, 193–204. [Google Scholar] [CrossRef]
- Intan, B.; Murat, S.; Khalili, P.; Fromme, P. Impact Damage Detection in Composite Panels us-ing Guided Ultrasonic Waves. In Proceedings of the 40th Annual Review of Progress in Quantitative Nondestructive Evaluation: Incorporating the 10th International Conference on Barkhausen Noise and Micromagnetic Testing, Baltimore, MD, USA, 21–26 July 2013; pp. 286–293. [Google Scholar] [CrossRef]
- Papa, I.; Lopresto, V.; Langella, A. Ultrasonic inspection of composites materials: Application to detect impact damage. Int. J. Lightweight Mater. Manuf. 2020, 4, 37–42. [Google Scholar] [CrossRef]
- Okabe, T.; Yashiro, S. Damage detection in holed composite laminates using an embedded FBG sensor. Compos. Part A Appl. Sci. Manuf. 2012, 43, 388–397. [Google Scholar] [CrossRef]
- Werneck, M.M.; Allil, R.C.S.B.; Ribeiro, B.A.; de Nazaré, F.V.B. A Guide to Fiber Bragg Grating Sensors. In Current Trends in Short- and Long-Period Fiber Gratings; Intech: London, UK, 2013; pp. 1–24. [Google Scholar]
- Materials, C. Overview of Fiber Optic Sensor Technologies for Strain/Temperature Sensing Applications in Composite Materials. Sensors 2016, 16, 99. [Google Scholar] [CrossRef]
- Kinet, D.; Megret, P.; Goossen, K.W.; Qiu, L.; Heider, D.; Caucheteur, C. Fiber Bragg Grating Sensors toward Structural Health Monitoring in Composite Materials: Challenges and Solutions. Sensors 2014, 14, 7394–7419. [Google Scholar] [CrossRef] [PubMed]
- Takeda, S.I.; Yokozeki, T.; Ogasawara, T. Damage monitoring of polymer-lined carbon fiber-reinforced plastic using small-diameter fiber Bragg grating sensors. J. Reinf. Plast. Compos. 2015, 34, 454–462. [Google Scholar] [CrossRef]
- Guo, Z.; Feng, J.; Wang, H.; Hu, H.; Zhang, J. Fiber Bragg Grating Sensors for Fatigue Monitoring of Composite. Polym. Polym. Compos. 2013, 21, 553–560. [Google Scholar] [CrossRef]
- Chiang, C.C.; Shin, C.S.; Lin, C.L. Application of the embedded optical fiber Bragg grating sensors in detecting the internal fatigue damage of Gr/epoxy laminated composites. Chin. J. Mech. Eng. 2006, 27, 801–807. [Google Scholar]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]








| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 142 | 1900 | ||
| 9 | 51 | ||
| 9 | 51 | ||
| 0.32 | 1100 | ||
| 0.46 | 130 | ||
| 0.32 | 130 | ||
| 4.6 | 72 | ||
| 3.08 | 72 | ||
| 4.6 | 70 | ||
| 50 | 75 | ||
| 0.25 | 0.75 | ||
| 1620 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 9.7 | 55 | ||
| 6.5 | 120 | ||
| 6.5 | 120 | ||
| 0.28 | 1.45 | ||
| 0.495 | 1570 | ||
| 0.495 |
| Grid Number | Number of Grid Cells (Units) | Simulation Limit Load (N) |
|---|---|---|
| 1 | 4320 | 23,024 |
| 2 | 6624 | 22,418 |
| 3 | 10,752 | 20,321 |
| 4 | 20,792 | 20,568 |
| 5 | 31,320 | 20,564 |
| Group | Quantity | Number | Application |
|---|---|---|---|
| A | 3 | A1~A3 | Quasi-static test |
| B | 3 | B1~B3 | Fatigue test (δ = 0.7) |
| C | 3 | C1~C3 | Fatigue test (δ = 0.75) |
| D | 3 | D1~D3 | Fatigue test (δ = 0.8) |
| E | 4 | E1~E4 | Fatigue damage evolution |
| Specimen | Elastic Limit Load (N) | Ultimate Load (N) |
|---|---|---|
| A1 | 7063 | 20,801 |
| A2 | 8608 | 20,860 |
| A3 | 8485 | 19,545 |
| Load Factor | Specimen Life (Times) | Average Value | ||
|---|---|---|---|---|
| 0.7 | B1 | B2 | B3 | 440,071 |
| 438,920 | 440,260 | 441,032 | ||
| 0.75 | C1 | C2 | C3 | 311,114 |
| 310,670 | 321,323 | 301,350 | ||
| 0.8 | D1 | D2 | D3 | 254,563 |
| 254,362 | 254,563 | 254,763 | ||
| Load Factor | Fatigue Life (Times) | Difference (Times) | Relative Errors | |
|---|---|---|---|---|
| Experimental Average Value | Simulated Value | |||
| 0.7 | 440,071 | 480,000 | 39,929 | 9.07% |
| 0.75 | 311,114 | 340,000 | 28,886 | 9.28% |
| 0.8 | 254,563 | 280,000 | 25,437 | 9.99% |
| Load Factor | Inflection Point | Experiment Strain (Cycle Times) | Simulation Displacement (Cycle Times) | Experiment Residual Stiffness (Cycle Times) | Simulation Residual Stiffness (Cycle Times) |
|---|---|---|---|---|---|
| 0.7 | Point 1 | 19,300 | 20,459 | 39,080 | 41,065 |
| Point 2 | 415,867 | 380,689 | 382,236 | 379,770 | |
| 0.75 | Point 1 | 19,780 | 21,609 | 39,571 | 39,811 |
| Point 2 | 299,392 | 280,574 | 260,470 | 279,728 | |
| 0.8 | Point 1 | 19,881 | 20,344 | 39,937 | 40,125 |
| Point 2 | 239,635 | 220,459 | 220,815 | 219,644 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, G.; Yan, X.; Gao, X.; Xiao, J. Experimental and Numerical Studies on Fatigue Characteristics of CFRP Shaft Tube. Appl. Sci. 2022, 12, 8933. https://doi.org/10.3390/app12188933
Ding G, Yan X, Gao X, Xiao J. Experimental and Numerical Studies on Fatigue Characteristics of CFRP Shaft Tube. Applied Sciences. 2022; 12(18):8933. https://doi.org/10.3390/app12188933
Chicago/Turabian StyleDing, Guoping, Xiaoyu Yan, Xiaoling Gao, and Jieliang Xiao. 2022. "Experimental and Numerical Studies on Fatigue Characteristics of CFRP Shaft Tube" Applied Sciences 12, no. 18: 8933. https://doi.org/10.3390/app12188933
APA StyleDing, G., Yan, X., Gao, X., & Xiao, J. (2022). Experimental and Numerical Studies on Fatigue Characteristics of CFRP Shaft Tube. Applied Sciences, 12(18), 8933. https://doi.org/10.3390/app12188933





