Crack Extension Analysis of Atmospheric Stress Corrosion Based on Peridynamics
Abstract
:1. Introduction
2. Materials and Methods
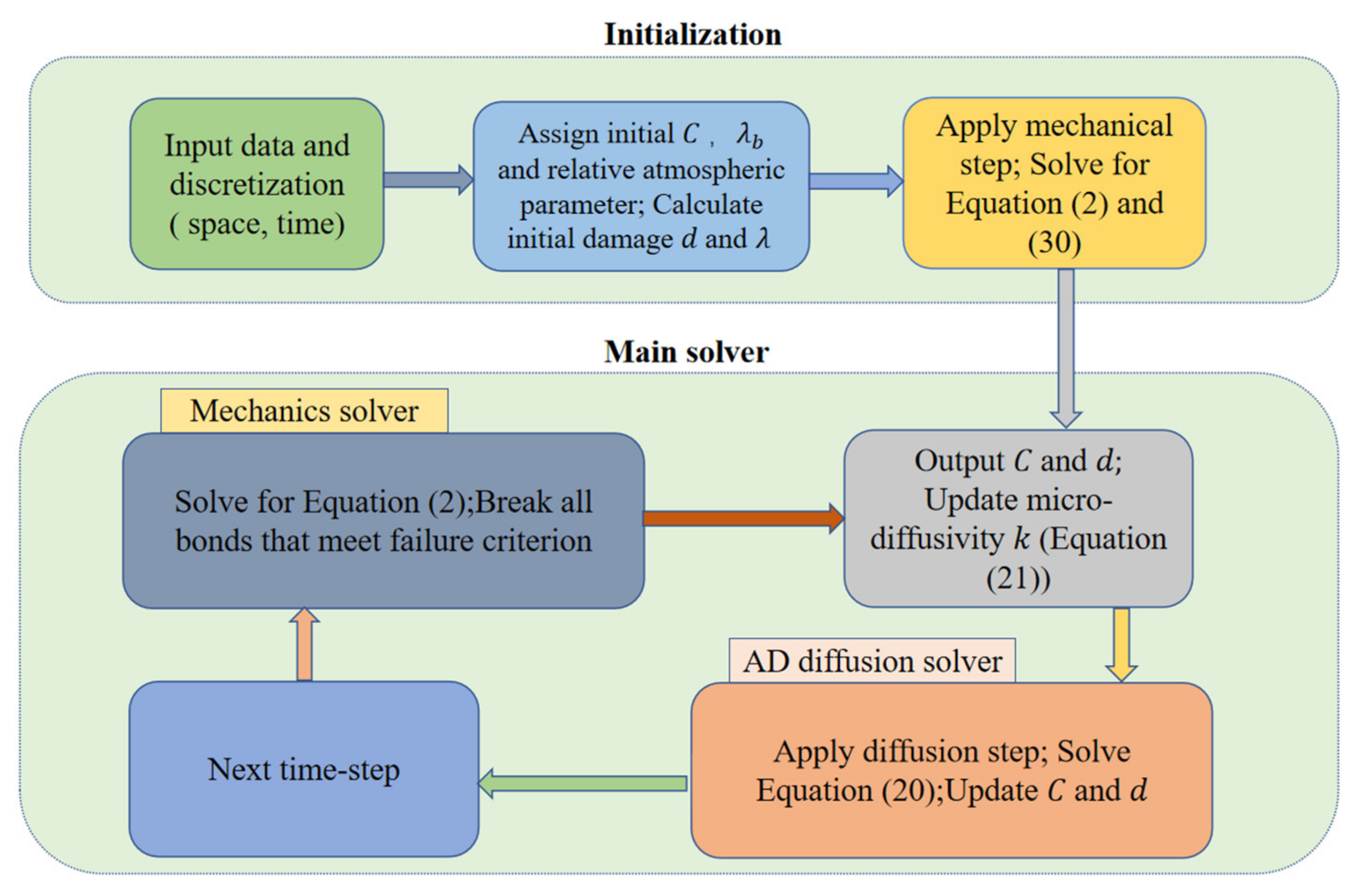
2.1. Atmospheric Stress Corrosion Coupling Model with Peridynamics
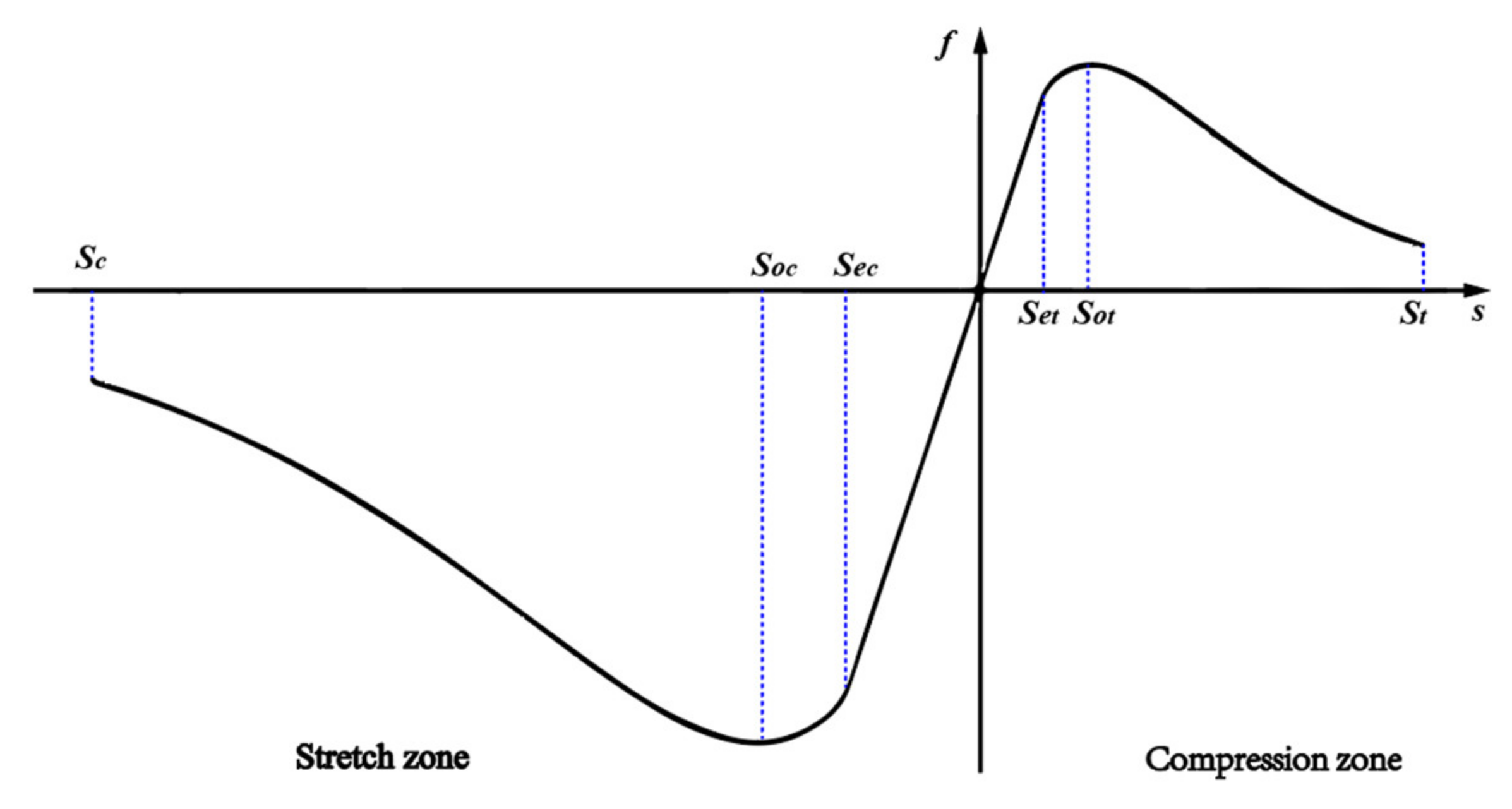
2.1.1. Peridynamics Fracture Model
2.1.2. Atmospheric Corrosion Model
- (1)
- Dry atmospheric corrosion: There is no liquid film coating on the metal surface. It is mostly generated by pure chemical reactions and its corrosion efficiency and destruction are often modest.
- (2)
- Humid atmospheric corrosion: There is a 10 nm–1 liquid film coating on the metal surface. This thin liquid film is generated on a metal surface via capillary action, adsorption, or chemical condensation. Atmospheric oxygen travels considerably more readily through the water film on the metal surface than through the liquid layer when totally submerged.
- (3)
- Wet atmospheric corrosion: There is a 1 –1 mm liquid film coating on the metal surface. It is broadly compatible with the electrochemical corrosion mechanism in the body solution.
2.1.3. Peridynamics Anodic Dissolution Model
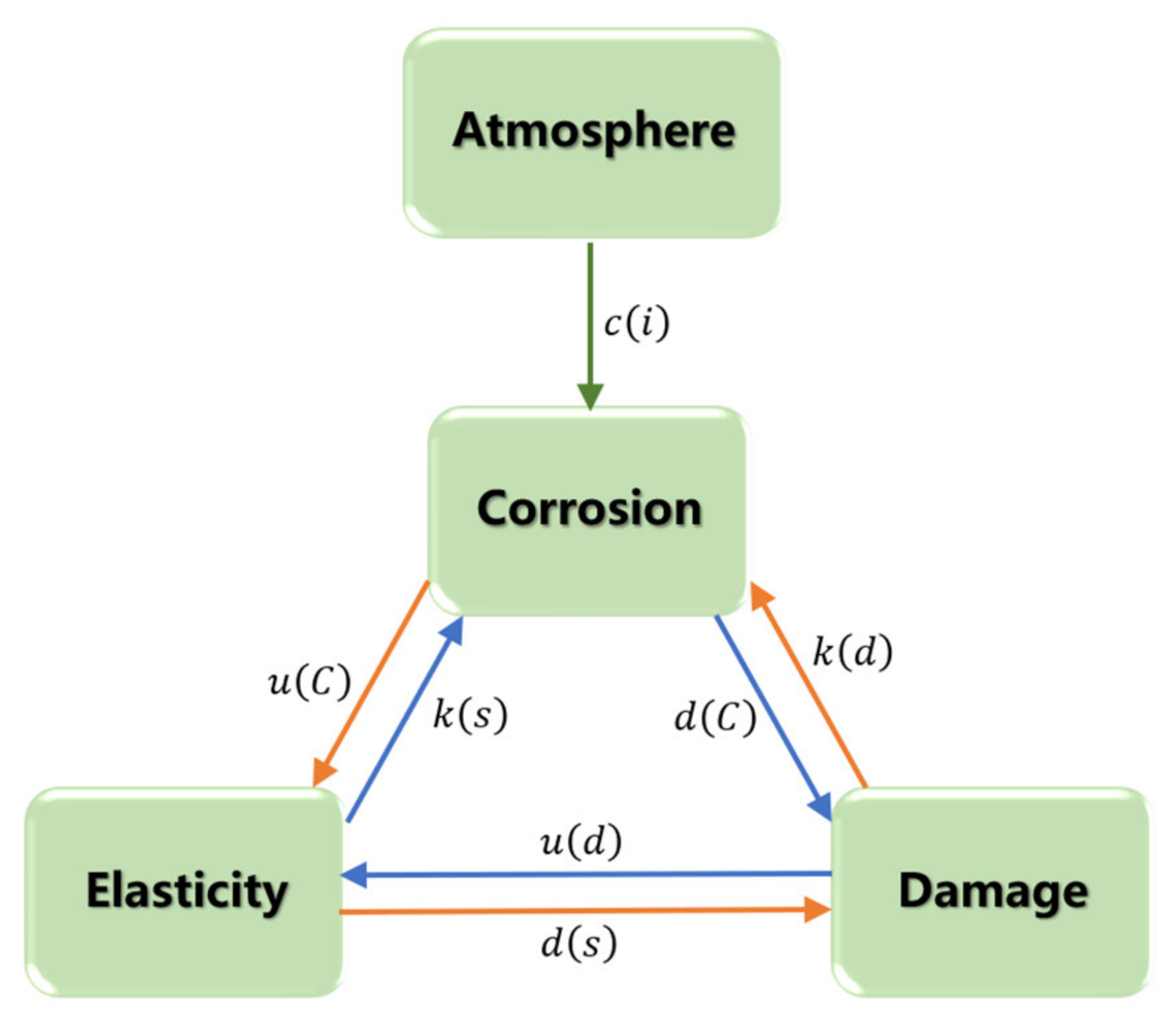
2.1.4. Atmospheric Corrosion–Fracture Coupling Model with Peridynamics
2.2. Simulation of Atmospheric Stress Corrosion Fracturing in 304 Stainless Steel
2.2.1. Experiment
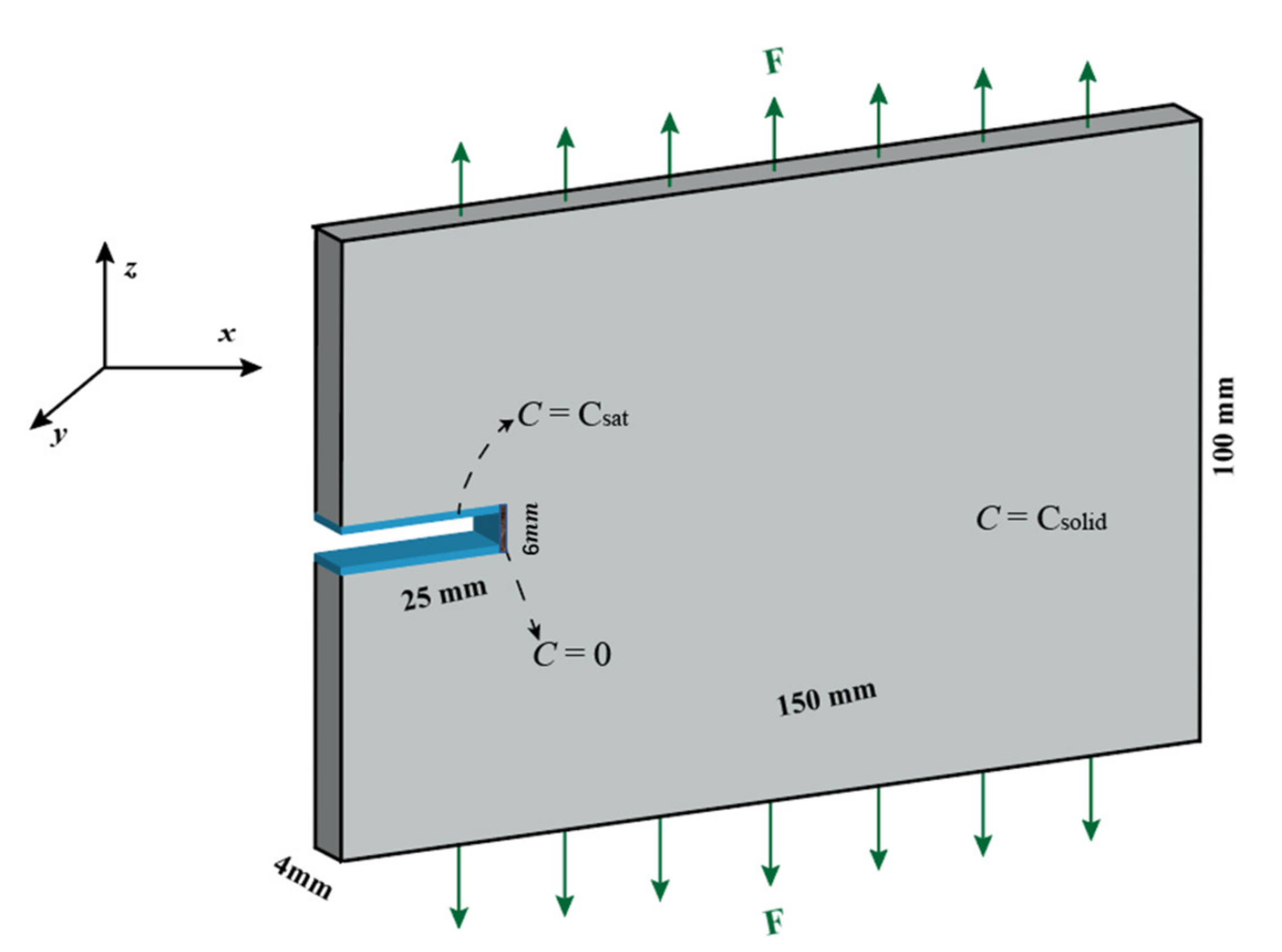
2.2.2. Calculation Model Setup
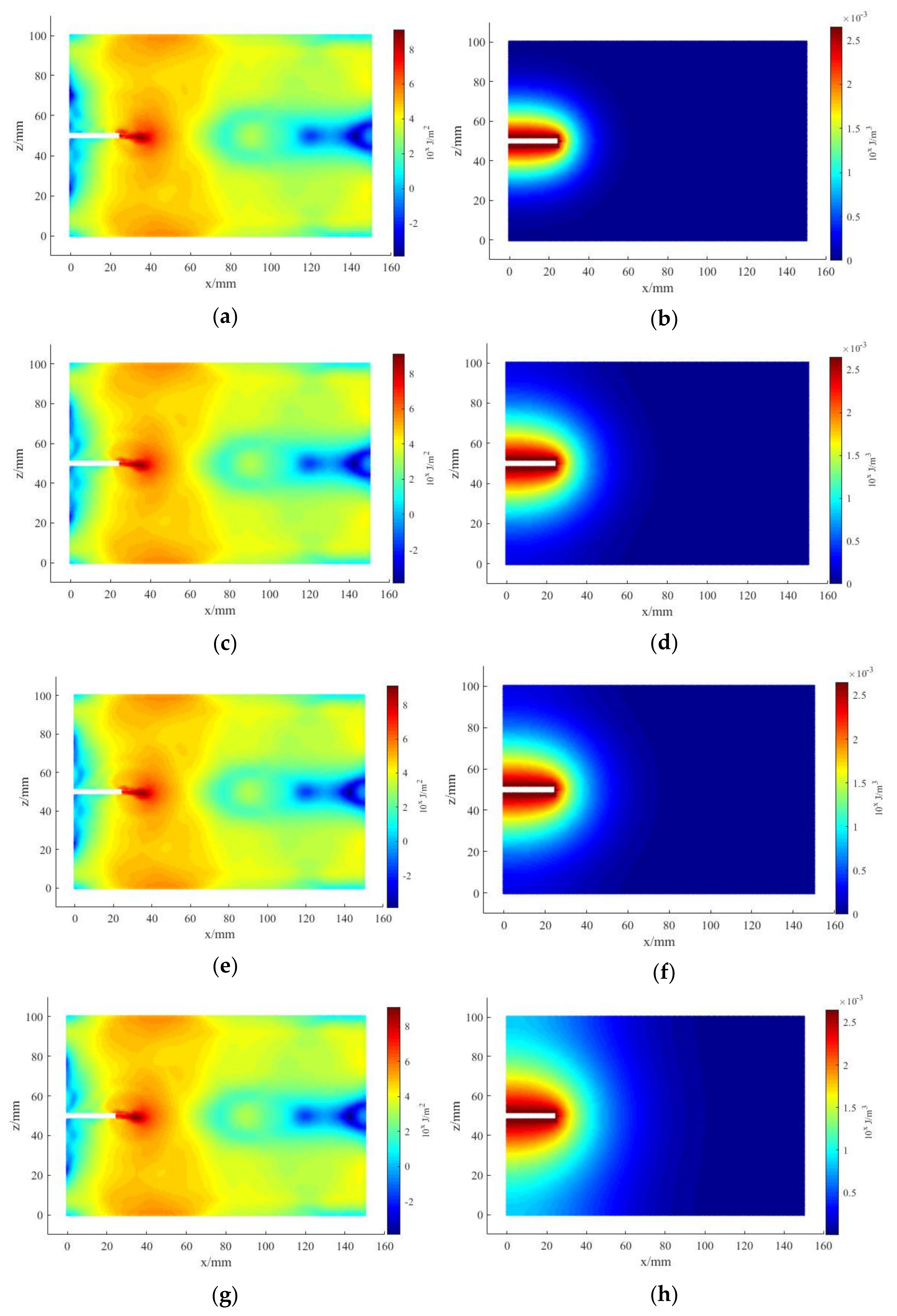
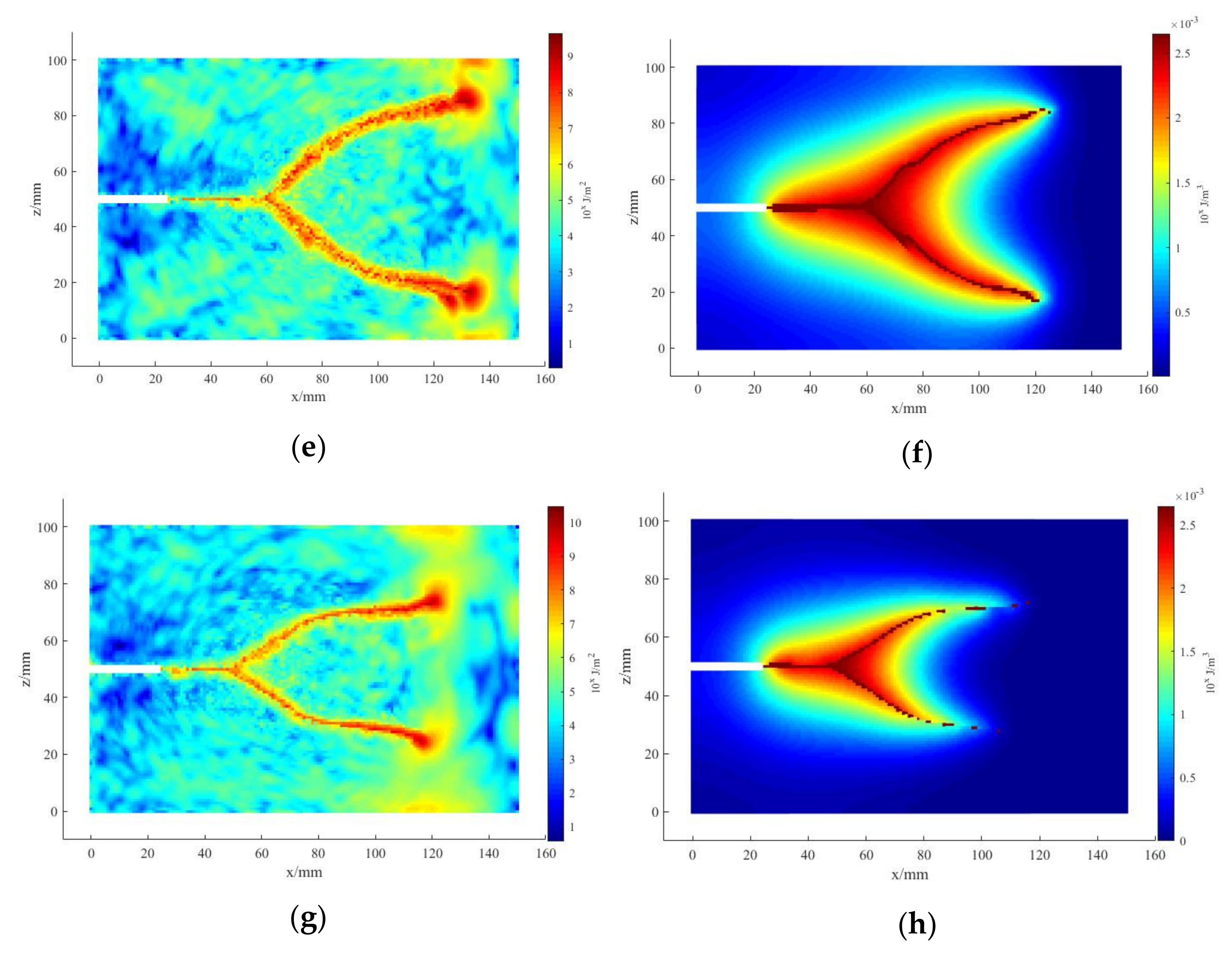
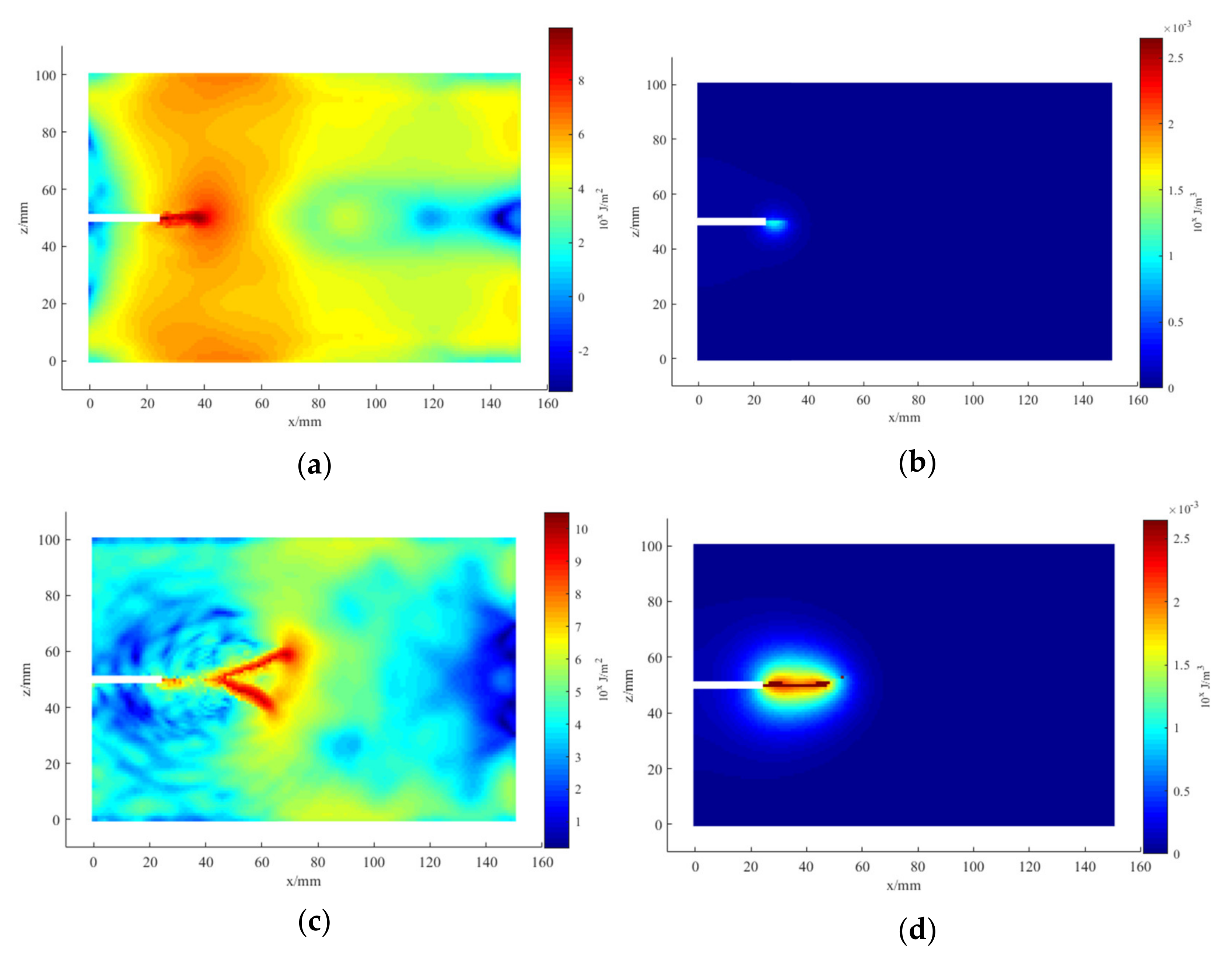
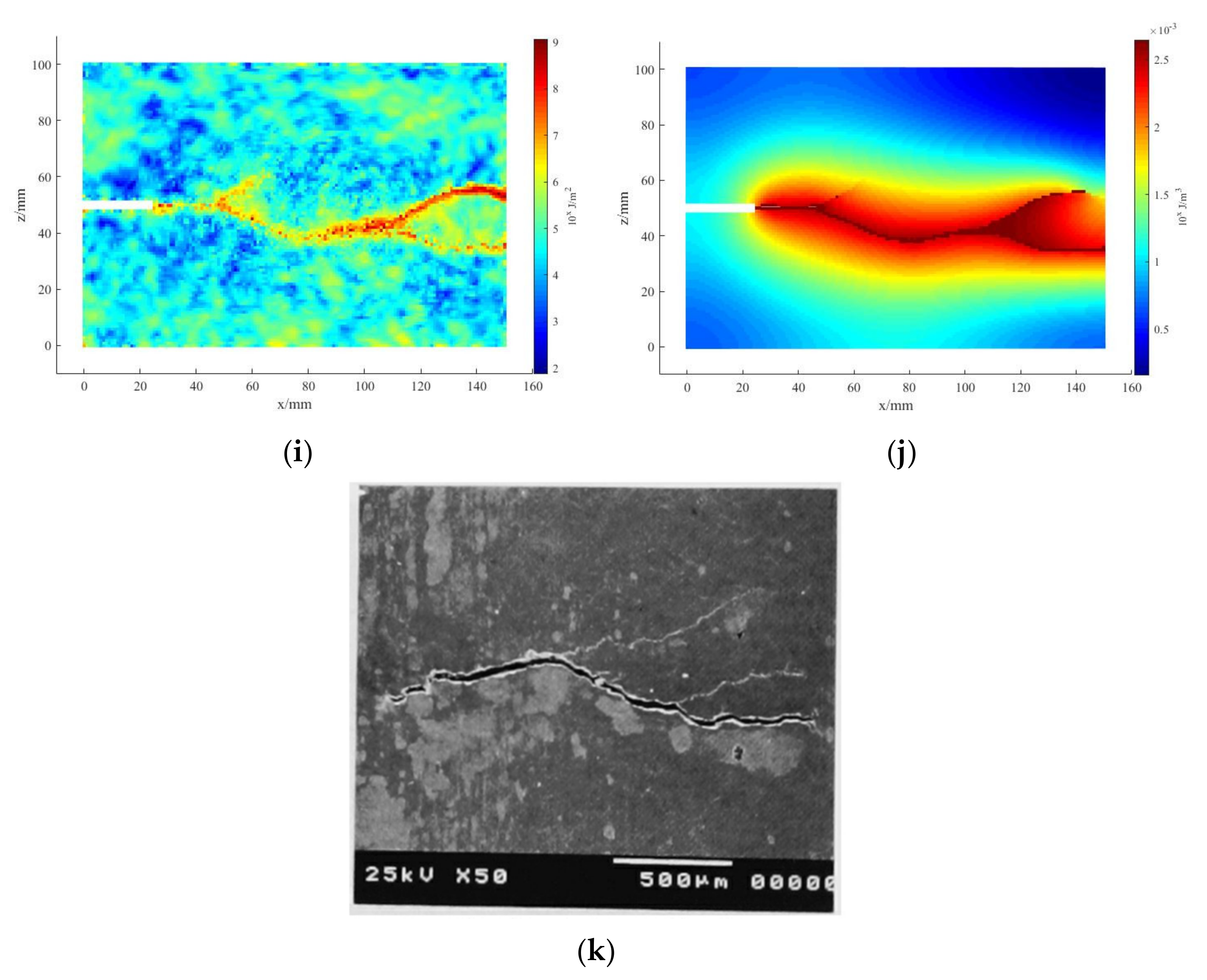
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hansson, C.M. The Impact of Corrosion on Society. Met. Mater. Trans. A 2011, 42, 2952–2962. [Google Scholar] [CrossRef]
- Koushik, B.G.; Steen, N.V.D.; Mamme, M.H.; Van Ingelgem, Y.; Terryn, H. Review on modelling of corrosion under droplet electrolyte for predicting atmospheric corrosion rate. J. Mater. Sci. Technol. 2020, 62, 254–267. [Google Scholar] [CrossRef]
- Ramamurthy, S.; Atrens, A. Stress corrosion cracking of high-strength steels. Corros. Rev. 2013, 31, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Flanagan, W.; Bastias, P.; Lichter, B. A theory of transgranular stress-corrosion cracking. Acta Met. et Mater. 1991, 39, 695–705. [Google Scholar] [CrossRef]
- Lu, Y.; Peng, Q.; Sato, T.; Shoji, T. An ATEM study of oxidation behavior of SCC crack tips in 304L stainless steel in high temperature oxygenated water. J. Nucl. Mater. 2005, 347, 52–68. [Google Scholar] [CrossRef]
- Dadfarnia, M.; Martin, M.L.; Nagao, A.; Sofronis, P.; Robertson, I.M. Modeling hydrogen transport by dislocations. J. Mech. Phys. Solids 2015, 78, 511–525. [Google Scholar] [CrossRef]
- Jiang, D.; Carter, E.A. First principles assessment of ideal fracture energies of materials with mobile impurities: Implications for hydrogen embrittlement of metals. Acta Mater. 2004, 52, 4801–4807. [Google Scholar] [CrossRef]
- Barnoush, A.; Asgari, M.; Johnsen, R. Resolving the hydrogen effect on dislocation nucleation and mobility by electrochemical nanoindentation. Scr. Mater. 2012, 66, 414–417. [Google Scholar] [CrossRef]
- Lynch, S. Hydrogen embrittlement phenomena and mechanisms. Corros. Rev. 2012, 30, 105–123. [Google Scholar] [CrossRef]
- Leyson, G.; Grabowski, B.; Neugebauer, J. Multiscale description of dislocation induced nano-hydrides. Acta Mater. 2015, 89, 50–59. [Google Scholar] [CrossRef]
- Schindelholz, E.; Kelly, R.G. Wetting phenomena and time of wetness in atmospheric corrosion: A review. Corros. Rev. 2012, 30, 135–170. [Google Scholar] [CrossRef]
- Simillion, H.; Dolgikh, O.; Terryn, H.; Deconinck, J. Atmospheric corrosion modeling. Corros. Rev. 2014, 32, 73–100. [Google Scholar] [CrossRef]
- Steen, N.V.D.; Simillion, H.; Dolgikh, O.; Terryn, H.; Deconinck, J. An integrated modeling approach for atmospheric corrosion in presence of a varying electrolyte film. Electrochim. Acta 2016, 187, 714–723. [Google Scholar] [CrossRef]
- Stratmann, M.; Streckel, H. The Investigation of the Corrosion of Metal Surfaces, Covered with Thin Electrolyte Layers—A New Experimental Technique. Ber. Der Bunsenges. Für Phys. Chem. 1988, 92, 1244–1250. [Google Scholar] [CrossRef]
- Nishikata, A.; Ichihara, Y.; Tsuru, T. Electrochemical impedance spectroscopy of metals covered with a thin electrolyte layer. Electrochim. Acta 1996, 41, 1057–1062. [Google Scholar] [CrossRef]
- Nishikata, A.; Ichihara, Y.; Hayashi, Y.; Tsuru, T. Influence of Electrolyte Layer Thickness and pH on the Initial Stage of the Atmospheric Corrosion of Iron. J. Electrochem. Soc. 1997, 144, 1244–1252. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, W.; Wang, J.; Peng, X.; Wang, Y.; Zhang, P.; Wang, H.; Gao, C. Study of corrosion behavior of carbon steel under seawater film using the wire beam electrode method. Corros. Sci. 2014, 80, 523–527. [Google Scholar] [CrossRef]
- Shi, Y.; Tada, E.; Nishikata, A. A Method for Determining the Corrosion Rate of a Metal under a Thin Electrolyte Film. J. Electrochem. Soc. 2015, 162, C135–C139. [Google Scholar] [CrossRef]
- Chung, K.-W.; Kim, K.-B. A study of the effect of concentration build-up of electrolyte on the atmospheric corrosion of carbon steel during drying. Corros. Sci. 2000, 42, 517–531. [Google Scholar] [CrossRef]
- Ito, M.; Ooi, A.; Tada, E.; Nishikata, A. In Situ Evaluation of Carbon Steel Corrosion under Salt Spray Test by Electrochemical Impedance Spectroscopy. J. Electrochem. Soc. 2020, 167, 101508. [Google Scholar] [CrossRef]
- Saeedikhani, M.; Steen, N.V.D.; Wijesinghe, S.; Vafakhah, S.; Terryn, H.; Blackwood, D.J. Moving Boundary Simulation of Iron-Zinc Sacrificial Corrosion under Dynamic Electrolyte Thickness Based on Real-Time Monitoring Data. J. Electrochem. Soc. 2020, 167, 041503. [Google Scholar] [CrossRef]
- Simillion, H.; Steen, N.V.D.; Terryn, H.; Deconinck, J. Geometry influence on corrosion in dynamic thin film electrolytes. Electrochim. Acta 2016, 209, 149–158. [Google Scholar] [CrossRef]
- Gupta, D.; Eom, H.-J.; Cho, H.-R.; Ro, C.-U. Hygroscopic behavior of NaCl–MgCl2 mixture particles as nascent sea-spray aerosol surrogates and observation of efflorescence during humidification. Atmospheric Chem. Phys. 2015, 15, 11273–11290. [Google Scholar] [CrossRef] [Green Version]
- Schindelholz, E.; Risteen, B.E.; Kelly, R.G. Effect of Relative Humidity on Corrosion of Steel under Sea Salt Aerosol Proxies. J. Electrochem. Soc. 2014, 161, C460–C470. [Google Scholar] [CrossRef]
- Cole, I.; Ganther, W.D.; Sinclair, J.D.; Lau, D.; Paterson, D.A. A Study of the Wetting of Metal Surfaces in Order to Understand the Processes Controlling Atmospheric Corrosion. J. Electrochem. Soc. 2004, 151, B627–B635. [Google Scholar] [CrossRef]
- Cole, I.; Azmat, N.S.; Kanta, A.; Venkatraman, M. What really controls the atmospheric corrosion of zinc? Effect of marine aerosols on atmospheric corrosion of zinc. Int. Mater. Rev. 2009, 54, 117–133. [Google Scholar] [CrossRef]
- Cole, I.; Paterson, D.A. Modelling aerosol deposition rates on aircraft and implications for pollutant accumulation and corrosion. Corros. Eng. Sci. Technol. 2009, 44, 332–339. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Meth. Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Schlangen, E.; van Mier, J.G.M. Simple lattice model for numerical simulation of fracture of concrete materials and structures. Mater. Struct. 1992, 25, 534–542. [Google Scholar] [CrossRef]
- Silling, S. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- De Meo, D.; Diyaroglu, C.; Zhu, N.; Oterkus, E.; Siddiq, M.A. Modelling of stress-corrosion cracking by using peridynamics. Int. J. Hydrogen Energy 2016, 41, 6593–6609. [Google Scholar] [CrossRef] [Green Version]
- Madenci, E.; Yaghoobi, A.; Barut, A.; Phan, N. Peridynamic Modeling of Compression after Impact Damage in Composite Laminates. J. Peridynamics Nonlocal Model. 2021, 3, 327–347. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Chen, Z.; Bobaru, F. Peridynamic Modeling of Repassivation in Pitting Corrosion of Stainless Steel. Corrosion 2017, 74, 393–414. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Chen, Z.; Bobaru, F. Peridynamic Modeling of Intergranular Corrosion Damage. J. Electrochem. Soc. 2018, 165, C362–C374. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, G.; Bobaru, F. The Influence of Passive Film Damage on Pitting Corrosion. J. Electrochem. Soc. 2015, 163, C19–C24. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Chen, Z.; Li, S.; Bobaru, F. A peridynamic mechano-chemical damage model for stress-assisted corrosion. Electrochim. Acta 2019, 323, 134795. [Google Scholar] [CrossRef]
- Chen, Z.; Jafarzadeh, S.; Zhao, J.; Bobaru, F. A coupled mechano-chemical peridynamic model for pit-to-crack transition in stress-corrosion cracking. J. Mech. Phys. Solids 2020, 146, 104203. [Google Scholar] [CrossRef]
- Ran, X.; Qian, S.; Zhou, J.; Xu, Z. Crack propagation analysis of hydrogen embrittlement based on peridynamics. Int. J. Hydrogen Energy 2021, 47, 9045–9057. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Wu, W.; Li, X.; Zhao, J. Crack growth behaviour of E690 steel in artificial seawater with various pH values. Corros. Sci. 2019, 164, 108336. [Google Scholar] [CrossRef]
- Gong, K.; Wu, M.; Xie, F.; Liu, G.; Sun, D. Effect of Cl− and rust layer on stress corrosion cracking behavior of X100 steel base metal and heat-affected zone in marine alternating wet/dry environment. Mater. Chem. Phys. 2021, 270, 124826. [Google Scholar] [CrossRef]
- Gong, K.; Wu, M.; Liu, G. Stress corrosion cracking behavior of rusted X100 steel under the combined action of Cl− and HSO3− in a wet–dry cycle environment. Corros. Sci. 2020, 165, 108382. [Google Scholar] [CrossRef]
- Chen, W.; Hao, L.; Dong, J.; Ke, W. Effect of sulphur dioxide on the corrosion of a low alloy steel in simulated coastal industrial atmosphere. Corros. Sci. 2014, 83, 155–163. [Google Scholar] [CrossRef]
- Hu, Y.; Dong, C.; Sun, M.; Xiao, K.; Zhong, P.; Li, X. Effects of solution pH and Cl− on electrochemical behaviour of an Aermet100 ultra-high strength steel in acidic environments. Corros. Sci. 2011, 53, 4159–4165. [Google Scholar] [CrossRef]
- Ives, M.; Lu, Y.; Luo, J. Cathodic reactions involved in metallic corrosion in chlorinated saline environments. Corros. Sci. 1991, 32, 91–102. [Google Scholar] [CrossRef]
- Liu, Z.; Du, C.; Zhang, X.; Wang, F.; Li, X. Effect of pH value on stress corrosion cracking of X70 pipeline steel in acidic soil environment. Acta Met. Sin. (English Lett.) 2013, 26, 489–496. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Gao, K.; Qiao, L.; Chu, W. The correspondence between susceptibility to SCC of brass and corrosion-induced tensile stress with various pH values. Corros. Sci. 2002, 44, 2367–2378. [Google Scholar] [CrossRef]
- Lu, Q.; Wang, L.; Xin, J.; Tian, H.; Wang, X.; Cui, Z. Corrosion evolution and stress corrosion cracking of E690 steel for marine construction in artificial seawater under potentiostatic anodic polarization. Constr. Build. Mater. 2019, 238, 117763. [Google Scholar] [CrossRef]
- Katona, R.; Carpenter, J.; Knight, A.; Bryan, C.; Schaller, R.; Kelly, R.; Schindelholz, E. Importance of the hydrogen evolution reaction in magnesium chloride solutions on stainless steel. Corros. Sci. 2020, 177, 108935. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Silling, S.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Wang, J.; Qian, S. Spallation Analysis of Concrete Under Pulse Load Based on Peridynamic Theory. Wirel. Pers. Commun. 2020, 112, 949–966. [Google Scholar] [CrossRef]
- Bobaru, F.; Duangpanya, M. The peridynamic formulation for transient heat conduction. Int. J. Heat Mass Transf. 2010, 53, 4047–4059. [Google Scholar] [CrossRef]
- Bobaru, F.; Duangpanya, M. A peridynamic formulation for transient heat conduction in bodies with evolving discontinuities. J. Comput. Phys. 2012, 231, 2764–2785. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, K.; Rao, K.P. Effect of microstructure on stress corrosion cracking behaviour of austenitic stainless steel weld metals. Mater. Sci. Eng. A 1991, 142, 79–85. [Google Scholar] [CrossRef]
- Qiao, L.; Mao, X. Thermodynamic analysis on the role of hydrogen in anodic stress corrosion cracking. Acta Met. Mater. 1995, 43, 4001–4006. [Google Scholar] [CrossRef]
- Mayuzumi, M.; Arai, T.; Hide, K. Chloride Induced Stress Corrosion Cracking of Type 304 and 304L Stainless Steels in Air. Zairyo-to-Kankyo 2003, 52, 166–170. [Google Scholar] [CrossRef]
- Qiao, L.; Mao, X.; Chu, W. The role of hydrogen in stress-corrosion cracking of austenitic stainless steel in hot MgCl2 solution. Met. Mater. Trans. A 1995, 26, 1777–1784. [Google Scholar] [CrossRef]
- Nyrkova, L.; Melnichuk, S.; Osadchuk, S.; Lisovyi, P.; Prokopchuk, S. Investigating the mechanism of stress corrosion cracking of controllable rolling pipe steel X70 in near-neutral environment. Mater. Today Proc. 2021, 50, 470–476. [Google Scholar] [CrossRef]
- Chiari, L.; Komatsu, A.; Fujinami, M. Defects Responsible for Hydrogen Embrittlement in Austenitic Stainless Steel 304 by Positron Annihilation Lifetime Spectroscopy. ISIJ Int. 2021, 61, 1927–1934. [Google Scholar] [CrossRef]
- Haruna, T.; Shoji, Y.; Hirohata, Y. Hydrogen Absorption Rate into Fe with Rust Layer Containing NaCl during Atmospheric Corrosion in Humidity-controlled Air. ISIJ Int. 2021, 61, 1079–1084. [Google Scholar] [CrossRef]
- Zhou, C.; Ye, B.; Song, Y.; Cui, T.; Xu, P.; Zhang, L. Effects of internal hydrogen and surface-absorbed hydrogen on the hydrogen embrittlement of X80 pipeline steel. Int. J. Hydrogen Energy 2019, 44, 22547–22558. [Google Scholar] [CrossRef]




| C | Si | Mn | P | S | Ni | Cr | Fe |
|---|---|---|---|---|---|---|---|
| 0.06% | 0.61% | 0.95% | 0.028% | 0.011% | 8.12% | 18.10% | Bal. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, C.; Qian, S.; Zhang, J. Crack Extension Analysis of Atmospheric Stress Corrosion Based on Peridynamics. Appl. Sci. 2022, 12, 10008. https://doi.org/10.3390/app121910008
Tan C, Qian S, Zhang J. Crack Extension Analysis of Atmospheric Stress Corrosion Based on Peridynamics. Applied Sciences. 2022; 12(19):10008. https://doi.org/10.3390/app121910008
Chicago/Turabian StyleTan, Can, Songrong Qian, and Jian Zhang. 2022. "Crack Extension Analysis of Atmospheric Stress Corrosion Based on Peridynamics" Applied Sciences 12, no. 19: 10008. https://doi.org/10.3390/app121910008
APA StyleTan, C., Qian, S., & Zhang, J. (2022). Crack Extension Analysis of Atmospheric Stress Corrosion Based on Peridynamics. Applied Sciences, 12(19), 10008. https://doi.org/10.3390/app121910008






