Calibration and Testing of Discrete Element Simulation Parameters for Sandy Soils in Potato Growing Areas
Abstract
:1. Introduction
2. Soil Physical Property Parameters
2.1. Purpose of the Experiment
2.2. Test Materials
2.2.1. Soil Preparation with Different Water Content
2.2.2. Soil Preparation with Different Firmness
2.3. Test Methods and Equipment
2.3.1. Determination of Angle of Repose in Soil with Different Moisture Content
2.3.2. Determination of Rolling Friction Angle of Soil with Different Moisture Content
2.3.3. Direct Shear Test for Soil with Different Moisture Content and Firmness
2.3.4. Lateral Limitless Compressive Test for Soil with Different Moisture Content and Firmness
2.4. Experimental Results
2.4.1. Rest Angle and Friction Coefficient of Soil with Different Water Content
2.4.2. Results of Direct Shear Tests of Soil with Different Moisture Content and Firmness
2.4.3. Results of Lateral Limitless Compressive Test of Soil with Different Moisture Content and Firmness
3. Soil Parameter Discrete Element Calibration
3.1. Purpose of the Experiment
3.2. Soil Particle Simulation Parameters and Discrete Element Modeling
3.3. Discrete Element Parameter Calibration and Result Analysis
3.3.1. Evaluation Indicators
3.3.2. Plackett–Burman Test
3.3.3. Steepest Climb Test
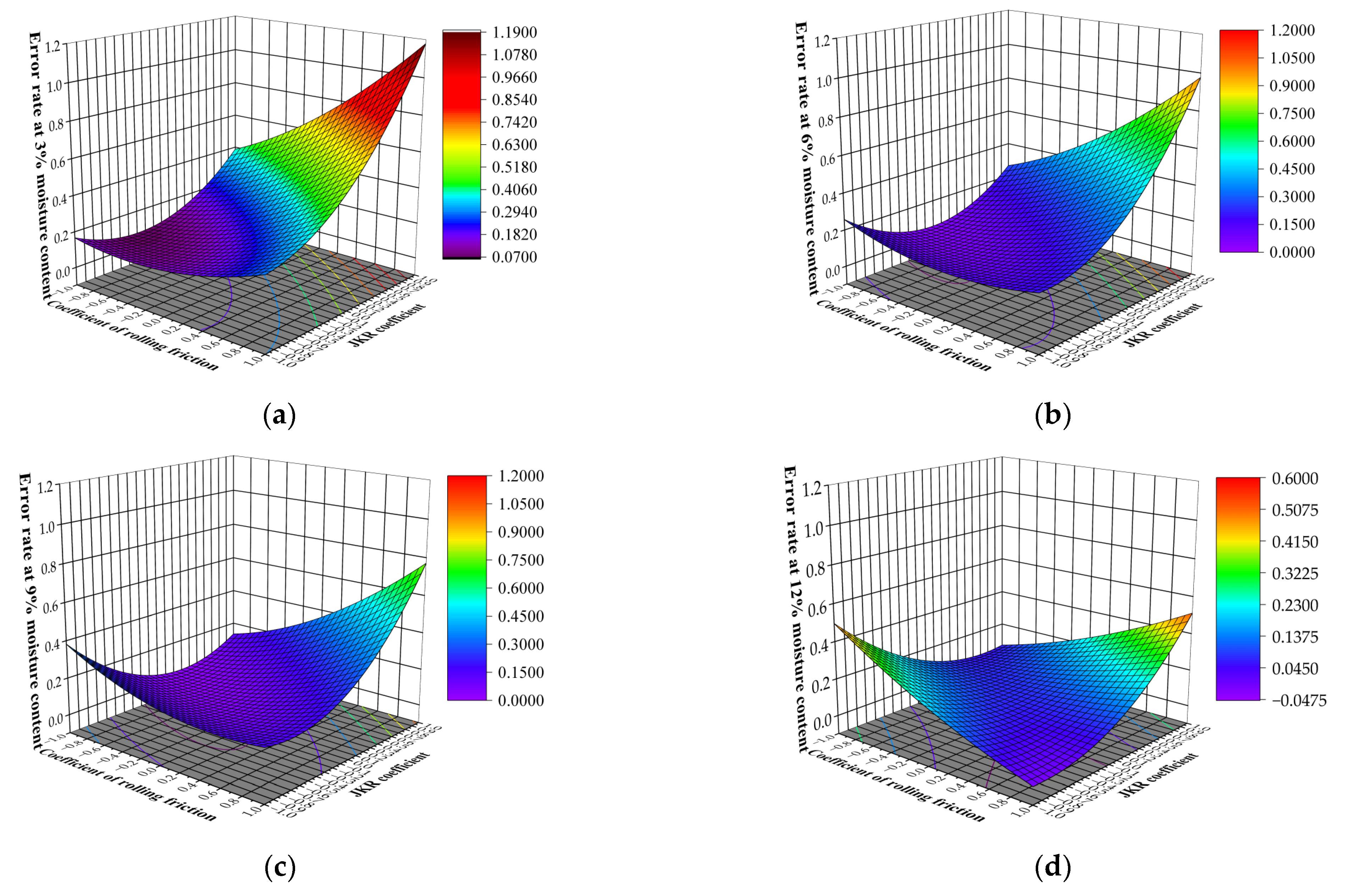
3.3.4. Box–Behnken Test Design and Analysis of Results
3.4. Discrete Element Contact Parameter Calibration Validation
3.5. Soil Direct Shear Test Discrete Element Simulation
3.6. Discrete Element Simulation of the Soil Lateral Limitless Compressive Test
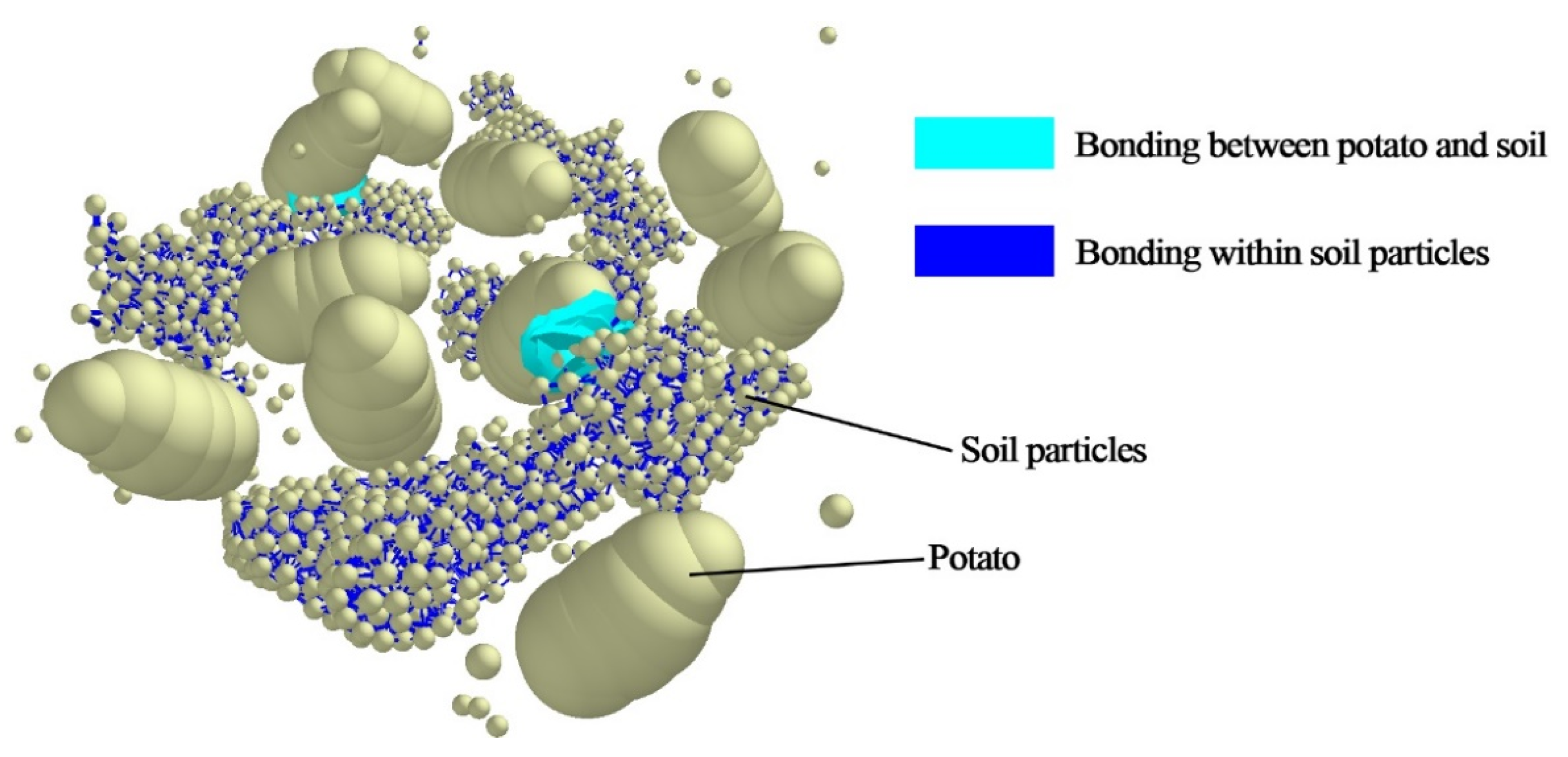
3.7. Discrete Meta-Simulation of Potato–Soil Mixtures
4. Discussion
4.1. Calibration of Soil Contact Parameters
4.2. Calibration of Soil Bonding Parameters
5. Conclusions
- Based on EDEM 2020 software, the recovery coefficient, static friction coefficient, rolling friction coefficient, and JKR surface energy factor between soil particles and between soil and 65 Mn steel were selected as the test factors at 3, 6, 9, and 12%, the rest angle error rate of the physical and simulation tests was used as the evaluation index, and the Plackett–Burman test was used to screen the significant factors: JKR surface energy, interparticle recovery coefficient, and interparticle rolling friction factor of soil.
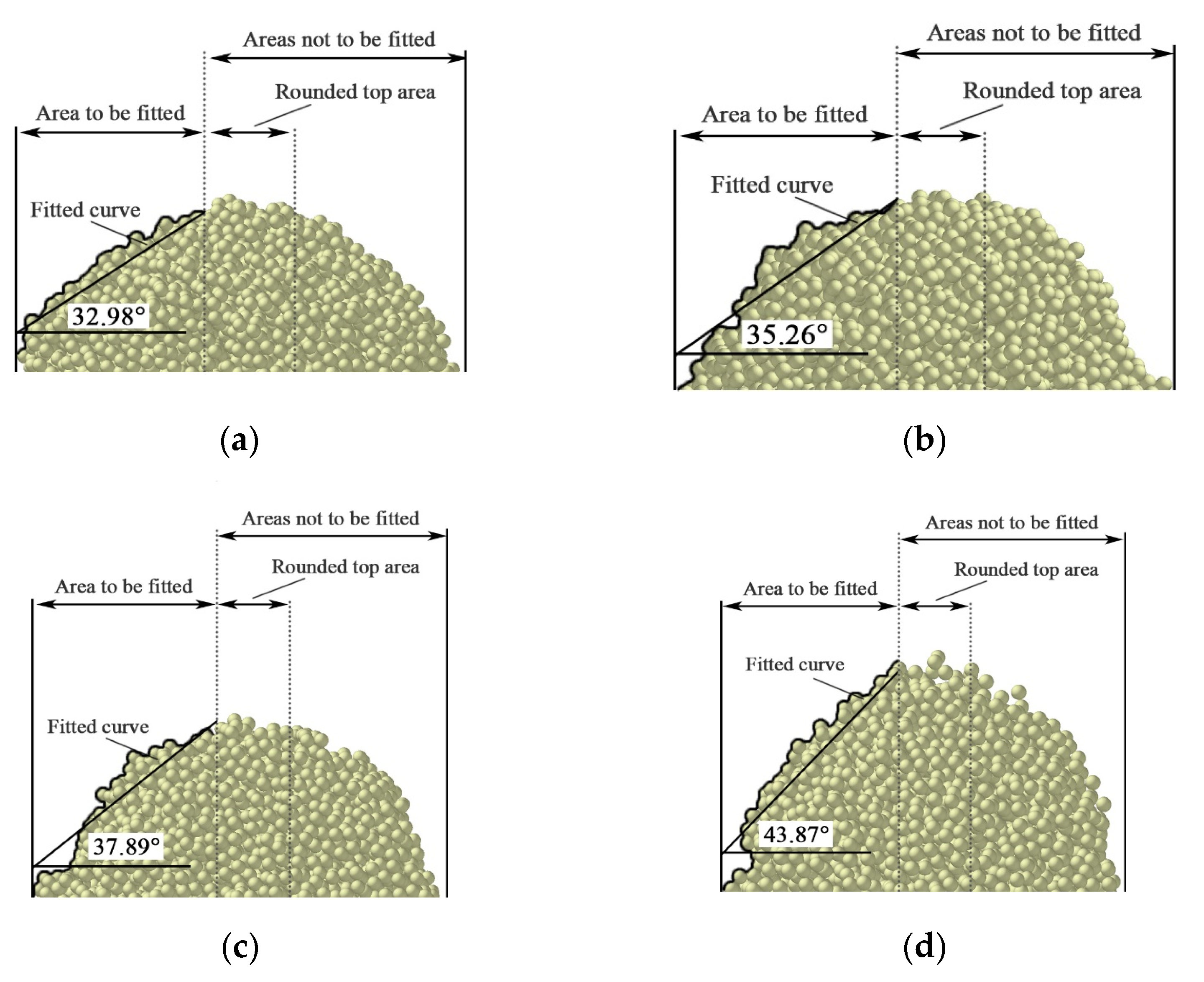
- A single simulation of multiple Box–Behnken response surface analysis was performed to optimize the model. The JKR surface energy coefficients were obtained as 0.3558, 0.356, 0.363, and 0.371 for soil with moisture contents of 3, 6, 9, and 12%, respectively, and the interparticle rolling friction was 0.188, 0.15, 0.193, and 0.338, respectively. The simulation was carried out using the above parameters, and the simulation rest angle was obtained as 32.98°, 35.26°, 37.63°, and 41.80°, respectively, with a maximum error rate of 4.72%.
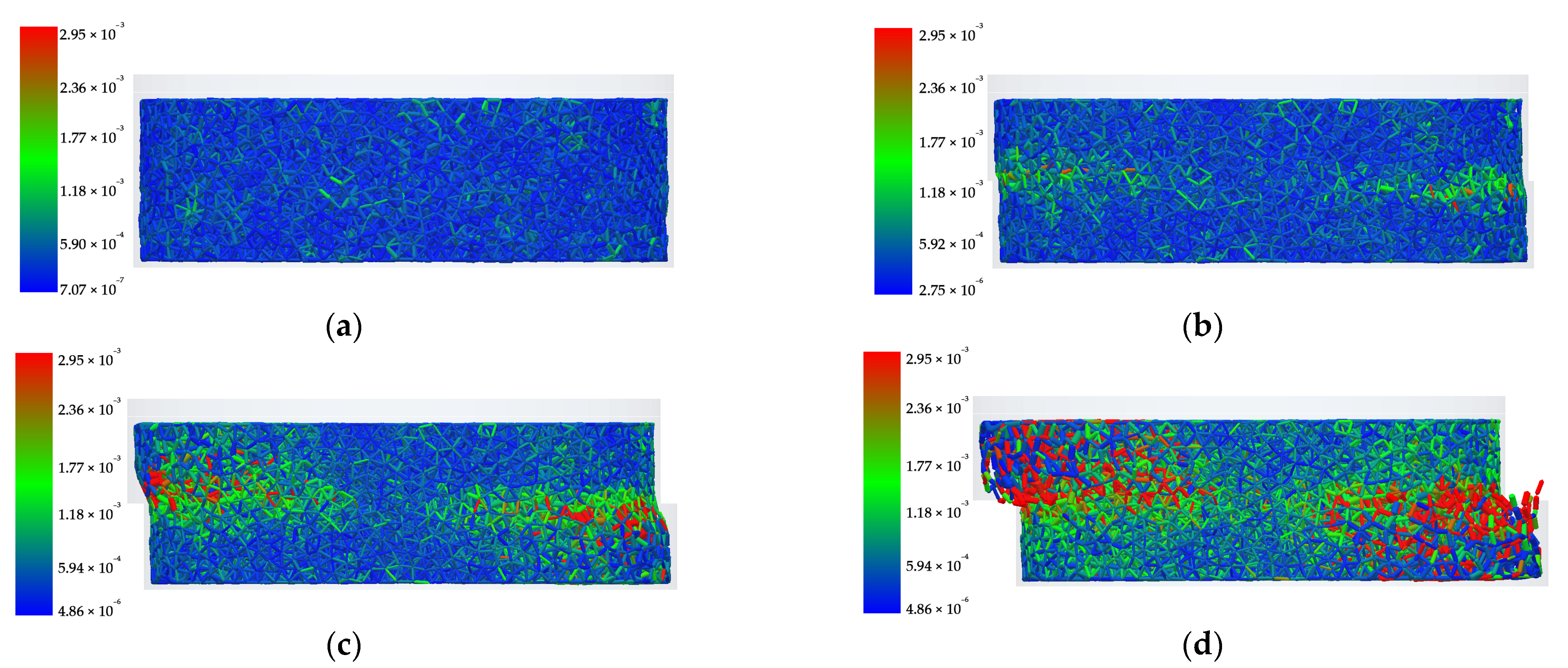
- The parameters required for the bonding key of the EDEM simulation were obtained using direct shear and lateral limitless compression tests. The EDEM simulation approach combining direct shear and unconfined compression tests was proposed to obtain the force distribution images of bonds in the shear and compression processes. The error rates of the simulation and physical tests for the direct shear test were distributed in the range of 3.71–6.53%, and those of simulation and physical tests for the unconfined compression test were distributed in the range of 0.6–8.07%, which were within tolerable limits, and the overall trend was consistent.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, Z.; Li, H.; Su, G. Development of potato harvester with buffer type potato-impurity separation sieve. Trans. Chin. Soc. Agric. Eng. 2019, 35, 1–11. [Google Scholar]
- Ding, W.; Zhu, J.; Chen, W. Simulation calibration of highland barley contact parameters based on EDEM. J. Chin. Agric. Mech. 2021, 42, 114–121. [Google Scholar] [CrossRef]
- Li, X.; Du, Y.; Liu, L.; Zhang, Y.; Guo, D. Parameter calibration of corncob based on DEM. Adv. Powder Technol. 2022, 33, 103699. [Google Scholar] [CrossRef]
- Coetzee, C.J.; Els, D.N.J.; Dymond, G.F. Discrete element parameter calibration and the modelling of dragline bucket filling. J. Terramechanics 2009, 47, 33–44. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Liu, D.; Xie, F.; Ashwehmbom, L.G.; Tang, Z.Z. Calibration of discrete element parameters and experimental verification for modelling subsurface soils. Biosyst. Eng. 2021, 212, 215–227. [Google Scholar] [CrossRef]
- Wen, X.; Fang, F.; Liu, Y. Research on stacking angle of coal particles and parameter calibration on EDEM. China Saf. Sci. J. 2020, 30, 114–119. [Google Scholar] [CrossRef]
- Wang, L.; Fan, S.; Chen, H. Calibration of contact parameters for pig manure based on EDEM. Trans. Chin. Soc. Agric. Eng. 2020, 36, 95–102. [Google Scholar]
- Rui, Z.; Dianlei, H.; Qiaoli, J.; Yuan, H.; Jianqiao, L. Calibration methods of sandy soil parameters in simulation of discrete element method. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2017, 48, 49–56. [Google Scholar] [CrossRef]
- Fang, H. Research on the straw-soil-rotary blade interaction using discrete element method. Master’s Thesis, Nanjing Agriculture University, Nanjing, China, 2016. [Google Scholar]
- Ding, Q.; Ren, J.; Adam, B.E.; Zhao, J.; Ge, S.; Li, Y. DEM analysis of subsoiling process in wet clayey paddy soil. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2017, 48, 38–48. [Google Scholar] [CrossRef]
- Ajmal, M.; Roessler, T.; Richter, C.; Katterfeld, A. Calibration of cohesive DEM parameters under rapid flow conditions and low consolidation stresses. Powder Technol. 2020, 374, 22–32. [Google Scholar] [CrossRef]
- Yu, W.; Liu, R.; Yang, W. Parameter Calibration of Pig Manure with Discrete Element Method Based on JKR Contact Model. AgriEngineering 2020, 2, 367–377. [Google Scholar] [CrossRef]
- Xing, J.; Zhang, R.; Wu, P. Parameter calibration of discrete element simulation model for latosol particles in hot areas of Hainan Province. Trans. Chin. Soc. Agric. Eng. 2020, 36, 158–166. [Google Scholar]
- Liu, Y.; Zhao, J.; Qi, H. Parameters calibration of discrete element of clay soil in yam planting area. J. Hebei Agric. Univ. 2021, 44, 99–105. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, M.; Liu, Y.; Gao, K.; Su, B.; Qi, Y. Measurement and calibration of DEM parameters of lunar soil simulant. Acta Astronaut. 2022, 191, 169–177. [Google Scholar] [CrossRef]
- Jba, A.; Ma, A.; Ying, C.B.; Zz, B. Calibration of discrete element parameters of crop residues and their interfaces with soil. Comput. Electron. Agric. 2021, 188, 106349. [Google Scholar]
- Aikins, K.A.; Ucgul, M.; Barr, J.B.; Jensen, T.A.; Antille, D.L.; Desbiolles, J.M. Determination of discrete element model parameters for a cohesive soil and validation through narrow point opener performance analysis. Soil Tillage Res. 2021, 213, 105123. [Google Scholar] [CrossRef]
- Wei, Z.; Su, G.; Li, X. Parameter Optimization and Test of Potato Harvester Wavy Sieve Based on EDEM. Ransactions Chin. Soc. Agric. Mach. 2020, 51, 109–122. [Google Scholar]
- Song, Z.; Li, H.; Yan, Y. Calibration Method of Contact Characteristic Parameters of Soil inMulberry Field Based on Unequal-diameter Particles DEM Theory. Trans. Chin. Soc. Agric. Mach. 2022, 53, 21–33. [Google Scholar]
- Wang, Y. Soil Wind Erosion Characteristics and Wind Erosion Estimation in Dry Farming Areas of Wuchuan County. Master’s Thesis, Inner Mongolia Agriculture University, Hohhot, China, 2019. [Google Scholar]
- Chinese Academy of Inspection and Quarantine; China Chemical Economic and Technological Development Center. Chemicals-Test method for particlesize analysis of soils. In General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China; Standardization Administration of the People’s Republic of China: Beijing, China, 2011; Volume GB/T 27845-2011, p. 20. [Google Scholar]
- China Renewable Energy Engineering Institute; Nanjing Hydraulic R lesearch Institute. Standard for geotechnical testing method. In Ministry of Housing and Urban-Rural Development of the People’s Republic of China; State Administration for Market Regulation: Beijing, China, 2019; Volume GB/T 50123-2019, p. 717. [Google Scholar]
- Xiao, Z.; Tian, H.; Zhang, T. Parameter calibration of discrete element numerical simulation for the dedusting sieve of corn straw feed. J. China Agric. Univ. 2022, 27, 172–183. [Google Scholar]
- Xie, F.; Wu, Z.; Wang, X. Calibration of discrete element parameters of soils based on unconfined compressive strength test. Trans. Chin. Soc. Agric. Eng. 2020, 36, 39–47. [Google Scholar]
- Li, G.; Gu, K.; Wang, X. An experimental study of the unconfined compressive strength characteristics of the expansive soil with cracks. Hydrogeol. Eng. Geol. 2022, 49, 62–70. [Google Scholar] [CrossRef]
- Yang, W.; Liu, H.; Xie, H. Mesoscopic Parameter Calibration Method of Accumulated Debris Materials Based on Direct Shear Test and Simulation Verification. Adv. Eng. Sci. 2022, 54, 46–54. [Google Scholar] [CrossRef]
- Sun, Y.; Shao, L.; Fan, Z. Experimental research on Poisson’ s ratio of sandy soil. Rock Soil Mech. 2009, 30, 63–68. [Google Scholar] [CrossRef]
- Research Institute of Forestry Chinese Academy of Forestry-Forest Soil Laboratory. Determination of soil particle density in forest soil; forestry industry standards; Standardization Administration of the People’s Republic of China: Beijing, China, 1999; Volume LY/T 1224-1999, p. 3P, A4. [Google Scholar]
- Modenese, C. Numerical Study of the Mechanical Properties of Lunar Soil by the Discrete Element Method. Ph.D. Thesis, University of Oxford, Oxford, UK, 2013. [Google Scholar]
- Johnson, K.L.; Kendall, K.; Roberts, A. Surface Energy and the Contact of Elastic Solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1971, 324, 301–313. [Google Scholar]
- Xia, R.; Li, B.; Wang, X.; Li, T.; Yang, Z. Measurement and calibration of the discrete element parameters of wet bulk coal—ScienceDirect. Measurement 2019, 142, 84–95. [Google Scholar] [CrossRef]
- Li, Y.; Li, F.; Xu, X.; Shen, C.; Meng, K.; Chen, J.; Chang, D. Parameter calibration of wheat flour for discrete element method simulation based on particle scaling. Trans. Chin. Soc. Agric. Eng. 2019, 35, 320–327. [Google Scholar]
- Roessler, T.; Katterfeld, A. DEM parameter calibration of cohesive bulk materials using a simple angle of repose test. Particuology 2019, 45, 105–115. [Google Scholar] [CrossRef]
- Zhang, S.; Tekeste, M.Z.; Li, Y.; Gaul, A.; Liao, J. Scaled-up rice grain modelling for DEM calibration and the validation of hopper flow. Biosyst. Eng. 2020, 194, 196–212. [Google Scholar] [CrossRef]
- Liang, R.; Chen, X.; Jiang, P.; Zhang, B.; Meng, H.; Peng, X.; Kan, Z. Calibration of the simulation parameters of the particulate materials in film mixed materials. Int. J. Agric. Biol. Eng. 2020, 13, 29–36. [Google Scholar] [CrossRef]
- Nguyen, N.K.; Borkowski, J.J. New 3-level response surface designs constructed from incomplete block designs. J. Stat. Plan. Inference 2008, 138, 294–305. [Google Scholar] [CrossRef]
- Maba, B.; Res, A.; Epo, A.; Lsv, A.; Lae, A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar]
- Li, H.; van den Driesche, S.; Bunge, F.; Yang, B.; Vellekoop, M.J. Optimization of on-chip bacterial culture conditions using the Box-Behnken design response surface methodology for faster drug susceptibility screening. Talanta 2019, 194, 627–633. [Google Scholar] [CrossRef] [PubMed]
- Dop, A.; Pac, B. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar]
- Wang, M.; Feng, Y.T.; Zhao, T.T.; Wang, Y. Modelling of sand production using a mesoscopic bonded particle lattice Boltzmann method. Eng. Comput. 2019, 36, 691–706. [Google Scholar] [CrossRef] [Green Version]
- Quist, J.; Evertsson, C.M. Cone crusher modelling and simulation using DEM. Miner. Eng. 2015, 85, 92–105. [Google Scholar] [CrossRef]
- Manso, J.; Marcelino, J.; Caldeira, L. Effect of the clump size for bonded particle model on the uniaxial and tensile strength ratio of rock. Int. J. Rock Mech. Min. Sci. 2019, 114, 131–140. [Google Scholar] [CrossRef]
- Jiang, Y.; Luan, H.; Wang, Y.; Wang, G.; Wang, P. Study on Macro–Meso Failure Mechanism of Pre-fractured Rock Specimens Under Uniaxial Compression. Geotech. Geol. Eng. 2018, 36, 3211–3222. [Google Scholar] [CrossRef]
- Johansson, M.; Quist, J.; Evertsson, M.; Hulthén, E. Cone crusher performance evaluation using DEM simulations and laboratory experiments for model validation. Miner. Eng. 2017, 103, 93–101. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, G.; Xue, D. An approach to calibration of BPM bonding parameters for iron ore. Powder Technol. 2020, 381, 245–254. [Google Scholar] [CrossRef]


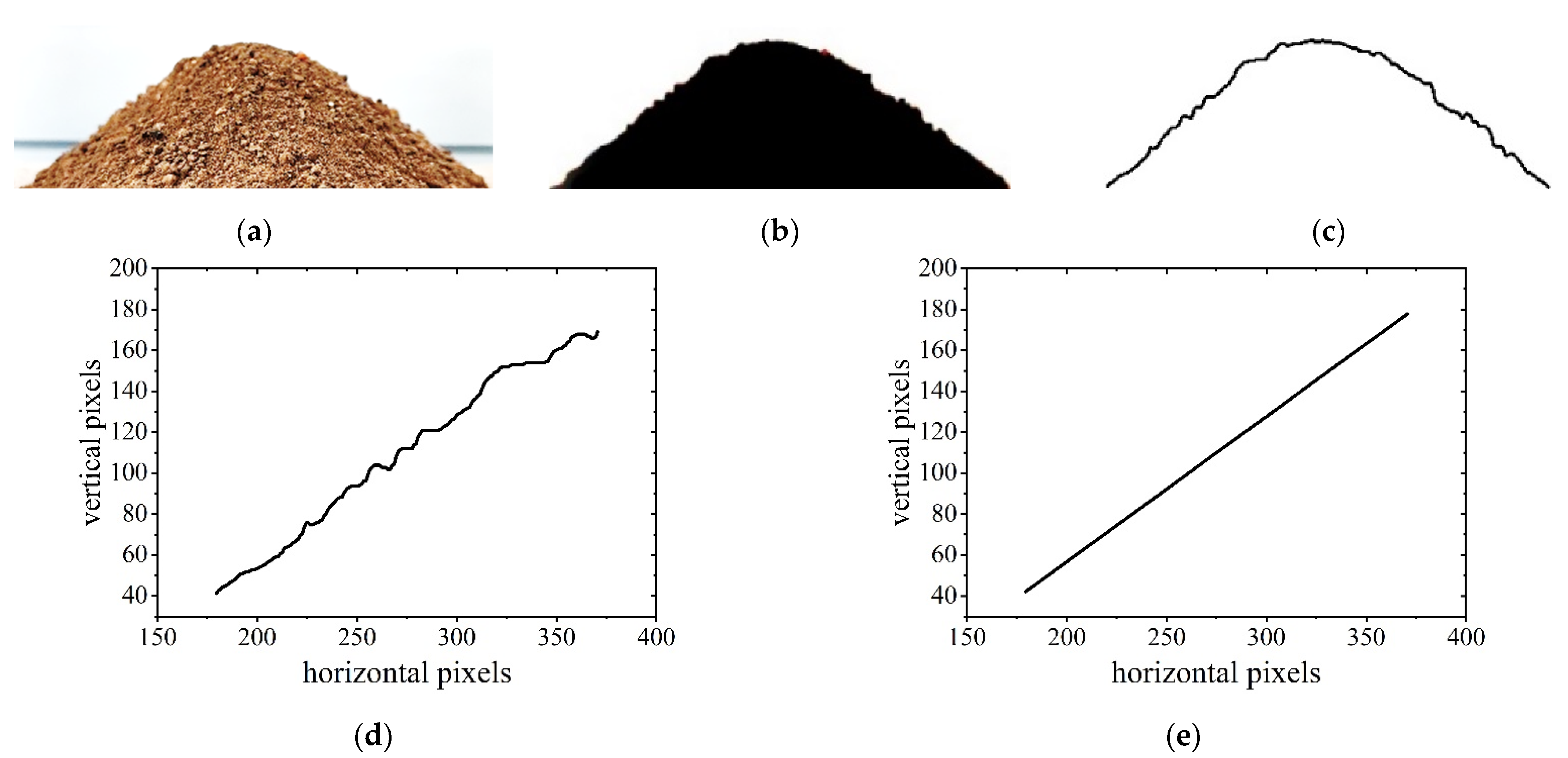


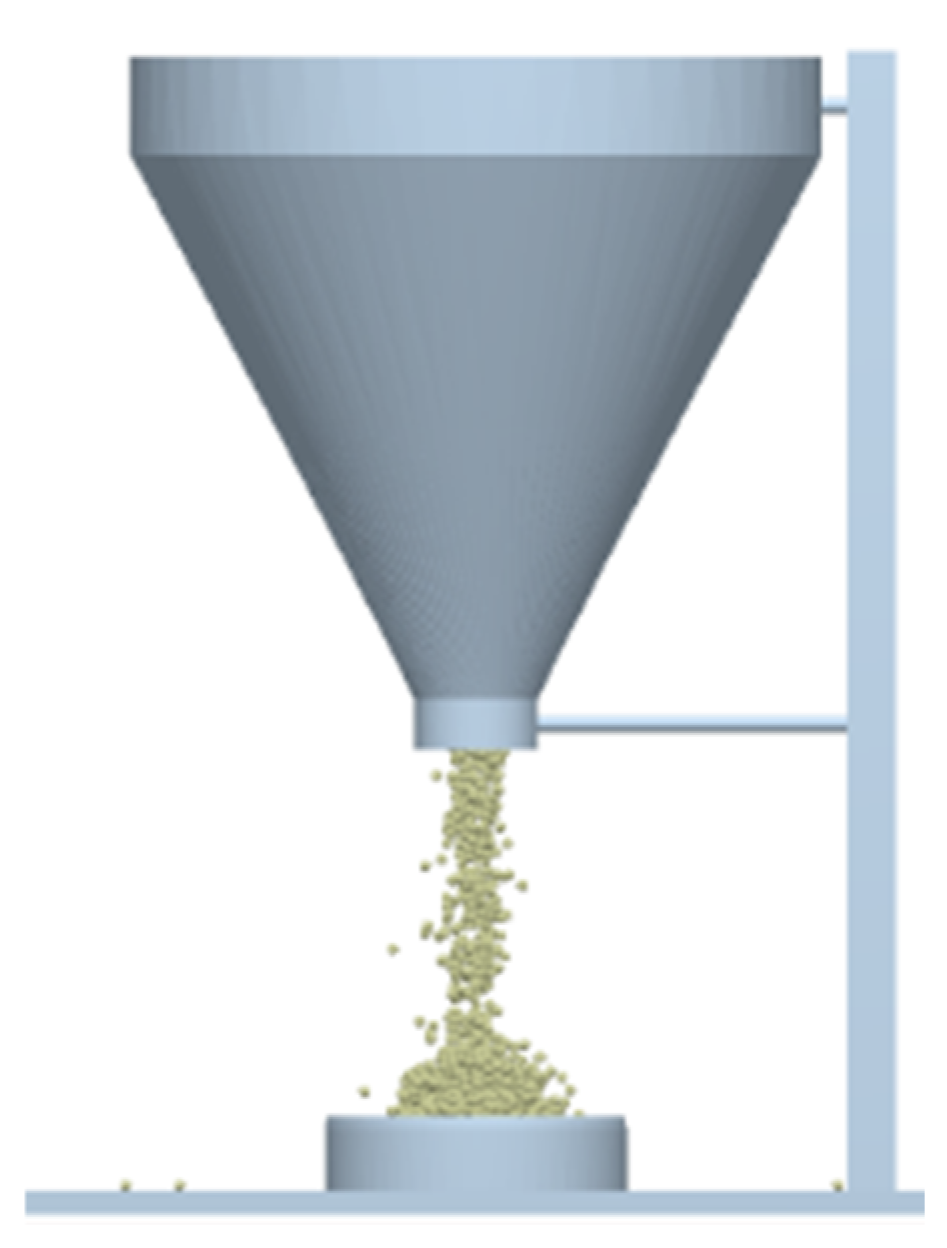
| Water Content | Static Friction Coefficient (μ1) | Rolling Friction Coefficient (μ2) | Resting Angle(°) | ||
|---|---|---|---|---|---|
| Min | Max | Min | Max | ||
| 3% | 0.6400 | 0.7813 | 0.1663 | 0.2543 | 32.76 |
| 6% | 0.7265 | 0.8098 | 0.1877 | 0.2095 | 35.53 |
| 9% | 0.7813 | 0.8391 | 0.2543 | 0.3249 | 37.89 |
| 12% | 0.9014 | 0.9325 | 0.3265 | 0.3839 | 43.87 |
| Water Content (%) | Solidity (MPa) | Cross-Sectional Area (mm2) | Direct Shear Displacement (mm) | Cohesion C (α = 0) (MPa) | Internal Friction Angle φ (°) | Tangential Stiffness per Unit Area N (m·m2) |
|---|---|---|---|---|---|---|
| 6 | 0.34 | 3000 | 5 | 0.0165 | 32.5 | 3.3000 × 106 |
| 0.945 | 0.0282 | 38.4 | 5.6480 × 106 | |||
| 1.55 | 0.0587 | 32.3 | 1.1734 × 107 | |||
| 2.155 | 0.0563 | 40.3 | 1.1262 × 107 | |||
| 2.76 | 0.0626 | 37.3 | 1.2514 × 107 | |||
| 3 | 1.55 | 0.0866 | 21.5 | 1.7314 × 107 | ||
| 9 | 0.0575 | 35.4 | 1.1490 × 107 | |||
| 12 | 0.0818 | 19.2 | 1.6360 × 107 |
| Water Content (%) | Solidity (MPa) | Load (N) | Section Correction Radius (mm) | Corrected Area (mm2) | Axial Displacement (mm) | Compressive Strength without Lateral Limit (MPa) | Normal Stiffness per Unit Area N (m·m2) |
|---|---|---|---|---|---|---|---|
| 6 | 0.34 | 298.6 | 31.83 | 3182.9011 | 2.87 | 0.0943 | 3.2688 × 107 |
| 0.945 | 856 | 33.56 | 3538.2929 | 1.99 | 0.2431 | 1.2157 × 108 | |
| 1.55 | 895.6 | 33.25 | 3473.2270 | 2.41 | 0.2591 | 1.0700 × 108 | |
| 2.155 | 916.2 | 31.21 | 3060.1126 | 2.96 | 0.3006 | 1.0115 × 108 | |
| 2.76 | 1060 | 33.75 | 3578.4704 | 2.32 | 0.2962 | 1.2773 × 108 | |
| 3 | 1.55 | 34.4 | 28.92 | 2627.5225 | 1.14 | 0.0114 | 1.1484 × 107 |
| 9 | 994 | 33.79 | 3586.9577 | 1.02 | 0.2771 | 2.7168 × 108 | |
| 12 | 1043 | 32.14 | 3245.2011 | 2.73 | 0.3205 | 1.1775 × 108 |
| Parameters | Materials | |
|---|---|---|
| Soil Particles | Steel | |
| Poisson’s ratio | 0.2 | 0.3 |
| Shear modulus (MPa) | 79,000 | |
| Modulus of elasticity (MPa) | 13.5 | |
| Density (kg/m3) | 1380 | 7865 |
| Parameter | Code | Low Level(−1) | High Level (+1) | Level Selection Source |
|---|---|---|---|---|
| Soil–65 Mn steel recovery factor | 0.2 | 0.5 | [19] | |
| Soil–65 Mn steel static friction coefficient | 0.5 | 1.2 | [19] | |
| Soil–65 Mn steel rolling friction coefficient | 0.05 | 0.4 | [19] | |
| Soil–soil recovery factor | 0.15 | 0.75 | [20] | |
| Soil–soil static friction coefficient | 0.6 | 1.0 | Friction coefficient determination | |
| Soil–soil rolling friction coefficient | 0.1 | 0.4 | Friction coefficient determination | |
| JKR water content model coefficient | 0 | 0.75 | [24] |
| No. | Factors | Rest Angle (°) | ||||||
|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | ||
| 1 | 1 | −1 | 1 | −1 | −1 | −1 | 1 | 40.07 |
| 2 | 1 | −1 | 1 | 1 | −1 | 1 | −1 | 18.63 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 32.47 |
| 4 | −1 | 1 | 1 | 1 | −1 | 1 | 1 | 46.20 |
| 5 | −1 | 1 | 1 | −1 | 1 | −1 | −1 | 14.00 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 36.37 |
| 7 | 1 | 1 | 1 | −1 | 1 | 1 | −1 | 32.96 |
| 8 | −1 | −1 | −1 | 1 | 1 | 1 | −1 | 25.97 |
| 9 | −1 | −1 | 1 | 1 | 1 | −1 | 1 | 22.16 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 41.97 |
| 11 | 1 | −1 | −1 | −1 | 1 | 1 | 1 | 64.70 |
| 12 | 1 | 1 | −1 | 1 | −1 | −1 | −1 | 4.69 |
| 13 | −1 | 1 | −1 | −1 | −1 | 1 | 1 | 72.16 |
| 14 | 1 | 1 | −1 | 1 | 1 | −1 | 1 | 21.72 |
| 15 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 9.15 |
| Source | DF | Standardized Effect | MS | Impact Rate | p-Value | Significance |
|---|---|---|---|---|---|---|
| Models | 8 | 613.49 | 96.66% | <0.001 | *** | |
| X1 | 1 | 0.3722 | 3.91 | 0.08% | 0.723 | |
| X2 | 1 | 0.6005 | 10.18 | 0.20% | 0.57 | |
| X3 | 1 | 1.3233 | 49.44 | 0.97% | 0.234 | |
| X4 | 1 | 5.0889 | 731.13 | 14.40% | 0.007 | ** |
| X5 | 1 | 0.5114 | 7.38 | 0.15% | 0.627 | |
| X6 | 1 | 8.0859 | 1845.89 | 36.36% | <0.001 | *** |
| X7 | 1 | 8.7801 | 2176.4 | 42.87% | <0.001 | *** |
| Bend | 1 | 83.59 | 1.65% | 0.136 | ||
| Error | 6 | 28.23 | 3.34% | |||
| Total | 14 | 100.00% |
| No | Factors | Resting Angle (°) | Error Rate (°) | |||||
|---|---|---|---|---|---|---|---|---|
| X4 | X6 | X7 | 3% | 6% | 9% | 12% | ||
| 1 | 0.15 | 0.10 | 0 | 15.22 | 0.5354 | 0.5716 | 0.5984 | 0.6530 |
| 2 | 0.25 | 0.15 | 0.125 | 31.72 | 0.0317 | 0.1072 | 0.1630 | 0.2769 |
| 3 | 0.35 | 0.20 | 0.250 | 41.76 | 0.2748 | 0.1754 | 0.1020 | 0.0480 |
| 4 | 0.45 | 0.25 | 0.375 | 39.96 | 0.2198 | 0.1247 | 0.0545 | 0.0890 |
| 5 | 0.55 | 0.30 | 0.500 | 42.61 | 0.3007 | 0.1993 | 0.1244 | 0.0286 |
| 6 | 0.65 | 0.35 | 0.625 | 45.26 | 0.3816 | 0.2739 | 0.1944 | 0.0318 |
| 7 | 0.75 | 0.40 | 0.750 | 68.95 | 1.1047 | 0.9407 | 0.8196 | 0.5718 |
| No. | Factors | Rest Angle (°) | Error Rate (°) | |||||
|---|---|---|---|---|---|---|---|---|
| X4 | X6 | X7 | 3% | 6% | 9% | 12% | ||
| 1 | 0(0.45) | −1 (0.15) | 1 (0.625) | 42.65 | 0.3017 | 0.2003 | 0.1255 | 0.0279 |
| 2 | −1 (0.25) | 1 (0.35) | 0 (0.375) | 51.36 | 0.5678 | 0.4456 | 0.3556 | 0.1708 |
| 3 | 0 | 1 | 1 | 68.57 | 1.0932 | 0.9300 | 0.8098 | 0.5631 |
| 4 | 0 | 0 (0.25) | 0 | 39.01 | 0.1907 | 0.0979 | 0.0295 | 0.1108 |
| 5 | 0 | −1 | −1 (0.125) | 24.28 | 0.2590 | 0.3168 | 0.3593 | 0.4467 |
| 6 | 0 | 1 | −1 | 45.37 | 0.3849 | 0.2769 | 0.1974 | 0.0342 |
| 7 | 1 (0.65) | −1 | 0 | 33.50 | 0.0227 | 0.0570 | 0.1157 | 0.2363 |
| 8 | 1 | 1 | 0 | 47.39 | 0.4465 | 0.3337 | 0.2506 | 0.0802 |
| 9 | −1 | 0 | −1 | 32.50 | 0.0080 | 0.0854 | 0.1423 | 0.2592 |
| 10 | 1 | 0 | −1 | 33.06 | 0.0093 | 0.0694 | 0.1274 | 0.2463 |
| 11 | 0 | 0 | 0 | 41.67 | 0.2720 | 0.1728 | 0.0997 | 0.0502 |
| 12 | 1 | 0 | 1 | 55.43 | 0.6919 | 0.5600 | 0.4628 | 0.2634 |
| 13 | −1 | 0 | 1 | 59.33 | 0.8110 | 0.6698 | 0.5658 | 0.3523 |
| 14 | −1 | −1 | 0 | 34.53 | 0.0540 | 0.0282 | 0.0887 | 0.2129 |
| Source | 3% Moisture Content | 6% Moisture Content | 9% Moisture Content | 12% Moisture Content | ||||
|---|---|---|---|---|---|---|---|---|
| p-Value | Significance | p-Value | Significance | p-Value | Significance | p-Value | Significance | |
| Models | 0.0092 | ** | 0.006 | ** | 0.0036 | ** | 0.0065 | ** |
| X4 | 0.4593 | 0.4435 | 0.3511 | 0.3246 | ||||
| X6 | 0.0027 | ** | 0.0027 | ** | 0.0047 | ** | 0.6462 | |
| X7 | 0.0012 | ** | 0.0014 | ** | 0.0019 | ** | 0.2138 | |
| X4 × X6 | 0.7215 | 0.4642 | 0.3723 | 0.3452 | ||||
| X4 × X7 | 0.6353 | 0.62 | 0.5421 | 0.5182 | ||||
| X6 × X7 | 0.0385 | ** | 0.0075 | ** | 0.0015 | ** | 0.0003 | *** |
| X42 | 0.4837 | 0.9241 | 0.2809 | 0.1086 | ||||
| X62 | 0.2402 | 0.1431 | 0.0489 | ** | 0.1895 | |||
| X72 | 0.0281 | ** | 0.0061 | ** | 0.0018 | ** | 0.0034 | ** |
| Lack of Fit | 0.0728 | Not significant | 0.1107 | Not significant | 0.1672 | Not significant | 0.1882 | Not significant |
| R2 | 0.9499 | 0.9583 | 0.9661 | 0.9568 | ||||
| Adeq Precision | 11.8888 | 13.2918 | 14.0464 | 11.8414 | ||||
| Parameter | 3% Moisture Content | 6% Moisture Content | 9% Moisture Content | 12% Moisture Content |
|---|---|---|---|---|
| Soil–soil recovery coefficient | 0.45 | 0.45 | 0.45 | 0.45 |
| Soil–soil rolling friction coefficient | 0.188 | 0.15 | 0.193 | 0.388 |
| JKR surface energy coefficient | 0.3558 | 0.3560 | 0.3630 | 0.371 |
| Water Content (%) | Solidity (MPa) | Cross-Sectional Area (mm2) | Direct Shear Displacement (mm) | Peak Shear Force (N) | Error Rate (%) | |
|---|---|---|---|---|---|---|
| Physical Tests | Simulation Test | |||||
| 6 | 0.34 | 3000 | 5 | 149.4 | 143.9 | 3.68 |
| 0.945 | 183.1 | 176.3 | 3.71 | |||
| 1.55 | 197.4 | 184.5 | 6.53 | |||
| 2.155 | 209.2 | 198.9 | 4.92 | |||
| 2.76 | 262.9 | 246.5 | 6.24 | |||
| 3 | 1.55 | 157.3 | 162.3 | 3.18 | ||
| 9 | 204.9 | 192.8 | 5.91 | |||
| 12 | 165.3 | 174.7 | 5.69 | |||
| Water Content (%) | Solidity (MPa) | Peak Axial Force or 15% Axial Strain Corresponding Pressure(N) | Error Rate (%) | |
|---|---|---|---|---|
| Physical Test | Simulation Test | |||
| 6 | 0.34 | 94.253634 | 101.83 | 8.04 |
| 0.945 | 243.05506 | 226.13 | 6.96 | |
| 1.55 | 259.12501 | 273.9 | 5.70 | |
| 2.155 | 300.64253 | 289.11 | 3.84 | |
| 2.76 | 296.21595 | 311.23 | 5.07 | |
| 3 | 1.55 | 11.417599 | 10.59 | 7.25 |
| 9 | 277.11506 | 299.47 | 8.07 | |
| 12 | 320.4732 | 318.555 | 0.60 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Xie, S.; Liu, F.; Guo, Y.; Liu, C.; Shang, Z.; Zhao, X. Calibration and Testing of Discrete Element Simulation Parameters for Sandy Soils in Potato Growing Areas. Appl. Sci. 2022, 12, 10125. https://doi.org/10.3390/app121910125
Li J, Xie S, Liu F, Guo Y, Liu C, Shang Z, Zhao X. Calibration and Testing of Discrete Element Simulation Parameters for Sandy Soils in Potato Growing Areas. Applied Sciences. 2022; 12(19):10125. https://doi.org/10.3390/app121910125
Chicago/Turabian StyleLi, Junru, Shengshi Xie, Fei Liu, Yaping Guo, Chenglong Liu, Zhenyu Shang, and Xuan Zhao. 2022. "Calibration and Testing of Discrete Element Simulation Parameters for Sandy Soils in Potato Growing Areas" Applied Sciences 12, no. 19: 10125. https://doi.org/10.3390/app121910125






