Effect of Grating Ruling Machine System Errors on Grating Spectral Performance
Abstract
:1. Introduction
- (1)
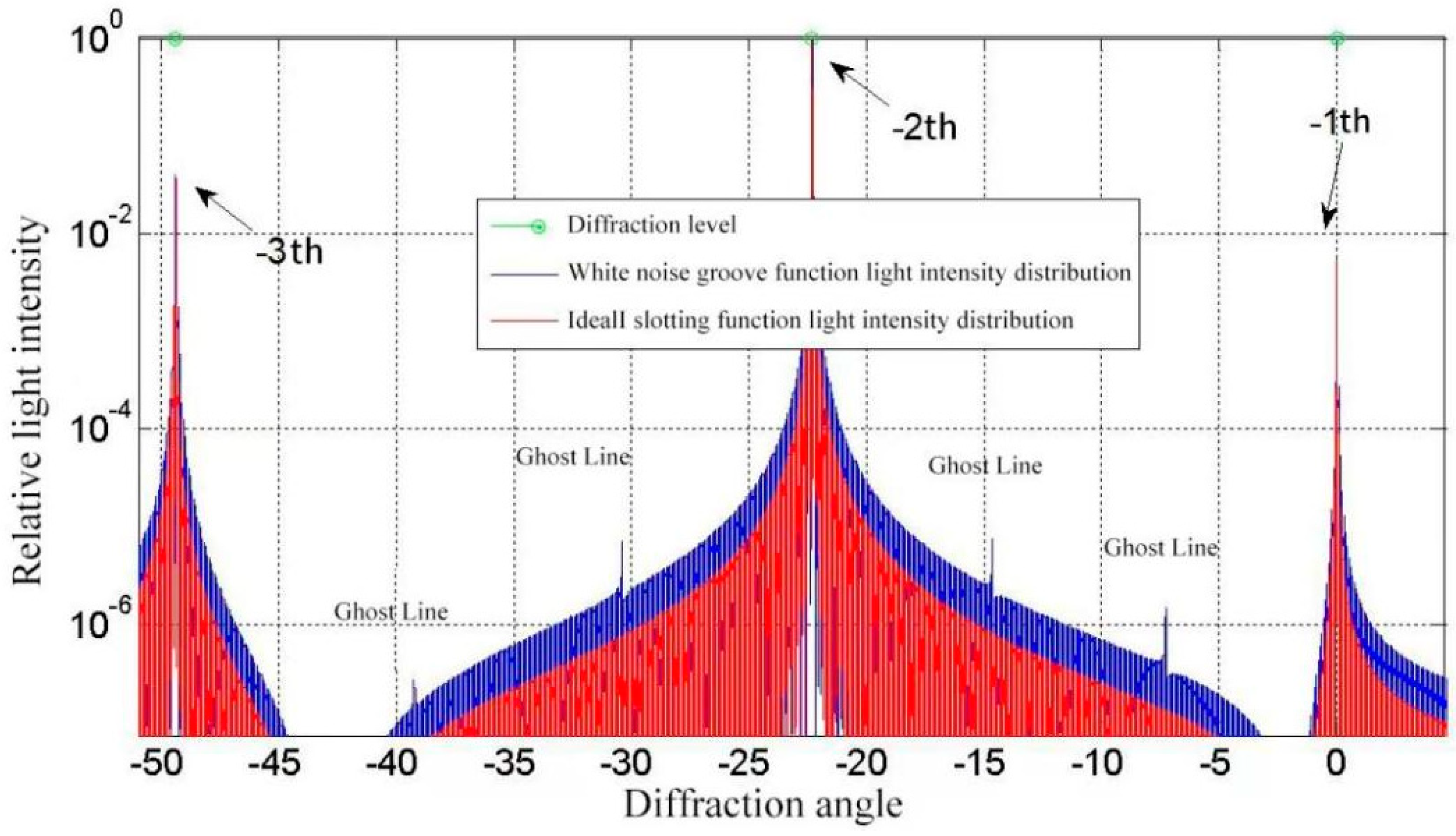
- Based on the scalar diffraction theory of grating groove function, the physical phenomenon of light source splitting after grating interference and diffraction is described, and the complex amplitude distribution of light source under the action of a diffraction grating on the diffraction screen is obtained. The complex amplitude distribution can give the position and intensity distribution information of the diffraction light and then analyze the influence of the ruling error on the grating ghost line and stray light.
- (2)
- In order to eliminate the ghost line and stray light error, which affect the grating performance in the grating ruling process, the worm gear and screw are mechanically corrected.
- (3)
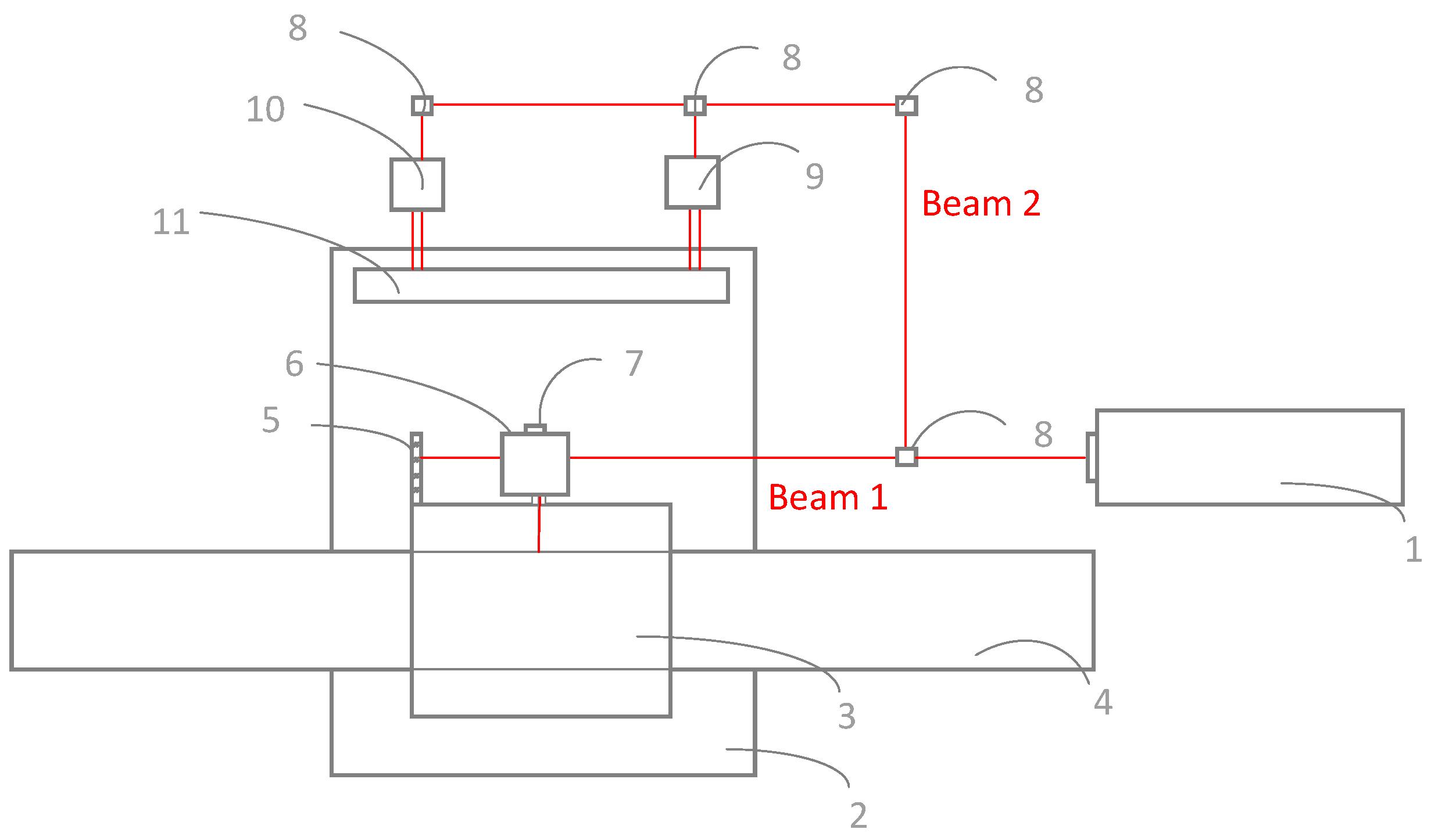
- The measurement’s optical path of random error is established. The grating ruling error is controlled by an active control system, and the error compensation system is optimized. To improve the performance index of the ruling grating.
2. Error Analysis of Grating Ruling Machine
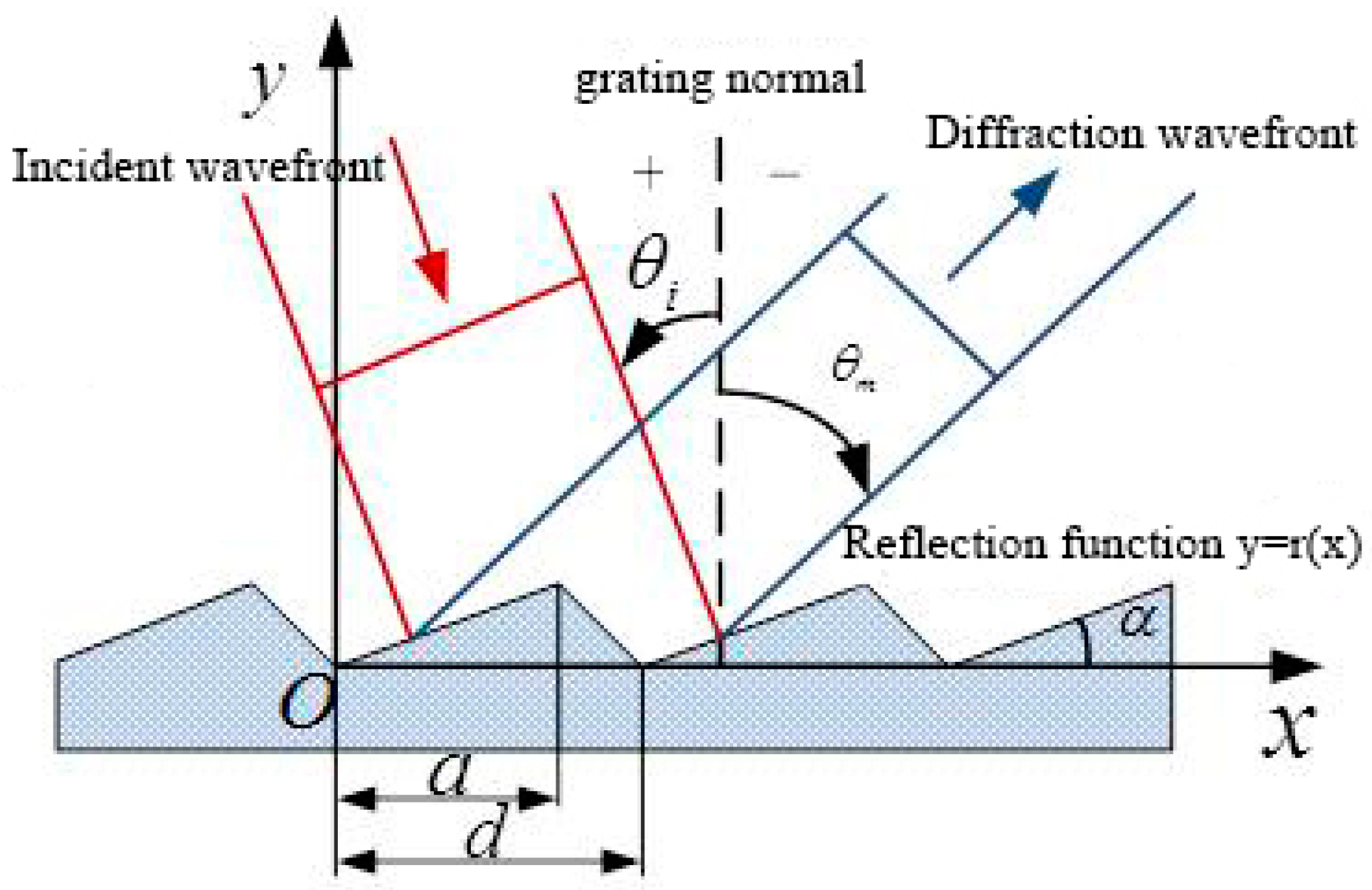
2.1. Ideal Grating Energy Distribution Solution
2.2. The Impact of Periodic Grooving Errors on Grating Performance Indicators
2.3. Effect of Screw Error on Grating Spectral Performance
2.3.1. Influence of Lead Screw Error on Grating Performance
2.3.2. Effect of Worm Gear Error on Grating Spectral Performance
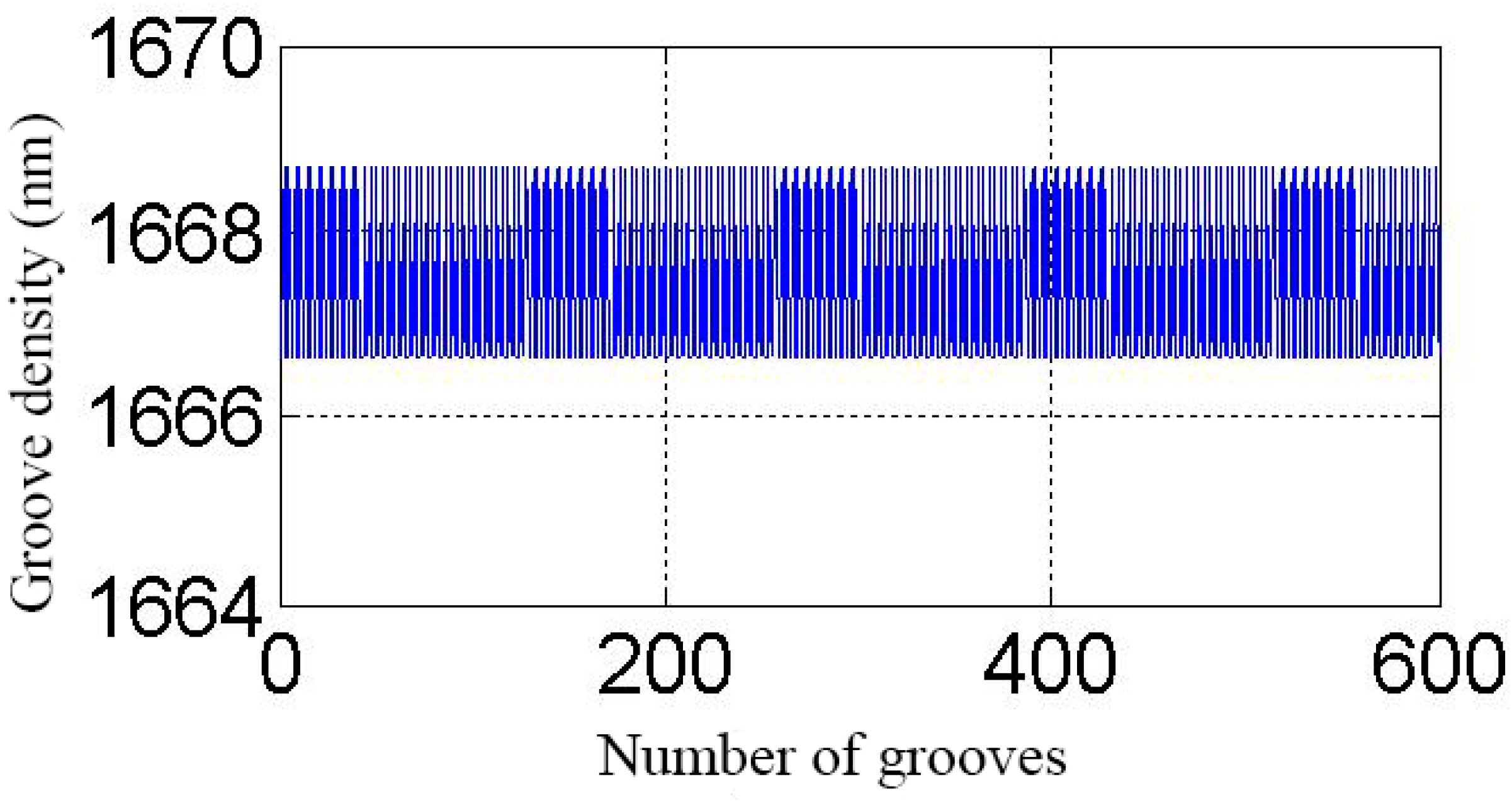
2.3.3. The Random Grooving Error on Spectral Performance
3. Grating-Groove Error Correction
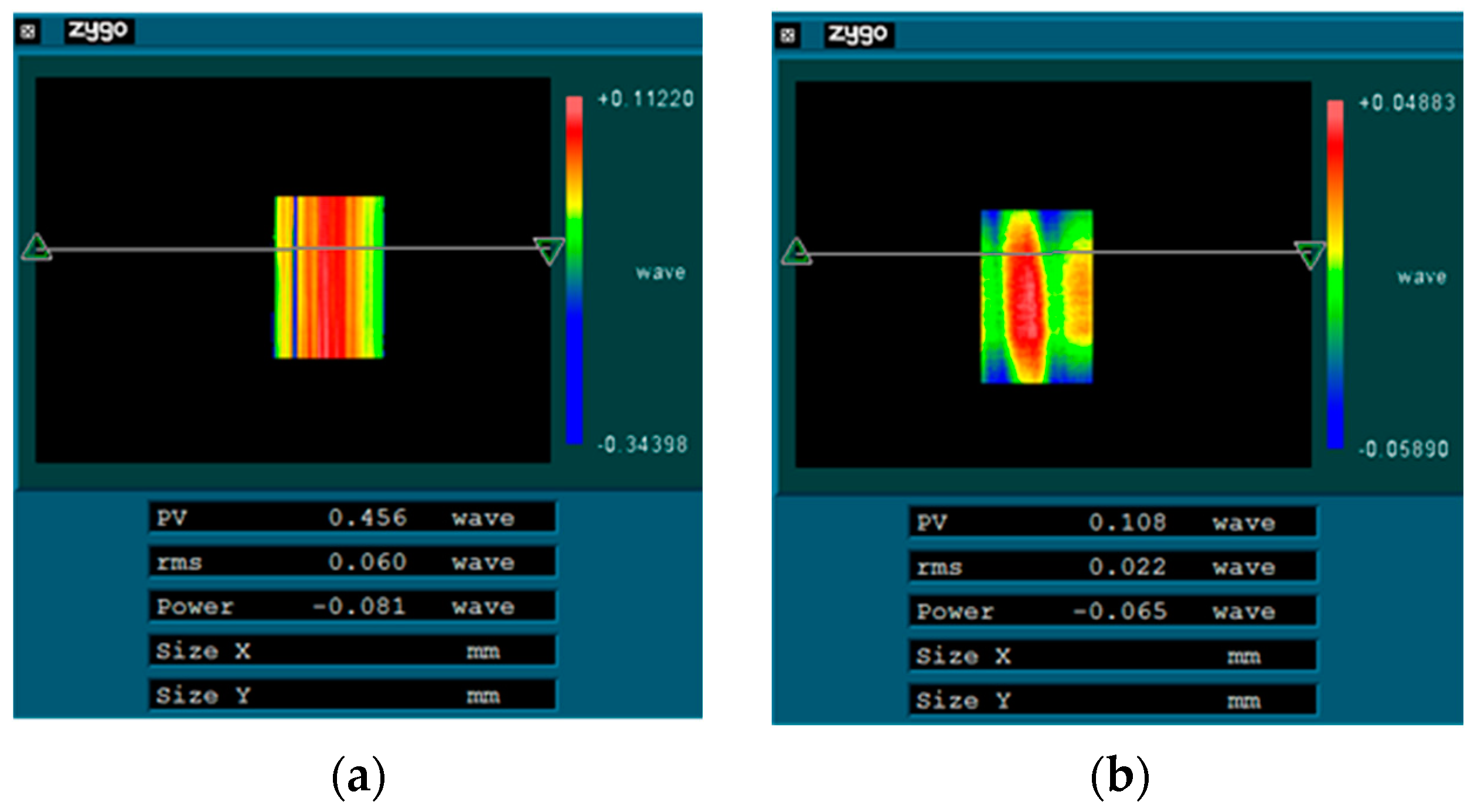
4. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Definition
| Z | Distance between grating and diffraction screen |
| U | Optical vibration distribution function |
| ϕ | Grating groove phase function |
| r | Grating groove transmission function |
| e | Light source illumination function |
| t | Diffraction hole transmission function |
| I | Optical-intensity distributed-function |
| D | Grating constant |
| a | Effective reflector width of grating groove |
| Incident angle | |
| Diffraction angle | |
| α | Blaze angle |
| m | Diffraction order |
| N | Number of grating grooves |
| d | Grating groove spacing |
| m | Grating diffraction order |
| λ | Blaze wavelength |
References
- Bao, G.; Li, P. Diffraction Grating Theory. In Maxwell’s Equations in Periodic Structures; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Chen, Z.; Özbek, A.; Rebling, J.; Zhou, Q.; Deán-Ben, X.L.; Razansky, D. Multifocal structured illumination optoacoustic microscopy. Light Sci. Appl. 2020, 9, 1473–1481. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Zhao, Y.; Zeng, L. Low-stray-light gratings fabricated with scanning exposure method based on Lloyd’s mirror for a high-contrast near-eye display in augmented reality. Appl. Opt. 2022, 61, 5626–5632. [Google Scholar] [CrossRef]
- Zhai, Z.; Cao, Q.; Gao, T.; Liu, D.; Lv, Q.; Wang, Q.; Xiong, Z.; Feng, W. Beam shaping with high energy utilization and uniformity using gradient orthogonal gratings. Appl. Opt. 2021, 60, 5104–5109. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Ruiz, M.R.; Carballar, A. Fiber Bragg Grating-Based Optical Signal Processing: Review and Survey. Appl. Sci. 2021, 11, 8189. [Google Scholar] [CrossRef]
- Li, Y.-L.; Wang, D.; Chu, F.; Lee, S.-D.; Zheng, Y.-W.; Wang, Q.-H. Tunable liquid crystal grating based holographic 3D display system with wide viewing angle and large size. Light Sci. Appl. 2022, 11, 188. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, Q.; Shen, N.; Ding, H. Experimental investigation and numerical analysis of mechanical ruling for an Aluminum-Coated Diffraction Grating. J. Manuf. Sci. Eng. 2017, 139, 021003. [Google Scholar] [CrossRef]
- Pan, Q.; Chen, X.; Zhou, J.; Zhao, Z.; Shen, Q. Design and measurement of convex grating in conical diffraction Offner spectrometer. Opt. Eng. 2019, 58, 025109. [Google Scholar] [CrossRef]
- Gao, J.; Chen, P.; Wu, L.; Yu, B.; Qian, L. A review on fabrication of blazed gratings. J. Phys. D Appl. Phys. 2021, 54, 313001. [Google Scholar] [CrossRef]
- Liu, X.-Q.; Cheng, R.; Zheng, J.-X.; Yang, S.-N.; Wang, B.-X.; Bai, B.-F.; Chen, Q.-D.; Sun, H.-B. Wear-resistant blazed gratings fabricated by etching-assisted femtosecond laser lithography. J. Lightwave Technol. 2021, 39, 4690–4694. [Google Scholar] [CrossRef]
- Heusinger, M.; Banasch, M.; Zeitner, U.D. Rowland ghost suppression in high efficiency spectrometer gratings fabricated by e-beam lithography. Opt. Express 2017, 25, 6182–6190. [Google Scholar] [CrossRef]
- Chen, H.-K.; Ni, Z.-J.; Huang, Y.-S.; Xu, B.-L.; Zhang, D.-W. Low-stray-light concave holographic gratings processed by combining the methods of photoresist hot-melting and oxygen-ion ashing. Appl. Opt. 2020, 59, 3942–3950. [Google Scholar] [CrossRef] [PubMed]
- Harrison, G.R. The Production of Diffraction Gratings I. Development of the Ruling Art. J. Opt. Soc. Am. 1949, 39, 413–426. [Google Scholar] [CrossRef]
- Harrison, G.R. Interferometric Control of Grating Ruling with Continuous Carriage Advance. J. Opt. Soc. Am. 1955, 45, 112–120. [Google Scholar] [CrossRef]
- Ding, W.; Huao, Y.; Zhang, D. Analysis of the ruling error requirements for echelle grating. Guangdian Gongcheng Opto-Electron. Eng. 2013, 40, 68–75. [Google Scholar]
- Li, X.; Qi, B. Influence and Revising Method of Machine-Ruling Grating Line′s Curve Error, Location Error on Plane Grating′ Performance. Chin. J. Lasers 2013, 40, 0308009. [Google Scholar]
- Mi, X.; Yu, H.; Yu, H.; Zhang, S.; Li, X.; Yao, X.; Qi, X.; Wan, Q. Correcting groove error in gratings ruled on a 500-mm ruling engine using interferometric control. Appl. Opt. 2017, 56, 5857–5864. [Google Scholar] [CrossRef]
- Yao, X.; Cui, J.; Yu, H.; Qi, X.; Mi, X.; Jiang, Y.; Wang, M.; Li, X. An improved accuracy-measuring method in manufacturing the lead screw of grating ruling engine. Precis. Eng. 2017, 49, 344–353. [Google Scholar] [CrossRef]
- Yu, H.; Li, X.; Zhu, J.; Yu, H.; Qi, X.; Feng, S. Reducing the line curvature error of mechanically ruled gratings by interferometric control. Appl. Phys. B 2014, 117, 279–286. [Google Scholar] [CrossRef]
- Cong, M.; Qi, X.; Mi, X.; Yu, H.; Li, X.; Lu, Y. Influence of incident light angles on mosaic grating errors in optical path for grating replication and mosaic. Opt. Precis. Eng. 2017, 25, 3027–3033. [Google Scholar] [CrossRef]
- Yang, G.; Qi, X.; Mi, X.; Zhang, S.; Yu, H.; Yu, H.; Li, X. Separation detection and correction of mosaic errors in mosaic gratings based on two detection lights with the same diffraction order and different incident angles. Opt. Lasers Eng. 2020, 139, 106281. [Google Scholar] [CrossRef]
- Lu, Y.; Qi, X.; Mi, X.; Shan, J.; Yu, H.; Li, X.; Lu, Y. Detection and Calculation of Mosaic Grating Error Based on Wavefront Method. Acta Opt. Sin. 2016, 36, 0505001. [Google Scholar]
- Yang, C.; Yu, H.; Li, X. Real time monitoring technology for full aperture grating diffraction wavefront with high frequency error. Opt. Commun. 2019, 452, 428–433. [Google Scholar] [CrossRef]
- Yang, C.; Guo, J.; Yue, L. Error analysis of a ruled grating and mechanism optimization of a grating ruling machine. Appl. Opt. 2022, 61, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Mi, X.; Zhang, S.; Qi, X.; Yu, H.; Yu, H.; Lin, Y.; Yao, X.; Jiang, S.; Zhou, J. Effect of the changes in refractive index of air on grating diffraction wavefront. Opt. Commun. 2020, 457, 124716. [Google Scholar] [CrossRef]

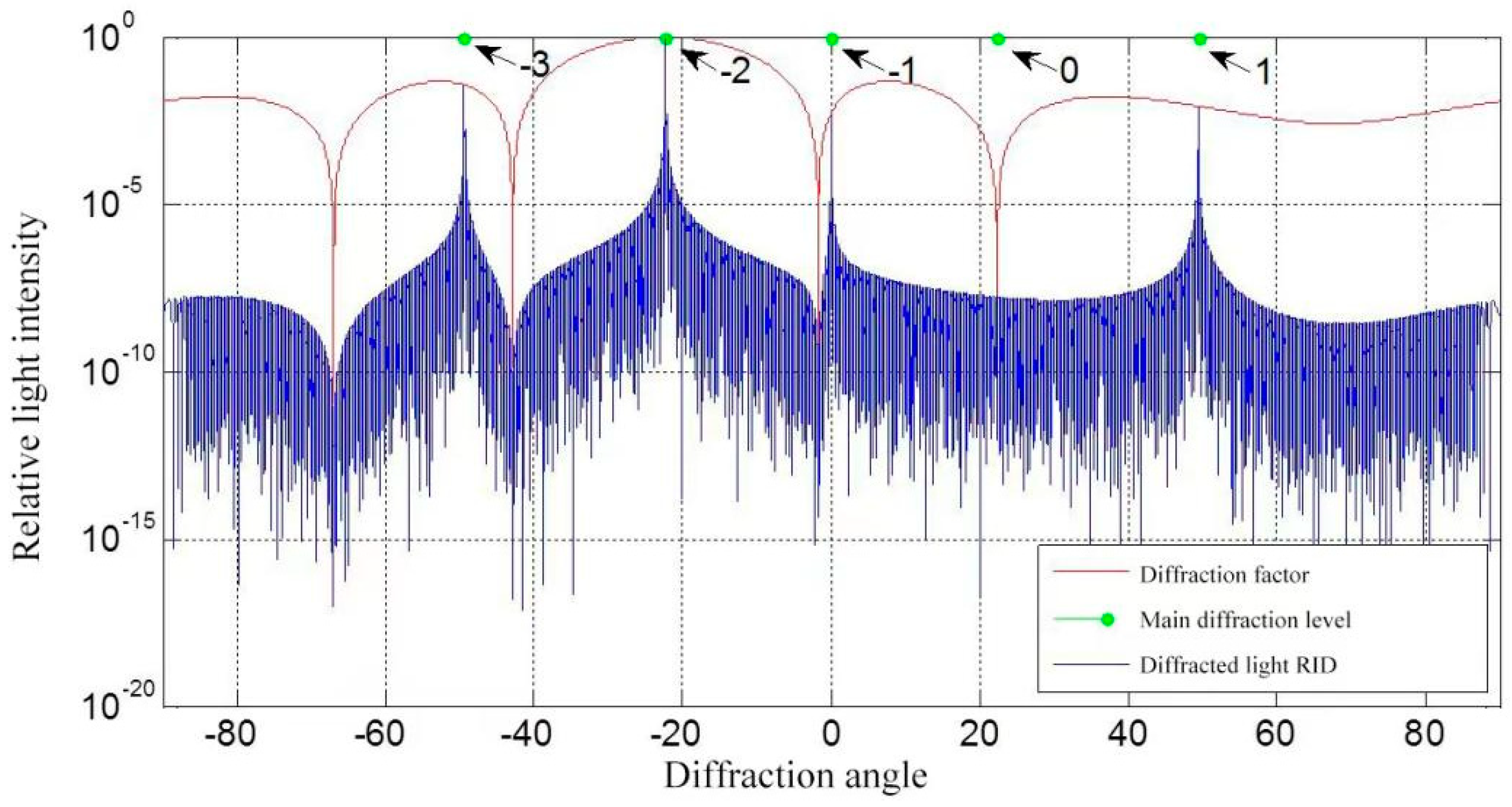


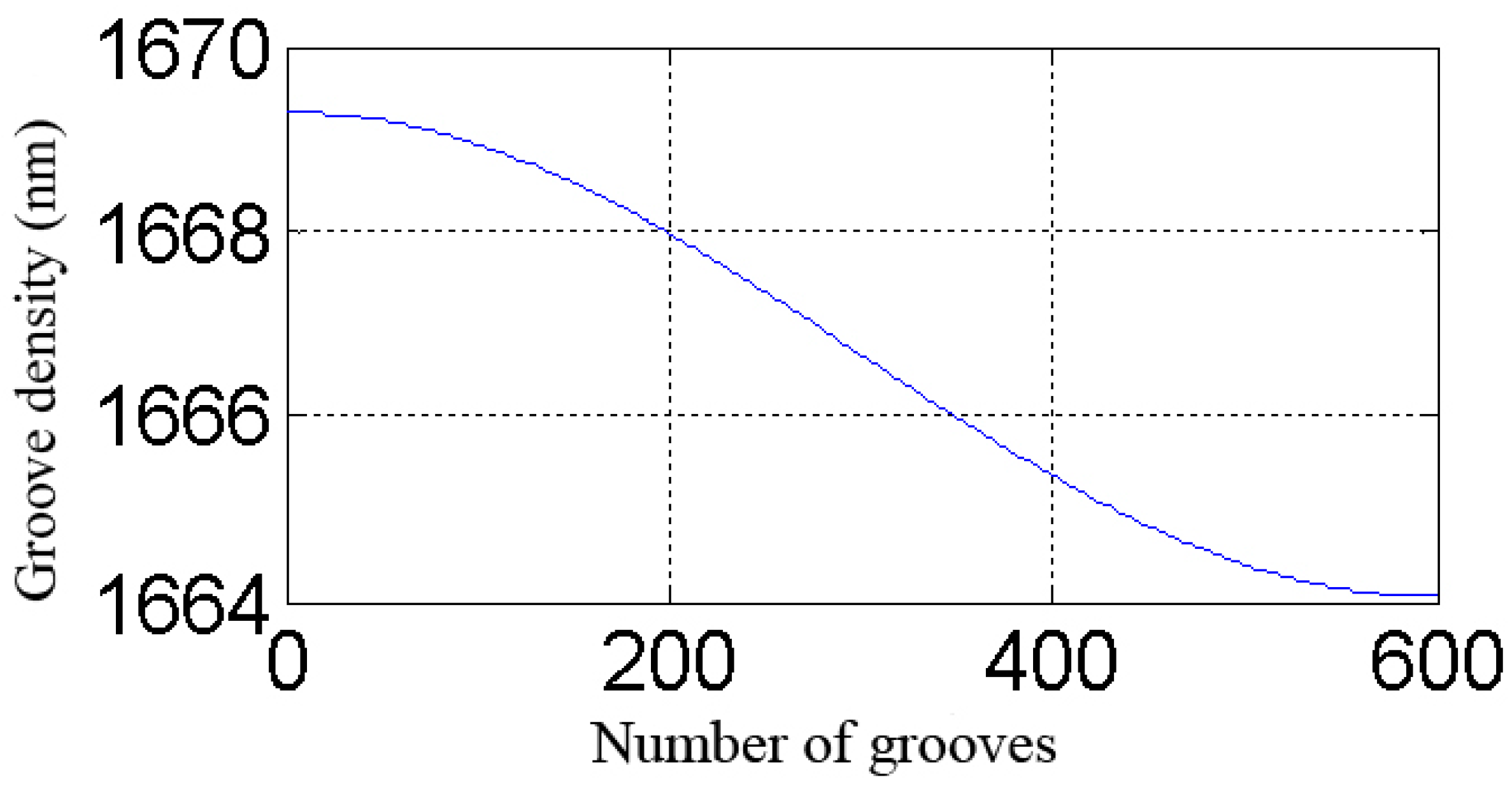
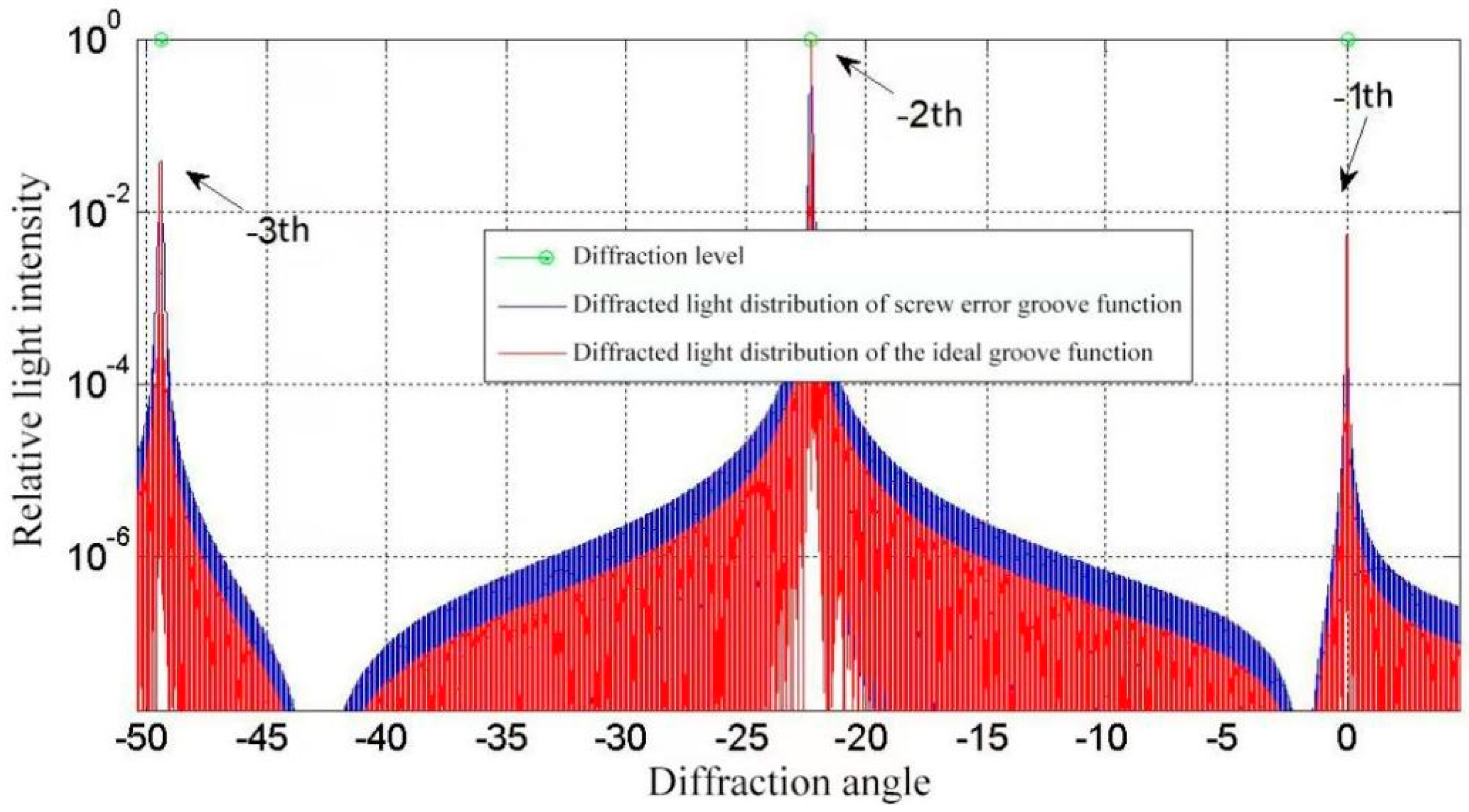






| Groove Density | Wavelength | Blaze Angle | Blaze Level | Error Distribution |
|---|---|---|---|---|
| 600 g/mm | 632.8 nm | 22° | −2 | −10 nm, 10 nm, ⋯ |
| Groove Density | Wavelength | Blaze Angle | Blaze Level | Error Distribution |
|---|---|---|---|---|
| 600 g/mm | 632.8 nm | 22° | −2 | −10 nm, 10 nm, ⋯ |
| Groove Density | Wave Length | Blaze Angle | Blaze Level | Error Distribution |
|---|---|---|---|---|
| 600 g/mm | 632.8 nm | 22° | −2 | White noise, extreme values ± 10 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Chen, X. Effect of Grating Ruling Machine System Errors on Grating Spectral Performance. Appl. Sci. 2022, 12, 10174. https://doi.org/10.3390/app121910174
Yang C, Chen X. Effect of Grating Ruling Machine System Errors on Grating Spectral Performance. Applied Sciences. 2022; 12(19):10174. https://doi.org/10.3390/app121910174
Chicago/Turabian StyleYang, Chao, and Xu Chen. 2022. "Effect of Grating Ruling Machine System Errors on Grating Spectral Performance" Applied Sciences 12, no. 19: 10174. https://doi.org/10.3390/app121910174
APA StyleYang, C., & Chen, X. (2022). Effect of Grating Ruling Machine System Errors on Grating Spectral Performance. Applied Sciences, 12(19), 10174. https://doi.org/10.3390/app121910174





