Analysis of an Elasto-Hydrodynamic Seal by Using the Reynolds Equation
Abstract
1. Introduction
2. Materials and Methods
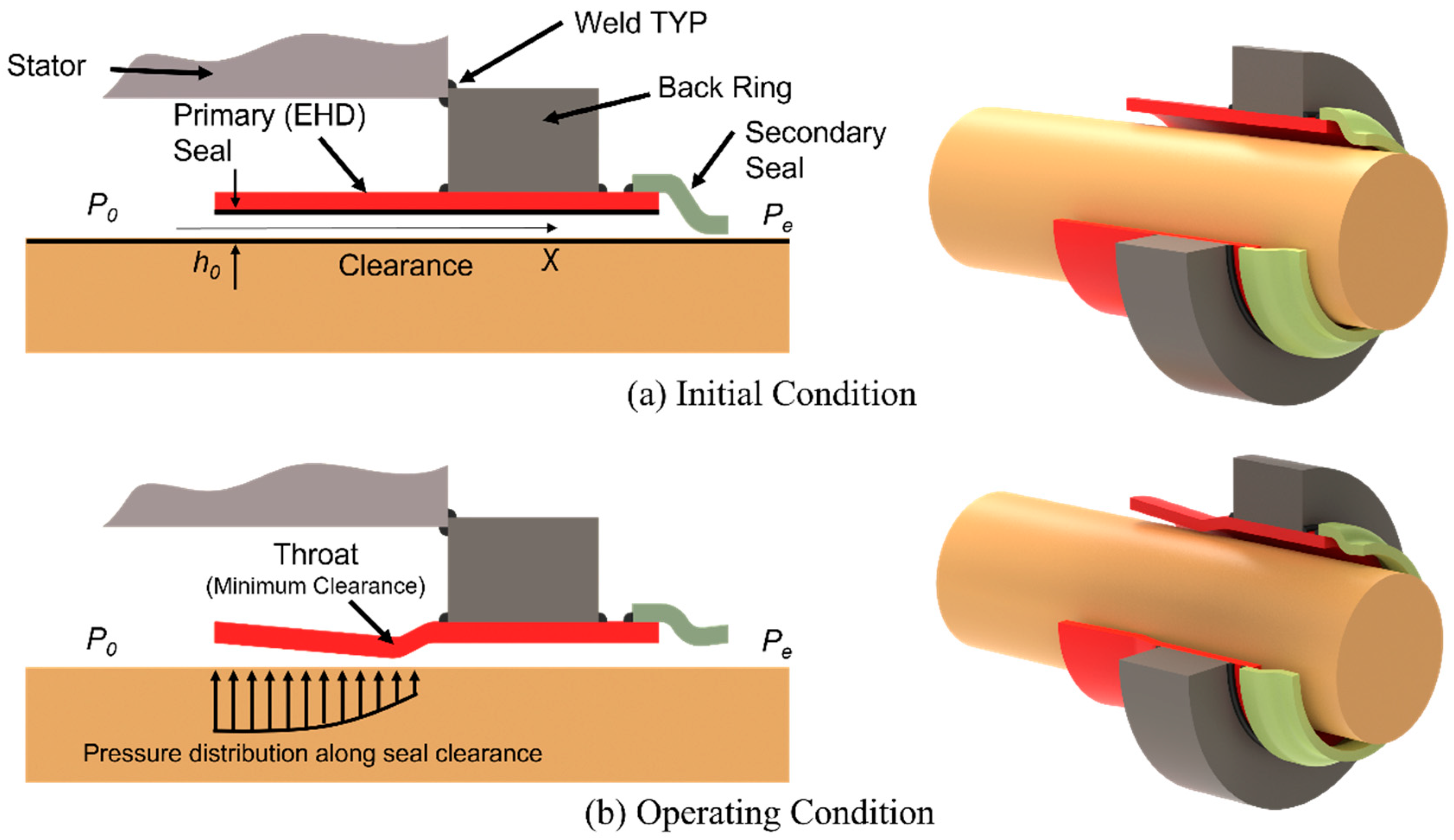
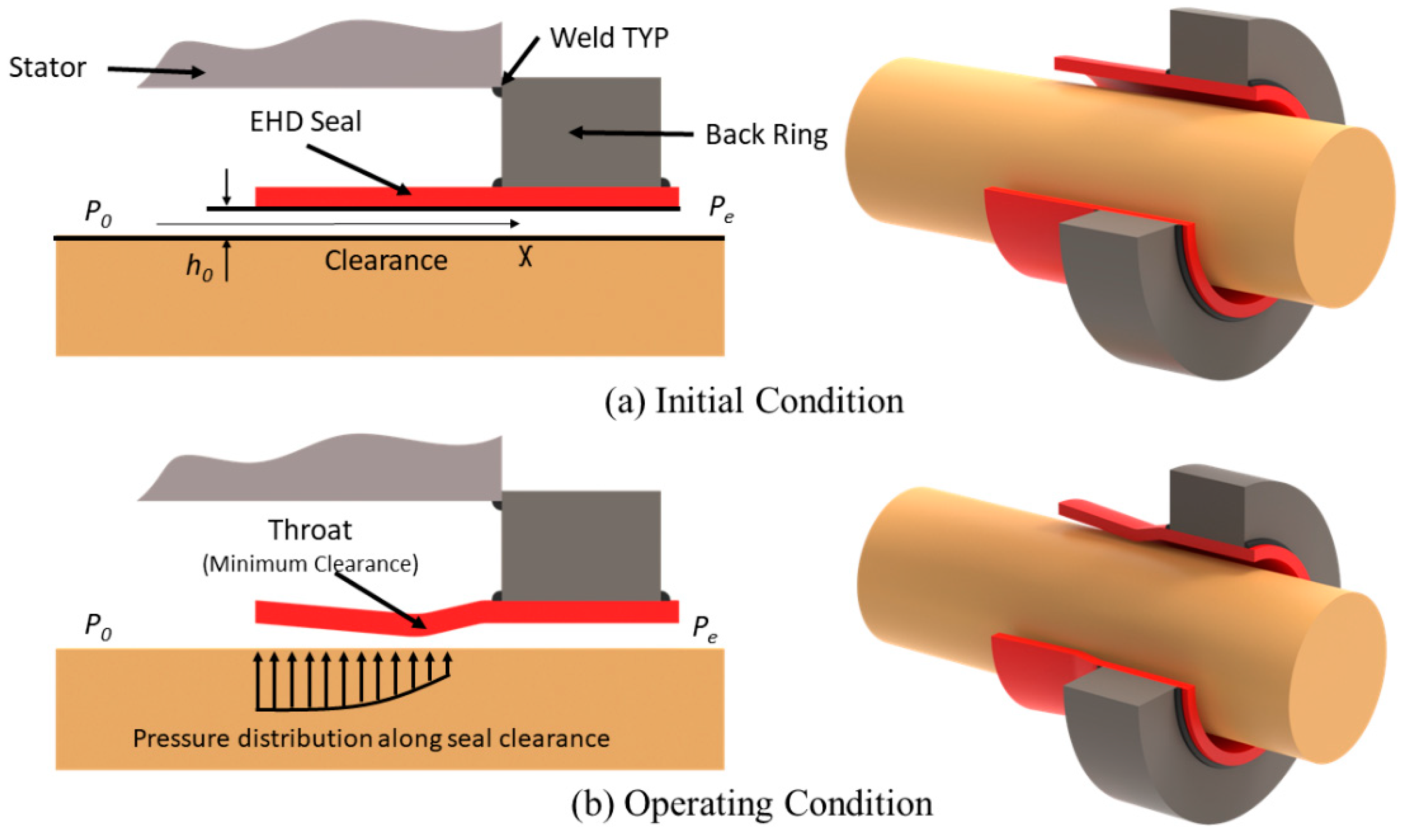
2.1. Proposed EHD Seal Design
- Low Leakage. The self-regulated minimum clearance throttles the sCO2 leaking flow, improving the cycle efficiency.
- Minimal Wear. The EHD seal operates in non-contact conditions.
- Low Cost. The simple sleeve structure results in low seal cost and minimal wear, saving maintenance costs.
- No Stress Concentration. The EHD seal design eliminates sharp angles and stress concentration risks. The deformations on the seal will be minimal, which ensures that the seal will always stay in the linear elastic region on a typical stress-strain curve.
- Smoother startup. The secondary seal will be integrated to the primary seal to provide sealing at the startup, which will enable active sealing for the whole operating range (0–11 MPa, from the cold start to operating conditions).
2.2. Design Methodology
- -
- The flow is steady. There is no sudden impact assumed between the sleeve and the rotor as it is assumed that the pressure is increased gradually.
- -
- The flow is laminar. The laminar flow assumption was validated after the simulations (see Figure 11)
- -
- The flow is in 1D and along the shaft axis only. Because of the high-pressure differentials along the seal clearance, the very high majority of the flow occurs in the x-direction. The viscous effects due to the rotation of the sleeve are strongly dominated by the pressure differentials in the x-direction.
- -
- The rotational effects of the rotor are neglected since the majority of the flow is in the axial direction of the rotor and viscous effects are negligible as the working fluid is gas. Thus, both the flow and solid domains are modeled as axisymmetric, and the inertial terms are omitted from the governing equations of motion of the seal. This assumption was validated in Figure 10.
- -
- The back ring, the stator, and the rotor are not modeled, and the deformations of these rigid structures are assumed to be zero. This can be achieved by proper design of the seal.
- -
- The rotor and the sleeve were assumed to be concentric in this study. This can be achieved by proper design of the seal.
3. Results and Discussions
3.1. Analytical Solution of a Simplified Case
3.2. Proof-of-Concept Studies

3.3. Parametric Studies
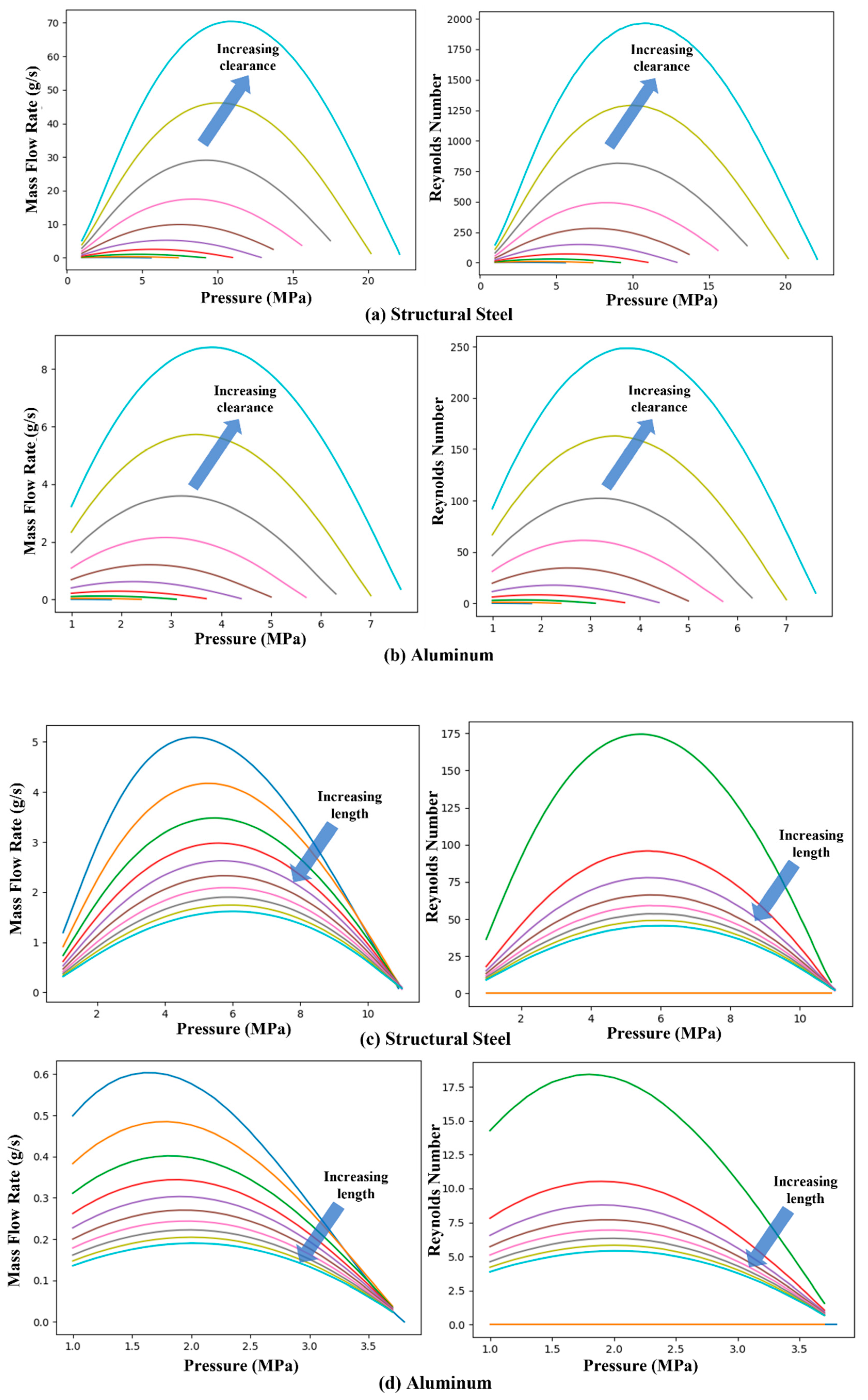
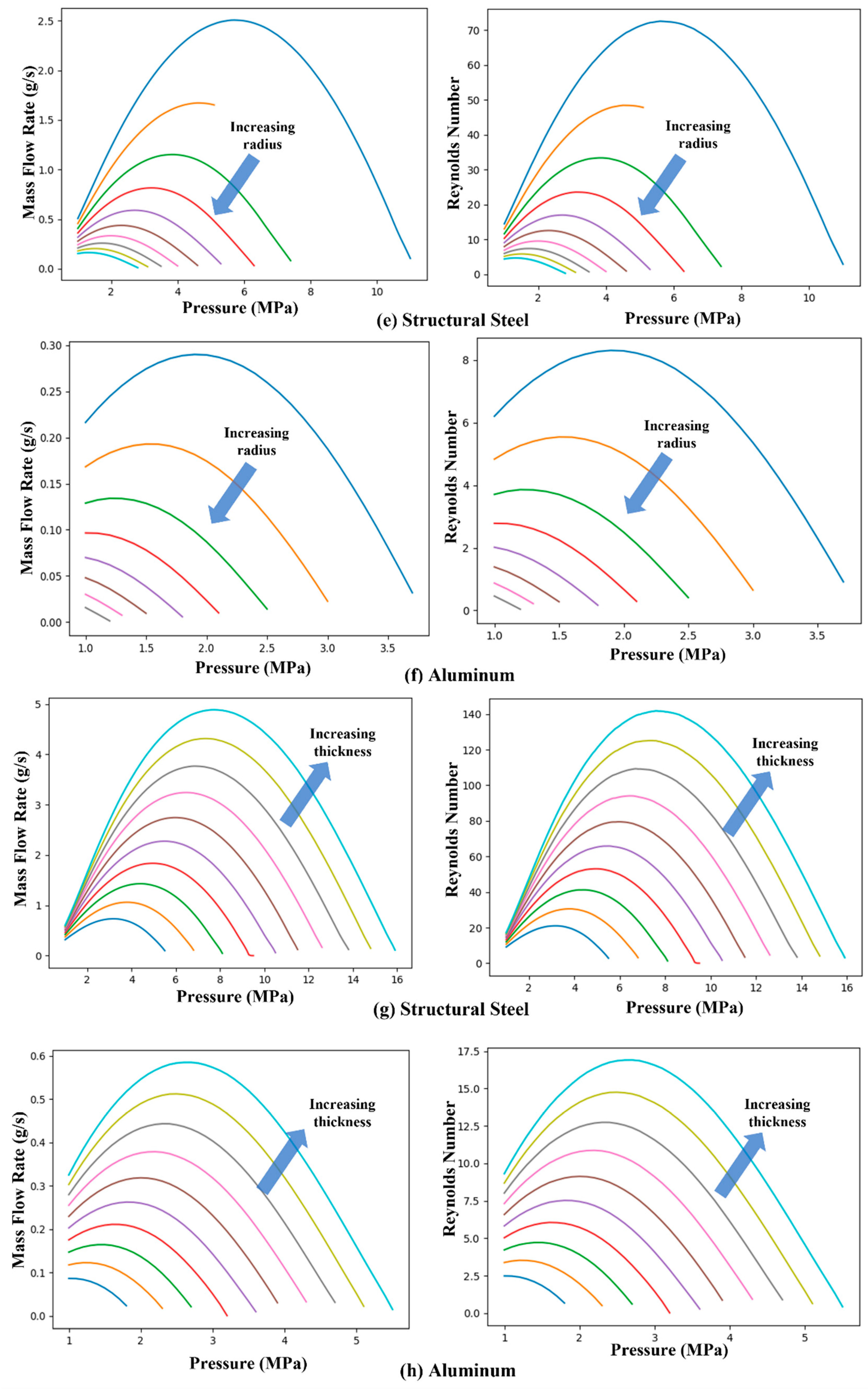
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| P0 | Inlet pressure | Pa |
| Pe | Outlet pressure | Pa |
| ρ | Density | Kg/m3 |
| h | Film thickness/clearance | m |
| μ | Dynamic viscosity | Pa s |
| p | Pressure | Pa |
| va | Rotational velocity of the rotor | m/s |
| vb | Rotational velocity of the sleeve | m/s |
| T | Temperature | K |
| σ | Cauchy stress tensor | N/m2 |
| F | Body force per unit volume | N/m3 |
| Displacement/deformation in the structure | m | |
| R | Gas constant | kJkg−1·K−1 |
| Hamiltonian operator | - | |
| Change in clearance | m | |
| r | Radius | m |
| rrotor | Rotor radius | m |
| EHD seal thickness | m | |
| Lseal | EHD seal length | m |
| x | Length along the clearance | m |
| FEM | Finite Element Method | - |
References
- Ho, C.K.; Carlson, M.; Garg, P.; Kumar, P. Technoeconomic Analysis of Alternative Solarized s-CO2 Brayton Cycle Configurations. J. Sol. Energy Eng. Trans. ASME 2016, 138, 5. [Google Scholar] [CrossRef]
- Neises, T.; Turchi, C. A comparison of supercritical carbon dioxide power cycle configurations with an emphasis on CSP applications. Energy Procedia 2014, 49, 1187–1196. [Google Scholar] [CrossRef]
- Wright, S.A.; Fuller, R.; Pickard, P.S.; Vernon, M.E.; Radel, R.F.; Vernon, M.E. Supercritical CO2 Brayton Cycle Power Generation Development Program And Initial Test Results. In Proceedings of the ASME Power Conference, Power 2009, Albuquerque, NM, USA, 21–23 July 2009; Power 2009-81081. pp. 573–583. [Google Scholar]
- Turchi, C.S.; Neises, T.W.; Wagner, M.J. Thermodynamic Study of Advanced Supercritical Carbon Dioxide Power Cycles for Concentrating Solar Power Systems. J. Solar Energy Eng. 2013, 135, 1–7. [Google Scholar] [CrossRef]
- Justak, J.F.; Doux, C. Self-Acting Clearance Control for Turbine Blade outer Air Seals. ASME Turbo Expo 2009, 3, 9. [Google Scholar] [CrossRef]
- Dinc, S.; Demiroglu, M.; Turnquist, N.; Mortzheim, J.; Goetze, G.; Maupin, J.; Hopkins, J.; Wolfe, C.; Florin, M. Fundamental design issues of brush seals for industrial applications. Proc. ASME Turbo Expo 2001, 3, 1–10. [Google Scholar] [CrossRef]
- Schlumberger, A. Film Riding Seals for Rotary Machines. U.S. Patent 9587746B2, 6 February 2014. [Google Scholar] [CrossRef]
- Salehi, M.; Heshmat, H. On the fluid flow and thermal analysis of a compliant surface foil bearing and seal. Tribol. Trans. 2000, 43, 318–324. [Google Scholar] [CrossRef]
- Ferguson, J.G. Brushes As High Performance Gas Turbine Seals. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the Gas Turbine and Aeroengine Congress, 6–9 June 1988, Amsterdam, The Netherlands; American Society of Mechanical Engineers: New York, NY, USA; ISBN 978-0-7918-7919-1. [CrossRef]
- Zhao, H.; Su, H.; Chen, G. Analysis of total leakage of finger seal with side leakage flow. Tribol. Int. 2020, 150, 106371. [Google Scholar] [CrossRef]
- Heshmat, J.L.C.H.; Walton, J. Technology Readiness of 5th and 6th Generation Compliant Foil Bearing for 10 MWE S-CO2 Turbomachinery Systems. In Proceedings of the 6th International Supercritical CO2 Power Cycles Symposium, Pittsburgh, PA, USA, 27–29 March 2018; pp. 1–29. Available online: https://www.researchgate.net/publication/324227375%0A“Technology (accessed on 9 September 2022).
- Moore, J.; Lawson, S. Development of Oxy-Fuel Combustion Turbines with CO2 Dilution for Supercritical Carbon Dioxide Based Power Cycles. 2018; p. 38. Available online: https://netl.doe.gov/sites/default/files/2019-01/FE0031620-Kickoff.pdf (accessed on 9 September 2022).
- Trivedi, D.; Bidkar, R.A.; Wolfe, C.; Zheng, X. Film-stiffness characterization for supercritical CO2 film-riding seals. Proc. ASME Turbo Expo 2018, 5B-2018, 1–10. [Google Scholar] [CrossRef]
- Laxander, A.; Fesl, A.; Hellmig, B. Development And Testing of Dry Gas Seals For Turbomachinery In Multiphase CO2 Applications. In Proceedings of the 3rd European Supercritical CO2 Conference, Paris, France, 19–20 September 2019; pp. 1–12. [Google Scholar] [CrossRef]
- Chapman, P. A High Performance Dry Gas Seal for High Temperature and Pressure Supercritical CO2 Power Cycles. 2019. Available online: https://www.osti.gov/biblio/1506975 (accessed on 9 September 2022).
- Bidkar, R.A.; Sevincer, E.; Wang, J.; Thatte, A.M.; Mann, A.; Peter, M.; Musgrove, G.; Allison, T.; Moore, J. Low-Leakage Shaft-End Seals for Utility-Scale Supercritical CO2 Turboexpanders. J. Eng. Gas Turbines Power 2017, 139, 1–8. [Google Scholar] [CrossRef]
- Dowson, D. A generalized Reynolds equation for fluid-film lubrication. Int. J. Mech. Sci. 1962, 4, 159–170. [Google Scholar] [CrossRef]
- Gong, R.Z.; Li, D.Y.; Wang, H.J.; Han, L.; Qin, D.Q. Analytical solution of Reynolds equation under dynamic conditions. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 416–427. [Google Scholar] [CrossRef]
- Wu, S.R. A penalty formulation and numerical approximation of the Reynolds-Hertz problem of elastohydrodynamic lubrication. Int. J. Eng. Sci. 1986, 24, 1001–1013. [Google Scholar] [CrossRef]
- Morris, S.; Sellier, M.; al Behadili, A.R. Comparison of lubrication approximation and Navier-Stokes solutions for dam-break flows in thin films. arXiv 2017, arXiv:1708.00976. [Google Scholar]
- Tibos, S.M.; Georgakis, C.; Harvey, K.; Teixeira, J.A. Detailed Study on Stiffness and Load Characteristics of Film-Riding Groove Types Using Design of Experiments. J. Eng. Gas Turbines Power 2017, 139, 9. [Google Scholar] [CrossRef]
- Conry, T.F.; Wang, S.; Cusano, C. A roynolds-eyring equation for elastohydrodynamic lubrication in line contacts. J. Tribol. 1987, 109, 648–654. [Google Scholar] [CrossRef]
- Habchi, W.; Eyheramendy, D.; Bair, S.; Vergne, P.; Morales-Espejel, G. Thermal elastohydrodynamic lubrication of point contacts using a Newtonian/generalized Newtonian lubricant. Tribol. Lett. 2008, 30, 41–52. [Google Scholar] [CrossRef]
- Habchi, W.; Eyheramendy, D.; Vergne, P.; Morales-Espejel, G. A full-system approach of the elastohydrodynamic line/point contact problem. J. Tribol. 2008, 130, 1–10. [Google Scholar] [CrossRef]
- Habchi, W. A numerical model for the solution of thermal elastohydrodynamic lubrication in coated circular contacts. Tribol. Int. 2014, 73, 57–68. [Google Scholar] [CrossRef]
- Björling, M.; Habchi, W.; Bair, S.; Larsson, R.; Marklund, P. Towards the true prediction of EHL friction. Tribol. Int. 2013, 66, 19–26. [Google Scholar] [CrossRef]
- Habchi, W.; Demirci, I.; Eyheramendy, D.; Morales-Espejel, G.; Vergne, P. A finite element approach of thin film lubrication in circular EHD contacts. Tribol. Int. 2007, 40, 1466–1473. [Google Scholar] [CrossRef]
- Paulson, N.R.; Sadeghi, F.; Habchi, W. A coupled finite element EHL and continuum damage mechanics model for rolling contact fatigue. Tribol. Int. 2017, 107, 173–183. [Google Scholar] [CrossRef]
- Cesmeci, S.; Hassan, R.; Hassan, M.F.; Ejiogu, I.; DeMond, M.; Xu, H.; Tang, J. An Innovative Elasto-Hydrodynamic Seal Concept for Supercritical CO2 Power Cycles. In Proceedings of the ASME 2021 Power Conference, Virtual, Online, 20–21 July 2021; p. V001T04A002. [Google Scholar] [CrossRef]
- Lyathakula, K.R.; Cesmeci, S.; Hassan, M.F.; Xu, H.; Tang, J. A Proof-of-Concept Study of a Novel Elasto-Hydrodynamic Seal for Supercritical CO2 Turbomachinery Applications. In Proceedings of the ASME 2022 Power Conference, Pittsburgh, PA, USA, 18–19 July 2022. [Google Scholar] [CrossRef]
- Lyathakula, K.R.; Cesmeci, S.; DeMond, M.; Xu, H.; Tang, J. Physics-Informed Deep Learning-Based Modeling of a Novel Elastohydrodynamic Seal for Supercritical CO2 Turbomachinery. In Proceedings of the ASME 2022 Power Conference, Pittsburgh, PA, USA, 18–19 July 2022. [Google Scholar] [CrossRef]
- Peterson, W.; Russell, T.; Sadeghi, F.; Berhan, M.T. A Strongly Coupled Finite Difference Method–Finite Element Method Model for Two-Dimensional Elastohydrodynamically Lubricated Contact. J. Tribol. 2020, 142, 1–8. [Google Scholar] [CrossRef]
- Feldermann, A.; Neumann, S.; Jacobs, G. CFD simulation of elastohydrodynamic lubrication problems with reduced order models for fluid–structure interaction. Tribol.—Mater. Surfaces Interfaces 2017, 11, 30–38. [Google Scholar] [CrossRef]
- Lohner, T.; Ziegltrum, A.; Stemplinger, J.P.; Stahl, K. Engineering Software Solution for Thermal Elastohydrodynamic Lubrication Using Multiphysics Software. Adv. Tribol. 2016, 2016, 6507203. [Google Scholar] [CrossRef]
- Bearings, H.; Theory, P. A CFD-Based Frequency Response Method Applied in the Determination of Dynamic Coefficients of hydrodynamic bearings. Part 1: Theory. Lubricants 2019, 7, 23. [Google Scholar] [CrossRef]
- Chen, Q. Analysis of Soft- Elastohydrodynamic Lubrication Line Contacts on Finite Thickness. J. Tribol. 2018, 140, 1–8. [Google Scholar] [CrossRef]
- Sellier, M.; Lee, Y.C.; Thompson, H.M.; Gaskell, P.H. Thin film flow on surfaces containing arbitrary occlusions. Comput. Fluids 2009, 38, 171–182. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Jamari, J.; Susilowati, S.; Pujiastuti, C.; Setiyana, B.; Pasaribu, A.H.; Ammarullah, M.I. Fluid on a Heterogeneous Slip/No-Slip Journal Bearing System Based on CFD-FSI Method. Fluids 2022, 7, 225. [Google Scholar] [CrossRef]
- Xu, H.; Lei, T. A ringless high pressure moving seal up to 1200 mpa. Tribol. Trans. 1994, 37, 767–770. [Google Scholar] [CrossRef]
- Xu, H.P.; Wong, P.L.; Zhang, Z.M. An EHL Analysis of an All-Metal Viscoelastic High-Pressure Seal. J. Tribol. 1999, 121, 916–920. [Google Scholar] [CrossRef]
- Wong, P.L.; Xu, H.; Zhang, Z. Performance evaluation of high pressure sleeve seal. Wear 1997, 210, 104–111. [Google Scholar] [CrossRef]
- COMSOL. COMSOL Multiphysics User’s Guide; COMSOL: Stockholm, Sweden, September 2005. [Google Scholar]
- Lemmon, M.O.W.; Eric, B.; Ian, H.; Huber, M.; McLinden, L. Thermophysical Properties of Fluid Systems; National Institute of Standard & Technology: Gaithersburg, MD, USA, 2022. [Google Scholar] [CrossRef]
- COMSOL. Structural Mechanics Module User’s Guide, COMSOL MultiphysicsR v. 5.2 a; COMSOL AB: Stockholm, Sweden; Available online: www.comsol.com (accessed on 9 September 2022).
- COMSOL. CFD Modules User’s Guide, COMSOL MultiphysicsTM v. 5.4.; COMSOL AB: Stockholm, Sweden, 2018. [Google Scholar]
- Pick, R.J.; Harris, H.D. Morrison and Parry Seals for Water Pressures up to 345 MPa. J. Pressure Vessel Technol. 1980, 102, 84–89. [Google Scholar] [CrossRef]
- Parry, J.S.C. University of Bristol, Development of Reciprocating Seals for Very High Pressures (45000 lb per in2). In Proceedings of the Third International Conference on Fluid Sealing, Cambridge, England, 1 January 1967. P.C-6-69-c6-80. [Google Scholar]
- Dean, T.J.; Elligsen, R.A.; Mohaupt, U.H. High Pressure Sealing Characteristics of Metallic Sleeve Seals. MRS Online Proc. 1984, 22, 249–252. [Google Scholar] [CrossRef]
- Pick, D.J.B.R.J. Dimensional Parameters Influencing the Behavior of the Morrison Unsupported Area Seal. J. Eng. Industry 1970, 92, 755–758. [Google Scholar] [CrossRef]
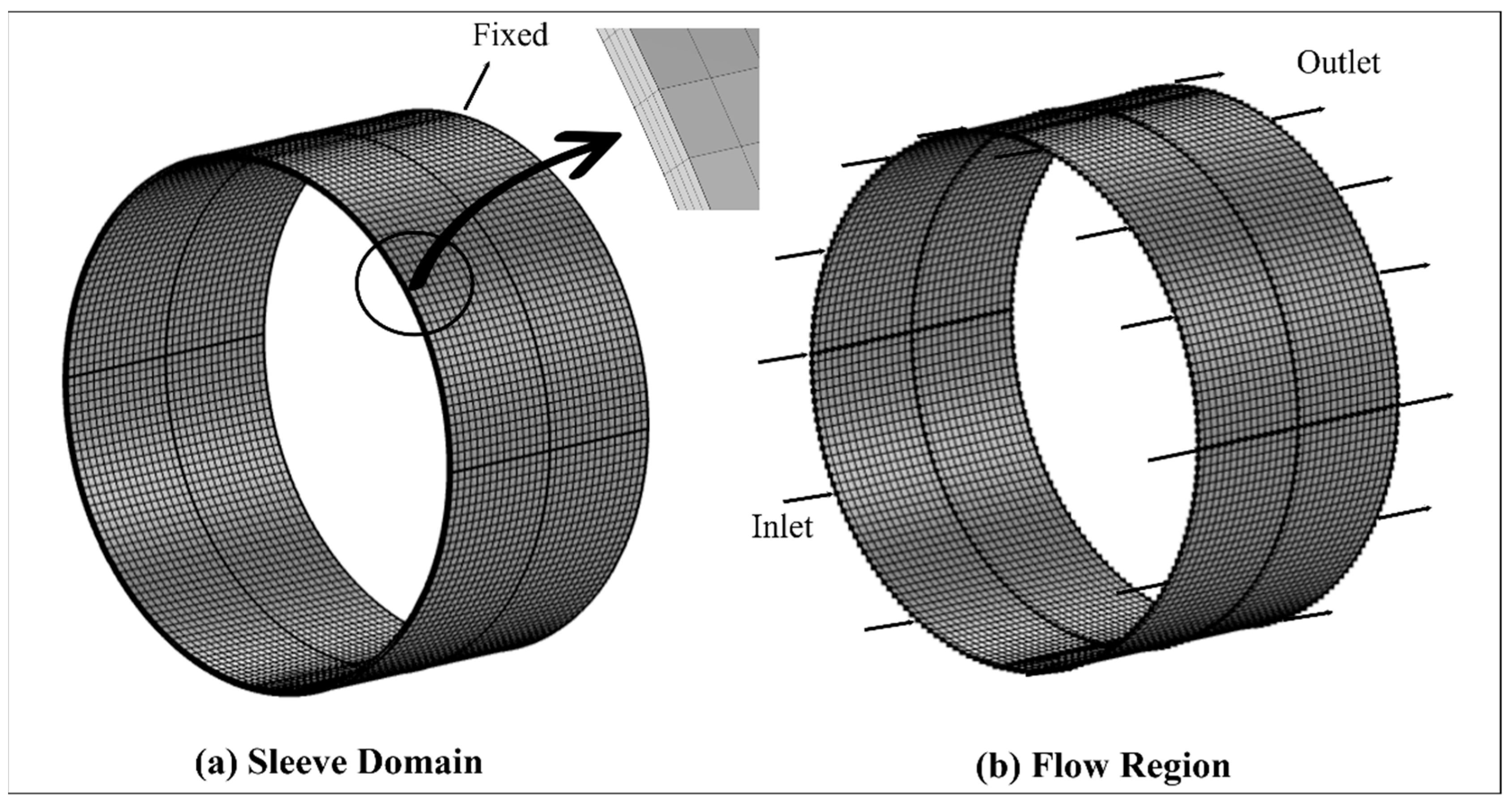
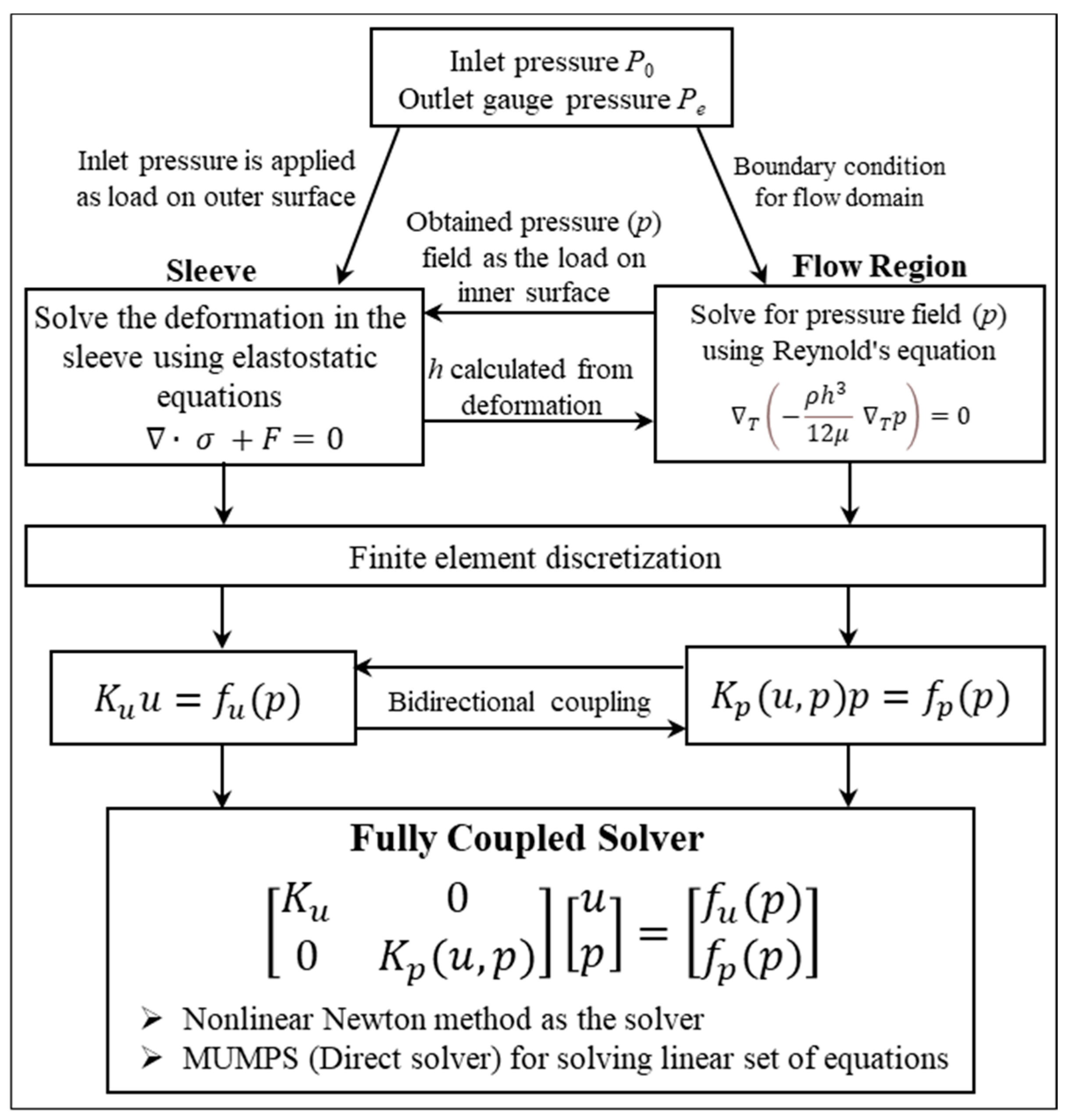
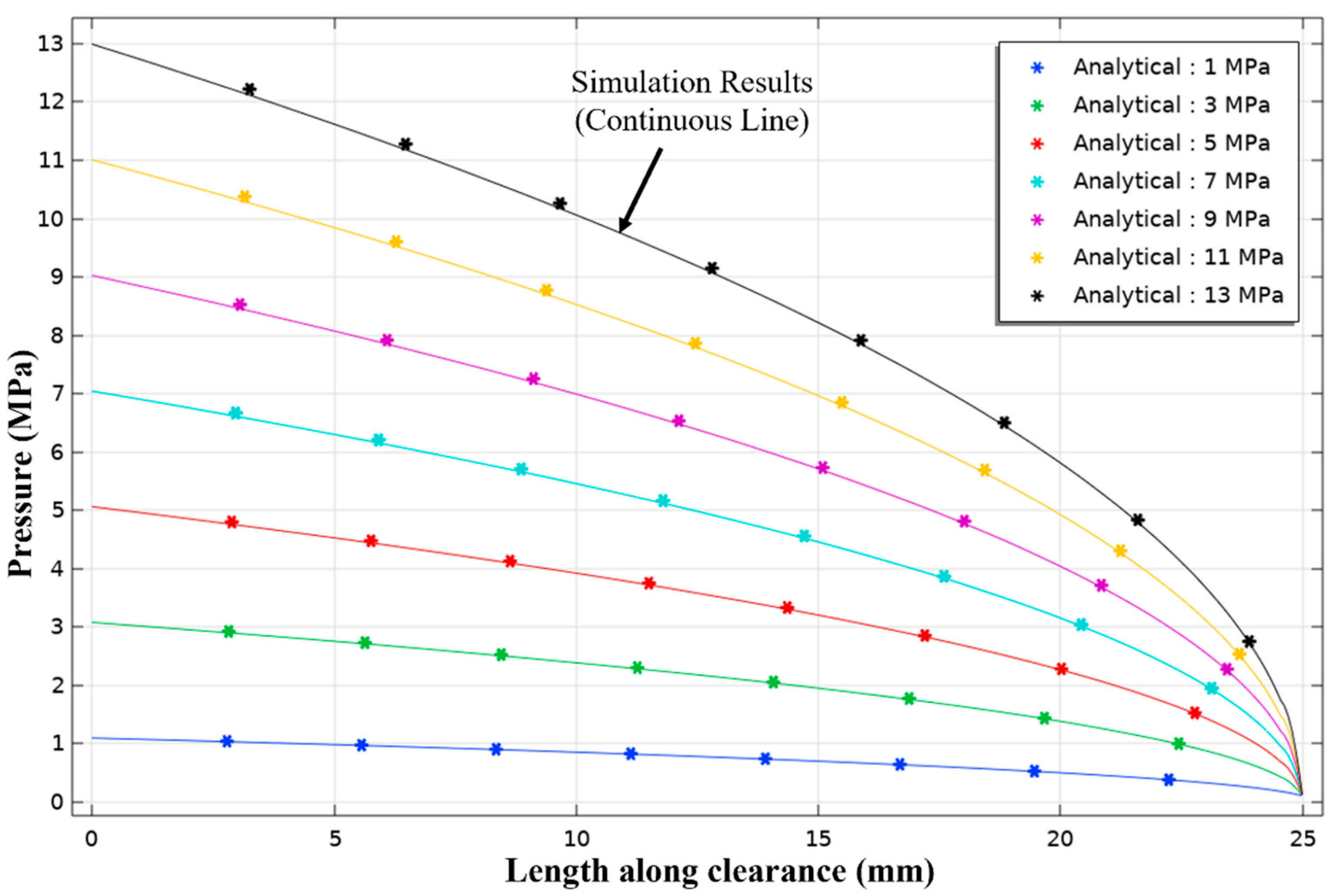
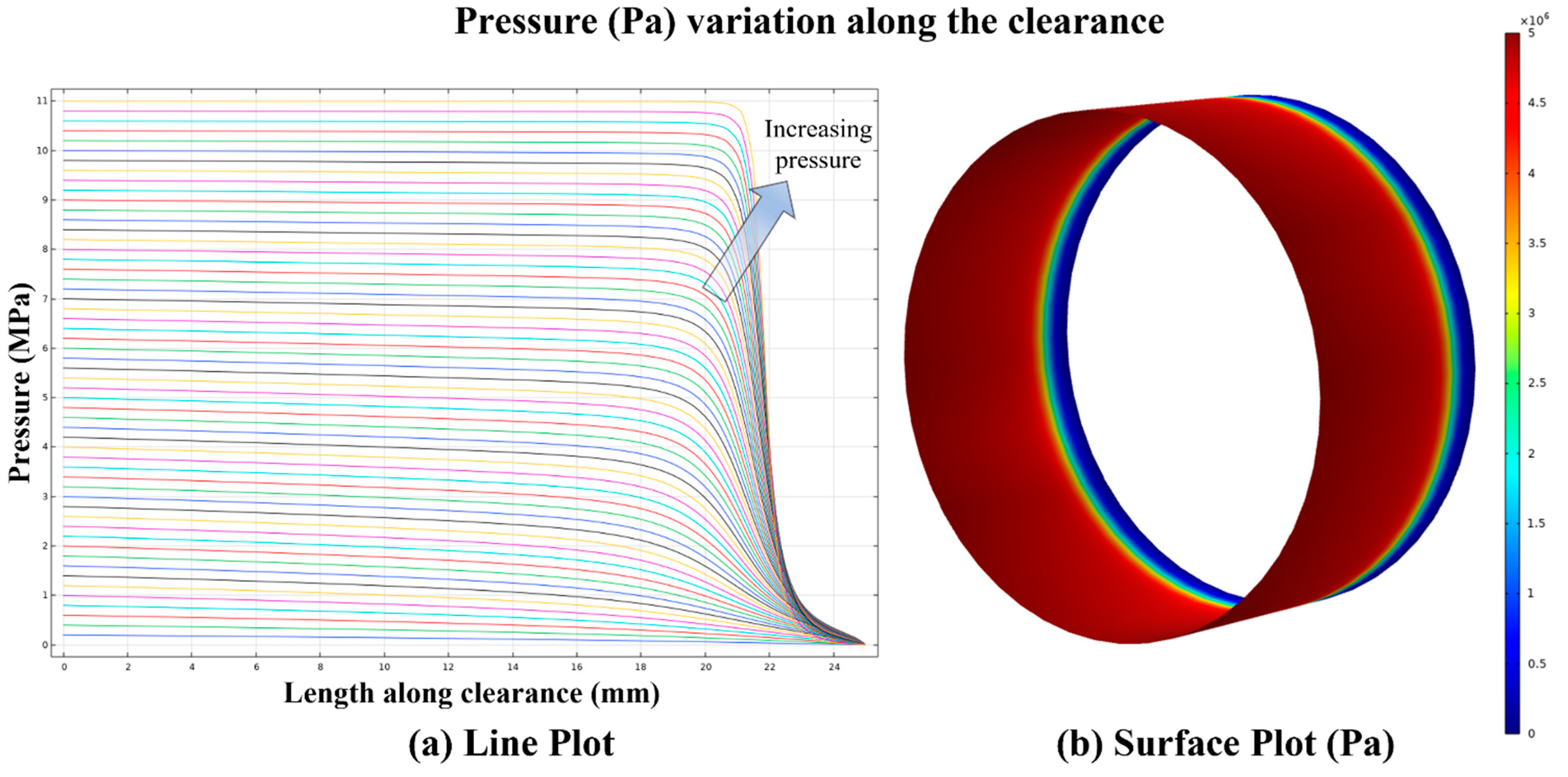

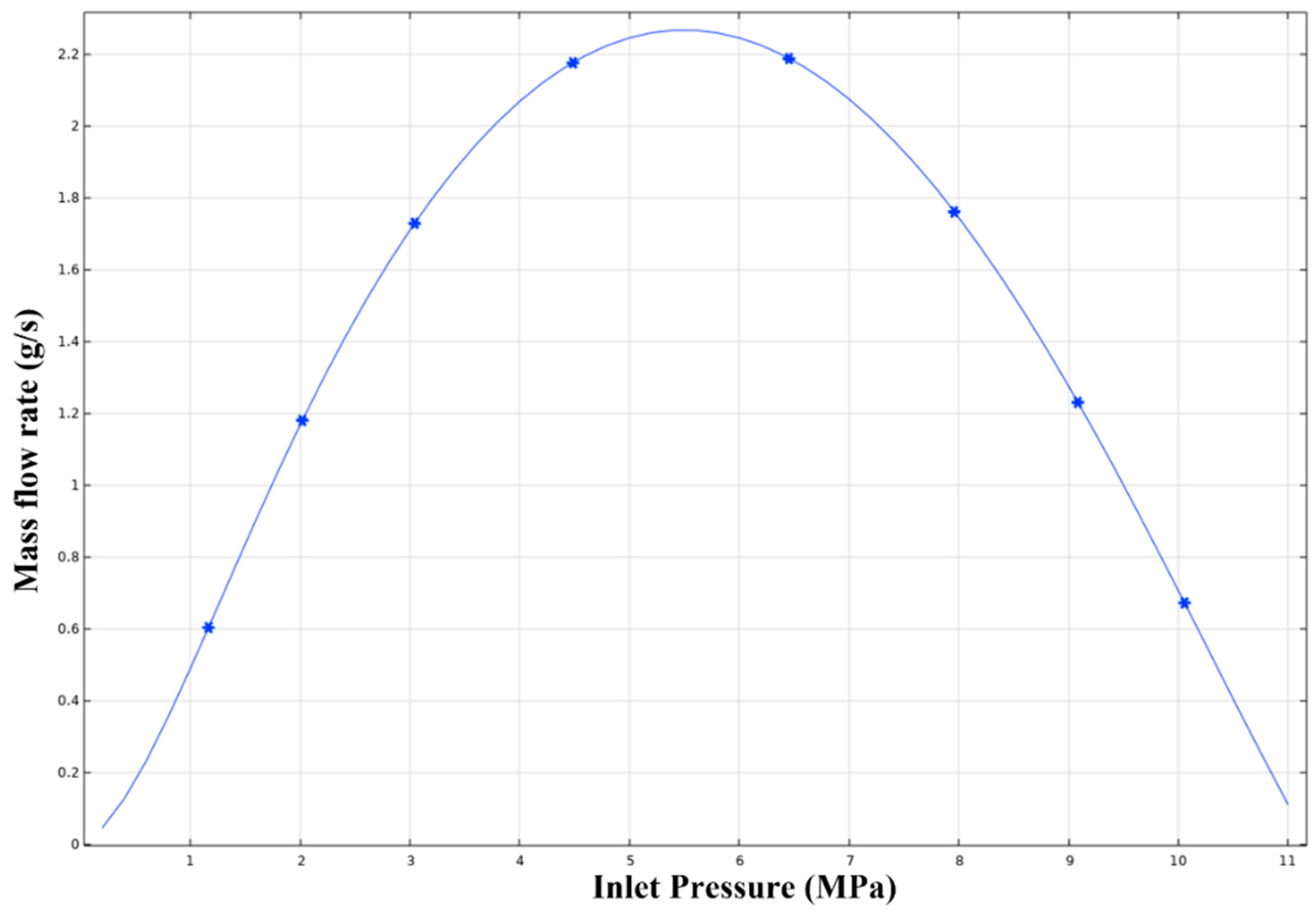
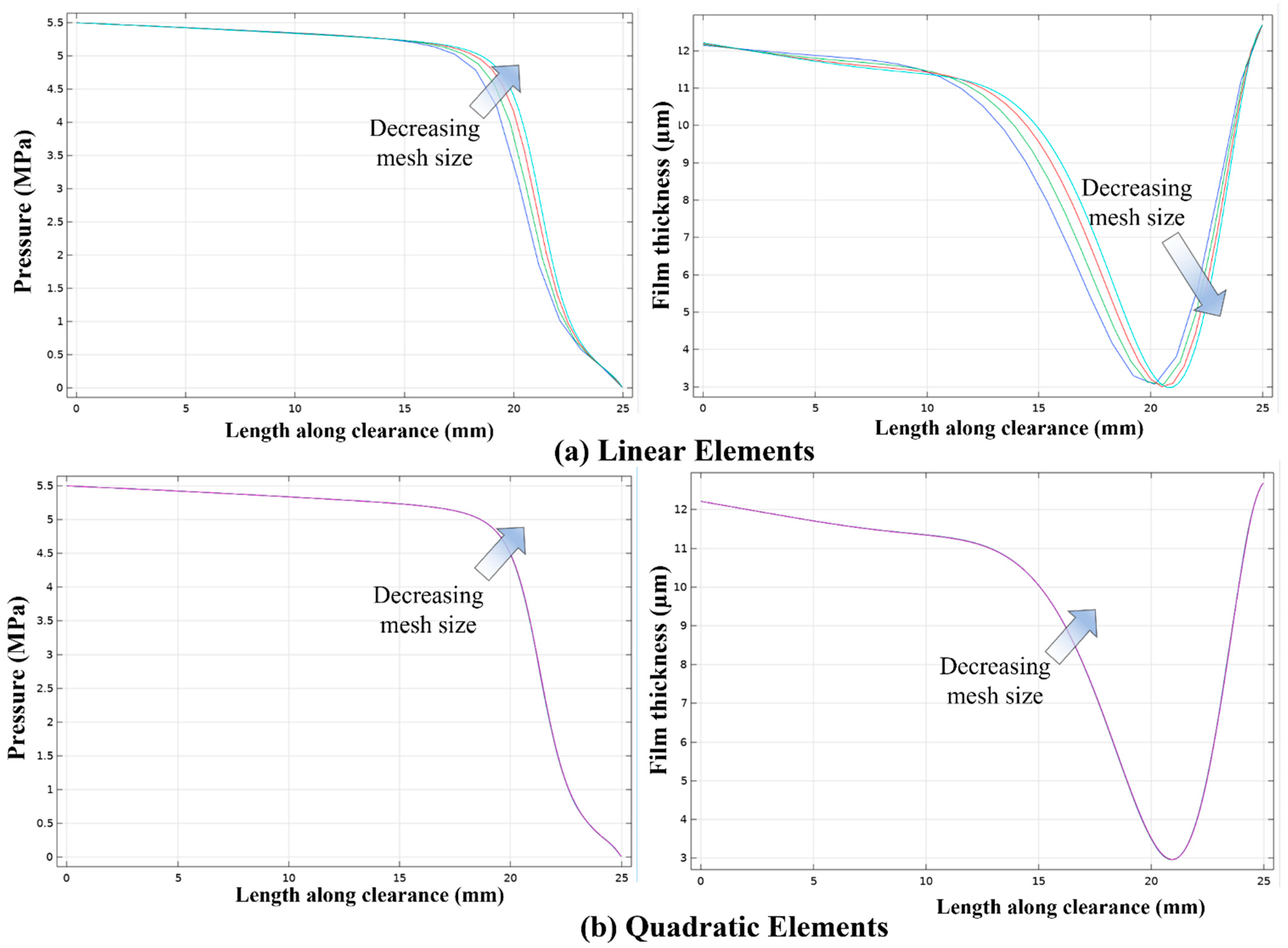
| Property/Parameter | Value |
|---|---|
| Rotor radius (rrotor) | 25.4 mm |
| EHD seal thickness (tseal) | 0.5 mm |
| EHD seal length (Lseal) | 25.0 mm |
| Initial clearance (h0) | 0.0127 mm |
| Dynamic viscosity of CO2 (µ) | f(P, T) |
| Young’s modulus of the steel seal (E) | 2 × 1011 N/m2 |
| Young’s modulus of the aluminum seal (E) | 70 × 109 N/m2 |
| Density of CO2 (ρ) | f(P, T) |
| Working pressure (P0) | Varying |
| Ambient pressure (Pe) | 0 Gauge |
| Gas constant of CO2 | 0.1889 kJ/(kg·K) |
| Parameter | Range |
|---|---|
| EHD seal initial clearance, h0 | 0.00635–0.0254 mm |
| EHD seal length, Lseal | 12.7–38 mm |
| Rotor radius, rrotor | 25.4–50.8 mm |
| EHD seal thickness, tseal | 0.25–0.75 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cesmeci, S.; Lyathakula, K.R.; Hassan, M.F.; Liu, S.; Xu, H.; Tang, J. Analysis of an Elasto-Hydrodynamic Seal by Using the Reynolds Equation. Appl. Sci. 2022, 12, 9501. https://doi.org/10.3390/app12199501
Cesmeci S, Lyathakula KR, Hassan MF, Liu S, Xu H, Tang J. Analysis of an Elasto-Hydrodynamic Seal by Using the Reynolds Equation. Applied Sciences. 2022; 12(19):9501. https://doi.org/10.3390/app12199501
Chicago/Turabian StyleCesmeci, Sevki, Karthik Reddy Lyathakula, Mohammad Fuad Hassan, Shuangbiao Liu, Hanping Xu, and Jing Tang. 2022. "Analysis of an Elasto-Hydrodynamic Seal by Using the Reynolds Equation" Applied Sciences 12, no. 19: 9501. https://doi.org/10.3390/app12199501
APA StyleCesmeci, S., Lyathakula, K. R., Hassan, M. F., Liu, S., Xu, H., & Tang, J. (2022). Analysis of an Elasto-Hydrodynamic Seal by Using the Reynolds Equation. Applied Sciences, 12(19), 9501. https://doi.org/10.3390/app12199501






