Study on Reinforcement Mechanism and Reinforcement Effect of Saturated Soil with a Weak Layer by DC
Abstract
:1. Introduction
1.1. Background
1.2. Dynamic Compaction
1.3. Main Research Contents
2. The Fluid–Solid Coupling Model and FEM Implementation
2.1. u-U-p Formulation
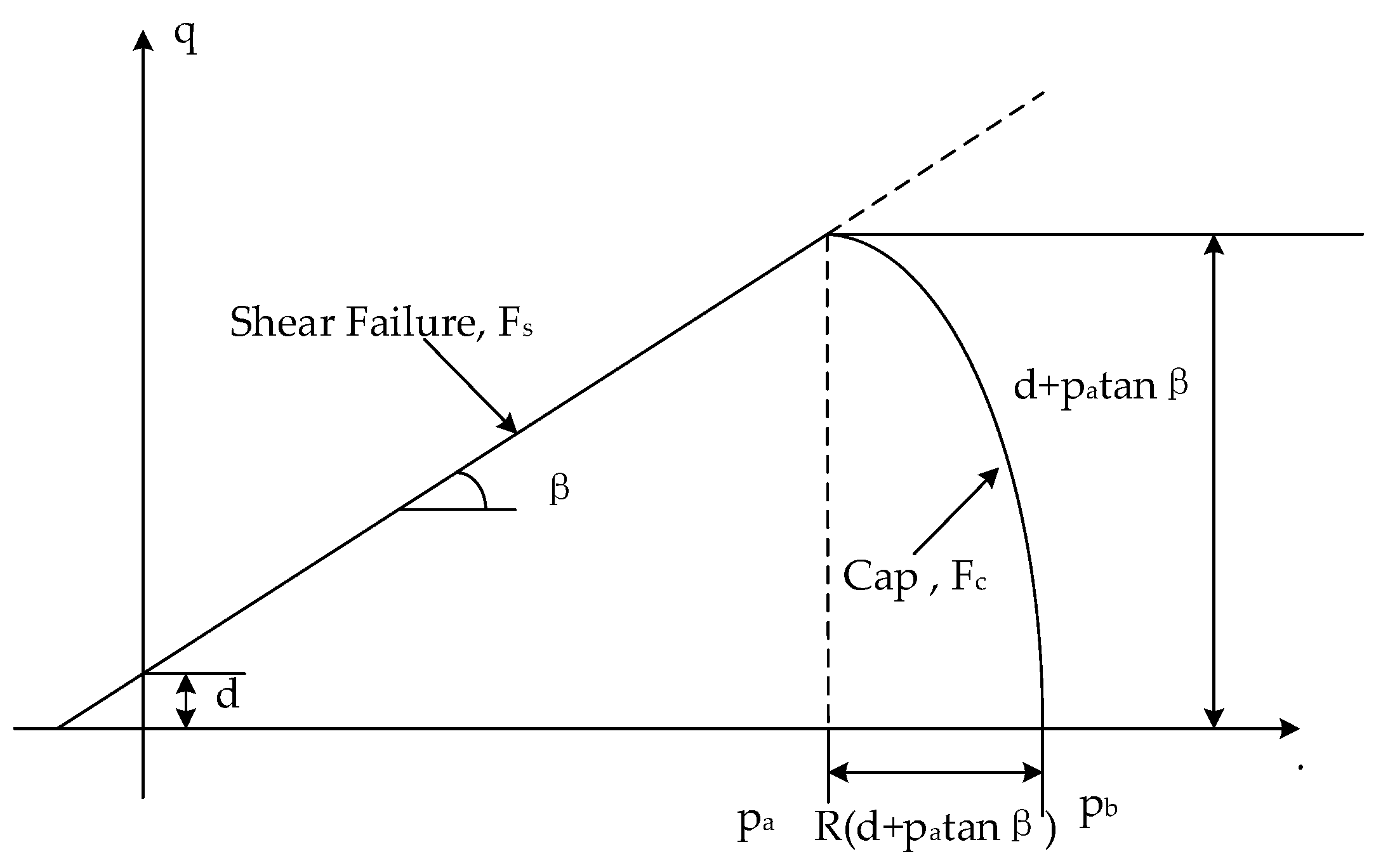
2.2. Constitutive Model for Soil in DC
3. Validation of the Numerical Method
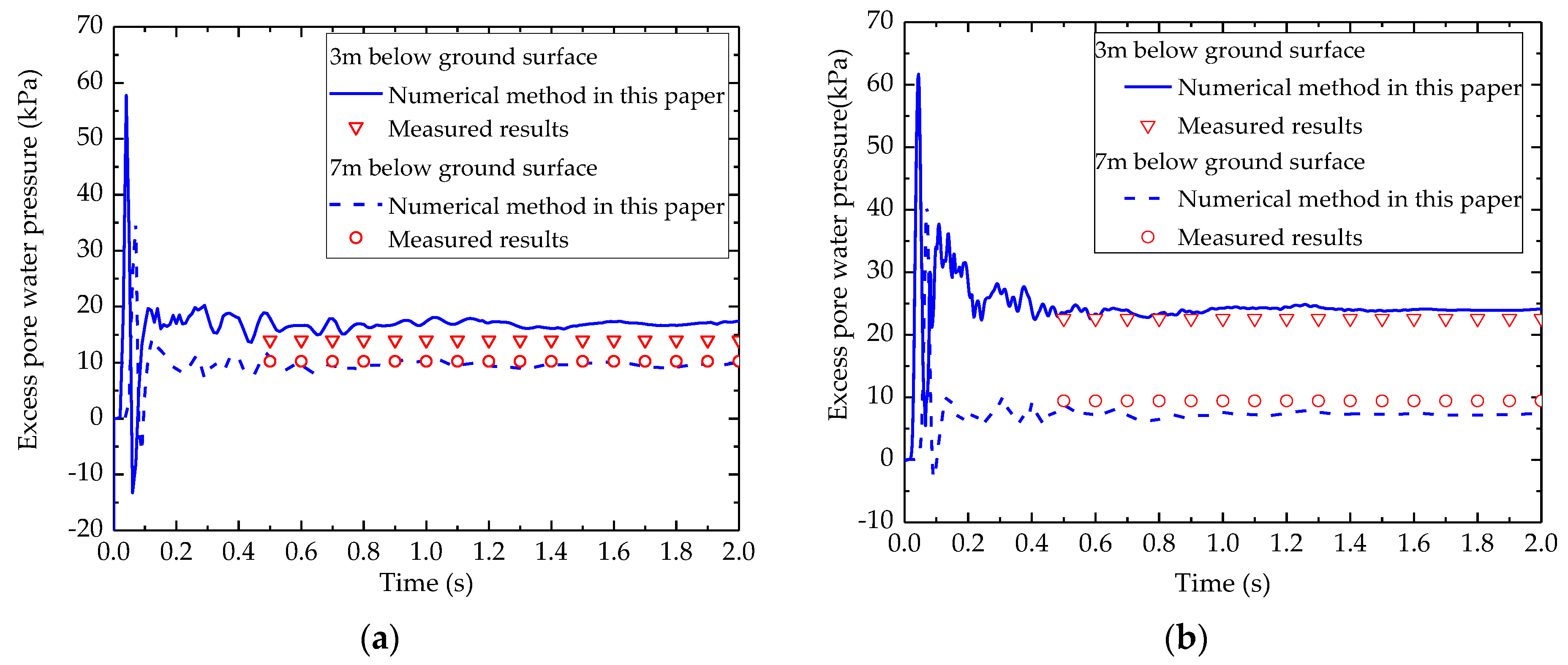
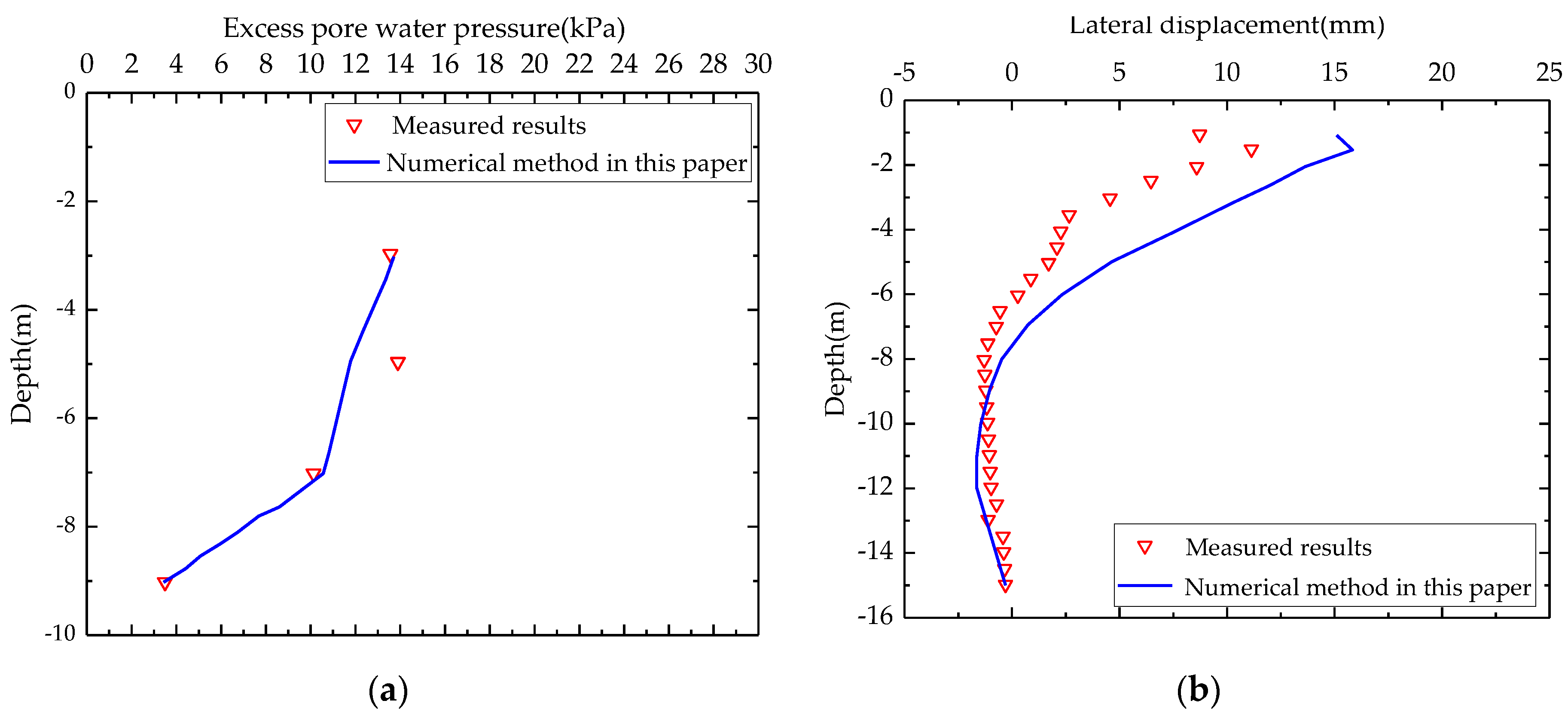
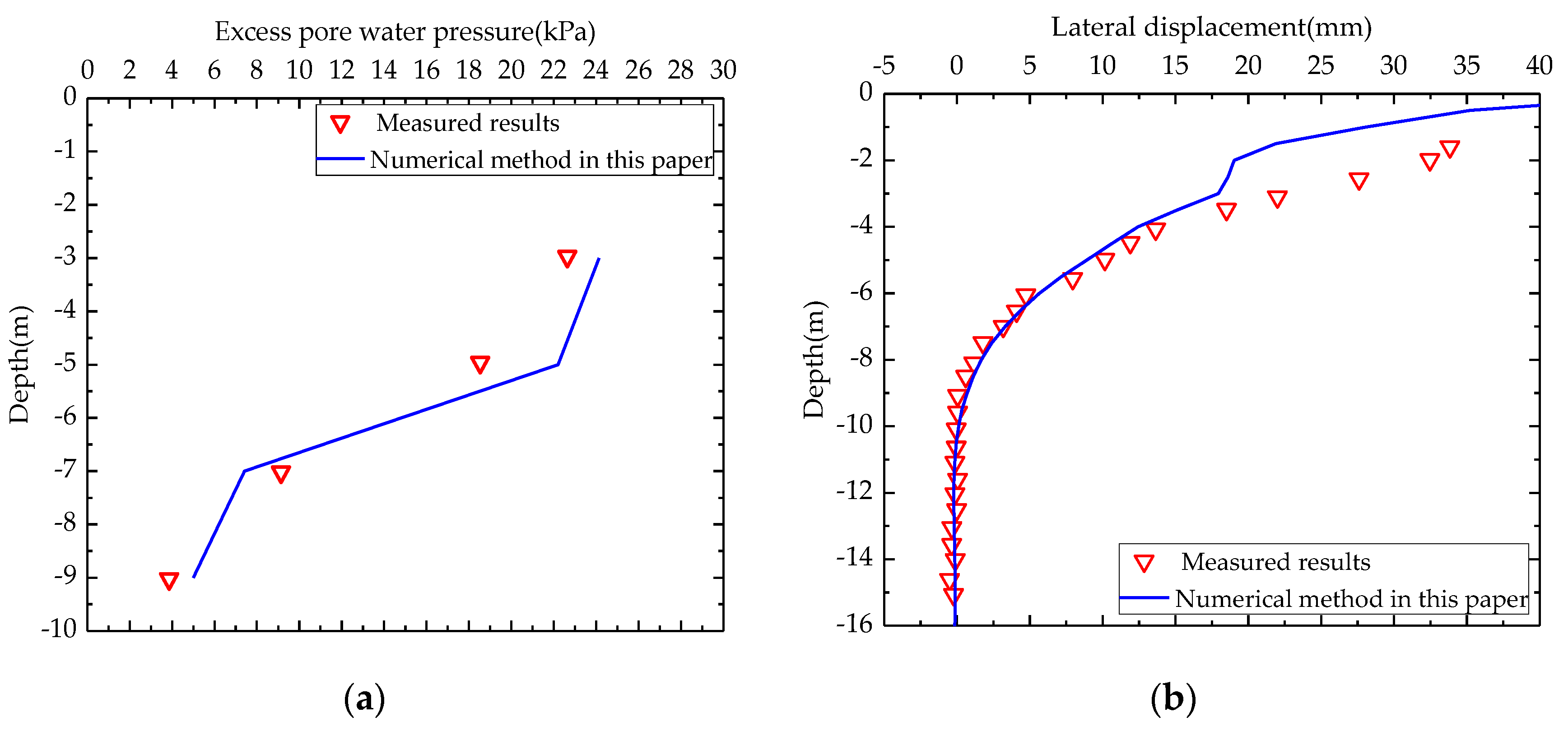
3.1. Pore Water Pressure and Lateral Displacement
3.2. Reinforcement Effect
4. Numerical Analysis
4.1. Improvement Mechanism of Nonhomogeneous Saturated Soil Foundation under DC
4.2. Parametric Analysis
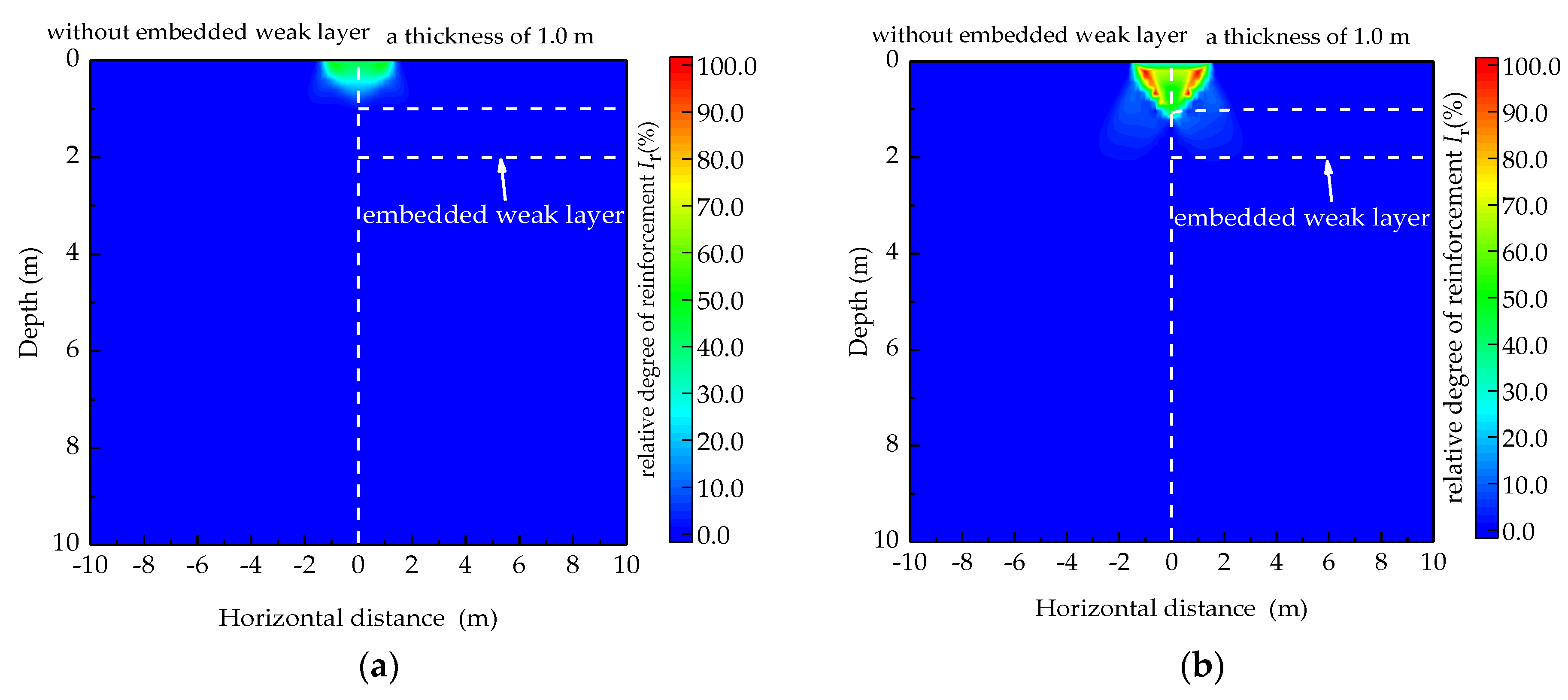
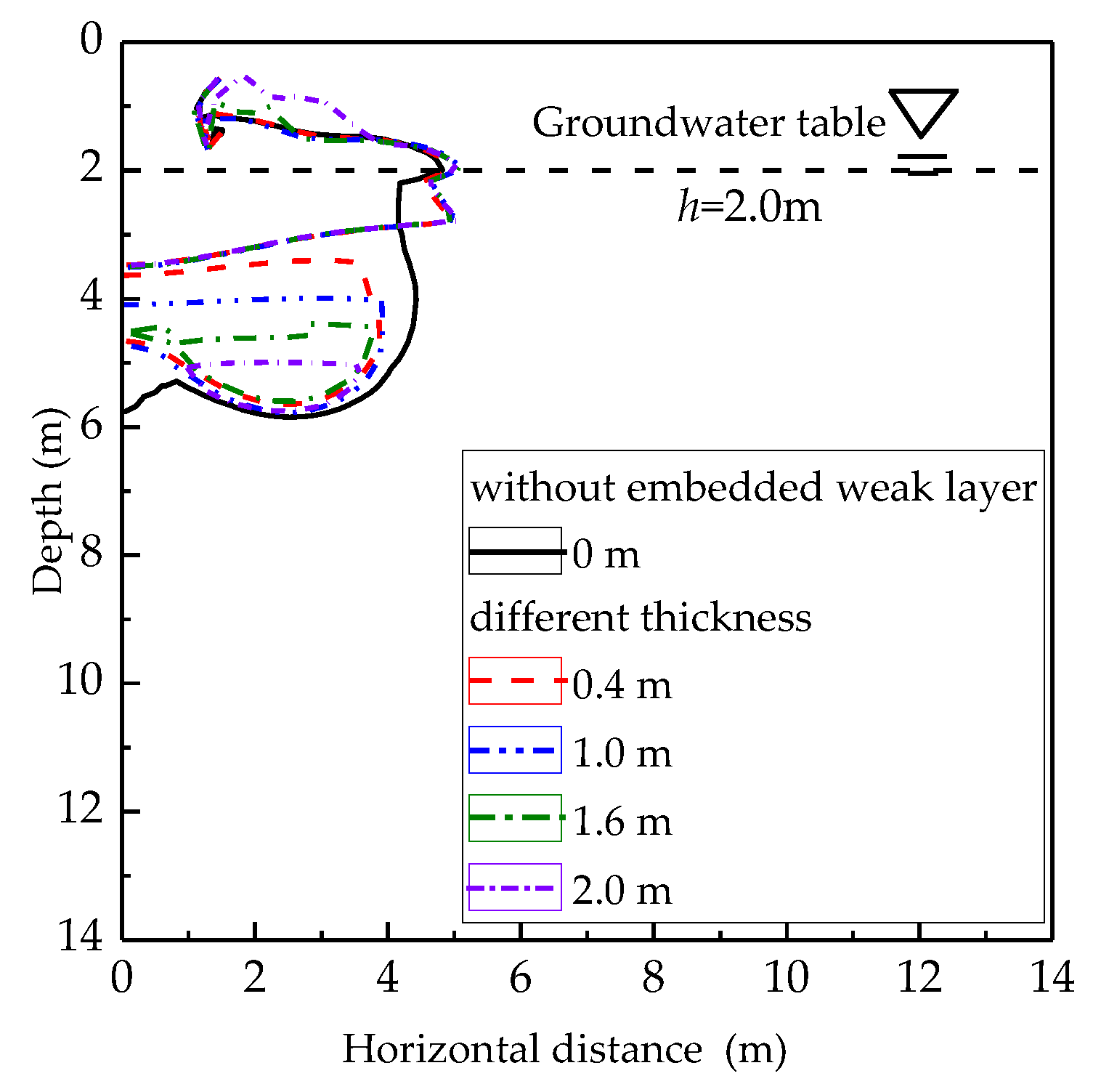
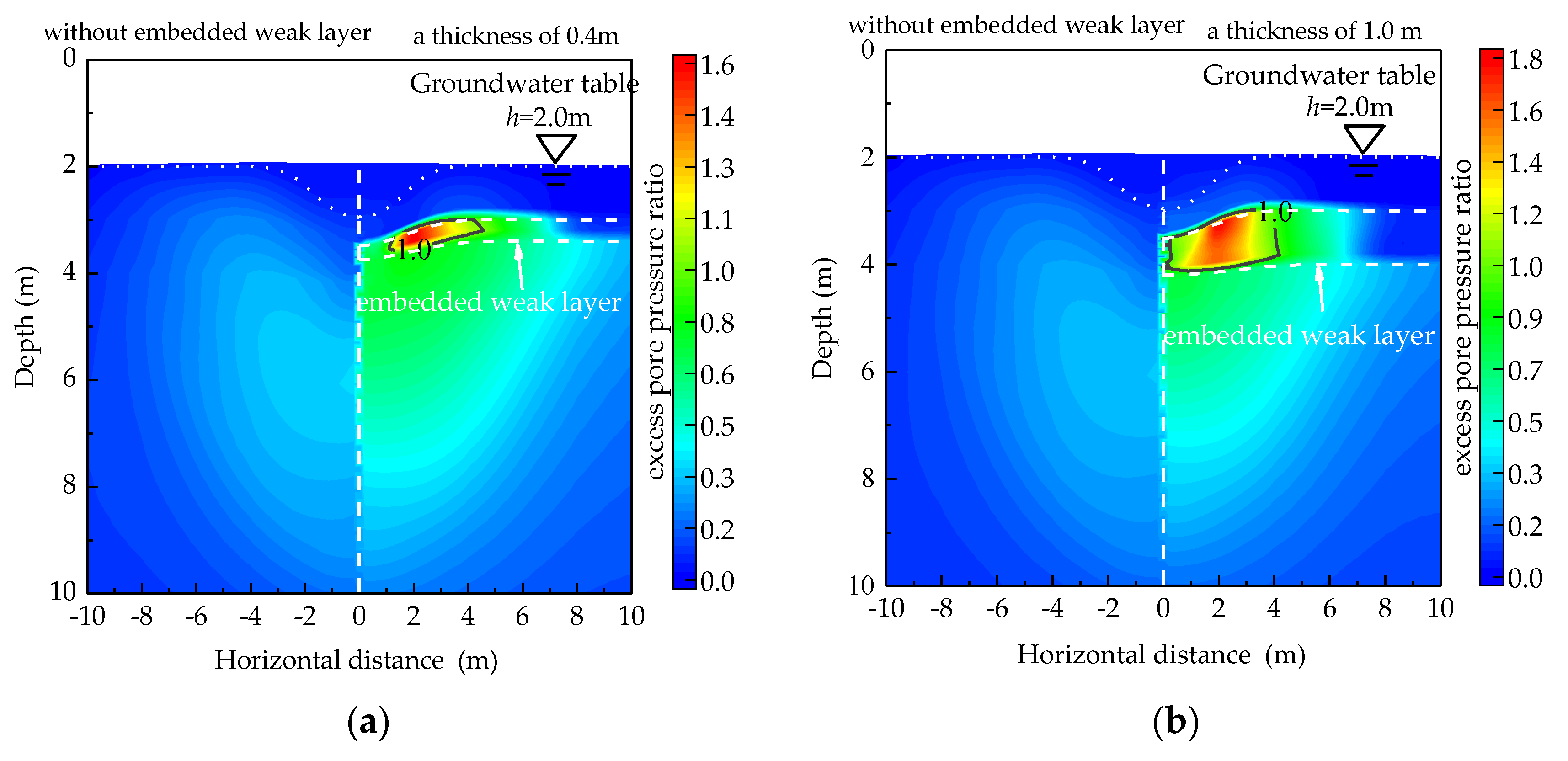
4.2.1. Influences of Thickness of the Embedded Weak Layer
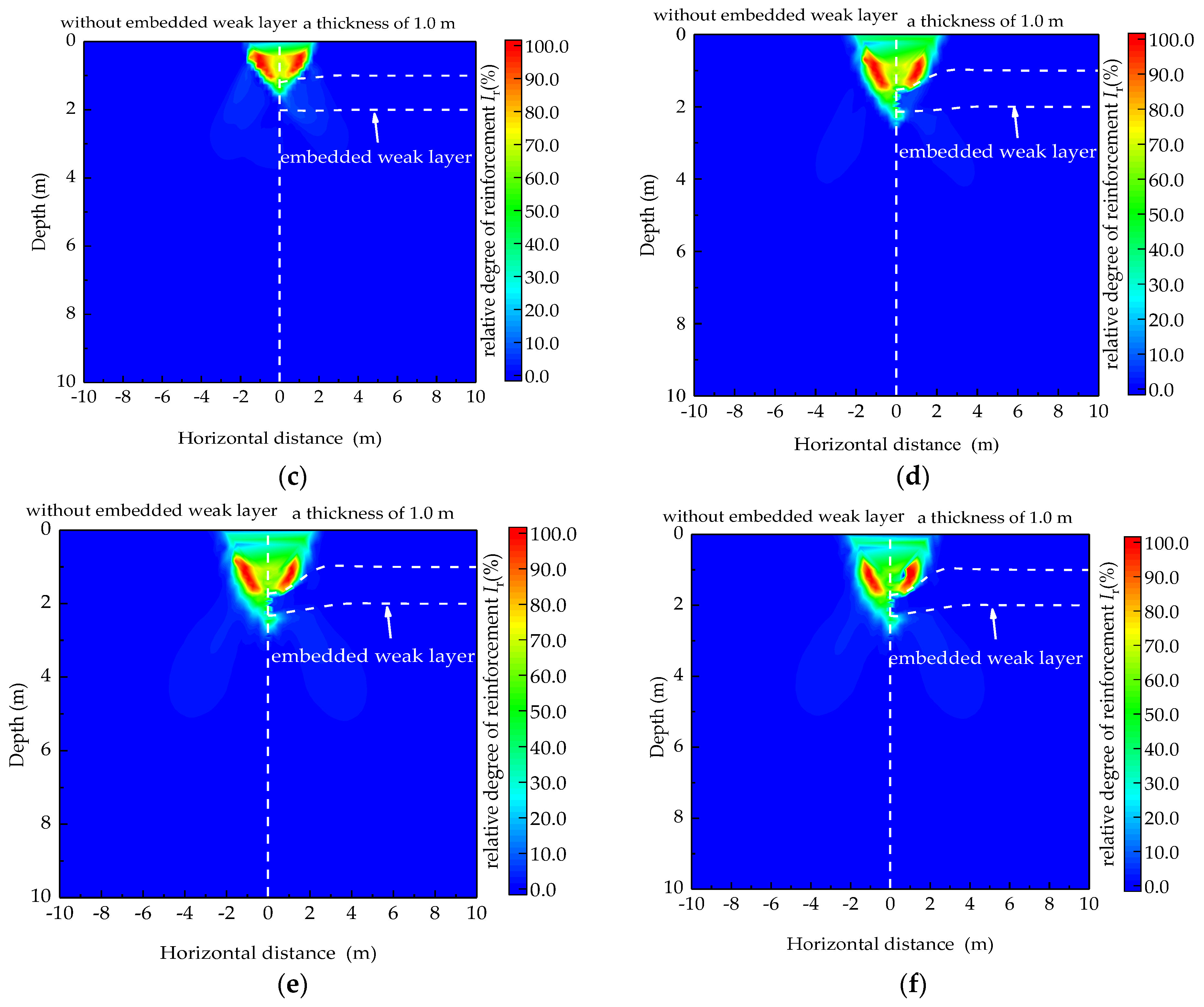
4.2.2. Influences of Depth of the Embedded Weak Layer
4.2.3. Effect of Tamping Energy
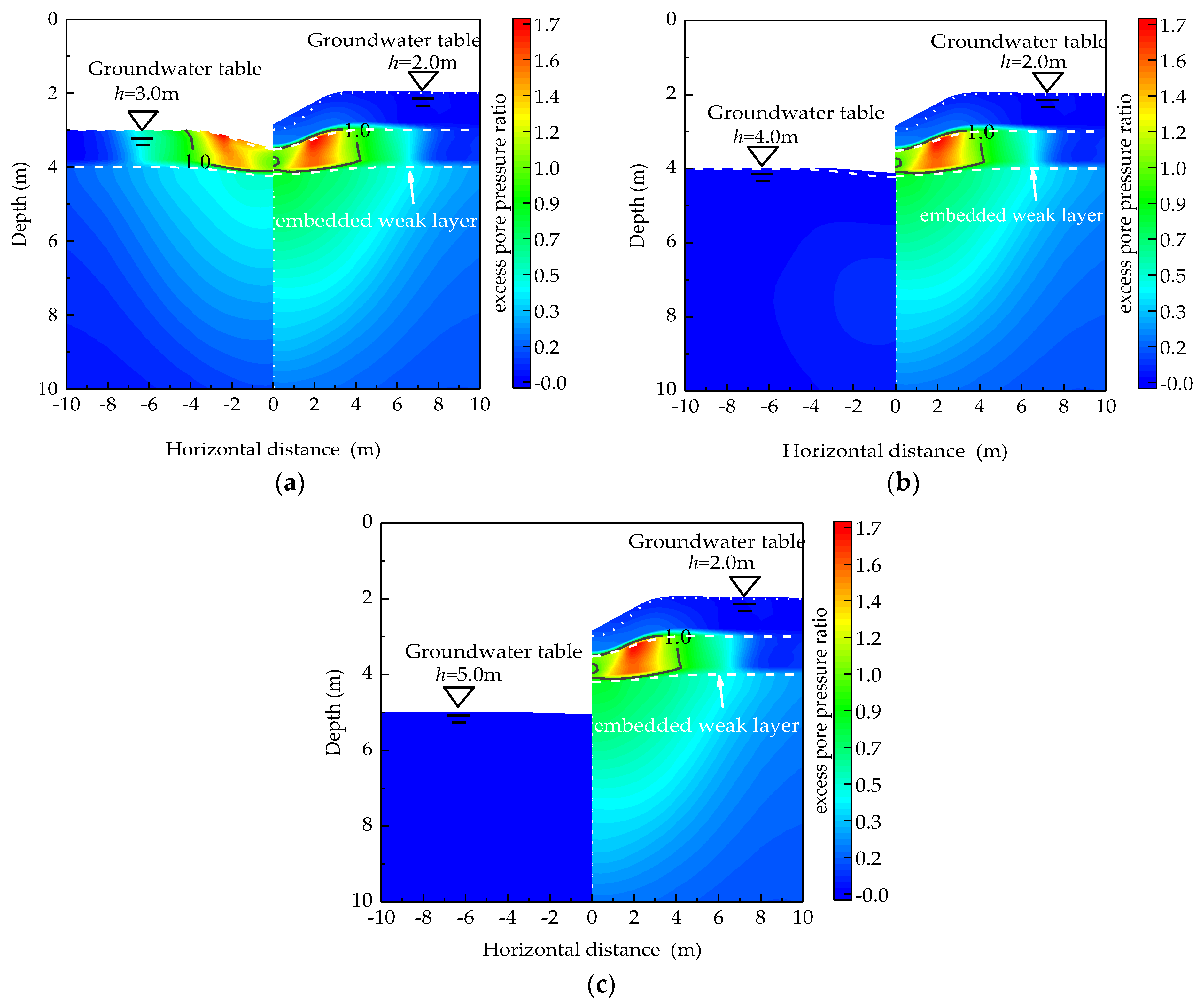
4.2.4. Effect of Groundwater Table
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hasheminezhad, A.; Bahadori, H. Seismic response of shallow foundations over liquefiable soils improved by deep soil mixing columns. Comput. Geotech. 2019, 110, 251–273. [Google Scholar] [CrossRef]
- Bahadori, H.; Farzalizadeh, R.; Barghi, A.; Hasheminezhad, A. A comparative study between gravel and rubber drainage columns for mitigation of liquefaction hazards. J. Rock Mech. Geotech. Eng. 2018, 10, 924–934. [Google Scholar] [CrossRef]
- Bahadori, H.; Motamedi, H.; Hasheminezhad, A.; Motamed, R. Shaking table tests on shallow foundations over geocomposite and geogrid-reinforced liquefiable soils. Soil Dyn. Earthq. Eng. 2020, 128, 105896. [Google Scholar] [CrossRef]
- Jun, C.A.I.; Zhang, J.; Guangyin, D.U.; Han, X.I.A. Application of the dynamic compaction method for ground improvement of collapsible loess in Qinhai. Teknik Dergi 2022, 33, 11455–11472. [Google Scholar]
- Majik, R.K.; Savoikar, P.P. Ground modification techniques for deep soft soils sites in Goa region. In Ground Improvement and Reinforced Soil Structures; Springer: Singapore, 2022; pp. 409–421. [Google Scholar]
- Bo, M.W.; Na, Y.M.; Arulrajah, A.; Chang, M.F. Densification of granular soil by dynamic compaction. Proc. Inst. Civ. Eng. Ground Improv. 2009, 162, 121–132. [Google Scholar] [CrossRef]
- Feng, S.J.; Tan, K.; Shui, W.H.; Zhang, Y. Densification of desert sands by high energy dynamic compaction. Eng. Geol. 2013, 157, 48–54. [Google Scholar] [CrossRef]
- Shenthan, T.; Nashed, R.; Thevanayagam, S.; Martin, G.R. Liquefaction mitigation in silty soils using composite stone columns and dynamic compaction. Earthq. Eng. Eng. Vib. 2004, 3, 39–50. [Google Scholar] [CrossRef]
- Cao, Y.C.; Wang, W.T. Seabed ground improvement in coastal reclamation area by heavy tamping after rockfilling displacement. Mar. Georesources Geotechnol. 2007, 25, 1–14. [Google Scholar] [CrossRef]
- Mayne, P.W.; Jones, J.S., Jr.; Dumas, J.C. Ground response to dynamic compaction. J. Geotech. Eng. 1984, 110, 757–774. [Google Scholar] [CrossRef]
- Nashed, R. Liquefaction Mitigation Of Silty Soils Using Dynamic Compaction; State University of New York at Buffalo: New York, NY, USA, 2006. [Google Scholar]
- Feng, S.J.; Shui, W.H.; Tan, K.; Gao, L.Y.; He, L.J. Field evaluation of dynamic compaction on granular deposits. J. Perform. Constr. Facil. 2011, 25, 241–249. [Google Scholar] [CrossRef]
- Feng, S.J.; Du, F.L.; Shi, Z.M.; Shui, W.H.; Tan, K. Field study on the reinforcement of collapsible loess using dynamic compaction. Eng. Geol. 2015, 185, 105–115. [Google Scholar] [CrossRef]
- Lee, F.H.; Gu, Q. Method for estimating dynamic compaction effect on sand. J. Geotech. Geoenviron. Eng. 2004, 130, 139–152. [Google Scholar] [CrossRef]
- Wang, W.; Chen, J.J.; Wang, J.H. Estimation method for ground deformation of granular soils caused by dynamic compaction. Soil Dyn. Earthq. Eng. 2017, 92, 266–278. [Google Scholar] [CrossRef]
- Dou, J.; Chen, J.; Wang, W. Method for estimating the degree of improvement in soil between adjacent tamping locations under dynamic compaction. Int. J. Geomech. 2019, 19, 04019134. [Google Scholar] [CrossRef]
- Zhou, C.; Jiang, H.; Yao, Z.; Li, H.; Yang, C.; Chen, L.; Geng, X. Evaluation of dynamic compaction to improve saturated foundation based on the fluid-solid coupled method with soil cap model. Comput. Geotech. 2020, 125, 103686. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, C.; Qi, H.; Yao, K.; Yao, Z.; Wang, K.; Ji, P.; Li, H. Evaluation on improvement zone of foundation after dynamic compaction. Appl. Sci. 2021, 11, 2156. [Google Scholar] [CrossRef]
- Perucho, A.; Olalla, C. Dynamic consolidation of a saturated plastic clayey fill. Proc. Inst. Civ. Eng. Ground Improv. 2006, 10, 55–68. [Google Scholar] [CrossRef]
- Feng, S.J.; Lu, S.F.; Shi, Z.M.; Shui, W.H. Densification of loosely deposited soft soils using the combined consolidation method. Eng. Geol. 2014, 181, 169–179. [Google Scholar] [CrossRef]
- Feng, S.J.; Du, F.L.; Chen, H.X.; Mao, J.Z. Centrifuge modeling of preloading consolidation and dynamic compaction in treating dredged soil. Eng. Geol. 2017, 226, 161–171. [Google Scholar] [CrossRef]
- Jia, M.; Cheng, J.; Liu, B.; Ma, G. Model tests of the influence of ground water level on dynamic compaction. Bull. Eng. Geol. Environ. 2021, 80, 3065–3078. [Google Scholar] [CrossRef]
- Abdizadeh, D.; Pakbaz, M.S.; Nadi, B. Numerical modeling of lateral dynamic compaction on the slope in dry sand. KSCE J. Civ. Eng. 2021, 25, 398–403. [Google Scholar] [CrossRef]
- Yao, K.; Yao, Z.Y.; Song, X.G.; Shang, Q.S. Test study of pore water pressure during dynamic compaction at the subgrade of highway in the Yellow River Flood Area. In Advanced Materials Research; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2012; Volume 374, pp. 436–439. [Google Scholar]
- Yao, K.; Rong, Y.; Yao, Z.; Shi, C.; Yang, C.; Chen, L.; Zhang, B.; Jiang, H. Effect of water level on dynamic compaction in silty ground of Yellow River alluvial plain. Arab. J. Geosci. 2022, 15, 1–16. [Google Scholar] [CrossRef]
- Chen, X.Y.; Guo, B.X.; Xie, Y.L.; Ma, Y.F. Field Test on influencing factors and vibration law of dynamic compaction for sand foundation. Pet. Eng. Constr. 2016, 42, 64–68. (In Chinese) [Google Scholar]
- Song, X.G.; Sun, R.S.; Dong, H.; Liu, X.L.; Wang, K.; Bo, M.; Sang, X.R. Field test of foundation dynamic compaction about soft interlayer structure in yellow river flood area. J. Archit. Civ. Eng. 2018, 35, 26–32. (In Chinese) [Google Scholar]
- Jia, M.; Zhao, Y.; Zhou, X. Field studies of dynamic compaction on marine deposits. Mar. Georesources Geotechnol. 2016, 34, 313–320. [Google Scholar] [CrossRef]
- Ye, F.; Goh, S.; Lee, F. A method to solve biot’s uu formulation for soil dynamics applications using the abaqus/explicit platform. Numer. Methods Geotech. Eng. 2010, 417–422. [Google Scholar]
- Ye, F.; Goh, S.H.; Lee, F.H. Dual-phase coupled u–U analysis of wave propagation in saturated porous media using a commercial code. Comput. Geotech. 2014, 55, 316–329. [Google Scholar] [CrossRef]
- Zhou, C.; Yao, K.; Rong, Y.; Lee, F.H.; Zhang, D.; Jiang, H.; Yang, C.; Yao, Z.; Chen, L. Numerical investigation on zone of improvement for dynamic compaction of sandy ground with high groundwater table. Acta Geotech. 2022, 1–15. [Google Scholar] [CrossRef]
- Yao, Z.; Zhou, C.; Lin, Q.; Yao, K.; Satchithananthan, U.; Lee, F.H.; Wang, S. Effect of dynamic compaction by multi-point tamping on the densification of sandy soil. Comput. Geotech. 2022, 151, 104949. [Google Scholar] [CrossRef]
- Helwany, S. Applied Soil Mechanics with ABAQUS Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Miao, L.; Chen, G.; Hong, Z. Application of dynamic compaction in highway: A case study. Geotech. Geol. Eng. 2006, 24, 91–99. [Google Scholar] [CrossRef]
- Yi, J.T.; Zhang, L.; Ye, F.J.; Goh, S.H. One-dimensional transient wave propagation in a dry overlying saturated ground. KSCE J. Civ. Eng. 2019, 23, 4297–4310. [Google Scholar] [CrossRef]
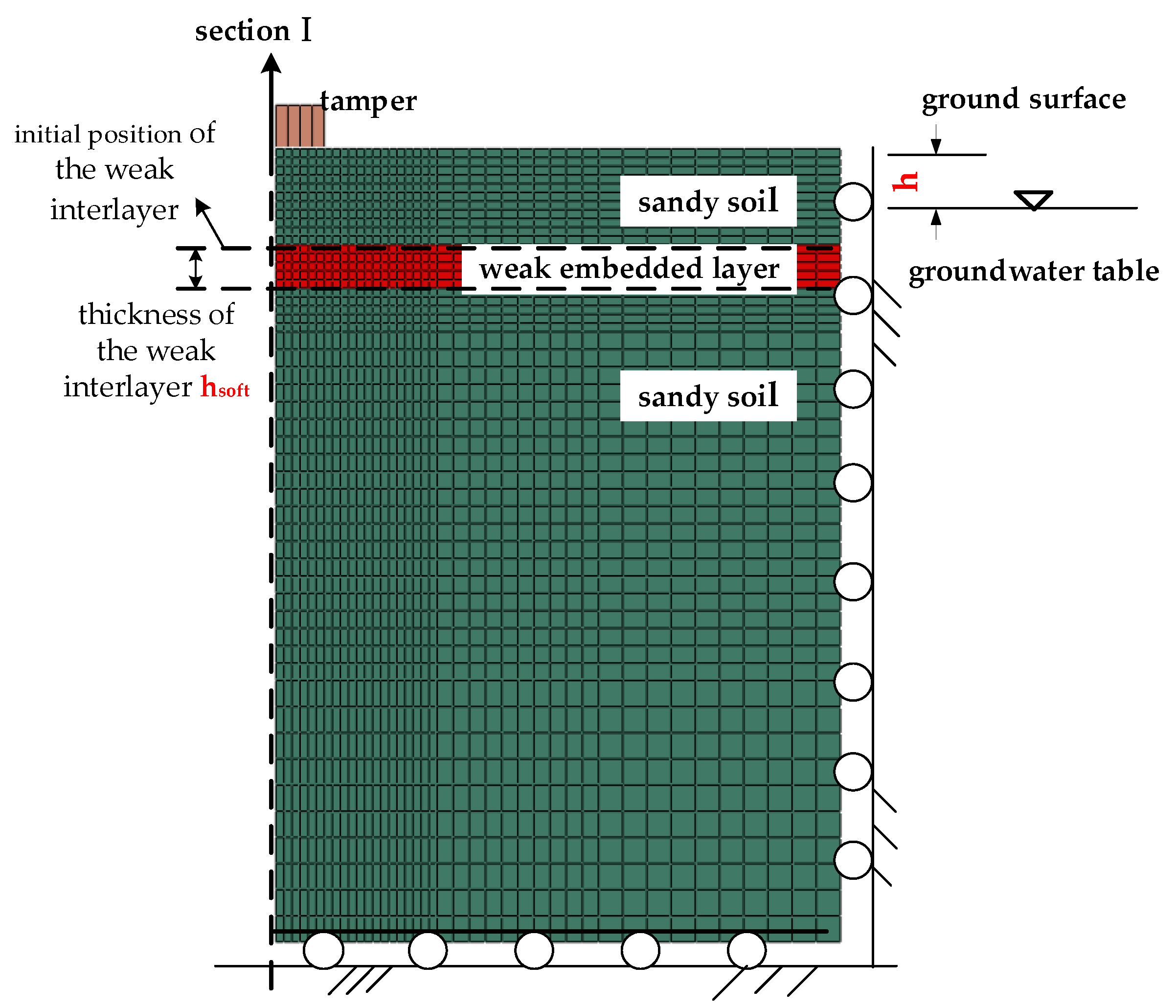
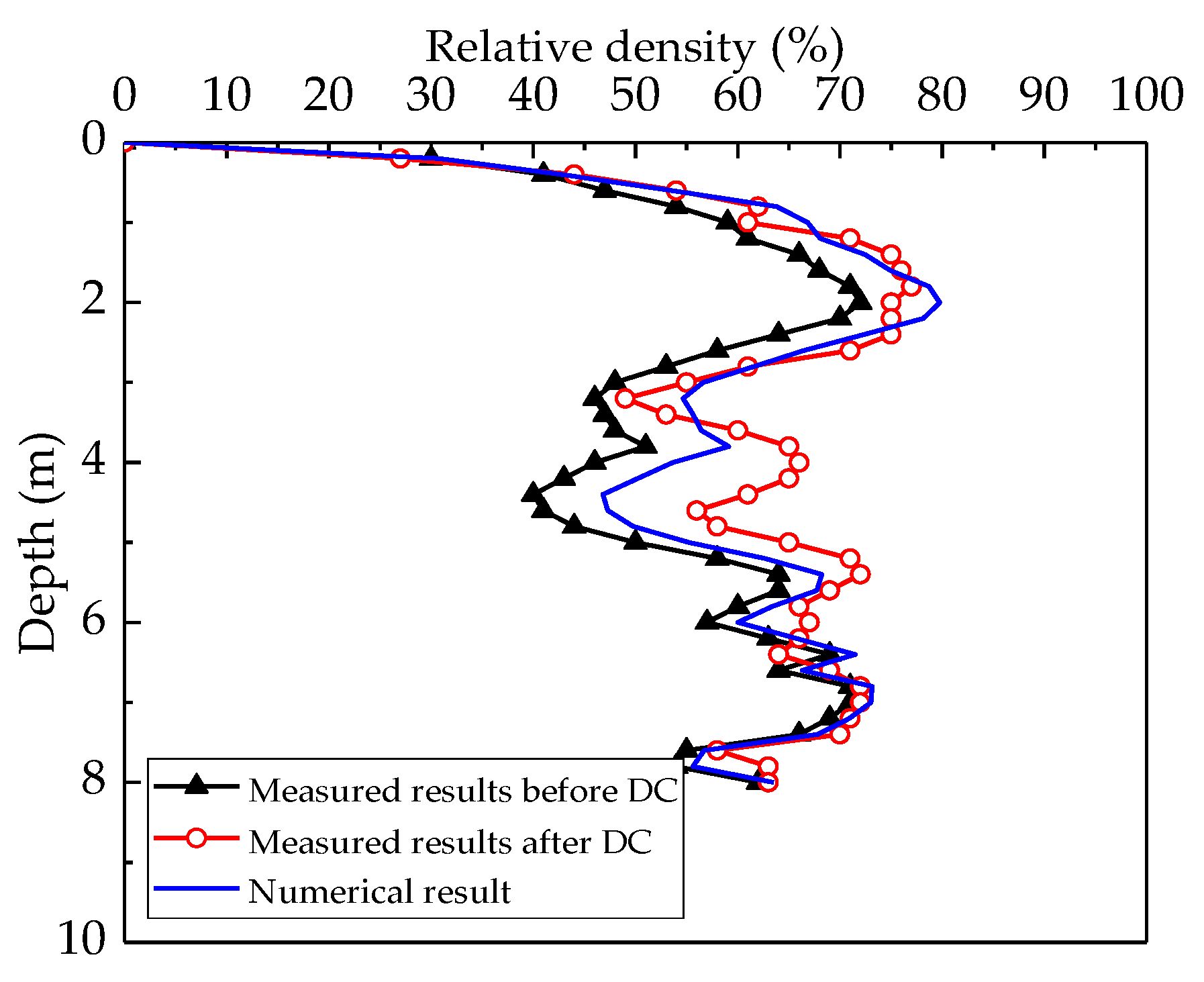
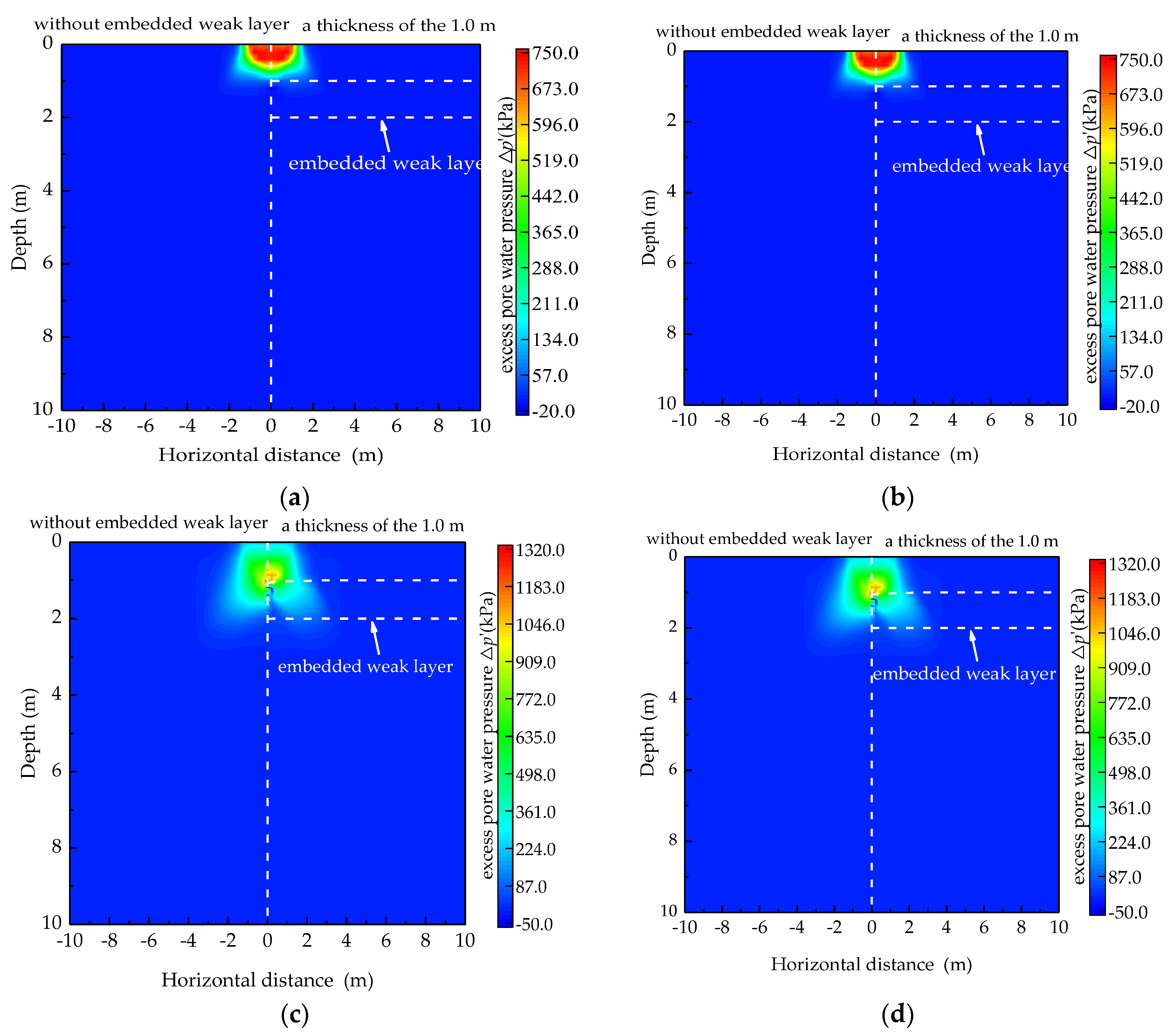

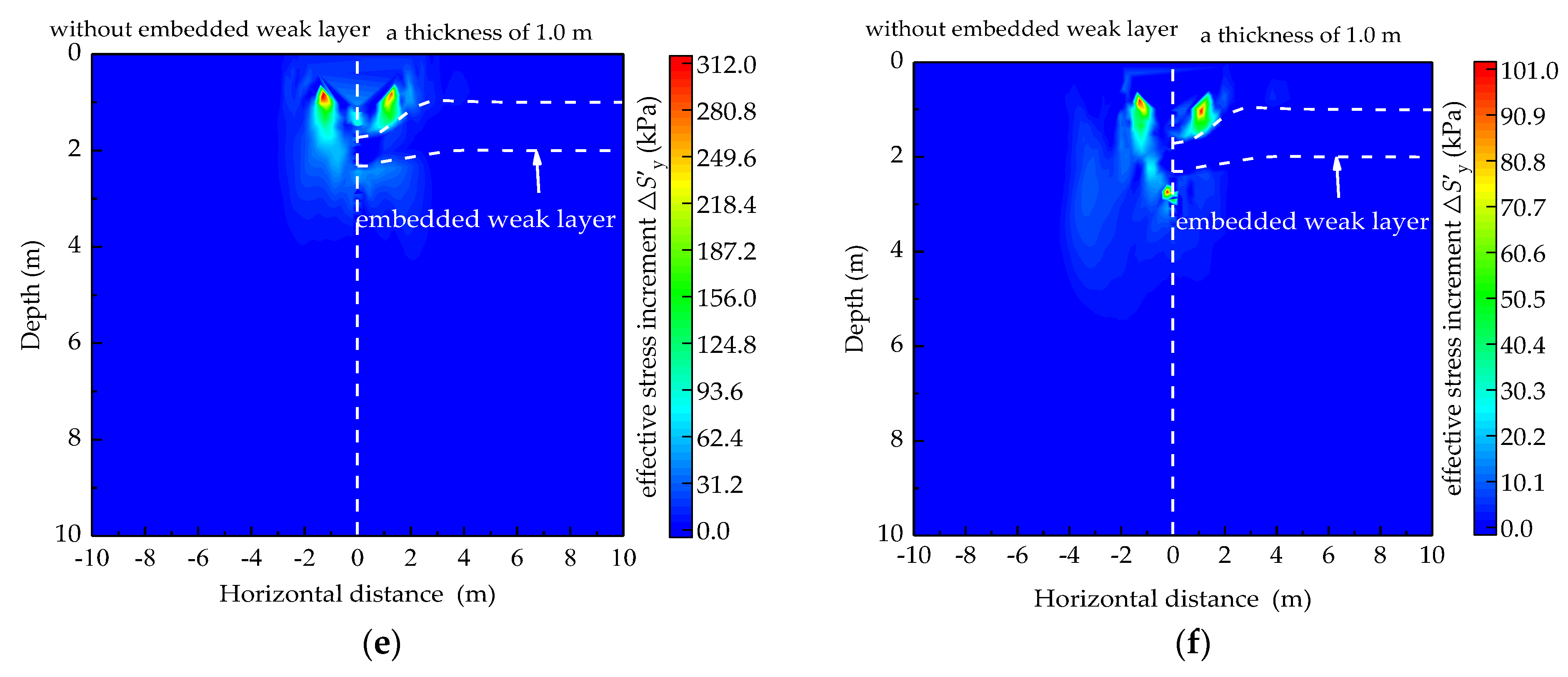

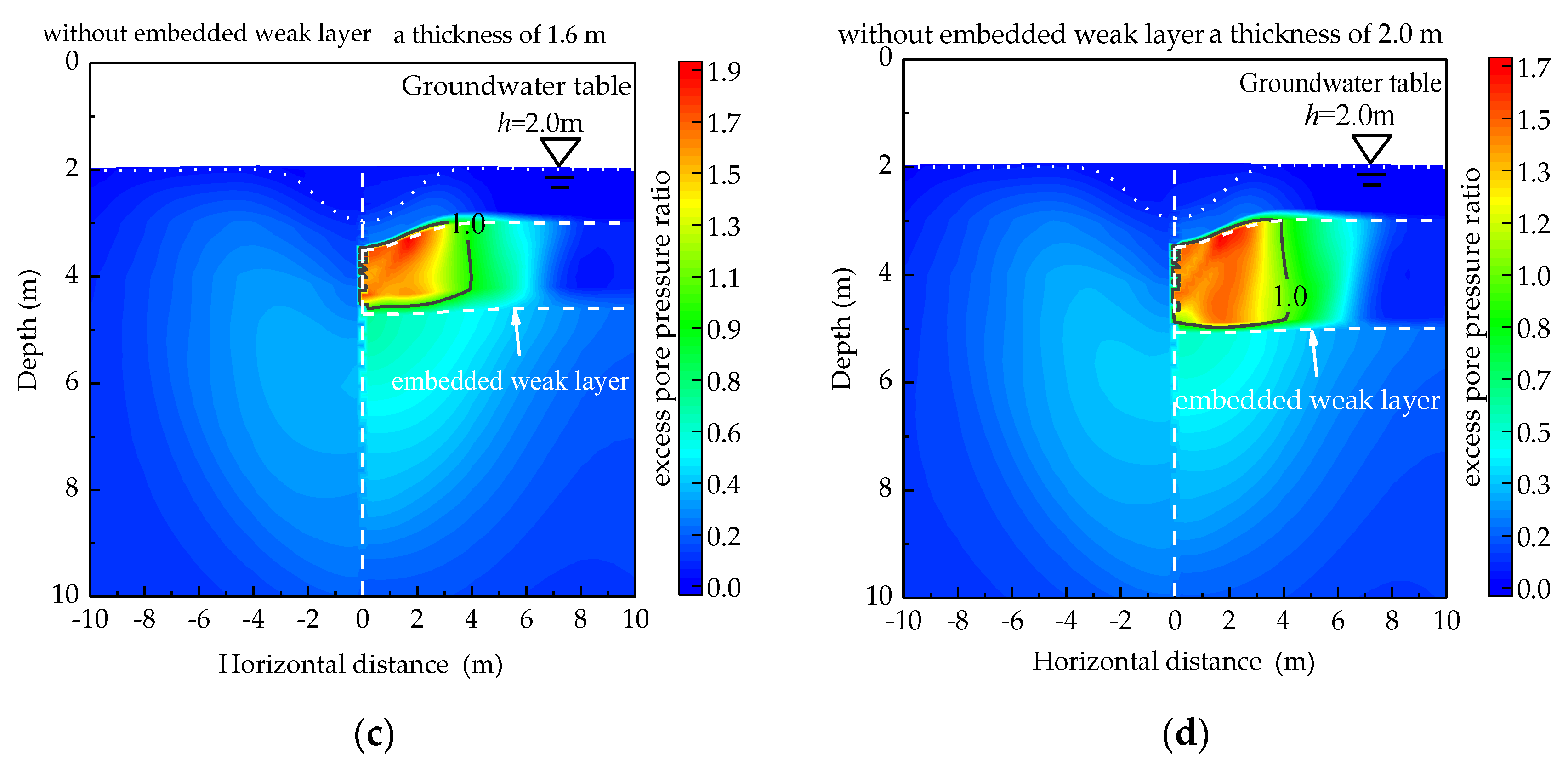


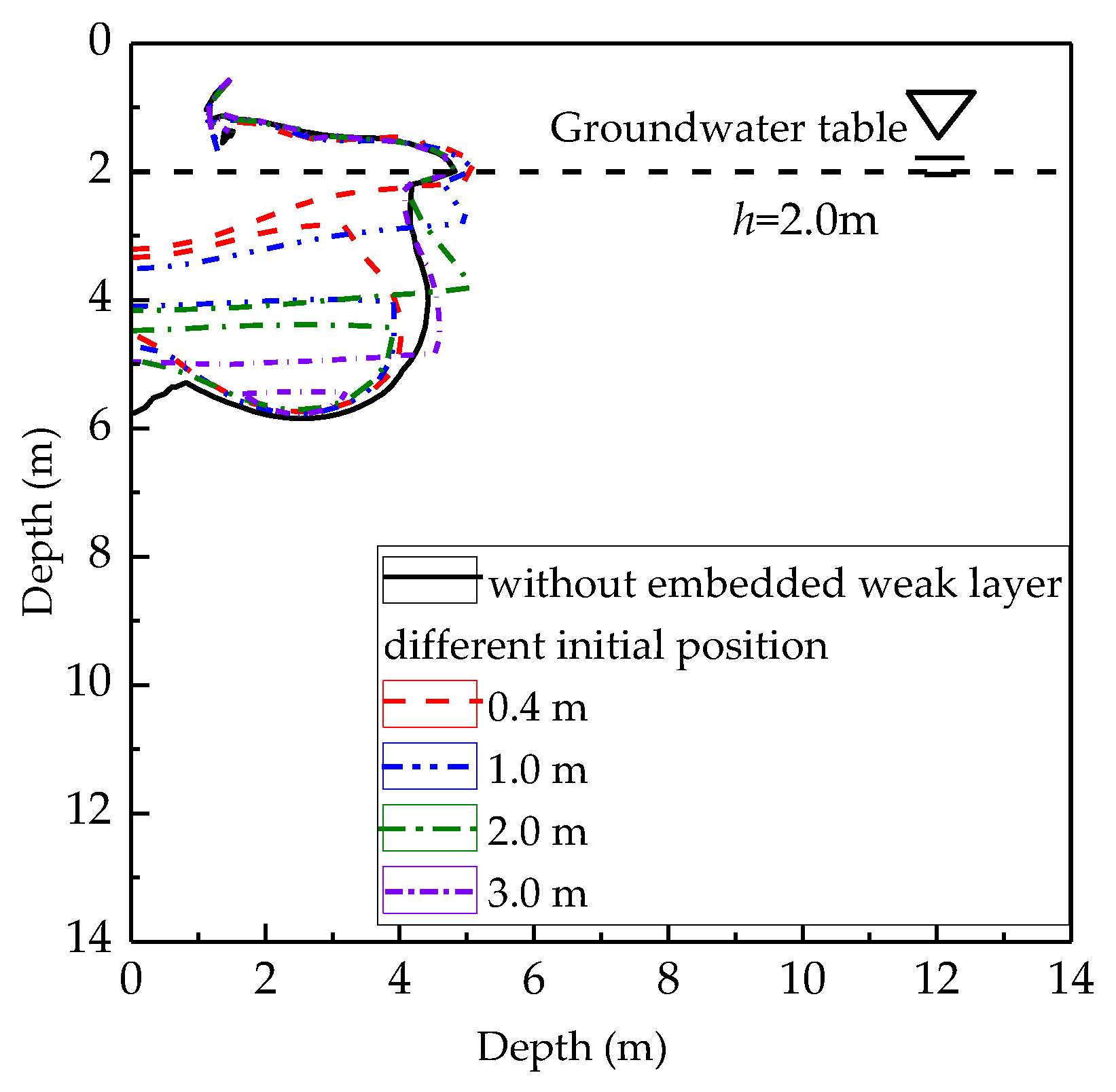
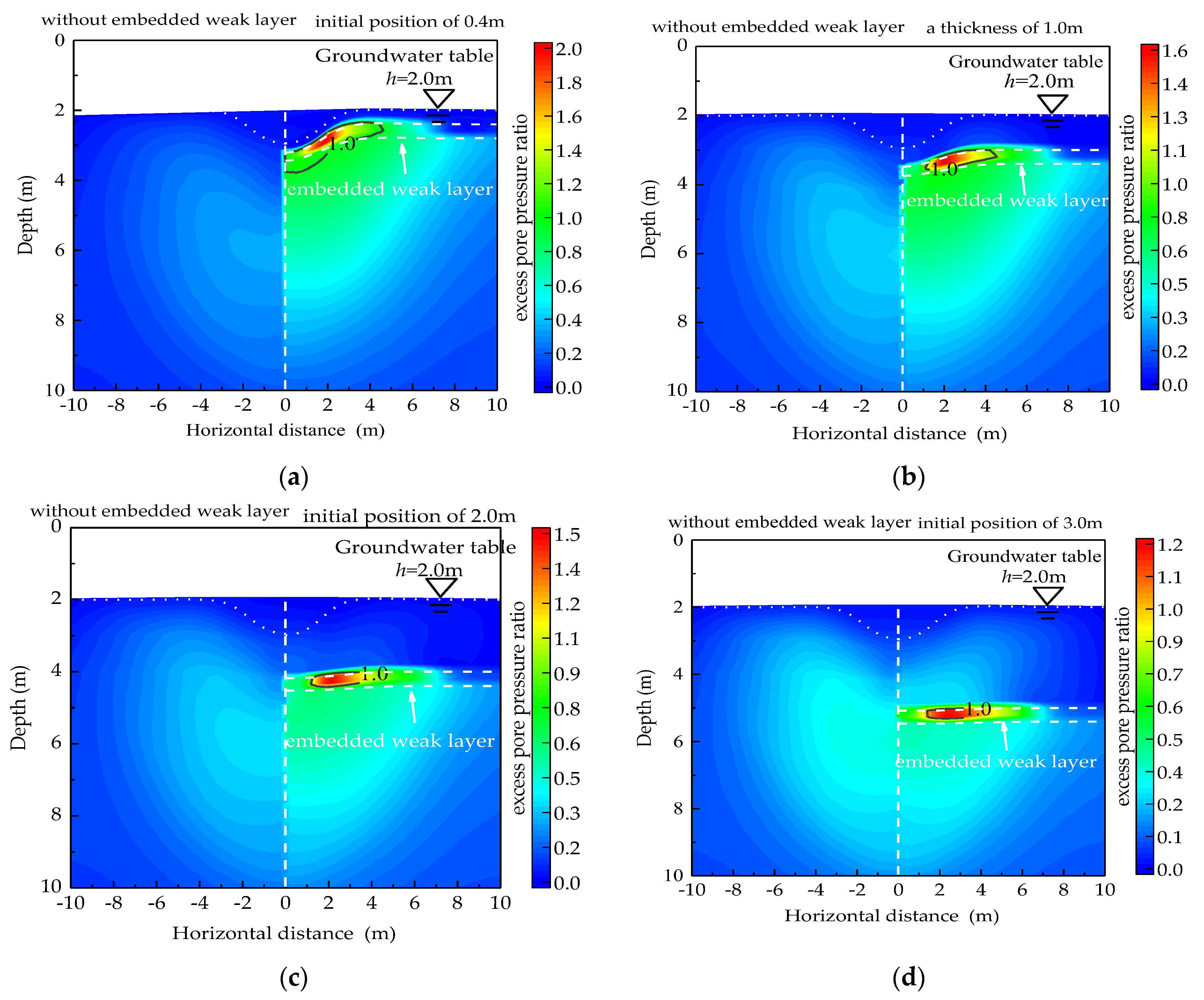
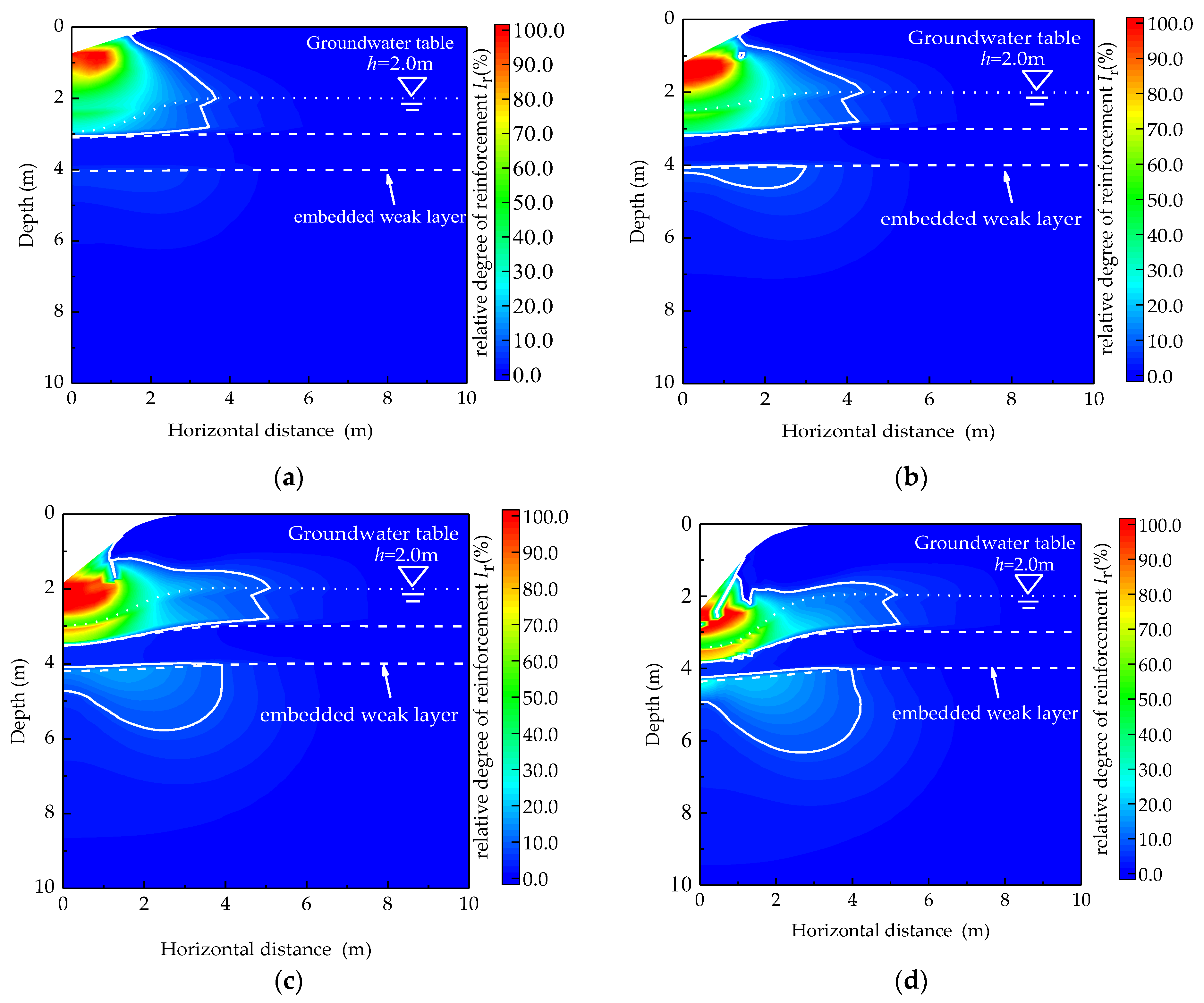
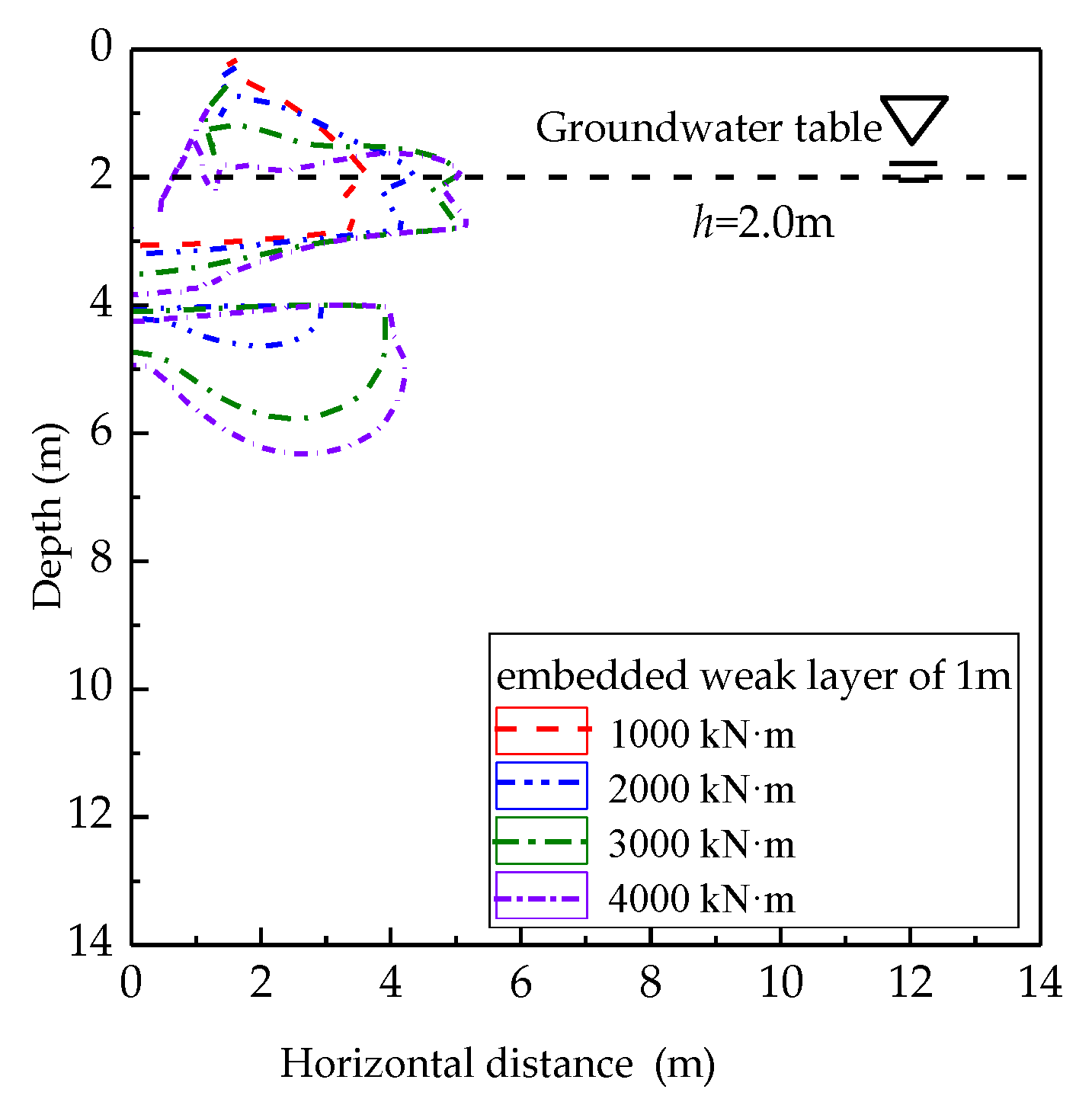
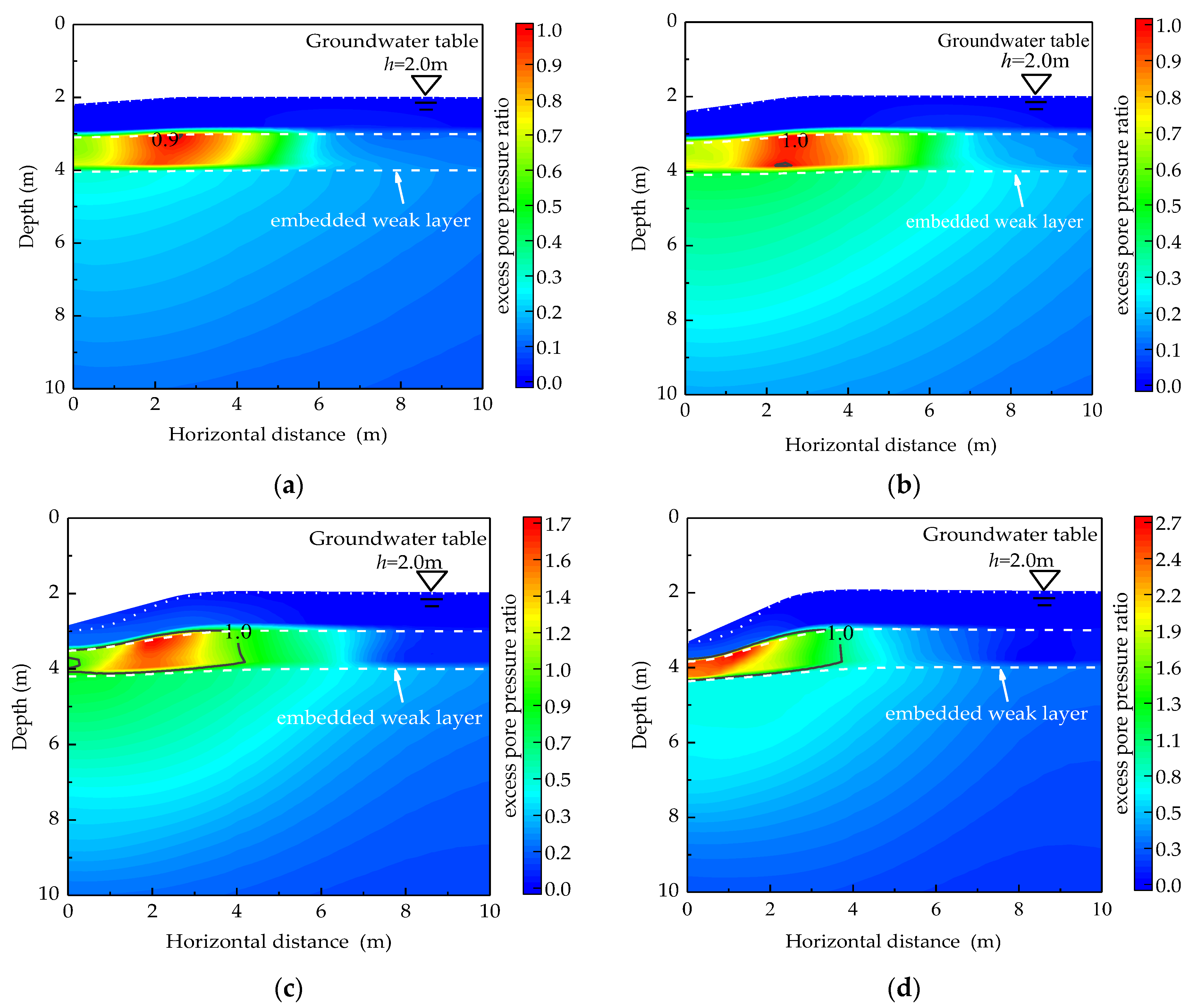
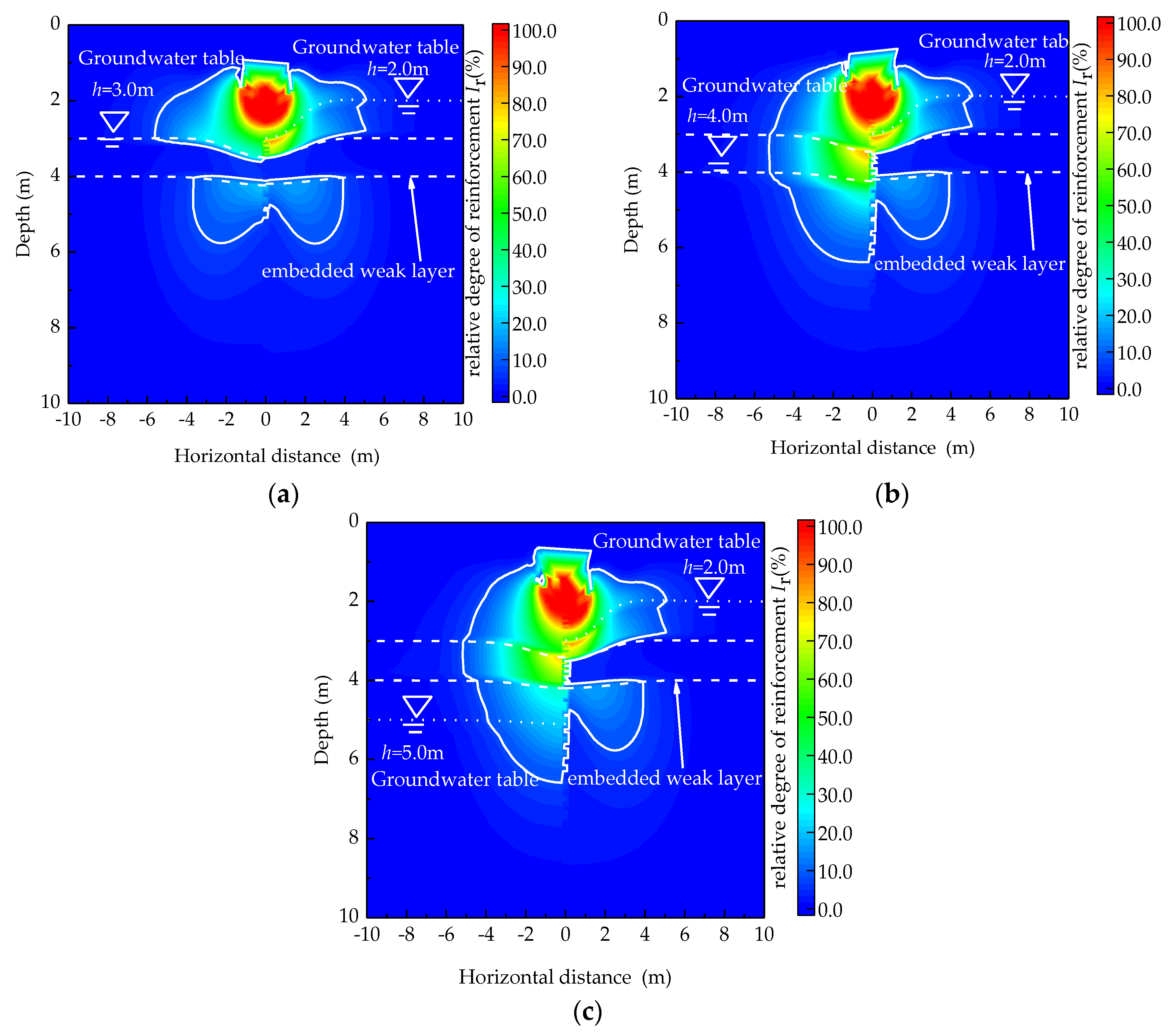
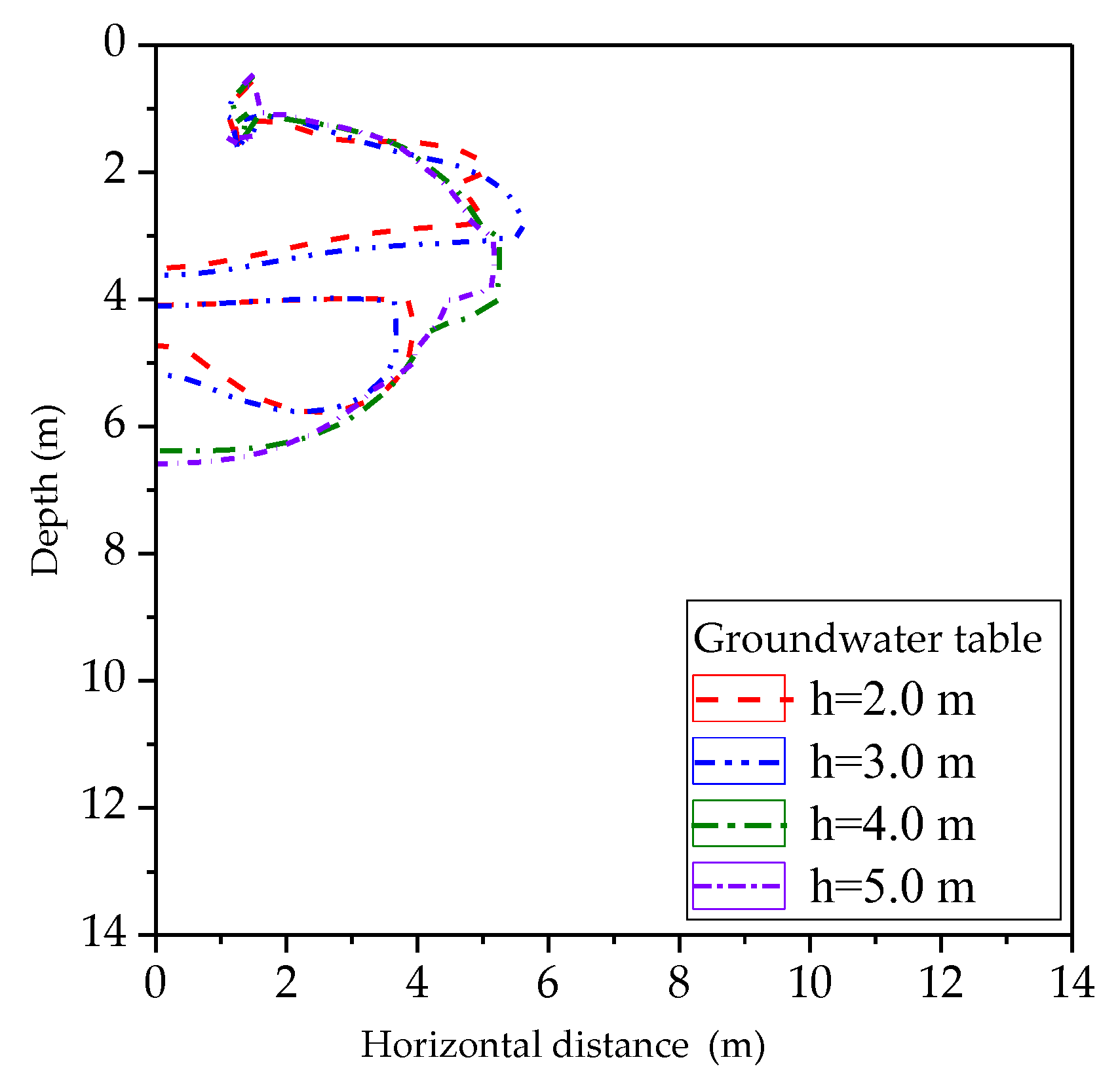
| Reference | Ground Stratum | Research Questions | Main Conclusion | Investigation Method |
|---|---|---|---|---|
| Lee, F. H., & Gu, Q. [14] | Uniform | A two-dimensional finite element method based on the cap model is used to study the influence of different construction parameters and soil properties on the reinforcement effect by DC. | This paper proposes a chart method for predicting the reinforcement effect of sandy soil foundation. | Numerical method |
| Wang et al. [15] | Uniform | Ls-dyna was used to investigate influence of different parameters of DC and soil properties’ conditions. | This paper presents a estimation method for ground deformation of granular soils caused by DC. | Numerical method |
| Dou et al. [16] | Uniform | A three-dimensional finite element analysis is conducted to investigate the influence of soil properties, different parameters of DC on the soil improvement between adjacent tamping locations by multi-point tamping. | This paper proposes a method for estimating the degree of final soil improvement between adjacent tamping locations. | Numerical method |
| Zhou et al. [17] | Uniform | This paper developed a the fluid–solid coupled method incorporating the cap model to analyze the improvement on saturated foundation by DC. | This paper focuses on the two key elements, which influenced improvement of saturated foundation: groundwatertable and sitecondition. | Numerical method |
| Zhou et al. [18] | Uniform | A three-dimensional (3D) finite element (FE) model based on cap modelis established to deal with the problem of the factors affecting the sandy soil improvement effect. | A formula considering the various factors of DC is put forward to predict the reinforcement effect by DC | Numerical method |
| Perucho, A., & Olalla, C. [19] | a plastic clayey fill in a port area | Dynamic consolidation was used to reinforce a plastic clay in the infill port area. | Dynamic consolidation proved to be an effective form of soft foundation treatment for plastic clayey fill in a port area. | Field test |
| Feng et al. [20] | soft soils | The dynamic consolidation (heavy tamping) is performed in a site with loosely deposited soft soils in the Yangtze River Delta of China. | The allowable bearing capacity and the depth of improvement after DC meet the design requirements. | Field test |
| Feng et al. [21] | Uniform | A novel method of modeling preloading consolidation and DC in centrifuge are developed in this study. | The results of test are comprehensively analyzed and discussed to have a better understanding of preloading consolidation and DC. | Centrifuge test |
| Jia et al. [22] | Uniform | Model tests of DC on sand with different groundwater tables are performed to investigate the effect of groundwater depth in DC. | Through the comparison of dynamic responses of soils, dewatering is used for the treatment of saturated soil with groundwater. | Model tests |
| Abdizadeh et al. [23] | Uniform | ABACUS 6.14 software is used to simulate three-dimensional model of lateral DC in the slope. | Impact velocity is the major factor that influences soil improvement for three different slope. | Numerical method |
| Soil Layer | ρ (kg/m3) | E (Mpa) | v | φ | c (kPa) | R | W | D (kPa−1) |
|---|---|---|---|---|---|---|---|---|
| Sand | 1500 | 25.0 | 0.30 | 30° | 10 | 4.33 | 0.4 | 0.00018 |
| Weak layer | 1500 | 10.0 | 0.30 | 0° | 10 | 4.33 | 0.5 | 0.0003 |
| Sand | 1500 | 25.0 | 0.30 | 30° | 10 | 4.33 | 0.4 | 0.00018 |
| Soil Layer | ρf (kg/m3) | k (m/s) | v | Ks (kPa) | Kf (kPa) | n |
|---|---|---|---|---|---|---|
| Sand | 1000 | 10−2 | 0.30 | 1 × 104 | 2.0 × 1011 | 0.4382 |
| Weak layer | 1000 | 10−7 | 0.30 | 1 × 104 | 2.0 × 1011 | 0.4382 |
| Sand | 1000 | 10−2 | 0.30 | 1 × 104 | 2.0 × 1011 | 0.4382 |
| Case | Groundwater Table (m) | Depth of Soft Interlayer (m) | Thickness of Soft Interlayer (m) | Tamping Energy (kN·m) |
|---|---|---|---|---|
| 1 | 2.0 | 3.0 | 0.4 | 3000 |
| 2 | 2.0 | 3.0 | 1.0 | 3000 |
| 3 | 2.0 | 3.0 | 1.6 | 3000 |
| 4 | 2.0 | 3.0 | 2.0 | 3000 |
| 5 | 2.0 | 0.4 | 0.4 | 3000 |
| 6 | 2.0 | 1.0 | 0.4 | 3000 |
| 7 | 2.0 | 2.0 | 0.4 | 3000 |
| 8 | 2.0 | 3.0 | 0.4 | 3000 |
| 9 | 2.0 | 3.0 | 1.0 | 1000 |
| 10 | 2.0 | 3.0 | 1.0 | 2000 |
| 11 | 2.0 | 3.0 | 1.0 | 3000 |
| 12 | 2.0 | 3.0 | 1.0 | 4000 |
| 13 | 3.0 | 3.0 | 1.0 | 3000 |
| 14 | 4.0 | 3.0 | 1.0 | 3000 |
| 15 | 5.0 | 3.0 | 1.0 | 3000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhou, C.; Xin, G.; Long, G.; Zhang, W.; Li, C.; Zhuang, P.; Yao, Z. Study on Reinforcement Mechanism and Reinforcement Effect of Saturated Soil with a Weak Layer by DC. Appl. Sci. 2022, 12, 9770. https://doi.org/10.3390/app12199770
Li J, Zhou C, Xin G, Long G, Zhang W, Li C, Zhuang P, Yao Z. Study on Reinforcement Mechanism and Reinforcement Effect of Saturated Soil with a Weak Layer by DC. Applied Sciences. 2022; 12(19):9770. https://doi.org/10.3390/app12199770
Chicago/Turabian StyleLi, Jialei, Chong Zhou, Gongfeng Xin, Guanxu Long, Wenliang Zhang, Chao Li, Peizhi Zhuang, and Zhanyong Yao. 2022. "Study on Reinforcement Mechanism and Reinforcement Effect of Saturated Soil with a Weak Layer by DC" Applied Sciences 12, no. 19: 9770. https://doi.org/10.3390/app12199770
APA StyleLi, J., Zhou, C., Xin, G., Long, G., Zhang, W., Li, C., Zhuang, P., & Yao, Z. (2022). Study on Reinforcement Mechanism and Reinforcement Effect of Saturated Soil with a Weak Layer by DC. Applied Sciences, 12(19), 9770. https://doi.org/10.3390/app12199770






