Three-Dimensional Analytical Calculation and Optimization of Plate-Type Permanent Magnet Electrodynamic Suspension System
Abstract
:1. Introduction
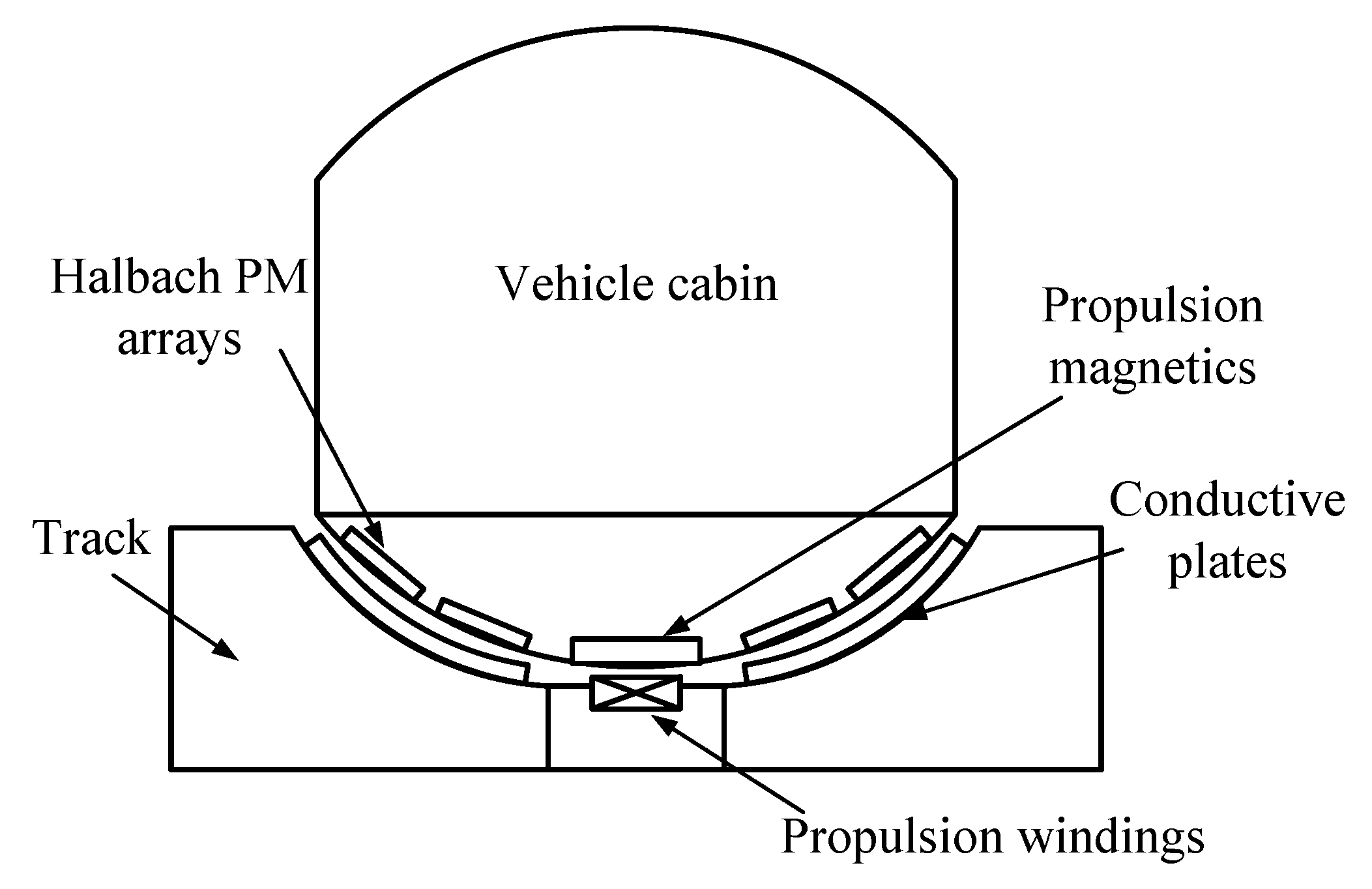
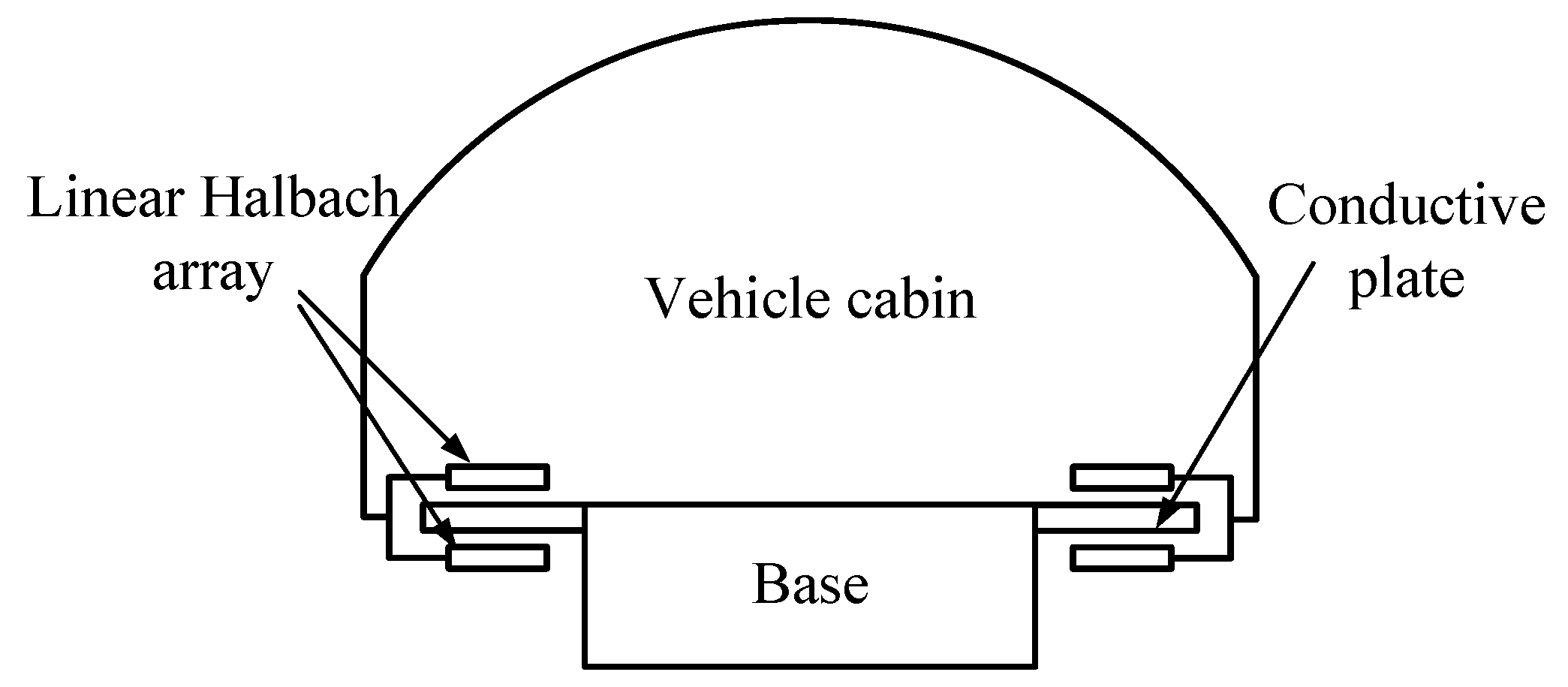
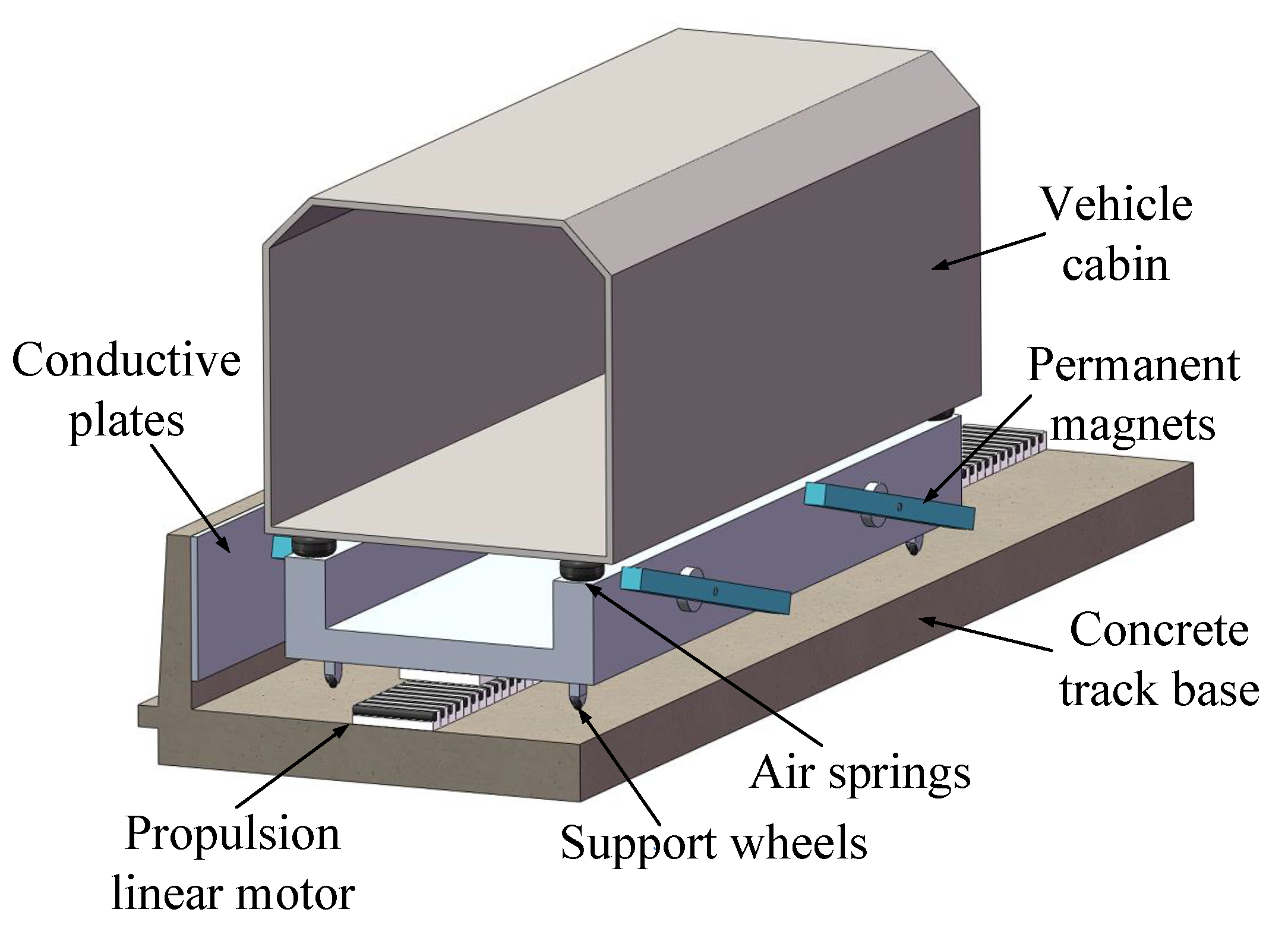
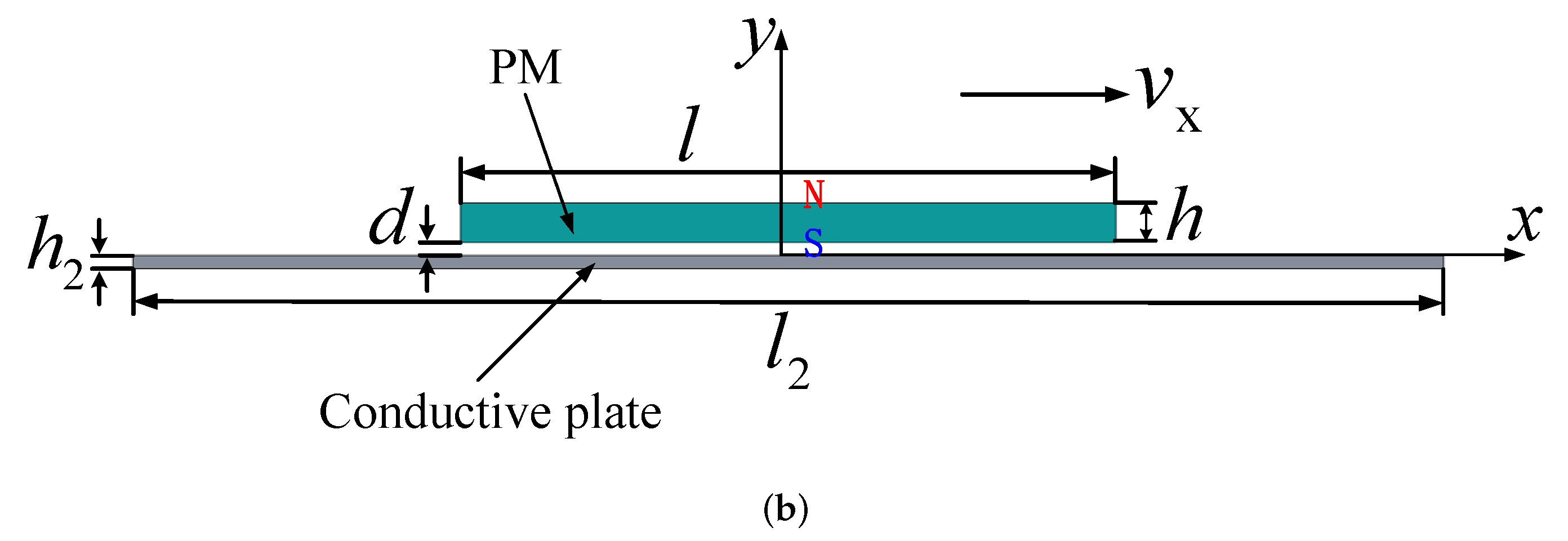
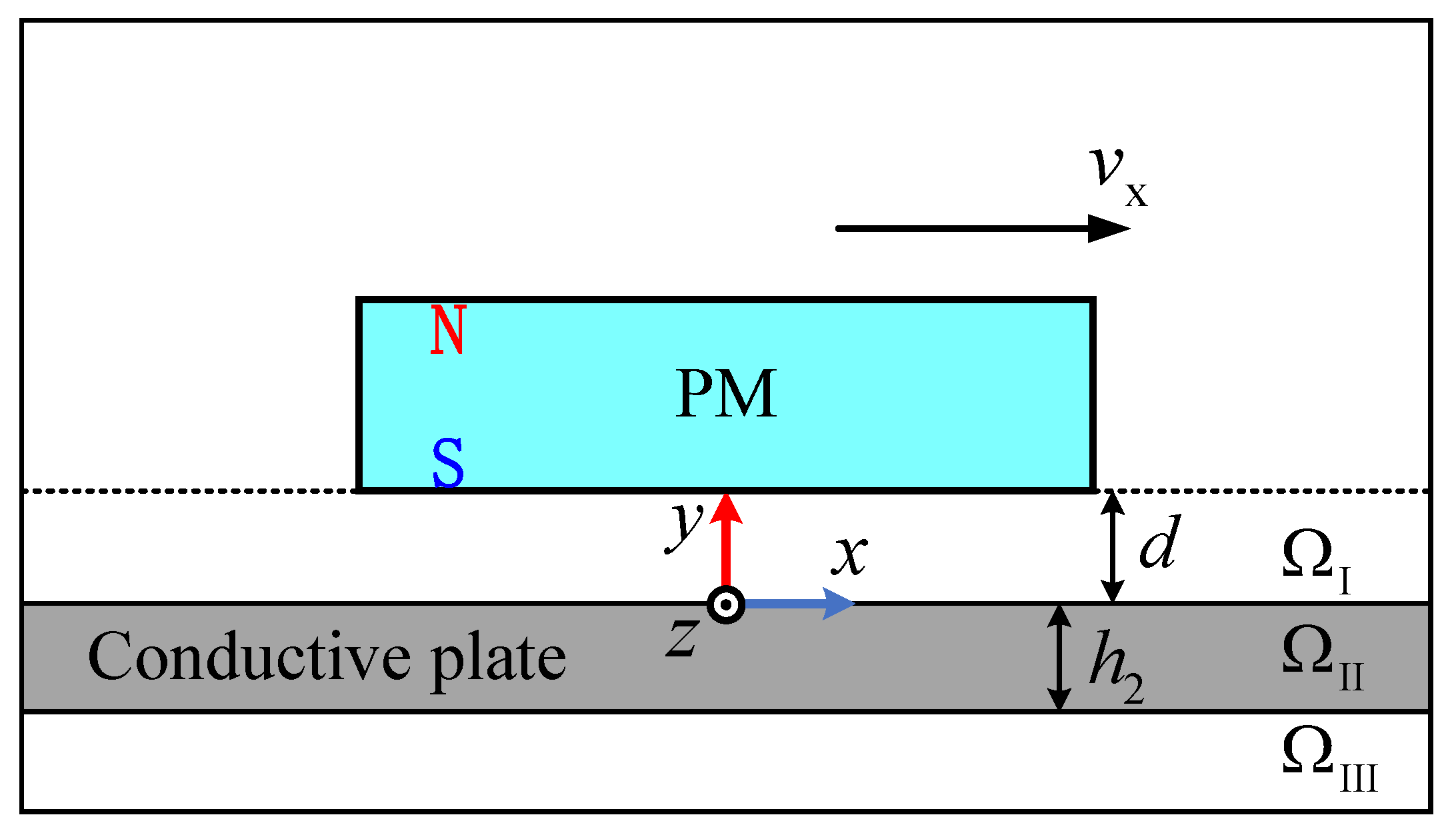
2. Structure of the Suspension System
3. Analytical Model Calculation and Validation
3.1. Analytical Calculation
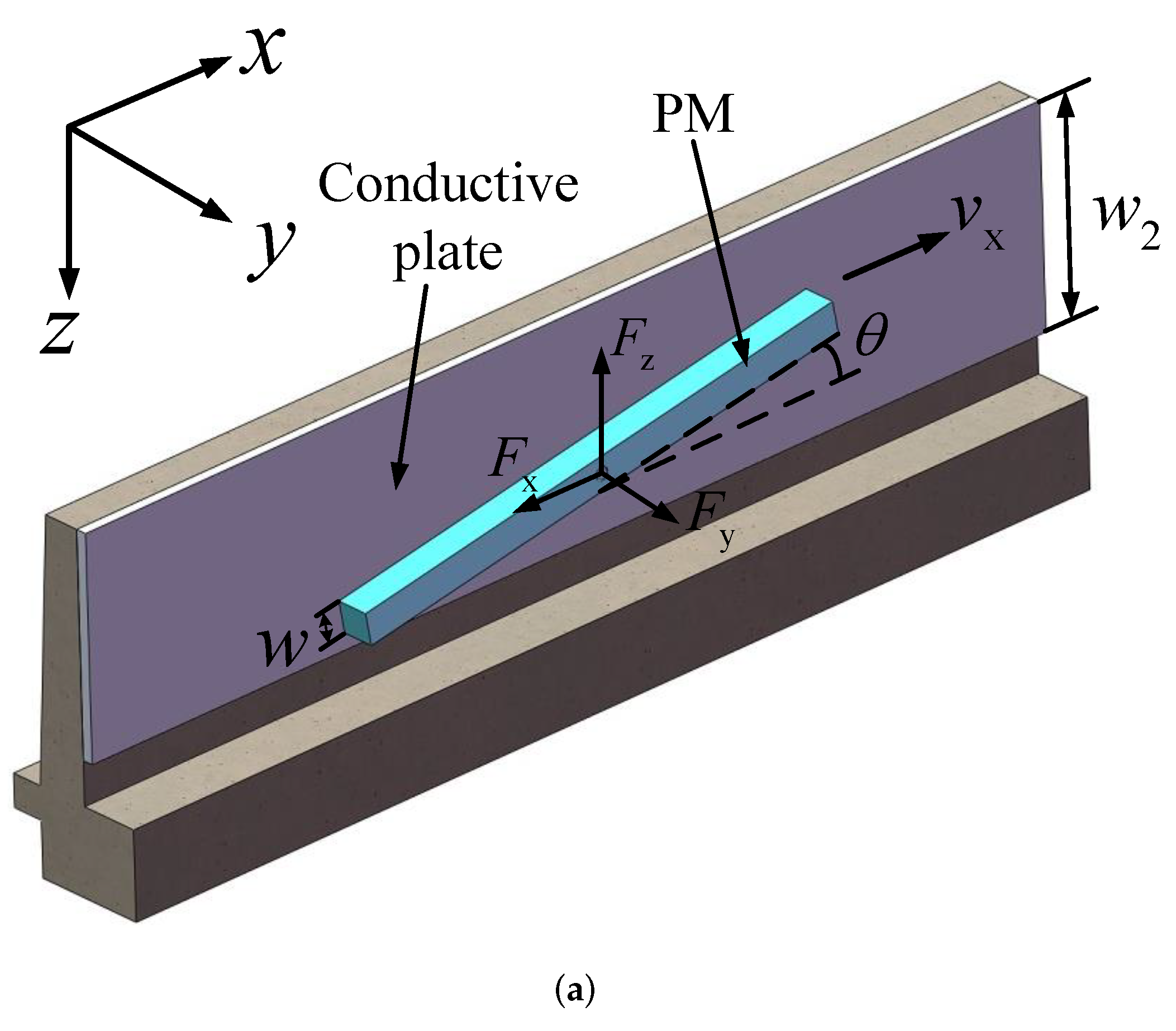
3.1.1. Establishment of Equation
- The length and width of the conductive plate are large enough to be regarded as infinite, and the thickness is finite.
- The conductive plate is continuous with constant conductivity and is nonmagnetic.
- The PM can move translationally along the x, y and z-axes.
- The moving speed of the PM is much less than the speed of light, which makes the frequency of the magnetic field low enough, and the system approximates a quasi-static model.
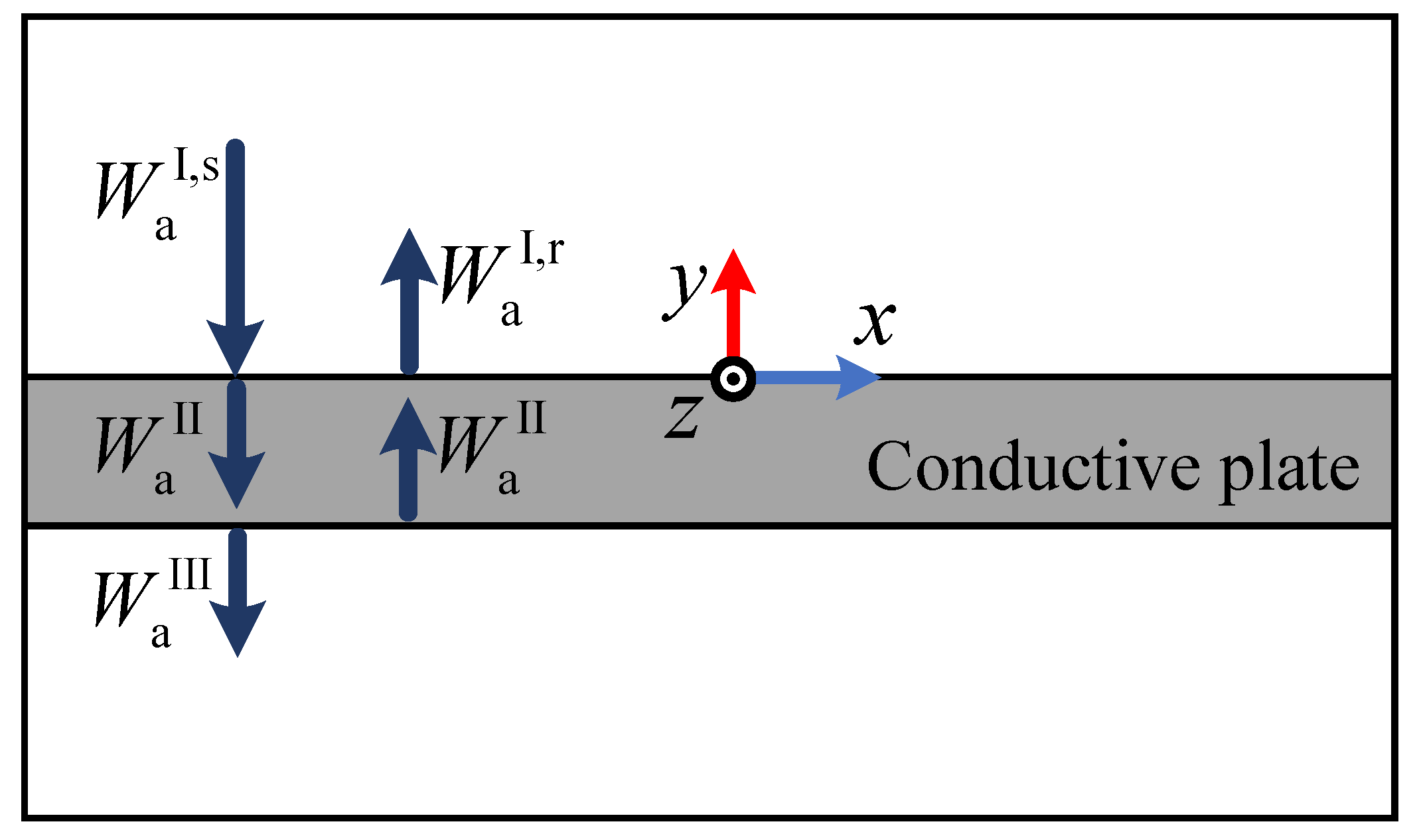
3.1.2. Boundary Conditions
3.1.3. Solution of Equations
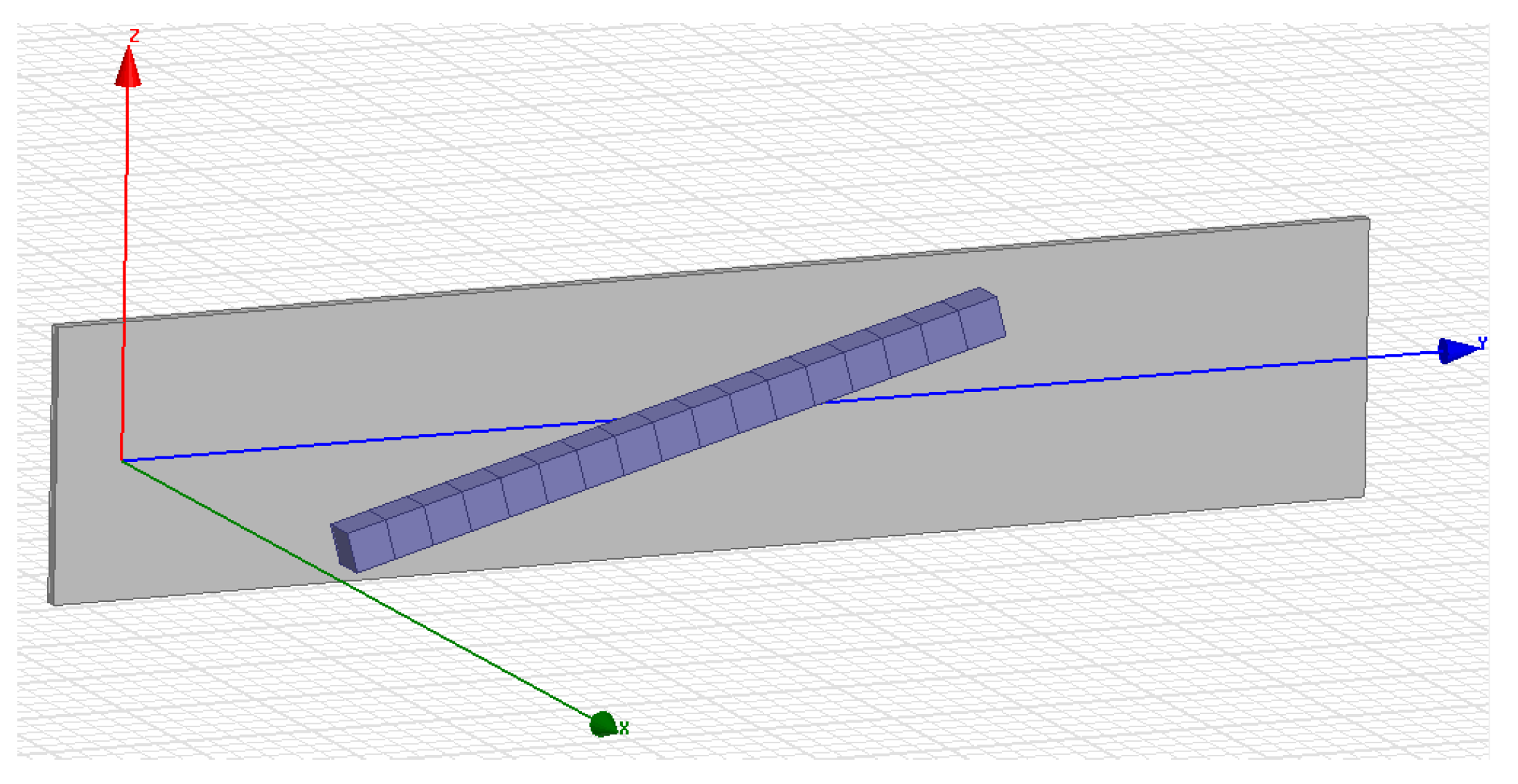
3.2. FEA Calculation
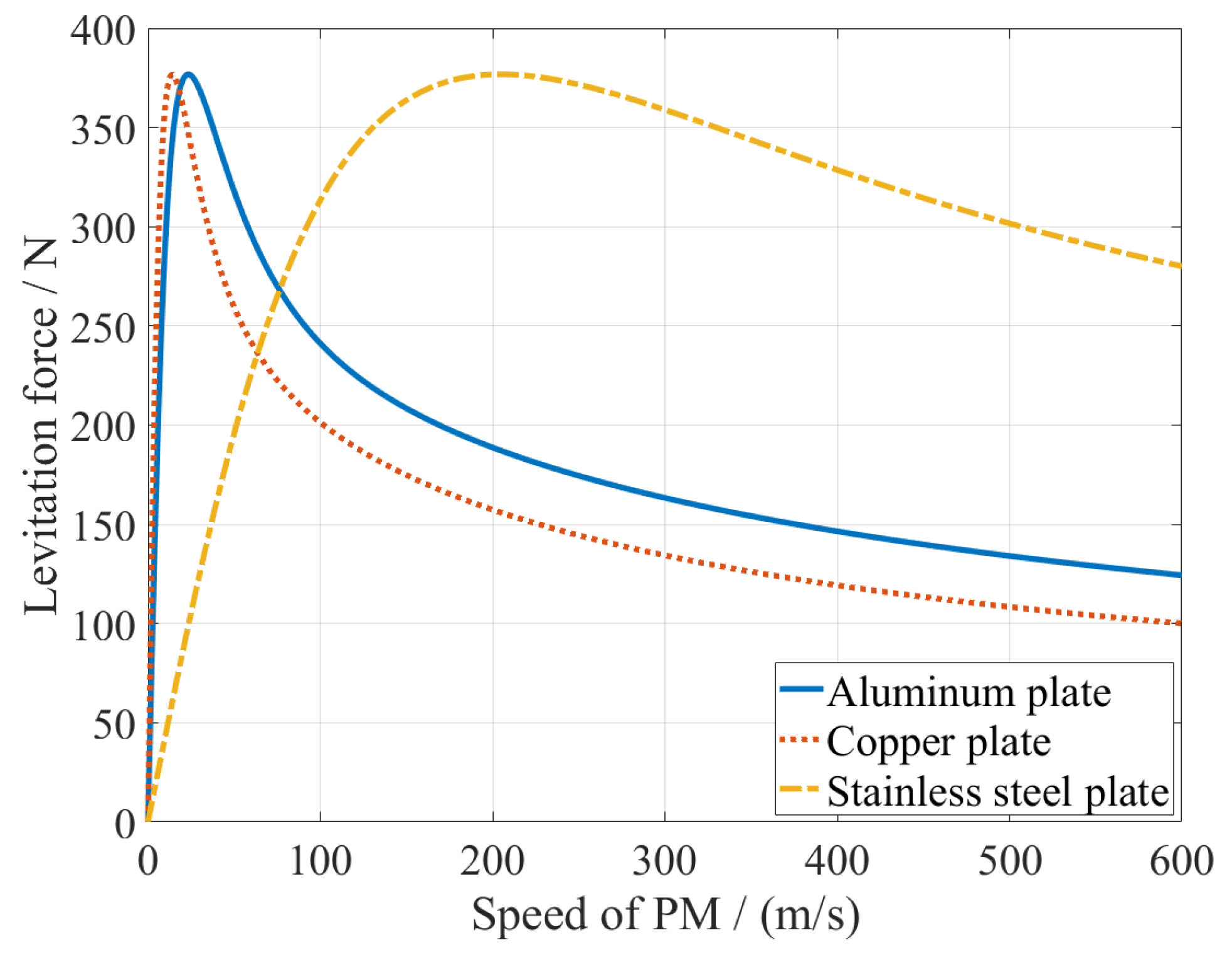
3.3. Validation of Calculation Results
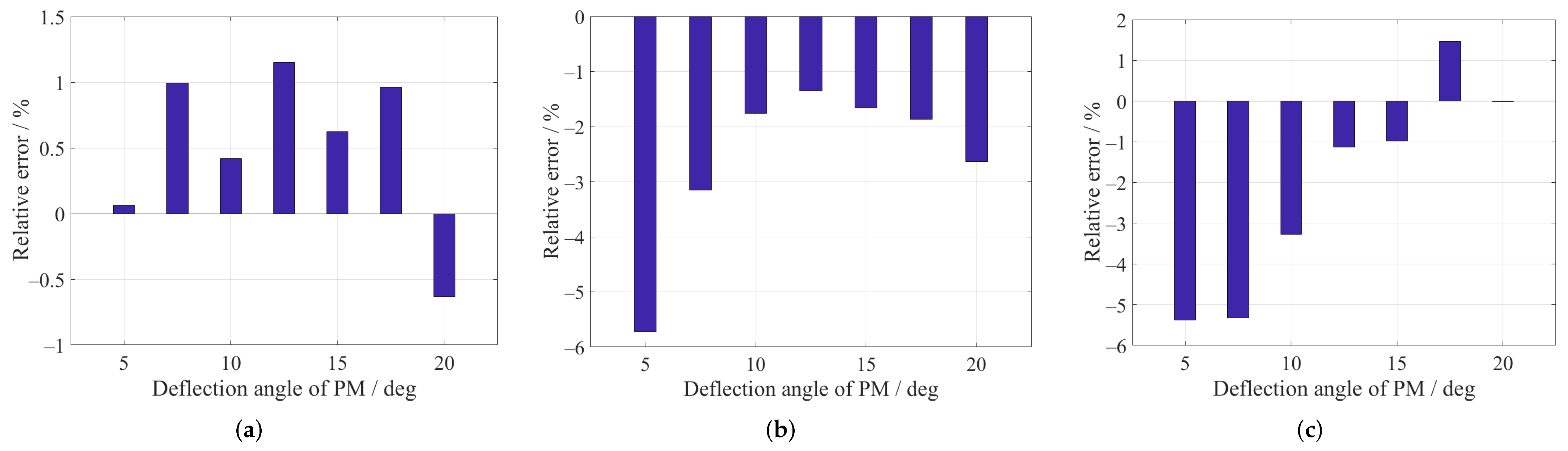
3.3.1. Electromagnetic Forces Validation
3.3.2. Magnetic Field Validation
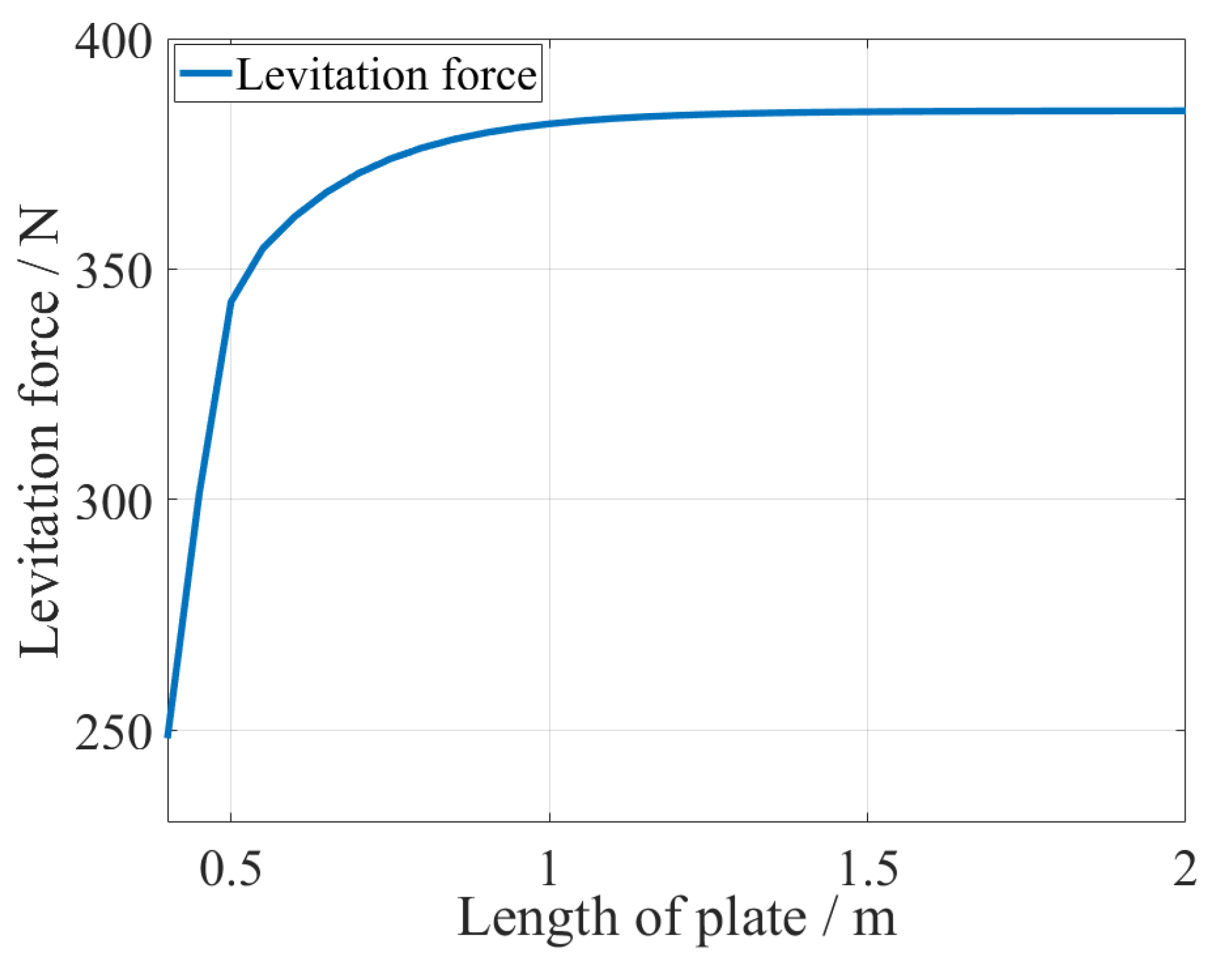
4. Size Optimization of the PM
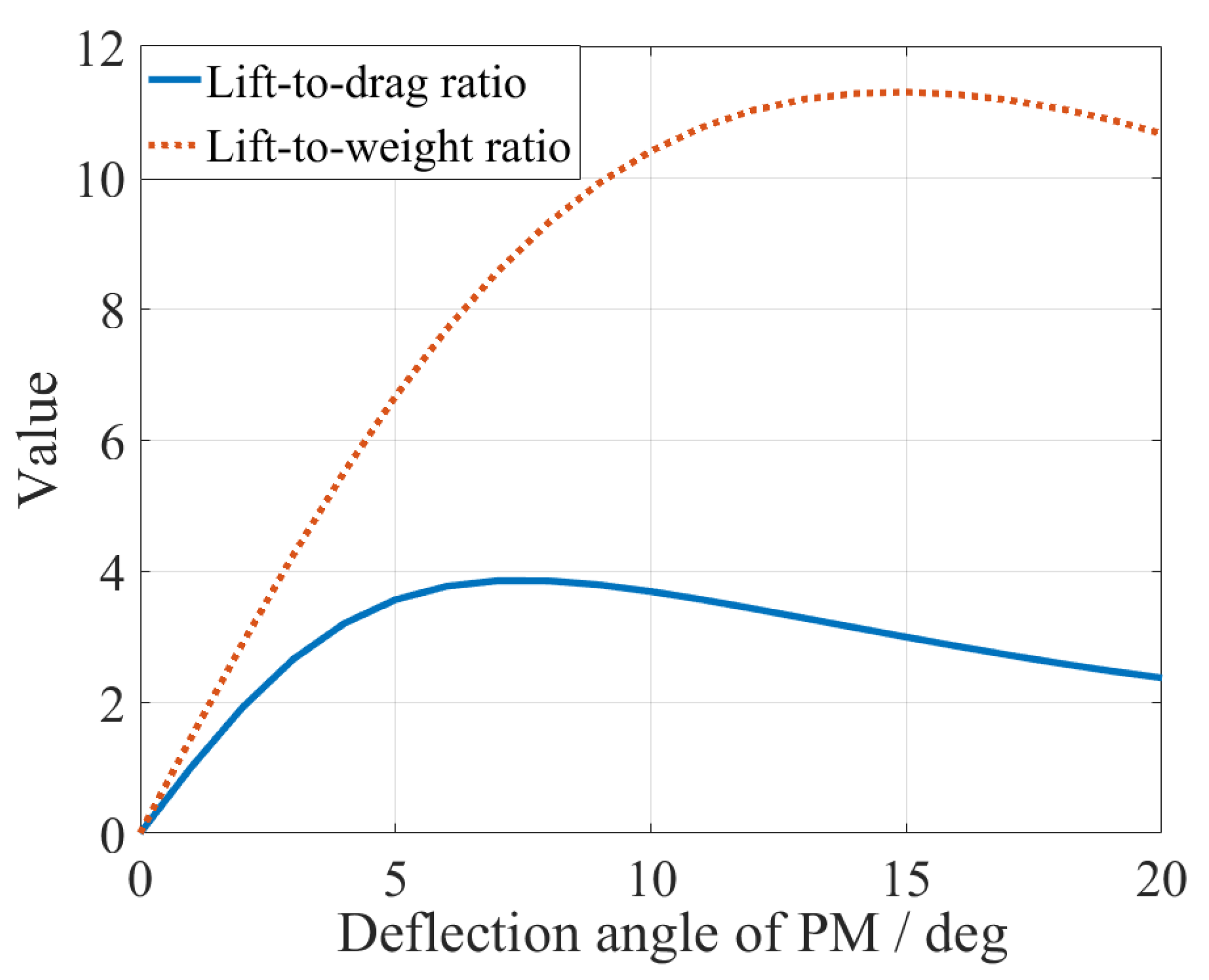
4.1. Optimization Objectives
4.2. Multi-Objective Particle Swarm Optimization Algorithm
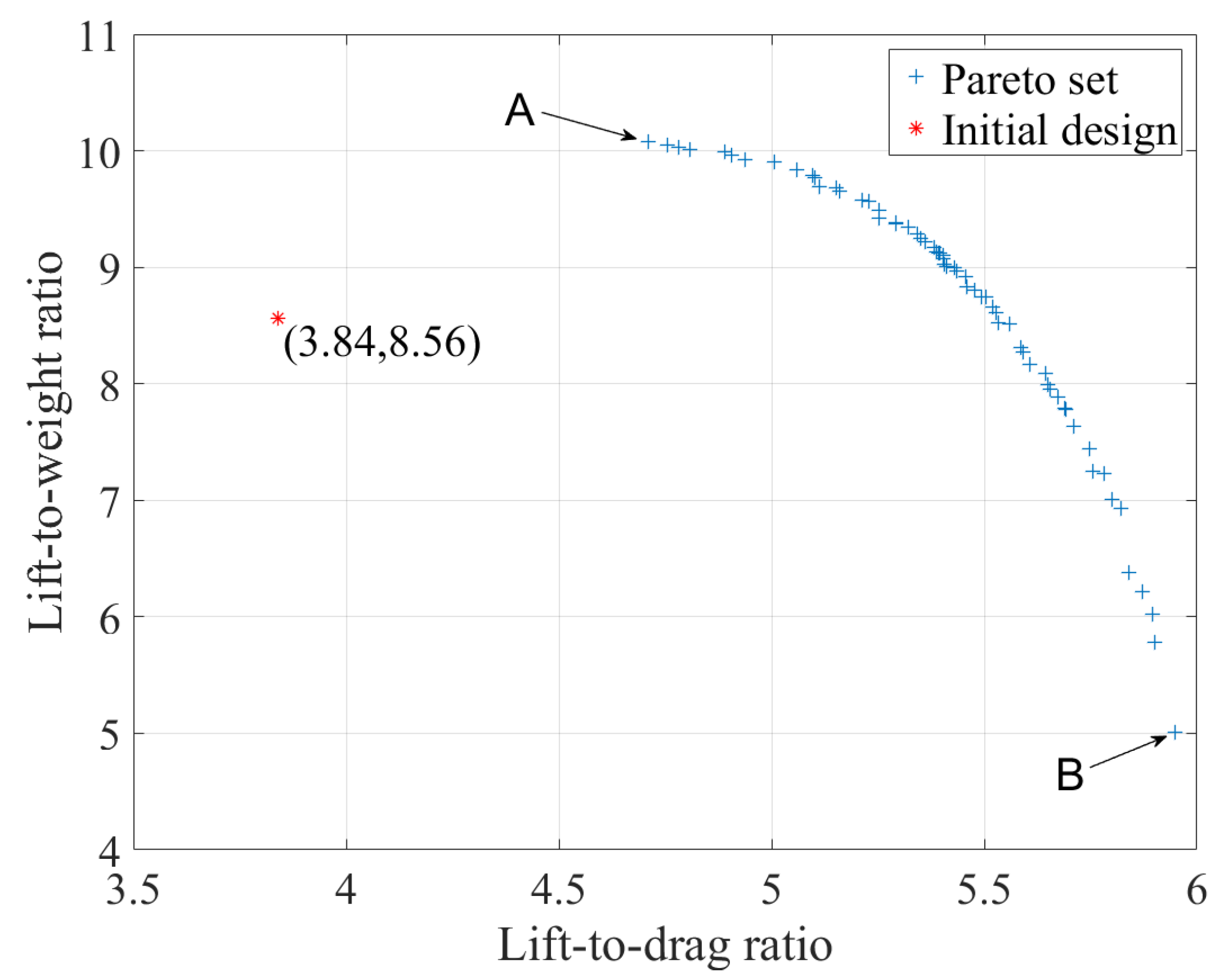
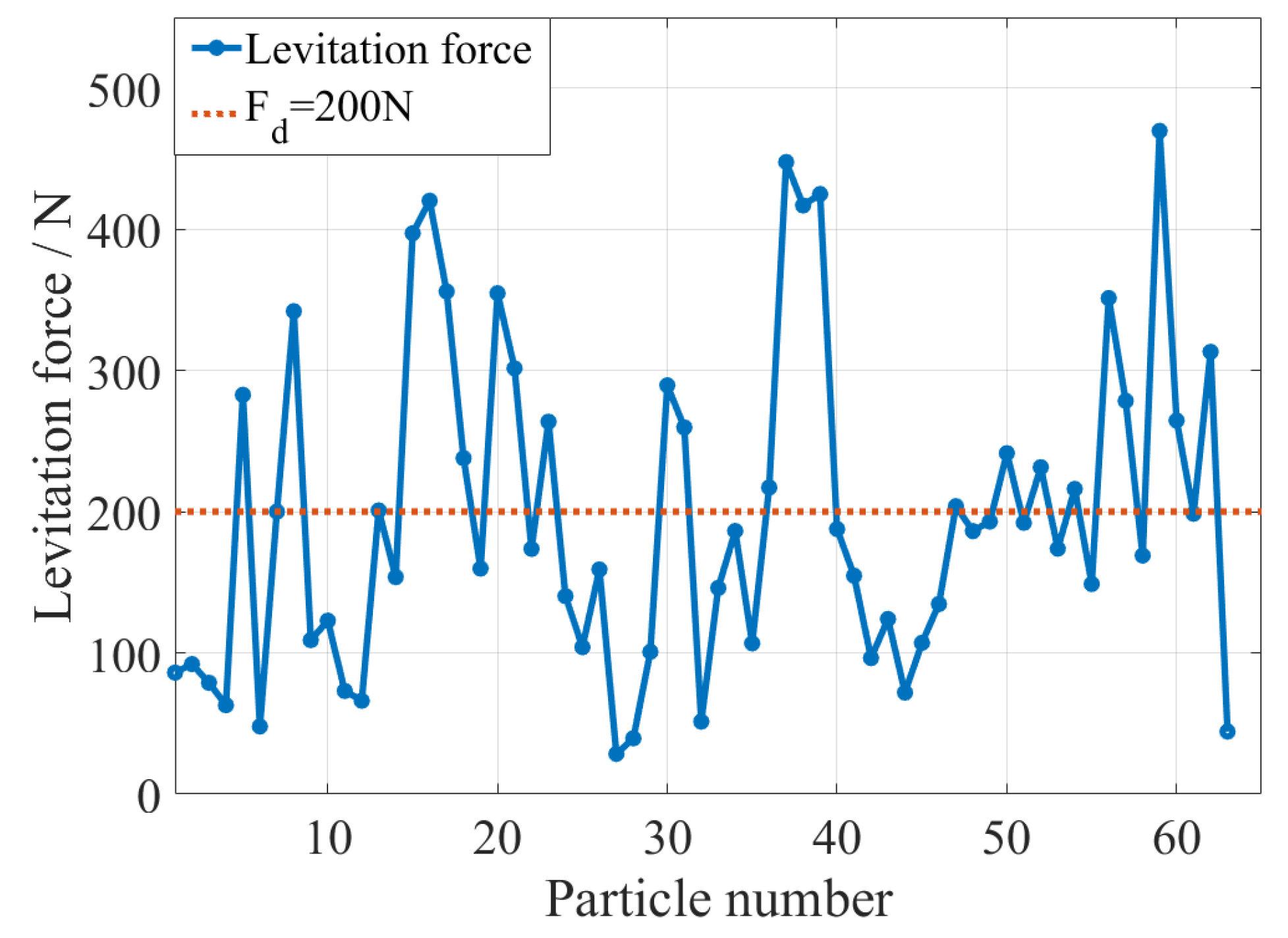
4.3. Optimization Results
5. Results
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, Z.; Li, J.; Zhou, D. Study of a null-flux coil electrodynamic suspension structure for evacuated tube transportation. Symmetry 2019, 11, 1239. [Google Scholar] [CrossRef] [Green Version]
- Montgomery, D.B. Kinematical Analysis for the Second Suspension System of the Mid-Low-Speed Maglev Vehicle. In Proceedings of the MAGLEV’2004, Shanghai, China, 26–28 October 2004. [Google Scholar]
- Fang, J.; Montgomery, D.B.; Roderick, L. A Novel MagPipe Pipeline Transportation System Using Linear Motor Drives. Proc. IEEE 2009, 97, 1848–1855. [Google Scholar] [CrossRef]
- Wang, R.; Yang, B.; Gao, H. Nonlinear Feedback Control of the Inductrack System Based on a Transient Model. J. Dyn. Syst. Meas. Control 2021, 143, 1–13. [Google Scholar] [CrossRef]
- Malewicki, D.J. Data Entry-March 31, 2052: A Retrospective of Solid-State Transportation Systems. Proc. IEEE 1999, 87, 680–687. [Google Scholar] [CrossRef]
- Malewicki, D.J. Silicon is About to Change the World-Again! Proc. IEEE 2009, 97, 1750–1753. [Google Scholar] [CrossRef]
- Fang, J.; Radovinsky, A.; Montgomery, D.B. Dynamic Modeling and Control of the Magplane Vehicle. In Proceedings of the MAGLEV’2004, Shanghai, China, 26–28 October 2004. [Google Scholar]
- Guo, Z.; Zhou, D.; Chen, Q.; Yu, P.; Li, J. Design and Analysis of a Plate Type Electrodynamic Suspension Structure for Ground High Speed Systems. Symmetry 2019, 11, 1117. [Google Scholar] [CrossRef] [Green Version]
- Bird, J.; Lipo, T.A. Modeling the 3-D Rotational and Translational Motion of a Halbach Rotor Above a Split-Sheet Guideway. IEEE Trans. Magn. 2009, 45, 3233–3242. [Google Scholar] [CrossRef]
- Theodoulidis, T.P.; Kriezis, E.E. Impedance Evaluation of Rectangular Coils for Eddy Current Testing of Planar Media. NDT E Int. 2002, 35, 407. [Google Scholar] [CrossRef]
- Musolino, A.; Rizzo, R.; Tripodi, E. Travelling Wave Multipole Field Electromagnetic Launcher: An SOVP Analytical Model. IEEE Trans. Plasma Sci. 2013, 41, 1201–1208. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Li, Y.; Li, Y. Three-dimensional Analytical Calculation of Plate-type Double Permanent Magnet Electrodynamic Suspension. J. Railw. Eng. Soc. 2019, 36, 29–34. [Google Scholar]
- Chen, Y. Characteristic Analysis of Electromagnetic Forces Created by Low-speed PM Electrodynamic Suspension. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2015. [Google Scholar]
- Gou, X.; Yang, Y.; Zheng, X. Analytic Expression of Magnetic Field Distribution of Rectangular Permanent Magnets. Appl. Math. Mech. 2004, 3, 271–278. [Google Scholar]
- Ooi, B.T.; Eastham, A.R. Transverse Edge Effects of Sheet Guideways in Magnetic Levitation. IEEE Trans. Power Appar. Syst. 1975, 94, 72–80. [Google Scholar] [CrossRef]
- Paul, S. Three-Dimensional Steady State and Transient Eddy Current Modeling. Ph.D. Thesis, University of North Carolina at Charlotte, Charlotte, NC, USA, 2014. [Google Scholar]
- Kong, L.; Wang, J.; Zhao, P. Solving the Dynamic Weapon Target Assignment Problem by an Improved Multiobjective Particle Swarm Optimization Algorithm. Appl. Sci. 2021, 11, 9254. [Google Scholar] [CrossRef]
- Wu, C.; Li, G.; Wang, D. 3-D Analytical Modeling and Electromagnetic Force Optimization of Permanent Magnet Electrodynamic Suspension System. Trans. China Electrotech. Soc. 2021, 36, 924–934. [Google Scholar]
- Chen, G.; Wu, Y.; Gao, L.; Liu, M.; Ma, X. Optimization of Submarine Resistance Based on MOPSO. Ship Build. China 2020, 61, 392. [Google Scholar]
- Abido, M.A. Multiobjective Evolutionary Algorithms for Electric Power Dispatch Problem. IEEE Trans. Evol. Comput. 2006, 10, 315–329. [Google Scholar] [CrossRef]


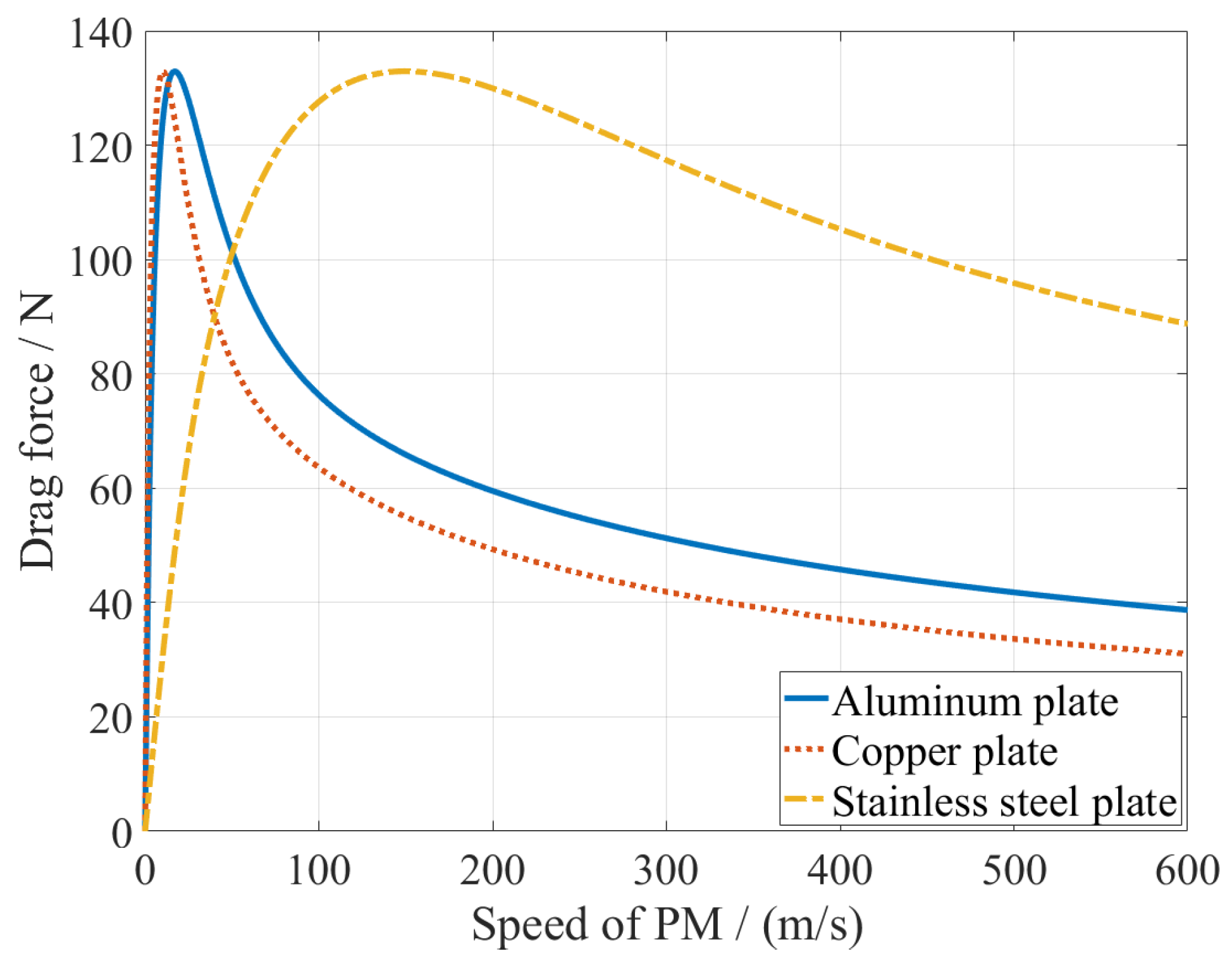
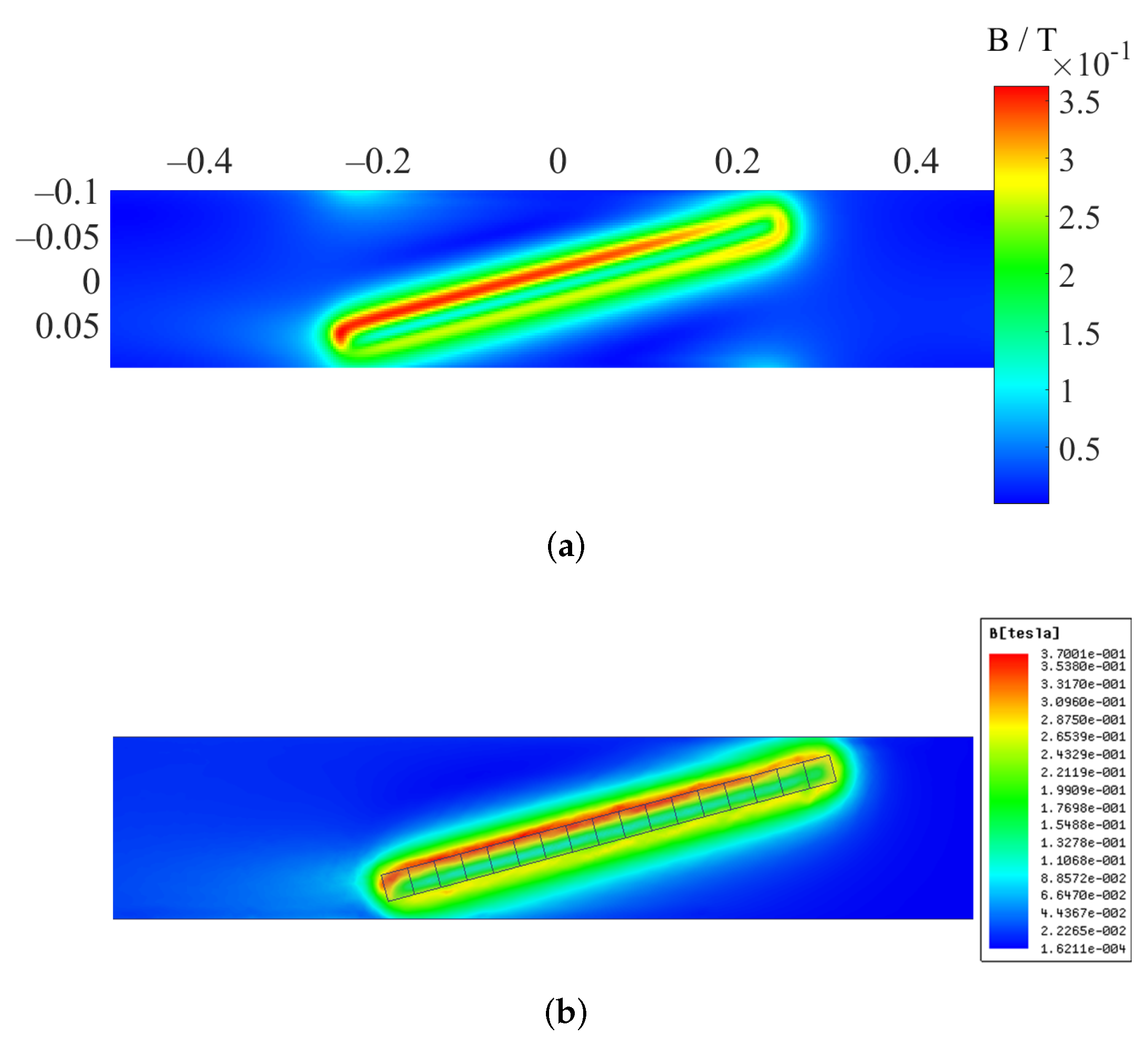


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| l | 0.51 m | 0.20 m | |
| w | 0.03 m | 0.01 m | |
| h | 0.03 m | d | 0.01 m |
| coercivity of PM | A/m | 30 m/s | |
| 1 m | S/m |
| Parameter | Value |
|---|---|
| Number of particles N | 100 |
| Maximum iterative number | 100 |
| Inertia factor | |
| Learning factor | |
| Learning factor |
| Design | Lift-to-Drag Ratio | Lift-to-Weight Ratio | l (m) | w (m) | h (m) | Dominant Value |
|---|---|---|---|---|---|---|
| Particle No. 7 | 5.383 | 9.169 | 0.751 | 0.024 | 0.016 | 0.017 |
| Particle at point A | 4.711 | 10.073 | 0.767 | 0.034 | 0.022 | 0.012 |
| Particle at point B | 5.947 | 5.010 | 0.750 | 0.010 | 0.010 | 0.012 |
| Initial design | 3.841 | 8.559 | 0.510 | 0.030 | 0.030 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Tan, Y.; Yang, Q.; Chen, Q.; Zhou, D.; Li, J. Three-Dimensional Analytical Calculation and Optimization of Plate-Type Permanent Magnet Electrodynamic Suspension System. Appl. Sci. 2022, 12, 9926. https://doi.org/10.3390/app12199926
Liu M, Tan Y, Yang Q, Chen Q, Zhou D, Li J. Three-Dimensional Analytical Calculation and Optimization of Plate-Type Permanent Magnet Electrodynamic Suspension System. Applied Sciences. 2022; 12(19):9926. https://doi.org/10.3390/app12199926
Chicago/Turabian StyleLiu, Mingxin, Yiqiu Tan, Qing Yang, Qiang Chen, Danfeng Zhou, and Jie Li. 2022. "Three-Dimensional Analytical Calculation and Optimization of Plate-Type Permanent Magnet Electrodynamic Suspension System" Applied Sciences 12, no. 19: 9926. https://doi.org/10.3390/app12199926





