Evaluation of the Strength Characteristics of Silty-Clayey Soils during Freezing-Thawing Cycles

Abstract

Destructuring settlements due to frost heave during the structures’ exploitation are often not taken into account at the designing stage, although they are indirectly related to the bearing capacity of the soils. The objective of this research was analyzing the effect of the number of freezing-thawing cycles on the strength characteristics of soils. A paired experiment with various initial parameters (void ratio, initial moisture content, and the number of freezing-thawing cycles) was carried out. According to the experimental results, the cohesion largely depends on the above parameters which might lead to its decrease by up to three times. The angle of internal friction demonstrated an indefinite behavior during the freeze-thaw cycles, which is confirmed by a literature review. Freezing–thawing cycles significantly decrease the soil bearing capacity: up to 44% after 10 freezing-thawing cycles for soil with $e=0.55$ and $w=16.5\%$. However, in the case of $e=0.75$ and $w=22.6\%,$ it increased by 33%. A program based on the least-squares method was used to calculate the approximation coefficients of the dependence describing the changes in strength characteristics from the abovementioned parameters. Changes in strength characteristics must be taken into account when designing structures, as they can lead to additional settlement or even subsidence of the foundations.

1. Introduction

Many scientists around the world have observed changes in soil moisture and density during freeze–thaw cycles and, accordingly, a change in bearing capacity, directly related to engineering characteristics [1,2,3]. Options for addressing these impacts were investigated by [4,5,6]. Russian scientists from the Soviet era, including M.N. Goldstein, A.M. Pchelintsev, E.P. Shusherina, and N.A. Tsytovich [7,8,9,10,11], have studied the influence of the number of freezing-thawing cycles on the mechanical properties of soils and contributed to the development of methods for strengthening base soils subject to freezing [12,13].

A significant part of the conducted experiment deals with road construction in areas with seasonally frozen soils, as well as problems associated with freezing-thawing of the roadway and its subgrade, such as settlement, frost heaving, and slope sliding (Ling et al., 2009; Li et al., 2016; Tebaldi et al., 2016) [14,15,16].

Destructuring settlement and heave settlement during the exploitation of buildings and structures are not taken into account in most construction design standards, although they are indirectly related to the strength characteristics of the soil. According to [17], the vertical deformation of foundations on a natural base is determined as the sum of four components Equation (A1) (Appendix A): calculated settlement, elastic settlement, destructuring settlement, and heave settlement.

Destructuring settlement $S_{destr}$ and heave settlement $S_{heave}$ are not taken into account by domestic standards [18] and are indirectly related to the strength characteristics of soil. The change to these characteristics caused by freezing-thawing is studied in this paper.

Many geotechnical scientists have paid great attention to studying the changes caused by freezing in the cohesion and the angle of internal friction of the soil as these are the main strength characteristics. It is generally accepted that with an increase in the number of freezing-thawing cycles, cohesion decreases, but the stabilized value of cohesion after several freezing-thawing cycles remains controversial [19,20,21,22,23,24]. However, some results show that cohesion increases or defies the obvious law when exposed to freezing-thawing [25]. Studies of changes in the angle of internal friction of soil are rather contradictory: according to some studies [1,21,22,25], the angle of internal friction increases; according to other studies [19], it decreases or remains constant [24,26,27]. Some studies note the inconsistent nature of the change in the angle of internal friction during freezing-thawing [20,23,28]. One way or another, the obtained scientific results are difficult to apply in engineering practice unambiguously. In 2018, Wang et al. were the first to propose a mathematical equation using correction factors for calculating the shear strength of soil during freezing-thawing, which had never been considered before [21]. However, the dependence is only for clays with a moisture content of 18.5%.

The purpose of this research is to analyze and to study the mathematical dependence of changes in the strength characteristics of clayey soils with different void ratios and initial moisture content due to freezing-thawing cycles.

2. Materials and Methods

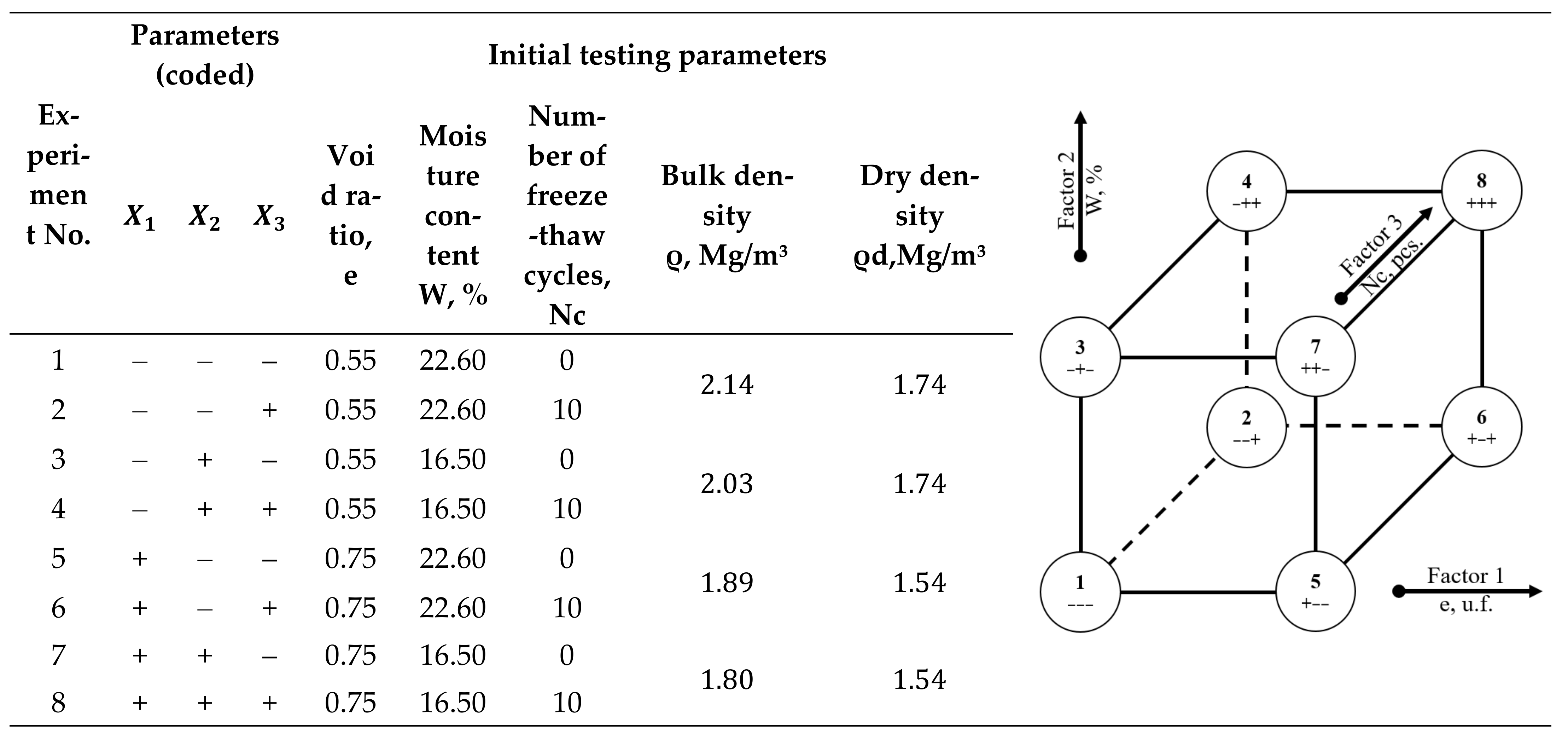
The southern area of the Tyumen region of the Russian Federation contains silty-clayey soils which are considered as frost-susceptible soils, resulting in severe frost heave during the winter time. Remolded clay loam samples with the particle density 2.70 g/cm³ were compacted in accordance with the Russian State Standard GOST 30416-2012 “Soils. Laboratory testing. General” [29]. The samples were compacted in three layers, with the required density and moisture content. The specimens were prepared as cylinders in metal rings of 71.5 mm in diameter and 35 mm in height. Physical characteristics of the soils are presented in Table 1.

Table 1. Physical characteristics of the soil.

No.	Designation	Indicator	Unit	Value
1	${\rho }_s$	Density of soil particles	g/cm3	2.70
2	$w_P$	Plastic limit	-	0.15
3	$w_L$	Liquid limit	-	0.27
4	$I_P$	Plasticity index	-	12.1
5	$I_L$	Liquidity index	-	0.375

In the experiment, four paired samples were considered for testing with varied initial settings (Table 1). However, only one sample of the pair was subjected to 10 freeze–thaw cycles and the second remained in its original state.

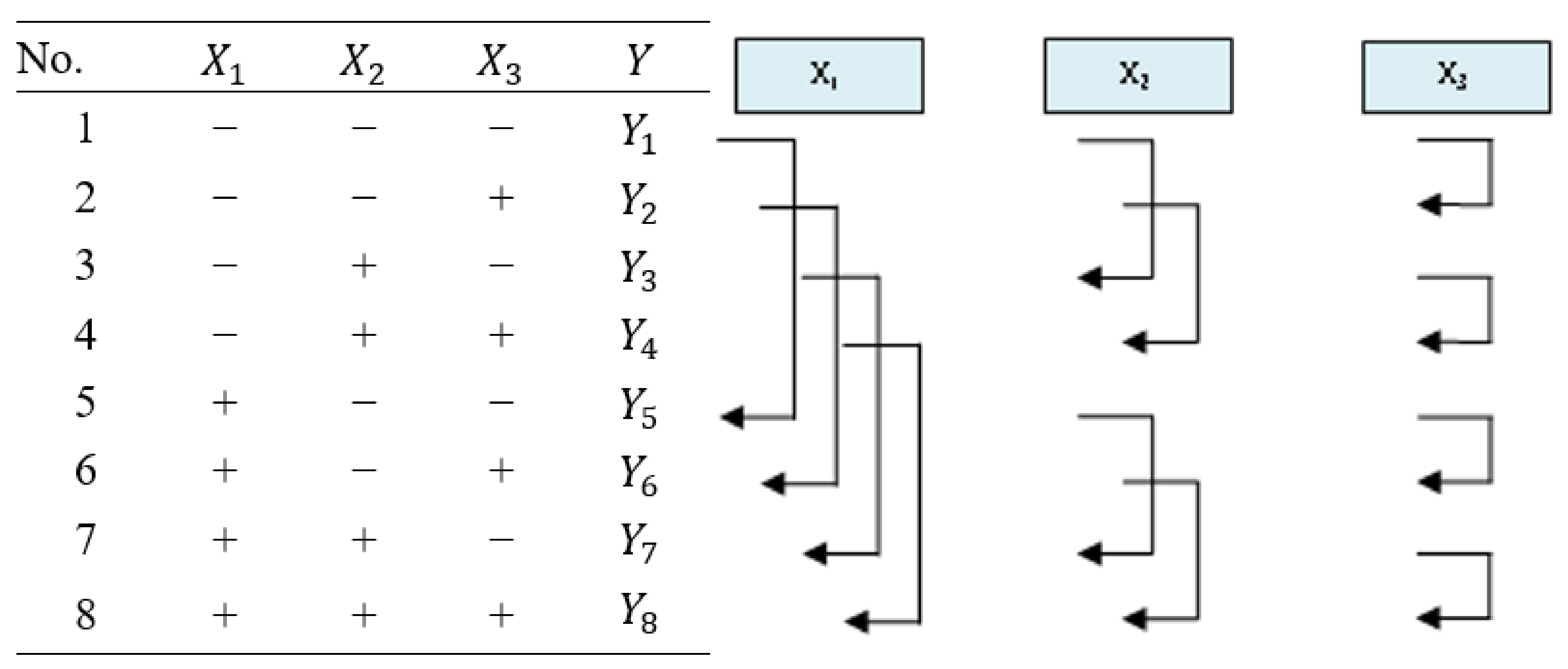
As part of the study, a two-level analysis was carried out based on three parameters. Each experimental set was formed from a pair made up of a soil sample subjected to the freeze–thaw cycles, and one that remained unaffected (Figure 1). The three variable parameters in the sample preparation are introduced below:

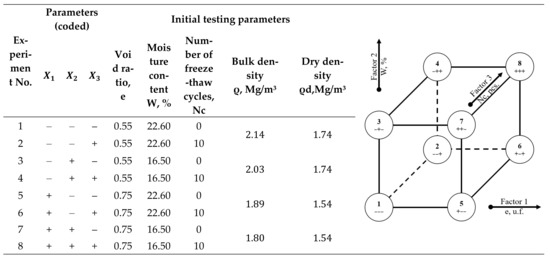
Figure 1. Graphical representation of the experiment matrix.

• Soil void ratio: low level at 0.55 unit fractions (“−” level) and high level at 0.75 unit fractions (“+” level);
• Initial soil moisture content: conventionally designated as low level at 22.6% (“−” level) and high level at 19.5% (“+” level), which corresponds to the high-plastic and semi-solid consistency of soil;
• Number of freezing-thawing cycles: low level at 0 cycles (“−” level) and high level at 10 cycles (“+” level).

The experiment set matrix is presented in Table 2.

Table 2. Direct shear test results.

Sample No.	Angle of Internal Friction φ, °	Cohesion c, kPa
1	8	36
2	12	24
3	12	39
4	13	28
5	12	13
6	18	3
7	12	26
8	13	25

According to Russian Standard GOST 25100-2020 “Soils. Classification” [30] the degree of saturation in soil samples #1–2 is classified as fully saturated ($Sr\approx 1.00$), samples #3–6 as semi-saturated ($Sr=0.81$), and samples #7–8 as slightly wet ($Sr=0.59$).

The samples were frozen at a temperature of −20 °C and thawed at 20 °C, with the freezing time and thawing time each being 12 h. The specimens were covered with sleeves during the freeze–thaw cycling to prevent the evaporation of water. The all-round freezing method with constant temperature was applied for the freeze–thaw cycle test in a closed system without a water supply. The samples were placed in metal rings without normal stress.

The engineering properties of soil samples after freeze–thaw cycles were determined using a direct shear apparatus, according to GOST 12248-2010 “Soils. Laboratory methods for determining the strength and strain characteristics” [31]. Four shear tests were conducted with normal stresses 100, 150, 200, and 300 kPa. After conducting experiments under each set of conditions and processing the results of the direct shear test, the data were analyzed to determine the influence of each of the studied factors [32].

The assessment of the effect of each parameter (${\mathit{X}}_{\mathbf{1}}$, ${\mathit{X}}_{\mathbf{2}}$, and ${\mathit{X}}_{\mathbf{3}})$ for the designed three-parameter two-level experiment is presented in Figure 2. In this case, we have four pairwise comparisons for each parameter that give the effect grade values. As an example, the main effect of the parameter ${\mathit{X}}_{\mathbf{1}}$ is considered, which is calculated as the average of these four comparisons. The effect of ${\mathit{X}}_{\mathbf{1}}$ is regarded as the average of the four Ys at the high level of ${\mathit{X}}_{\mathbf{1}}$ minus the average of the four Ys at the low level of ${\mathit{X}}_{\mathbf{1}}$. The results of the eight experiments carried out were used to calculate the ${\mathit{X}}_{\mathbf{2}}$ and ${\mathit{X}}_{\mathbf{3}}$ effects in a similar way (by subtracting the average Y value at the low parameter level from the average Y value at the high parameter level). Here, Y parameters are the results of the direct shear test in terms of angle of internal friction and cohesion.

Figure 2. The assessment of the effect of each parameter,${\mathit{X}}_1$, ${\mathit{X}}_2$, and ${\mathit{X}}_3$, for the designed three-parameter two-level experiment.

Thus, the actual effect of parameters ${\mathit{X}}_{\mathbf{1}}$, ${\mathit{X}}_{\mathbf{2}},$ and ${\mathit{X}}_{\mathbf{3}}$ was calculated using Equations (A2)–(A4).

The most important advantage of factorial design of an experiment is that it allows one to evaluate the interactions between parameters. Interaction means that the influence of one parameter depends on the value (level) of one or more other parameters. The simplest type of interactions are two-factor (${\mathit{X}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{2}}, {\mathit{X}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{3}} \mathrm{and} {\mathit{X}}_{\mathbf{2}}{\mathit{X}}_{\mathbf{3}}$); the interaction of higher-order factors here is ${\mathit{X}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{2}}{\mathit{X}}_{\mathbf{3}}$.

3. Results

The results of the direct shear test for each paired experimental sample set are presented in Table 2, where samples 2, 4, 6, 8 were those subjected to 10 freeze–thaw cycles, and samples 1, 3, 5, 7 were their analogs in the original state of density and moisture content, as presented in Table 3.

Table 3. Calculation of the actual effect of factors and their interactions.

No.	Factor			Parameters (Coded)			Additional Calculations				Result
	e, u.f.	W, %	Nc, pcs	${\mathit{X}}_1$	${\mathit{X}}_2$	${\mathit{X}}_3$	${\mathit{X}}_1{\mathit{X}}_2$	${\mathit{X}}_1{\mathit{X}}_3$	${\mathit{X}}_2{\mathit{X}}_3$	${\mathit{X}}_1{\mathit{X}}_2{\mathit{X}}_3$	φ, °	c, kPa
1	0.55	22.6	0	−	−	−	1	1	1	−1	8	36
2	0.55	22.6	10	−	−	+	1	−1	−1	1	12	24
3	0.55	16.5	0	−	+	−	−1	1	−1	1	12	39
4	0.55	16.5	10	−	+	+	−1	−1	1	−1	13	28
5	0.75	22.6	0	+	−	−	−1	−1	1	1	12	13
6	0.75	22.6	10	+	−	+	−1	1	−1	−1	18	3
7	0.75	16.5	0	+	+	−	1	−1	−1	−1	12	26
8	0.75	16.5	10	+	+	+	1	1	1	1	13	25
Actual effect
Δφ, °				2.50	0.00	3.00	−2.50	0.50	−2.00	−0.50
Δc, kPa				−15.00	10.50	−8.50	7.00	3.00	2.50	2.00

The actual interaction effect between the factors can be calculated by multiplying the interaction factors and the subsequent sum of the products of the obtained value by the result of the experiment in Table 4. For example, the actual effect of interaction of factors ${\mathit{X}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{2}}$ is calculated with Equations (A5)–(A7). The actual effect of interaction of factors ${\mathit{X}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{3}}$ and ${\mathit{X}}_{\mathbf{2}}{\mathit{X}}_{\mathbf{3}}$, as well as ${\mathit{X}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{2}}{\mathit{X}}_{\mathbf{3}}$, was calculated similarly.

Table 4. Average effect of factors ${\mathit{X}}_1$, ${\mathit{X}}_2$, and ${\mathit{X}}_3$ on the strength characteristics of soils.

$\mathbf{Average} \mathbf{Effect} \mathbf{of} \mathbf{Factors} \mathbf{on} \frac{\mathit{\phi }, °}{\mathit{c}, \mathit{k}\mathit{P}\mathit{a}}$
Factor (Coded)		Level (−)	$\mathit{Y}{\left(-\right)}_{\mathit{a}\mathit{v}\mathit{g}}$	Level (+)	$\mathit{Y}{\left(+\right)}_{\mathit{a}\mathit{v}\mathit{g}}$	Effect $\left[\mathit{Y}{\left(+\right)}_{\mathit{a}\mathit{v}\mathit{g}}-\mathit{Y}{\left(-\right)}_{\mathit{a}\mathit{v}\mathit{g}}\right]$
${\mathit{X}}_1$	E, u.f.	0.55	$\frac{11.25}{31.75}$	0.75	$\frac{13.75}{16.75}$	$\frac{2.50 \left(18\%\right)}{-15.00 \left(47\%\right)}$
${\mathit{X}}_2$	W, %	22.6	$\frac{12.50}{19.00}$	16.5	$\frac{12.50}{29.50}$	$\frac{0.00 \left(0\%\right)}{10.50 \left(36\%\right)}$
${\mathit{X}}_3$	Nc	0	$\frac{11.00}{28.50}$	10	$\frac{14.00}{20.00}$	$\frac{3.00 \left(21\%\right)}{-8.50 \left(30\%\right)}$

The results of statistical analysis revealed that the void ratio of soil had the greatest effect on the change in the angle of internal friction: with the void ratio e = 0.75, the angle of internal friction was, on average, 2.50° (18%) greater with e = 0.55. The soil moisture content and the number of freezing-thawing cycles had a lesser effect, and the latter factor led to an increase in the angle of internal friction by an average of 3.00° (21%).

Void ratio and initial moisture content had the greatest effect on the change in cohesion; both factors had a negative effect on the characteristic (15.00 and 10.50 kPa, which corresponds to 47% and 36%). With a lower number of freeze–thaw cycles, the soil had a higher cohesion by 8.50 kPa on average, which corresponds to 30%. (Table 4).

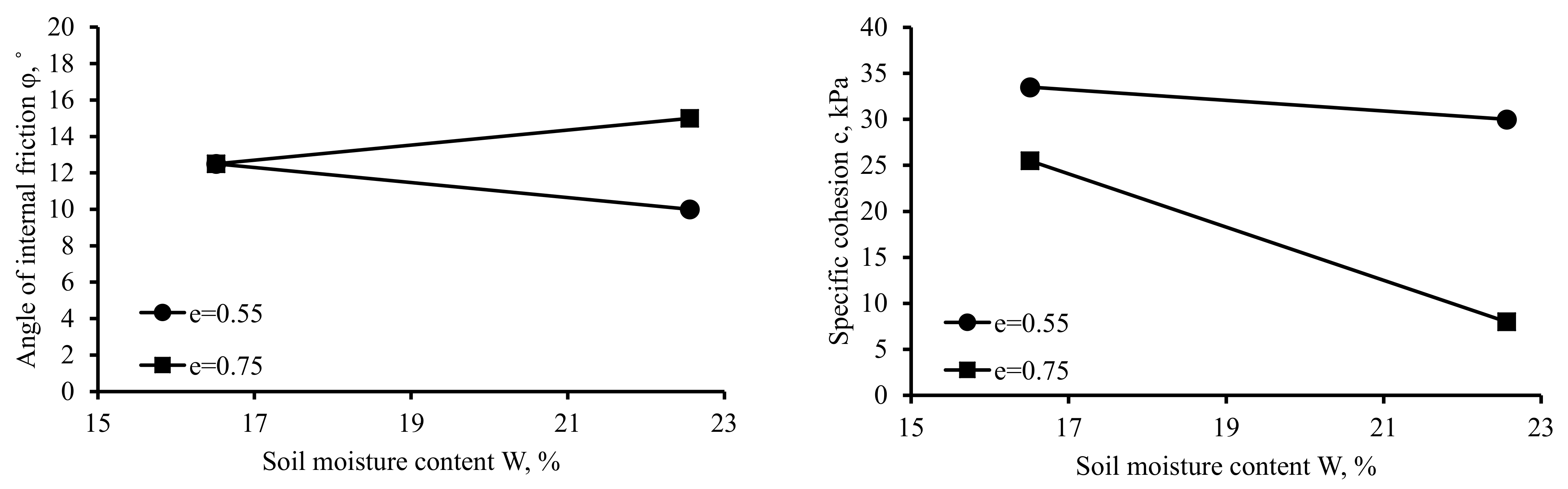
Statistical analysis of the experimental data results (Figure 3) showed that the void ratio and the soil moisture content both had a significant effect on the strength characteristics of the soil. The angle of internal friction of soil with a void ratio of 0.55 decreased on average by 2.5° (20%) if the moisture content increased from 16.5% to 22.6%. However, the angle of internal friction of soil with a void ratio of 0.75 increased by 2.50° (17%) if the moisture content increased within the above limits. It is important to note that with an initial soil moisture content of 22.6%, the angle of internal friction of soil with a void ratio of 0.55 was 5.00° (33%) lower (Figure 3).

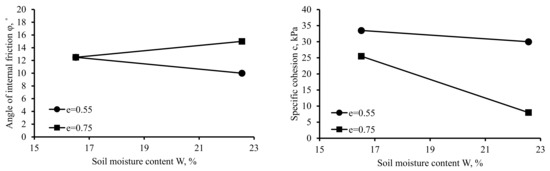
Figure 3. Effect of the interaction of factors ${\mathit{X}}_1{\mathit{X}}_2$ on the strength characteristics of soil.

The cohesion of soil with a void ratio of 0.55 decreased by 3.50 kPa (10%) if the moisture content increased within the above range, and that of soil with a void ratio e = 0.75 decreased by 17.50 kPa (69%). With an initial soil moisture content of 16.5%, the cohesion of soil with a void ratio of 0.55 was 8.00 kPa (24%) higher, and with an initial soil moisture content of 22.6% it was higher by 22.00 kPa, i.e., by 73% (Figure 3).

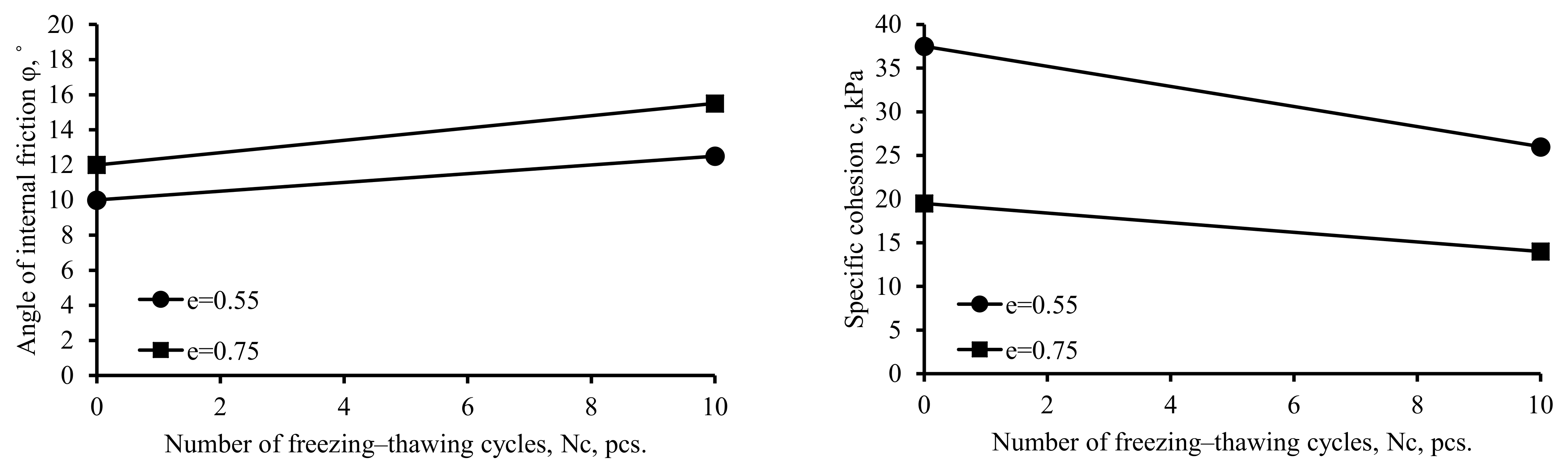
The combination of the void ratio and the number of freezing-thawing cycles also had a significant effect on the strength characteristics of the soil. (Figure 4).

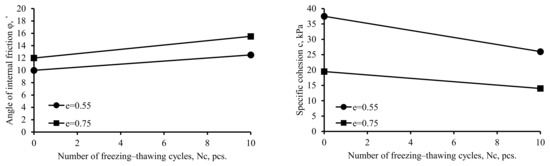
Figure 4. Effect of the interaction of factors ${\mathit{X}}_1{\mathit{X}}_3$ on the strength characteristics of soil.

The angle of internal friction of soil with a void ratio of 0.55 increased by 2.5° (20%) during freezing-thawing cycles. The angle of internal friction of soil with a void ratio of 0.75 increased by 3.50° (23%) during freezing-thawing cycles. It should be noted that the angle of internal friction of soil with a void ratio of 0.55 was 2.0° (17%) lower, without freezing-thawing. The angle of internal friction of soil with a void ratio of 0.55 was 3° (19%) lower during freezing-thawing.

Cohesion of the soil during freezing-thawing cycles dropped drastically by 11.50 kPa (31%) and 5.50 kPa (28%) for soil with void ratios of 0.55 and 0.75, respectively. The cohesion of soil with a void ratio of 0.55 was 18.00 kPa (48%) higher without the effect of freezing-thawing. The cohesion of soil with a void ratio of 0.55 was 12.00 kPa (46%) higher during freezing-thawing cycles. Cohesion was revealed to be the most sensitive parameter influenced by the freeze-thaw cycles.

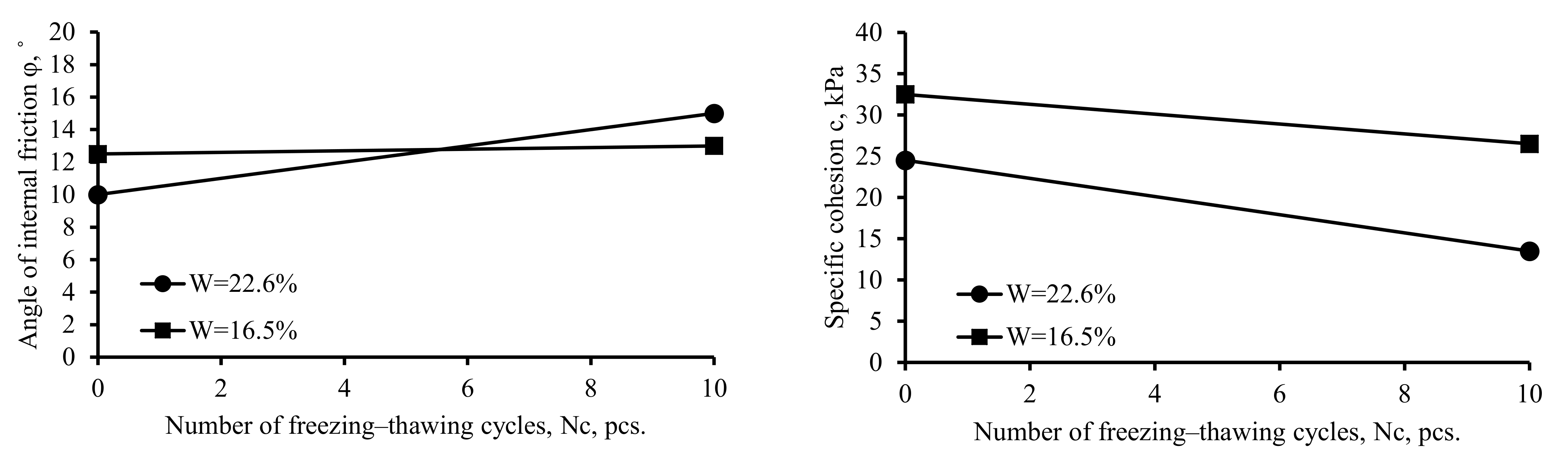
In addition, the average effect of both the initial soil moisture content and the number of freezing-thawing cycles on the cohesion and the angle of internal friction was considered. The results are shown in Figure 5.

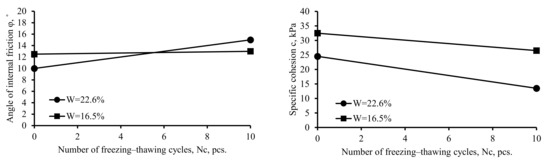
Figure 5. Effect of the interaction of factors ${\mathit{X}}_2{\mathit{X}}_3$ on the strength characteristics of soil.

The angle of internal friction of soil with an initial moisture content of 16.5% did not change during freezing-thawing. However, the angle of internal friction of soil with an initial moisture content of 22.6% increased by 5° (33%) during freezing-thawing. It should be noted that the angle of internal friction of soil with an initial moisture content of 22.6% was 2.50° (20%) lower without freezing-thawing. The angle of internal friction of soil which underwent 10 freezing-thawing cycles was 2.00° (13%) higher for the soil with the initial moisture content of 22.6%.

The cohesion of soil with initial moisture contents of 16.5% and 22.6% decreased by 11.00 kPa (45%) and 6.00 kPa (18%), respectively, during freezing-thawing. It is important to note that the cohesion of soil without freezing-thawing was lower by 8.00 (25%) for the soil with an initial moisture content of 22.6%.

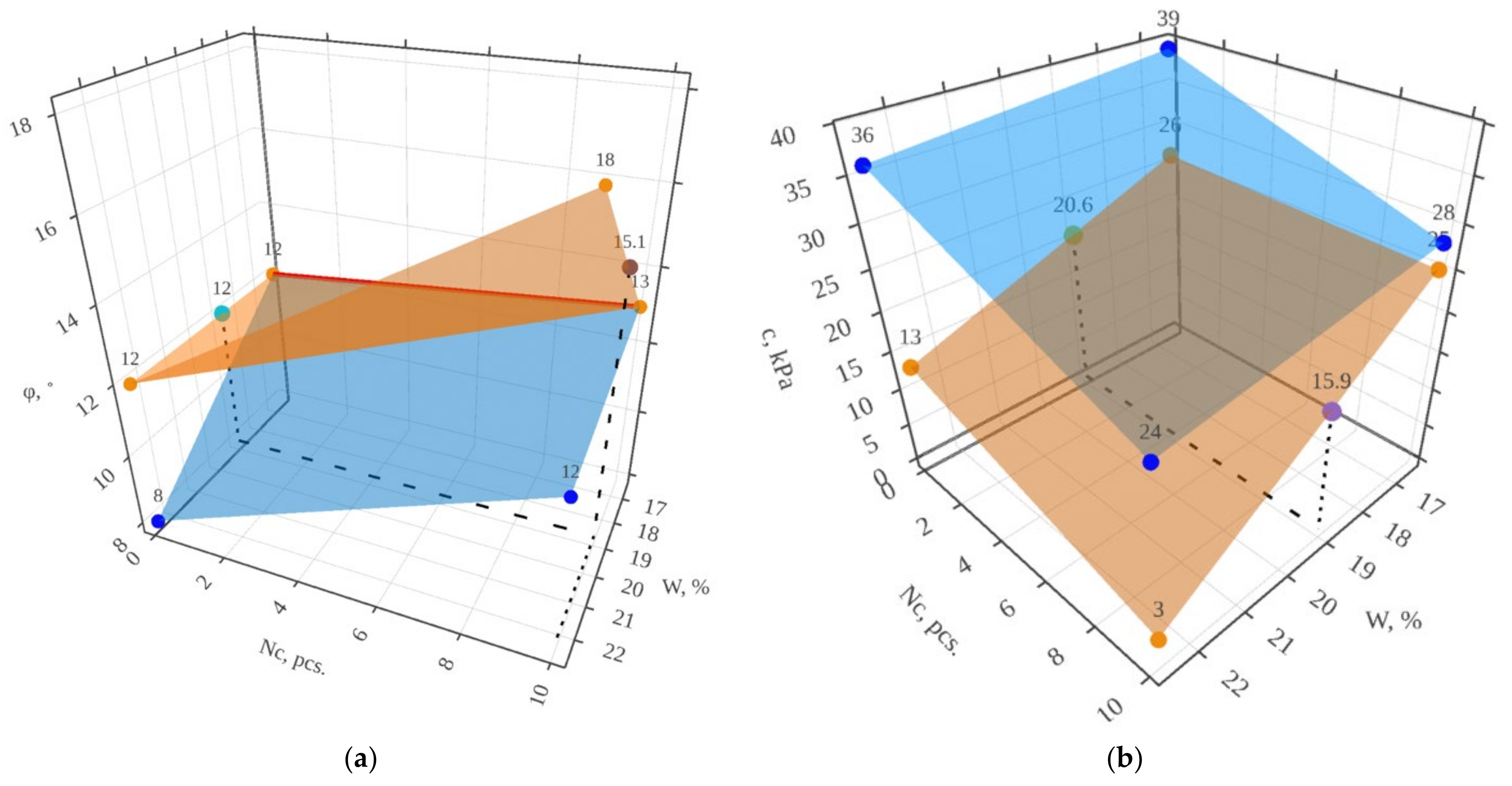
In a three-dimensional way, the described dependence can be represented as shown in Figure 6. An intermediate value of the soil strength characteristic can be found by using the presented graphical dependence. Figure 6a shows the intermediate value of the internal friction angle for soil with a void ratio equal to 0.75, with 10 freezing-thawing cycles, and with an initial moisture content of 19.0%. The resulting value is 15.1°.

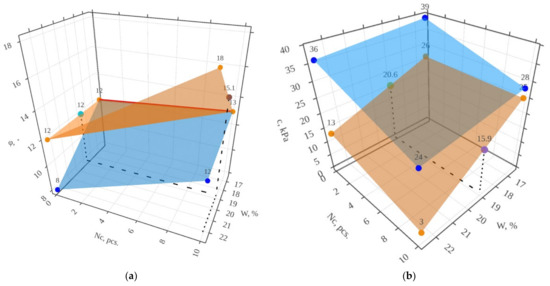
Figure 6. Dependence of the strength characteristics of soil on the void ratio, initial moisture content, and the number of freezing-thawing cycles, shown in a three-dimensional manner: (a)—for the angle of internal friction; (b)—for cohesion.

In addition, Figure 6a indicates the uncertainty of the behavior of the angle of internal friction depending on the void ratio. Thus, at a moisture content of 22.6%, the angle of internal friction is lower for soil with a void ratio of 0.55. However, if the moisture content decreases, the nature of the change in characteristics, depending on the void ratio, changes in the opposite direction, forming a line of intersection of two planes. At the same time, the change in cohesion depending on the void ratio is unambiguous, which is shown in Figure 6b. Figure 6a shows the intermediate value of the cohesion for the soil with a void ratio equal to 0.75, with 10 freezing-thawing cycles and with an initial moisture content of 19.0%. The resulting value is 15.9 kPa.

4. Discussion

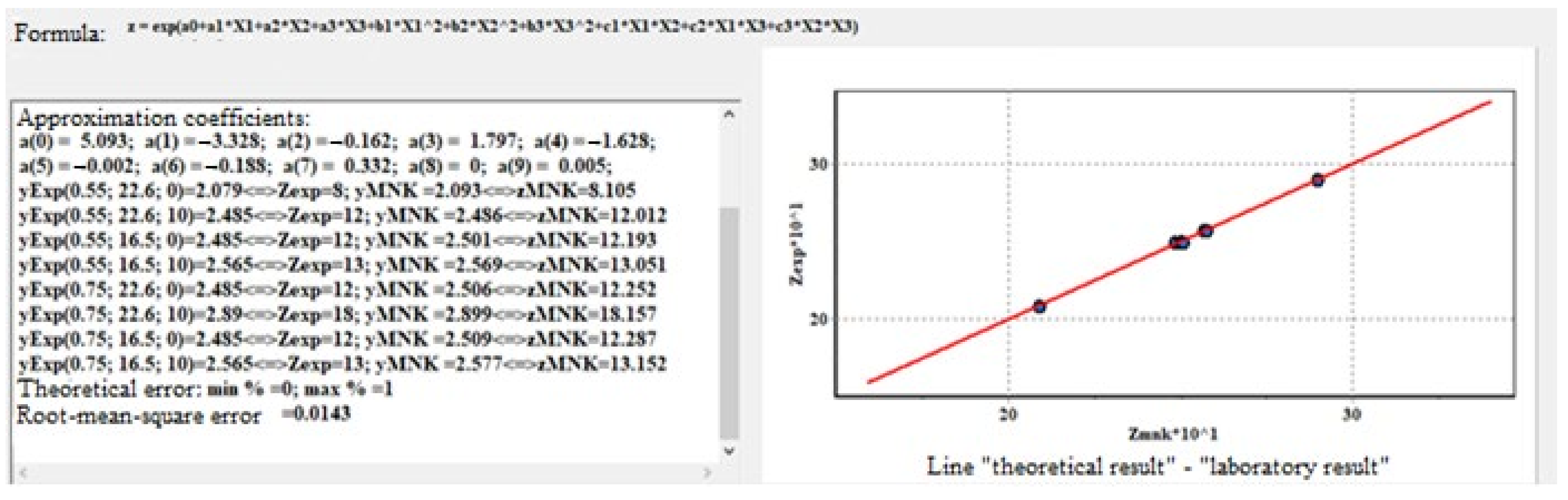
Based on the results of laboratory research, a dependence was derived that allows to determine the angle of internal friction or cohesion on the given data of void ratio, initial soil moisture, and number of freeze–thaw cycles. A program based on the least-squares method has the following form:

$$y=e^{a_0+a_1{X}_1+a_2{X}_2+a_3{X}_3+b_1{X}_1{}^2+b_2{X}_2{}^2+b_3{X}_3{}^2+c_1{X}_1{X}_2+c_2{X}_1{X}_3+c_3{X}_2{X}_3}$$

(1)

where ${\mathit{a}}_{\mathit{i}}, {\mathit{b}}_{\mathit{i}}, \mathrm{and} {\mathit{c}}_{\mathit{i}}$ is the approximation coefficient;

${\mathit{X}}_{\mathbf{i}}$ is the value of the factor under study.

The developed program for calculating the dependence of the desired parameter on the given values allows us to process the results of a three-factor experiment. The general view of the program is presented in Figure 7. The figure shows the results of calculating the approximation coefficients for the angle of internal friction.

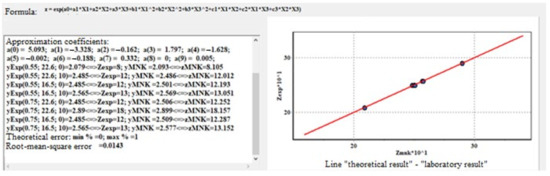
Figure 7. General view of the program.

For the angle of internal Friction (2) and Cohesion (3), the mathematical dependence can be represented as follows:

$$y=e^{5.093-3.328·X_1-0.162·X_2+1.797·X_3-1.628·X_1{}^2-0.002·X_2{}^2-0.188·X_3{}^2+0.332·X_1{X}_2+0.005·X_2{X}_3}$$

(2)

$$y=e^{2.696+10.277·X_1-0.129·X_2-4.049·X_3+5.206·X_1{}^2+0.019·X_2{}^2+0.436·X_3{}^2-1.057·X_1{X}_2-0.192·X_1{X}_3-0.012·X_2{X}_3}$$

(3)

where $X_i$ is the value of the factor under study ($X_1$ is the soil void ratio; $X_2$ is the initial soil moisture content; $X_3$ is the number of freezing-thawing cycles).

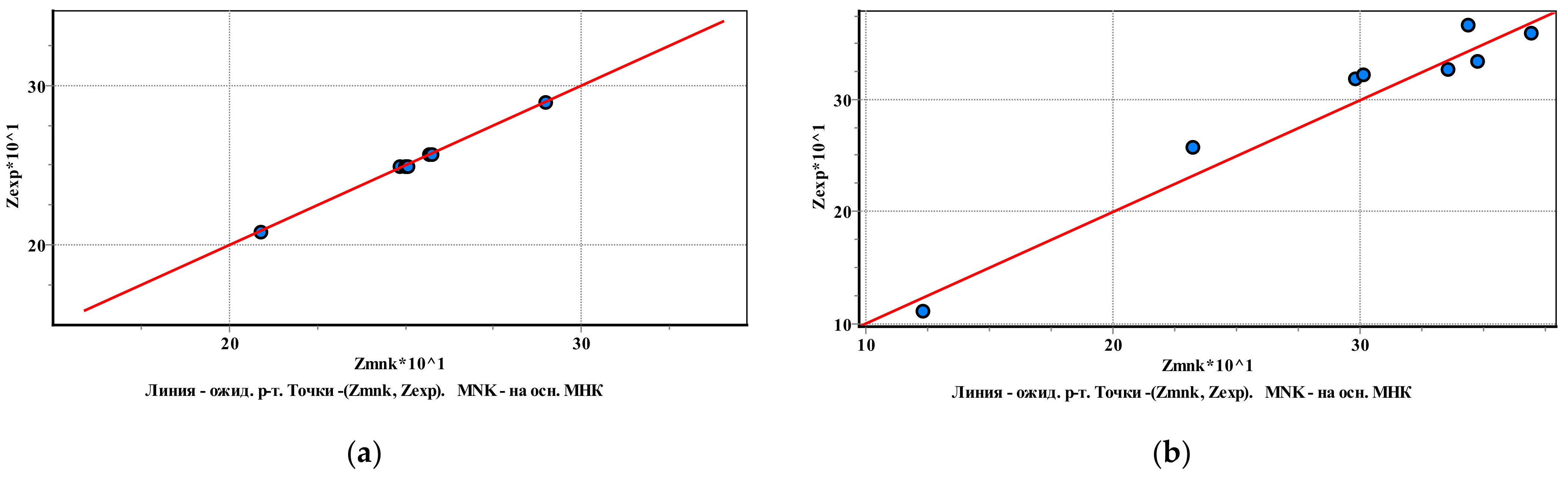
Figure 8 shows a graph of the correspondence of the results of laboratory and theoretical values of strength characteristics. The axis of the abscissa indicates the value of the characteristic calculated according to Equations (2) and (3). The axis of the ordinate represents the value of the characteristic obtained as a result of laboratory studies. With perfect correspondence, the points should be located on the line $Y=X$. Figure 8 shows that the closest correspondence is observed for the angle of internal friction.

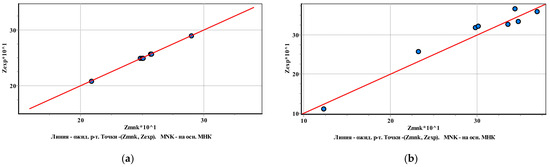
Figure 8. The correspondence of the results of laboratory and theoretical values of strength characteristics: (a)—angle of internal friction; (b)—cohesion.

Thus, by setting the values of void ratio, initial soil moisture, and number of freeze–thaw cycles, it becomes possible to calculate the angle of internal friction and/or cohesion for each type of soil. However, the presented dependencies work correctly only near the points of interest. Therefore, additional tests are required inside the cube (Figure 1) to clarify these mathematical dependences.

5. Example Calculation of Engineering Characteristics of Soil Bases by the Proposed Analytical Method

In order to verify the proposed method, in this subsection, the following example was considered to determine the angle of internal friction and cohesion and compare it with the calculated values; the bearing capacity of the soil was determined according to the standard [18] of the Russian Federation. According to the design standards, when calculating the strains of the soil base of building foundations, the average pressure under the foundation footing should not exceed the design soil resistance R, which is calculated by Equation (4) in accordance with SP 22.13330.2016 “Soil bases of buildings and structures” [18] which allows the determination of the linear load in the soil base,

$$R=\frac{{\gamma }_{c1}{\gamma }_{c2}}{k}\left[M_{\gamma }{k}_{z}b{\gamma }_{II}+M_q{d}_l{\gamma }_{II}^{\prime }+\left(M_q-1\right)d_b{\gamma }_{II}^{\prime }+M_c{c}_{II}\right]$$

(4)

As an example, below is the calculation of the general case of strength characteristics with the following initial data:

• The foundation footing width $\mathit{b}\mathbf{=}\mathbf{10} \mathbf{m}$, therefore ${\mathit{k}}_{\mathit{z}}\mathbf{=}\frac{{\mathit{z}}_{\mathbf{0}}}{\mathit{b}}\mathbf{+}\mathbf{0.2}\mathbf{=}\mathbf{1}$.
• The foundation depth ${\mathit{d}}_{\mathit{l}}\mathbf{=}\mathbf{5} \mathbf{m}$.
• The basement depth ${\mathit{d}}_{\mathit{b}}$ is assumed equal to 2 m in accordance with SP 22.13330.2016 [18].
• The building has a rigid structure; the ratio of the length of the structure to its height L/H is less than 1.5.
• The strength characteristics of the soil are determined by direct tests, therefore $\mathit{k}\mathbf{=}\mathbf{1}$.
• Depending on the calculated angle of internal friction, coefficients ${\mathit{M}}_{\mathit{\gamma }}$, ${\mathit{M}}_{\mathit{q}},$ and ${\mathit{M}}_{\mathit{c}}$ are taken according to SP 22.13330.2016 [18].
• The soil base is homogeneous, i.e., ${\mathit{\gamma }}_{\mathit{I}\mathit{I}}\mathbf{=}{\mathit{\gamma }}_{\mathit{I}\mathit{I}}^{\prime }$.
• Coefficients ${\mathit{\gamma }}_{\mathit{c}1}$ and ${\mathit{\gamma }}_{\mathit{c}2}$ are accepted according to SP 22.13330.2016 [18], depending on the type of soil and its initial moisture content.

Table 5 is a summary of the calculation results of determining the engineering characteristics by the analytical method. Here, ${\mathit{\phi }}_{\mathit{n}}$ and ${\mathit{c}}_{\mathit{n}}$ are the normative values of angle of internal friction and cohesion determined in the laboratory, whereas ${\mathit{\phi }}_{\mathit{I}\mathit{I}}$ and ${\mathit{c}}_{\mathit{I}\mathit{I}}$ are design values.

Table 5. Calculation of the engineering characteristics by the analytical method.

Indicator	Experiment No.
	No.1	No.5	No.3	No.7	No.2	No.6	No.4	No.8
	No Freezing–Thawing Cycles				10 Freezing–Thawing Cycles
	$\mathit{e}=0.55$	$\mathit{e}=0.75$	$\mathit{e}=0.55$	$\mathit{e}=0.75$	$\mathit{e}=0.55$	$\mathit{e}=0.75$	$\mathit{e}=0.55$	$\mathit{e}=0.75$
	$$\begin{gathered} \mathit{w}=22.6\mathit{\%} \\ {\mathit{I}}_{\mathit{L}}>0.5 \end{gathered}$$ (High-Plastic)		$$\begin{gathered} \mathit{w}=16.5\mathit{\%} \\ {\mathit{I}}_{\mathit{L}}<0.25 \end{gathered}$$ (Semi-Solid)		$$\begin{gathered} \mathit{w}=22.6\mathit{\%} \\ {\mathit{I}}_{\mathit{L}}>0.5 \end{gathered}$$ (High-Plastic)		$$\begin{gathered} \mathit{w}=16.5\mathit{\%} \\ {\mathit{I}}_{\mathit{L}}<0.25 \end{gathered}$$ (Semi-Solid)
${\phi }_n$, º	8	12	12	12	12	18	13	13
${\gamma }_{g\phi }$	1.217	1.196	1.049	1.539	1.298	1.042	1.630	1.585
$c_n$, kPa	36	13	39	26	24	3	28	25
${\gamma }_{gc}$	1.161	1.887	1.055	2.448	1.670	5.59	2.716	2.08
${\phi }_{II}$, º	6	10	12	8	9	17	8	8
$c_{II}$, kPa	31	7	37	11	14	1	10	12
${\gamma }_{c1}$	1.1		1.25		1.1		1.25
${\gamma }_{c2}$	1		1.1		1		1.1
$M_{\gamma }$	0.10	0.18	0.23	0.14	0.16	0.39	0.14	0.14
$M_q$	1.39	1.73	1.94	1.55	1.64	2.57	1.55	1.55
$M_c$	3.71	4.17	4.42	3.93	4.05	5.15	3.93	3.93
${\gamma }_{II}, \mathrm{kN}/{\mathrm{m}}^3$	21.35	18.91	20.3	17.98	21.35	18.91	20.3	17.98
R, kPa	331.54	279.85	612.29	312.85	322.58	419.40	340.14	318.25

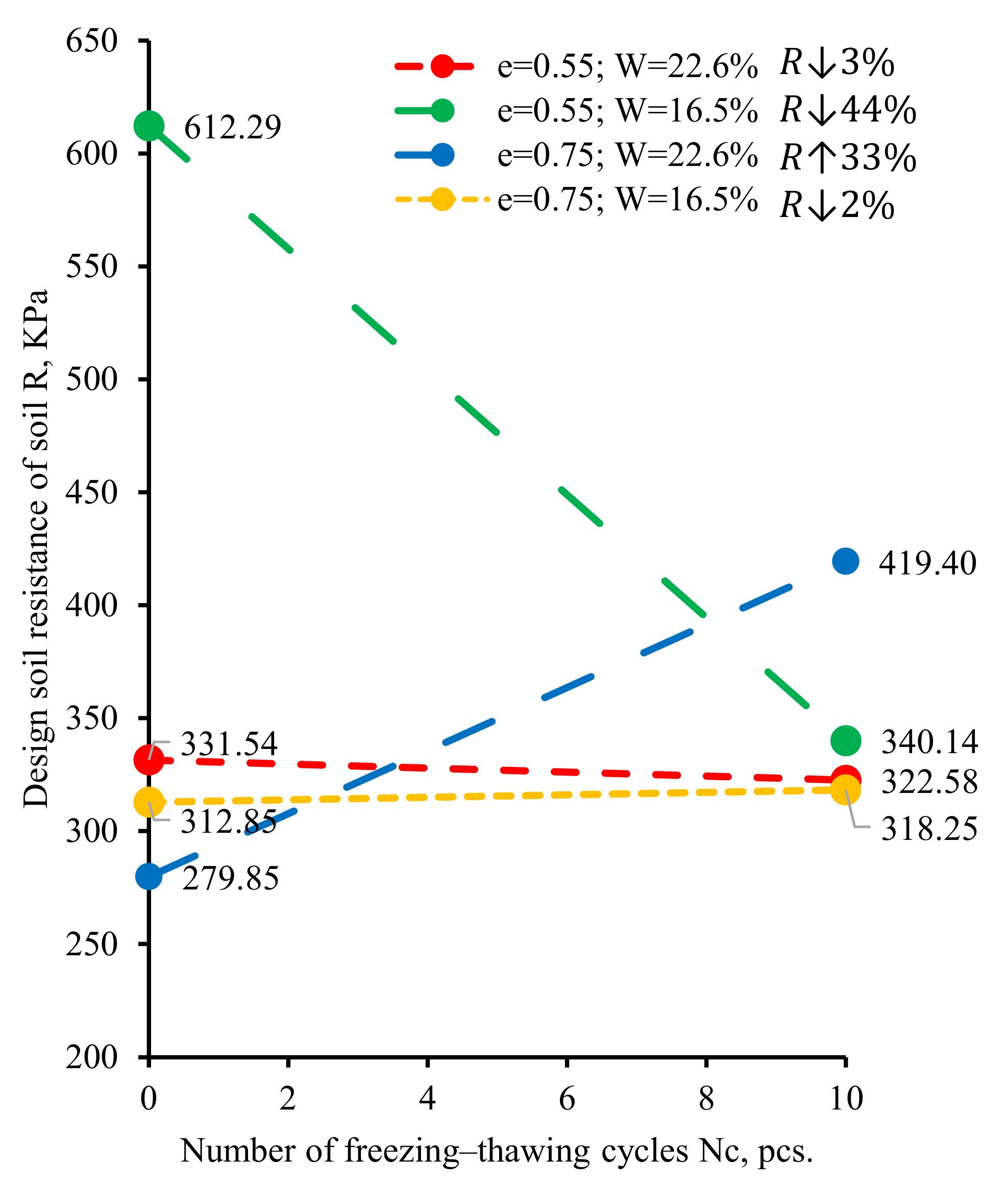
As can be seen from the results in Table 5, Figure 9, the freezing-thawing cycles significantly reduced the bearing capacity of the soil base. The largest decrease in design soil resistance R was by up to 44% after 10 freezing-thawing cycles, which was observed for the soils with $\mathit{e}=0.55$ and $\mathit{w}\mathbf{=}\mathbf{16.5}\mathbf{\%}$. For the soils with initial characteristics $\mathit{e}\mathbf{=}\mathbf{0.75}$ and $\mathit{w}\mathbf{=}\mathbf{22.6}\mathbf{\%}$, the design soil resistance increased by 33% after freezing-thawing cycles, which is obviously associated with additional soil compaction.

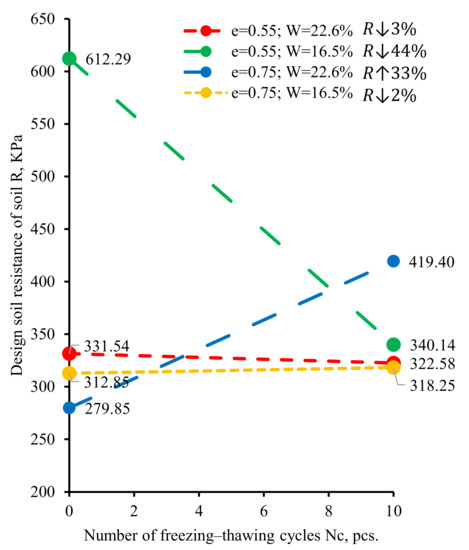
Figure 9. Dependence of design soil resistence from the number of freezing-thawing cycles.

Thus, in the case of an unfavorable combination of the type of soil, its condition, and environmental factors, if a decrease in the design soil resistance is not taken into account, additional settlement of the upper soil base layer may also be not accounted for. This is due to its non-linear operation at an average pressure exceeding R. In some cases, this can lead to soil uplift from under the building foundation and its significant subsidence.

6. Conclusion

In this work, a three-parameter paired experiment was conducted in order to analyze the influence of void ratio, initial moisture content, and the number of freezing-thawing cycles on the engineering characteristics of soil, such as angle of internal friction and cohesion. According to the results of the study, the following outcomes were highlighted:

• The factors under study greatly affect the cohesion of the soil and, together, can decrease it by up to three times. The angle of internal friction has an indefinite behavior when the parameters under study change, which is confirmed by the literature review. Consequently, taking into account the reduction in cohesion is mandatory in engineering practice, whereas taking into account the change in the angle of internal friction is only recommended.
• A program based on the least-squares method was used to calculate the approximation coefficients of the dependence describing the changes in strength characteristics from the abovementioned parameters under study based on experiment results. Thus, by setting the values of void ratio, initial soil moisture, and number of freeze–thaw cycles, it became possible to calculate the angle of internal friction and/or cohesion for each type of soil.
• Freezing–thawing cycles significantly decreased the bearing capacity of the soils: by 44% after 10 freezing-thawing cycles for soil with e = 0.55 and w = 16.5%. However, in the case of e = 0.75 and w = 22.6%, the bearing capacity of the soils increased by 33%, exceeding all expectations. Such changes in strength characteristics must be taken into account when designing structures, as they can lead to additional settlement or even subsidence of the foundations during the freezing-thawing cycles while exploiting.