Crouch Gait Analysis and Visualization Based on Gait Forward and Inverse Kinematics
Abstract
:1. Introduction
2. Materials and Methods
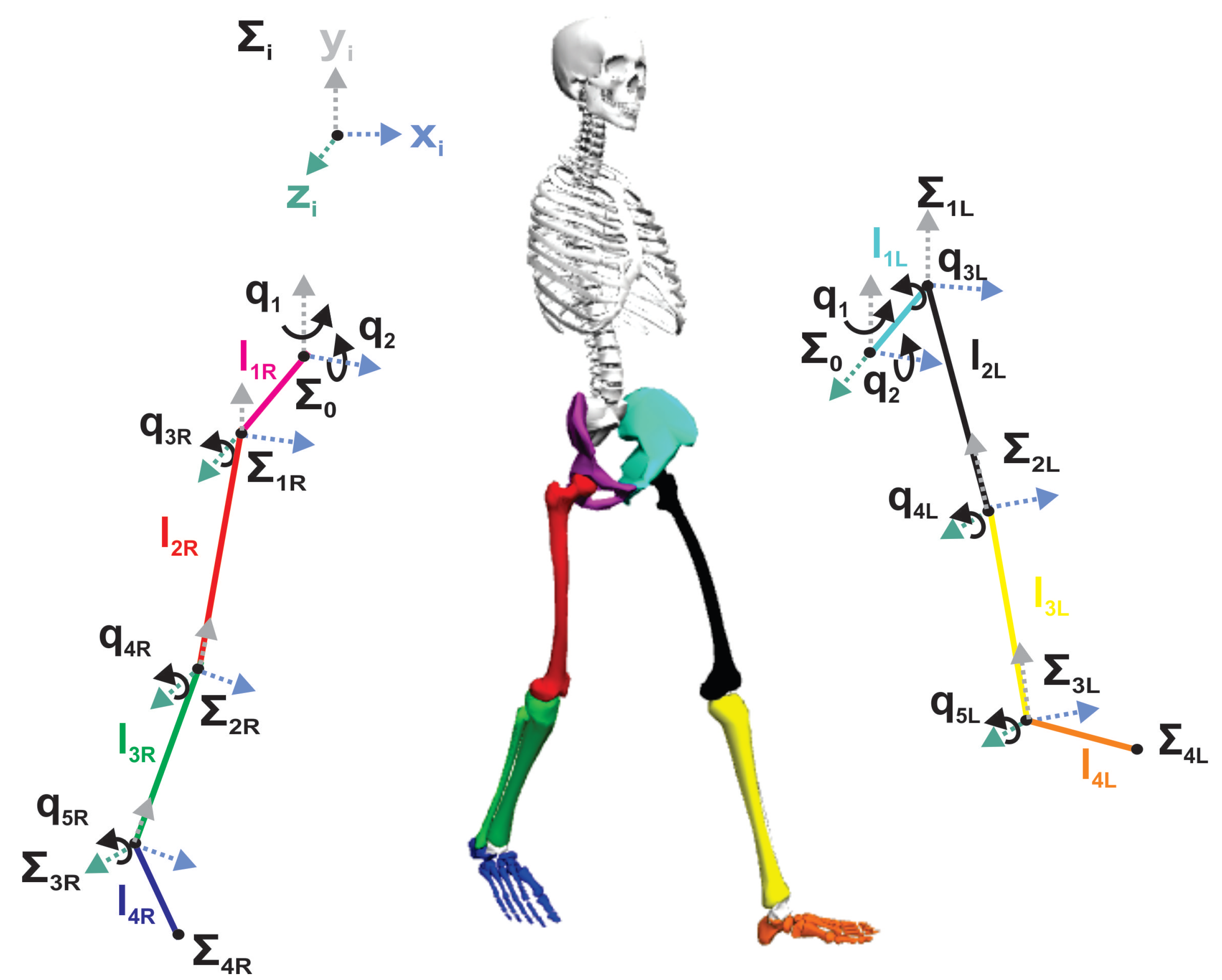
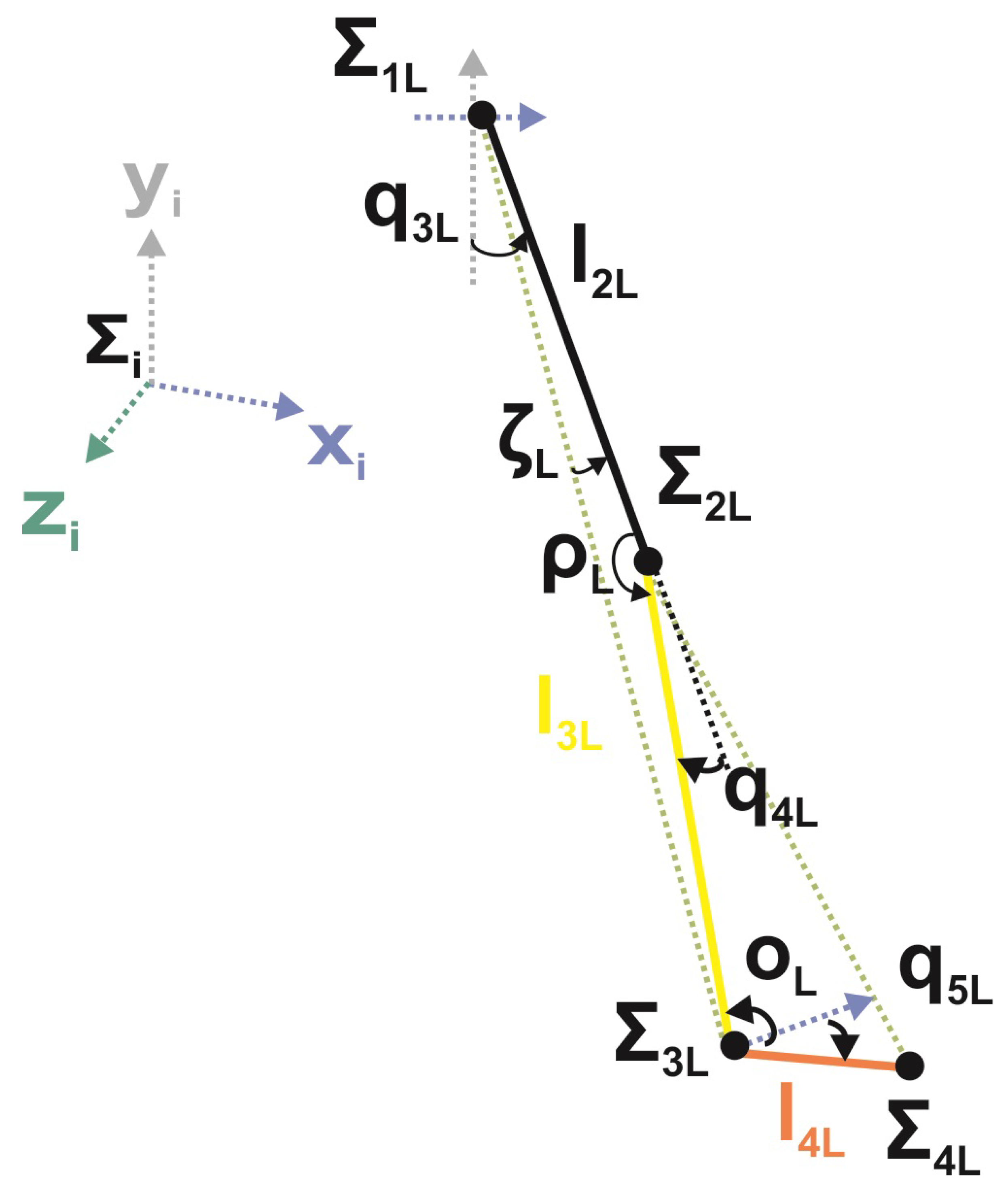
2.1. Gait Forward Kinematics
2.1.1. Quaternions Algebra for Rotations
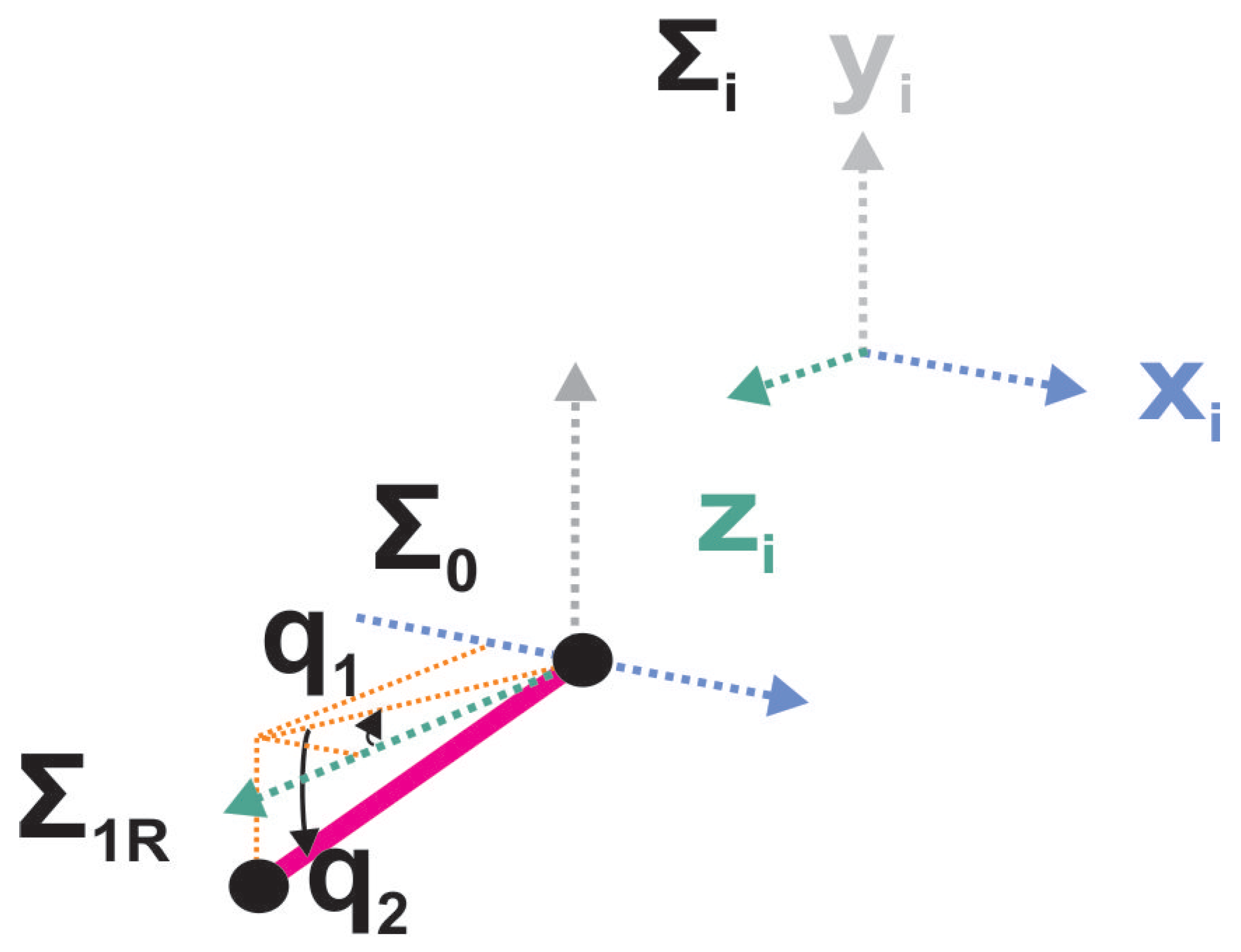
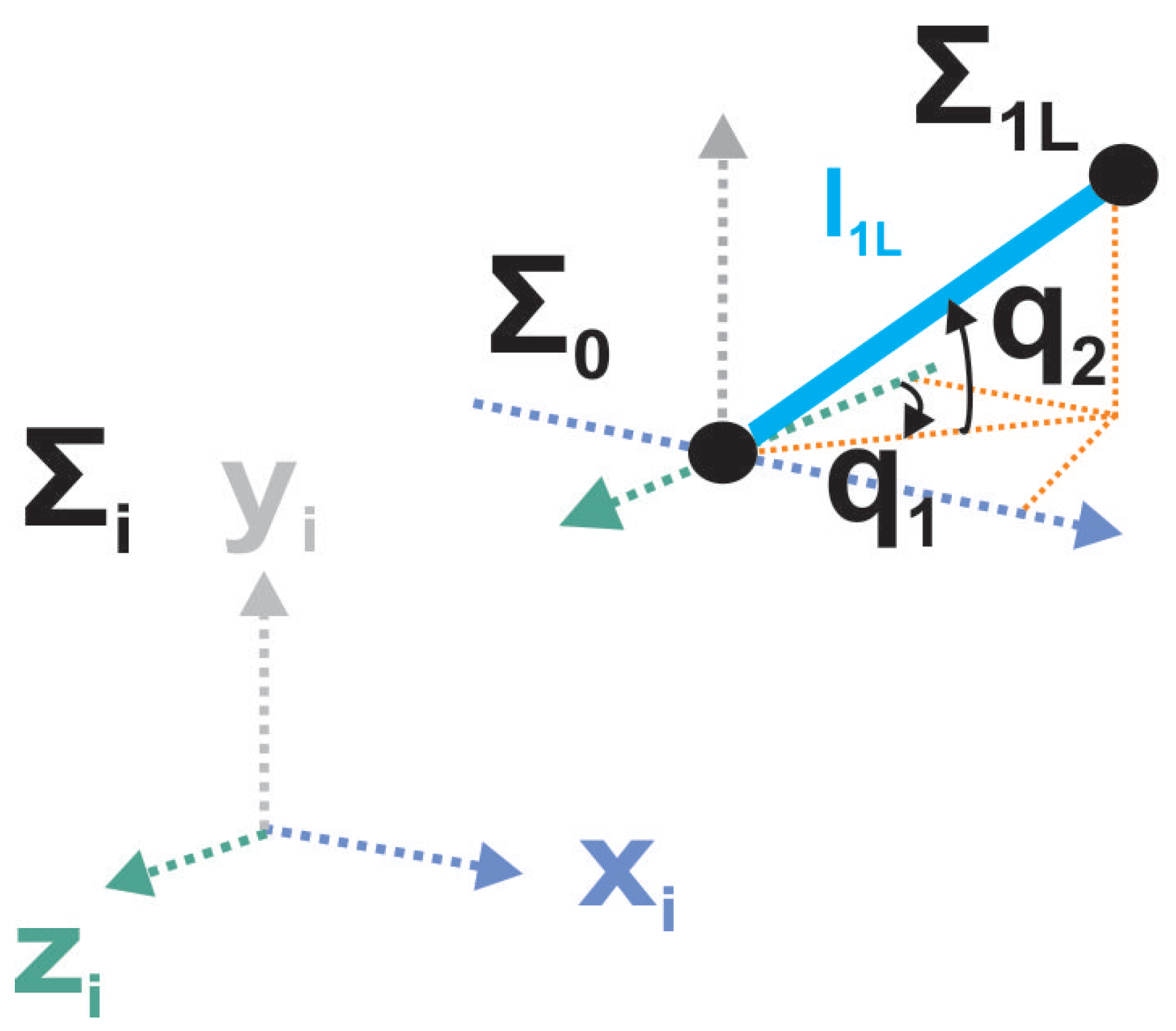
2.1.2. Gait Forward Kinematics Using Quaternions Algebra
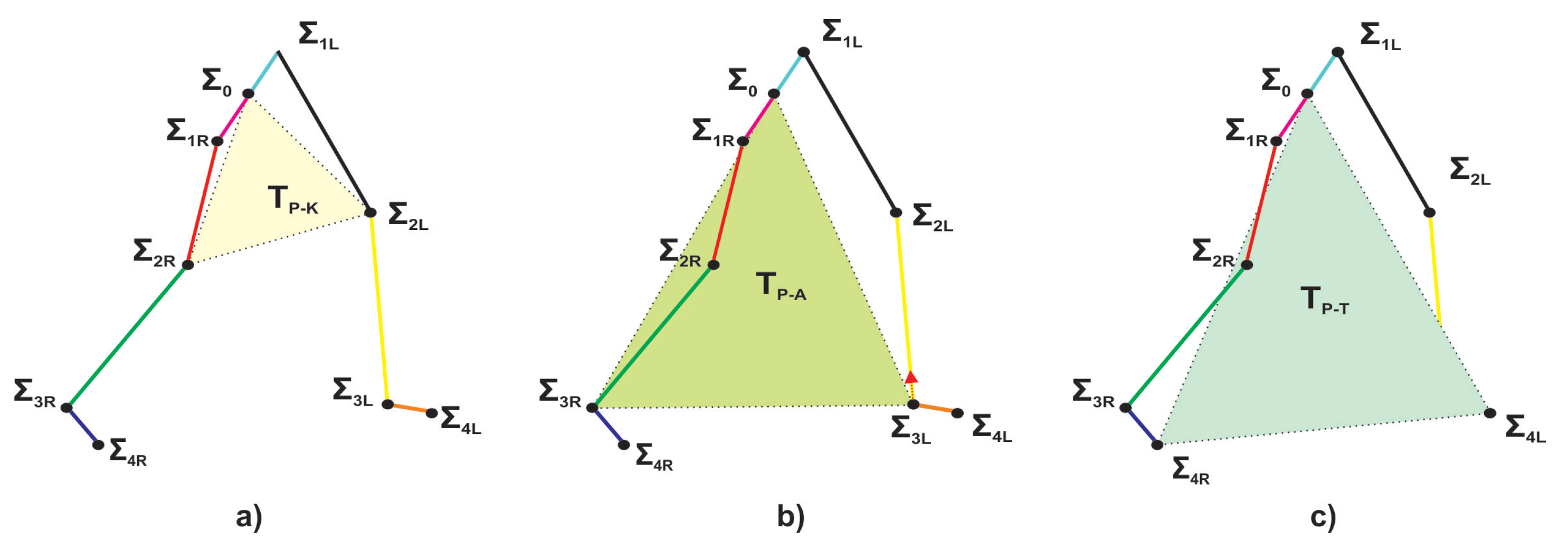
2.1.3. Parameters of Workspace for Gait Analysis
2.2. Gait Inverse Kinematics
Parameters on Joint Space for Gait Analysis
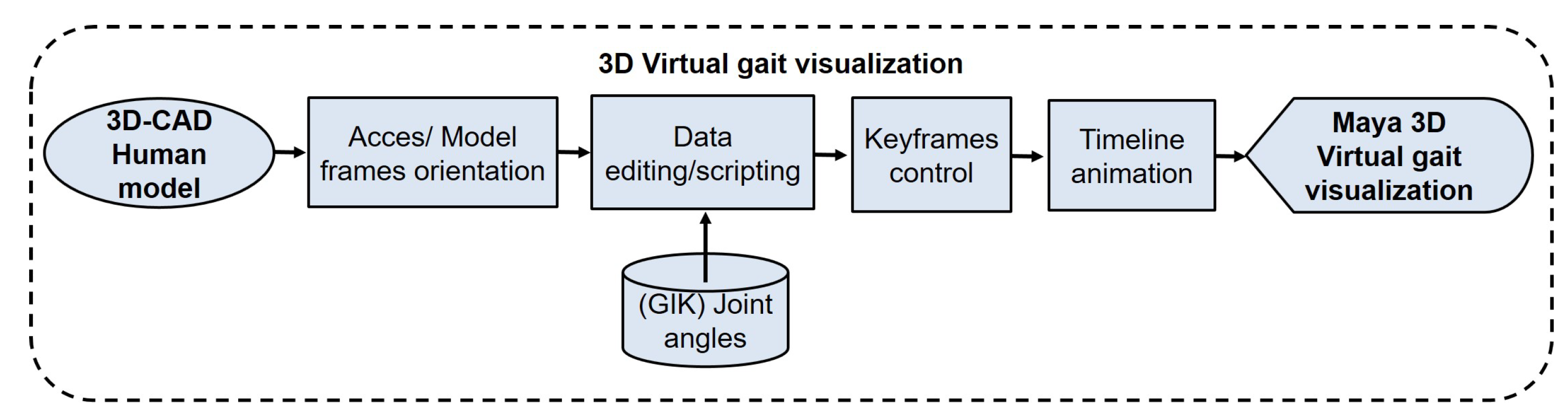
2.3. Virtual Gait Visualization
3. Results
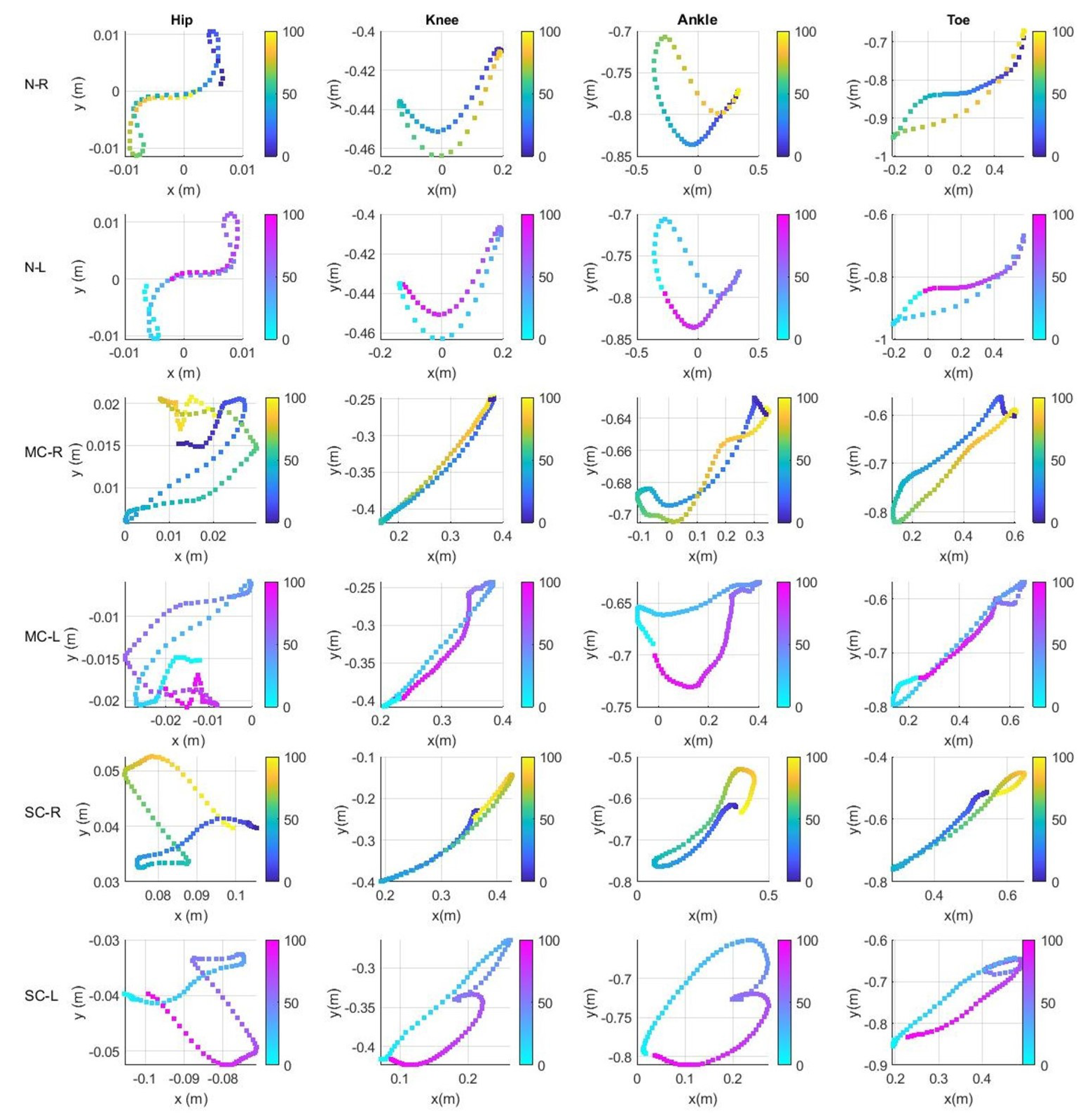
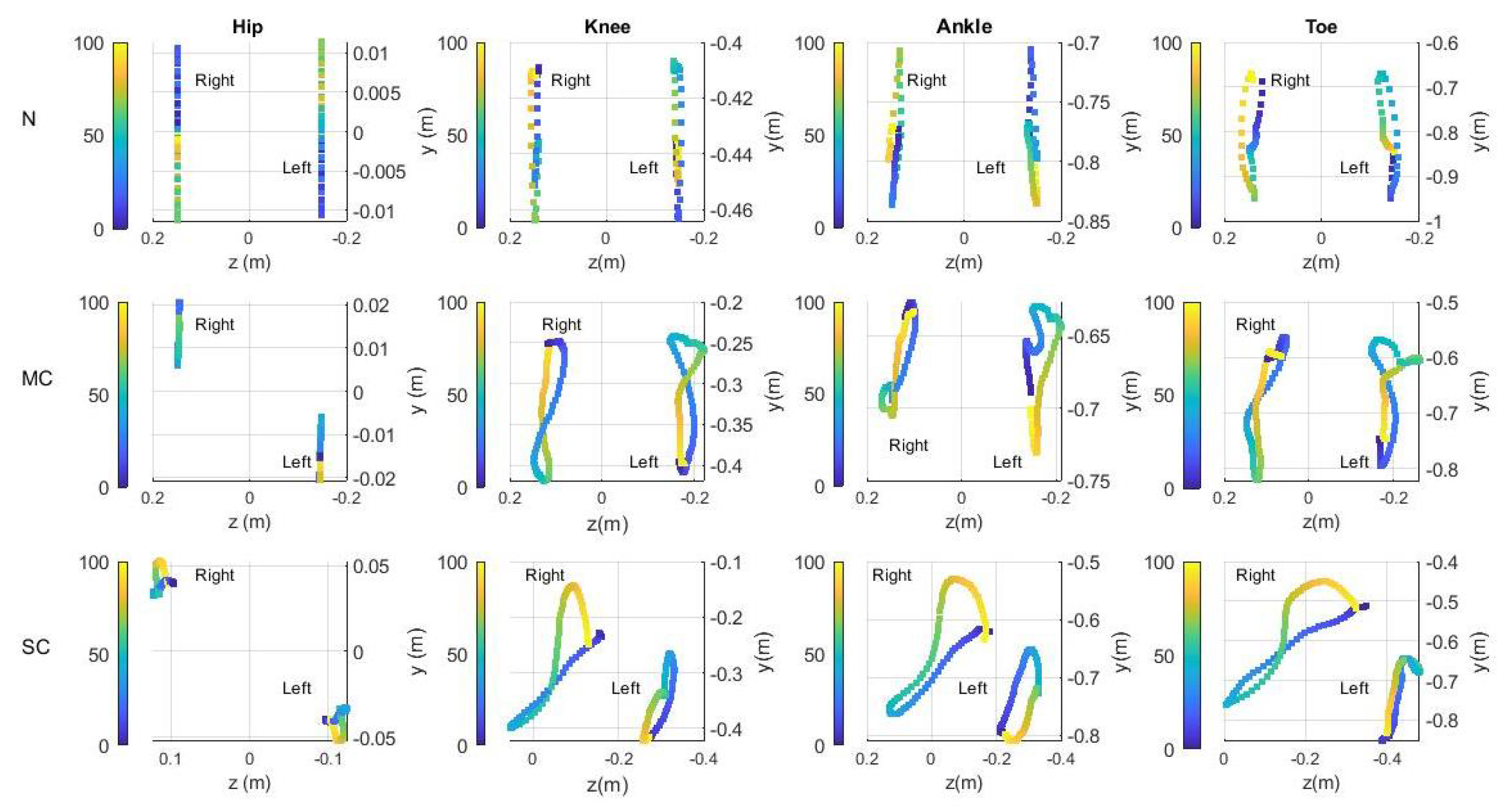
3.1. Gait Analysis on the Workspace
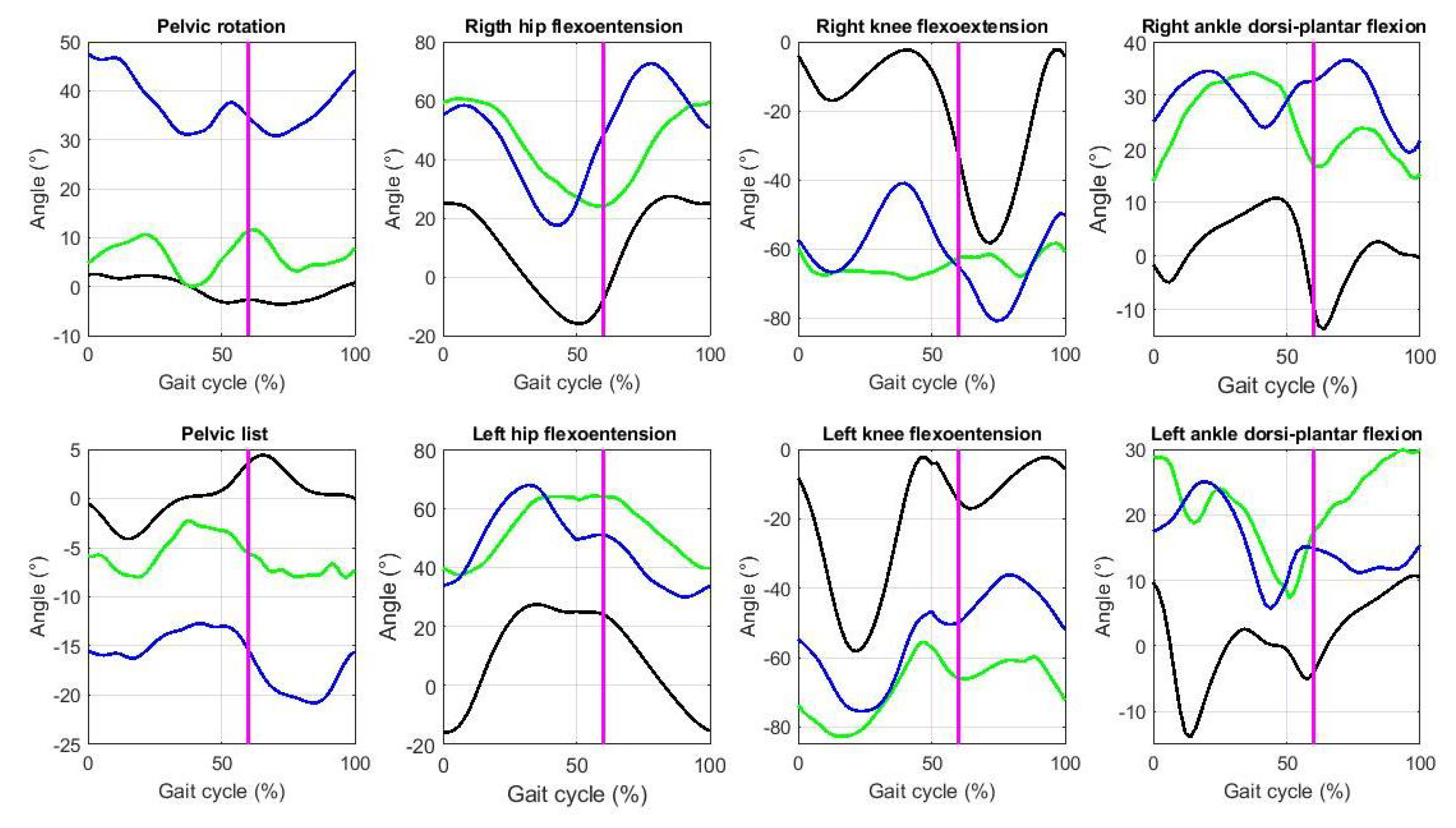
3.2. Gait Analysis on the Joint Space
3.3. Virtual Gait Visualization
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stergiou, N. Biomechanics and Gait Analysis; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Whittle, M.W. Gait Analysis: An Introduction; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Beaulieu, M.L.; Lamontagne, M.; Beaulé, P.E. Lower limb biomechanics during gait do not return to normal following total hip arthroplasty. Gait Posture 2010, 32, 269–273. [Google Scholar] [CrossRef]
- Ogihara, H.; Tsushima, E.; Kamo, T.; Sato, T.; Matsushima, A.; Niioka, Y.; Asahi, R.; Azami, M. Kinematic gait asymmetry assessment using joint angle data in patients with chronic stroke—A normalized cross-correlation approach. Gait Posture 2020, 80, 168–173. [Google Scholar] [CrossRef]
- Smith, M.C.; Stinear, J.; Stinear, C.M. The effects of unilateral step training and conventional treadmill training on gait asymmetry in patients with chronic stroke. Gait Posture 2021, 87, 156–162. [Google Scholar] [CrossRef]
- Kobsar, D.; Barden, J.M.; Clermont, C.; Wilson, J.; Ferber, R. Sex differences in the regularity and symmetry of gait in older adults with and without knee osteoarthritis. Gait Posture 2022, 95, e192–e197. [Google Scholar] [CrossRef]
- Munteanu, S.; Barton, C. Lower limb biomechanics during running in individuals with Achilles tendinopathy: A systematic review. J. Sci. Med. Sport 2010, 13, e74–e75. [Google Scholar] [CrossRef]
- Yamada, M.; Aoyama, T.; Mori, S.; Nishiguchi, S.; Okamoto, K.; Ito, T.; Muto, S.; Ishihara, T.; Yoshitomi, H.; Ito, H. Objective assessment of abnormal gait in patients with rheumatoid arthritis using a smartphone. Rheumatol. Int. 2012, 32, 3869–3874. [Google Scholar] [CrossRef]
- Chinn, L.; Dicharry, J.; Hart, J.M.; Saliba, S.; Wilder, R.; Hertel, J. Gait kinematics after taping in participants with chronic ankle instability. J. Athl. Train. 2014, 49, 322–330. [Google Scholar] [CrossRef] [Green Version]
- Saad, A.; Zaarour, I.; Guerin, F.; Bejjani, P.; Ayache, M.; Lefebvre, D. Detection of freezing of gait for Parkinson’s disease patients with multi-sensor device and Gaussian neural networks. Int. J. Mach. Learn. Cybern. 2017, 8, 941–954. [Google Scholar] [CrossRef]
- Xu, H.; Li, X.; Shi, Y.; An, L.; Taylor, D.; Christman, M.; Morse, J.; Merryweather, A. Hospital bed height influences biomechanics during bed egress: A comparative controlled study of patients with Parkinson disease. J. Biomech. 2021, 115, 110116. [Google Scholar] [CrossRef]
- Ramadoss, P.; Rapetti, L.; Tirupachuri, Y.; Grieco, R.; Milani, G.; Valli, E.; Dafarra, S.; Traversaro, S.; Pucci, D. Whole-Body Human Kinematics Estimation using Dynamical Inverse Kinematics and Contact-Aided Lie Group Kalman Filter. arXiv 2022, arXiv:2205.07835. [Google Scholar]
- Kainz, H.; Modenese, L.; Lloyd, D.; Maine, S.; Walsh, H.; Carty, C. Joint kinematic calculation based on clinical direct kinematic versus inverse kinematic gait models. J. Biomech. 2016, 49, 1658–1669. [Google Scholar] [CrossRef]
- Barki, A.; Kendricks, K.; Tuttle, R.F.; Bunker, D.J.; Borel, C.C. Extraction of human gait signatures: An inverse kinematic approach using Groebner basis theory applied to gait cycle analysis. In Proceedings of the Active and Passive Signatures IV; SPIE: Bellingham, WA, USA, 2013; Volume 8734, pp. 138–151. [Google Scholar]
- Parent, A.; Pouliot-Laforte, A.; Dal Maso, F.; Cherni, Y.; Marois, P.; Ballaz, L. Muscle fatigue during a short walking exercise in children with cerebral palsy who walk in a crouch gait. Gait Posture 2019, 72, 22–27. [Google Scholar] [CrossRef]
- Dussault-Picard, C.; Mohammadyari, S.; Arvisais, D.; Robert, M.; Dixon, P. Gait adaptations of individuals with cerebral palsy on irregular surfaces: A Scoping Review. Gait Posture 2022, 96, 35–46. [Google Scholar] [CrossRef]
- Rethlefsen, S.A.; Blumstein, G.; Kay, R.M.; Dorey, F.; Wren, T.A. Prevalence of specific gait abnormalities in children with cerebral palsy revisited: Influence of age, prior surgery, and Gross Motor Function Classification System level. Dev. Med. Child Neurol. 2017, 59, 79–88. [Google Scholar] [CrossRef]
- Cho, S.; Lee, K.D.; Park, H.S. A Mobile Cable-Tensioning Platform to Improve Crouch Gait in Children With Cerebral Palsy. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 1092–1102. [Google Scholar] [CrossRef]
- Lerner, Z.F.; Damiano, D.L.; Park, H.S.; Gravunder, A.J.; Bulea, T.C. A robotic exoskeleton for treatment of crouch gait in children with cerebral palsy: Design and initial application. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 650–659. [Google Scholar] [CrossRef]
- Adil, S.; Al Jumaily, A.; Anam, K. AW-ELM-based Crouch Gait recognition after ischemic stroke. In Proceedings of the 2016 5th International Conference on Electronic Devices, Systems and Applications (ICEDSA), Ras Al Khaimah, United Arab Emirates, 6–8 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Jahnsen, R.; Villien, L.; Aamodt, G.; Stanghelle, J.; Holm, I. Musculoskeletal pain in adults with cerebral palsy compared with the general population. J. Rehabil. Med. 2004, 36, 78–84. [Google Scholar] [CrossRef] [Green Version]
- Opheim, A.; Jahnsen, R.; Olsson, E.; Stanghelle, J.K. Walking function, pain, and fatigue in adults with cerebral palsy: A 7-year follow-up study. Dev. Med. Child Neurol. 2009, 51, 381–388. [Google Scholar] [CrossRef]
- Rose, J.; Gamble, J.G.; Burgos, A.; Medeiros, J.; Haskell, W.L. Energy expenditure index of walking for normal children and for children with cerebral palsy. Dev. Med. Child Neurol. 1990, 32, 333–340. [Google Scholar] [CrossRef]
- O’Sullivan, R.; Marron, A.; Brady, K. Crouch gait or flexed-knee gait in cerebral palsy: Is there a difference? A systematic review. Gait Posture 2020, 82, 153–160. [Google Scholar] [CrossRef]
- Spong, M.W.; Vidyasagar, M. Robot Dynamics and Control; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Ho, T.; Kang, C.G.; Lee, S. Efficient closed-form solution of inverse kinematics for a specific six-DOF arm. Int. J. Control. Autom. Syst. 2012, 10, 567–573. [Google Scholar] [CrossRef]
- Kucuk, S.; Bingul, Z. Inverse kinematics solutions for industrial robot manipulators with offset wrists. Appl. Math. Model. 2014, 38, 1983–1999. [Google Scholar] [CrossRef]
- Dulęba, I.; Opałka, M. A comparison of Jacobian-based methods of inverse kinematics for serial robot manipulators. Int. J. Appl. Math. Comput. Sci. 2013, 23, 373–382. [Google Scholar] [CrossRef] [Green Version]
- Di Vito, D.; Natale, C.; Antonelli, G. A comparison of damped least squares algorithms for inverse kinematics of robot manipulators. IFAC-PapersOnLine 2017, 50, 6869–6874. [Google Scholar] [CrossRef]
- Hamilton, W. First Motive for naming the Quotient of two Vectors a Quaternion. Elem. Quaternions 1866, 110–113. [Google Scholar]
- Cohen, A.; Shoham, M. Hyper Dual Quaternions representation of rigid bodies kinematics. Mech. Mach. Theory 2020, 150, 103861. [Google Scholar] [CrossRef]
- Özgür, E.; Mezouar, Y. Kinematic modeling and control of a robot arm using unit dual quaternions. Robot. Auton. Syst. 2016, 77, 66–73. [Google Scholar] [CrossRef]
- Baker, R.; Leboeuf, F.; Reay, J.; Sangeux, M. The conventional gait model-success and limitations. Handb. Hum. Motion 2018, 489–508. [Google Scholar]
- Lin, C.J.; Guo, L.Y.; Su, F.C.; Chou, Y.L.; Cherng, R.J. Common abnormal kinetic patterns of the knee in gait in spastic diplegia of cerebral palsy. Gait Posture 2000, 11, 224–232. [Google Scholar] [CrossRef]
- Rodda, J.; Graham, H.K.; Nattrass, G.; Galea, M.P.; Baker, R.; Wolfe, R. Correction of severe crouch gait in patients with spastic diplegia with use of multilevel orthopaedic surgery. JBJS 2006, 88, 2653–2664. [Google Scholar] [CrossRef]
- Steele, K.M.; Seth, A.; Hicks, J.L.; Schwartz, M.S.; Delp, S.L. Muscle contributions to support and progression during single-limb stance in crouch gait. J. Biomech. 2010, 43, 2099–2105. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Soh, G.S. A study on estimation of planar gait kinematics using minimal inertial measurement units and inverse kinematics. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 6911–6914. [Google Scholar]
- Roy, G.; Mukherjee, S.; Das, T.; Bhaumik, S. Single Support Phase Gait Kinematics and Kinetics for a Humanoid Lower Limb Exoskeleton. In Proceedings of the 2020 IEEE Region 10 Symposium (TENSYMP), Dhaka, Bangladesh, 5–7 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 138–141. [Google Scholar]
- Catelli, D.S.; Cotter, B.; Lamontagne, M.; Grammatopoulos, G. Spine, Pelvis and Hip Kinematics—Characterizing the Axial Plane in Healthy and Osteoarthritic Hips. Appl. Sci. 2021, 11, 9921. [Google Scholar] [CrossRef]
- Surer, E.; Kose, A. Methods and technologies for gait analysis. In Computer Analysis of Human Behavior; Springer: Berlin/Heidelberg, Germany, 2011; pp. 105–123. [Google Scholar]
- Bethi, S.R. Exergames for telerehabilitation. arXiv 2020, arXiv:2006.10110. [Google Scholar]
- Thikey, H.; van Wjick, F.; Grealy, M.; Rowe, P. A need for meaningful visual feedback of lower extremity function after stroke. In Proceedings of the 2011 5th International Conference on Pervasive Computing Technologies for Healthcare (PervasiveHealth) and Workshops, Dublin, Ireland, 23–26 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 379–383. [Google Scholar]
- Uzor, S.; Baillie, L. Recov-R: Evaluation of a home-based tailored exergame system to reduce fall risk in seniors. ACM Trans. Comput.-Hum. Interact. (TOCHI) 2019, 26, 1–38. [Google Scholar] [CrossRef]
- Pacheco, T.B.F.; de Medeiros, C.S.P.; de Oliveira, V.H.B.; Vieira, E.R.; De Cavalcanti, F. Effectiveness of exergames for improving mobility and balance in older adults: A systematic review and meta-analysis. Syst. Rev. 2020, 9, 1–14. [Google Scholar] [CrossRef]
- Cardenas, A.; Warner, D.; Switzer, L.; Graham, T.N.; Cimolino, G.; Fehlings, D. Inpatient Exergames for Children with Cerebral Palsy following Lower Extremity Orthopedic Surgery: A Feasibility Study. Dev. Neurorehabilit. 2021, 24, 230–236. [Google Scholar] [CrossRef]
- Veilleux, L.N.; Raison, M.; Rauch, F.; Robert, M.; Ballaz, L. Agreement of spatio-temporal gait parameters between a vertical ground reaction force decomposition algorithm and a motion capture system. Gait Posture 2016, 43, 257–264. [Google Scholar] [CrossRef]
- Filtjens, B.; Ginis, P.; Nieuwboer, A.; Slaets, P.; Vanrumste, B. Automated freezing of gait assessment with marker-based motion capture and multi-stage spatial-temporal graph convolutional neural networks. J. Neuroeng. Rehabil. 2022, 19, 1–14. [Google Scholar] [CrossRef]
- Gumroad. Skeleton Maya Rig, 2022. Available online: https://truongcgartist.gumroad.com/l/bdbxF (accessed on 30 May 2022).
- Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; et al. OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLoS Comput. Biol. 2018, 14, e1006223. [Google Scholar] [CrossRef] [Green Version]
- John, C.T.; Seth, A.; Schwartz, M.H.; Delp, S.L. Contributions of muscles to mediolateral ground reaction force over a range of walking speeds. J. Biomech. 2012, 45, 2438–2443. [Google Scholar] [CrossRef] [Green Version]
- Tadano, S.; Takeda, R.; Miyagawa, H. Three dimensional gait analysis using wearable acceleration and gyro sensors based on quaternion calculations. Sensors 2013, 13, 9321–9343. [Google Scholar] [CrossRef] [PubMed]





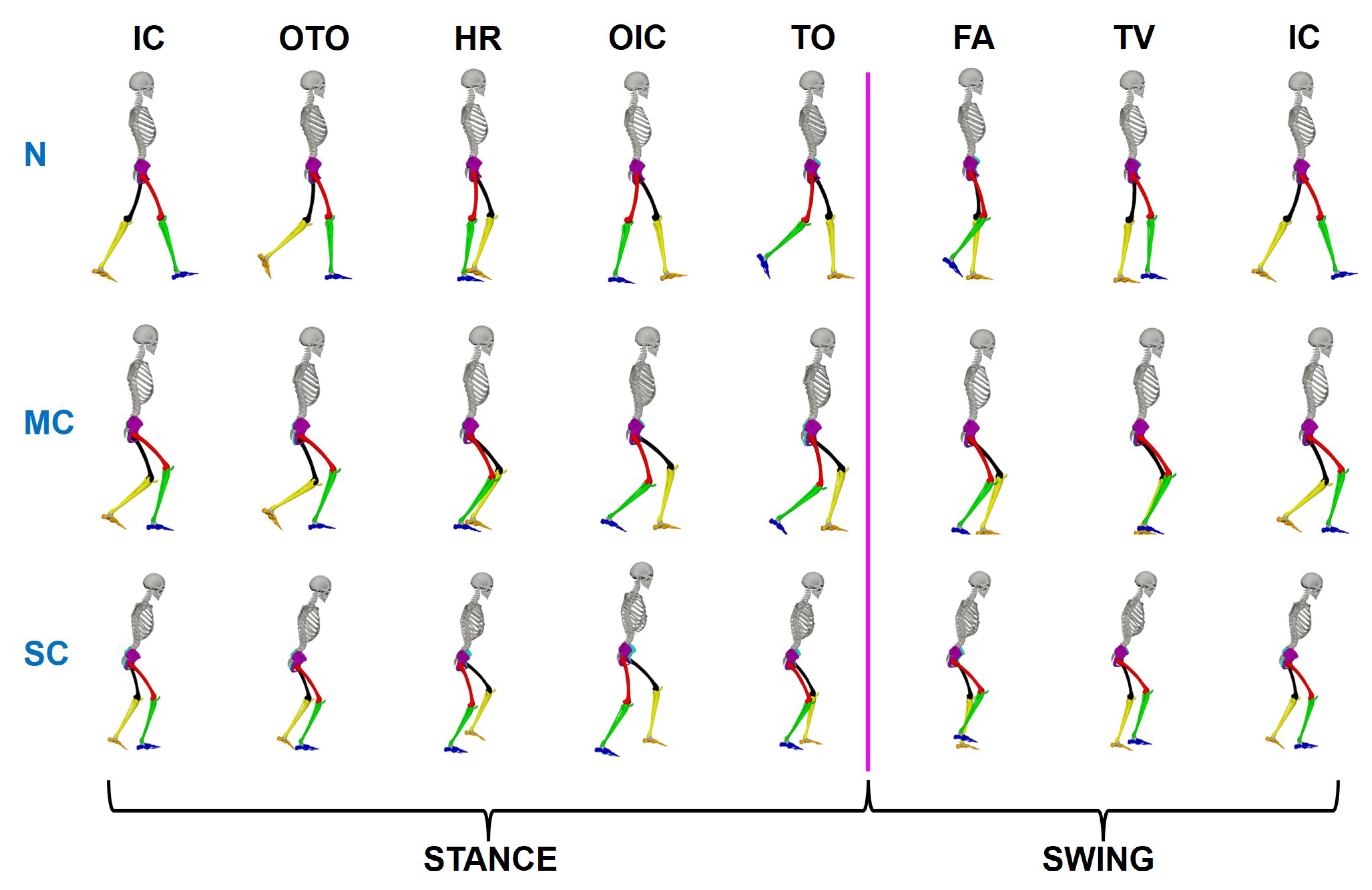


| Normal (N) | Mild Crouch (MC) | Severe Crouch (SC) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| METRIC | MEAN | STD | RMS | MEAN | STD | RMS | MEAN | STD | RMS |
| (m) | 0.373 | 0.049 | 0.376 | 0.350 | 0.038 | 0.352 | 0.346 | 0.038 | 0.348 |
| (m) | 0.520 | 0.138 | 0.538 | 0.432 | 0.092 | 0.441 | 0.381 | 0.058 | 0.386 |
| (m) | 0.563 | 0.157 | 0.584 | 0.459 | 0.107 | 0.471 | 0.405 | 0.066 | 0.410 |
| (m) | 0.081 | 0.008 | 0.08 | 0.077 | 0.007 | 0.077 | 0.076 | 0.007 | 0.076 |
| (m) | 0.203 | 0.053 | 0.209 | 0.147 | 0.030 | 0.150 | 0.136 | 0.025 | 0.138 |
| (m) | 0.239 | 0.065 | 0.248 | 0.178 | 0.041 | 0.183 | 0.161 | 0.031 | 0.164 |
| Normal (N) | Mild Crouch (MC) | Severe Crouch (SC) | ||||
|---|---|---|---|---|---|---|
| −3.576 | 2.560 | 0.020 | 11.617 | 30.78 | 47.611 | |
| −4.097 | 4.413 | −8.047 | −2.270 | −20.783 | −12.690 | |
| −15.921 | 27.418 | 23.992 | 60.633 | 17.488 | 72.673 | |
| −15.897 | 27.419 | 37.455 | 64.153 | 29.942 | 67.872 | |
| −58.234 | −2.270 | −68.687 | −58.242 | −80.684 | −40.947 | |
| −58.207 | −2.271 | −82.737 | −55.463 | −75.453 | −36.203 | |
| −13.785 | 10.741 | 13.798 | 34.151 | 19.187 | 36.610 | |
| −13.919 | 10.749 | 7.345 | 29.921 | 5.692 | 25.056 | |
| Normal (N) | Mild Crouch (MC) | Severe Crouch (SC) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| JA | ||||||||||||
| −0.65 | 2.29 | 2.35 | 1.10 | 6.27 | 3.17 | 7.02 | 1.12 | 37.10 | 5.33 | 37.47 | 1.01 | |
| 0.22 | 2.33 | 2.31 | 1.29 | −5.97 | 1.88 | 6.25 | 1.04 | −16.20 | 2.65 | 16.41 | 1.01 | |
| 9.71 | 15.68 | 18.31 | 1.12 | 44.42 | 13.42 | 46.39 | 1.04 | 48.53 | 16.97 | 51.39 | 1.06 | |
| 9.71 | 15.66 | 18.29 | 1.12 | 52.95 | 9.91 | 53.87 | 1.02 | 47.16 | 12.17 | 48.69 | 1.03 | |
| −19.98 | 18.31 | 26.98 | 1.35 | −64.85 | 2.79 | 64.91 | 1.00 | −60.71 | 11.22 | 61.73 | 1.02 | |
| −19.98 | 18.30 | 26.97 | 1.35 | −68.32 | 8.48 | 68.84 | 1.01 | −54.06 | 12.76 | 55.53 | 1.02 | |
| 1.15 | 6.39 | 6.42 | 1.25 | 24.66 | 6.51 | 25.49 | 0.39 | 29.81 | 4.82 | 30.19 | 1.01 | |
| 1.12 | 6.42 | 6.46 | 1.25 | 21.53 | 6.20 | 22.40 | 1.04 | 15.29 | 5.20 | 16.14 | 1.05 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Islas, J.-C.; Dominguez-Ramirez, O.-A.; Lopez-Ortega, O.; Peña-Ramirez, J.; Ordaz-Oliver, J.-P.; Marroquin-Gutierrez, F. Crouch Gait Analysis and Visualization Based on Gait Forward and Inverse Kinematics. Appl. Sci. 2022, 12, 10197. https://doi.org/10.3390/app122010197
Gonzalez-Islas J-C, Dominguez-Ramirez O-A, Lopez-Ortega O, Peña-Ramirez J, Ordaz-Oliver J-P, Marroquin-Gutierrez F. Crouch Gait Analysis and Visualization Based on Gait Forward and Inverse Kinematics. Applied Sciences. 2022; 12(20):10197. https://doi.org/10.3390/app122010197
Chicago/Turabian StyleGonzalez-Islas, Juan-Carlos, Omar-Arturo Dominguez-Ramirez, Omar Lopez-Ortega, Jonatan Peña-Ramirez, Jesus-Patricio Ordaz-Oliver, and Francisco Marroquin-Gutierrez. 2022. "Crouch Gait Analysis and Visualization Based on Gait Forward and Inverse Kinematics" Applied Sciences 12, no. 20: 10197. https://doi.org/10.3390/app122010197
APA StyleGonzalez-Islas, J.-C., Dominguez-Ramirez, O.-A., Lopez-Ortega, O., Peña-Ramirez, J., Ordaz-Oliver, J.-P., & Marroquin-Gutierrez, F. (2022). Crouch Gait Analysis and Visualization Based on Gait Forward and Inverse Kinematics. Applied Sciences, 12(20), 10197. https://doi.org/10.3390/app122010197







