Study on the Penetration Characteristics of Water Entry Rod Projectile into Liquid Cabin at an Attack Angle

Abstract

The penetration of a projectile into a warship broadside liquid cabin is usually a non-ideal penetration process. To explore the protective effects of the broadside liquid cabin of a large warship against the non-ideal penetration of rod projectiles and to provide reference for the design of new liquid cabin structures, ballistic impact tests of rod projectiles penetrating the liquid cabin at different attack angles were carried out. Combined with numerical calculation, the impact of the attack angle on the water entry and penetration characteristics of the projectile into the liquid cabin as well as their failure modes were studied. The overturning and yawing of the projectile in water were analyzed. The pressure load characteristics in the liquid cabin and the deformation/failure modes of the projectile and the liquid cabin were identified. The results showed that: multiple overturning and yawing occur in the projectile with an initial attack angle during penetration into liquid; the yaw direction is mainly affected by the initial attack angle and projectile attitude; the projectile mainly undergoes four basic failure modes, namely, asymmetric mushrooming at the projectile nose, side erosion, overall plastic bending and fracture; the actual failure of the projectile is a combination of the basic failure modes; the overall plastic bending and fracture are mainly related to the length to diameter ratio, initial attack angle and initial projectile velocity; the front plate of the liquid cabin may undergo tearing along the central plastic hinge line of the plate: at a small attack angle, the tear is “I” shaped, and at a large attack angle, it is “X”-shaped.

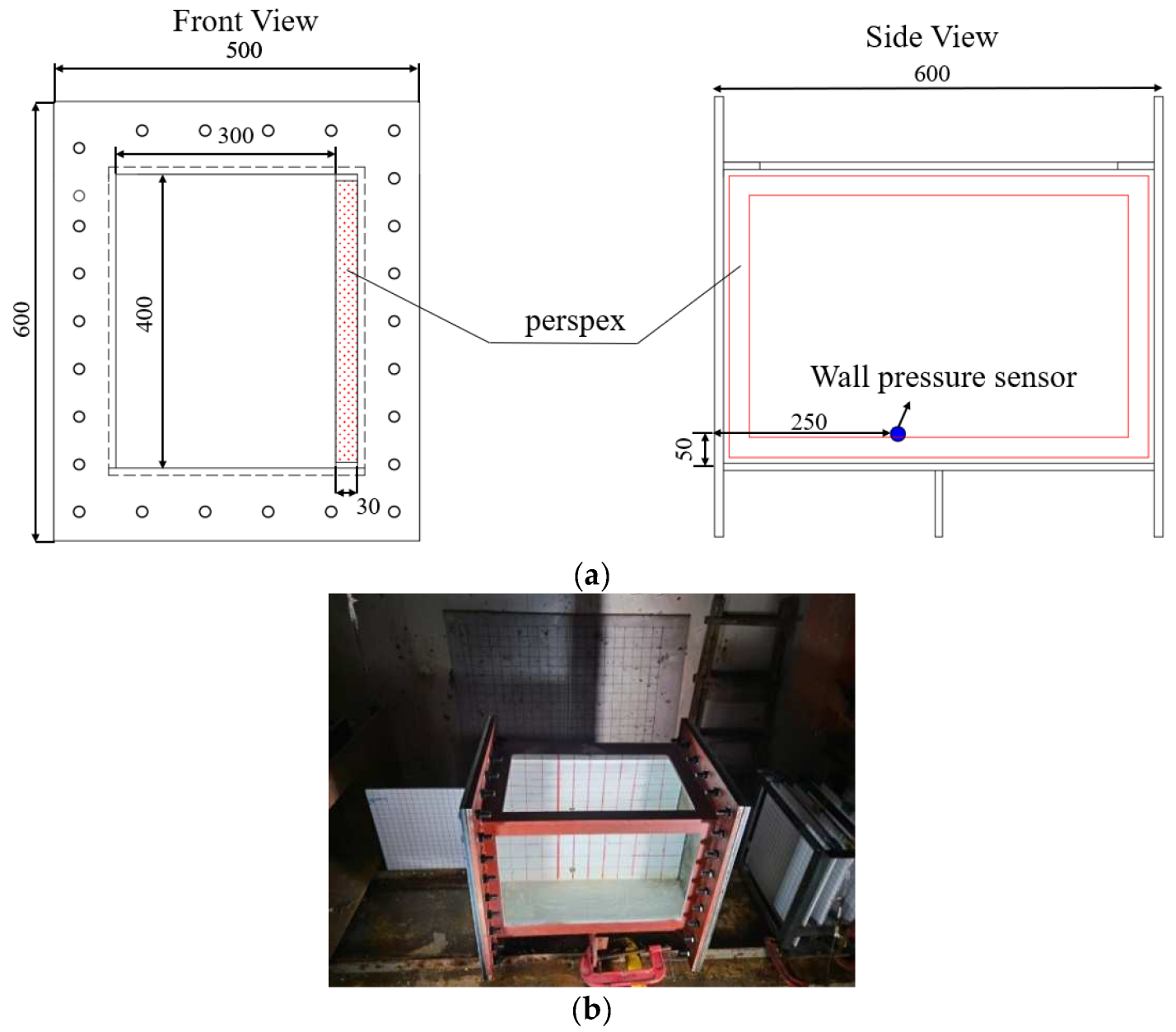
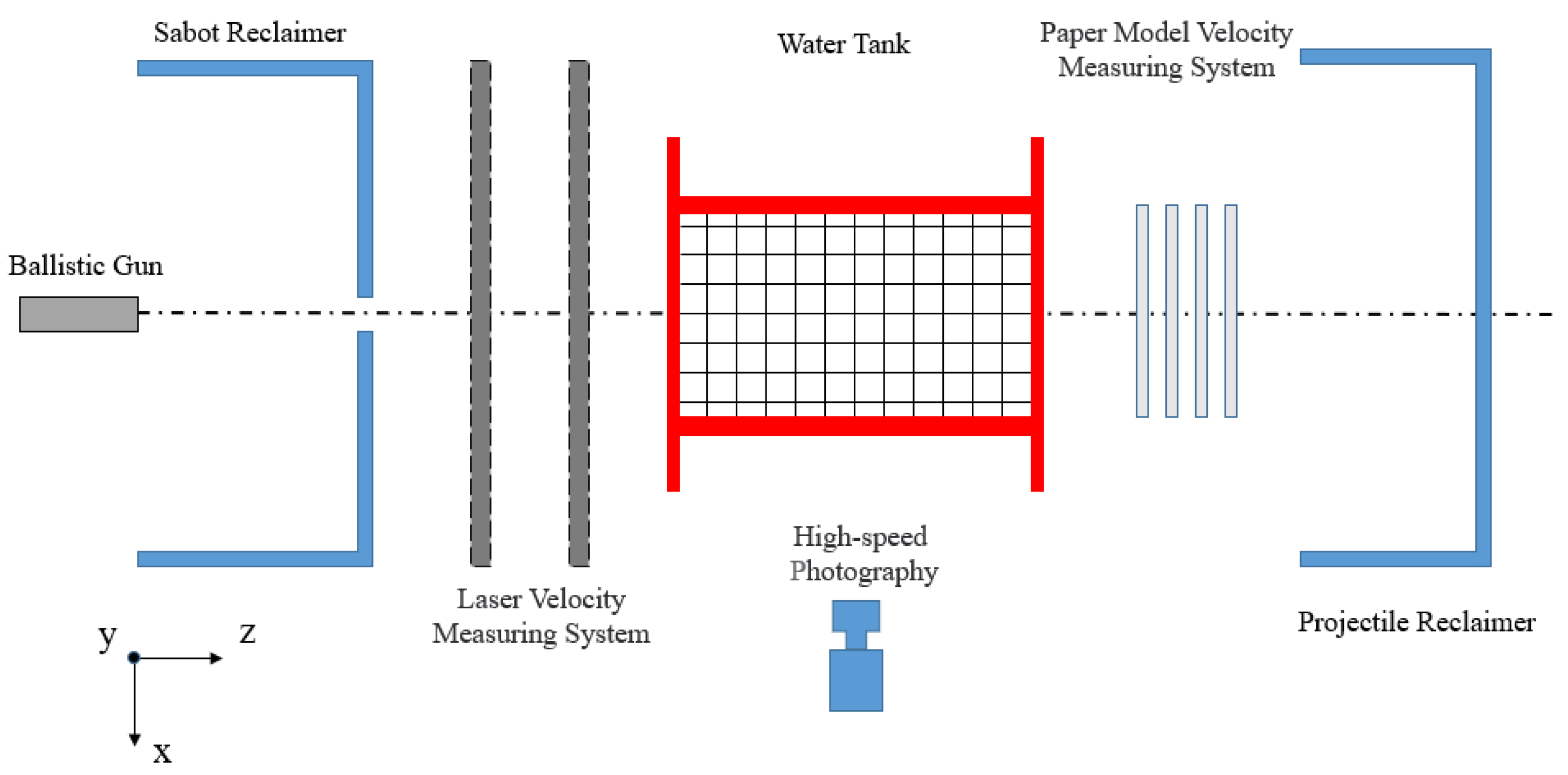
1. Introduction

To improve the penetration and destructive capabilities of projectiles, anti-armor weapons are widely equipped with rod projectiles with large length to diameter ratio (L/D ratio), strong anti-interference ability, good flight stability, high energy density and strong armor-piercing ability [1], whereas underwater weapons mostly adopt explosively formed projectiles (EFPs) [2,3]. As the warship broadside can be easily attacked by anti-ship weapons due to its large area, liquid cabin structures are often set on the broadside to protect the inner structure against penetration or armor-piercing damage caused by fragments and debris generated by the warhead shell and the outer plate of the cabin [4]. However, before penetrating into the liquid cabin, the projectile inevitably interacts with the stiffened plate and other obstacles in the empty cabin, changing the ballistic characteristics such as attitude angle of the projectile or causing asymmetric deformation of the projectile, and thus affecting its penetration capability [5]; when attacking underwater targets, torpedoes and projectiles usually enter the water at an attack angle; thus, it is of great significance to study the non-ideal water entry of rod projectiles for warship protection.

Generally, the water entry of projectiles can be divided into four stages: (1) Impact stage. As a projectile impacts the water at a high speed, causing a large impact force on the projectile, the projectile nose is prone to mushrooming deformation, and meanwhile the impact by the projectile leads to the formation of high-speed shock waves in the water, which propagates in a semicircle [6]. (2) Flow formation stage. After being impacted, the water will be separated by the projectile and flow away from its sides as the projectile moves forward, resulting in cavitation. Whip can be easily observed in this stage, where the pressure on the projectile is far less than that in the impact stage. (3) Open cavity stage. The cavity generated after the water entry of the projectile does not disappear immediately. It is still connected with the air at the water surface. As the projectile moves, the cavity gradually expands. When the projectile moves forward in the cavity, the uneven contact between the projectile nose and the water cause projectile swinging, resulting in ballistic instability. At the same time, due to tail swing, the tail contacts the cavity, causing tail flap, which further increases the uneven force on the projectile, leading to greater yaw [7,8]. (4) Closed cavity stage. After formation for some time, the cavity closes at a point on or below the water surface. Cavity closure may generate jet. When the jet strikes the cavity wall and causes its deformation, or hits the projectile and changes its trajectory, the projectile will detach from the cavity, leading to a significant change in the direction of projectile movement [9,10].

At present, the water entry problem of projectiles is generally studied from two perspectives: a projectile penetrating the free water, such as the water entry of aerial torpedo and spacecraft; a projectile penetrating the liquid tank, such as the penetration of a projectile into an aircraft fuel tank, and fragments penetrating the broadside liquid cabin. Researchers have conducted extensive research on the penetration of rod projectiles under ideal conditions.

In terms of the ideal penetration of projectiles into free water, Karman [11] proposed the added mass method to calculate the water entry impact load, and derived the formula of the water entry impact load using the conservation of momentum; Wagner [12] considered the lifting of water surface based on Karmans work, and introduced the wave influence factor to optimize the theory; Cointe [13] established a two-dimensional water entry impact model through progressive matching; Takagi [14] employed the potential method to accurately calculate the added mass, water entry velocity and penetration depth, which were in good agreement with the test results; Mojtaba [15] considered the transient model of cavity shape and established a complete model of the water entry of cylindrical projectile. Alekseevskii [16] and Tate [17] built a theoretical analysis model of the penetration of long-rod projectiles into semi-fluid medium. However, the water entry of projectile is a three-dimensional phenomenon. Both the fluid flow and projectile movement are asymmetric, and the forces involved are quite complex [18]. Chen [19] conducted experiments and found that projectile tumbling and yaw occurred in the cases of both vertical and oblique water entry of the projectile. Projectile tumbling occurs due to the change of the pitch angular velocity when the hydrodynamic force acting on the projectile nose does not pass through the center of gravity of the projectile, resulting in the so-called “whip” phenomenon [20]. Li Tianxiong [21] verified by numerical simulation that symmetrical projectiles also undergo ballistic yawing during vertical water entry.

With respect to the ideal penetration of a projectile into a liquid-filled structure, this process involves not only the interaction between the projectile and water, but also the interaction between water and the liquid tank. As the projectile penetrates the liquid tank, its energy is transferred to the water and tank structure, causing high pressure on them. This phenomenon is called hydrodynamic ram (HRAM) [22]. Researchers have studied the HRAM effect caused by impact on liquid-filled structures from various aspects: (1) Pressure load characteristics. Shi [23] verified that the rise time of initial shock waves under the HRAM effect is in microseconds; Gao [24] experimentally demonstrated that cavitation load is the dominant factor of liquid-filled cell failure; Li [25,26,27] summarized the load characteristics of rod projectiles penetrating the liquid-filled structure through penetration test and numerical calculation. Then, according to the load characteristics, he divided different areas to establish a simplified calculation model, and compared the structure protection performance; Disimile [28] adopted high-speed photography to show the generation of pressure waves and how the cavitation region expands and collapses. (2) Remaining projectile characteristics. Deletombe [29] proposed that the projectile will undergo overturning, deformation or even fracture when interacting with the water medium; Shen [30,31,32] analyzed the rule of the mushrooming deformation of the projectile and its influence on penetration resistance by tests and numerical calculations of fragments penetrating the liquid cabin, and proposed the formulas for calculating penetration resistance and velocity considering the influence of projectile deformation. (3) Structural deformation and failure. Artero and Nishida [33,34] found through tests and numerical calculations that water will cause secondary damage to the fluid-filled tubes, thus reducing the structural strength, and that the damage to the rear plate is more serious; David [35] conducted high-velocity impact test at 1000–3000 m/s with fluid-filled aluminum alloy containers, and the wall plate exhibited petal cracking.

In terms of water entry under non-ideal penetration conditions, which includes oblique water entry, water entry with an attack angle and water entry of asymmetric projectiles, currently, a large number of studies are focused on the water entry of asymmetric projectiles and oblique water entry. Takashi Isobe [36] performed oblique water entry tests using projectiles of various shapes, and had the following findings: when the projectile nose is moving in the water, the fluid exerts a lift force on it because of the cavitation caused by projectile motion; due to the pressure difference between the upper and lower surfaces of the projectile, cavitation occurs on the two surfaces is not symmetrical, and then the amount of water displaced by the projectile on the free surface side is less than the other side; thus, the pressure on this side is lower, resulting in asymmetric pressure on the upper and lower surfaces, thus exerting a lift force on the projectile and causing projectile ricochet; the nose shape of the projectile greatly affects the ballistic stability in water: the flat-nosed projectile has better ballistic stability underwater, the sharp-nosed projectile is prone to ballistic instability, and the ogive-nosed projectile tend to overturn in the early stage of water entry [37,38,39,40]; compared with symmetric nose, after the asymmetric nose enters the water, a non-axial component exists in the hydrodynamic force on the nose [41], and an overturning moment acts on the projectile, changing its attitude angle. This further affects the hydrodynamic force on the projectile, leading to the nonlinear increase in the overturn and yaw of the projectile [42,43]. The more asymmetric the projectile nose is, the worse the attitude and trajectory stability of the projectile is, and the projectile is prone to instability and inclination, which leads to yaw.

There are much less studies on the water entry by a projectile at an attack angle. Li [44] used numerical calculation to simulate the vertical water entry by a projectile at a small attack angle, and found that under certain attack angles, the projectile tail contacts with the cavity, thus reducing the ballistic stability, and that the spinning of the projectile in water has little impact on ballistic stability. However, Truscott [45,46] found that the spinning motion of the projectile induces a lateral force on the projectile, resulting in a curved trajectory. Yao [47] studied the water entry by the underwater vehicle through numerical simulation and revealed that positive attack angles suppress projectile whipping, whereas negative attack angles aggravate this phenomenon; therefore, ballistic change easily occurs under negative attack angles. Liang Jingqi [48] conducted a study using the LS-DYNA program and found that greater attack angle leads to faster axial velocity attenuation of the projectile, and thus greater overturning angle and projectile velocity. Wang Zhen [49] studied the oblique water entry of projectile at small attack angles with LS-DYNA, and discovered that the attack angle determines the direction and magnitude of the moment on the projectile nose.

To sum up, detailed investigations on the residual characteristics, pressure load characteristics and structural deformation of projectiles have been conducted through the ideal penetration test of the water-entry projectile. During the oblique water entry, entry with an angle of attack and water entry of an asymmetric projectile, ballistic yaw will occur. Among these cases, the penetration at an attack angle has been less investigated, and numerical calculation is the main method adopted. Few experimental studies have been carried out on the water entry by high-velocity projectiles with attack angles because the initial attack angle is difficult to realize in ballistic tests and is not conducive to ballistic control. Therefore, in the present study, the tests of high-velocity rod-shaped projectiles penetrating the liquid cabin at various attack angles are performed, and the overturning and yawing of the projectile in water, the pressure load characteristics and the deformation/failure modes of the projectile and the liquid cabin are analyzed by combining experimental tests with numerical calculations.

2. Experimental and Numerical Methods

2.1. Ballistic Experiment Design

2.1.1. Water Tank Model

Two types of cylindrical rod projectiles with a diameter of 14.5 mm and lengths of 23.5 mm and 29 mm are employed in the test. The projectile material is 45# steel.

As shown in Figure 1, the water tank is designed with a volume of 300 × 400 × 600 mm, with no cover on the upper side to simulate the free surface of the liquid cabin of an actual warship. The front and rear plates of the water tank have flange structures to facilitate the connection with the target. The front and rear plates and the pressplate are connected with the water tank using bolts with a diameter of 15 mm. A rubber pad is added between the target plate and the water tank to keep water tightness. One side of the water tank is made of 30 mm thick polymethyl methacrylate (organic glass) for the convenience of high-speed photography. On the other side, 50 mm gridlines are drawn for the calculation of the position and velocity of the projectile in water. The front plate is 2 mm thick, and the rear plate 4 mm thick. The material of the water tank and front/rear plates is Q235 steel.

2.1.2. Experimental Equipment and Setup

A 14.5 mm ballistic gun is used to fire the projectiles (bullets). The sabot is designed to be not closely fit with the projectile, so that initial disturbances can be generated after the projectile exits the bore, leading to the formation of the initial attack angle as the projectile impacts the target. The initial attack angle is obtained by the combination of high-speed photography and analysis of the breach morphology of the front wall of the water tank. A sabot collector is set to avoid the influence of sabot on the tests.

A laser speed measuring system is installed at the front side of the water tank (liquid cabin) to measure the initial velocity of the projectile (Figure 2a), and a target-net speed measuring system and a projectile recovery box are set at the rear side to measure the residual velocity of the projectile and recover the remaining projectile, respectively. The laser speed measurement system uses Chengdu Test TST6260 transient signal tester, the maximum sampling can reach 20 Msps.

The X213 high-speed camera made by Revealer Company in Hefei, China, is used to observe the projectile attitude in water and the cavitation process (Figure 2b). It shoots at 10,000 frames per second, i.e., one picture is taken every 100 us.

To measure the pressure load in water, a wall pressure sensor with a measuring range of 0~68 MPa and a sampling frequency of 1 MHz is set at a position 5 mm from its center to the bottom of the water tank (Figure 1a).

The experimental setup is shown in Figure 3.

2.2. Brief Experimental Results

Three penetration tests are conducted with the water tank, and the initial physical state and initial projectile velocity are recorded. Since the rear plate of the water tank have been perforated, the residual velocity of the projectile is not measured. After the tests, the residual projectile mass and its displacement in all directions are obtained through measurements. The test conditions and results are shown in

Table 1. Test conditions and results.

Test No.	Y-Axis Attack Angle (°)	Z-Axis Attack Angle (°)	Total Attack Angle (°)	Projectile Length	L/D Ratio	Projectile Weight M (g)	Initial Velocity V0 (m/s)	Residual Weight of Projectile M (g)	Displacement cm
									X	Y	Total
1	−30	−40	−50	23.5	1.6	29.9	1016.0	29.08	3.3	−1.9	3.8
2	−15	66	67	23.5	1.6	29.3	991.1	29.56	−0.6	6.8	6.83
3	25	38	45	29	2	37.3	1004.9	36.54	3.5	5.6	6.6

.

2.3. Numerical Calculation Model and Effective Verification

2.3.1. Numerical Model

The water tank model is simplified as shown in Figure 4. The models are built with SolidWorks, and Hypermesh is used to generate grids. The solid structures such as the projectile and target plate use Lagrangian solid elements; the side walls of the water tank do not involve damage and deformation; therefore, Lagrangian shell elements are used for them. The water domain is constructed in the water tank, the air domain is established outside the water tank; Eulerian elements are adopted for the water and air domains, and the common node approach is applied, so as to realize the flow of water and air.

The projectile is divided into 14 equal parts in the radial direction, 16 equal parts in the circumferential direction, and 1.2 mm grids along the length direction. The grid of the water and air domains is 4 mm in size, and the grids are refined in the central area with a size of 2 mm. The grids of the front and rear plates of the water tank are divided into 1 mm cube elements. Because side walls are thick and can be regarded as rigid walls, their grid size is 5 mm.

2.3.2. Numerical Calculation Method

As the numerical calculation involves the fluid flow and the interaction between fluid and structure, the fluid-solid coupling algorithm in the LS-DYNA R10 software is used. The LAGRANGE_IN_SOLID card is used to realize the structure-fluid coupling. Since gravity cannot be ignored during the projectile’s water entry, the LOAD_BODY command is employed to set the gravity field in the Eulerian domain, and the INITIAL_HYDROSTATIC_ALE command is set to define the hydrostatic pressure in the water domain. The contact between the projectile, the steel plate and water tank are set to ERODING_SURFACE_TO_SURFACE.

2.3.3. Material Model

(a)

Q235 steel

The water tank and steel plate are made of Q235 steel. The Cowper-Symonds constitutive model is adopted, and its dynamic yield strength σ_d is:

$${\sigma }_d=\left({\sigma }_0+\frac{E{E}_h}{E-E_h}{\epsilon }_p\right)[1+\left(\frac{\dot{\epsilon }}{D}{)}^{1/n}\right]$$

(1)

where σ₀ is the static yield strength, E is the elastic modulus, E_h is the strain hardening modulus, $\dot{\epsilon }$ is the equivalent strain rate, and D and n are the strain rate parameters.

Table 2. Material parameters of Q235 steel.

Parameter	Value	Parameter	Value	Parameter	Value
Yield strength σ0 /MPa	235	n	5	Failure strain εf	0.28
Strain hardening modulus Eh/MPa	250	D(s−1)	40.4

lists the material parameters.

(b)

45# steel

The material of the projectile is 45# steel, and Johnson–Cook constitutive model is selected:

$$\sigma =\left(A+B{\epsilon }_p{}^n\right)\left(1+C\ln \frac{{\stackrel{·}{\epsilon }}_p}{{\stackrel{·}{\epsilon }}_{po}}\right)\left[1-{\left(\frac{T-T_0}{T_m-T_0}\right)}^m\right]$$

(2)

where σ Is the dynamic yield strength of steel, ε_p is the plastic strain, A is the static yield limit, B is the strain hardening modulus, n is the strain hardening index C is the strain rate coefficient, ε_p0 is the critical strain rate, m is the thermal softening index, T is the temperature, T_m is the melting point of the material, and T₀ is the room temperature.

The J-C failure model is adopted to describe the failure of the materials:

$${\epsilon }_f=\left\{D_1+D_2\exp \left[D_3\frac{{\sigma }_h}{{\sigma }_{eff}}\right]\right\}\left[1+D_4\ln {\dot{\epsilon }}^{\ast }\right]\left(1+D_5{T}^{\ast }\right)$$

(3)

where D₁–D₅ are material parameters, σ_eff is the von Mises stress, σ_h is the hydrostatic pressure of the material under the triaxial stress, T* = (T − T_r)/(T_m − T_r) is the dimensionless temperature, T_r is the room temperature, and T_m is the melting point of the material.

The material parameters of the projectile are presented in

Table 3. Mechanical parameters of the projectile.

Parameter	Value	Parameter	Value	Parameter	Value
shear modulus G/GPa	80.8	C	0.0483	Tm/K	1793
A/MPa	335	m	0.804	T0/K	300
B/MPa	350	D1	0.8	D2	0.76
n	0.782	D3	1.57	D4	0.005
Cv/J·(kg·K)−1	477	D5	−0.84

.

(c)

Water

The Grüneisen equation of state (EOS) is adopted for water:

$$P=\frac{{\rho }_0{C}^2\mu \left[1+\left(1-\frac{{\gamma }_0}{2}\right)\mu -\frac{a}{2}{\mu }^2\right]}{{\left[1-\left(S_1-1\right)\mu -S_2\frac{{\mu }^2}{\mu +1}-S_3\frac{{\mu }^3}{{\left(\mu +1\right)}^2}\right]}^2}+\left({\gamma }_0+\mathrm{a}\mu \right)E$$

(4)

where ρ₀ is the density, C is the speed of sound, γ₀ is the Grüneisen parameter, μ = ρ/ρ₀−1, a is volume correction, and S₁, S₂ and S₃ are curve fitting parameters.

(d)

Air

When air is an ideal gas without viscosity, its EOS is a linear polynomial:

$$P=C_0+C_1\mu +C_2{\mu }^2+C_3{\mu }^3+\left(C_4+C_5\mu +C_6{\mu }^2\right)E$$

(5)

where C₀–C₆ are the parameters and E is the internal energy. Let C₀ = C₁ = C₂ = C₃ = C₆ = 0, C₄ = C₅ = γ − 1, so that it has ideal gas characteristics, where γ is the adiabatic exponent. The material parameters of water and air are shown in

Table 4. Material parameters of fluid.

Parameter	ρ0 (kg/m3)	νd	C (m/s)	S1	S2	S3	γ0	a	C4	C5	E0 (J/m3)
water	1000	0.89	1448	1.98	0	0	0.11	3			0
air	1.22								0.4	0.4	2.53 × 105

.

2.3.4. Verification of Calculation Results

Numerical calculation is performed according to the attack angle and initial projectile velocity measured in the tests. The calculation results are compared with the experimental data. With the measured projectile positions in water at different times, the corresponding velocities can be calculated and fitted. The velocity comparison is shown in Figure 5, and the maximum error is within 15%. It can be considered that the velocity attenuation trend of the numerical calculation is in good agreement with the experimental results.

Figure 6 gives a comparison between the measured load curve in the projectile water entry test and numerically calculated loads. The shock wave peak overpressure measured in Test 1 is 19.1 MPa, and the initial shock wave pressure in the simulation is 15.6 MPa, with an error of 18%, whereas the error between simulation and experimental results in Test 3 is 22%. The reason for this difference is: the grids in the water domain are slightly larger, so the shock wave attenuation speed is faster than the actual situation; however, reducing the grid size will increase the computing time at a geometric rate. Therefore, it is considered that the numerical calculation gives reasonable results on the premise of ensuring accuracy, and the error is within the acceptable range.

Figure 7 and

Table 5. Comparison between experimental and calculated residual mass of the projectile.

Test No.	Projectile Mass M (g)	Residual Mass of Projectile in Test M (g)	Residual Mass of Projectile in Simulation M (g)	Error Value (%)
1	29.9	29.08	28.24	2.84
2	29.3	29.56	29.03	1.81
3	37.3	36.54	36.52	0.05

show a comparison of the remaining projectile after the test and numerical simulation. The side erosion unique to the water entry of the projectile at an attack angle and the asymmetric shape of the nose are successfully simulated, and the error between the calculated and experimental residual mass is very small, demonstrating that the failure modes of the projectile obtained by numerical calculation agrees well with the experimental data.

To sum up, the proposed numerical calculation methods and numerical models can well simulate the water entry of the projectile, and check with the experimental data, striking a good balance between accuracy and efficiency.

2.4. Test Conditions

To study the influence of the initial attack angle and initial velocity on the deformation morphology of the liquid cabin and the projectile after the penetration of the projectile into the liquid cabin, 30 working conditions for the projectile with a diameter of 14.5 mm and a length of 69.6 mm (L/D ratio = 4.8) penetrating the liquid cabin are investigated using the numerical calculation method. TEST/FEM indicates that ballistic impact test is used in this working condition, supplemented by numerical calculation method, whereas FEM uses the finite element algorithm verified in Section 2.3 for calculation. The specific working conditions are listed in

Table 6. Test conditions.

Condition No.	Initial Velocity V0 (m/s)	Attack Angle (°)	Test Method	Condition No.	Initial Velocity V0 (m/s)	Attack Angle (°)	Test Method
No. 1	1016	−50	TEST/FEM	No. 18	1200	60	FEM
No. 2	991	67	TEST/FEM	No. 19	1600	0	FEM
No. 3	1004	45	TEST/FEM	No. 20	1600	15	FEM
No. 4	400	0	FEM	No. 21	1600	30	FEM
No. 5	400	15	FEM	No. 22	1600	45	FEM
No. 6	400	30	FEM	No. 23	1600	60	FEM
No. 7	400	45	FEM	No. 24	2000	0	FEM
No. 8	400	60	FEM	No. 25	2000	15	FEM
No. 9	800	0	FEM	No. 26	2000	30	FEM
No. 10	800	15	FEM	No. 27	2000	45	FEM
No. 11	800	30	FEM	No. 28	2000	60	FEM
No. 12	800	45	FEM	No. 29	2400	0	FEM
No. 13	800	60	FEM	No. 30	2400	15	FEM
No. 14	1200	0	FEM	No. 31	2400	30	FEM
No. 15	1200	15	FEM	No. 32	2400	45	FEM
No. 16	1200	30	FEM	No. 33	2400	60	FEM
No. 17	1200	45	FEM	No. 34	1200	8	FEM

.

3. Results and Analysis

3.1. Overturning and Yawing during Underwater Penetration of Projectile at an Attack Angle

Figure 8 shows the photos of the three groups of tests taken by the high-speed camera. After the projectile enters the water with an attack angle, the cavitation region generated by its high-velocity motion is asymmetric and curved. This is because the penetration attitude and trajectory of the projectile with an attack angle are not stable in water, and the penetration direction of the projectile at the moment it enters the water is related to the initial attack angle of the projectile. In the case of positive initial attack angles, the projectile tends to yaw upward such as in Tests 2 and 3; in the case of negative initial attack angles, the projectile tends to yaw downward, such as in Test 1 (the anticlockwise rotation of the attack angle about the axis is defined as positive attack angle and the clockwise rotation as negative one).

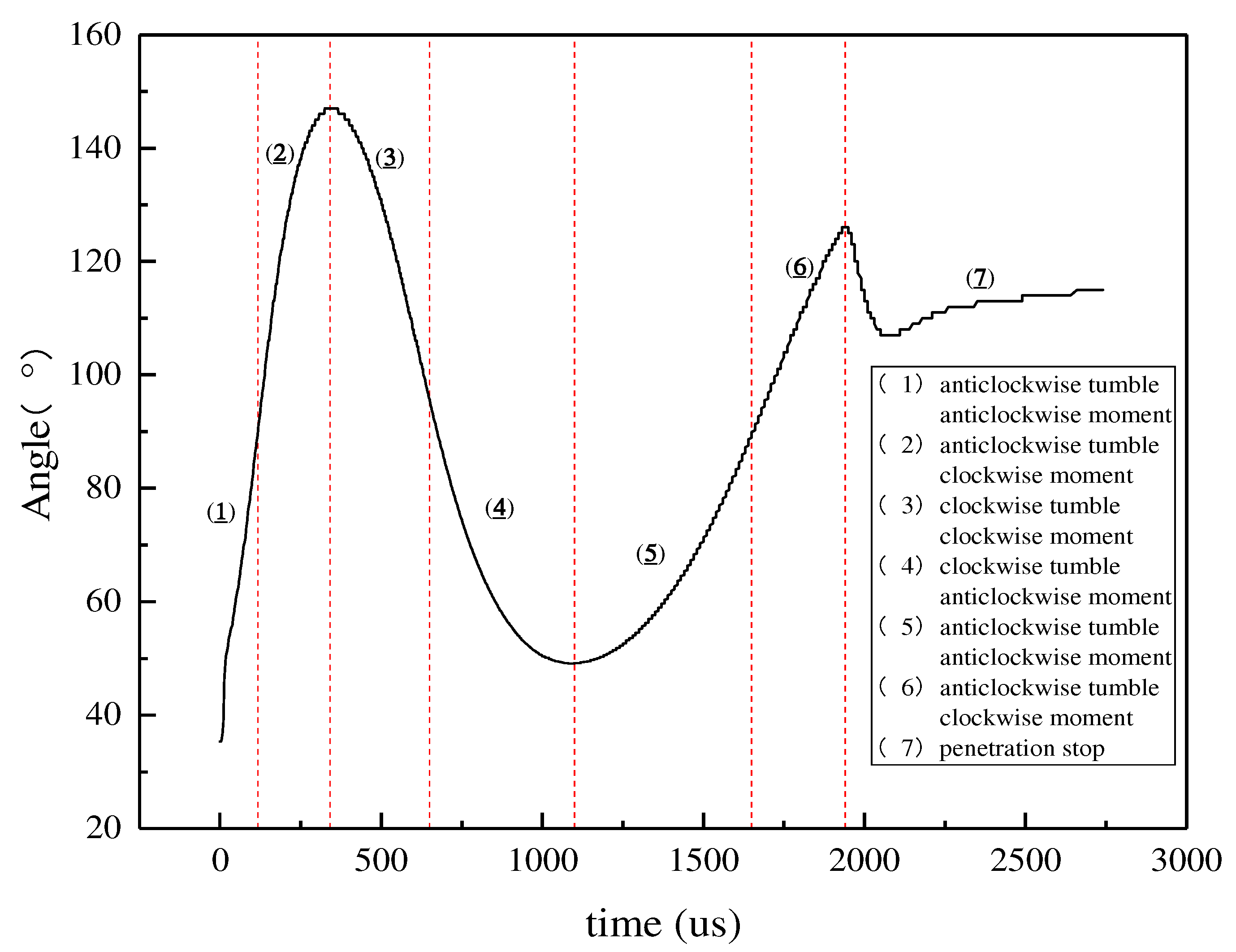
The attitude angle of the projectile in water is an important factor affecting the yaw of the projectile. Taking Test 3 as an example, it can be clearly observed from the photos that the attitude of the projectile keeps changing, overturning anticlockwise first and then clockwise. The attitude angle of the projectile on the XY plane, its Y-axis velocity and displacement are read from numerical calculations (Figure 9, Figure 10 and Figure 11). When the projectile enters the water with its nose up, the nose and lower side of the projectile are the main positions contacting with water. Because the lower side of the projectile is subjected to the dynamic pressure of the water, which is perpendicular to the contact surface, a lift force is exerted on the projectile, generating a Y-direction velocity, leading to the upward yawing of the projectile. At this time, the force exerted by water on projectile nose is the largest. Due to the existence of the attitude angle of the projectile, the force does not pass through the center of mass of the projectile, and the resultant force is on the upper side of the center of mass. This gives an anticlockwise overturning moment to the projectile, leading to the anticlockwise overturning of the projectile. At t = 130 us, the projectile overturns to the maximum incident flow area (around 90°), and the resultant force on the projectile basically passes through its center of mass. However, as the projectile continues to overturn anticlockwise due to inertia, the original “tail” of the projectile turns over to the “nose” position, and the direction of the resultant force on the projectile becomes downward. The Y-axis velocity of the projectile starts to decrease, and the resultant force is below the projectile’s center of mass; thus, the projectile is subjected to a clockwise overturning moment, which generates an angular acceleration in the opposite direction to the overturning direction, and the anticlockwise overturning velocity decreases gradually. At t = 342 us, the angular velocity of the projectile declines to 0 rad/s, the projectile starts to overturn clockwise, and the Y-axis velocity of the projectile is increasing smaller. When the projectile overturns clockwise to the maximum incident flow area, the projectile starts to be subjected to an anticlockwise moment; thus, the angular velocity starts to decrease, the resultant force becomes upward, and the Y-axis velocity increases; finally, as the projectile contacts the back plate, the penetration ceases.

In summary, during projectile penetration into liquid at an attack angle, the projectile is always in the overturning state. Due to the change of the projectile position contacting with water, the projectile will undergo overturning many times. The yaw of the projectile is affected by the attack angle and attitude angle as the two angles determine the direction of the force on the projectile during penetration. As the initial velocity during water entry is large, greater dynamic pressure on the projectile leads to greater Y-direction component. Therefore, the yaw velocity of the projectile is fast at the initial stage of water entry; when the second overturn occurs, the projectile velocity becomes smaller, and the Y-direction component of the projectile is also smaller; thus, the trajectory tends to be stable with a relatively small yaw velocity at the later stage of water entry.

3.2. Analysis of Residual Characteristics of Projectile Penetrating into Liquid Cabin at an Attack Angle

Figure 12 shows the deformation and failure morphology of the projectiles after the penetration tests under various attack angles. Mass abrasion occurs in both radial and axial directions of the projectile (the residual mass increases due to high-temperature fusion of the projectile and front plate fragments in Test 2). Compared with water entry under normal penetration (Figure 4d), the water entry projectile with an attack angle undergoes obvious asymmetric deformation. In the radial direction, one side of the projectile presents overall wavy erosion, whereas the other side shows no deformation; in the axial direction, one side of the projectile undergoes mushrooming deformation, and the other side suffers slight mass loss.

Adiabatic shear failure occurs during the high-velocity projectile impact on the target plate, generating a large amount of heat. As the heat is transferred to the projectile, the yield strength of the projectile is reduced, causing mushrooming and erosion to the projectile nose; the sides of the projectile with an attack angle also impacts the front plate, causing “strip” erosion. The impacted part of the front plate drives the nearby region to move backward, and the velocity of the plate exceeds that of the projectile. Then, a gap is produced between the projectile and the front plate after the initial impact, and as the projectile moves forward, its side impacts the front plate again, causing “strip” erosion to this side again; after multiple impacts, the side shows wavy erosion. After the projectile enters the water, one side and the nose of the projectile are impacted by the water, leading to erosion and mushrooming deformation of the projectile; due to the reduced velocity of the projectile after water entry, its deformation in water is relatively small; cavitation occurs on the other side of the projectile due to its high-velocity motion; the projectile on this side is always in the cavitation region and does not contact with the water; thus, deformation does not occur to this side; when the projectile impacts the rear plate, a small deformation occurs as the velocity at this time has been completely decayed.

In conclusion, when the initial velocity of the projectile is 1000 m/s, the penetration into the front plate takes the shortest time but is the main stage when projectile failure occurs, featuring a small deformation and mass abrasion of the projectile.

The failure morphology of the high-velocity rod projectile is studied by numerical calculation. The specific working conditions are shown in Figure 13.

As the front plate is thin, the penetration of the high-velocity projectile into liquid is the main stage of projectile failure. As can be seen from Figure 13, the projectile enters the water at a high velocity, which causes great deformation of the projectile. When projectile water entry is under normal penetration, the projectile undergoes erosion-mushrooming deformation, and the greater the velocity, the more serious the erosion; when projectile water entry is under penetration at an attack angle, the projectile undergoes a large overall deformation at 15~30°, and the overall plastic bending occurs at 1600 m/s. The reason is: an overturning moment is generated on the projectile under asymmetric loads, leading to the bending stress on the cross-section of the projectile; the critical section of the projectile reaches the yield limit under the combined action of axial compressive stress and bending stress; at this time, the plastic hinge line is formed in this section, leading to overall plastic bending deformation of the projectile; when the incident velocity is large enough, such as 2400 m/s, the critical section breaks directly, such as No. 30 and 31; however, when the initial attack angle is greater than 30°, only side erosion occurs during the high-velocity water entry of the projectile, and certain bending deformation also occurs when the incident velocity is high enough (No. 32); when the L/D ratio of the projectile is large enough, a large part of the projectile still undergoes deformation at low velocities and small attack angles; taking No. 33 as an example, the projectile with a L/D ratio of 10 at 1200 m/s undergoes bending when the attack angle is 8°. There are four failure modes of the projectile during its penetration into the liquid cabin: mushrooming, erosion, plastic bending and fracture. The failure phase diagram of the projectile penetrating the liquid cabin at different attack angles and initial velocities can be drawn. Figure 14 is the failure phase diagram of the penetration of the rod projectile with a L/D ratio of 4.8 into the liquid cabin.

In summary, at low projectile velocities, its penetration into the front plate is the main stage of failure, and at high velocities, the penetration into the liquid is the main stage of failure. The failure modes of the projectile are determined by its initial velocity, attack angle and L/D ratio. The projectile with an attack angle undergoes asymmetric deformation. When the attack angle is in the range of 15~30°, overall deformation is most likely to occur. At low velocities, overall plastic bending deformation occurs and with the increase in velocity, fracture will occur. When the attack angle is greater than 30°, the failure mode of the projectile is side erosion, but with the increasing initial velocity of the projectile, the range of the attack angle that leads to the overall deformation of the projectile also expands. The larger the L/D ratio, the more easily the overall plastic bending occurs to the projectile.

3.3. Analysis of Pressure Load Characteristics of Liquid Cabin

Figure 15 shows the pressure load curve of the bottom of the middle position of the water tank measured in Test 3. As shown in the figure, the pressure loading on the side wall of the projectile during water entry can be divided into three stages: the initial shock wave stage, the cavitation loading stage, and the cavity collapse stage.

In the initial shock wave stage, the projectile perforates the front plate and then penetrates into the water, causing a huge acceleration of the previously static liquid relative to the projectile. This acceleration generates a shock wave that propagates in the water in an arc (Figure 16a). Peak value of initial pressure and cavitation load are shown in

Table 7. Peak value and specific impulse of initial pressure and cavitation load.

Test No.	Kinetic Energy (J)	Initial Peak Pressure (MPa)	Specific Impulse of Initial Pressure (MPa·us)	Peak Cavitation Load (MPa)	Specific Impulse of Cavitation Load (MPa·us)
1	15,432	19.1	450	8.3	2516
3	18,799	22.9	502	9.1	2617

. The initial shock wave has the largest peak pressure, which is 19.1 MPa in Test 1 and 22.9 MPa in Test 3 through measurement. Since the L/D ratio and initial velocity of the projectiles in the two tests are different, the ratio of their kinetic energy is 0.821, and the ratio of the two initial shock wave peak pressures is 0.83. This indicates that under the same water tank structure and projectile shape, the initial shock wave peak pressure has a linear relationship with the kinetic energy of the projectile. The larger the kinetic energy, the larger the initial peak pressure.

Then, in the cavitation loading stage, the projectile penetrates into the water at a high velocity and displaces the water, which converts the kinetic energy of the projectile into the kinetic energy of the water. A cavity is formed on the moving path of the projectile, and the water keeps squeezing the water tank due to cavity expansion, causing the cavitation load. In Test 1, the specific impulse of the initial shock wave measured on the side wall is 450 MPa·us, and that of the cavitation load is 2516 MPa·us; in Test 3, the specific impulse of the initial shock wave is 502 MPa·us, and that of the cavitation load is 2617 MPa·us. The peak pressure of the cavitation load is much smaller than the initial shock wave load. However, due to its long duration, the specific impulse of the cavitation load is about five times that of the initial shock wave. Therefore, the cavitation load is the main load causing the side wall failure of the water tank. The ratio of the specific impulse of the initial shock wave to the kinetic energy ratio of the projectile is basically the same. As the kinetic energy increases, the specific impulse of the initial shock wave increases significantly. The reason is: the initial shock wave propagates at a speed in the water close to the speed of sound, and the initial shock wave is affected by the rarefaction waves in all directions; thus, the shock wave pressure decays quickly with a short action time, and the shock wave duration is the same. Therefore, the larger peak value of the shock wave leads to larger specific impulse, but there is little difference between the cavitation load and the specific impulse.

As the kinetic energy of the projectile is continuously converted into the kinetic energy of the water, the water level rises. Under the influence of the backflow of disturbed water during cavity expansion, the air flow between the cavitation bubble and the atmosphere is cut off, and the cavity is closed at the entry hole. At this time, there are lots of gas and water vapor in the cavity, hence the formation of the cavitation bubble, which has the largest potential energy. Due to the pressure difference between the inside and outside of the bubble, its wall contracts, and the bubble gradually shrinks; in this process, the potential energy of the bubble is converted into kinetic energy, and negative pressure is generated in the water tank, which lasts for a long time, but the absolute value of the load is small; thus, it barely causes damage to the structure. With the contraction of the bubble, the gas in the bubble is compressed, leading to the increase in pressure and the formation of a high-pressure region, and then the bubble collapses, followed by bubble expansion again. At this time, shock waves are generated, and most of the energy in the bubble is converted into impact energy. Thereafter, the bubble keeps expanding and collapsing until all energy is dissipated. Due to the existence of the free surface in the water tank and the pressure sensor located at the bottom of the side wall of the water tank, the measured shock wave load for bubble collapse is relatively small (Figure 15). The cavity collapse pressure measured by Disimilea was very large, even exceeding the initial shock pressure. On the one hand, because the measuring points were arranged near the ballistic axis, and the cavity collapse also occurred on the ballistic axis, the measured pressure was large; on the other hand, the liquid-filled tank used was a closed tank with a large volume, resulting in a large cavity and higher pressure value generated during cavity collapse.

To investigate the effect of attack angle on the loads during the projectile penetrating the liquid cabin, No. 29–33 are selected for investigation, and the loads on the side walls of the water tank and at the horizontal distance of 7.5 cm between the front/rear plates and the center are measured. According to Figure 17, as the attack angle of the projectile increases, the initial shock wave pressure load on the side walls of the tank tends to increase first and then decrease; meanwhile, due to improved attack angle, the area of the projectile in contact with water increases, resulting in greater water disturbance, so the load on the front plate keeps increasing; on the contrary, the pressure load on the rear plate decreases with the increasing attack angle for the following reasons: when the projectile enters the water at the velocity of 2400 m/s; meanwhile, the wave velocity in the water is only 1500 us, and the projectile separates from the shock wave after water entry for a period of time; at this time, the projectile yaws, and the measuring point on the rear plate is far away from the projectile axis; the increasing attack angle leads to greater projectile yaw and farther measuring point from the axis, and thus the pressure load on the rear plate decreases with the increasing attack angle. The initial shock wave propagates far away in a hemispherical shape, and the pressure along the wave arc decreases with the angle of the wave moving away from the ballistic axis. The measuring point on the front plate is more than 90° away from the axis, and the measuring point on the rear plate is near the axis, so at small attack angles, the pressure load on the rear plate is greater than that on the front plate; as the attack angle increases, the pressure load on the front plate increases but decreases on the rear plate, with the former exceeding the latter. The specific impulse change in the initial shock wave loads on the front and rear plates is consistent with the variation law of the shock wave pressure peak, but the specific impulse change of the cavitation load on the front plate is not significant. The reason is: as the projectile enters the water, a large cavitation region is generated, resulting in the measuring point on the front plate entering the cavitation region only after being subjected to cavitation loading for a short period of time, not the complete cavitation load.

3.4. Analysis of Failure Modes of Liquid Cabin

Figure 18 presents the deformation morphology and failure diagrams and scanned contours of the front and rear plates before and after the tests. As illustrated, the front plate of the water tank undergoes shear plugging failure and thin film bulging deformation during the projectile penetration into the water tank at a high velocity. When the high-velocity projectile impacts the steel plate at an attack angle with water medium as the “dynamic support”, the support of water improves the rigidity of the steel plate. As the front plate is thin, the impact on the target plate by the high-velocity projectile causes adiabatic shearing. The light blue color at the edge of the perforation hole is caused by the release of a large amount of heat during the contact between the projectile and the target. Because projectile penetration is at an attack angle, the shape of the hole is not circular, similar to the shape of the projectile nose, but rectangular, similar to the shape of the side of the projectile. The initial shock wave is generated after the projectile impacts the water and enters it. As the shock wave is close to the front plate, it bulges outward after being impacted. Then, due to the long cavitation, the water in the tank moves around and squeeze the front plate, leading to the wide bulging deformation of the front plate. However, when Wu conducted the penetration test with the water tank, the front plate was depressed, which was caused by the negative pressure induced by bubble contraction on the front plate due to the closure of the tank. In the present paper, as the tank is not covered, there is no plate depression. Comparing the plate deflection, we see that the kinetic energy of the projectile increases, but the deflection of the front plate does not increase apparently. This is explained by the fact that the front plate mainly undergoes thin film bulging deformation caused by the cavitation load, and the specific impulse of the cavitation load in the three groups of tests is basically the same.

Due to the large thickness and stiffness of the rear plate, it has no obvious thin film bulging deformation. Since the projectiles used in Tests 1 and 3 have different masses and L/D ratios, under the same initial velocity, their kinetic energy varies, leading to very different failure modes of the rear plate. In Test 1, the rear plate mainly undergoes bulging and dishing deformation. Due to the long water domain, the incident shock wave generated after the water entry of the projectile is weakened to some extent when reaching the rear plate, having a small influence on the rear plate; as the projectile approaches the rear plate during penetration, a high-pressure region is produced at the position around the projectile nose as the projectile squeezes the water, and this high-pressure region acts on the rear plate, causing dishing deformation; then, the projectile impacts the rear plate, causing bulging deformation. After Test 3, the rear plate has annular breaches and radial cracks. The reason is: as the projectile moves in the water with an attack angle, it keeps overturning; it always has a large attack angle and a certain angular velocity upon reaching the rear plate; as the edge of the projectile nose first touches the target, which is similar to the penetration of a sharp-nosed projectile, the rear plate undergoes severe plastic deformation, and then the material is squeezed toward the cratering position by the sharp nose, causing annular breaches and radial cracks at the edge of the breaches; as the penetration continues, more cracks are generated and developed into petaling failure. In Tests 1 and 3, the kinetic energy ratio of the projectiles is 0.82, and the maximum deflection ratio of the rear plates is 0.60, which indicates that when the rear plate is approaching the ballistic limit, the impact force on the rear plate is increased by the projectile’s pushing of the water; thus, the rear plate is subjected to the high pressure of the water and the impact of the projectile, resulting in two failures; the coupling effect of the two failures aggravates the damage to the rear plate.

Figure 19 shows the failure morphology of the liquid cabin after the penetration of the projectile with a L/D ratio of 4.8 and a velocity of 1600 m/s and at different attack angles (No. 19–23). As the attack angle increases, the breach in the front plate enlarges. During normal penetration, the front plate undergoes shear plugging-thin film bulging deformation, and the breach is circular. When an attack angle exists, the load applied by the projectile changes from a point load to a line load; thus, the area in contact with the target increases, and the shear plugging breach is rectangular. After the water entry of projectile, which is subjected to the shock wave pressure and cavitation load, the front plate undergoes bulging deformation; at the same time, the plate is subjected to the surface load of the water. Based on the classical yield line theory, the plastic hinge line in the rectangular plate is as shown in Figure 20, where the plate tears along the plastic hinge line. Since more water is displaced by the water entry projectile with an attack angle, the initial shock wave pressure and cavitation load on the front plate increase with the increasing attack angle: in the range of 15~30°, the front plate shows “I”-shaped tear along the plastic hinge line; in the range of 45~60°, the front plate is subjected to a greater load, and thus shows the “X”-shaped tear along the plastic hinge line.

As the attack angle increases, the breach in the rear plate gradually decreases for the following reason: the projectile with an attack angle is subjected to greater drag in water; therefore, the projectile velocity decays faster; moreover, the front plate undergoes overall failure in advance under high attack angles; the liquid pressure is unloaded from the front plate, which reduces the damage to the rear plate; in the case of normal penetration, the rear plate undergoes dishing–petaling deformation; with the increase in the attack angle, the breach in the rear plate changes from the petal shape to the strip shape; in the range of 30~45°, the rear plate undergoes dishing- “I” tearing; at 60°, the projectile cannot perforate the rear plate; therefore, the rear plate exhibits dishing–bulging deformation.

4. Conclusions

In this paper, an effective numerical calculation method was obtained through the model test of the projectile penetrating the liquid tank and the numerical calculation verification with the experimental data. The deformation and failure modes of the projectile after penetration at attack angles, the trajectory and attitude change of the projectile in water were explored, and the load strength on the side walls and the failure modes of the front and rear plates during the penetration of the projectile into the water tank were analyzed. The main conclusions are as follows:

(a)

There are four basic failure modes after the projectile penetrating the liquid cabin at attack angles: asymmetric mushrooming at the nose, side erosion, overall plastic bending and fracture. The overall plastic bending and fracture are mainly related to the L/D ratio, initial attack angle and initial projectile velocity; at low velocities, the main failure occurs during the penetration into the front plate; at high velocities, the main failure occurs during the penetration into the water.

(b)

In the case of the rod projectile with a L/D ratio of 2 and a velocity of 1600 m/s, the projectile was more prone to overall deformation at the attack angles in the range of 15~30°. At low velocities, the overall plastic bending deformation occurred, whereas with the increasing velocity, fracture failure occurred; when the attack angle was above 30°, the failure mode of the projectile was side erosion, but as the initial velocity increased, the range of the attack angle that led to the overall deformation of the projectile also expanded. The larger the L/D ratio, the more easily the projectile undergoes overall plastic bending failure.

(c)

After the projectile entered the water at an attack angle, the overturning moment was generated due to the uneven force on the projectile, and the projectile was at a state of constant overturning. Due to the change of the position contacting with the water, the projectile overturned many times, and projectile yaw occurred; the yaw direction was mainly affected by the initial attack angle and projectile attitude.

(d)

After the water entry of the projectile, the side walls of the water tank were mainly affected by three stages of loading: the initial shock wave pressure loading, the cavitation loading and the cavity collapse loading. As the attack angle increased, the peak load of the initial shock wave pressure on the front plate increased gradually, whereas the initial shock wave pressure load on the rear plate decreased gradually.

(e)

After the penetration of the projectile into the water tank, the failure modes of the front plate were mainly shear plugging, thin film bulging deformation and tearing failure. At certain velocities, with the increasing attack angle, the front plate underwent tearing along the plastic hinge line; under small attack angles, the tear was “I” shaped, and under large attack angles, it was “X” shaped; the rear plate mainly underwent dishing-bulging deformation; when the rear plate approached the ballistic limit, annular breaches and circumferential cracks were produced.